1 Introduction

The supersonic flow of charged particles from the hot corona of the Sun along with the magnetic field constitutes solar wind. This magnetized plasma can be classified into fast and slow wind based on their source of origin. The fast wind originates from open coronal holes that are uniform and stable. Its composition resembles that of the photosphere. The fast wind is Alfvén wave dominated (Ovenden, Shah, and Schwartz, 1983). Alfvén waves are transverse magnetohydrodynamic waves in which ions oscillate with magnetic tension on the magnetic field lines as the restoring force. Large-amplitude Alfvén waves propagating away from the Sun are considered to belong to the causes of coronal heating and acceleration of the solar wind (De Pontieu et al., 2007; Jess et al., 2009; McIntosh et al., 2011; Morton et al., 2012; Tomczyk et al., 2007). The slow wind originates from the lower solar latitude and is highly variable in terms of their speed, density, temperature, etc. Its composition resembles that of the corona (Schwenn, 1990). Alfvén waves in the fast wind evolve in the inner heliosphere getting weaker as the wind moves away from the Sun. Fast wind Alfvénicity becomes equal to that of slow wind near 0.3 AU. The slow wind turbulence is less Alfvénic compared to the fast wind and shows no radial dependence (Bruno and Carbone, 2013).

Systems in nature can be described either by linear or nonlinear models. Nonlinear models are generally more suitable for most real world systems (Kaplan and Glass, 1995). Thus nonlinear time series tools are essential to understand the dynamics of real world systems. Development of chaos theory and related techniques, applied to time series data, gives more potential to recover the underlying dynamics of the real world system from its complex temporal behavior (Abarbanel and Gollub, 1996; Ott, 2002; Abarbanel et al., 1993; Grassberger, Schreiber, and Schaffrath, 1991; Kugiumtzis, Lillekjendlie, and Christophersen, 1994; Lillekjendlie, Kugiumtzis, and Christophersen, 1994; Schuster, 1988; Kantz and Schreiber, 2004). Nonlinear time series analysis using chaos theory has been widely used in a variety of fields such as social science, astronomy, and physics (Schreiber, 1999). “Time delay embedding” is a method used in nonlinear time series analysis to reconstruct the phase space from single scalar time series data. In a dissipative system, time evolution trajectories in phase space converge to an invariant set called an attractor (Takens, 1981; Sauer, Yorke, and Casdagli, 1991). The static, as well as dynamic aspect of the attractors, are obtained by using certain nonlinear time series quantifiers such as correlation dimension, \(D_{2}\), correlation entropy, \(K_{2}\), and multifractal analysis, etc. (Mayer-Kress, 2012). A complexity measure which quantifies the geometry and shape of the attractor of a dynamical system is called the correlation dimension \(D_{2}\). The variation of \(D_{2}\) with embedding dimension \(M\) can be effectively used to characterize the measured time series data, since it is a measure of the dimension of the underlying attractor generated from the time series. For a random process, \(D_{2}\) increase continuously with embedding dimension \(M\), but for a chaotic process, \(D_{2}\) saturates for some value of \(M\). Correlation entropy \(K_{2}\) represents the rate at which information is lost due to exponential divergence of trajectories in phase space in the case of a chaotic system (Ott, 2002). For a chaotic system, correlation entropy \(K_{2}\) saturates as the embedding dimension \(M\) increases, but \(K_{2}\) tends to zero as \(M\) tends to infinity for a random process. Multifractal analysis is an effective method to provide a statistical description of the strange attractors of a chaotic system.

Time series data available from the real world systems are affected by noise. A direct application of nonlinear techniques to the real world data may give spurious results if the noise component masks or dominates the inherent nonlinearity in the data. The effect of noise in the real world data can be effectively reduced by using nonlinear noise reduction techniques (Davies, 1994; Grassberger et al., 1993; Kantz et al., 1993; Kostelich and Schreiber, 1993; Schreiber, 1993).

The first step to begin the nonlinear time series analysis is hypothesis testing to confirm that the data are not resulting from a stochastic random process. Surrogate analysis is the method used for the hypothesis testing in the nonlinear time series analysis (Theiler et al., 1992; Schreiber and Schmitz, 1996). The surrogate analysis also helps us to get an idea about the noise present in real world data (Harikrishnan et al., 2006). We use both \(D_{2}\) and \(K_{2}\) as a discriminating parameter (between noise and nonlinearity) in the surrogate analysis. The correlation entropy \(K_{2}\) is more effective than the correlation dimension \(D_{2}\) in the presence of colored noise which is correlated random process with the power varying with frequency as \(1/(f^{\alpha })\) with the index \(\alpha \) ranging from 1 to 2 (Kennel and Isabelle, 1992; Redaelli, Plewczyński, and Macek, 2002). The colored noise present in real world data gives a well saturated value of \(D_{2}\), whereas pure white noise is scale free.

As solar wind dynamics contain information about coronal heating and solar wind acceleration, it is desirable to characterize these properties using time series analysis tools. The chaotic nature of the solar wind plasma is evident from the nonlinear time series analysis of slow speed solar wind, the interplanetary magnetic field, and the solar wind radio pulsation (Macek and Obojska, 1998, 1997; Macek and Redaelli, 2000; Pavlos et al., 1992; Polygiannakis and Moussas, 1994b,a). The multifractality of the solar wind chaotic attractor and change of the degree of multifractality as the wind evolves radially out from the Sun has also been studied using nonlinear time series tools (Macek, 2002, 2003, 2007; Marsch and Tu, 1994; Marsch, Tu, and Rosenbauer, 1996; Marsch and Tu, 1997; Carbone, 1993; Burlaga, 1991, 2001). The solar wind plasma studies are still relevant as many questions regarding solar wind plasma dynamics, radial evolution of the wind, the interaction of individual flow, etc., still remain unanswered. It is the turbulent nature of the solar wind plasma that demands the nonlinear time series tools for its analysis.

In the present study, we use an automated non-subjective algorithm scheme proposed by Harikrishnan et al. (2006), Harikrishnan, Misra, and Ambika (2009), Harikrishnan et al. (2009) for the computation of \(D_{2}\), \(K_{2}\) and the multifractal analysis. The method of computation is more useful for the comparison of the nonlinear measures computed from data and surrogates (as compared to methods based on TISEAN package). We use the TISEAN package to generate surrogate using Amplitude Adjusted Fourier Transformation (AAFT) procedure (Hegger, Kantz, and Schreiber, 1999; Hegger and Schreiber, 2002).

Our study mainly focuses on the radial dependence of the chaotic nature of the wind and how Alfvén waves influence the nonlinear and chaotic nature of the wind. We make a detailed nonlinear analysis of the radial evolution of the solar wind plasma in the inner heliosphere using our automated non-subjective algorithm scheme. Our algorithm allows us to compare the dynamics of solar wind plasma at different heliocentric distances in the presence of noise. It helps us to study the dynamics of solar wind plasma without using the nonlinear noise reduction methods. The nonlinear Alfvén waves in the solar wind are more dominant in the inner heliosphere. The Alfvén waves have a stochastic random nature (Ovenden, Shah, and Schwartz, 1983). The surrogate analysis provides an excellent qualitative estimate of noise in our data. It motivates us to study the change in the Alfvén wave in the solar wind as it radially flows out from the Sun.

Our paper is arranged as follows. Section 2 describes the data used for analysis. A detailed description of the methods used for the analysis of our data is given in Section 3. Results are presented in Section 4. Discussion and conclusion of our study are given in Section 5

2 Solar Wind Data

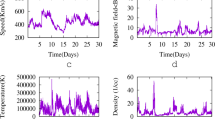
In the present study, we use radial component of velocity of solar wind plasma flow recorded in situ by Helios 2 at three different distances 0.3 AU, 0.7 AU and 0.9 AU during its primary mission to the Sun. The observed data at three different distances are from the same co-rotating stream during three consecutive solar rotation. We divide the selected data at each heliospheric distances into two data sets; one continuous fast wind data set and another continuous slow wind data set. Each data set includes near about 6000 data points and the time interval between each data point is \(\Delta t = 40.5~\text{s}\). The solar wind plasma used in our analysis is presented in Figure 1. Table 1 gives the heliocentric distances and the periods of different solar wind streams used in our analysis.

Figure 1
figure 1

Plot of the slow (left panel) and the fast (right panel) solar wind measured at different radial distance from the Sun.

Full size image
Table 1 Details of solar wind data used in our analysis.
Full size table

3 Nonlinear Measures Used for the Analysis

The Takens delay embedding method is used to reconstruct the entire phase space of the system from a single scalar time series output of the system. A multi-dimensional embedding space is created from the scalar time series \(s(t_{i})\) by choosing a suitable value of embedding dimension \(M\) and delay time \(\tau \) (Takens, 1981; Sauer, Yorke, and Casdagli, 1991)

$$ X_{n} = \bigl[s(t_{i}),s(t_{i} + \tau ), \ldots..,s\bigl(t_{i} + (M-1)\tau \bigr) \bigr]. $$
(1)

The attractor in phase space is characterized by computing the correlation dimension \(D_{2}\), the correlation entropy \(K_{2}\) and the multifractal spectrum. Grassberger and Procaccia (1983a,b, 1984) used the time delay embedding method in the algorithm proposed for the computation of \(D_{2}\) and \(K_{2}\). In the present study, we use an automated modified Grassberger and Procaccia (GP) algorithm.

3.1 Correlation Dimension \(D_{2}\)

The correlation dimension quantifies the static aspect of the underlying attractor, such as the geometry of the attractor. Correlation dimension \(D_{2}\) is defined as

$$ D_{2} =\lim_{R \rightarrow 0} \frac{d \log C_{M}(R)}{d\log R} .$$
(2)

Here \(C_{M}(R)\) is the correlation sum. It is calculated as finding the relative number of data points within a distance \(R\) from a particular \(i\)th data point, say \(p_{i}(R)\) in phase space,

$$ p_{i}(R) = \lim_{N_{v}\rightarrow \infty } \frac{1}{N_{v}} \sum_{j=1,j \neq i}^{N_{v}} H\bigl(R - | \vec{x_{i}} - \vec{x_{j}}|\bigr), $$
(3)

where \(N_{v}\) is the total number of reconstructed vectors and \(H\) is the Heaviside step function. Averaging this quantity over randomly selected centers \(N_{c}\) gives the correlation sum

$$ C_{M}(R) =\frac{1}{N_{c}}\sum_{i=1}^{N_{c}}p_{i}(R). $$
(4)

The correlation dimension measures how the correlation sum scales with distance in the embedded space.

3.2 Correlation Entropy \(K_{2}\)

Correlation entropy is the dynamic measure of the underlying attractor. It represents the rate at which the information is created when trajectories evolve in phase space (Ott, 2002). The relation connecting correlation entropy \(K_{2}\) and correlation sum \(C_{M}(R)\) is

$$ K_{2} \Delta t = \lim_{R \rightarrow 0} \lim _{M \rightarrow \infty } \lim_{N \rightarrow \infty } \log \biggl( \frac{C_{M}(R)}{C_{M+1}(R)} \biggr) . $$
(5)

Here \(\Delta t\) is the time step between successive values in the time series.

In our modified scheme, we use a non-subjective algorithm approach for identifying the scaling region in the correlation sum for the computation of the correlation entropy \(K_{2}\) and the correlation dimension \(D_{2}\). The modified Grassberger and Procaccia (GP) algorithm computes several \(D_{2}\) and \(K_{2}\) for different values of \(R\) in the scaling region for a fixed \(M\) value and taking an average of these values. The error in \(D_{2}\) and \(K_{2}\) is the mean of the standard deviation of each value from this average value. The detailed algorithm is given in the papers of Harikrishnan, Misra, and Ambika (2009) and Harikrishnan et al. (2006).

3.3 Multifractal Spectrum

Chaotic dynamical systems always have strange attractors. The multifractal formalism is critical in determining the strange attractors present in dynamical systems and also providing a new statistical description to these sets. Strange attractors formed in the phase space due to the stretching and folding of trajectories have multifractal structure. Strange attractors always have a spectrum of dimension \(D_{q}\), where the index \(q\) varies from \(-\infty \) to \(+\infty \) (Hentschel and Procaccia, 1983).

Since the dimension represents a scaling index, the spectrum of dimension implies that the chaotic attractor, in general, involves a range of scaling indices. In other words, different parts of the attractor scales differently. This spectrum of scaling indices is represented by what is called a multifractal spectrum. To get a formal definition of this, we divide the attractor into \(M\) dimensional cube of side \(\epsilon \). Let \(N_{j}\) be the number of points in the \(j\)th cube and \(N_{T}\) be the number of points on the attractor; then \(p_{j}(\epsilon ) = \frac{N_{j}}{N_{T}}\), the probability for the \(j\)th box.

This \(p_{j}(\epsilon )\) scale with \(\epsilon \) is given by

$$ p_{j}(\epsilon )\propto \epsilon ^{\alpha _{j}}, $$
(6)

where \(\alpha _{j}\) is the scaling index for the \(j\)th cube. The number of cubes \(g(\alpha )d\alpha \) having scaling index in the range \(\alpha \) and \(\alpha + d\alpha \) also varies as

$$ g(\alpha )\propto \epsilon ^{-f(\alpha )}, $$
(7)

where \(f(\alpha )\) represent fractal dimension with singularity strength \(\alpha \). The \(D_{q}\) to \(f(\alpha )\) transformation is done by using the Legendre transformation (Atmanspacher, Scheingraber, and Wiedenmann, 1989).

The generalized correlation dimension \(D_{q}\) is defined as

$$ D(q) = \lim_{R \rightarrow 0 } \frac{ d(\log C^{q }_{M}(R))}{d(\log ( R)) }, $$
(8)

where \(C^{q}_{M}(R)\) is the generalized correlation sum and is given by

$$ C^{q}_{M}(R) = \Biggl[\frac{1}{N_{c}}\sum _{i}^{N_{c}}\Biggl(\frac{1}{N_{v}} \sum_{j=1,j\neq i}^{N_{v}}H\bigl(R -|\vec{X_{i}} -\vec{X_{j}}|\bigr)\Biggr)^{q-1}\Biggr]^{\frac{1}{q-1}} . $$
(9)

The generalized correlation dimension is also obtained by using a non-subjective algorithm approach proposed by Harikrishnan et al. (2009). In this approach, an analytic form of the \(f(\alpha )\) function is first assumed to be

$$ f(\alpha ) = A(\alpha -\alpha _{min})^{\gamma _{1}}(\alpha _{max}- \alpha )^{\gamma _{2}}, $$
(10)

where \(A\), \(\gamma _{1}\), \(\gamma _{2}\), \(\alpha _{max}\), \(\alpha _{min}\) are set of parameters used to characterize a particular \(f(\alpha )\) curve. Here “\(\alpha _{min}\)” and “\(\alpha _{max}\)” represent the extreme values of “\(\alpha \)” and “\(\gamma _{1}\)” and “\(\gamma _{2}\)” specify the slope of the profile at the extreme points.

The above function satisfies the following conditions which are characteristic of any typical \(f(\alpha )\) curve:

  1. i)

    It is a single valued function between \(\alpha _{max}\) and \(\alpha _{min}\).

  2. ii)

    It has a single maximum.

  3. iii)

    \(f(\alpha _{max})=f(\alpha _{min}) =0\).

  4. iv)

    By imposing a condition on \(f(\alpha )\) it can be shown that \(0<\gamma _{1}\), \(\gamma _{2}<1\).

The important steps in the algorithm for the computation of \(f(\alpha )\) are

  1. i)

    First set the parameters \(\alpha _{max}\cong D_{+\infty }\), \(\alpha _{min} \cong D_{-\infty }\), \(\alpha _{1}\cong D_{1}\) and choose a value \(\gamma _{1}\) in the range [\(0,1\)].

  2. ii)

    Use the input parameters and find the value of \(\gamma _{2}\), \(A\).

  3. iii)

    Compute \(f(\alpha )\) in the range \(\alpha _{min}\) to \(\alpha _{max}\).

  4. iv)

    Obtain \(D_{q}\) curve from \(f(\alpha )\) using the inverse Legendre transformation.

  5. v)

    Adjust the input parameters to obtain a \(D_{q}\) spectrum that best matches with \(D_{q}\) spectrum obtained from the time series.

  6. vi)

    The final \(f(\alpha )\) is obtained from the best fit \(D_{q}\) curve.

4 Results

Figure 2 presents the projection of attractor on to the two-dimensional subspace of the phase space for the fast and the slow solar wind at different radial distances from the Sun in the inner heliosphere. For the faithful comparison of the attractor, all the time series data are changed to a uniform deviate. Numerically, the time series is transformed into the range 0 to 1 which makes the embedding space unity. The attractor for the slow solar wind is shown in the left panel. The geometry of the attractor of the slow speed wind shows not much variation as the wind flows out from the Sun. The right panel shows the attractor for the fast wind in the inner heliosphere. The spread of attractor in phase space is greater for fast wind near 0.3 AU and 0.7 AU than the attractor near 0.9 AU. This result indicates that the percentage of white noise in the fast wind is higher in the inner heliosphere, and it is decreasing as the wind flows away from the Sun.

Figure 2
figure 2

Plot of the reconstructed phase space for the slow (left panel) and the fast (right panel) solar wind.

Full size image

To determine the noise in the solar wind data in the inner heliosphere, we perform a surrogate analysis using the correlation dimension \(D_{2}\) and the correlation entropy \(K_{2}\) as discriminating parameters. The correlation entropy \(K_{2}\) is a more effective discriminator in the presence of colored noise. In the present study, we made ten surrogates for each solar wind time series based on the AAFT procedure using the TISEAN code. Figure 3 presents the results of the surrogate analysis for all the solar wind with the correlation dimension \(D_{2}\) as a discriminating measure. The fast wind near 0.3 AU and 0.7 AU shows a stochastic random behavior whereas the fast wind near 0.9 AU shows a slight deviation from its stochastic nature. A saturated value of correlation dimension \(D_{2}\) is obtained for the slow solar wind and its surrogates. It indicates the presence of colored noise in the slow solar wind. The results of the surrogate analysis using the correlation entropy \(K_{2}\) as a discriminating parameter are shown in Figure 4. The result obtained in the second surrogate analysis test also supports the results obtained in the first method. The colored noise contamination is more evident in the second method.

Figure 3
figure 3

Surrogate analysis of the slow (left panel) and the fast (right panel) solar wind using correlation dimension \(D_{2}\) as discriminating parameter.

Full size image
Figure 4
figure 4

Surrogate analysis of slow (left panel) and fast (right panel) solar wind using correlation entropy \(K_{2}\) as a discriminating parameter.

Full size image

We calculated the correlation dimension \(D_{2}\) of the solar wind flow, and the results are shown in Figure 5. The value of the correlation dimension \(D_{2}\) of the slow solar wind is decreasing as it flows away from the Sun. Based on the above result, this change in \(D_{2}\) value does not indicate any change in dynamics but confirms that white noise in the data decreases with distance from the Sun. This result also supports the presence of colored noise in the data. In the case of the fast wind, the presence of white noise is more dominant and behaves as a stochastic random process. However, near 0.9 AU the fast solar wind shows evidence of \(D_{2}\) saturation with \(M\). It indicates that the percentage of the white noise in the fast wind is more near the Sun and its percentage is slowly decreasing with distance from the Sun.

Figure 5
figure 5

Variation of the correlation dimension \(D_{2}\) with the embedding dimension \(M\) for the slow (left panel) and the fast (right panel) solar wind.

Full size image

The results of the computation of the correlation entropy \(K_{2}\) for different types of solar wind flow are shown in Figure 6. The results also suggest that slow wind in the inner heliosphere does not show any dynamical modulation with distance from the Sun. The results of the correlation entropy \(K_{2}\) for the fast wind also support its stochastic random nature.

Figure 6
figure 6

Variation of the correlation entropy \(K_{2}\) with the embedding dimension \(M\) for the slow (left panel) and the fast (right panel) solar wind. Several \(K_{2}\) values are computed for different values of \(R\) in the scaling region for a fixed \(M\) value and an average of these values are taken. The error in \(K_{2}\) is the mean of the standard deviation of each value from this average value.

Full size image

Finally, we show results of the multifractal analysis of both the slow and the fast wind in the inner heliosphere. The spectrum of dimension \(D_{q}\) of the strange attractors as a function of \(q\) for the fast and the slow wind are shown in Figure 7. The \(D_{q}\) versus \(q\) curve for the fast wind becomes steeper as the wind move away from the Sun, whereas the steepness of the curve for the slow wind shows no significant variation as the wind moves away from the Sun. Therefore one can say that both the slow and the fast wind in the inner heliosphere are the multifractal. The degree of multifractality of the fast wind increases with an increase in radial distance from the Sun and the degree of multifractality of the slow wind does not vary with radial distance from the Sun. The \(f(\alpha)\) spectrum computed from the best fit \(D_{q}\) curve for both slow and fast wind are shown in Figure 8. The width of the \(f(\alpha)\) spectrum for the fast wind increases as the wind moves away from the Sun, whereas the width for the slow wind show no significant variation. These observations also support the previous result. The narrow width of \(f(\alpha)\) spectrum for the fast wind in the inner heliosphere supports white noise dominance in the wind because as the white noise in the data increase then the \(f(\alpha)\) spectrum tends more and more towards a delta function.

Figure 7
figure 7

The spectrum of generalized dimension for the slow (left panel) and the fast (right panel) solar wind.

Full size image
Figure 8
figure 8

The \(f(\alpha )\) spectrum for the slow (left panel) and the fast (right panel) solar wind.

Full size image

5 Discussion and Conclusion

Nonlinear studies of the radial evolution of the solar wind provide a deeper understanding of the solar wind dynamics. The solar wind is a complex real world system. Its complex dynamics and evolution can be obtained from the comparison of nonlinear analysis results of the solar wind plasma at different radial distances from the Sun in the inner heliosphere. Our results confirm the deterministic chaotic nature of slow solar wind plasma as found in the previous studies. The previous studies have analyzed a change of dynamic of slow solar wind in the inner heliosphere using methods such as false nearest neighbors, average mutual information, etc. But in the present study, we analyzed this problem in a detailed manner using correlation dimension \(D_{2}\), correlation entropy \(K_{2}\), surrogate analysis and multifractal analysis and obtained the same as previous result. Our results also give a good qualitative estimate of noise present in the slow solar wind in the inner heliosphere. Our results show that white noise and colored noise are present in the slow solar wind near the Sun and the colored noise become more and more dominant noise with an increase in distance from the Sun. The fast wind dynamics change in the inner heliosphere contrary to the slow solar wind. Our present study also analyzed these results in detail. We found that the fast wind in the inner heliosphere is a stochastic random process and a deviation from this stochastic character is found near 0.9 AU. The multifractal analysis done in our study clearly shows a dynamic change of the fast wind in the inner heliosphere. Also, we found that dominant noise present in the fast wind is white noise which decreases with an increase in radial distance from the Sun. The white noise masks the actual dynamics of the fast wind in the inner heliosphere.

Surrogate analysis in the present study strongly provides the following observation. White noise is present in both the fast and the slow wind. The presence of white noise is greater in the fast wind than in the slow wind. The white noise in both fast and slow wind decreases with increasing radial distance from the Sun, and this radial variation is more evident in the fast wind. The Alfvénic fluctuations in the solar wind have stochastic nature. Thus, we interpret stochastic random element in the solar wind as outward propagating Alfvén waves. The incompressive nature of Alfvénic fluctuations inhibits damping and leads to it dominating solar wind turbulence. The Alfvénic fluctuations are more dominant in the fast wind than in the slow wind. These Alfvénic fluctuations fade with increasing heliocentric distance. Our results indicate that the complex dynamics of the solar wind are characterized by a nonlinear process occurring at the source of origin and is convected along with the wind. The presence of large-amplitude Alfvén waves in the wind increases the stochastic nature of wind.

Based on the nonlinear analysis of the slow solar wind near 0.3 AU, the interplanetary magnetic field and the temperature near 1 AU, and radio pulsation have been confirming that the solar wind generates by some nonlinear process in the corona (Macek and Obojska, 1997, 1998; Macek and Redaelli, 2000; Pavlos et al., 1992; Polygiannakis and Moussas, 1994b,a; Kurths and Herzel, 1987). Hydrodynamic turbulence and intermittency characteristics of the solar wind plasma in the inner heliosphere have been obtained from previous work based on the multifractal analysis of solar wind data (Macek, 2002, 2003; Marsch and Tu, 1994; Marsch, Tu, and Rosenbauer, 1996; Marsch and Tu, 1997). These pieces of knowledge are still not enough to unveil the nature of solar wind that pervades the interplanetary space.

The results obtained in our work are in good agreement with the previous studies. Our results could be relevant in the sense that the radial evolution of the solar wind is very much related to Alfvén waves in the wind. The Alfvén wave-dominated fast wind is a stochastic random process and the less Alfvénic slow wind is chaotic. Our results set two important questions; the first is whether the Alfvén wave dominance in the fast wind masks the actual dynamics of the fast wind and the second is whether the different dynamics of both slow and fast wind is due to the source of origin or due to the Alfvén wave influence. To answer these questions, we need a detailed future study about solar wind plasma in the inner heliosphere and outer heliosphere. The future studies based on the data available from new missions like Parker Solar Probe and Solar Orbiter will provide a better idea about the solar wind source because these missions approach more closely to the Sun than Helios mission. These two missions will give more information regarding the source and evolution of slow solar wind. The information about Alfvénic slow wind closer to the Sun will be provided by Parker Solar Probe and, more about the source of solar wind plasma will be provided by Solar Orbiter.