A Rapid, Manual Method to Map Coronal-Loop Structures of an Active Region Using Cubic Bézier Curves and Its Applications to Misalignment Angle Analysis

Abstract

A rapid and flexible manual method is described that maps individual coronal loops of a 2D EUV image as Bézier curves using only four points per loop. Using the coronal loops as surrogates of magnetic-field lines, the mapping results restrict the magnetic-field models derived from extrapolations of magnetograms to those admissible and inadmissible via a fitness parameter. We outline explicitly how the coronal loops can be employed in constraining competing magnetic-field models by transforming 2D coronal-loop images into 3D field lines. The magnetic-field extrapolations must satisfy not only the lower boundary conditions of the vector field (the vector magnetogram) but also must have a set of field lines that satisfies the mapped coronal loops in the volume, analogous to an upper boundary condition. This method uses the minimization of the misalignment angles between the magnetic-field model and the best set of 3D field lines that match a set of closed coronal loops. The presented method is an important tool in determining the fitness of magnetic-field models for the solar atmosphere. The magnetic-field structure is crucial in determining the overall dynamics of the solar atmosphere.

1 Introduction

Solar images have always been important in acquiring an understanding of the physics of the Sun. From the first photographic images of the solar corona in 1851, to Hale’s spectroheliograph chromospheric images of 1891, to Lyot’s coronagraph images of 1931, to Skylab’s X-ray images of 1973, and to today’s Solar Dynamics Observatory’s images, image analysis has played a pivotal role in the development of solar physics. Starting in April 2010, the operation of the Solar Dynamics Observatory, with its two primary imaging instruments of the extreme ultraviolet (EUV) multiple-wavelength spectroheliograph, the Atmospheric Imaging Assembly (AIA) and the combined vector magnetograph and Dopplergraph instrument, the Helioseismic and Magnetic Imager (HMI), have provided unparalleled observations of the magnetically dominated structure of the solar atmosphere (Lemen et al. 2012; Schou et al. 2012). In particular, the coronal-loop structures in the solar atmosphere are clearly defined by AIA at high resolution (1.5 arcsec) and high temporal cadence of (1 image/12 second) over the EUV spectral range (9.4 – 33.5 nm) using a set of spectral filters covering a temperature range of 0.06 – 20 MK (Aschwanden and Boerner 2011; Reeves and Golub 2011; Pesnell, Thompson and Chamberlain 2012). HMI provides photospheric vector magnetograms every 90 – 135 seconds, and is normally averaged into 12-minute products. The HMI data provide the base magnetic field for the corona, as well as dopplergrams and continuum filtergrams (Scherrer et al. 2012). Use of the AIA data to define precisely the loop structures, which are surrogates for magnetic-field lines, provides a definitive diagnostic for admissible and inadmissible magnetic-field solutions.¹ The magnetic-field models for the solar atmosphere are decisive and crucial in determining the overall dynamics of the atmosphere leading to flares and coronal mass ejections and the form of the outflowing solar wind. The geometry of the magnetic-field lines can be used

• i) to determine the variability of the magnetic-field strength with height which is important in determining the plasma-β ratio,

• ii) to understand the non-potential magnetic structures of the solar atmosphere, which is critical in estimating the magnetic free energy,

• iii) to study the open/closed topology of the magnetic field by defining the foot points of the field lines and specifying the open-field lines, and

• iv) to constrain the possible magnetic reconnection scenarios in the corona.

To date, the best method to delineate the coronal structures in an active region employing EUV imagery is through a manual method of tracing each curvilinear feature, even though extensive research has been carried out into automating the process (Aschwanden et al. 2008; Aschwanden 2010). This manual success is due to the exceptional mental process of being able to recognize in context a single loop in a complex image where the unshaped, overlaying, and discontinuous loops may have low contrast and ill-defined endpoints; albeit with personal biases. In this article, we exploit this manual process of visual recognition by introducing an easy curve-matching process. This method uses only four points per loop, which are moved through a simple user-interaction process allowing the curve to be rapidly overlaid onto the selected loop in an image. The total resulting curve is stored by using only four coordinate points: the control points. The interactive computer process is implemented to allow various co-spatial magnetograms and EUV filtergrams to be viewed sequentially. This improvement allows the recognition of the overall loop structure by studying the loops at various emission temperatures, and allows the loop identification to include information on the arrangement of the underlying photospheric magnetic flux. The use of photospheric and chromospheric images also helps determine the tentative location of the coronal foot points by allowing the selection to be consistent with magnetic features and lower atmospheric emission features at the end points of the loop. The rationale of this approach is discussed in the following sections.

2 Parametric Bézier Curve

A coronal loop in a EUV image is seen as a curvilinear feature in the projected two-dimensional image plane. These enhanced coronal-loop features trace the magnetic field that contains the EUV-emitting plasma. They appear distinct in the EUV images because the pressure is enhanced by about ten times over the ambient pressure and have plasma temperatures between 10⁴ – 10⁶ K, and, in the common closed form, span from positive to negative magnetic-field regions (Priest 1982; Aschwanden 2001, 2002). Because the magnetic pressure dominates the plasma pressure, the coronal features trace the curve of the magnetic-field lines (Gary 2001). The closed magnetic loops in an active region are generally the brightest due to the plasma trapping of the magnetic field. As a mathematical construct, the center of these loops is a locus of a point moving with one degree of freedom, e.g. u, along the curve. The geometric modeling of the curves can be efficiently described by parametric equations (Klimchuk et al. 1992; Klimchuk 2000). In 2D, the curves are described by the functions x=x(u) and y=y(u) of a parameter u, which allows lines tangent to the coordinate axes, bounded lines, and lines independent of the image coordinate systems. One class of parametric curves is the Bézier curves. We refer the reader to Mortenson (1997) for a detailed discussion of these curves and their general properties.

The major advantages of using Bézier curves to map the coronal features are

• i) they provide a method to change the shape of the curve with only a few parameters in order to match a coronal loop,

• ii) the variation of the simple parameters changes the shape of the curve in a predictable manner,

• iii) the curve automatically starts and ends at the user-defined foot points, and

• iv) the curves and their derivatives with respect to the parameter u exist and can be determined at every point along the curve by a simple analytic equation.

Given a value of u (0≤u≤1), a position point [X(x,y)] along the curve is determined. The predictable nature of the changes in the curve is due, in part, to the Bézier curve being invariant under affine transformations (combinations of translation, rotation, scaling, or shear) and there is a simple geometric algorithm (the de Casteljau construction (Mortenson 1997)) for constructing the curve.

The general 2D Bézier curve of degree n can be written in the form

$$ {\bf X}(x,y) = f(u) = \sum_{i=0}^n {\bf P}_{i+1} \beta_{n,i}(u),\quad u\in[0,1], $$

(1)

where β _n,i is the $n{\rm{th}}$-degree polynomial basis function, the Bernstein polynomials,

$$ \beta_{n,i}(u) = \frac{n!}{i!(n-i)!} u^i (1-u)^{n-i} , $$

(2)

and P _j (j=1,…,n+1) are position vectors (x _j ,y _j ) called control points and are the vector parameters that control the shape of the curve (Mortenson 1997, Equation (4.2)). [n.b. In this article, P _j indexing starts with 1, this is different from Mortenson’s indexing, which starts from 0.] The Bézier curves interpolate between the first and last control points and are tangent to the first and last sides of an open polygon formed by connecting the P _j (x,y) points. The Bézier curve lies within the convex hull of the polygon control points (as shown in Figure 1).

Figure 1

An example of a using cubic (n=3) Bézier curve to fit a coronal loop on a SDO AIA 171 Å filtergram taken in the northern area of the active region AR 11117 on 25 October 2010. From frames (a) to (f), the control points are moved to have the curve match the loop captured in frame (f). The field of view is ≈4.5×5.3 arcmin².

We can generally restrict the curves that trace projected coronal loops to the class of cubic (n=3) Bézier splines. The essence of this assumption is that the coronal loops show normally at most one inflection point, which can be handled by the cubic Bézier curve. We will later quantify this assumption by comparing Bézier curve approximations to a set of field lines generated for an active region by a magnetic-field solution extrapolated from a solar magnetogram. The parametric cubic Bézier curve is given explicitly by

$$\begin{aligned} {\bf X}(x,y) &= {\bf f}(u) \\ &= (1-u)^3 {\bf P}_1(x_1,y_1 ) + 3u (1-u)^2 {\bf P}_2(x_2,y_2 ) \\ &\quad{}+ 3 u^2 (1-u) {\bf P}_3(x_3,y_3) + u^3 {\bf P}_4 (x_4,y_4 ) , \end{aligned}$$

(3)

where P ₁ and P ₄ are the control points associated with the coronal-loop foot points under the appropriate assumption which are to be described. For simplicity, the curves for the coronal loops are assumed non-segmented, i.e. non-composite curves. However, if necessary, high-order curves can be accommodated by a composite of cubic Bézier curves joined end to end. In this case, the control points at the joints are joined preserving the position and tangent continuities.

To improve loop recognition, high spatial-frequency image filtering or image time-differencing techniques could be implemented to help delineate the coronal loops. However, our current method does not apply these methods, to avoid inducing artifacts. For example, a few observed coronal-loop features might be artificially generated by line-of-sight integration effects of overlapping coronal objects, but even these would be shaped by the magnetic-field structures in the low-plasma-β corona (Gary 2001). We assume that each visible loop is a magnetic-field surrogate and use un-enhanced imagery.

Figure 1 shows a sequence of six images in which the cubic Bézier control points are moved, until in frame F the curve visibly overlays a loop in the AIA 171 Å filtergram. As the line segments or the open polygons formed by the four points ${\bf P}_{1}, {\bf P}_{2}, {\bf P}_{3}$, and ${\bf P}_{4}$ expand from a straight line to embrace the 171 Å loop which is captured in the last frame, the points ${\bf P}_{1}$ and ${\bf P}_{4}$ are placed at the foot points and initially ${\bf P}_{2}$ and ${\bf P}_{3}$ are placed at equal distances between the end points. Then the points ${\bf P}_{2}$ and ${\bf P}_{3}$ are moved outward along the two tangent lines at the nearest foot points, respectively. The length of the resulting curve is given by

$$ L = \int_0^1 \bigg|\frac{\partial{\bf f}(u)}{\partial u} \bigg|\, \mathrm {d}u , $$

(4)

which can be evaluated numerically (Bancisk and Juhasz 1999). For Figure 1(f), the coronal-loop arclength L is 190 arcsec or 137 Mm, which is about 100 times the cross-sectional width of the loop. For a particular point on the coronal loop, the tangent vector is ${\bf T} = \mathrm{d} {\bf X}(x,y)/\mathrm{d}s$ where the s is the differential of arclength, ds=(dx ²+dy ²)^1/2. For Bézier curves, the normalized tangent vector can be written as

$$ \bf{T} = \frac{ \frac{\partial{\bf f}(u)}{ \partial u}}{|\frac {\partial{\bf f}(u)}{ \partial u} |} , $$

(5)

where

$$ \frac{\partial{\bf f}(u)}{\partial u} = \sum_{i=0}^n \,[{\bf P}_{i+2}-{\bf P}_{i+1}] \beta_{n-1,i}(u) . $$

(6)

Equation (6) allows one to calculate equally spaced steps along a Bézier curve, even though equal steps in u are not equal Euclidean steps. The normal vector is ${\bf N} = \kappa^{-1} \mathrm{d}{\bf T}/\mathrm{d}s$, where κ is the curvature or the reciprocal of the radius of curvature, ρ=κ ⁻¹ = |[1+(dy/dx)²]^3/2/d² y/dx ²|. The average radius of curvature is

$$ \rho_{\mathrm{ave}} = \frac{1}{L} \int_0^L \rho(s) \, \mathrm{ds}. $$

(7)

For this example, ρ _ave=86 arcsec or 63 Mm (with ρ _min=28 Mm). The width of the coronal loop, two arcsec, is only 2 % of the arclength (Aschwanden 2011; Aschwanden and Boerner 2011). By visual inspection, the peak-to-peak error in fitting is estimated to be about the same value. This value is typical of the fitting that is achieved by this manual method.

In order to estimate the errors of using a cubic Bézier curve to map the center line of the coronal loop, we will assume that the variety of coronal-loop structures can be approximated by a set of potential-field lines. This then allows the loop coordinates to be numerically compared to a Bézier fit. A computer algorithm was implemented to determine the control points ${\bf P}_{2}$ and ${\bf P}_{3}$ that minimizes the difference between a cubic Bézier curve and a known magnetic-field line. The process starts with having ${\bf P}_{1}$ and ${\bf P}_{4}$ at the foot points (or end points) of the field lines. The cubic Bézier curve fit is found by varying the respective two middle control points, ${\bf P}_{2}$ and ${\bf P}_{3}$, along the nearest foot-point tangents, ${\bf P}^{\prime}_{1}$ and ${\bf P}^{\prime}_{4}$, such that the distances between equally spaced points on the coronal loop (field line) and the Bézier curve are minimized in the root-mean-square sense. Two Euclidean distances [ϵ ₂ and ϵ ₃] are introduced such that ϵ ₂ is the distance between ${\bf P}_{2}$ and ${\bf P}_{1}$ along the field-line tangent at ${\bf P}_{1}$, and ϵ ₃ is the distance between ${\bf P}_{3}$ and ${\bf P}_{4}$ along the field-line tangent at ${\bf P}_{4}$. The placement of ${\bf P}_{2}$ and ${\bf P}_{3}$ is then generated by minimizing the square root of the sum of the squared differences between equally divided points [α] on the Bézier curve [$\bf{f}$] and the field-line [$\bf{r}$] loops, as a function of ϵ ₂ and ϵ ₃:

$$ \chi= \Biggl[~ \frac{1}{m} \sum _{\alpha=1}^m \bigl[ {\bf f}(u_\alpha,\epsilon _2,\epsilon_3) - {\bf r}_\alpha \bigr]^2 ~ \Biggr]^{1/2} . $$

(8)

This determines the best fit for a Bézier curve to the potential-field line.

To quantify the use of the cubic (n=3) Bézier curve over higher-degree curves, we use the above minimization process to compare the differences between the cubic curves and a series of field lines generated from a known magnetic-field configuration. The magnetic field is a ten-dipole fit to the longitudinal magnetogram of AR 11117. The parameters of the ten dipoles (i.e. dipole magnetic-field strengths and locations) are determined by minimizing the RMS differences between the sum of longitudinal magnetic field at the photosphere of the set of dipoles and the planar longitudinal magnetogram. Applying the minimization procedure to a set of randomly generated field lines, the curve-fitting results are shown in Figure 2 and are given in Table 1. These data imply that the single cubic Bézier curve is sufficient for most studies. The RMS error of Equation (8) of the Bézier curve fit is less than 5 % of the length of the curve. Only when there is a large (90^∘) kink in the 2D image of the loop is there difficulty in matching the loop with a single cubic Bézier curve, and in the manual process this mismatch is quickly determined. The RMS fit error of 5 % is comparable to the 4.5 Mm width of the a typical 100 Mm coronal loop observed by Transition Region and Coronal Explorer (TRACE: Aschwanden and Boerner 2011). Hence it is expected that the cubic Bézier curve can be fitted within the width of the observed loop. Of course, a composite curve could be implemented if higher criteria are required.

Figure 2

Cubic Bézier curves (black) are fitted and compared to the potential magnetic-field lines (light gray) for the active region AR 11117 using a ten-dipole fit to the HMI magnetogram (25 October 2010, 20:58 UT) (background). The background magnetogram (5 by 5 arcmin²) is in false-color with red showing the direction of the field toward the observer and blue away from the observer.

Table 1 Statistical study of the suitability of the cubic Bézier curves to map magnetic fields. The potential-field loop of length L in arcsec is given with the mean RMS error and the percent deviation of RMS/L.

As a result of obtaining a cubic Bézier fit to a coronal-loop image, one can extend the process to extract the coronal-loop pixels and straighten out the loop. This straightened loop can be used to study

• i) the fitness of the loop to the curve, i.e. to determine how straight the coronal loop is when the Bézier curve is straightened out,

• ii) the cross-sectional characteristics of the coronal loops, and

• iii) the influence of the near-by and cross-cutting loops (Klimchuk et al. 1992).

This analysis using the straightened loop is to be discussed later but here we discuss the extraction and straightening process. The technique generates two curves parallel to the cubic Bézier fit on opposite sides of the loop.

Figure 3(a), shows, at a specific parameter value [u] the normal vector direction to the field line [${\bf{ N}}/{\|{\bf N} \|}$] and the tangent vector [${{\bf T}}/{\|{\bf T} \|}$]. If we extend the normal direction out in both directions along the curve we obtain two parallel lines (Figure 3(b)). The respective Bézier curves, f _upper(u) and f _lower(u), for these two lines can be obtained from Equation (3), where the values of the corresponding parametric values [u _a and u _b ] for two selected middle control points [${\bf P}_{a}$ and ${\bf P}_{b}$] for the upper and lower curves, are known.

Figure 3

The process of straightening the cubic Bézier curve (a) by generating two parallel lines (b) and segmenting the region into equal steps of the parametric equation (c). An example of a gridded 10×10 segment of the Bézier path (d) with its irregular quadrilateral shape which is translated into a rectangle form (e) in the loop-straightening process. In frame (a), the normal vector direction to the field line is blue and the tangent vector is orange.

These two parallel cubic Bézier curves can be subdivided into segments by using the parametric values u _i =i/M, i=0,…,M. The individual widths of the subdivided segments of the fit are not all the same since the arclength is not a linear function of u. This division is shown in Figure 3(c), with one segment highlighted in yellow and with M=100. The four quadrilateral corners of a segment are given by f _upper(u _i ), f _lower(u _i ), f _upper(u _i+1), and f _lower(u _i+1). The collection of segments can be straightened by making each segment into rectangles with a width of the arclength distance of the segment, and the height is the fixed distance between the outer parallel Bézier curves as shown in Figure 3(d).

The curved segments, Figure 3(c), do not have parallel sides and are not oriented normal to the image-plane axes; hence the image points associated within these segments must be calculated by breaking the area down via a linear interpolation of each of the four sides. A resultant 10×10 grid is shown in the example given in Figure 3(d) for a segment. We use these straightening and curve-fitting techniques as major elements for fitting and checking the Bézier curve fits. Although not yet implemented, an additional improvement in our method could use this straightening segment and perform a cost-function analysis for fine adjustments of the placement of the middle control points (Conlon and Gallagher 2010). The selection of coronal-loop foot points are discussed next.

3 Determining the End Points – The Foot Points

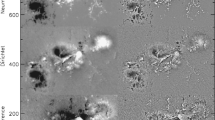
Because the coronal-heating process remains unknown, there are many proposed coronal-heating models. Aschwanden lists a set of coronal-heating models broken down into eight subgroups (Aschwanden 2002, p. 361). The heating processes in the models belonging to nearly all subgroups are driven by photospheric motions and/or by magnetic-field processes that are connected to the photosphere. The exception is the one subgroup that relates to magnetic instabilities in the corona itself and does not necessarily relate directly back to the photosphere. However, in general, it is expected that there should be a photospheric or chromospheric signature to the heating process even though this signature may not completely specify the process. For example, transient events (e.g. nanoflares) produce energy and outflows consistent with plasma heating and have been related to coronal loops (Aschwanden 2002). In the manual selection process we examine the foot-point locations (see Figure 4 and the four enlargements in Figure 5) in the EUV continuum and the longitudinal field strength in order to associate the foot-point location with heating surrogates.

Figure 4

SDO data of active region AR 11140 on 4 January 2011 at 00:00 UT: (top) AIA 171 Å  filtergram, (middle) AIA 1700 Å  filtergram, and (bottom) HMI longitudinal magnetogram, with enlarged selected foot-point views, to the left. As indicated by the circles, multiple wavelength views of the regions around possible foot-point locations help to limit the foot-point origin. The fields of view are 6.0×0.4 arcmin² and 0.7×0.4 arcmin², respectively.

Figure 5

The main panel for selecting and mapping the coronal loops by foot-point adjustments. The first and last control-point subframe locations for the magnetic field and 1700 Å continuum regions are shown below the active region. There are keys to switch the main-panel backround view through the AIA filters and HMI data sets.

The foot points of coronal loops, in many cases, are not definitely determined by visual inspection from a single wavelength filtergram. For those cases in which the end points of the loops are not definite due to the overlapping of loops, the lack of definition and contrast, and the fading of the loop at one of the foot points, we can use two approaches. The first is to use the full set of filtergrams from AIA to augment a particular filtergram and the second is to use photospheric and chromospheric signatures as proxies. The heated coronal loops have a temperature distribution along the axial direction of the loop. This implies that the loop heating or cooling is reflected to some degree by the dynamics and heating signatures at the foot points (see, e.g., Berger and Title 2001; Aschwanden 2002; Yurchyshyn et al. 2010). Magnetic structures have been related to the coronal-loop foot points (see, e.g., Schrijver and Title 2002; Katsukawa and Tsuneta 2005). Also using TRACE and Solar and Heliospheric Observatory/Michelson Doppler Imager (SOHO/MDI) data, dipole magnetic features were related to large scale loops (Schrijver and Title 2002). Both hot and cool loops have been found to be rooted in 1 kG photospheric fields using Yohkoh, SOHO, and TRACE data. The foot points are identified with some specific magnetic feature or chromospheric emission at the base of the corona (cf. Figure 4). An additional improvement in the manual foot-point selection process would be to devise and test various algorithms for selecting the nearest possible heating site using EUV images, magnetograms, and Doppler maps (De Pontieu et al. 2009).

Because of the relation between coronal heating and various foot-point signatures in the photosphere or chromosphere, locating the foot points of the coronal loops should be employed using these signatures. We employ these signatures in our coronal-loop fitting by adding additional panels to the main computer panel (Figure 5). The four additional subpanels show enlarged portions of the images around the two foot points of the Bézier curve. The magnetograms and the 1700 Å continuum panels are updated continuously and the control points [${\bf P}_{1}$ and ${\bf P}_{4}$] are moved to fine tune these foot points to coincide with the enhancement in the magnetic flux and UV emission.

4 The Manual Program

In the manual mapping, we have developed a Mathematica^® program that provides a simple interface to view alternately the EUV filtergrams and magnetograms and provide manipulation and storage of the control points, as well as expanded views of the foot-point regions. As seen in Figure 5, the main coronal-mapping program provides a simple switching mode to change the background between AIA and HMI images. The control points are selected to map a particular coronal loop in this data set. Furthermore, as the foot points are adjusted, the expanded views of the two foot-point regions (enlarged by a factor of two) in both the EUV continuum and longitudinal field are updated and allow suitable foot-points’ adjustment and selection. The data are stored and then the next loop is mapped, all at a rapid pace of only a few seconds per loop.

In order to obtain the EUV images needed for the coronal-loop identification there are several alternatives, e.g. Heliophysics Event Knowledgebase (HEK: Hurlburt et al. 2012), Virtual Solar Observatory (VSO: sdac.virtualsolar.org) web pages, SolarSoftWare software (SSW: www.lmsal.com/solarsoft ) and Joint Science Operations Center data request forms (JSOC: www.jsoc.Stanford.edu ). Here we discuss only JHelioviewer. JHelioviewer ( www.jhelioviewer.org ) is a visualization tool for SDO, AIA, and HMI data based on the JPEG 2000 image-compression standard, which gives a highly compressed, quality progressive, and region-of-interest based form of image search and acquisition (Mueller et al. 2009). These features make it relevant for NASA’s Solar Dynamics Observatory data since the observatory is providing more than a terabyte of image data per day. The use of the browser allows the capturing of the AIA filtergrams and HMI magnetograms. One of the primary advantages of the JHelioviewer software lies in its ability, in part, to cross-reference the data sets and solar events from various instruments and spacecraft and to allow the capture of selected regions of interest for later analysis.

After browsing for specific data in JHelioviewer, the user created the state file and images upon exiting. This state file can be modified to select particular fields of view (center, width, and height in meters) and, if needed, reopened with the new coordinates.

In Figure 6, panels (a) and (b), show more details of the elements of the manual mapping program. Figure 6(a) shows a full set of field lines that has been mapped by selecting and moving the Bézier control points, and illustrates the benefits of switching between background images. For each curve the four Bézier points determine the full curve and are stored for analysis. Figure 6(b) shows, for one loop, a selected Bézier curve and the four associate control points. Using the method to straightening the line, the fit can be checked, as shown in Figure 6(c). Further improvement of the program might automate small corrections through a cost analysis that makes slight adjustments automatically to fit the coronal loop.

Figure 6

Panel (a): first row, a set of open and closed field lines is shown on the 171 Å filtergram and the HMI LOS magnetogram for AR 11117 on 12 October 2010 at 18:30 UT (7.2×5.4 arcmin²). Panel (b): the loop to be straightened is shown with the active region (2.9×2.1 armin²). The loop is clearly defined leaving the following sunspot but weakens and disappears as it enters the preceding sunspot region. A manual method allows the intuitive connection of disjointed coronal loops within the context of the entire region, albeit subjective, per loop, with consistent total structure. Panel (c): the Bézier curve has been straightened and the resulting associated emission for the coronal loop is displayed.

5 Determining the Best 3D Magnetic Field Model

The 2D parametric cubic Bézier curve fit to an imaged coronal loop can be generalized to 3D with only two additional scalar parameters, and this 3D loop can be used to constrain 3D magnetic-field models. This section discusses this generalization. The 2D cubic Bézier curve (from Equation (1)) is given by

$$ {\bf X}(x,y) = {\bf f}(u) = \sum_{i=0}^3 {\bf P}_{i+1} \beta_{n,i}(u), $$

(9)

where ${\bf P}_{j}$ are 2D position vectors (x _j ,y _j ), and can be extended to 3D, by having the positions vector be 3D vectors, i.e. ${\bf P}_{j} = (x_{j},y_{j},z_{j})$. Hence, writing Equation (9) in the 3D form, we have

$$\begin{aligned} {\bf R}(x,y,z) &= {\bf F}(u) \\ &=\bigl[\bigl[ (1-u)^3 x_1 + 3u(1-u)^2 x_2 + 3 u^2 (1-u) x_3 + u^3 x_4 \bigr], \\ &\quad\; \bigl[ (1-u)^3 y_1 + 3u(1-u)^2 y_2 + 3 u^2 (1-u) y_3 + u^3 y_4 \bigr], \\ &\quad\; \bigl[ (1-u)^3 z_1 + 3u(1-u)^2 z_2 + 3 u^2 (1-u) z_3 + u^3 z_4 \bigr] \bigr] . \end{aligned}$$

(10)

The ${\bf X}(x,y)$ curve is the 2D projection of the 3D curve ${\bf R}(x,y,z)$ onto the z=0 plane. Figure 7 illustrates this projection geometry. Assuming ${\bf P}_{1}$ and ${\bf P}_{4}$ are the photospheric foot points of a coronal loop, Figure 7 shows that by changing only z ₂ and z ₃ for the matched Bézier control points, a 3D curve agrees with the fitted coronal loop in 2D projection. Therefore, if we can determine z ₂ and z ₃, we have the 3D coronal-loop structure, i.e. a 3D magnetic-field line.

Figure 7

The cubic Bézier connection between the 3D and 2D projections. Dashed blue line: a 2D cubic Bézier curve in the z=0 plane, defined by the control points ${\bf P}_{i}(x_{i},y_{i}), i\in(1,4)$. If the control points ${\bf P}_{1}$ and ${\bf P}_{4}$ become 3D vectors, via ${\bf}(x_{1},y_{1},0)$ and ${\bf P}_{4}(x_{4},y_{4},0)$, and if we define ${\bf P}^{\prime}_{2}$ and ${\bf P}^{\prime}_{3}$ as ${\bf P}^{\prime}_{2}(x_{2},y_{2},z_{2})$ and ${\bf P}^{\prime}_{3}(x_{3},y_{3},z_{3})$, then we define the 3D cubic Bézier curve (dark red) by the introduction of two parameters: z ₂ and z ₃. The two curves are related by having points lying at the same location in the image plane.

Next, a method to determine z ₂ and z ₃ is discussed in terms of minimizing the coronal magnetic-field line tangents [${\bf B}_{\mathrm{obs}}({\bf R})$] with a theoretical magnetic-field model [${\bf B}_{\mathrm{theo}}({\bf R})$]. At a 3D position [${\bf R}$], we define the misalignment angle $\mu({\bf R})$, 0≤μ≤π (De Rosa et al. 2009; Aschwanden and Malanushenko 2013) as

$$ \mu({\bf R})= \cos^{-1}{ \biggl[ \frac{{\bf B}_{\mathrm{theo}}({\bf R}) \cdot {\bf B}_{\mathrm{obs}}({\bf R})}{ |{\bf B}_{\mathrm{theo}}({\bf R})| |{\bf B}_{\mathrm{obs}} ({\bf R}) |} \biggr]}, $$

(11)

where the angle μ is defined in terms of ${\bf R}$ and the associated field directions for the observed and theoretical magnetic fields. For the entire loop, a characteristic misalignment angle is defined by the equation

$$ \xi= \frac{1}{\Gamma} \sum_{k=1}^{\Gamma} \mu({\bf R}_k), $$

(12)

where the sum is over Γ=100 equi-spaced points along a field line and Γ has the same value for all loop lengths. Hence from the preceding paragraphs, we define, for the jth loop, a similar overall characteristic misalignment angle ξ _j [z _j2,z _j3] for the 3D Bézier coronal fit, where the position z-coordinates are determined by

$$ z[z_{j2},z_{j3}]=(1-u)^3 z_{j1}+3u (1-u)^2 z_{j2} +3 u^2 (1-u) z_{j3}+ u^3 z_{j4} , $$

(13)

where z _j1 and z _j4 are the estimated foot-point positions at z=0, and z _j2 and z _j3 are initially unknown. Hence given a 3D magnetic-field extrapolation model [${\bf B}^{m}_{\mathrm{theo}}(x)$], where m is the model number, and using the 3D Bézier loop construction we can construct the characteristic misalignment angle for the jth loop and mth theoretical magnetic-field model assuming values for z ₂ and z ₃:

$$ \xi_j^m [z_{j2},z_{j3}] = \frac{1}{\Gamma} \sum_{k=1}^{\Gamma} \cos^{-1}\biggl[ \frac{{\bf B}_{\mathrm{theo}}^m ({\bf R}_k [z_{j2},z_{j3}] ) \cdot {\bf B}_{\mathrm{obs}} ({\bf R}_k [z_{j2},z_{j3}])}{ (|{\bf B}_{\mathrm{theo}}^m({\bf R}_k [z_{j2},z_{j3}])| |{\bf B}_{\mathrm{obs}} ({\bf R}_k [z_{j2},z_{j3}]) |)}\biggr] . $$

(14)

The final set of values for z _j2 and z _j3 (i.e. $z_{j2}^{*}$ and $z_{j3}^{*}$), are determined by the values that minimize $\xi_{j}^{m}$, i.e.

$$ \xi_j^m \bigl[z_{j2}^*,z_{j3}^* \bigr]= \mbox{min}_{z_2, z_3} \bigl[ \xi_j^m [z_{j2},z_{j3} ] \bigr] . $$

(15)

Using the best-fit parameters $z_{j2}^{*}$ and $z_{j3}^{*}$, we define a global parameter [Φ] using all of the N loops for each model:

$$ \Phi[m]= \frac{1}{N} \sum _j^N \xi_j^m \bigl[z_{j2}^*,z_{j3}^* \bigr]. $$

(16)

We define this as a measure of the goodness of fit for each model. The best magnetic model representation for the corona is given by the model which satisfies min _m [Φ[m]]. Assuming that all the models extrapolate the same photospheric vector magnetic field then this procedure allows a selection of the best model that agrees with the coronal loops.

Figure 8 shows the misalignment of the tangent Bézier vectors and the normalized magnetic-field directions associated with a field lines in AR 11117 (see Figure 2), in which the middle-two cubic Bézier control points are given increasingly vertical displacements z ₂ and z ₃. The resulting characteristic misalignment angles (Equation (14)) decrease from 36^∘  to 0.5^∘. The photospheric projection of the field line is fitted by a root-mean-squared 2D Bézier curve and then the middle control points are given vertical displacements with the resulting curve becoming 3D with the addition of non-zero values for z ₂ and z ₃. The minimum characteristic misalignment error is not zero, in part from three sources of errors resulting from i) the finite integration steps for the initial field lines, ii) an imperfect match of the cubic Bézier curve to the projected field line (2 % RMS error), and iii) the RMS minimization determination of z ₂ and z ₃. However, the resulting 3D cubic Bézier curve is a good representation of the numerical field line with an RMS displacement error of 3.3 % compared to the arc length of the field line.

Figure 8

The reduction of the misalignment of the tangent Bézier vectors and the normalized magnetic-field directions as displacements z ₂ and z ₃ are increased. The blue arrows are tangents to the Bézier curve and the red arrows are the normalized magnetic-field directions at the same point. The black line is the original field line generated from a ten-dipole magnetic-field model (Figure 2, Loop A). From bottom to top, the associated characteristic misalignment angles are 36.70, 29.75, 23.00, 16.61, 10.70, 5.33, 0.51 (minimum), and 3.78 degrees.

By forcing the end points of the cubic Bezier curve (${\bf P}_{1}$ and ${\bf P}_{4}$) onto the photosphere, the misalignment-angle minimization process then has a single global minimum for all the coronal loops used in this study. A follow-on study, now in progress, also allows z ₁ (or z ₄) to have a vertical displacement, and we minimize the coronal loops displacements with three free z-parameters. We simulate an open field line by having one end point in the corona and one on the photosphere. We are also exploring having all four control points with a vertical displacement, although it might be problematic in finding a global minimum; however, this would negate the necessity of assuming photospheric foot points.

This method could be used to determine the linear force-free parameters in minimum dissipation rate (MDR) models (Gary 2009) to distinguish the best nonlinear-force-free model, or to select the source-surface height of a potential-field source model (De Rosa et al. 2009; Malanushenko et al. 2012).

The active region AR 11117 was used in a comparison example (Wu et al. 2012; Tadesse et al. 2012; Jiang et al. 2012). Figure 9 shows the results of a potential-field extrapolation compared with the 3D time-dependent data-driven MHD solution of Wu et al. (2012). Also for comparison, the NLFFF minimum dissipative rate (MDR) model is included (Hu and Dasgupta 2008; Hu et al. 2010). The MHD is obviously superior in generating field lines closer to the observed coronal loops. This superiority is, in part, caused by using the full photospheric vector magnetic field in the model and having no global parameters as is the case for the other two models which use constant-LFFF parameters. Using Equation (16) we can determine a quantitative comparison between these three models. The results of the analysis for the three models is shown in Table 2, where 25 closed coronal loops were used. This analysis assumed the identified loops were closed, i.e. both ends of the loop were coronal foot points at z=0. Obviously this assumption is only asserted, but it relies on checking the polarity of the assumed foot points and the general geometry of model field lines. Having a number of Bézier-fitted coronal loops allows the statistics to be in favor of the majority being actually closed loops. In the current process we assume that the foot points are actually at or very near the photosphere level, although later work will allow these foot points to be also elevated in the minimization procedure. For the initial investigation these foot-point values are zero, to simplify the test of the method.

Figure 9

For active region AR 11117, a comparison of field lines from a potential magnetic field (panel (a)), a minimization of energy dissipation rate process (panel (b)), and a data-driven MHD magnetic field (panel (c)) are shown with AIA 171 Å coronal loops mapped by cubic Bézier curves. The background is the LOS HMI magnetogram (3.3×2.1 arcmin²). The field lines (red) of each model are generated from the end points (foot points) of Bézier mapped coronal loops. Bézier coronal loops are colored yellow if they appear to be closed field lines, and green if they appear to be open field lines. The agreement of the projected field lines with the Bézier coronal-loop curves visibly improves from (a) to (c).

Table 2 The misalignment angle results comparing three magnetic-field models, using 3D Bézier curve fits to 25 coronal loops, characterized as closed field lines.

For the three magnetic-field models studied (potential, MDR, and MHD) the respective misalignment angles are 32.7^∘, 28.8^∘, and 27.6^∘. The calculation had a physical volume of 200×128×100 arcsec³. Of particular interest are the resulting magnetic-energy values in the volume corresponding to 4.12, 4.47, and 4.90×10³² ergs. There is an almost inverse linear correspondence between the energy and the misalignment angle, with an extrapolated zero misalignment angle having an energy of about twice the potential energy. However, we have only three points, and it will be interesting to see if we can verify this trend in future studies. Furthermore, in the context of several previous studies employing the misalignment angle, the derived misalignment angles of Table 2 are consistent. In a comparison of nonlinear-force-free-magnetic-field (NLFFF) models, De Rosa et al. (2009) derived the misalignment angles of the model in comparison with Solar TErrestrial RElations Observatory (STEREO) data for active region AR 10953. The mean misalignment angles of these NLFFF models ranged from 24^∘ to 44^∘  with the minimum being, surprisingly, associated with a potential-field model; there does not seem to be a linear correspondence between the energies and the misalignment angles of these NLFFF models. The field lines employed in this study were at the periphery of the active region and hence the study was affected by the lack of knowledge of the side and upper boundary conditions. The boundary conditions, the weakness of the transverse-field measurements, and pre-processing the data could also affect these results significantly giving the potential field a smaller misalignment angle. Two additional articles using STEREO data have calculated the misalignment angle employing submerged dipoles, with and without currents, to model the magnetic fields (Sandman and Aschwanden 2011; Aschwanden 2013). Each of these articles effectively describes modeling the STEREO observed field lines, that is, these models are to achieve the best fit to the observed field lines and do not take into account magnetic transverse-field measurements, nor do they employ any solar plasma parameters. Without electric currents, for four active regions employing from 70 to 200 loops, the peak misalignment angles ranged from 11.2^∘to 17.8^∘  compared to the potential (PFSS) range of results from 19^∘  to 32^∘. In both cases there were numerous misalignment angles greater than the value corresponding to the peak of the distribution of all misalignment angles. Therefore, our results using the 3D Bézier approach seem consistent with these previous results and show a promising new method to compare competing magnetic-field models.

6 Conclusion

Although our manual technique is rapid, it is not an automated technique. The manual process should allow automated techniques to improve via a learning process. In a recent article, Aschwanden (2010) reported on a promising technique that automatically identifies the position of segments of coronal loops with the number extracted approaching the number of segments obtained by visual identifications. The method used is based on oriented-directivity tracing of curvilinear features and takes advantage of the specific property that coronal loops have large curvature radii compared with their widths. In this article one can find references to other automated approaches for coronal-loop identifications. We hope that our visual identification process and the application of employing Bézier curves described above can be used to improve these automated processes via a cognitive, intelligent, or hierarchical temporal memory computing, i.e. learning from experience, cf. Banda, Angryk, and Martens (2013). In particular, these new methods need to employ global connections and foot-point selections to actually provide a complete closed magnetic-field line.

Similar investigations have been performed by other research groups. For example, Malanushenko, Longcope, and McKenzie (2009) and Malanushenko, Yusuf, and Longcope (2011) use a piecewise-cubic-spline function for a coronal loop (i.e. two cubic Hermite splines were used to fix one loop where each spline was defined by two end points and the tangents at the end points) and searches for linear-force-free field solutions curves in both its force-free parameter and height for each best-fit field line to infer the twist of the lines. In order to investigate the twist in the coronal magnetic field, various calculations have been performed to select field lines from different LFFF and NLFFF models to determine the free parameter [α] which gives the best fit of the coronal lines (Lim et al. 2007; Lopez Fuentes, Klimchuk, and Demoulin 2006; Malanushenko, Longcope, and McKenzie 2009; Aschwanden and Malanushenko 2013; Aschwanden et al. 2012b). When the two STEREO spacecraft had the proper angular separation, STEREO investigations have provided unique 3D reconstructions to allow testing of various extrapolation models (Aschwanden and Malanushenko 2013; Aschwanden et al. 2012a, 2012b). Our approach presented here is similar to the STEREO method investigated by Aschwanden (2013); however, we have used a cubic Bézier curve-fitting approach with applications for distinguishing competing magnetic-field models. The 3D cubic Bézier spline (n=3) has two anchor points at the ends and two middle control points, which allow non-planar curves.

The importance of employing coronal-loop images in selecting the magnetic-field model arises in part from the difficulty of measuring the photospheric magnetic field. Wiegelmann and Inhester (2010) and Wiegelmann et al. (2010) addressed the implication of the vector-magnetogram errors for deriving a nonlinear-force-free magnetic-field model. The effect of the 180^∘  uncertainty in the polarization measurement of the transverse magnetic field and its relatively weaker signal introduces errors in the magnetic-field extrapolations. These uncertainties can be ameliorated by using the coronal-loop information on the direction of the magnetic-field lines and connectivity, hence the need to map the coronal loops and extract their information for an improved assessment of magnetic-field models, e.g. see De Rosa et al. (2009).

In summary, we have described a rapid and flexible manual method based on cubic Bézier splines to represent the EUV coronal loops of an active region. The technique uses only four points per field line, which allows a computer-efficient and rapid algorithm. Since the coronal loops are used as surrogates of magnetic-field lines, the Bézier mapping can restrict the magnetic-field models derived from extrapolations of magnetograms to those admissible and inadmissible, since the magnetic-field extrapolations must satisfy not only the lower boundary conditions of the vector field, the vector magnetogram, but also must have a set of field lines that satisfies the additional conditions in the volume, akin to supplying an upper boundary condition. Figure 10 summarizes this process, from data to the result of the goodness of fit parameter [Φ] for a model. The tool and program are important in determining the magnetic-field models for the solar atmosphere which are crucial in determining the overall dynamics of the solar atmosphere. In subsequent articles we will apply this technique to compare various magnetic-field extrapolation models. For active-region analysis, the generalizations of this technique of coronal-loop identification and misalignment analysis can also be used for iterating a specific solar-atmosphere model to improve its 3D reconstruction of the corona. Such results will lead to a better understanding of the 3D plasma motion along the magnetic-field lines and magnetic-field oscillations, as well as to an overall modeled magnetic field consistent with observed coronal loop structure, and they will improve understanding of the solar-atmosphere dynamics.

Figure 10

Flow chart for the selection of the best numerical coronal magnetic-field model for an active region. Using the numerical criteria determined from the misalignment angles of the 3D Bézier curve fits to best closed coronal loops, the compatibility of the models to coronal observations can be determined numerically.