1 Introduction

Let G be a bounded set in \({\mathbb {R}}^d,\ d>1,\) and let \(M(x), x\in G,\) be a family of symmetric positive definite matrices, which are unknown. The main goal of this work is to estimate the integral curve \(x(t), t\ge 0,\) starting at a known fixed point \(a\in G\) and driven by a vector field \(v(M(x)), x\in G,\) based on the observations

$$\begin{aligned} \{(X_j, {Y}(X_j)), j=1,\dots ,n\},\quad Y(X_j)=BM(X_j)+\Sigma ^{1/2}(X_j)\Xi _j, \end{aligned}$$

where \(X_j, j=1,\dots ,n,\) are discrete locations in G, B is a known matrix, and the second term on the right represents random errors. For our purpose, the vector field v(M(x)) will generally consist of the leading eigenvectors of the tensors M(x). The integral curve \(x(t), t\ge 0,\) is defined as a solution of the ODE

$$\begin{aligned} \frac{dx(t)}{dt}=v(M(x(t))),\quad t\ge 0, \;\, x(0)=a \end{aligned}$$
(1)

or equivalently of the integral equation \( x(t)=a+\int _0^t v(M(x(s)))ds. \) The other parts of the model will be explained in the next sections. Below we give the motivation and application from brain imaging research.

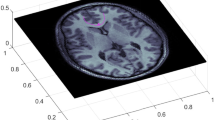
Diffusion tensor magnetic resonance imaging (DTI) is a prominent method for using magnetic fields to measure the degree to which water molecules are diffusing along particular 3D directions at every location in a biological specimen; e.g., see Bammer et al. (2009), Beaulieu (2002), Chanraud et al. (2010), Mukherjee et al. (2008a, b). Because water is constrained to diffuse along, but not across, the wire-like axons that carry an electrical charge from neuron to neuron in the human brain, tracing trajectories along prominent water diffusion directions through volumetric brain DTI data sets has attracted considerable scientific attention as a means for mapping the axon architecture of the brain. Given raw DTI data, consisting of component images that quantify the amount of water diffusion along particular 3D directions, the fiber trajectory tracing problem for DTI has traditionally been formulated in terms of estimating a \(3\times 3\) positive definite matrix called the diffusion tensor that represents the statistics of water diffusion over every direction on a 3D sphere; differential equations that model particle motion through the field of diffusion tensor leading eigenvectors are then solved (Fig. 1).

Fig. 1
figure 1

A 2D slice of a 3D DTI data set. DTI provides a \(3\times 3\) positive definite matrix at each location in 3D; the leading eigenvector of this matrix (direction shown in blue) indicates the most prominent direction along which water molecules are diffusing locally. The fractional anisotropy of the matrix (FA) is a function of the three matrix eigenvalues that gives a univariate summary of how anisotropic, i.e. strongly preferential along a single spatial direction, the water diffusion is (higher FA is whiter). a A map of fractional anisotropy (FA) derived from DTI data, with whiter pixels representing locations where the diffusion tensor is dominated by its leading eigenvalue. The FA map is overlaid with the vector field of leading eigenvectors. b The FA map is overlaid with the diffusion tensor field represented by ellipses. The major axis of each ellipse is oriented along the leading eigenvector direction and the minor axis is oriented along the second eigenvector direction. The major axis is scaled to have unit length and the minor axis is scaled according to the ratio of the second eigenvalue to the leading eigenvalue. c The FA map is overlaid with an example fiber tracing with 95 % confidence ellipsoids based on the proposed method. (Color figure online)

Full size image

However, DTI component images contain a notoriously high amount of noise relative to the water diffusion signal, resulting in noisy estimation of the diffusion tensor and leading eigenvectors; see, e.g., Gudbjartsson and Patz (1995), Hahn et al. (2006, 2009), Zhu et al. (2007, 2009). This in turn causes erroneous trajectory estimates that can in turn lead to spurious scientific findings; see Basser and Pajevic (2000), Zhu et al. (2009). This problem led to the development of a class of methods, termed probabilistic tractography, that provides estimates of uncertainty in fiber trajectories. These approaches are generally based on the use of sampling to explore the space of possible diffusion tensors, leading eigenvectors, or fiber trajectories. For example, Bayesian frameworks have been presented for estimation of parameters such as leading eigenvector directions or trajectory curve characteristics; Markov chain Monte Carlo (MCMC) is then used to explore the space of parameter values; see, e.g., Parker and Alexander (2003), Friman et al. (2006), and Basser et al. (2000). Bootstrap has also been used to repeatedly simulate novel diffusion tensors or leading eigenvectors based on subsets of component images; see, e.g., Jones (2003), Lazar and Alexander (2005), Behrens et al. (2003). Uncertainty is assessed in terms of variability of estimates across bootstrap samples. The key computational limitation of these approaches is the burden of drawing large numbers of samples from high-dimensional spaces. The key theoretical limitations of these approaches are the use of parametric models, and a lack of theoretical justification of why the method would converge, and if it converges how fast. In addition, prior distributions over parameter values required for MCMC need to be determined, usually through heuristic arguments; it is not adequate to simply provide non-informative priors because these assign non-zero prior probabilities to tensors that are not positive definite. See Chap. 8.2 in Gelman et al. (2004) on limitations of the Bayesian framework in this regard. Additionally, bootstrap can be misleading since it resamples from the given model, which could be inappropriate to start with. In order for bootstrap to work, one needs to prove its consistency, which is often equivalent to establishing asymptotic normality, and the functional that makes up the statistic of interest needs to be continuous with respect to the underlying distribution of observations; see, e.g. Mammen (1992) for more on what is needed for bootstrap to work and classical situations when it fails. Whether these necessary conditions are met by DTI has not been explored in depth. See also Yuan et al. (2008) for a discussion of various issues associated with use of bootstrap in DTI.

An alternative to probabilistic tractography is to use smoothing estimators to trace the fiber trajectory, and quantify uncertainty in closed form using rigorous theoretically-driven bounds on errors. For example, Koltchinskii et al. (2007) used a Nadaraya–Watson kernel smoothing estimator for the vector field combined with a plug-in estimator for the integral curve, under an assumption of additive vector field noise. This approach yields asymptotically normal estimators of integral curves as the number of spatial locations grows, it enjoys the optimal rate of convergence locally and globally, and provides closed-form estimates of integral curve uncertainty through the covariance of a limiting Gaussian process; see Sakhanenko (2010, 2011). This approach would need to identify locations along the integral curve trajectory where multiple distinct principal eigenvector directions appear viable, as is common in DTI data, and begin new integral curve trajectories along each of these directions. Complete characterizations of uncertainty in fiber trajectories are then assembled by linking together all such branching integral curves together with their uncertainty estimates. The key limitation of this approach is that the input to fiber tracing is assumed to be a vector field of “true” diffusion tensor leading eigenvectors that have been perturbed by an additive noise, thus ignoring the possibility that the estimation error in the diffusion tensor itself may give rise to more complex noise structures in the leading eigenvector field.

This paper provides an integral curve estimator that gives a more realistic and complete account of how noise in DTI data impacts fiber trajectory estimation by modeling how noise in the component images enters into the estimation of diffusion tensors and leading eigenvectors. We show that under certain geometric and smoothness assumptions the properly normalized difference between our estimator and the true integral curve, as a random process, converges weakly to a Gaussian process. This allows us to provide an asymptotically normal estimator of the integral curve at a point and to use the covariance matrix of the Gaussian process to construct confidence ellipsoids for fixed points along the integral curve. We then show that the Koltchinskii et al. estimator only converges to this Gaussian process in very limited, unrealistic situations: when the magnitudes of image noise and water diffusion are relatively small, and when the gradient of the leading eigenvector field is near constant along the integral curve. As described above, in the common case that integral curve tracing encounters a location whose leading eigenvector direction is ambiguous, we begin traces of new integral curves along each plausible eigenvector direction, and build complete descriptions of a fiber trajectory by linking together all such branching integral curves emanating from a given starting point.

The rest of the paper is organized as follows. Notation and our framework are described in Sect. 2. We formulate the three-step estimation procedure in Sect. 3. Important definitions and conditions are gathered in Sect. 4. The main theoretical results, and the step-by-step algorithm (including a test for branching), are in Sect. 5. We give a theoretical comparison between our approach and that of Koltchinskii et al. (2007) in Sect. 6. We illustrate how our method works on artificial data in Sect. 7 and on real DTI data in Sect. 8. We draw conclusions and discuss our findings in Sect. 9. Proofs are gathered in the Appendix.

2 Notation and framework

Throughout the paper all vectors are columns and \(u^*\) denotes the transposition of a vector or a tensor u. In brain imaging applications d is typically 2 or 3, G represents a region of a brain, and M(x) provides a representation of the spatial distribution of water diffusion at x. DTI makes the estimation of M(x) possible by collecting a set of N component images, each of which uses magnetic field gradients to measure the relative amount of water diffusion at x along a spatial direction represented by \(b\in {\mathbb {R}}^d\). This relative water diffusion measurement is denoted by S(x, b). If these measurements are collected along at least \(d(d+1)/2\) such directions, and the spatial distribution of water diffusion at each x is assumed to be ellipsoidal, then there is sufficient data to estimate a diffusion tensor M(x) such that for any spatial direction b, S(x, b) is estimated as follows: \( \log \bigg (\frac{S(x,b)}{S_0(x)}\bigg )=:y(x, b)=- c b^*M(x) b+\sigma (x, b)\xi . \) Here \(S_0\) is a baseline signal level measured in the absence of a magnetic field gradient; the constant c depends only on the hydrogen gyromagnetic ratio, the gradient pulse sequence design, duration and other timing parameters of the imaging procedure (see, e.g., Basser and Pierpaoli 1998); \(\sigma \) is a positive function that adds noise to the measurement that may depend on x and b; and \(\xi \) is a random variable with mean zero and variance one. In the absence of noise this relationship is known as the Stejskal–Tanner equation.

For a tensor \(A\in \mathbb {R}^{d^2}\), let \(A_{kl}, k, l =1,\dots ,d\) be its components. For convenience let \(d_0:=d(d+1)/2\). For a symmetric tensor \(A\in \mathbb {R}^{d^2}\) we define a \(d_0\)-dimensional vector \(\mathbf{A}\) that consists of stacked rows of the upper triangular part of the tensor A, i.e. \(\mathbf{A}=(A_{11}, A_{12},\dots , A_{1d}, A_{22}, A_{23}, \dots , A_{2d},\dots , A_{(d-1)(d-1)}, A_{(d-1)d}, A_{dd})^*.\) Note that for any two symmetric tensors \(A, F\in \mathbb {R}^{d^2}\) the trace of their product can be calculated as \(\sum _{k, l=1}^d A_{kl}F_{kl}=\mathbf{A}H\mathbf{F},\) where H is a diagonal matrix with ones and twos on the diagonal. For example, for \(d=3\) the diagonal of H is (1, 2, 2, 1, 2, 1).

Given N magnetic field gradient directions \(\{ b_1, \dots , b_{N} \}\), there is a fixed \(N\times d_0\) matrix B that is related to the set of spatial gradient directions and timing parameters of the imaging procedure (its kth row is proportional to \(\mathbf{F}H\) with \(F=b_kb_k^*\), \(k=1,\dots ,N\)). At a fixed location \(x\in \mathbb {R}^{d}\), we observe the \(N\times m\) tensor Y(x) such that

$$\begin{aligned} {Y}(x)=B\mathbf{M}(x)I_m^*+{\Sigma }^{1/2}(x){\Xi }_x\quad \mathrm{with}\quad I_m=(1,\dots ,1)^*\in \mathbb {R}^m, \end{aligned}$$
(2)

where the columns of Y(x) are \(Y_i \in \mathbb {R}^{N}, i=1,\dots ,m,\) and for a fixed x the \(N \times N\) tensor \(\Sigma \) is symmetric positive definite; the \(N\times m\) tensor \(\Xi _x\) is a random noise. Note that this is a linear model with the fixed design.

Throughout the paper, for a symmetric tensor A, its maximal eigenvalue is denoted by \(\lambda (A)\). When it is simple (not repeated) the corresponding unit length eigenvector is denoted by v(A). Under certain conditions on the tensor field \(M(x), x\in G,\) the vector field v(M(x)) is unique locally around the integral curve, which in turn exists and is unique. Because water diffuses preferentially along the directions of travel of axon fibers that connect disparate regions of the brain to each other, tracing such integral curves along prominent diffusion directions can result in \(x(t), t\ge 0,\) described in (1), that are geometric representations of those axon fibers. There are various downstream applications of the fiber curves; for example, structural connectivity analysis makes use of such fiber trajectories to infer the degree to which two distinct brain regions appear to be connected to each other, in effect quantifying the capacity of two brain regions to communicate with each other.

3 Three-step estimation procedure

The goal of our three step estimation procedure is to (1) regularize the input tensor field, (2) convert it to a vector field representation that allows integral curve tracing, and (3) perform the integral curve tracing. As a preliminary step one needs to estimate the tensor M(x) at a fixed location \(x\in G\) from the raw Y measurements. There are various ways to do so. For instance, the ordinary least squares estimator of \(M(x), x\in G,\) is

$$\begin{aligned} \tilde{\mathbf{M}}(x)=\frac{1}{m} (B^* B)^{-1} B^* {Y}(x)I_m, \end{aligned}$$
(3)

provided \((B^*B)^{-1}\) exists. It is the most popular choice in the DTI literature. Another estimate is the weighted least squares estimator of \(M(x), x\in G,\) which is studied extensively in the work of Zhu et al. (2007, 2009).

Our estimation procedure is as follows:

  • Step (i): Smoothed tensor field estimation At each location \(x\in G\), a smoothed estimate \(\hat{\mathbf{M}}_{n}(x)\) of the tensor field is constructed using the following kernel smoothing estimator:

    $$\begin{aligned} \hat{\mathbf{M}}_{n}(x)=\frac{1}{nh_n^d}\sum _{j=1}^n K\bigg (\frac{x-X_j}{h_n}\bigg )\tilde{\mathbf{M}}(X_j), \end{aligned}$$
    (4)

    where K is a kernel function and \(h_n\) is the bandwidth.

  • Step (ii): Leading eigenvector estimation For each \(x\in G\), the eigenvector \(v(\hat{M}_n(x))\) corresponding to the simple maximal eigenvalue \(\lambda (\hat{M}_n(x))\) is calculated. This quantity is an estimator of the true unknown eigenvector v(M(x)) of M(x) corresponding to the simple maximal eigenvalue \(\lambda (M(x))\) under certain conditions on M(x).

  • Step (iii): Integral curve estimation We estimate \(x(t), t\ge 0,\) starting at a fixed known point \(a\in G\) driven by the vector field \(v(M(x)), x\in G,\) by a plug-in estimator \(\hat{X}_n(t), t\ge 0,\) which is a solution of the ODE

    $$\begin{aligned} \frac{d\hat{X}_n(t)}{dt}=v(\hat{M}_n(\hat{X}_n(t))), t\ge 0, \quad \hat{X}_n(0)=a \end{aligned}$$
    (5)

    or equivalently of the integral equation \( \hat{X}_n(t)=a+\int _0^t v(\hat{M}_n(\hat{X}_n(s)))ds. \) In practice this ODE is solved numerically; see Sect. 5.

In Step (i), isotropic kernel smoothing prevents diffusion tensors outside white matter tract regions from exerting an influence on tensor characteristics. Near tract boundaries, the bandwidth can be chosen small enough that diffusion tensors outside the tract region exert little influence on the averaging operation.

Step (ii) depends on the existence of a single, unambiguous leading eigenvector v(M(x)) that represents the principal direction of water diffusion at \(x\in G\). However, in DTI, it is common to have multiple distinct water diffusion directions at x; this especially occurs at locations where distinct fibers cross each other. We first identify these locations through a statistical test based on the difference between the maximal and the next to maximal eigenvalues of the tensor field. Asymptotical null distribution of this test statistic is normal. The test rejects the null hypothesis of one single unambiguous leading eigenvalue for small values of the test statistic. These locations are referred to as branching points in the fiber trajectory since they suggest locations where fibers diverge or cross.

At these branching points, we modify model (2) so that the observations Y(x) arise from a mixture of two underlying tensors \(M^{(1)}(x)\) and \(M^{(2)}(x)\), which have the same simple maximal eigenvalue but different leading eigenvectors \(v(M^{(1)}(x))\) and \(v(M^{(2)}(x))\):

$$\begin{aligned} {Y}(x)= B(\pi \mathbf{M}^{(1)}(x)+(1-\pi )\mathbf{M}^{(2)}(x))I_m^*+{\Sigma }^{1/2}(x){\Xi }_x. \end{aligned}$$
(6)

The mixing coefficient \(\pi \) determines the relative contributions of \(M^{(1)}(x)\) and \(M^{(2)}(x)\) to Y(x). A variety of standard clustering techniques can be applied to estimate \(M^{(1)}(x)\) and \(M^{(2)}(x)\) as well as \(\pi \). Below, we use k-means clustering with 2 clusters performed on observations \(Y(X_j), j=1,\dots ,n,\) within a local neighborhood around x, and set \(\pi \) to a constant 0.5. The neighborhood is defined to be the set of locations surrounding x that influence the smoothing of M(x), as determined by the tensor smoothing kernel K and the associated bandwidth \(h_n\): see Eq. (4). A detailed description of this procedure is in Sect. 5.

During the numerical estimation of the fiber trajectory, if any location \(\hat{X}_n(t)\) is determined to be a branching point, trajectory tracing halts there, and two new integral curve tracings are initiated from the branching point, one each along directions \(v(M^{(1)}(x))\) and \(v(M^{(2)}(x))\). After this process terminates, the final answer for the estimated trajectory initiating from the starting point a consists of the collection of \(\hat{X}_n(t)\) estimators that represent trajectory segments running between a, branching points, and terminal points. This approach allows us to deal with the common case of branching points while maintaining theoretically rigorous estimation of integral curves over fiber segments in between them.

4 Foundations for main results

In what follows, for a number, a vector or a tensor w we denote the sum of its squared components as \(|w|^2\). For a scalar field, a vector field or a tensor field w we denote the tensor of derivatives of its components by \(\nabla w\). More precisely, for a function \(w: \mathbb {R}^d\rightarrow \mathbb {R}\) the components of the vector \(\nabla w(x)\) are \({\partial w(x)}/{\partial x_k}, k=1,\dots ,d\). For a vector field \(w: \mathbb {R}^{d^2}\rightarrow \mathbb {R}^d\) the components of the vector \(\nabla w(M)\) are \({\partial w_j(M)}/{\partial M_{kl}}, j, k, l = 1,\dots ,d\), so \(\nabla w\) is a \(d\times d^2\) tensor. Somewhat opposite, for a tensor field \(w: \mathbb {R}^{d}\rightarrow \mathbb {R}^{d^2}\) the components of the vector \(\nabla w(x)\) are \({\partial w_{kl}(x)}/{\partial x_{j}}, j, k, l = 1,\dots ,d\), so \(\nabla w\) is a \(d^2\times d\) tensor. The Kroneker symbol is \(\delta _{kl}=1\) for \(k=l\) and 0 for \(k\ne l\).

The following conditions are required:

  1. (A1)

    G is a bounded open set in \(\mathbb {R}^d\) with Lebesgue measure 1. It contains the support of the twice continuously differentiable everywhere symmetric positive definite tensor field \(M: \mathbb {R}^d\rightarrow \mathbb {R}^{d^2}\). Moreover, \(M(\cdot )\) has the simple eigenvalues everywhere in its support (See Sect. 5 for a relaxation of this requirement).

  2. (A2)

    The initial point a is inside of the support of \(M(\cdot )\).

  3. (A3)

    There exists a number \(T>0\) such that for all \(t_{1}, t_{2}\in (0, T)\) with \(t_1\ne t_2,\) \(x(t_1)\ne x(t_2)\).

  4. (A4)

    Locations \(\{X_j, j\ge 1\}\) are independent uniformly distributed in G.

  5. (A5)

    We observe \( \{(X_j, {Y}_{i}(X_j)), i=1,\dots ,m, j=1,\dots ,n\}, \) obeying the model \( {Y}(X_j)=B\mathbf{M}(X_j)I_m+{\Sigma }^{1/2}(X_j){\Xi }_j \) with a fixed non-random known real-valued \(N\times d_0\) tensor B, an unknown continuous on G symmetric positive definite \(N\times N\) tensor field \({\Sigma }: \mathbb {R}^d\rightarrow \mathbb {R}^{N^2},\) and unobservable random \(N\times m\) tensors \({\Xi }_j, j=1,\dots ,n\). Recall \(N\ge d_0\). Additionally, we assume that \(B^*B\) is invertible and \({\mathbb {E}}{\Sigma }_{kl}^4(X_1)<\infty , 1\le k, l\le N\).

  6. (A6)

    The columns of random noise matrices \({\Xi }_j, j\ge 1,\) are i.i.d. as \(\Xi \) and independent of locations. Additionally, components of the matrix \(\Xi \) satisfy \({\mathbb {E}}{\Xi }_{ki}=0,\) \({\mathbb {E}}{\Xi }_{ki}{\Xi }_{li}=\delta _{kl},\) and \({\mathbb {E}}{\Xi }^4_{ki}<\infty \) for all \(i=1,\dots ,m, 1\le k, l\le N\).

  7. (A7)

    The kernel K is nonnegative and twice continuously differentiable on its bounded support. Moreover, \(\int _{\mathbb {R}^d} K(x)dx=1, \int _{\mathbb {R}^d} xK(x)dx=0.\)

  8. (A8)

    The bandwidth \(h_n\) satisfies the condition \(\ nh_n^{d+3}\rightarrow \beta >0\) as \(n\rightarrow \infty \), where \(\beta \) is a known fixed number.

Condition (A1) requires the region G to be a locally contiguous region of the brain.

Conditions (A1) and (A2) guarantee that a unique solution \(x(t), t\in [0, T],\) of (1) exists and stays inside G; see formula (9) below. Condition (A1) can be relaxed to assume that \(M(\cdot )\) has simple eigenvalues in a neighborhood of a that contains the curve \(x(t), t\in [0, T]\). For more details on existence, uniqueness, and smoothness of tensor fields and the associated eigenvector fields see Kato (1980).

Condition (A3) prohibits cycles in the integral curve. This is not restrictive; when a cycle is detected, one needs to estimate the integral curve over just one period.

Analogous versions of the main results can be proven when condition (A4) is changed to allow diffusion tensor measurements arranged in a non-random, regular grid of locations as is typical in practice. Furthermore, the typical number of locations n in a DTI data set is on the order of hundreds of thousands or millions; for sample sizes this large, a regular grid of locations is fairly well approximated by uniform i.i.d. locations.

Condition (A6) means that noise is determined independently at each location. Given the physics of MRI acquisition, this assumption may be unrealistic. But this assumption is typical for the state of the art in diffusion MRI; it is built into the near-ubiquitous Rician noise model for example. Accounting for spatially correlated noise structures in theoretical models of DTI will require methodological advances that are beyond the scope of the current study.

Condition (A6) also requires that the noise is white: zero-mean and with no correlations among the diffusion tensor entries. Previous researchers have noted that the popular Rician noise model for DTI is well approximated by such a white noise model in the event that the ratio of Rician model’s mean to standard deviation is moderate to large. Because this is typically the case in real-world DTI studies, our white noise model is a realistic representation of DTI noise; see Zhu et al. (2007) and references therein.

If the second moments of K are finite, \(\nabla K\) and \(\nabla ^2 K\) are uniformly bounded, and the functions \(\Lambda _2\) and \(\Lambda _4\) defined in the proof of Theorem 1 are integrable, then condition (A7) can be relaxed to accommodate them, even if their support is infinite. For instance, this is the case for Gaussian kernels.

Finally, note that formula (3) can be rewritten as

$$\begin{aligned} \tilde{\mathbf{M}}(X_j)=\mathbf{M}(X_j)+{\varvec{\Gamma }}_{ j}, \quad {\varvec{\Gamma }}_{j}=\frac{1}{m} (B^*B)^{-1}B^*{\Sigma }^{1/2}(X_j){\Xi }_jI_m,\quad j\ge 1, \end{aligned}$$
(7)

where \({\varvec{\Gamma }}_j\) denotes a \(d_0\)-vector representation of a random tensor in \(\mathbb {R}^{d^2}\), \(j\ge 1\). Note that due to condition (A6) random tensors \({\varvec{\Gamma }}_j, j\ge 1,\) are i.i.d. and we have for all \(j\ge 1\), \({\mathbb {E}}{\varvec{\Gamma }}_{j}=0\) and

$$\begin{aligned} {\mathbb {E}}({\varvec{\Gamma }}_{j}{\varvec{\Gamma }}_{j}^*|X_j)= & {} \frac{1}{m^2} (B^*B)^{-1}B^*{\mathbb {E}}[{\varvec{\Sigma }}^{1/2}(X_j){\varvec{\Xi }}_1 I_mI_m^*{\varvec{\Xi }}_1({\Sigma }^{1/2}(X_j))^*]B(B^*B)^{-1} \\= & {} \frac{1}{m}(B^*B)^{-1}B^*{\varvec{\Sigma }}(X_j)B(B^*B)^{-1}=:\Sigma _{\Gamma }(X_j), \end{aligned}$$

where \(\Sigma _{\Gamma }: \mathbb {R}^d\rightarrow \mathbb {R}^{d_0^2}\) is a tensor field. We remark that if the matrix B is a square matrix, i.e. \(N=d_0\), and it is invertible then we can simplify \(\Sigma (\cdot )=\frac{1}{m} (B^*{\Sigma }(\cdot )B)^{-1}\).

5 Main results

First, let us introduce lemmas that are required to prove the key theoretical result.

Lemma 1

Suppose conditions (A1)–(A8) hold. Then \( {\mathbb {E}}\sup _{x\in \mathbb {R}^d}|\hat{M}_n(x)-M(x)|^2\le \frac{C}{nh_n^{d+2}} \) for sufficiently large n with a finite constant C.

Consequently, we have \( \sup _{x\in \mathbb {R}^d}|\hat{M}_n(x)-M(x)|\rightarrow ^P 0\quad \mathrm{as}\quad n\rightarrow \infty . \)

Lemma 2

Suppose conditions (A1)–(A8) hold. Then \( \sup _{x\in \mathbb {R}^d}|\nabla \hat{M}_n(x)-\nabla M(x)|\rightarrow ^P 0\) as \(n\rightarrow \infty . \)

Lemma 3

Suppose conditions (A1)–(A8) hold. Then \( \sup _{t\in [0, T]}|\hat{X}_n(t)-x(t)|\rightarrow ^P 0\) as \(n\rightarrow \infty . \)

Lemma 4

Suppose conditions (A1)–(A8) hold. Then \(\hat{M}_n(x)\) is symmetric for all \(x\in G\) and all n. Moreover, \( P(\hat{M}_n(x)\ \mathrm{is}\ \mathrm{positive}\ \mathrm{definite}\ \mathrm{for}\ \mathrm{all}\ x\in G)\rightarrow 1 \) as \(n\rightarrow \infty \).

In order to formulate the main result of this paper we need the following definitions. As in the work of Koltchinskii et al. (2007) define for \( u\in \mathbb {R}^d\)

$$\begin{aligned} \Psi (u)=\int _{\mathbb {R}^d} K(z)K(z+u)dz,\quad \psi (u)=\int _{\mathbb {R}} \Psi (\tau u)d\tau . \end{aligned}$$

Let \(U: \mathbb {R}^2\rightarrow \mathbb {R}^{d^2}\) be the Green’s function, defined as the solution of the following PDE

$$\begin{aligned} \frac{\partial U(t,s)}{\partial t}=\nabla v(M(x(t)))\nabla M(x(t))U(t,s),\quad U(s,s)={\mathbb I}. \end{aligned}$$

For a vector field \(w: \mathbb {R}^{d^2}\rightarrow \mathbb {R}^d\) let \(\tilde{\nabla }w\) be the \(d\times d_0\) tensor of its derivatives \({\partial w}/{\partial \mathbf{M}_i}, i=1,\dots ,d_0\). For a \(d^2\times d^2\) tensor A and vector \(z\in \mathbb {R}^d\) let \(\langle Az, z\rangle \) be the \(d^2\)-vector with components \( \langle Az, z\rangle _{kl}=\sum _{q,r=1}^d A_{kl,qr}z_qz_r,\ 1\le k, l\le d. \)

The main theorem follows.

Theorem 1

Suppose conditions (A1)–(A8) hold. Then the sequence of stochastic processes

$$\begin{aligned} \sqrt{nh_n^{d-1}}(\hat{X}_n(t)-x(t)),\quad t\in [0, T], \end{aligned}$$

converges weakly in the space of \({\mathbb {R}}^d\)-valued continuous functions on [0, T] to the Gaussian process \(\mathcal{G}(t), t\in [0, T],\) with mean

$$\begin{aligned} \mu _{\beta }(t)=0.5\sqrt{\beta }\int _0^t\int _{\mathbb {R}^d} U(t,s)\nabla v(M(x(s)))K(z)\langle \nabla ^2 M(x(s))z,z\rangle dz ds \end{aligned}$$

and covariance

$$\begin{aligned} C(t_1, t_2)= & {} \int _0^{t_1\wedge t_2}\psi (v(M(x(s))))U(t_1,s){\tilde{\nabla }} v(M(x(s))) \\&\times \, H[\mathbf{M}(x(s))\mathbf{M}^*(x(s))+\Sigma _{\Gamma }(x(s))]H\tilde{\nabla }v(M(x(s)))^*U^*(t_2,s) ds. \end{aligned}$$

Notice that \(\mu _{\beta }(t), t\ge 0,\) satisfies the following ODE

$$\begin{aligned} \frac{d\mu _{\beta }(t)}{dt}= & {} \nabla v(M(x(t)))\nabla M(x(t))\mu _{\beta }(t) \\&+\,0.5\sqrt{\beta }\nabla v(M(x(t)))\int _{\mathbb {R}^d}K(z)\langle \nabla ^2 M(x(t))z, z\rangle dz,\quad \mu _{\beta }(0)=0. \end{aligned}$$

By the same token \(C(t,t), t\ge 0,\) satisfies the following ODE: \(C(0,0)=0\),

$$\begin{aligned} \frac{dC(t,t)}{dt}= & {} \nabla v(M(x(t)))\nabla M(x(t)) C(t,t)+ C(t,t)(\nabla v(M(x(t)))\nabla M(x(t)))^* \\&+\,\psi (v(M(x(t))))\tilde{\nabla }v(M(x(t)))H[\mathbf{M}(x(t)) \mathbf{M}^*(x(t))\\&+\,\Sigma _{\Gamma }(x(t))]H\tilde{\nabla }v(M(x(t)))^*. \end{aligned}$$

Thus, Theorem 1 allows us to track the estimated curve, the mean function, and the covariance function in small steps sequentially and simultaneously, and construct confidence ellipsoids along the curve. This will be illustrated in Sects. 7 and 8.

Sketch of proof The proof of this result, provided in the Appendix, has several steps. First, we show that \(\hat{X}_n(t)-x(t), t\in [0, T],\) is approximated by a process \(Z_n(t), t\in [0, T],\) which is the solution of a linear integral equation and can be explicitly written as a linear operator transformation of \(\hat{M}_n(\cdot )-M(\cdot )\). And \(Z_n(t), t\in [0, T],\) happens to be a sum of i.i.d. terms. Second, we find the asymptotical mean and covariance of \(Z_n\). Finally, we show that the sequence \(\sqrt{nh_n^{d-1}}(Z_n(t)-{\mathbb {E}}Z_n(t)), t\in [0, T],\) converges to a Gaussian process due to Lyapunov’s condition and asymptotical equicontinuity.

Connectivity tests This result allows us to apply Theorem 2 from Koltchinskii et al. (2007) to perform tests of connectivity that are commonly of interest in studies of DTI data: given a starting location a, the test is concerned with whether the integral curve originating at a passes through a given subregion in G. We formulate this test in terms of estimating the squared Euclidean distance between the integral curve and a one-point region \(r\in G\); also see Koltchinskii and Sakhanenko (2009).

Corollary 1

Suppose conditions (A1)–(A8) hold. Moreover, suppose there exists the unique point \(\tau \in (0, T)\) such that \(\min _{t\in [0, T]}|x(t)-r|^2=|x(\tau )-r|^2\). If \(x(\tau )\ne r\) then the sequence \( \sqrt{nh_n^{d-1}}\bigg [\min _{t\in [0, T]}|{\hat{X}}_n(t)-r|^2-|x(\tau )-r|^2\bigg ] \) is asymptotically normal with mean \(2\mu _{\beta }(\tau )^*(x(\tau )-r)\) and variance \(4(x(\tau )-r)^*C(\tau , \tau )(x(\tau )-r)\). If \(x(\tau )= r\) then the sequence \(nh_n^{d-1}\min _{t\in [0, T]}|{\hat{X}}_n(t)-r|^2\) converges in distribution to a random variable \(|Z|^2-(v(M(x(\tau )))^*Z)^2\), where Z is a normal random variable with mean \(\mu _{\beta }(\tau )\) and variance \(C(\tau , \tau )\).

This corollary can be used to test whether an integral curve starting at a point \(a\in G\) passes closely by the point r. See Koltchinskii and Sakhanenko (2009) for details and proofs.

5.1 Implementation

The complete algorithm for obtaining integral curve estimator together with confidence ellipsoids has the following steps.

  1. 1.

    Initialize \(q=0, t_q=0, \hat{X}_n(t_0)=a, \mu _{\beta }(t_0)=0, C(t_0,t_0)=0\).

  2. 2.

    Track the estimated integral curve using Euler’s method, given a fixed \(\delta >0\) and small time steps \(t_{q}=q\delta , q=0,1,2,\dots \) Footnote 1:

    $$\begin{aligned} \hat{X}_n(t_q)\approx \hat{X}_n(t_{q-1})+\delta v(\hat{M}_n(\hat{X}_n(t_{q-1}))),\quad \hat{X}_n(0)=a. \end{aligned}$$
  3. 3.

    Approximate \(\nabla ^2\hat{M}_{n}(x)\), \(\nabla \hat{M}_{n}(x)\) and \(\hat{\Sigma }_n(x)\) as follows:

    $$\begin{aligned} \tilde{\Sigma }_{\Gamma , n}(X_j)= & {} \frac{1}{m}\sum _{i=1}^m(Y_{i}(X_j)-B\tilde{\mathbf{M}}(X_j))(Y_{i}(X_j)-B\tilde{\mathbf{M}}(X_j))^*,\quad j=1,\dots ,n, \\ \hat{\Sigma }_{n}(x)= & {} \frac{1}{nh_n^d}\sum _{j=1}^n K((x-X_j)/h_n)\tilde{\Sigma }_{\Gamma , n}(X_j), \quad x\in G, \\ \nabla \hat{M}_{n}(x)= & {} \frac{1}{n\tilde{h}_n^{d+1}}\sum _{j=1}^n \nabla K\bigg (\frac{x-X_j}{\tilde{h}_n}\bigg )\tilde{M}(X_j), \quad x\in G,\quad n\tilde{h}_n^{d+1}\rightarrow \infty , \\ \nabla ^2\hat{M}_{n}(x)= & {} \frac{1}{n\tilde{\tilde{h}}_n^{d+2}}\sum _{j=1}^n \nabla ^2 K\bigg (\frac{x-X_j}{\tilde{\tilde{h}}_n}\bigg )\tilde{M}(X_j), \quad x\in G,\quad n\tilde{\tilde{h}}_n^{d+1}\rightarrow \infty . \end{aligned}$$

    And, approximate \(\nabla v(M(x))\) by \(\nabla v(\hat{M}_n(x))\) using the relationship (9) in the proof of Lemma 3, i.e.

    $$\begin{aligned} \frac{\partial v_p(\hat{M}_n(x))}{\partial M_{kl}}=(1-0.5\delta _{kl})&\bigg [ (\lambda (\hat{M}_n(x))I_d-\hat{M}_n(x))^+_{pk}v_l(\hat{M}_n(x)) \\&+(\lambda (\hat{M}_n(x))I_d\!-\!\hat{M}_n(x))^+_{pl}v_k(\hat{M}_n(x)) \bigg ],\quad 1\!\le \! p, k, l\!\le \! d, \end{aligned}$$

    where \(A^+\) stands for the Moore–Penrose inverse of a matrix A.

  4. 4.

    Approximate \(\mu _{\beta }(t_q), q\ge 1,\) as

    $$\begin{aligned} \hat{\mu }_{\beta }(t_q)\approx & {} \hat{\mu }_{\beta }(t_{q-1})+\delta \nabla v(\hat{M}_n(\hat{X}_n(t_{q-1})))\nabla \hat{M}_n(\hat{X}_n(t_{q-1}))\hat{\mu }_{\beta }(t_{q-1}) \\&+\,0.5\delta \sqrt{\beta }\nabla v(\hat{M}_n(\hat{X}_n(t_{q-1})))\int _{\mathbb {R}^d}K(z)\langle \nabla ^2\hat{M}_n(\hat{X}_n(t_{q-1}))z, z\rangle dz. \end{aligned}$$
  5. 5.

    Approximate \(C(t_q,t_q)\) as

    $$\begin{aligned} \hat{C}(t_q, t_q)\approx & {} \hat{C}(t_{q-1}, t_{q-1})+\delta \nabla v(\hat{M}_n(\hat{X}_n(t_{q-1})))\nabla \hat{M}_n(\hat{X}_n(t_{q-1}))\hat{C}(t_{q-1},t_{q-1}) \\&+\,\delta \hat{C}(t_{q-1},t_{q-1})\nabla \hat{M}_n(\hat{X}_n(t_{q-1}))^*\nabla v(\hat{M}_n(\hat{X}_n(t_{q-1})))^* \\&+\,\delta \psi (v(\hat{M}_n(\hat{X}_n(t_{q-1})))) \tilde{\nabla }v(\hat{M}_n(\hat{X}_n(t_{q-1}))) \\&\times \, [\hat{\mathbf{M}}_n(\hat{X}_n(t_{q-1}))\hat{\mathbf{M}}_n(\hat{X}_n(t_{q-1}))+\Sigma _{\Gamma }(\hat{X}_n(t_{q-1}))] \\&\times \, \tilde{\nabla }v(\hat{M}_n(\hat{X}_n(t_{q-1})))^*,\quad q\ge 1. \end{aligned}$$
  6. 6.

    Approximate the \(100(1-\alpha )\%\) confidence ellipsoid for \(x(t_q), q\ge 1,\) as

    $$\begin{aligned} P\bigg \{|\hat{C}(t_q,t_q)^{-1/2}(\sqrt{nh_n^{d-1}}(\hat{X}_n(t_q)-x(t_q))-\hat{\mu }_{\beta }(t_q))|\le R_{\alpha }\bigg \}\approx 1-\alpha , \end{aligned}$$

    where \(P(|Z|\le R_{\alpha })=1-\alpha \) for a standard normal vector Z in \({\mathbb R}^d\).

  7. 7.

    Repeat steps 2–6 until \(t_q\) reaches T.

5.2 Kernel smoothing bandwidth selection

Finally, we remark on how to select \(\beta \) in the bandwidth \(h_n=(\beta /n)^{1/(d+3)}\). One approach is to estimate the \(\beta \) that minimizes the mean integrated squared error (MISE) between the estimated and the true integral curves. MISE is asymptotically equivalent to the following expression

$$\begin{aligned} \mathrm{MISE}:= & {} {\mathbb {E}}\int _0^T (\hat{X}_n(t)-x(t))^*(\hat{X}_n(t)-x(t)) dt \\\approx & {} n^{-4/(d+3)}\bigg [\beta ^{4/(d+3)}\int _0^T \mu _1(t)^*\mu _1(t)dt + \beta ^{-(d-1)/(d+3)}\int _0^T \mathrm{tr} C(t, t)dt\bigg ], \end{aligned}$$

which is minimized by \(\beta =0.25(d-1)\int _0^T \mathrm{tr} C(t, t)dt\bigg [\int _0^T \mu _1(t)^*\mu _1(t)dt\bigg ]^{-1}\). An interleaved estimation procedure for \(\beta \) would thus consist of starting with an initial \(\beta \) estimate, estimating \(\mu _1\) and C accordingly, re-estimating \(\beta \) based on these \(\mu _1\) and C, and so on.

5.3 Modeling locations with multiple fiber directions

Note that the covariance of the limiting Gaussian process in Theorem 1 goes to infinity as the second largest eigenvalue of \(M(\cdot )\) (call this \(\phi (M(\cdot ))\)), approaches the largest eigenvalue \(\lambda (M(\cdot ))\). More precisely, some components of the gradient \(\tilde{\mathbf{\nabla }}v(M(x))\) in the integrand of \(C(t_1, t_2), t_1, t_2\in [0, T],\) are proportional to \((\lambda (M(x))-\phi (M(x)))^{-2}\) for a point x on the curve \(x(t), t\in [0, T]\). Our approach is to devise a theoretically grounded test for this situation, and when it occurs we decompose the tensor \(M(\cdot )\) into components, each of which has a dominant leading eigenvalue.

Branching point detection We develop a test for branching based on the difference between the two largest eigenvalues of the estimated tensor field \(\hat{M}_n(\cdot )\). Let w(A) be the eigenvector corresponding to the second largest eigenvalue \(\phi (A)\) of a \(d\times d\) matrix A. We utilize the following result.

Proposition 1

Suppose conditions (A1)–(A8) hold. For any fixed \(x\in G\)

$$\begin{aligned} \sqrt{nh_n^d}\bigg ((\lambda (\hat{M}_n(x)) -\lambda (M(x)))-(\phi (\hat{M}_n(x))-\phi (M(x)))\bigg ) \end{aligned}$$

is asymptotically normal with mean 0 and variance \(\sigma ^2_{\lambda }(x)+\sigma ^2_{\phi }(x)-2\sigma _{\lambda , \phi }(x)\), where

$$\begin{aligned} \sigma ^2_{\lambda }(x)= & {} \int K^2(u) du {\varvec{\Delta }}_v(x)^* H [\mathbf{M}(x)\mathbf{M}^*(x)+{\Sigma }_{\Gamma }(x)] H{\varvec{\Delta }}_v(x), \\ \sigma ^2_{\phi }(x)= & {} \int K^2(u) du {\varvec{\Delta }}_w^*(x) H [\mathbf{M}(x)\mathbf{M}^*(x)+{\Sigma }_{\Gamma }(x)] H{\varvec{\Delta }}_w(x), \\ \sigma _{\lambda , \phi }(x)= & {} \int K^2(u) du {\varvec{\Delta }}_v^*(x) H [\mathbf{M}(x)\mathbf{M}^*(x)+{\Sigma }_{\Gamma }(x)] H{\varvec{\Delta }}_w(x) \end{aligned}$$

with \({\varvec{\Delta }}_v\) being a vector representation of the matrix \(\Delta _v\) with entries \(\Delta _{v, ij}=(2-\delta _{ij})v_i({M})v_j({M})\) and \({\varvec{\Delta }}_w\) being a vector representation of the matrix \(\Delta _w\) with entries \(\Delta _{w, ij}=(2-\delta _{ij})w_i({M})w_j({M})\).

Combining this result with Theorem 1 by means of the delta method allows us to construct the following test. We reject the null hypothesis of no branching at a location \(\hat{X}_n(t_{q+1}), q\ge 1,\) if

$$\begin{aligned}&\lambda (\hat{M}_n(\hat{X}_n(t_{q+1}))) -\phi (\hat{M}_n(\hat{X}_n(t_{q+1})))< \lambda (\hat{M}_n(\hat{X}_n(t_{q}))) -\phi (\hat{M}_n(\hat{X}_n(t_{q}))) \\&\quad -\varepsilon _{\alpha }(nh_n^d)^{-1/2}[\hat{\sigma }^2_{\lambda } (\hat{X}_n(t_q)) +\hat{\sigma }^2_{\phi }(\hat{X}_n(t_q))-2\hat{\sigma }_{\lambda , \phi }(\hat{X}_n(t_q))]^{1/2}, \end{aligned}$$

where \(\hat{\sigma }^2_{\lambda }, \hat{\sigma }^2_{\phi }\), and \(\hat{\sigma }_{\lambda , \phi }\) are obtained from \(\sigma ^2_{\lambda }, \sigma ^2_{\phi }\), and \(\sigma _{\lambda , \phi }\) using the estimators \(\hat{M}_n\) and \(\hat{\Sigma }_n\) instead of M and \(\Sigma _{\Gamma }\) and \(P(0<Z<\varepsilon _{\alpha })=\alpha \) for a standard normal variable Z.

Tensor decomposition at branching points Whenever a branching point is detected at a location x, we use 2-means clustering method to group the raw DTI measurements \(Y(X_j), j=1,\dots ,n,\) for \(X_j\) that are within the averaging window of the smoothing kernel K into clusters, using the Euclidean distance between \(Y(X_j)\) as a measure of their similarity. Assuming that the branching point consists of the confluence of two distinct fiber orientations, the two clusters are expected to correspond to those two orientations respectively. The two diffusion tensors \(\mathbf{M}^{(1)}(x)\) and \(\mathbf{M}^{(2)}(x)\) are estimated from the two clusters individually. We trace two new integral curves beginning at x that initially move along the \(v(\mathbf{M}^{(1)}(x))\) and \(v(\mathbf{M}^{(2)}(x))\) directions, and repeat the branching test where these two curves arrive.

We apply this to the synthetic tensor field in Fig. 2. This is a linear combination of a circular tensor field (from the example in Sect. 7) with a circle radius of 0.25 and a horizontal tensor field in the strip \(|x_2|<0.05\) with the same maximal eigenvalues as the circular tensor field. We use a mixture model with \(\pi =0.5\) for the locations where the tensor fields overlap. Noise is added to the raw measurements Y with the matrix \(\Sigma =[1, 0.8, 0.8; 0.8, 1, 0.8; 0.8, 0.8, 1]\). The method successfully identifies the branching point and traces both fibers.

Fig. 2
figure 2

A test for branching points and a mixture model for diffusion tensors at such points can be used to apply the integral curve tracing method to locations where fibers diverge or cross. The point where the semi-circular and horizontal tensor regions overlap is successfully detected as a branching point, and separate integral curves are traced along both trajectories. a The \(2\times 2\) tensor field \(\tilde{M}\) is visualized through ellipses. Here \(m=8, n=4900, \delta =0.02, \beta =0.001\). b FA map is overlaid with estimated fiber trajectories and 95 % confidence ellipses based on our method and 2-means clustering near the branching point. The initial point is (\(0.1, -0.2291\)). We use \(\alpha =0.1\) for testing. (Color figure online)

Full size image

6 Theoretical comparison of \(\hat{X}_n\) with Koltchinskii et al. (2007) estimator

Here we compare our estimator with that of the most similar fiber tracing approach to ours, due to Koltchinskii et al. (2007). They estimate fiber trajectories with closed-form uncertainty estimates, given noise-corrupted leading eigenvectors without reference to the raw DTI measurements. That is, they assume input data \((X_j, V_j), j=1,\dots ,n,\) where \(V_j=v(M(X_j))+\xi _j\) is the leading eigenvector direction at \(X_j\) that has been corrupted with i.i.d. noise variables \(\xi _j\) drawn from a distribution with mean zero and covariance \(\Sigma _{K}\). Given noise of the form \(\xi _j=\Sigma _K(X_j)^{1/2}\eta _j\) with i.i.d., mean 0, variance 1, random vectors \(\eta _j, j=1,\dots ,n\) that are also drawn independently at each \(X_j\), and given conditions similar to (A1)–(A8), the difference between their estimator \(\hat{X}_n^{K}(t), t\in [0, T],\) and the true integral curve \(x(t), t\in [0, T],\) normalized by \(\sqrt{nh_n^{d-1}}\) converges weakly in the space of \({\mathbb {R}}^d\)-valued continuous functions on [0, T] to the Gaussian process \(\mathcal{G}^{K}(t), t\in [0, T].\) The mean of this process is

$$\begin{aligned} \mu ^{K}_{\beta }(t)=0.5\sqrt{\beta }\int _0^t\int _{\mathbb {R}^d} U(t,s)K(z)\langle \frac{\partial ^2}{\partial x^2}v(x(s))z,z\rangle dz ds \end{aligned}$$

and the covariance is

$$\begin{aligned} C^{K}(t_1, t_2)= & {} \int _0^{t_1\wedge t_2}\psi (v(M(x(s))))U(t_1,s)[v(M(x(s)))v^*(M(x(s))) \\&+\,\Sigma _K(x(s))]U^*(t_2,s) ds. \end{aligned}$$

Next, we show the three specific simplifications that must be made to our tensor and noise models that are required to reduce it down to the special case covered by the Koltchinskii et al. (2007) estimator.

The first required simplification is to model the noise applied to M(x) as a first-order perturbation that moves M(x) within a very local neighborhood. Consider the following first order approximation for an observation \( v(M(X_j)+\Gamma _j)=v(M(X_j))+\tilde{\nabla }v(M(X_j))H{\varvec{\Gamma }}_j+ \alpha _1(|\Gamma _j|^2), \) where the vector-function \(\alpha _1(u)/|u|^2, u\in \mathbb {R}^d,\) is bounded in a small neighborhood around 0. Note that the covariance matrix of the linear term \(v(M(X_j))+\tilde{\nabla }v(M(X_j))H{\varvec{\Gamma }}_j\) is \(\tilde{\nabla }v(M(X_j))H\Sigma _{\Gamma }H\tilde{\nabla }v(M(X_j))^*\); this covariance matrix is required to be the same as \(\Sigma _K(X_j)\) for the measurement to comply with the Koltchinskii et al. (2007) model.

The second required simplification is to assume that we have almost a constant gradient of v with respect to M along the integral curve. Specifically, the second derivatives of v with respect to x must be simplified by the following: \( \frac{\partial ^2}{\partial x^2}v(M(x))=\nabla ^2 v(M(x))\nabla M(x)\nabla M(x)+\nabla v(M(x))\nabla ^2 M(x) =\nabla v(M(x))\nabla ^2 M(x)(1+\alpha _2(x)), \) where the vector function \(\alpha _2(x), x\in \mathbb {R}^d,\) is continuous at 0, and \(\alpha _2(0)=0\).

The third required simplification is to assume that v is almost linear with respect to M, i.e. \( v(M(x))=\tilde{\nabla }v(M(x))H\mathbf{M}(x)+\alpha _1(|M|^2(x)), x\in G. \) Putting these simplifications together, for all \(t\in [0, T]\) and \(z\in \mathbb {R}^d\) we have \(v(M(x(t)))\approx \tilde{\nabla }v(M(x(t)))H\mathbf{M}(x(t))\) and \(\nabla v(M(x(t)))\langle \nabla ^2 M(x(t))z, z\rangle \approx \langle \frac{\partial ^2}{\partial x^2}v(M(x(t)))z, z \rangle \).

Through these three simplifications we arrive at the model of Koltchinskii et al. (2007), which can be thought of as a very restricted special case of our model. To apply the Koltchinskii model, both the noise \(\Gamma \) and the tensor M must be relatively small along the integral curve and \(\nabla v(M)\) should be nearly fixed as M varies along the curve. These assumptions are unrealistic for real-world DTI data; this may explain why the Koltchinskii estimator fails to accurately follow fiber trajectories in the simulated examples in the next section.

7 Synthetic examples

7.1 Comparison with Koltchinskii et al. (2007) approach

We first provide two synthetic examples that compare how our estimator and that of Koltchinskii et al. (2007) behave when applied to separate cases that do and do not violate the assumptions of the Koltchinskii model. The first example shows a curved trajectory of constant curvature in a tensor field corrupted by noise that violates the assumptions of Koltchinskii et al. (2007). The second example comes close to satisfying this assumption. However, we show that in both cases, our estimator provides integral curve estimators that have similar accuracy compared to the Koltchinskii estimator, but lower covariance.

7.1.1 Circular trajectories

For the first example, we consider a 2D tensor field corresponding to a circular fiber trajectory. Let \(G=[-0.5, 0.5]^2\). Let the true tensor field and the eigenvector corresponding to the maximal eigenvalue be

$$\begin{aligned} \begin{array}{ll} M(x)=\left( \begin{array}{ll} 1+\frac{x_2^2}{x_1^2+x_2^2} &{} \quad \frac{-x_1x_2}{x_1^2+x_2^2}\\ \frac{-x_1x_2}{x_1^2+x_2^2} &{} \quad 1+\frac{x_1^2}{x_1^2+x_2^2}\\ \end{array} \right) ,&{}\quad v(M(x))=\left( \begin{array}{l} \frac{-x_2}{\sqrt{x_1^2+x_2^2}}\\ \frac{x_1}{\sqrt{x_1^2+x_2^2}}\\ \end{array} \right) .\\ \end{array} \end{aligned}$$

The eigenvalues are 2 and 1. The true integral curves are circles centered at the origin. The directions are \(b_1=(1, 0)^*, b_2=(0, 1)^*, b_3=2^{-1/2}(1, 1)^*\), so the design matrix is \(B=[-1, 0, 0; 0, 0, -1; -0.5, -1, -0.5]\). This common type of gradient direction setup is referred to as orthogonal or pyramidal gradient encoding in the DTI literature.

For each random location \(X_j, j=1,\dots ,n,\) we simulate m vectors \(Y_i\in \mathbb {R}^3\) according to the model \(Y_i=BM(X_j)+\Sigma ^{1/2}(X_j)\xi _{j, i}, j=1,\dots ,n, i=1,\dots ,m,\) with independent standard normal 3D vectors \(\xi _{j, i}\) and two choices for \(\Sigma \). The first submodel, \(\Sigma =[1, 0.8, 0.8; 0.8, 1, 0.8; 0.8, 0.8, 1]\), is a constant matrix; the second submodel is \(\Sigma (x)=0.01\mathbf{M(x)}\mathbf{M(x)}^*, x\in G\). In all simulations we use the bandwidth \(h_n=(n/\beta )^{1/5}\) and the standard 2D Gaussian kernel.

Fig. 3
figure 3

The solid black curves with blue confidence ellipsoids correspond to the estimated integral curves using our approach. The solid green curves with cyan confidence ellipsoids correspond to the estimated integral curves using the method of Koltchinskii et al. (2007). The solid red curves are the true integral curves. The initial point is (\(0.1, -0.2291\)). We use a 95 % confidence level. Here \(m=8, n=20^2=400, \delta =0.005, \beta =0.001\). a The matrix \(\Sigma \) is fixed for all the locations. b The matrix \(\Sigma \) is of the second order with respect to the tensor M. (Color figure online)

Full size image

Both methods yield integral curve estimates that are very close to the true curve (Fig. 3). However, the covariances of the Koltchinskii et al. (2007) estimator are much higher than those of our estimator in both submodels. For the first sub-model with a fixed \(\Sigma \), the Euclidean norm of the covariance matrix \(C^K\) is 20–35 times higher than the norm of C along the first third of the curve, then this ratio decreases gradually to 1.2 at the end of the curve. For the second sub-model, the ratio of the norms of \(C^K\) and C is also 20–30 for the first third of the curve and reduces to 5–6 at the end of the curve. This is to be expected since the matrices between U and \(U^*\) in the covariance of the limiting Gaussian processes are \(r^4[\cos ^2 2s, -\sin 4s\sin ^2 2s/16; -\sin 4s\sin ^2 2s/16, \sin ^2 s\sin ^2 2s/4 ]+O(\Sigma _{\Gamma }), s\in [0, T],\) and \([\sin ^2 s, -\sin 2s/2; -\sin 2s/2, \cos ^2 s]+ O(\Sigma _K), s\in [0, T],\) for our and Koltchinskii et al.’s (2007) methods respectively. Both covariance matrices \(\Sigma _{\Gamma }\) and \(\Sigma _K\) are small and \(r=1/4\) for the true integral curve.

7.1.2 Nearly additive vector field noise

For the second example, we attempt to design a tensor field and a noise model that come as close as possible to meeting the additive eigenvector field noise assumption of Koltchinskii et al. (2007), for \(d=3\) and \(G=[0, 1]^3\). It is not difficult to show that there are no special cases for which our tensor field noise model exactly yields the additive eigenvector field noise. Therefore, we start with vectors \(v_1(x)=(-(x_2-0.5), x_1-0.5, 1/(2\pi ))^*, v_2(x)=(x_1-0.5, x_2-0.5, 0)^*, v_3(x)=(x_2-0.5, -(x_1-0.5), 2\pi ((x_1-0.5)^2+(x_2-0.5)^2))^*\). Then let the corresponding unit vectors \(V_1(x), V_2(x), V_3(x)\) be the eigenvectors of M(x) for the corresponding eigenvalues (10, 2, 1). We use an orthogonal gradient encoding with 6 directions: \(b_1=(1, 0, 0)^*\), \(b_2=(0, 1, 0)^*\), \(b_3=(0, 0, 1)^*\), \(b_4=2^{-1/2}(0, 1, 1)^*\), \(b_5=2^{-1/2}(1, 0, 1)^*\), \(b_6=2^{-1/2}(1, 1, 0)^*\).

For each random location \(X_j, j=1,\dots ,n,\) we simulate m vectors \(Y\in \mathbb {R}^6\) according to the model \(Y_i=BM(X_j)+\Sigma ^{1/2}(X_j)\xi _{j, i}, j=1,\dots ,n, i=1,\dots ,m,\) with independent standard normal 6D vectors \(\xi _{j, i}\) and two choices for \(\Sigma \). The first submodel is \(\Sigma =0.01[1,\dots ,1]\in \mathbb {R}^{6^2}\) a constant matrix; the second submodel is \(\Sigma _{\Gamma }(x)=0.01(x_1, 0.1x_1, 0, 0, 0, 0; 0.1x_1, x_1, 0.1x_1, 0, 0, 0; 0, 0.1x_1, x_1, 0, 0, 0; 0, 0, 0, x_2, 0.1x_2, 0; 0, 0, 0, 0.1x_2, x_2, 0; 0, 0, 0, 0, 0, x_3)\) for \(x\in G\). e Koltchinskii et al. (2007) estimator to the perturbed eigenvector fields \(v(\tilde{M}(X_j)), j=1,\dots ,n.\) In all the simulations we use the bandwidth \(h_n=(n/\beta )^{1/6}\) and the standard 3D Gaussian kernel K.

Figure 4 demonstrates that both procedures approximate the true integral curve nicely. Comparing the methods with respect to covariance, our estimator has much tighter confidence ellipsoids than those for the estimator of Koltchinskii et al. (2007). The ratio of the Euclidean norms of the covariance matrices \(C^K\) and C is about 100 along the curve for both submodels. Again, this is expected from the theoretical comparison of covariance expressions similar to those done for the 2D example.

Fig. 4
figure 4

The solid black curves with blue confidence ellipsoids correspond to the estimated integral curves using our approach. The solid green curves with cyan confidence ellipsoids correspond to the estimated integral curves using the method of Koltchinskii et al. (2007). The solid red curves are the true integral curves. The initial point is (0.75, 0.5, 0.25). We use a 95 % confidence level to calculate the confidence ellipsoids. Here \(m=8, n=11^3=1331, \delta =0.005, \beta =0.1\). a The matrix \(\Sigma \) is fixed. b The matrix \(\Sigma \) varies with location. (Color figure online)

Full size image

7.2 Comparison with Behrens et al. (2003) approach

We consider a popular probabilistic tractography approach by Behrens et al. (2003). This approach uses wild bootstrap to obtain a sample of eigenvector directions at each voxel, then applies Monte Carlo Markov chain (MCMC) sampling to those eigenvector direction samples to generate a set of trajectory samples emanating from a given seed location. It is implemented in an open source package of programs known as the FMRIB diffusion toolbox. We use two synthetic examples to illustrate its differences from our approach. The first is a thin, curved trajectory that resembles the letter C. In the second example we mix the letter C with a straight flat trajectory, thus producing a trajectory pattern shaped like the letter Y. These two general patterns are commonly observed in real diffusion MRI scans of the human brain: the corpus callosum is a major inter hemispheric white matter tract, many of whose fibers are shaped like the letter C; and there are many examples of fiber tracts that converge, diverge, or ”kiss,” thus leading to a Y-like splitting of trajectories. We show that in both cases, our method provides better geometrical representations with theoretically well understood statistical properties, using a fixed amount of computation.

FMRIB produces two main outputs: a set of fiber trajectories emanating from a seed location, resulting from its MCMC sampling; and an occupancy image—an image representing how many of those trajectories pass through each voxel in the space of the input image. Our approach provides a different type of output: a mean trajectory and point wise covariance matrices representing possible deviations from that mean. To be fair to FMRIB, we did not wish to calculate a mean trajectory or pointwise covariances from their outputs, since this step could introduce artifacts that were never intended by the authors of FMRIB. Instead, we show our trajectory means and covariances side by side with their trajectory samples for qualitative comparison. We also created p-value maps as introduced in Koltchinskii et al. (2007), and compare those to the FMRIB occupancy images. More precisely, we calculate the p-value of the test of the null hypothesis that a fiber starting at the initial point reaches a point in the slice, using our connectivity tests as in Corollary 1. Then for all points in the slice we visualize their corresponding p-values in color.

For the first example we have \(d=3, G=[0, 1]^3\). We start with the unit vectors parallel to \((x_2, x_1, 0)^*, (-x_1, x_2, 0)^*, (0, 0, x_3)\). Those serve as the eigenvectors of M(x) with the corresponding eigenvalues (10, 2, 1) for locations in G satisfying \(|\sqrt{x_1^2+x_2^2}-0.5|<0.05\) and \(|x_3-0.5|<0.05\). We use the same orthogonal gradient encoding as in the previous example, \(m=1\), and the independent normal vectors \(\xi _j, j=1,\dots ,n\) with means 0 and variances 0.01. We use a regular grid with 50 knots for \(x_1\) and \(x_2\) and 25 knots for \(x_3\). Thus the sample size is \(n=62{,}500\).

Figure 5a shows the eigenvector field calculated at the grid points and projected on one of two horizontal slices that contain the bundle of fibers. The initial point for the tracking procedure is chosen in the first of the two slices. Figure 5b shows our p-value map. Figure 5c and d provide visualizations of the FMRIB occupancy images. The scale for the slice \(z=0.52\) is 100 times higher than the scale for the slice \(z=0.48\) that contains the initial point. Figure 5e shows 400 of the total of 10,000 MCMC tracks emanating from the initial point. Figure 5f provides our estimated trajectory with 95 % confidence ellipsoids along it.

Fig. 5
figure 5

C-template. a Projection of the eigenvector field on the slice \(z=0.48\). b P-value map for slice \(z=0.48\). The initial point is (0.47, 0.01706, 0.48). Here \(\delta =0.02, \beta =0.0001\). c Slice \(z=0.48\). Visualization of how many MCMC tracks terminated at each point. The order is \(10^{-43}.\) d Slice \(z=0.52\). Visualization of how many MCMC tracks terminated at each point. The order is \(10^{-41}.\) e 400 out of 10,000 MCMC tracks. f Our estimator together with pointwise 95 % confidence ellipsoids. (Color figure online)

Full size image

Most of the trajectory samples from FMRIB are short and are concentrated near the initial point. They also deviate substantially outside the plane in which the C-shaped trajectory was defined. The number of trajectory samples—10,000—is provided as a default parameter setting by FMRIB, but there are no theoretically valid reasons to determine an optimal number of samples. Meanwhile, our approach provides theoretically grounded visualizations of the statistical uncertainty of our estimator that conform well to the general shape of the “C” (Fig. 5b, f), and the uncertainty estimates were calculated using closed-form expressions.

To construct the second example we take the tensor from the previous example and mix it with the tensor whose eigenvectors are parallel to \((1, 1, 0)^*, (-1, 1, 0)^*\) and \((0, 0, 1)^*\). The eigenvalues are 10, 2, 1. This second tensor exists only for locations in G such that \(|x_1-x_2|<0.05, x_1>0.32, x_2>0.32, |x_3-0.5|<0.05\). We use the mixing weight \(\pi =0.5\) for the locations where these tensors mix.

Figure 6 has the same sub-figures as Fig. 5. We again observe that MCMC trajectory samples tend to be short and concentrated near the initial point. They trace out the letter C much better than the remaining part of letter Y. The Y pattern is almost non-existent on Fig. 6e, where only one track out of 400 traces the diagonal. It seems to appear on Fig. 6c, while part of the letter C disappears, but the scale is 1/100-th of the scale of Fig. 6d, where there is no Y pattern present. On contrary, our procedure traces out the Y pattern completely but provides very wide confidence ellipsoids for the diagonal part. This indicates high uncertainty of the estimator in the diagonal part of the letter Y. The p-value map shows similar results, again suggesting that our estimator provides superior geometric representation of the underlying tensor field and the uncertainty of trajectories through it.

Fig. 6
figure 6

Y-template. Note that the Y pattern is almost non-existent on e, where only one track out of 400 traces the diagonal. It seems to appear on c, while part of the letter C disappears, but the scale is 1/100-th of the scale of d, where there is no Y pattern present. a Slice \(z = 0.48\). The initial point is (0.47, 0.01706, 0.48). Here \(N = 6 \), \( m = 1\), \(n = 62{,}500\) ; \(\delta = 0.02\), \(\beta = 0.0001\). b P-value map for slice \(z = 0.48\). The initial point is (0.47, 0.01706, 0.48). Here \( \delta = 0.02 \), \( \beta = 0.00005 \). c Slice \(z = 0.48\). Visualization of how many MCMC tracks terminated at each point. The order is \(10^-43\). d Slice \(z = 0.52\). Visualization of how many MCMC tracks terminated at each point. The order is \(10^-41\). e 400 out of 10,000 MCMC tracks. f Our estimator together with pointwise 95 % confidence ellipsoids. (Color figure online)

Full size image

8 Application to real brain imaging data

Our method was applied to a DTI scan of an elderly individual who volunteered for research at the UC Davis Alzheimer’s Disease Center. Imaging was performed at the UC Davis Imaging Research Center on a 1.5T GE Signa Horizon LX Echospeed system. The single-shot spin-echo echo planar imaging DTI sequence had acquisition parameters including: TE: 94 ms, TR: 8000 ms, Flip angle: 90 degrees, Slice thickness: 5 mm, slice spacing: 0.0 mm, FOV: 22 cm \(\times \) 22 cm, Matrix: \(128 \times 128\), B-value: 1000 s/mm\(^{2}\). Each acquisition included collection of 2 images with no gradient applied and 4 diffusion-weighted images acquired along each of 6 gradient directions. The directions are \(b_1=2^{-1/2}(1, 0, 1)\), \(b_2=2^{-1/2}(1, 0, -1)\), \(b_3=2^{-1/2}(0, 1, 1)\), \(b_4=2^{-1/2}(0, -1, 1)\), \(b_5=2^{-1/2}(1, 1, 0)\), \(b_6=2^{-1/2}(-1, 1, 0)\). This is referred to as the oblique double gradient encoding in the DTI literature. The dataset contains observations of Y on a regular grid with \(128\times 128\times 19\) locations. The voxel dimensions are \(1.875 \times 1.875 \times 5\) mm in the x, y and z directions, respectively. We scale the grid to \(G=[0, 1]^2\times [0, 3/8].\) The dataset has \(m=4\). The matrix B corresponding to the gradient directions is \(B=-0.25(1, 0, 2, 0, 0, 1; 1, 0, -2, 0, 0, 1; 0, 0, 0, 1, -2, 1; 0, 0, 0, 1, 2, 1; 1, -2, 0, 1, 0, 0; 1, 2, 0, 1, 0, 0)\).

We used the standard 3D Gaussian kernel K, bandwidths \(h_n=(n/\beta )^{-1/6}\), \(\tilde{h}_n=(n/\beta )^{-1/4}\log n\), \(\tilde{\tilde{h}}_n=(n/\beta )^{-1/5}\log n\) with \(\beta =0.0001\). Reducing \(\beta \) did not change results substantially, while increasing it produced very wide averaging windows so several tracts were averaged together.

First, for comparison we also estimated the fibers based on the noisy eigenvector field calculated at grid points using the method of Koltchinskii et al. (2007). Part of the vector field is shown in Fig. 7b. We also used Euler’s method and the same choice of the kernel and bandwidths.

We chose initial points in the center of the corpus callosum, one of the major tracts of white matter fibers in the brain. The corpus callosum fibers trace out U-shaped trajectories that run from the left side of the brain to the right.

Figure 7a shows illustrations of the estimated integral curves overlaid onto a horizontal slice of the DTI data. It demonstrates that our estimator keeps closer to the true integral curve than the Koltchinskii et al. (2007) estimator. Moreover, the confidence ellipsoids are wider for their estimator. Theirs are extended in the z direction. The Euclidean norm of the covariance matrices for our estimator at the ends of the tract is on the order of 0.0007, while it is 0.02 for Koltchinskii et al.’s (2007) estimator. A comparison of Fig. 7c and d suggests that our estimators are closer to the true fibers while all of the Koltchinskii et al.’s (2007) estimators drift away from the true U-shaped trajectory of the fiber. Choosing a smaller \(\beta \) to shrink the averaging window does not change the overall performance of their estimator.

Fig. 7
figure 7

Comparison of our estimator with that of Koltchinskii et al. (2007) on a real DTI data set. a The solid black curve with blue confidence ellipsoids corresponds to the estimated integral curve using our approach. The solid green curve with cyan confidence ellipsoids corresponds to the estimated integral curve using the method of Koltchinskii et al. (2007). We traced the fiber for 40 steps with \(\delta =0.005\). We used a 95 % confidence level to define the confidence ellipsoids. b The eigenvector field \(v(\tilde{M}(X_j)), j=1,\dots ,n,\) is shown for the region in a. c Several fibers are estimated using our procedure with 95 % confidence ellipsoids. d Several fibers are estimated using the procedure of Koltchinskii et al. (2007) with 95 % confidence ellipsoids. (Color figure online)

Full size image

Second, for comparison we consider a popular tractography approach by Behrens et al. (2003). Figure 8 has the same parts as Fig. 5. Upon its inspection we again observe that MCMC tracks tend to be short and concentrated near the initial point. Also quite a lot of them deviate in the z-direction. Note that scale is different for Fig. 8c and d. These MCMC tracks do not trace out the underlying letter U on FA map. On the contrary, our procedure traces out the letter U and it provides nice confidence ellipsoids that lay completely inside the fiber. The p-value map shows similar results.

Fig. 8
figure 8

Comparison of our approach with a probabilistic tractography approach due to Behrens et al. (2003). The initial point is (0.47, 0.01706, 0.48). Here \(N=6, m=2, n=311{,}296\). a FA map for slice \(z=9/19\) is overlaid with the principle eigenvector field. b P-value map for the selected fiber in slice \(z=9/19\) is constructed with \(\delta =0.02, \beta =0.00005\). c Slice \(z=9/19\). Visualization of how many MCMC tracks terminated at each point. The order is \(10^{-43}\). d Slice \(z=10/19\). Visualization of how many MCMC tracks terminated at each point. The order is \(10^{-41}\). e Slice \(z=9/19\). 400 out of 10,000 MCMC tracks. f Slice \(z=9/19\). Our estimator together with pointwise 95 % confidence ellipsoids. Here \(\delta =0.02, \beta =0.00005\). (Color figure online)

Full size image

9 Discussion and conclusion

A great number of scientific analyses based on tracing axonal fibers through DTI data have been published, many of which rely on probabilistic tractography to deal with the uncertainty inherent to the fiber trajectories. Yet, the theoretical statistical properties of these probabilistic tractography algorithms are not well understood, and they are computationally burdensome due to the need for sampling from a high-dimensional distribution. This work addresses the theoretical and computational problems by developing a rigorous statistical framework that provides theoretically-grounded fiber trajectory estimates, along with closed-form solutions for confidence regions. We use a nonparametric approach to model the tensor field, its leading eigenvector field and the corresponding integral curve. We derive asymptotical theory for the proposed estimator. Applications to synthetic and real human brain DTI data suggest that our method provides realistic trajectory tracing with tighter confidence ellipsoids than a more restrictive nonparametric approach. It also yields more intuitive geometric representations and realistic output images than a popular probabilistic approach due to Behrens et al. (2003).

Besides its firmer theoretical foundations, the proposed method is also advantageous over probabilistic tractography in terms of computational complexity. The proposed method requires \(O(n^{3/(d+3)})\) operations to estimate the integral curve when a kernel with bounded support is used, and O(n) operations for Gaussian or other kernels. It requires \(O(n^2)\) operations for the calculation of asymptotical covariance, which is needed to construct confidence ellipsoids. The constants in front of these \(O(\cdot )\) terms are on the order of hundreds. In contrast, the estimator based on a probabilistic tractography approach due to Behrens et al. (2003) requires \(O(n\tau _n)\) operations, where \(\tau _n\) is an average number of iterations needed for MCMC to converge. To obtain ad hoc bootstrapped confidence regions, one needs \(O(n\tau _n)\) operations with an extremely large constant; there is no firm theoretical upper bound on \(\tau _n\) either. Behrens et al. (2003) used 20,000,000\(n\tau _n\) iterations in their experiments. While in principle, the number of MCMC iterations required for any individual data set may be lower than this, in practice the number of iterations required is completely arbitrary. In our simulation study our method took several minutes to run while the method of Behrens et al. (2003) took hours. A more comprehensive and fair comparison of real-world computational complexity between our method and probabilistic tractography methods such as that of Behrens et al. would require a large-scale Monte Carlo study involving repeated imaging of the same brain under the same conditions, followed by fiber tracing in each scan. For particular fiber tracts of interest, the different tracing methods applied to the repeated scans would then provide empirical distributions of integral curves, their uncertainties, and their run times. These distributions could be the basis for a fair comparison of the methods.

We showed that the one pre-existing method that provided theoretically rigorous trajectory confidence bounds, by Koltchinskii et al. (2007), is a special case of ours and that the asymptotical distribution of their estimator coincides with that of our estimator under strong restrictions on our model. We argued that the assumptions required by their model are too unrealistic for the method to be useful for DTI, and our experiments with real DTI data supported this view. In these experiments, the estimator of Koltchinskii et al. (2007) had covariance matrices with larger norms along the curve, and thus it had looser confidence ellipsoids. It also traced incorrect trajectories in regions with multiple fibers located in a close proximity. These experiments suggest that the theoretical rigor of our approach is actually relevant from the point of view of tract tracing applications.

Given that integral curve estimation becomes ill-conditioned at locations with multiple viable leading eigenvector directions, we first perform a preprocessing step to identify such locations, and if they are encountered during curve tracing, we begin separate integral curve traces along each viable direction. The full set of estimated trajectories emanating from a given point consists of the set of all these integral curve segments. Note that this does not introduce much more computation than a probabilistic tractography approach, which can be thought of as sampling trajectories over all such viable leading eigenvector directions. We do not think it is difficult to extend this approach to greater numbers of possible leading eigenvector directions; however, a key limitation of the current method is that uncertainty in whether or not a location constitutes a branching point is not translated into uncertainty in the tensors, eigenvectors, and integral curves. Instead, we apply a hard threshold to a branching point test statistic and use it to classify all locations as either absolutely branching points, or not. How to incorporate this branching point uncertainty into the model in a principled way is unclear. Progress in this area will be required to insure that all relevant sources of uncertainty are brought to bear on integral curve uncertainty.

In addition, it is unclear how this analysis extends to more elaborate mathematical representations of the water diffusion directional distribution that are ascendant in the current DTI literature. Some examples of these representations include diffusion tensors that are higher than second order, spherical deconvolution models, and spherical wavelet models; see Assemlal et al. (2011). To our knowledge, none of these models have been studied from the standpoint of theoretically rigorous statistical error analysis. Extending the current results to these novel diffusion representations will be an important next step for maintaining theoretically-sound integral curve tracing as diffusion MRI technology continues to advance.