Parameter estimation for reflected Ornstein–Uhlenbeck processes with discrete observations

Abstract

A parameter estimation problem for a one-dimensional reflected Ornstein–Uhlenbeck is considered. We assume that only the state process itself (not the local time process) is observable and the observations are made only at discrete time instants. Strong consistency and asymptotic normality are established. Our approach is of the method of moments type and is based on the explicit form of the invariant density of the process. The method is valid irrespective of the length of the time intervals between consecutive observations.

1 Introduction

We consider the parameter estimation problem for a one-dimensional reflected Ornstein–Uhlenbeck (ROU) process with infinitesimal drift $-\gamma x$ and infinitesimal variance ${\sigma }^{2}$, where $\gamma \in (0,\infty )$ and $\sigma \in (0,\infty )$. The ROU behaves like a standard OU process in the interior of its domain $(0,\infty )$. However, when it reaches the boundary zero, then the sample path returns to the interior in a manner that the “pushing” force is minimal. Our main interest in this model stems from the fact that the ROU process arises as the key approximating process for queueing systems with reneging or balking customers [see Ward and Glynn (2003a, b, 2005) and the references therein]. In such cases, the drift parameter $\gamma$ carries the physical meaning of customers’ reneging (or, balking) rate from the system. Other application areas of the ROU process include financial engineering and mathematical biology [see, e.g., Attia (1991), Bo et al. (2011a, 2010), Ricciardi (1985)].

Given a filtered probability space $\varLambda :=(\varOmega , {\mathcal {F}}, ({\mathcal {F}}_t)_{t\ge 0},{\mathbb {P}})$ with the filtration $({\mathcal {F}}_t)_{t\ge 0}$ satisfying the usual conditions, we define the ROU process $\{X(t):t\ge 0\}$ reflected at the boundary zero as follows. Let $\{X(t):t\ge 0\}$ be the strong solution [whose existence is guaranteed by an extension of the results of Lions and Sznitman (1984)] to the stochastic differential equation:

$$\begin{aligned} \left. \begin{array}{l} \mathrm{d}X(t)=-\gamma X(t) \mathrm{d}t + \sigma \mathrm{d}B(t) + \mathrm{d}L(t), \\ X(t)\ge 0 \quad \text{ for } \text{ all } t \ge 0,\\ \end{array} \right\} \end{aligned}$$

(1)

where $\gamma \in (0,\infty ), \sigma \in (0,\infty )$ and $B=(B(t))_{t\ge 0}$ is a one-dimensional standard Brownian motion on $\varLambda$. Here, $L=(L(t))_{t\ge 0}$ is the minimal non-decreasing and non-negative process, which makes the process $X(t)\ge 0$ for all $t\ge 0$. The process $L$ increases only when $X$ hits the boundary zero, so that

$$\begin{aligned} \int _{[0,\infty )}^{} I(X(t)>0)\mathrm{d}L(t)=0, \end{aligned}$$

(2)

where $I(\cdot )$ is the indicator function. It is often the case that the reflecting barrier is assumed to be zero in applications to queueing system, storage model, engineering, finance, etc. This is mainly due to the physical restriction of the state processes such as queue-length, inventory level, content process, stock prices and interest rates, which take non-negative values. We refer the reader to Harrison (1985) and Whitt (2002) for more details on reflected stochastic processes and their broad applications.

Our interest lies in the statistical inference for the ROU process defined in (1) and (2). More specifically, we would like to estimate the unknown drift parameter $\gamma \in (0,\infty )$ in the Eq. (1) based on discrete observations of the state process $\{X(t)\}_{t\ge 0}$. Fix a time interval $h>0$. We assume that $\left\{ X(kh): 1\le k\le n\right\}$ are known. The recent papers Bo et al. (2011b), Lee et al. (2012) studied the maximum likelihood estimator (MLE) and the sequential MLE for the drift parameter $\gamma$, respectively, based on the continuous time observations throughout a (fixed or random) time interval $[0,T]$. Moreover, they assume that the local time process $L=\{L(t)\}_{t\ge 0}$ is also observable. However, this means that the observer has the complete information on the system. It is evident that one often encounters practical difficulties to obtain a complete continuous observation of the sample path, and only the discrete time observations are possible.

In this paper, we overcome the afore-mentioned difficulties by assuming that only the state process $X=\{X(t)\}_{t\ge 0}$ (not the local time process $L$) is observable and only at discrete time instants. Our approach is based on the explicit form of the invariant density of the process and the method of moment type estimators together with the ergodic theorem. Hence, we bypass the obstacles associated with the transition densities of $X$ which are usually unknown except in very special cases, or oftentimes computationally cumbersome to handle.

One of the note-worthy advantages is that the method is valid irrespective of the time between consecutive observations $h$, and hence we do not require $h$ go to $0$ [see a recent work in the fractional Brownian motion case without reflection Hu and Song (2013)]. That means one does not need very frequent observations. Our method is, therefore, widely applicable in many practical situations involving models with ergodic diffusion processes (see comments in Sect. 5 for more details). However, we mention that our proposed approach does not allow to estimate $\gamma >0$ and $\sigma >0$ simultaneously (only $\gamma$ but not ${\sigma }^2$). This is due to some technical reasons (see Remark 1) presented in the expression of the invariant density of the process. This is sufficient when ${\sigma }^2$ is known. However, if ${\sigma }^2$ is unknown, we need to assume the data is of high frequency type. In this case, ${\sigma }^2$ can be estimated through a more conventional way (see Remark 6 for more details).

The remainder of the paper is organized as follows. In Sect. 2, we introduce the unique invariant density and prove an ergodic theorem, which is the crucial basis of the main results. We present the method of moment estimator and the main theoretical results in Theorems 1 and 2. Then in Sect. 3, we extend our method to the more general cases in which the multiple parameters are present and we try to jointly estimate them. Section 4 is devoted to the various numerical studies of the estimator. Section 5 concludes with some discussion and remarks on the further work.

2 Strong consistency and asymptotic normality

We shall use a result of Ward and Glynn (2003b) [see also Linetsky (2005)]. It can be proved that the process $\{X(t)\}_{t\ge 0}$ is ergodic (see Lemma 1 below) and the unique invariant density of $\{X(t)\}_{t\ge 0}$ is given [Ward and Glynn (2003b), Linetsky (2005)] by

$$\begin{aligned} p(x)=2\sqrt{\frac{2{\gamma }}{{\sigma }^2}} \phi \left( \sqrt{ \frac{ 2{\gamma }}{{\sigma }^2}} x\right) \,, \quad x\in [0,\infty ), \end{aligned}$$

(3)

where $\phi (u)=(2\pi )^{-1/2} e^{-\frac{u^2}{2}}$ is the (standard) Gaussian density function. The following result is based on basic stability theories of Markov processes and is crucial in our approach of constructing estimators.

Lemma 1

The discretely observed process $\{X(kh):k\ge 0\}$ is ergodic, namely, the following mean ergodic theorem holds: For any $x\in S:=[0,\infty )$ and any $f\in L_1(S,\mathcal B(S))$,

$$\begin{aligned} \lim _{n\rightarrow \infty }\frac{1}{n} \sum _{k=1}^n f(X(kh)) = \mathbb { E}\ [f(X(\infty ))]= \int _{0}^{\infty }f(x)p(x)dx \quad \text{ a.s. } [\mathbb {P}_x]. \end{aligned}$$

Proof

The continuous time process $\{X(t):t\ge 0\}$ and its $h$-skeleton $\{X(kh):k\ge 0\}$ share the same invariance measure $\pi$ on $S$: Let $P^t(x,A):={\mathbb {E}}_x[X(t)\in A]$ and $(P^t(x,A):x\in S, A\in \mathcal B(S))$ be the transition probability kernel of $X$. Then we have

$$\begin{aligned} ||P^t(x,\cdot )-\pi \{\cdot \}||\le ||P^{kh}(x,\cdot )-\pi \{\cdot \}|| \le ||P^{t+h}(x,\cdot )-\pi \{\cdot \}||, \end{aligned}$$

whenever $t\le kh \le t+h$ for some $h>0$. Therefore, it suffices to show that $X:=\{X(t): t\ge 0\}$ is bounded in probability on average and is a $T$-process [cf. Meyn and Tweedie (1993)]. Then the desired conclusion will follow from Theorem 8.1(i) of Meyn and Tweedie (1993). We note that the Markov process $X$ is Feller and $\lambda$-irreducible, where $\lambda$ is a Lebesgue measure on $S$ [see, e.g., Lemma 5.7 of Budhiraja and Lee (2007)]. Also, the cited lemma yields that the support of the maximal irreducibility measure for $X$ is all of $S$. Thus we have from Theorem 6.2.9 of Meyn and Tweedie (2009) that $X$ is a $T$-process. Then, owing to Theorem 3.2(ii) of Meyn and Tweedie (1993) we conclude that $X$ is bounded in probability on average since $X$ is a positive Harris recurrent process. $\square$

Recall the invariant density $p(x)$ in (3). After some algebraic computations, we obtain the following simple formula for the stationary moment: For all $\eta >-1, \eta \ne 0$,

$$\begin{aligned} {\mathbb {E}} |X(\infty )|^\eta = \int _{0}^{\infty } x^\eta p(x) \mathrm{d}x = {\varGamma }\left( \frac{\eta +1}{2}\right) \frac{\sigma ^\eta }{\sqrt{\pi }}{\gamma }^{-\eta /2}. \end{aligned}$$

(4)

Hence, a natural method of moment estimator of $\gamma$ is given by

$$\begin{aligned} \hat{\gamma }_{\eta , n } := \frac{{\left( {\varGamma }((\eta +1)/2)\right) ^{2/\eta } \sigma }^{2}}{\pi ^{1/\eta } }\left( \frac{1}{\frac{1}{n} \sum _{k=1}^n {|X(kh)|^{\eta } }}\right) ^{2/\eta } \end{aligned}$$

(5)

for an arbitrary $h>0$ and any $\eta >-1, \eta \ne 0$. [Note that the term $\sum _{k=1}^{n}|X(kh)|^\eta$ in the denominator is positive almost surely; cf. Appendix of Budhiraja and Lee (2007)]. Here, ${\varGamma }(\cdot )$ denotes the Gamma function. It is worthy to note that when $\eta =1$, we have

$$\begin{aligned} \hat{\gamma }_{ n}=\hat{\gamma }_{1, n}=\frac{{ \sigma }^{2}}{\pi }\left( \frac{1}{\frac{1}{n} \sum _{k=1}^n {|X(kh)| }}\right) ^{2 }. \end{aligned}$$

(6)

The following theorem shows the strong consistency of the estimators $\hat{\gamma }_{\eta , n}$ of $\gamma$.

Theorem 1

Fix any $\eta >-1, \eta \ne 0$ and any $h>0$. As $n\rightarrow \infty , \hat{\gamma }_{\eta , n} \rightarrow \gamma$ almost surely.

Proof

This is an immediate consequence of the ergodic theorem in Lemma 1 by setting $f(x)=|x|^\eta$. $\square$

Remark 1

Notice that, in the above approach, we cannot estimate $\gamma >0$ and $\sigma >0$ simultaneously. This is because the invariant density $p(x)$ in (3) is a function of $\frac{{\gamma }}{{\sigma }^2}$. We can use $p(x)$ to determine only $\frac{{\gamma }}{{\sigma }^2}$.

Remark 2

We note the persistent bias presence in the estimator $\hat{\gamma }_n=\hat{\gamma }_{1, n}$. The unconditional bias of $\hat{\gamma }_n$ is given by ${\mathbb {E}}[\hat{\gamma }_n-\gamma ]$. This will not in general be equal to zero because of Jensen’s inequality. The nonlinear transformation $g(x)=\frac{{\sigma }^{2}}{\pi }\left( \frac{1}{x}\right) ^2$ in (6) of the sample mean is a convex function, and it follows immediately from the Jensen’s inequality that its bias is positive. However, the unconditional bias of $\hat{\gamma }_n$ can be approximated using second order Taylor series expansion for $\hat{\gamma }_n$ around $\gamma$, which yields

$$\begin{aligned} {\mathbb {E}}[\hat{\gamma }_n-\gamma ]\approx \frac{1}{2}g''({\mathbb {E}} X(\infty )){\mathbb {E}}\left( \frac{1}{n}\sum _{k=1}^{n}|X(kh)|-{\mathbb {E}}X(\infty )\right) ^2. \end{aligned}$$

In practice, the first factor above $g''({\mathbb {E}}X(\infty ))$ can be approximated by plugging in the sample mean $g''\left( \frac{1}{n}\sum _{k=1}^{n}X(kh)\right)$ due to an ergodic theorem, and the second factor by the empirical variance of the sample mean. Therefore, one could use the following estimate as the bias correction term in practice:

$$\begin{aligned} \frac{{\sigma }^2}{\pi }\times \frac{3}{\left( \frac{1}{n}\sum _{k=1}^{n}|X(kh)|\right) ^4}\times \widehat{\mathrm{Var }}\left( \frac{1}{n}\sum _{k=1}^{n}|X(kh)|\right) . \end{aligned}$$

Next, we establish the central limit theorem.

Theorem 2

As $n\rightarrow \infty$,

$$\begin{aligned} \sqrt{n}(\hat{\gamma }_{\eta , n} - \gamma ) \Rightarrow N(0,\Sigma _\eta )\end{aligned}$$

(7)

where $\Sigma _\eta$ is a nonnegative constant.

Proof

Only the case $\eta =1$ will be treated here. The extension to general $\eta >-1$ is accomplished by a straightforward computation; it only increases the notational complexity. We notice that $\{X(kh): k\ge 0\}$ is a positive Harris chain with invariant probability $\pi$ with density $p(x)$ (recall Lemma 1). Furthermore, it can be shown that $\{X(kh): k\ge 0\}$ is $V$-uniformly ergodic with a function $V$ that grows exponentially [see Corollary 5.10 of Budhiraja and Lee (2007)], i.e., there exist $\rho \in (0,1)$ and $D\in (0,\infty )$ such that for all $x\in (0,\infty )$,

$$\begin{aligned} ||{P}^{n}(x,\cdot )-\pi ||_V\le DV(x){\rho }^{n}, \end{aligned}$$

(8)

where ${P}^{n}(x,A):=P_{nh}(x, A):={\mathbb {P}}_x(X(nh)\in A)$ is an $n$-step transition probability kernel of the chain $\{X(kh): k\ge 0\}$. (The positive constants $D$ and $\rho$ above depend on the parameter $\gamma$.) Therefore, the constant

$$\begin{aligned} \bar{\sigma }^2:= \mathrm{Var }_\pi [X(0)] + 2\sum _{k=1}^{\infty } \mathrm{Cov }_\pi (X(0), X(kh)) \end{aligned}$$

is well defined, non-negative and finite, and coincides with the asymptotic variance in

$$\begin{aligned} \sqrt{n} \left( \frac{1}{n} \sum _{k=1}^n {X(kh)} - {\mathbb {E}} X(\infty )\right) \Rightarrow N\left( 0, \bar{\sigma }^2\right) \end{aligned}$$

(9)

from Theorem 17.0.1(ii) of Meyn and Tweedie (2009). Letting $g(x)=\frac{{\sigma }^{2}}{\pi }\left( \frac{1}{x}\right) ^2$, the transform in (6), we get from the delta-method that $\sqrt{n}(\hat{\gamma }_n - \gamma ) \Rightarrow N(0,\varSigma _1)$ as $n\rightarrow \infty$, where the variance $\varSigma _1=\bar{\sigma }^2(g'({\mathbb {E}}(X(\infty ))))^2$. [Note that $g'({\mathbb {E}}(X(\infty )))$ exists and is non-zero valued because ${\mathbb {E}}(X(\infty ))$ is strictly positive]. From (4), it is explicitly given by $\varSigma _1=\bar{\sigma }^2\frac{4\pi {\gamma }^{3}}{\sigma ^2}$. $\square$

Remark 3

For the non-ergodic $(\gamma <0)$ and non-stationary $(\gamma =0)$ cases, our methods do not apply since it is based upon ergodic theorem and explicit form of a stationary density of the process. As a related work, the paper Bo et al. (2011b) deals with the ergodic case (i.e., $\gamma >0$) as well and establishes similar consistency and asymptotic normality for an ordinary MLE based on the continuous time observations. In contrast, the sequential estimations of Lee et al. (2012) do not need ergodicity of the process and their sequential MLE exhibits unbiasedness and exact normality for all $\gamma \in (-\infty ,\infty )$.

Remark 4

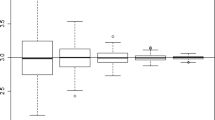
At the end of the preceding proof, an asymptotic variance in the CLT is given as $\varSigma _1=\bar{\sigma }^2\frac{4\pi {\gamma }^{3}}{\sigma ^2}$, where $\bar{\sigma }^2= \mathrm{Var }_\pi [X(0)] + 2\sum _{k=1}^{\infty } \mathrm{Cov }_\pi (X(0), X(kh))$ also depends on the parameter $\gamma >0$. When $\gamma >0$ is small, the process $(X_t)$ is more unstable, and therefore the terms ${\gamma }^{3}$ and $\bar{\sigma }^2$ compete with each other in $\varSigma _1$ as $\gamma$ gets smaller. Our numerical study in Sect. 4 indicates that the estimator actually performs better (in terms of mean squared error) when $\gamma >0$ is smaller; see Fig. 1 (when $\gamma =0.5$) and Fig. 2 (when $\gamma =0.05$).

Fig. 1

MSE of $\hat{\gamma }_{\eta , n }$ against $\eta$ (when $\gamma =0.5$)

Fig. 2

MSE of $\hat{\gamma }_{\eta , n }$ against $\eta$ (when $\gamma =0.05$)

In general, computation or estimation of the asymptotic variance $\bar{\sigma }^2$ is challenging and requires specialized techniques. We provide below a possible method of evaluating it. If the process is stationary, namely, if $X(0)$ has the invariant measure $\pi$, then $\bar{{\sigma }}^2$ may be computed in the following way. We denote $\langle f, g\rangle =\int _{[0, \infty )} f(x) g(x) dx$ and $P_{kh} g(X(0)) =\mathbb { E}\ (g(X(kh))$. We denote $g(x)=x$. Then

$$\begin{aligned} \bar{\sigma }^2&= \mathrm{Var }_\pi [X({0})] + 2\sum _{k=1}^{\infty } \mathrm{Cov }_\pi (X(0), X(kh))\nonumber \\&= \mathrm{Var }[X(\infty )] + 2\sum _{k=1}^{\infty } \left[ \mathbb { E}\ (X(kh) X(0))- \mathbb { E}\ (X(kh)) \mathbb { E}\ (X(0))\right] \nonumber \\&= \mathrm{Var }[X(\infty )] + 2\sum _{k=1}^{\infty } \left[ \mathbb { E}\ (P_{kh}g(X(0)) X(0))- \mathbb { E}\ (P_{kh} g(X(0))) \mathbb { E}\ (X(0))\right] \nonumber \\&= \mathrm{Var }[X(\infty )] + 2 \langle pg , \sum _ {k=1}^{\infty } ( P_{kh}g - \langle p, P_{kh} g{\rangle )\rangle }\nonumber \\&= \int _0^\infty \left( x-\frac{{\sigma }}{\sqrt{\pi {\gamma }}}\right) ^2 p(x) \mathrm{d}x + 2 \langle pg , f\rangle \, \nonumber \\ {}&= \frac{\sigma ^2}{\gamma }\left( \frac{1}{2}-\frac{1}{\pi }\right) + 2 \langle pg , f\rangle \,, \end{aligned}$$

(10)

where

$$\begin{aligned} f:=\sum _ {k=1}^{\infty } ( P_{kh}g - \langle p, P_{kh} g{\rangle )}. \end{aligned}$$

The above defined $f$ satisfies the following two properties. First, it is easy to verify that

$$\begin{aligned} \langle p, f\rangle =\int _0^\infty p(x) f(x) \mathrm{d}x=0. \end{aligned}$$

(11)

Second, if we apply $I-P_h$ to the equation defined by $f$, then we have

$$\begin{aligned} (I-P_h) f=P_h g, \quad \text{ and } \,\text{ hence }\quad f=(I-P_h)^{-1}g. \end{aligned}$$

(12)

We note that there is a method for evaluating the transition probability function operator $P_h$ [and $(I-P_h)^{-1}$] based on the results in Linetsky (2005). More precisely, one can employ a useful eigenfunction expansion for the transition density of the reflected process $X$ established in Section 5.2 in Linetsky (2005). We refer the reader to pages 450–451 therein for more details about the eigenfunction and eigenvalue computations using the Hermite functions. Thus the asymptotic variance $\bar{{\sigma }}^2$ can be computed by (10) with $f$ being given by (11) and (12).

3 Extension to multiple-parameter case

The method in the previous section is simple, yet powerful; it can be extended to the more general cases in which the multiple parameters are present. We consider the following more general ROU model:

$$\begin{aligned} \mathrm{d}X(t) = ({\alpha }-{\gamma }X(t)) \mathrm{d}t + {\sigma }\mathrm{d}B(t) + \mathrm{d}L(t), \end{aligned}$$

(13)

where $L = (L(t): t \ge 0)$ is the minimal nondecreasing process which makes $X(t)\ge 0$ for all $t\ge 0$. In the above model, ${\sigma }>0$ is known and the parameters ${\alpha }>0$ and ${\gamma }>0$ are deterministic but unknown. Our goal is to jointly estimate parameters ${\alpha }$ and ${\gamma }$.

It can be shown that the process $\{X(t)\}_{t\ge 0}$ in (13), as well as its discrete time $h$-skeleton process, is ($V$-uniformly) ergodic (recall Lemma 1 and see the proof of Theorem 4 below) and the unique invariant density of $X(t)$ is now given [Ward and Glynn (2003b), Linetsky (2005)] by

$$\begin{aligned} p(x)=\sqrt{\frac{2{\gamma }}{{\sigma }^2}} \frac{\phi \left( \sqrt{ \frac{ 2{\gamma }}{{\sigma }^2}} \left( x-\frac{{\alpha }}{{\gamma }}\right) \right) }{1-\varPhi \left( -\sqrt{\frac{2{\alpha }^2}{{\gamma }{\sigma }^2}}\right) },\quad x\in [0,\infty ), \end{aligned}$$

(14)

where $\phi (u)=(2\pi )^{-1/2} e^{-\frac{u^2}{2}}$ and $\varPhi (y) =\int _{-\infty }^y \phi (u) \mathrm{d}u$ are the Gaussian density and the error function, respectively. Notice that $\frac{\gamma }{\sigma ^2}$ behaves as a single factor in the above expression and therefore we are unable to estimate $\gamma$ and ${\sigma }^2$ simultaneously using $p(x)$ alone, as noted in Remark 1. Henceforth, we shall assume that ${\sigma }>0$ is known; however, when the data is of high frequency (i.e., $h\rightarrow 0$), one can then estimate the parameter ${\sigma }^2$ (see Remark 6).

We shall now construct our estimators. For $u\in {\mathbb {R}}$, denoting $g(u)=1-\varPhi (-\sqrt{\frac{2\alpha ^2}{\gamma \sigma ^2}}-\sqrt{\frac{\sigma ^2}{2\gamma }}u)$, we can obtain the following stationary moments from the Maclaurin series of the m.g.f. ${\mathbb {E}} e^{uX(\infty )}$:

$$\begin{aligned} {\mathbb {E}} X(\infty )&=\frac{\alpha }{\gamma }+\frac{1}{g(0)}\phi \left( -\sqrt{\frac{2\alpha ^2}{\gamma \sigma ^2}}\right) \sqrt{\frac{\sigma ^2}{2\gamma }},\end{aligned}$$

(15)

$$\begin{aligned} \frac{1}{2} {\mathbb {E}} X(\infty )^2&=\frac{\sigma ^2}{4\gamma }+\frac{\alpha ^2}{2\gamma ^2} +\frac{1}{g(0)}\phi \left( -\sqrt{\frac{2\alpha ^2}{\gamma \sigma ^2}}\right) \sqrt{\frac{\sigma ^2}{2\gamma }}\left( \frac{1}{2} \frac{\alpha }{\gamma }\right) . \end{aligned}$$

(16)

Motivated from the above expressions, we construct the following equations for the estimators based on the observation process $\{X(kh)\}_{k\ge 1}$:

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle \frac{1}{n} \sum _{k=1}^nX(kh) \approx \frac{\alpha }{\gamma }+\frac{1}{g(0)} \phi \left( -\sqrt{\frac{2\alpha ^2}{\gamma \sigma ^2}}\right) \sqrt{\frac{\sigma ^2}{2\gamma }},\\ \displaystyle \frac{1}{2n} \sum _{k=1}^nX(kh)^2 \approx \frac{\sigma ^2}{4\gamma } +\frac{\alpha ^2}{2\gamma ^2}+\frac{1}{g(0)}\phi \left( -\sqrt{\frac{2\alpha ^2}{\gamma \sigma ^2}}\right) \sqrt{\frac{\sigma ^2}{2\gamma }}\left( \frac{1}{2} \frac{\alpha }{\gamma }\right) . \end{array}\right. } \end{aligned}$$

(17)

Denote the terms on the left side by $T_{i,n},i=1,2.$ To obtain the estimators for ${\alpha }$ and ${\gamma }$, we set (17) to identities. On the right hand side of (17) we make the substitutions $x=\frac{\alpha }{\gamma }$ and $y=\sqrt{\frac{2\alpha ^2}{\gamma \sigma ^2}}$. Thus we can get the estimators $\hat{x}_n=\frac{\hat{\alpha }_n}{\hat{\gamma }_n}$ and $\hat{y}_n =\sqrt{\frac{2\hat{\alpha }_n^2}{\hat{\gamma }_n \hat{\sigma }_n ^2}}$ by solving the following equations

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle T_{1,n} = x+\frac{\phi (-y)}{1-\varPhi (-y)}\frac{x}{y}\,, \\ \displaystyle T_{2,n} = \frac{1}{2}\left[ x^2+\frac{x^2}{y^2}\right] +\frac{\phi (-y)}{1-\varPhi (-y)}\frac{x^2}{2y}. \end{array}\right. } \end{aligned}$$

(18)

In what follows we intend to obtain the estimators $\hat{x}_n=\frac{\hat{\alpha }_n}{\hat{\gamma }_n}$ and $\hat{y}_n =\sqrt{\frac{2\hat{\alpha }_n^2}{\hat{\gamma }_n \sigma ^2}}$ by using (18). We need to show that this system of two equations is solvable. Denote the right hand sides of (18) by $g_1(x,y)$ and $g_2(x,y)$, respectively. Let $A=\frac{\phi (-y)}{1-\varPhi (-y)}$ and $B=-1+A\frac{1}{y}-\frac{1}{y^2}.$ Then the Jacobian matrix $J$ of $(g_1, g_2)$ is given by

$$\begin{aligned} \left( \begin{array}{ll} 1+\dfrac{A}{y}, &{}\quad xAB \\ x+\dfrac{x}{y^2}+A\dfrac{x}{y}, &{}\quad -\dfrac{x^2}{y^3}+\dfrac{x^2}{2}AB \\ \end{array} \right) . \end{aligned}$$

(19)

The determinant of $J$ is

$$\begin{aligned} \det (J)&= -\frac{x^2}{y^3}-\frac{x^2AB}{2}-\frac{x^2A^2B}{2y}-\frac{Ax^2}{y^4} -\frac{x^2AB}{y^2}\\&= -\frac{x^2}{2y^3}\left( 2-Ay^3-3Ay+A^3y+A^2\right) . \end{aligned}$$

We claim that $\det (J)\ne 0$ for all $x,y>0$. To this end, it suffices to show that $2-Ay^3-3Ay>0$ for all $y>0.$ Note that $1-\varPhi (-y)=\frac{1}{2}+\int _0^y \phi (x)\mathrm{d}x$ in $A$ and then it is equivalent to show $F(y):=1+2\int _0^y \phi (x)\mathrm{d}x-\phi (y)(y^3+3y)>0$. However, $F'(y)=\phi (y)\left( y^4-1\right) =0$ implies that $y=1$ is the only critical point on $(0,\infty )$ and since we have $F''(1)>0, F(1)>0$, we can conclude that $F(y)>0$ for $y\in (0,\infty ).$ Therefore, from the inverse function theorem, there exists a continuous inverse function $h=(h_1,h_2)$ of $(g_1,g_2)$.

Recall that from the ergodic theorem, we have $T_{i, n}\rightarrow g_i(x, y), i=1,2$ almost surely. Since $h=(h_1,h_2)$ is a continuous function, the estimators defined by

$$\begin{aligned} \hat{x}_n := h_1(T_{1,n}, T_{2, n}),\quad \hat{y}_n := h_2(T_{1,n}, T_{2, n}) \end{aligned}$$

(20)

will converge almost surely to the parameters

$$\begin{aligned} x=h_1(g_1(x, y), g_2(x, y))=\frac{\alpha }{\gamma },\quad y=h_2(g_1(x, y), g_2(x, y))=\sqrt{\frac{2\alpha ^2}{\gamma \sigma ^2}}, \end{aligned}$$

respectively, as $n$ tends to infinity. This implies the following result.

Theorem 3

The estimators defined by

$$\begin{aligned} \hat{{\alpha }}_n:= \frac{\sigma ^2\hat{y}_n^2}{2\hat{x}_n},\quad \hat{{\gamma }}_n:=\frac{{\sigma }^2\hat{y}_n^2}{2\hat{x}_n^2} \,, \end{aligned}$$

(21)

where $\hat{x}_n$ and $\hat{y}_n$ are defined by Eq. (20), are strongly consistent for the parameters $({\alpha }, {\gamma })$.

In contrast to the single parameter case, the estimators $\hat{{\alpha }}_n$ and $\hat{{\gamma }}_n$ have only implicit expressions (via the inverse functions $h_1$ and $h_2$), and hence, bias correction terms are difficult to obtain in this case. However, it is not difficult to argue that $h_1$ and $h_2$ are continuously differentiable. Therefore, similar to Theorem 2, we establish the following CLT for the vector estimator $(\hat{{\alpha }}_n, \hat{{\gamma }}_n)$.

Theorem 4

As $n\rightarrow \infty$,

$$\begin{aligned} \sqrt{n}\left( (\hat{{\alpha }}_n, \hat{{\gamma }}_n)^T-({\alpha }, {\gamma })^T\right) \Rightarrow N(0, \varSigma )\, \end{aligned}$$

for some covariance matrix $\varSigma$, and its explicit expression is provided in (26) below.

Proof

From Cramér-Wold device, it is sufficient to establish the following one-dimensional CLT: for all $(a_1,a_2)\in \mathbb {R}^2, \sqrt{n}(a_1\hat{{\alpha }}_n+a_2\hat{{\gamma }}_n)$ converges in distribution to a univariate normal random variable. Then, since $h_1$ and $h_2$ are continuously differentiable, it is enough to show the following univariate CLT holds [cf. Theorem 4.1 of van der Vaart (1998)]: for all $(a_1,a_2)\in {\mathbb {R}}^2, \sqrt{n} (a_1T_{1,n}+a_2 T_{2,n})$ converges in distribution to some normal random variable. This result readily follows from an application of the CLT for $V$-uniformly ergodic Markov chains [cf. Chapter 17 of Meyn and Tweedie (2009)]. More precisely, Lemma 5.9 and Corollary 5.10 of Budhiraja and Lee (2007) establish the $V$-uniform ergodicity for the process $\{X(kh):k\ge 0\}$, where $V$ is an exponentially growing Lyapunov function. (Indeed, the key stability Condition 5.5 of Budhiraja and Lee (2007) is satisfied with $\delta =\alpha$ and taking $A=[0, \frac{2\alpha }{\gamma }]$ therein). For $x\in [0,\infty )$ and any $(a_1,a_2)\in {\mathbb {R}}^2$, we let $g(x)=a_1x+\frac{a_2}{2}x^2$. Then,

$$\begin{aligned} \sqrt{n} (a_1T_{1,n}+a_2 T_{2,n})= \frac{1}{\sqrt{n}}\sum _{k=1}^{n} g(X(kh))=:\frac{1}{\sqrt{n}}S_n(g), \end{aligned}$$

and also $g^2$ is $\pi$-integrable [where $\pi$ has a density $p(\cdot )$ in (14)]. An application of Theorem 17.3.6 of Meyn and Tweedie (2009) yields the desired univariate CLT. For a related functional CLT, we refer the reader to Theorem 4.4 of Glynn and Meyn (1996) for general $V$-uniform Markov processes and, also Corollary 5.11(7) of Budhiraja and Lee (2007) for a wide class of reflected diffusion processes.

To obtain an explicit expression for the covariance matrix $\varSigma$, we (i) use the bivariate CLT for $(T_{1,n}, T_{2,n})^T$, established as above, and then (ii) apply the bivariate delta method. From now on, let $\pi$ denote the stationary distribution of the process, namely, $X(\infty )\sim \pi$. The multivariate Markov chain CLT [see, e.g., Section 1.8.1 in Brooks et al. (2011)] says that, as $n\rightarrow \infty$,

$$\begin{aligned} \sqrt{n}\left( (T_{1,n}, T_{2,n})^T-\left( {\mathbb {E}}X(\infty ), \frac{1}{2} {\mathbb {E}}X(\infty )^2\right) ^T\right) \Rightarrow N(0, \bar{\varSigma }). \end{aligned}$$

(22)

The asymptotic covariance matrix $\bar{\varSigma }$ above is given by

$$\begin{aligned} \bar{\varSigma }:= \mathrm{Var }_\pi [F(X(0))] + 2\sum _{k=1}^{\infty } \mathrm{Cov }_\pi (F(X(0)), F(X(kh))), \end{aligned}$$

(23)

where, with a slight abuse of notation, $\mathrm{Var }_\pi [F(X(0))]$ denotes the $2\times 2$ matrix with the $(i,j)$-th entry $\mathrm{Cov }_\pi \{F_i(X(0)), F_j(X(0))\} (i,j\in \{1,2\})$ and $F_1(x):=x, F_2(x):=x^2/2$. Similarly, $\mathrm{Cov }_\pi (F(X(0)), F(X(kh)))$ denotes the matrix with the $(i,j)$-th component $\mathrm{Cov }_\pi \{F_i(X(0)), F_j(X(kh))\}$ for $i,j\in \{1,2\}$.

Next, we invoke the bivariate delta method. Recalling the estimators defined by (20) and (21), we define two maps

$$\begin{aligned} h: (x_1,x_2)\mapsto \left( h_1(x_1,x_2), h_2(x_1,x_2)\right) ,\quad \ell : (x_1, x_2)\mapsto \left( \frac{\sigma ^2x_2^2}{2x_1}, \frac{\sigma ^2x_2^2}{2x_1^2}\right) . \end{aligned}$$

Then, denoting $\varTheta :=\left( {\mathbb {E}}X(\infty ), \frac{1}{2} {\mathbb {E}}X(\infty )^2\right)$ [whose formulas are given in (15)–(16)], we have

$$\begin{aligned} \ell \circ h(T_{1,n}, T_{2,n})=(\hat{\alpha }_n, \hat{\gamma }_n)\quad \text{ and }\quad \ell \circ h(\varTheta )=(\alpha ,\gamma ). \end{aligned}$$

(24)

An application of bivariate delta method [see Theorem 3.1 of van der Vaart (1998)] to (22) yields that as $n\rightarrow \infty$

$$\begin{aligned} \sqrt{n}\left( h(T_{1,n}, T_{2,n})^T- h(\varTheta )^T\right) \Rightarrow N\left( 0, \widetilde{\varSigma }\right) \quad \text{ with }\quad \widetilde{\varSigma }=\nabla h(\varTheta ) \bar{\varSigma } \nabla h(\varTheta )^T, \end{aligned}$$

(25)

where $\nabla h(\varTheta )$ denotes the Jacobian matrix of $h$ evaluated at $\varTheta$. We note that sufficient conditions of the multivariate delta method [Theorem 3.1 of van der Vaart (1998)] are justified; all partial derivatives $\partial h_j(x)/\partial x_i$ exist for $x$ in a neighborhood of $\varTheta$ (note that $\varTheta _i>0, i=1,2$) and are continuous at $\varTheta$, which can be checked from the inverse of the Jacobian matrix $J$ of $g=(g_1,g_2)$ (i.e., an inverse map of $h$) displayed in (19) and its determinant. (Clearly, $\nabla h$ is non-singular at $\varTheta$.) Lastly, applying the bivariate delta method once more to (25), we have as $n\rightarrow \infty$

$$\begin{aligned} \sqrt{n}\left( \ell (h(T_{1,n}, T_{2,n}))^T- \ell (h(\varTheta ))^T\right) \Rightarrow N(0, \varSigma )\quad \text{ with }\quad \varSigma =\nabla \ell (h(\varTheta )) \widetilde{\varSigma } \nabla \ell (h(\varTheta ))^T. \end{aligned}$$

(26)

Again, this delta method is justified because a direct computation shows that all partial derivatives $\partial \ell _j(x)/\partial x_i$ exist for $x$ in a neighborhood of $h(\varTheta )$ and are continuous at $h(\varTheta )$, and clearly $\nabla \ell$ is non-singular at that point. Combining (24) and (26), we establish the desired result. $\square$

Remark 5

It does not seem to be possible to derive the explicit formula for the matrix $\bar{\varSigma }$ in (23). As a remedy, one can estimate it in the following way: (Step 1) Carry out parameter estimations, i.e., compute $(\hat{\alpha }_n, \hat{\gamma }_n)$. (Step 2) Using these estimates, simulate the independent $p$ copies of the process $X$ with the initial distribution being $\pi$ (recall its density function (of truncated normal random variable) is given in (14)). Denote them by $\widetilde{X}_m, m=1, \ldots , p$. (Step 3) From those Monte-Carlo samples, estimate the expectation appearing in the series of (23) via corresponding Monte-Carlo average: for instance, for large $p$, we can estimate

$$\begin{aligned} {\mathbb {E}}_\pi [F_i(X(0)) F_j(X(kh))]\approx \frac{1}{p}\sum _{m=1}^p F_i(\widetilde{X}_m(0)) F_j(\widetilde{X}_m(kh)). \end{aligned}$$

Alternatively, one might also use the batch mean method [see Section 1.10 of Brooks et al. (2011) and the references therein] using long-time simulation (instead of many independent $p$ copies as above). Basically, it divides the output $X(h), \ldots , X(nh)$ of a long simulation run into a number of (almost stationary) batches and uses the sample means of these batches (i.e., batch means) to approximate the steady state mean or variance.

Remark 6

The case when ${\sigma }>0$ is unknown: As we pointed out, when we fix the time between two consecutive observations $h>0$ it is hard to simultaneously estimate ${\sigma }^2$ and $\gamma$ by using our approach. However, if the data is of high frequency (which means $h\rightarrow 0$), then we can use the usual approach to estimate ${\sigma }^2$. More precisely, (assuming $\alpha =0$ for simplicity of presentation) let

$$\begin{aligned} \hat{{\sigma }}_n ^2&:= \frac{1}{T} \sum _{k=0}^{n-1} \left( X_{(k+1) h}-X_{kh}\right) ^2 \\&= \frac{1}{T} \sum _{k=0}^{n-1} \left( -\gamma \int _{kh}^{(k+1)h}X_s \mathrm{d}s + \sigma \left( B_{(k+1) h}-B_{kh}\right) + \left( L_{(k+1) h}-L_{kh}\right) \right) ^2\,, \end{aligned}$$

where $h=T/n$ for any fixed $T>0$. Then, it is easy to show that as $n\rightarrow \infty , \hat{{\sigma }}_n ^2$ converges to ${\sigma }^2$ in $L^2$ and therefore in probability. This is essentially due to the fact that the local time process $(L_t)_{t\ge 0}$ is non-decreasing and thus it is of bounded variation. Hence, the quadratic variation of $(L_t)$ as well as other cross-product terms in the summand above vanish over any interval $[0,T]$ as $n\rightarrow \infty$ (i.e., $h\rightarrow 0$).

4 Numerical results

We examine the numerical behavior of the proposed estimator $\hat{\gamma }_{\eta , n}$ in (5). For a simulation of the ROU, we adopt the numerical scheme presented in Lépingle (1995), which is known to yield the same rate of convergence as the usual Euler-Maruyama scheme. Denote the time between each discretization step by $h>0$ and we generate $N=1,000$ Monte Carlo simulations of the sample paths with $h=0.01$ and $n=100,000$ under the setting $\gamma = 0.5$ (for Table 1; Fig. 1) and $\sigma = 1$. For Fig. 2, $\gamma$ is set to be 0.05 while other parameters are kept the same.

Table 1 Bias, variance and MSE of the estimator $\hat{\gamma }_{\eta , n }$

Table 1 shows the tradeoff between bias and variance for estimators $\hat{\gamma }_{\eta , n }$ with a range of $\eta$ values. Although the case with $\eta =-0.5$ provides a legitimate estimator, its empirical performance is not satisfactory in practice. The estimator is biased downward for a choice of lower moment and as the moment $\eta$ increases, the bias goes up. Magnitude of bias is minimized at $\eta =4$. The variance tends to increase as $\eta$ increases. The empirical MSE (mean squared error) of the estimator is minimized at $\eta =2$ as shown in Fig. 1. Based on the numerical analysis, the estimator based on 2nd or 3rd moments is recommended. We find that it is quite challenging to theoretically compare the MSE’s of $\hat{\gamma }_{\eta , n }$ with different $\eta$ values. Computations of the variance, let alone the bias, seem to be cumbersome since the transition probability density [whose representation is available only through infinite series of eigenfunctions, cf. Section 5.2 in Linetsky (2005)] is not so tractable for such purposes.

5 Concluding remarks

We conclude the paper with a few remarks. We have considered a parameter estimation problem with discrete observations for a one-dimensional ROU process having a single (lower) barrier. Our method can be readily applied to the ROU processes with two-sided barriers $0$ and $r>0$. The unique invariant density is known in the literature, see, e.g. Section 5.1 of Linetsky (2005), which is given by

$$\begin{aligned} p(x)= \frac{\sqrt{2\gamma }}{\sigma }\frac{\phi \left( \frac{\sqrt{2\gamma }}{\sigma }x\right) }{\varPhi \left( \frac{\sqrt{2\gamma }}{\sigma }r\right) -\frac{1}{2}}, \quad x\in [0,r]. \end{aligned}$$

Hence its stationary moments can be calculated. However, in such cases, an explicit formula for the estimator of $\gamma$ [due to the presence of $\varPhi \left( \frac{\sqrt{2\gamma }}{\sigma }r\right)$] is not available and it needs to be computed numerically. Nonetheless, we can apply our parameter estimation method to Brownian motions with drift parameter $\mu \in \mathbb {R}$ on $[0,r]$, reflected at 0 and $r$, to obtain explicit form of estimators and their asymptotic properties. In this case, the stationary density is given as a simple modified exponential distribution $p(x)=2\mu {e}^{2\mu x}/({e}^{2\mu r}-1)$ for $x\in [0,r]$. In order to expand the applicability of our methods, we are currently working on the generalized ROU model with jumps [cf. Xing et al. (2009)], where the parameters of interest would be jump intensity as well as infinitesimal drift. We observe that our method provides a versatile approach in estimating parameters for the ergodic diffusion processes, in particular, with state constraints.