Physics and Mathematics as Interwoven Disciplines in Science Education

Abstract

The relationship between physics and mathematics is reviewed upgrading the common in physics classes’ perspective of mathematics as a toolkit for physics. The nature of the physics-mathematics relationship is considered along a certain historical path. The triadic hierarchical structure of discipline-culture helps to identify different ways in which mathematics is used in physics and to appreciate its contribution, to recognize the difference between mathematics and physics as disciplines in approaches, values, methods, and forms. We mentioned certain forms of mathematical knowledge important for physics but often missing in school curricula. The geometrical mode of codification of mathematical knowledge is compared with the analytical one in context of teaching school physics and mathematics; their complementarity is exemplified. Teaching may adopt the examples facilitating the claims of the study to reach science literacy and meaningful learning.

Physics is not mathematics, and mathematics is not physics. One helps the other. But… Richard Feynman ( 1965 )

1 Introduction

Much has been said about mathematics in relation to the physics curriculum. A common research effort in physics education considers what mathematics does to science and expands on how physics educators may manage this reality more effectively (e.g., Krieger, 1987; Pospiech et al., 2015; Redish and Kuo, 2015). Researchers investigate the problems that students have in applying mathematical tools, revealing the features of such an application. Pospiech et al., (2015) reported about the variety in students’ ability to preserve physics meaning in manipulating mathematical expressions. Other researches expanded on the manners that mathematics is used in physics instruction and the delicate multidimensional balance between formal representation and conceptual meaning (Karam and Krey, 2015). We intend to add to these efforts, considering physics and mathematics knowledge with respect to its representation in teaching. For that, we adopt a holistic perspective, putting to the fore different interests, values, structures, and forms of utilization of the two areas of knowledge.

The relationship between mathematics and physics is often perceived in education in a simplified and obscure manner. By studying the beliefs of students and teachers, one may find that some physics educators consider mathematics as a higher domain of physics, which is more solid, exact, and sophisticated. Educators often stipulate learning physics by a solid mathematics background. Others consider mathematics nothing more than a tool for physics, thus ignoring the specific nature of mathematics as well as of physics and their values. Still others believe that mathematics is an intellectual game, while physics treats real experience, the model-reality relationship. These and other beliefs documented in studies (e.g., Vinitsky and Galili, 2014; Vinitsky, 2015) are rooted in people’s activities and practical requirements as well as in the vast span of individual abilities, cognitive preferences, and worldviews.

This article tries to clarify the essential aspects of the physics-mathematics relationship. It complements the existing discourse of physics education by introducing a view of mathematics and physics as interwoven and interacting disciplines, which are nevertheless different in their nature and interests. This perspective reveals essential aspects of teaching contents leading to design of a more inclusive and representative curriculum of both disciplines. It may also encourage a better understanding of the disciplines by teachers of both classes projecting on the meaningful teaching and learning (Vinitsky and Galili, 2013).

Considering mathematics and physics as cultures structured in the triadic manner, nucleus-body-periphery (Tseitlin and Galili, 2005) may effectively facilitate the appreciation of the difference between these two domains of knowledge. In resolving complexity, the major resource leading to understanding the nature of the physics-mathematics relationship is the history of science. Therefore, we need to review the pertinent history to learn about the specific features of both domains.

We first deal with the existing complexity of the physics-mathematics relationship through considering their interaction along a historical path (section 2). We then try to clarify the symbiotic nature of that relationship (section 3) through using the triadic structure of a discipline-culture and classify various activities possessing mathematical nature (section 4). In the following, the article touches upon the difference between the geometrical and algebraic accounts of the same subjects taught in school classes, showing their difference. We argue for their complementarity in knowledge presentation (section 5). We conclude by considering the meaning of the presented analysis and its curricular implications (section 6).

2 Introduction to Interactive Complexity

Close relatives often have a complicated relationship and such is the case between physics and mathematics. As Einstein put it in a wise comment: “…one can really quarrel only with his brothers or close friends; others are too alien [for that]” (Einstein, 1949, p. 688). Physics and mathematics are two different areas of human intellectual activity which are deeply entangled and mutually dependent. Although the two remain distinct, they reciprocally contribute to each other and establish a symbiosis. A historical path might be illustrative here to help uncover the features of this particular relationship.

In classical Greece, when what we now call science was still young, physics was a part of a philosophy dealing with the causes of natural phenomena. They were considered in terms of pure qualitative accounts as processes taking place in time. Aristotle thoroughly distinguished physics from mathematics. For Aristotle, mathematics scrutinized the time independent [eternal] features and qualities of abstract objects, or their ideas (Ross, 1923/1995, p. 64; Losee, 2001, p. 12).¹ On the other hand, the term “physics” came from the Greek phusis, which, as pointed by Heidegger, suggested becoming or revealing (Inwood, 1999, p. 137). Indeed, the term is still used today in that sense, for example, when we say, “Tell me about the physics of the phenomenon”, referring to the mechanism and the processes resulting in the observed reality. This was Aristotle’s distinction between the two realms, on the one side, the knowledge of eternal and the static (mathematics) and, on the other, the dynamical and changing processes (physics).

Just after Aristotle, in Hellenistic science, the mathematical accounts of nature strongly entered into physics. This was a radical change: discovering general causes became insufficient in application and account. Euclid, Heron, and Ptolemy introduced exact mathematical tools into optics; Aristarchus, Hipparchus, and Ptolemy into astronomy; and Archimedes and Heron into mechanics.² Even so, one cannot claim that there was an abrupt revolutionary change, but rather a strong change of preferences. For example, already in Hellenic science, Eudoxus provided an account for the motion of the planets in accordance with the principles placed by Plato—circular, geocentric, and uniform motion. It was a superior, mathematically accurate product which anticipated the modern method of expansion in spherical harmonics. However, this magnificent invention was abandoned because of its complexity and was replaced by the Hellenistic account of celestial motion by means of deferent and epicycle due to Apollonius, Hipparchus, and Ptolemy (e.g., Dreyer, 1953, pp. 88–108). The latter method, even if it allowed a simpler quantitative account, was in a striking contradiction with the principles of Aristotelian physics and, in fact, split astronomy between mathematical and physical (Dijksterhuis, 1986, p. 68). The issue instigated a continuous critique through centuries.³

During the medieval period, the scholars of the Islamic world (which included a puzzle of Muslim, Jewish, and Christian contributors⁴) continued this trend of involvement mathematics in scientific exploration, especially in astronomy (geodesy) and optics.⁵ In Europe, Grosseteste and Roger Bacon⁶ argued for involving mathematics in natural philosophy. The scholars of the Merton School in Oxford, known as the Calculators for their expanding of mathematical relationship and quantification beyond mathematics, had already considered abstract motion by introducing its basic types of uniform and “uniformly changed” (constant acceleration) as well as instant velocity, as we still teach and learn at school. In fact, the Calculators were the first to see the functional dependence of distance and time—the mid-speed theorem—the formulas we often ascribe to Galileo⁷ in regular teaching. Oresme in Paris further encouraged mathematical intrusion into physics by introducing the graphical representation of motion in symbolic terms, as practiced ever since.

With the transition to modern science, in the seventeenth century, Galileo adopted the results of the medieval scholars and expanded their mathematical account of the imaginary world into the real world of physics experiments. For that, it was considered to be the founder of the modern science (Einstein, 1973). Galileo adopted the doctrine that nature, the real world, was originally designed in terms of geometrical objects⁸ and as such was to be understood in the same terms, that is, by mathematics. The problem became to identify the appropriate correspondence between the mathematical design and physical appearance—mathematical truth and physical truth—and to demonstrate their correspondence.⁹ For that, Galileo introduced the new method of employing experimentation and quantification, a striking change from the abstract methods of medieval physics. He knew very well that “…mathematical subtleties do very well in the abstract, but they do not work out when applied to sensible and physical matters” (Galilei, 1632/1967, p. 203).¹⁰ The experimental method required great intellectual effort when attempting to prove claims, as each step was fraught with errors, and its great successes came alongside even more numerous failures. This may be illustrated by the fact that the glorification of mathematical design, epitomized in the metaphor of The Book of Nature (Galilei, 1623/1957, p. 237) was made by Galileo in the context of his erroneous claim about the location of comets, an inadequate critique of Tycho Brahe’s view. The metaphorical book of nature apparently possessed contents, concepts, and ideas, beyond pure mathematical objects. The former which had to be infused with meaning gleaned from the real physical world and cemented together by means of mathematics; these together formed a theory.

Fig. 1

The medieval image (1230) of God as an architect of the universe from amorphous mass

The role of mathematics in revealing of the “laws of nature” continued to increase. For Kepler (1621), Descartes (1644), Huygens (1690) and, of course, Newton (1678), mathematical form was already essential in representing the world harmony. Newton produced a theory of mechanics that Galileo missed in his book of nature. It was the first fundamental theory of the Modern Science. Newton titled his book, The Mathematical Principles of the Natural Philosophy to distinguish from Descartes’ Principles of Philosophy. Both texts addressed the physical theory of the world. Yet, Newton’s advance was in making the theory itself mathematical, while Galileo had only used mathematics in the account models of reality in specific cases (falling, projectiles, elastic beam, etc.¹¹). Classical physics proceeded within the new standard − seeking a mathematical account of reality. However, the complexity of this norm and the mathematical tools available limited scientists at each period. Thus, Descartes skipped over any mathematical account of his central idea of vortex theory of the world machinery, and Newton failed to produce as a powerful theory of light as he did in mechanics. His theory of light remained empirical and qualitative (Shapiro, 1984; Galili, 2014).

The progress in mechanics that followed surpassed Newton’s Principia in both the complexity and the novelty of the mathematical account. Euler (1736), d’Alembert (1743), Lagrange (1788), and others established Analytical Mechanics by manipulating abstract mathematical forms in their accounts of motion by means of models, using more complex mathematical tools and new concepts such as energy, Lagrange function, and variation principle. Calculus replaced geometry which had been considered by Galileo¹² to be the best tool to treat physics knowledge and was still considered as a major tool in Newton’s Principia. Its most striking feature was the fact that Newton’s laws became central in the quantitative theory.¹³ In its later version, this theory became the classical mechanics which already derived Newton’s laws through variation principle of the least action (e.g., Landau and Lifshitz, 1976, p. 9).

In optics and electricity, the process of mathematization was slower but not less indicative. Newton failed to provide a mathematical theory of light which required differential equations with partial derivatives and the calculus of several variables. Major progress took place in the nineteenth century when the Fresnel-Arago wave theory could account for light diffraction and interference through the application of Huygens principle. It by far surpassed Newton’s idea of light rays deflection by the hypothetical attraction of light particles. The interference of light waves was a critical innovation feasible due to the growth in mathematical ability (Kipnis, 1991). What Huygens could not do, the new wave theory could: it accurately applied interference to waves. Yet, the enigma of the medium for light propagation (already faced by Aristotle) remained. The luminiferous ether was ascribed unrealistic features and escaped any detection (Whittaker, 1960). Yet, the problem was perceived as temporary. Ray theory succumbed to the overwhelming mathematical accuracy reached by wave optics and its precise account of numerous phenomena. The numerical successes were convincing, even if nobody knew the physical processes underpinning light waves.

2.1 Is Physical Theory a Set of Equations?

Significant progress towards the physical account was due to Faraday’s invention of lines of force, electric and magnetic. In a sense, this model revived the Aristotelian perspective of interaction in contact instead of the mysterious action at a distance introduced by Newton.¹⁴ The crossing of the lines of force by a conductor caused the electromagnetic induction in it—Faraday’s law. Maxwell promoted Faraday’s physical idea, framing it with the concept of field and making it the basis for his theory of electromagnetism—the first field theory (Maxwell, 1873; Whittaker, 1960). In his complex model, electrical charges (ions) were subject to the influence of a specific medium permeating the space (Darrigol, 2000; Martins, 2005). It was not simple, however, to imagine the mechanism of the interaction, and that was not the only challenge. Maxwell did it. As in the case of light, the mathematical account of electric and magnetic fields and electric charges appeared to be useful and powerful despite the cumbersome physical model introduced by Maxwell, in which electrically polarized matter was twisted and pressed. Yet, even the new theory formally accounted for all electromagnetic phenomena, it left the mechanical model in shade (ibid; Tweney, 2011). Helmholtz, who developed his own theory of electromagnetism (also involving a medium), asked his student, Hertz, to clarify the meaning of Maxwell’s theory. The answer of Hertz (1893/1962, p. 21) became renowned for its striking definition moving to the fore the mathematical account:

I know of no shorter or more definite answer than the following: − Maxwell’s theory is Maxwell’s system of equations. Every theory which leads to the same system of equations, and therefore comprises the same possible phenomena, I would consider as being a form or special case of Maxwell’s theory; every theory which leads to different equations, and therefore to different possible phenomena, is a different theory.

Is a theory just a set of equations? Is the underpinning explanatory model secondary to the equations working well for the “same possible phenomena”? Why did the wrong model of Maxwell, as we now know, produce correct equations? In fact, the success of the equations was not a miracle. Maxwell’s theory was designed to match a number of already known empirical laws: Coulomb’s law of the interaction between charges (equivalent to Gauss law), Faraday’s law of induction, Ampere’s law of interaction of current wires, and Bio-Savart magneto-static law for a long wire.¹⁵ Those empirically backed results guided Maxwell in his model, ascribing translation and rotation to the imaginary ether causing its stress, tension, and vortices represented by electric and magnetic fields (Darrigol, 2000, pp. 156, 260; Martins, 2005). The equations constructed by Maxwell for the fields effectively included all empirical laws. Therefore, the same set of equations remained valid in both Lorentz electrodynamics, which preserved ether, and in Einstein’s theory of special relativity, which dismissed the ethereal medium as superfluous.¹⁶ Eventually, the quantum field theory replaced the immersion in field with exchange of photons. Even so, nobody dismissed Maxwell’s field equations: they remained the major tool for problem-solving where the classical electromagnetism is valid. In quantum field theory, continuous fields and Maxwell equations remained valid as a model depicting collective behavior of large numbers of photons. Thus, equations play a very important role, but they do not fully represent the meaning of a theory. For that, more is required.

2.2 Form and Content

The interplay of physics and mathematics touches upon the important aspects of form and content in physics theories. For instance, what is common between the gravitational force acting on a pendulum and the elastic force acting on a body connected to a spring? The two are described by different formulas:

$$ F=- mg\ \alpha \kern0.5em \left( for\ smal\ \alpha \right)\kern0.5em \leftrightarrow \kern0.5em F=- kx $$

Though different in appearance, the two formulas share the same mathematical structure (linear functional dependence of force) and therefore point to a similar account of motion in the same terms of periods and oscillations, where mg replaces k and α replaces x. Such similarity in form may reveal an analogy between the mechanisms of the considered phenomena, while leaving space for their contextually different interpretations (e.g., Gorelik, 1959, p. 61). Likewise, the equations depicting oscillations in an RCL-circuit and those describing a mechanical pendulum (e.g., Alonso-Finn, 1967, p. 643) may suggest a certain similarity of the mechanisms underpinning these two physical settings. Understanding the nature of such an analogy implies a deeper understanding of physics, which is essential and not obvious. Yet, the similarity of mathematical form in the account of linear and rotational motions (e.g., Walker, 2008, p. 288), although helpful in problem-solving, masks the essential conceptual difference between linear and rotational motions. There remains the need to understand, they are “similar, but in what?” Though different, both linear and rotational motions yield conservation of linear and angular momentum, respectively (Hecht, 1994, pp. 116, 267). The formal proximity of the two is due to the continuous spatial symmetry, yet of different types, translational and rotational.

Physicists do not know in advance whether a prediction based on formal mathematical considerations will be confirmed by reality. For example, Maxwell’s equations would become more symmetrical if there were magnetic monopoles akin to electrical charges, but we know of none. Even so, mathematical structure serves as a suggestive guide which may lead to a new understanding through abduction. Despite the lack of symmetry for the absence of magnetic charges, Maxwell created symmetry of other terms in his third and fourth equations—the Faraday’s law of induction and the Ampere-Maxwell law—by introducing a new concept of displacement current, a counterpart of the electrical current (e.g., Alonso-Finn, 1967, p. 656). In that case, the symmetry of form guided to the understanding of current continuity in a more general sense as needed in an open electric circuit (that containing a capacitor).

2.3 Why Is Mathematics Successful?

The complexity of the physics-mathematics relationship has continued to occupy scientists and mathematicians. “Why is mathematics so successful?”—asked mathematician Wigner in 1969 (Wigner, 1995) referring to the success of mathematics in contemporary physics. As a physicist, Einstein (1921) dampened this enthusiastic claim when he said, “To the extent that the statements of mathematics represent reality, they are not certain, and to the extent that they are certain, they do not represent reality”. Nevertheless, the success of mathematics remains unquestionable. Actually, Einstein went further: “The most incomprehensible thing about the world is that it is at all comprehensible” (comprehensible, but not mathematical).

At first sight, it may seem mysterious that the effectiveness of science is echoed by the effectiveness of mathematics. However, an answer to this mystery may be suggested by an evolutionary perspective on the consolidation of human knowledge and the construction of its mathematical account. From an evolutionary perspective, corrective adjustments are repeatedly made to realign the mind to reality at each of multiple iterations during a long history of trial and error. A great number of failed attempts and corrections preceded the mathematical constructs presently used by us as successful accounts. Given this history and also the fact that “only a fraction of all mathematical concepts are used in physics”¹⁷ (Wigner, 1995, p. 229) the considered perfect match seems a lot less mystical. A better metaphor may be of a suit perfectly following the line of a body only after a great effort was invested by a tailor.¹⁸

Observing the success of mathematics, one may mention that different physical theories employ different mathematical apparatus. Each mathematical framework reflects certain specific aspects of reality in the mosaic of different pictures of the world. Einstein himself gave more than a hint regarding the relationship between mathematics and reality, describing Euclid’s geometry as the first physical theory (Einstein, 1921/2008):

Geometry thus completed is evidently a natural science; we may in fact regard it as the most ancient branch of physics… Its affirmations rest essentially on induction from experience, but not on logical inferences only. We will call this completed geometry “practical geometry,” and shall distinguish it in what follows from “purely axiomatic geometry.” The question whether the practical geometry of the universe is Euclidean or not has a clear meaning, and its answer can only be furnished by experience.

2.4 What Is There, in Physics, Beyond Math?

Physicists continually insist that physical claims are different from mathematical ones, and that the former are fundamental in a physics theory as providing meaning to the mathematical formalism:

A physical understanding is a completely unmathematical, imprecise, and inexact thing, but absolutely necessary for a physicist. (Feynman, 1966, p. 2–1) (Emphases added)

Physics is not mathematics, and mathematics is not physics. One helps the other. But in physics you have to have an understanding of the connection of words with the real world. It is necessary at the end to translate what you have figured out into English, into the world, into the blocks of copper and glass that you are going to do the experiments with. Only in that way can you find out whether the consequences are true. This is a problem which is not a problem of mathematics at all. (Feynman, 1965, p. 55)

Much earlier, Maxwell (1873, x-xi) referenced Faraday (1952), who was well known for his avoiding of any mathematics. Maxwell’s words were revealing:

… before I began the study of electricity I resolved to read no mathematics on the subject till I had first read through Faraday’s Experimental Researches of Electricity. I was aware that there was supposed to be a difference between Faraday’s way of conceiving phenomena and that of the mathematicians, so that neither they were satisfied with each other’s language. I had also the conviction that this discrepancy did not arise from either party being wrong…

As I proceeded with the study of Faraday, I perceived that his method of conceiving the phenomena was also a mathematical one, though not exhibited in the conventional form of mathematical symbols. I also found that these methods were capable of being expressed in the ordinary mathematical forms, and thus compared with those of the professional mathematicians.

For instance, Faraday, in his mind’s eye, saw lines of force traversing all space where the mathematicians saw centres of force attracting at a distance: Faraday saw a medium where they saw nothing but distance: Faraday sought the seat of the phenomena in real actions going on in the medium, they were satisfied that they had found it in a power of action at a distance impressed on the electric fluids.

What Maxwell saw as mathematical skill was an ability of Faraday to imagine a concrete and exact mechanism of certain phenomena which is unobservable per se, but existed in the sense of embedding physical manifestations.¹⁹

Another illuminating example of this intimate relationship, indispensable for the understanding of physics, may be perceived in the establishment of Einstein’s Theory of Special Relativity. Historians suggest that Special Relativity emerged in the course of intensive exploration of several different accounts of electromagnetic phenomena.²⁰ Alternative approaches yielded various mathematical formulas such as the Lorenz transformations, the Lorentz-Fitzgerald contraction of length, and the Lorenz “local time.” Then, Einstein entered the arena bringing a new physical structure of a theory as a knowledge drawing on a particular set of basic principles and concepts (Einstein, 1973). Mathematics could not resolve the debate over the different interpretations; something essential, the heart of the theory, was to be addressed. Darrigol (2000, p. 394) wrote:

Although the overall organization of Einstein’s theory was unique, its only major novelty was the reform of the basic concepts of space and time. To which we may add a new derivation of the Lorentz transformations without reference to the Maxwell’s equations, and a new derivation of the dynamics of the electron without specific model.

This “only major novelty” represented the greatest of conceptual revolutions in which people changed their account of nature, which was important far beyond physics. Many scholars²¹ discussed the revolution in people’s conceptions of time and space.²² Nersessian (1984, p. 134) specified some of the changes introduced by Einstein in 1905:

The shift from being a ‘state’ [of aether] to being an ‘independently existing thing’ [electro-magnetic field] is a major conceptual change, which, in this instance, occurred in conjunction with major changes in the fundamental concepts ‘space’, ‘time’, and, indeed, ‘physical’ itself.

These gross conceptual changes in the worldview and scientific epistemology provided classical electromagnetism (and the whole of physics worldview) the status of a relativistic foundation without any major change in the mathematical apparatus (Darrigol, 2000). The leap caused by Einstein was not in the mathematical account of reality per se, but rather in the fundamental physics concepts (the idea of a four-dimensional world, space-time unification, operational definitions of basic concepts, the requirement of covariance of physics laws). Yet, the further progress—the move to the general relativity and quantum theory—did require new mathematical methods, tensor analysis in relativity, and operators and generalized functions together with functional analysis in quantum physics. Physicists looked for the tools appropriate to match the new vision of the natural order: a covariant form of physics laws, a discrete spectrum of observables, and a wave-particle duality.

2.5 Who Takes the Lead?

The symbiotic relationship may pose the question whether science steers mathematics or vice versa? It seems that the answer oscillated throughout history. Perhaps the first example of mathematical priority in guiding knowledge exploration was the Pythagorean all-inclusive paradigm of nature as organized in accordance with proportions of natural numbers. For instance, Pythagoreans considered the distance from the Earth to the Moon and the other planets to fit numerical harmony (music of spheres²³), and Philolaus inferred the existence of a never observed central fire (Hestia) and a counter-Earth planet (Antichthon) only so as to reach the sacred number of ten.²⁴ But above all, it was the Pythagorean idolization of circular uniform motion (the theory of the world as concentric spheres was the apex of its implementation). Though not precisely observed but rather presumed, it became the most fundamental principle in the organization of cosmos and was heavily imprinted into the whole development up to modern science. The paradigm of numerical harmony greatly influenced the thinking of Plato, the founder of the theoretical approach to the knowledge of reality based on a mathematically driven epistemology. Though Aristotle gave another foundation to physical theory, namely causative and objective qualitative principles, a great many scientists (Copernicus, Galileo, Kepler, Descartes, Huygens, Newton, to name a few) retained some form of the Pythagorean-Platonist worldview in constructing modern science.

Perhaps the most important epistemological influence of the mathematics was imposing the procedure of a proof as an unconditional norm of any scientific claim. That radical change could be taken as the beginning of the Western science—the claims are proved, demonstrated in accordance with certain initially established rules.²⁵ This trend proceeded from the pre-scientific period (pre-Socratic natural philosophy) to the Hellenistic science where it reached its climax in the activities of Euclid and Archimedes (Neugebauer, 1993, p. 148; Montgomery and Kumar, 2016, p. 158). Using the Greek terms, it was the preference of knowledge as episteme over that of gnosis (e.g., Brunschwig and Lloyd, 2000) in the basic features of the nature of science, as we know it now.

It would be superficial, however, to equate the Platonist perspective with Pythagorean number mysticism. The renowned inscription above Plato’s Academy entrance in Athens of 387 BCE announced “Let no-one ignorant of geometry enter here”. Given that geometry was not a subject of learning or investigation in the Academy, one may interpret Plato’s intention as pointing to the methodological paradigm. Geometry—a cluster of hierarchically organized knowledge elements (axioms, postulates, definitions, theorems, and solved problems)—seemed to be an exemplar of a theoretical product and an effective tool for acquiring knowledge of logic and ideal forms to which the real world presented, in Plato’s view, only an imperfect manifestation.

Yet, Hellenistic science brought about a swing in that respect.²⁶ Archimedes, who excelled in both mathematics and physics, may serve to represent that period. It appears that in his mathematical investigations, Archimedes was guided by his previously performed mechanical measurements (triangulating weighing, equilibrium, pertinent mechanical models) (Pedersen and Pihl, 1974, pp. 110–113). In several places, he wrote about this approach (Archimedes, 1952a, p. 527):

…a certain geometrical theorem which had not been investigated before but has now been investigated by me, and which I first discovered by means of mechanics and then exhibited by means of geometry.

Further generalized, his method appeared in his writing to a colleague (Archimedes, 1952b, p. 569):

The proofs then of these theorems I have written in this book and now send to you. … I thought fit to write out for you and explain in detail in the same book the peculiarity of a certain method, by which it will be possible for you to get a start to enable you to investigate some of the problems in mathematics by means of mechanics. This procedure is, I am persuaded, no less useful even for the proof of the theorems themselves; for certain things first became clear to me by a mechanical method, although they had to be demonstrated by geometry afterwards because their investigation by the said method did not furnish an actual demonstration. But it is of course easier, when we have previously acquired, by the method, some knowledge of the questions, to supply the proof than it is to find it without any previous knowledge.

Mechanical experimentation guided Archimedes in his illuminating method of mathematical proof by exhaustion, providing unprecedented results regarding the center of gravity of complex objects, the laws of levers, and the areas and volumes of different solids and figures, flat and curved.

The next swing took place in medieval science. The Merton School in Oxford and Oresme in Paris followed a rationalistic philosophy in the program producing concepts of instantaneous velocity and acceleration—the mathematical account and representation of abstract motion which later led Galileo in his physical studies and provided an ideological basis for the invention of calculus by Newton and Leibnitz led by new physics needs.

In the following period of modern science, it was already not a swing in leadership but rather a fusion of roles. In the activities of Galileo, Kepler, Descartes, and Newton, one may clearly recognize the symbiotic relationship between mathematics and physics in which both partners led in turn. Thus, lacking a theory of mechanics, Huygens inferred the equivalence of his newly introduced centrifugal force with gravitational force. He drew solely on the similarity between the mathematical account of falling objects (Galileo’s result) and his own mathematical account of a body leaving a circular path in the straight motion along the tangent line (Huygens, 1659/1703).²⁷

Regarding modern science, one may claim that a practically synchronic development took place (Tzanakis, 2000, pp. 111–121). Newton developed calculus to match the immediate need in classical mechanics, the account of gravitational interaction varying in distance between objects possessing volume. Similarly, vector analysis was developed for Maxwell’s theory of electromagnetism by Gibbs and Heaviside to fill the need for representing three-dimensional abstract concepts (field, force, polarization) (Crowe, 1967). Dirac’s delta function was required by the account of continuous observables in quantum theory (Dirac 1958).²⁸ The mathematical account of quantum theory (von Neumann, 1955) was a necessity for the new theory representing the physical reality of the micro-world.

In contrast, the diachronic relationship is known from cases in which physicists looked to mathematical tools that were developed in the past but that were later abandoned. That happened in developing Einstein’s theory of special and general relativity which found appropriate tools developed earlier in mathematics, the non-Euclidian geometry of Lobachevski and tensor analysis by Ricci-Curbastro and Levi-Civita (Weinstein, 2012; Gutfreund and Renn, 2015, p. 22).

When physics enters unknown areas, especially those where the scale is vastly different from our regular environment, the mathematical account may provide the only meaning to the new physical objects. Thus, by solving the Schrodinger equation for the hydrogen atom, we can say something about the electron states and predict their spatial “probability distribution” within the atom. Since elementary particles are not directly observable, the term electron actually represents a compendium of the physical features mathematically represented and proved to be reliable in the experiments of certain types. This is what we mean by “knowing” what an electron is. Mathematical considerations led elementary particle physics to the discovery of antimatter due to the solutions of Dirac’s equation and of the omega-baryon drawing on the symmetry of the introduced table of quarks.²⁹ Astrophysics is another area where mathematics often leads exploration of reality in vastly different scales of time, distance, mass, and temperature, which are all inaccessible to laboratory experimentation. Until recently, investigation of gravitational waves was the realm of solely theoretical/computer manipulation with the equations of general relativity theory.

One may summarize in this respect. At the beginning of science and mathematics in the classical sense (as systems of knowledge arranged in fundamental theories), mathematics or physics could lead each other in accordance with the prevailing epistemology in the particular period. Starting with modern science, characterized by the methodological synthesis of rationalism and empiricism, the two realms were in a reciprocal relationship, each contributing to the other in parallel development.

3 Further Clarification of the Relationship

Our historical examination of the connection and interaction of physics with mathematics testifies that these two distinct areas of knowledge have mutually supported each other and were often explored by the same individuals. It would be inadequate, however, to adopt the common practice and to define mathematics solely as either a tool, language, or ultimate form of physical theory. To clarify the actual relationship, one should be explicit about the nature of physical and mathematical knowledge.

Mathematics operates with abstract, strictly defined objects. The most fundamental of these have been inspired by reality, but are simplified and idealized. Precise rules of logic relate these mathematical constructs combining them into clusters of coherent knowledge—mathematical theories and their derivatives. In a sense, one may define this activity as a cognitive game (Wigner, 1995).³⁰ The two halves of the game seem equally important: the objects being clearly defined and their logical treatment being rigorous (Feynman, 1965).³¹ Mathematics creates and operates in an imaginary (Platonic) world investigating the properties, features, and relationships between the abstract objects that make up this special world. These relationships can be far from obvious and mathematicians invest a great deal of imagination and intellectual effort in constructing the pertinent knowledge, which is often intricate and sophisticated.³²

Physics, by contrast, deals with the real world of inanimate objects creating theories regarding the world order, its regularity and embedded causality. Where it can, physics tries to be as rigorous as mathematics, but quickly finds that this is often impossible and, in a sense, unnecessary. Facing rich and complex reality, physicists must not be too strict, but flexible in rigor, and produce approximate idealized models trying not to overlook reality in a particular perspective.³³ As a result, it is necessary to compromise on rigor in favor of inclusiveness in a fundamental theory, especially at the stage of theory construction. In physics, the strength of a theory depends upon its feasibility, its success in problem-solving and successful predictions, the span of its validity in accounting for real objects and natural phenomena. Consequently, physics tempers generality with pragmatics, certainty with tentativeness, coherence with eclecticism, and precision with approximation. The grand ambition of any physics theory to reach an inclusive and precise account of Nature is always limited by certain category of objects, kind and dimensions, distance from the extremely versatile reality.

For all their difference, however, mathematics and physics remain closely interwoven in our culture which leads to recognizing their complementarity. Yet, this complementarity may acquire a specific meaning in a scientific investigation. It draws on the idea of Bohr in addressing the mutually exclusive accounts of the particle-wave nature of objects in the micro-world (Bohr, 1949/1959). Within this vision, complementarity suggests that the accuracies in determination of two conjugated quantities are in inverse relationship. Migdal (1990) applied this perspective to mathematics and physics. He observed that the more a study focuses on the conceptual qualitative account of reality, the less precise is its formal mathematical account, as if one comes at the “expense” of the other. Perhaps this is what Einstein (1921) meant when he stated: “As far as the laws of mathematics refer to reality, they are not certain; and as far as they are certain, they do not refer to reality”? Poincare (2003, p. 124) suggested actually the same when he wrote: “What is gained in exactness [math] it has lost in objectivity [physics]”.

4 A Holistic Perspective

4.1 Discipline-Culture Model

Many metaphors have been used to represent the nature of mathematics. For example, it is common to compare mathematics with language and in particular with grammar, as Courant and Robbins (1996) wrote:

Formal mathematics is like spelling and grammar – a matter of the correct application of local rules. Meaningful mathematics is like journalism – it tells an interesting story. Unlike journalism, the story has to be true. The best mathematics is like literature – it brings a story to life before your eyes and involves you in it, intellectually and emotionally.

Feynman added: it is our language and logic by which we know what step to make next (Feynman, 1965, p. 40): “Mathematics is a language plus reasoning; it is like a language plus logic. Mathematics is a tool for reasoning. … By mathematics it is possible to connect one statement to another.” This perspective has inspired the more inclusive metaphor, which is particularly popular in science education at schools, of mathematics as “the physicist’s toolkit”.

Is this enough for school education? Historians may disagree and show that pragmatics often hides the nature of mathematics behind its products and the rules to act. The similar projection of this perspective to physics may lead to identifying physics with its products. In that, one may end up ignoring the genus of both mathematics and science. Though practically effective and formally valid, the consumer perspective misses the important contents and may lead to the perception of physics solely as the way to reach its products missing the worldview and values shared in the community of scientists and educators.³⁴ Schools need to find a more appropriate way to represent the image of science and mathematics in regular teaching, which would not stray too far from either formalism or relevant conceptual knowledge. A presentation of scientific knowledge as a discipline-culture may provide a more adequate picture through creation of cultural content knowledge in a certain domain (Tseitlin and Galili, 2005; Galili, 2012).

The discipline-culture model represents the structure of a fundamental theory in physics using a triple code. The triadic structure includes a nucleus, a body, and a periphery. With regard to a theory, the nucleus contains the fundamentals (principles, paradigmatic model, and basic concepts of ontological and epistemological nature). The body contains the knowledge elements constructed using the fundamentals and affiliated empirical regularities, whereas the periphery includes alternative, rival or challenging concepts, ideas, and constructs conflicting with the nucleus in the relevant domain of reality (Fig. 2).³⁵ It is suggested that this model may support a proper representation of the domains of mathematics and physics and better illustrate the relationship between these two realms.

Fig. 2

Discipline-culture structure of a theory

By contrast, the elements of the periphery strengthen the identity of the nucleus, the foundations of the theory. Inclusion of the conceptual debate often provided by addressing the historical discourse makes the disciplinary knowledge cultural. Furthermore, the idea of periphery helps to represent the knowledge of two competing theories. For example, the two competing theories of classical and relativistic mechanics may be represented by the structure shown in Fig. 3.

Fig. 3

Comparison of two fundamental theories, classical and relativistic mechanics

Such a representation illustrates two important principles: (1) the nuclei of the different fundamental theories are essentially different—each is located in the periphery of the other, (2) there are elements of knowledge which may be treated by both theories. For example, the space-time concepts, while belong to nuclei of both theories, are essentially different. At the same time, though the mathematical accounts of relative motion in both theories are different, the relativistic account yields the classical result in the limit of infinite light speed (c→∞).³⁶ Elements such as these may be referred to the overlap of the two bodies of knowledge (the shaded area in Fig. 3). This way, one may represent the essentially compatible and incompatible elements of the two theories.

Here, we may expand that approach to represent physics and mathematics as knowledge domains (Fig. 4) and consider the status of knowledge elements within the triadic structure of the discipline-culture model (Vinitsky and Galili, 2014). Thus, the nucleus of physics will include ontological claims regarding reality, concepts, and conceptions. There will also be epistemological claims defining the ways of adoption and verification of knowledge, such as empirical testing and logical rules. The nucleus of mathematics, in its turn, will address the foundations of mathematical theories of abstract well-defined objects, certain systems of axioms (fundamental assumptions), and rigorous logical rules to follow in producing knowledge elements and proving their validity. While this representation misses the distinction between different theories within physics and mathematics, it may still facilitate the appreciation of the difference between these domains of knowledge and represent their relationship.

Fig. 4

Triadic structuring of the relationship between mathematics and physics

Physics and mathematics may share certain mathematical tools, but they keep with different epistemological commitments and operational meanings. Therefore, merely mentioning mathematical forms may be insufficiently representative, since the same elements may be consumed differently in physics and mathematics classes and textbooks, doing “math in math” and “math in physics” (Feynman, 1965; Redish and Kuo, 2015). Such are the knowledge elements located in area I in Fig. 4—the overlap of the two bodies of knowledge.

4.2 Examples of the Classification

The overlap of Area I (Fig. 4) is of special interest. It may be illustrated by the concept of derivative. In physics, the derivative establishes the instantaneous velocity and acceleration, specific heat capacity, conservative force, and density. In their use, taking a derivative implies a mere replacement of functions (sin with cos). However, from the perspective of mathematics, derivation deals with the limit of the ratio of infinitesimal increments, the uncertainty of the type $\frac{0}{0}$. Perceived as a problem, it was first treated by the scholars of the Merton School in Oxford in the fifteenth century who introduced the “specific” (intensive) concepts. Today, it is fully treated in calculus, while physics teachers introduce the instantaneous velocity without even mentioning the problem of uncertainty. Derivation is solely a technical procedure.

Similarly, area I includes specific “using physics in doing math” (Redish and Kuo, 2015), the manipulations without full recognition of mathematical rigor. Physics students may write in short hand $\frac{1}{0}=\infty$ —the expression lacking meaning in mathematics. A more serious example of this kind is the delta function of Dirac. Widely used in quantum mechanics, it became legitimate in mathematics only later as a “generalized function” (Schwarz, 1950).³⁷

Area II elements of mathematical knowledge include the treatments of irrational and transcendental numbers which attracted much effort to see whether they can find any regularity in the infinite fractions representing them.³⁸ While this and other problems possessed essential difficulty within certain mathematical theories,³⁹ they could obtain an approximate iterative solution with any accuracy required in practice.⁴⁰

Area III includes interesting objects often ignored in school curricula. Such is, for instance, dimensional analysis—manipulation with units of physical entities as if they were numbers in accordance with physics laws relating the corresponding entities. Since Pythagoras, mathematics has been active in the realm of pure numbers. Yet, physics deals with quantities possessing dimensions (sec, kg, watt) and the laws relating them organized in theories. The specific nature of manipulation among labeled quantities becomes striking from the very start—a special understanding of equality sign “=.” For instance, how could newton be equal to kg m/s²? This is not a question for mathematics, but an implication of the fundamental relationship between force, mass, and acceleration—Newton’s second law:

$Newton= kg\cdot \frac{m}{{\mathit{\sec}}^2}$ because: F = m⋅a.

Units of numerous physical entities are represented in dimensional form through fundamental units, such as, for the unit of force, Newton = M⋅L⋅T⁻². Thus, the equality sign “=” implies that any equation in physics has to be balanced in terms of the fundamental units. Dimensional analysis presents an important part of physical mathematics, which establishes strict rules by which physicists can check the legitimacy and dismiss inappropriate mathematical expressions. Thus, without any specific knowledge, a physicist says that the period of a pendulum can be $T=2\pi \cdot \sqrt{\frac{L}{g}}$ but cannot be $T=2\pi \cdot \sqrt{\frac{L^3}{g}}$ and energy can be E = mc² but cannot be E = mc³. Many results in physics could be anticipated (though not proved!) based solely on dimensional analysis.⁴¹

Another specific element of area III is scaling. While mathematical results are indifferent to the numerical magnitude, physical results might be crucially depended on it. Galileo was a pioneer of a specific analysis named scaling. He provided a paradigmatic example of such analysis by demonstrating the nonexistence of giants for mechanical reasons —insufficient strength of human bones to sustain the weight of giants. Indeed, with the increase of height, the strength of bones increases as the square of bone section, that is, in second power, while the load increases as its volume, that is, in cubic power (Galilei, 1638/1914, p. 131). That causes bones to collapse. This result, termed the Square-Cube Law has found essential use in explaining functioning of biological organisms (Allen, 2014, p. 176). For example, the fact that the heating of a body is proportional to its volume and the heat exchange with the environment is proportional to the surface area of the organism determines the features of many animals, influencing evolution (Szirtes, 2006).

Area IV (Fig. 4), the periphery of both realms, mathematics and physics, is important in its own right. This region may include elements/rules important in training for effective functioning in physics and mathematical classes independent of theoretical foundation of both disciplines. Such is “mental math”—performing mathematical calculations without a calculator, memorizing constants and numerical results without actual calculations, “verbal counting,” all remain important in education.⁴² The knowledge elements of other disciplines, such as computer science, science and mathematical pedagogy, addressing subjects from the perspective of different theories of knowledge may also belong here.

5 Geometrical and Algebraic Accounts in Education

Comparing mathematics with physics in holistic perspective, we ignored the difference among mathematical domains, which might be important to education. In particular, geometry and algebra present such fundamental domains of complex relationship.⁴³ The overlap of their body knowledge (area I in Fig. 4) includes the mathematical topics treated in geometric and algebraic ways. We consider them here as being of special interest with respect to education.

In the eyes of a mathematician, algebraic and geometric codifications of certain truth might be equally valid.⁴⁴ Yet, in this way, we may miss the cognitive aspect. Poincare (2003, pp. 120–121) mentioned that there were:

…two kind of minds – logicians like Weierstrass, for instance, and intuitionists like Riemann…. We have those who seek to create an image, and those who restrict themselves to combining empty forms, perfectly intelligible, and deprived by abstraction of all matter.

He clarified: “There is the same difference among our students. Some prefer to treat their problems ‘by analysis,’ as they say, others ‘by geometry’.” Poincare, however, praised this diversity and concluded: “…we must resign ourselves to the diversity of minds, or rather we must be glad of it.”⁴⁵

However, with respect to human perception, there is no symmetry of these approaches—the geometrical approach usually possesses far greater appeal to the wide population of learners and consumers of science. Even the algebraic account may appear as more general and, in a way, formally simpler, some mathematicians reject such simplicity as non-stimulating deep understanding of the subject matter on behalf of students (Arnold, 1998). The history of science provides evidence if one argues by recapitulation with respect to education.

The first algebraic results were introduced in Greek geometric algebra (Neugebauer, 1993, p. 149; Boyer, 1991, pp. 77–79). Katz (2009, pp. 60–66) depicted how the elements of knowledge we ascribe to algebra in our days were shown in Hellenistic mathematics by geometric means (Fig. 5).

Fig. 5

Geometrical form of proving algebraic statements. a (a + b)² = a² + 2ab + b². The area of the big square, side a + b, is divided to show the statement as a claim regarding areas. Lengths and areas are marked. b (a + b)² = 4ab + (a − b)². The area of the big square, side a + b, is divided in certain manner. The smaller square, side a − b, emerges in the center

Feynman (1965, pp. 46–47) pointed to the paramount structural schism in the history of mathematics emphasizing that pre-Hellenistic mathematics (he called it Babylonian though it was practiced also in Egypt as well as in Greece) was different from the Hellenistic one (he called Euclidian) for the fundamental epistemological change—invention of a hierarchical deductive cluster of knowledge elements, a theory by the latter. The opposition he made was that between isolated models and inclusive theory, and it is extremely important for understanding the nature of science. As such, this opposition is often relevant with respect to the ways of presenting algebra and geometry in introductory education. In any case, the image of a hierarchical theory possessing deductive design was commonly associated with the Euclidian theory of geometry. For a long period, from Hellenistic to modern science, in order to prove a statement or claim, it was often demonstrated by means of geometry (Galileo, Huygens, Newton).⁴⁶

Perhaps the most spectacular example of a special appeal of geometry was provided by Nicole Oresme in the fourteenth century by his famous, impressively elegant treatment of infinite series, which had remained unresolved since Zeno, illustrating the inability of Ancient Greeks to account for problems with infinity (Merzbach and Boyer, 2011, p. 241).

Consider two infinite series:

$$ \frac{1}{1}+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+\frac{1}{6} + \dots +\frac{1}{n}+\dots $$

(1)

and

$$ \frac{1}{1}+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32} + \dots +\frac{1}{2^n}+\dots $$

(2)

Both series are infinite and decreasing in magnitude of their terms. The two features—infinite decreasing in magnitude and infinite increasing in number—apparently contradict each other. Yet, the first series is diverging, and the second is converging. Both results were proved by Oresme; whereas the first was proved by regrouping of terms, the proof of the second one was methodologically innovative by its geometric nature (e.g., Babb, 2005). Oresme represented the case by areas (instead of segments) incorporating them all inside the square ABCD (Fig. 6).

Fig. 6

Geometric representation of summarizing series (2) by Oresme (excluding the first term)

In the eyes of Oresme, series (2) corresponded to summing the areas of rectangles ABB₁A₁, A₁B₁B₂A₂, and so on, which were obtained by the subsequent division of the original square by lines B₁A₁, B₂A₂ and so which bisect segments AD, A₁D, A₂D and so on. By appealing to visual areas, the result of this summation became obvious—the area of the square, which is 1:

$$ \frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32} + \dots +\frac{1}{2^n}+\dots \kern0.5em =1 $$

(3)

An amazing change in human perception apparently takes place in the move from an analytical (3) to a geometric (Fig. 6) form of representation of essentially the same mathematical claim. Addressing understanding, Poincare (2003, p. 121) mentioned that “creating an image” might be more elucidating than an “empty form,” though it does not preclude the need for a purely logical and accurate account.⁴⁷ An image of the subject of thinking may guide and stimulate it. Yet, keeping solely with a specific image may miss the exactness and logical rigor. Such “free” thinking in mathematics was addressed by Lakatos when discussing thought experiments (Lakatos, 1978b, p. 65). Lakatos mentioned that Greek mathematicians used the procedure of deykmine—preferring intuitive demonstration to rigor.

5.1 In the Mathematics Class

In education, the issue of imagery-supported thinking reappeared in the debate between V.I. Arnold and J.-P. Serre regarding mathematical education in France (Arnold, 1998, 2002). Serre defended the need for primary instruction drawing on set theory independent of visual geometrical images, which are less universal in representing mathematical ideas. Arnold, however, insisted on geometrical images as being crucial for instigating and guiding comprehension, furnishing human thinking on mathematical problems, proving axioms with meaning.⁴⁸

The first step in relating the world of numbers with the world of images was taken when the mathematicians of Ancient Greece realized the inability to correspond between numbers and length of segments. This achievement of Pythagoreans deserves a passionate presentation in a mathematics class. It claims that rational numbers cannot represent all lengths, and there are some lengths which require irrational numbers, those which do not correspond to ratio $\frac{m}{n}$. No reading on a ruler, measurement, can provide their magnitude exactly. Such was $\sqrt{2}$. Being perhaps the most unobvious fact proved in school mathematics, it often misses its full greatness in school teaching.

To prove the irrational nature of number $\sqrt{2}$, Pythagoreans used the theory of numbers. They showed that the numerator of any hypothetical representation of $\sqrt{2}$ as a ratio can be neither an odd nor even number, and therefore, $\sqrt{2}$ is not a ratio of whole numbers, but a number of a different kind—irrational number, an abstract idea (Table 1, left column). In geometric terms, however, the irrationality of $\sqrt{2}$ implies incommensurability of the hypotenuse and cathetus, the sides of a right-angled isosceles triangle of side-length 1 (Table 1, right column). The shown geometrical proof is rather in Euclidean spirit, though Euclid included the proof by Pythagoreans in his Elements, Book X (Hearth, 1921, p. 91).

Table 1 Proofs of irrationality of $\sqrt{2}$

The algebraic way starts with the assumption that $\sqrt{2}$ can be represented by certain irreducible ratio of real numerals m and n. Squaring the initial expression led to the inference that m was an even number and therefore can be represented as m = 2p. The substitution of 2p instead of m led to the inference that n was even. Being m and n even contradicts the initial assumption of m/n being an irreducible ratio.

The geometric way⁴⁹ to prove that $\sqrt{2}$ is irrational considers a right angle isosceles triangle ABC with right angle B. Comparison of AB (= 1) with AC (= $\sqrt{2}\Big)\ \mathrm{begins}\ \mathrm{with}$placing AB on AC (AB′) and erecting perpendicular B′A′. After establishing the equality of segments, BA′, B′A′, and B′C, one arrives at the need to proceed to the comparison of segments B′C and A′C. At that moment, one discovers being back at the beginning of the process, implying its being endless. This simple and elegant proof not only demonstrates the incommensurability of lengths but also provides an easy way to obtain irrational lengths through geometrical construction.

As another example of a dual account, we may mention the revealing perpendicularity and parallelism of lines by means of vector algebra and geometry. In plane geometry, parallelism is demonstrated using theorems considering pairs of angles. In spatial geometry, the issue of perpendicularity presents a subject of the theorem of “three perpendiculars” (e.g., Kiselov, 1892/2004, p. 222). However, in vector algebra, the perpendicularity corresponds to nullifying the scalar product: (a⋅b) = 0 and the parallelism—to proportionality of the correspondent vector coordinates. Though the algebraic approach is formally simpler, abandonment of the need to manipulate with objects in space significantly reduces cognitive training. To promote spatial imagery, the old pedagogy encouraged students making material models of solids (prisms, pyramids, cones, cylinders) including their combination. All these are removed from teacher’s arsenal when spatial geometry is replaced by vector algebra.

5.2 In the Physics Class

To illustrate the algebra-geometry opposition in physics teaching, we consider centripetal acceleration. Textbooks are split in the way they treat this subject. The vector treatment is relatively simple; given r the vector to the point in uniform circular motion with angular velocity ω, acceleration is provided by double differentiation (Table 2, left column). In comparison, the geometric derivation provides the result through a more elaborate procedure considering vectors of velocity at two subsequent instants and going to the limit of ∆t → 0 (Table 2, right column). Though the algebraic way is straightforward, more compact and therefore might look preferable, the geometric derivation possesses greater explanatory power. The process reveals to the learner the origin of the centripetal acceleration, its meaning, its magnitude, and its direction, which emerge in construction. That is unlike the algebraic derivation where the result is obtained following formal algorithm of derivation in vector calculus. The geometric treatment is, therefore, preferable for an introductory treatment of the kinematics of circular motion in physics class.

Table 2 Derivation of centripetal acceleration

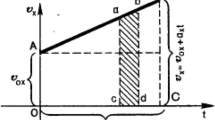
Our second example deals with the concept of the derivative, mentioned above, in the context of kinematics. It is common in teaching about the instant velocity or acceleration to provide their meaning through addressing the slope of the tangential line to the graph representing coordinate (or velocity) dependence of time (Fig. 7). This is, perhaps, the universal figure shared in most mathematics and introductory physics textbooks (e.g., Zeldovich, 2010, p. 26; Young and Friedman, 2012, p. 41). The reason for that is apparently the replacement of the sophisticated problem of $\underset{\Delta \mathrm{t}\to 0}{\lim}\frac{\Delta x}{\Delta t}$ signifying the uncertainty of $\frac{0}{0}$ with the obvious construction showing that the ratio of infinitesimals $\frac{\mathrm{dx}}{\mathrm{dt}}$ corresponds to the slope of the tangent to the curve x(t); ratio $\frac{{\mathrm{B}}_1\mathrm{C}}{\mathrm{AC}}$ results the processes of $\underset{\Delta \mathrm{t}\to 0}{\lim}\frac{\mathrm{BC}}{\mathrm{AC}}$. Possible complexity is postponed to further learning.

Fig. 7

Geometric representation of the meaning of instant velocity ${\mathrm{V}}_{\mathrm{x}}=\frac{\mathrm{dx}}{\mathrm{dt}}$ along x-coordinate

Masking the complexity, avoiding its analysis seeks making teaching and initial learning simpler. Yet, at the same time, it compromises meaningful learning of both mathematics, where the differential approach is the essence of calculus ideology, and physics, by missing the adequate presentation of mathematics as a discipline with specific interest and nature.^50,51

Our next example relates to physics teaching of perpendicularity. As mentioned in the previous section, perpendicularity in space is currently treated by means of vector analysis. Avoiding the need to imagine three lines mutually perpendicular in space (the theorem of three perpendiculars) projects on the skills required to grasp physics contents in mechanics (e.g., work function, torque) and electromagnetism. In the latter, introductory physics textbooks, seeking visual appeal, employ the so-called Fleming’s left- and right-hand rules (Fleming, 1902) (Fig. 8) in the account of electric motors and generators suggesting mnemonic rules to replace the formal relationship of vector cross product (F = q[V × B] with current density j instead of velocity V) and “Maxwell’s corkscrew rule” of vector analysis ($\mathit{\operatorname{curl}}\ \boldsymbol{E}=-\frac{\partial \boldsymbol{B}}{\partial t}\ \Big)\kern0.5em$(e.g., Chabay and Sherwood, 1995, p. 174, p. 540).

Fig. 8

Fleming’s right-hand rule for the electric motor context. (Fleming, 1902, p. 174)

Finally, we should at least mention the powerful elucidating effect of the geometrical representation of the theory of special relativity, suggested by Minkowski in 1907. Einstein (1905) introduced his theory in a purely analytical way⁵² actually establishing four-dimensional space-time world (Einstein and Infeld, 1938). This was the way the first textbooks presented the theory (e.g. Bergmann, 1942). Yet, the introduction of the new space-time metric (ds² = c²dt²-dx²) required Lobachevsky’s (non-Euclidian) geometry for geometrical representation, and that visualized the complicated claims of the theory making them “obvious” and thus pedagogically preferable. Modern textbooks of the special theory of relativity became inconceivable without manipulating with “world lines” and “light cone”.⁵³ All relativistic paradoxes are normally explained using geometric presentation.⁵⁴

We conclude that geometrical and algebraic accounts for reality differ in visual appeal and formal simplicity. They may differ in generality such as in analytical geometry that replaces graphs of curves with corresponding algebraic expressions. As such, a combination of both approaches corresponding to cultural (polyphonic) curricular approach could produce a richer representation of physical reality in a complementary perspective.

6 Concluding Remarks

Our discussion led us to appreciate the advantages and appropriateness of framing physics and mathematics curricula in discipline-cultural structure, in which each of the disciplines sees the other’s specific agenda, ontology, epistemology, and values.⁵⁵ We have reviewed the symbiosis of physics and mathematics from several perspectives. The two disciplines have emerged as different but closely connected and even overlapping, each penetrating the other. Throughout the long history, physics and mathematics have always fed each other with ideas, tools, products, and problems.

The individuality of the two areas (different nuclei) as well as their proximity (interwoven bodies) projects on science and mathematics curricula. Educators often teach both disciplines without emphasizing their specific identities in comparison. An implication of such comparison could upgrade the simplistic image: mathematics is not a toolkit or the language of physics, although it might serve as such. Nor does mathematics need to be isolated as a metaphor ignoring reality, although it can be. There is a wide spectrum of meanings and types of activities that make up these two realms of human intellectual enterprise. Considering the two as discipline-cultures may facilitate students’ understanding of both realms and visualize the conceptual variation, their common and different. Such perspective may stimulate meaningful learning of both disciplines.

The discipline-culture structure helps to classify various forms of mathematics used in physics. Some of these are currently missing from regular school curricula of both mathematics and physics: dimensional analysis, scaling, approximate and order of magnitude counting, numerical estimation. It is a loss, since they create specific elegance and virtuosity of physics as a method of exploration preserved in the tradition of generations in the performance by renowned physicists, Kapitza, Fermi, and Feynman, to name a few. Applied inside mathematics, to geometry and algebra, the cultural approach suggests a comparison of the approaches of both domains, thus enriching curriculum by complementarity. Applying geometrical method may appeal to a wider audience of science learners, making feasible their meaningful learning of science and serving as an important link between mathematics and physics contents.

This article addressed physics and mathematics in terms of their specific nature and suggests curricular changes. There is a need to upgrade school curricula with a cultural approach reviving the historical tradition and providing these disciplines with the features of liberal arts. It is such knowledge to be mastered at schools prior to the disciplinary advanced studies at universities. The contents of this article, the specific examples used in deriving its claims, may facilitate such a change as well as teachers’ presenting the corresponding topics in physics and mathematical classes.

Appendix

With regard to Greek science, one may illustrate the mentioned changes of epistemological preferences using the imagery appearing in Rafael’s fresco The School of Athens (1504) (Fig. 9). The first swing was from the Pythagorean number paradigm to Platonian theory first paradigm (the claim of initial ideal forms design). Still within the theoretical account, Aristotle changed the game and removed mathematics from the natural philosophy. He drew on the self-evident qualitative principles based on experience. The next change was the refinement of the Aristotelian empiricism returning mathematics to the theory of cosmos. That change facilitated the Hellenistic paradigm of the natural philosophy.

Fig. 9

a Using Rafael’s fresco The school of Athens (1504) to depict the dynamics of changes in the relationship of science (natural philosophy) and mathematics. Arrows and numbers point to the changes in time from left to right. 1—from Pythagoras and his “all are numbers” paradigm (its celebrating application—the harmonic intervals of musical octave (epogdoon b)—is shown on the table held for Pythagoras) to Plato’s theory first (rationalism); 2—from Plato to Aristotelian experience first (empiricism); and 3—from Aristotle to Hellenistic account by Euclid in the form of hierarchical deductive mathematical theory, geometry (a geometrical construction is shown on the tablet c)

During the scientific revolution of the seventeenth century, the depicted three epistemological preferences were still considered representative and were addressed by Hobbes (1660, Ch. 5) as three alternative ways to represent the knowledge of science:

For as arithmeticians teach to add and subtract in numbers, so the geometricians teach the same in lines, figures (solid and superficial), angles, proportions, times, degrees of swiftness, force, power, and the like; the logicians teach the same in consequences of words, adding together two names to make an affirmation, and two affirmations to make a syllogism, and many syllogisms to make a demonstration; and from the sum, or conclusion of a syllogism, they subtract one proposition to find the other. (Emphasis added)