Abstract
We consider multiclass queueing systems where the per class service rates depend on the network state, fairness criterion, and is constrained to be in a symmetric polymatroid capacity region. We develop new comparison results leading to explicit bounds on the mean service time under various fairness criteria and possibly heterogeneous loads. We then study large-scale systems with a growing number of service classes n (for example, files), \(m = \left\lceil {bn} \right\rceil \) heterogenous servers with total service rate \(\xi m\), and polymatroid capacity resulting from a random bipartite graph \({\mathcal {G}}^{(n)}\) modeling service availability (for example, placement of files across servers). This models, for example, content delivery systems supporting pooling of server resources, i.e., parallel servicing of a download request from multiple servers. For an appropriate asymptotic regime, we show that the system’s capacity region is uniformly close to a symmetric polymatroid—heterogeneity in servers’ capacity and file placement disappears. Combining our comparison results and the asymptotic ‘symmetry’ in large systems, we show that large randomly configured systems with a logarithmic number of file copies are robust to substantial load and server heterogeneities for a class of fairness criteria. If each class can be served by \(c_n=\omega (\log n)\) servers, the load per class does not exceed \(\theta _n=o\left( \min (\frac{n}{\log n}, c_n)\right) \), mean service requirement of a job is \(\nu \), and average server utilization is bounded by \(\gamma <1\), then for each constant \(\delta >1\), the conditional expectation of delay of a typical job with respect to the \(\sigma \)-algebra generated by \({\mathcal {G}}^{(n)}\) satisfies the following:
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In many shared network systems, service rate is allocated to ongoing jobs based on a fairness criterion, for example, \(\alpha \)-fair (\(\alpha \)F) (including max-min and proportional fair) as well as balanced fair (BF), and other greedy criteria [26]. When the network loads are stochastic a key open question is how the choice of fairness and network design will impact user perceived performance, for example, job delays, as well as the sensitivity of performance to heterogeneity in network resources and traffic loads. Motivated by this challenge, in this paper we take a step towards understanding these issues by investigating performance bounds for an interesting class of stochastic networks with symmetric polymatroid capacity under various fairness criteria.
The second question driving this paper is whether large scale systems can be designed to be inherently robust to heterogeneity and at what cost. Specifically, we consider centralized content delivery systems where a collection of servers deliver a proportionally large number of files. There has been substantial recent interest in understanding basic design questions for these systems, including, for example, [10, 14, 20, 24] and references therein: How should the number of file copies scale with the demand? What kinds of hierarchical caching policies are most suitable? How to best optimize storage/backhaul costs for unpredictable time-varying demands?
We consider a centralized system with several collocated servers. The replication of files across servers is kept static. We allow resource pooling, i.e., parallel file downloads from multiple servers akin to peer-to-peer systems. In principle, with an appropriate degree of storage redundancy, one can achieve much better peak service rates, exploit diversity in service paths, produce robustness to failures, and provide better sharing of pooled server resources. Intuitively when such systems have sufficient redundancy they will exhibit performance which is robust to limited heterogeneity in demands and server capacities, as well as to the fairness criterion driving resource allocation.
Some elements of content delivery infrastructure may see less pronounced heterogeneity in demands, for example, a centralized back end used to deliver files that are not available at distributed sites/caches. For such a system, with sufficient redundancy, enabling resource pooling for individual download requests could achieve scalable and robust performance.
1.1 Our contributions and organization
The contributions of this paper are threefold, each of independent interest, and collectively providing a significant step forward over what is known in the current literature.
-
(a.)
Performance bounds In Sects. 3, 4 we consider a class of systems with symmetric polymatroid capacity for which we develop several rate allocation monotonicity properties which translate to performance comparisons amongst fairness policies, and eventually give explicit bounds on mean delays. Specifically, we show that under homogeneous loads the mean delay achieved by greedy and \(\alpha \)F rate allocation, are bounded by that of BF allocation, which is computable. We then extend this upper bound to the case when the load is heterogeneous but ‘majorized by a symmetric load.’
-
(b.)
Uniform symmetry in large systems In Sect. 5 we consider a bipartite graph where nodes represent n job classes (files) and m servers with potentially heterogenous service capacity. The graph edges capture the ability of servers to serve the jobs in the given classes. If jobs can be concurrently served by multiple servers the system’s service capacity region is polymatroid. We show that for appropriately scaled large systems where the edge set is chosen at random (random file placement) the capacity region is uniformly close to a symmetric polymatroid.
-
(c.)
Performance robustness of large systems Combining these two results, in Sect. 6 we provide a simple performance bound for large-scale content delivery systems. More specifically, the performance under \(\alpha \)-fair rate allocation for a large system is upper-bounded by that under a system with smaller, symmetric, and approximate capacity region. The bound exhibits performance robustness in large systems with respect to variations in total system load, heterogeneity in load across the classes, and heterogeneity in server capacities, for \(\alpha \)-fair based resource allocation.
We have deferred some technical results to the appendix. Section 7 concludes the paper.
1.2 Related work
There is a substantial amount of related work. Yet the link between fairness in resource allocation and job delays in stochastic networks is poorly understood. The only fairness criterion for which explicit expressions or bounds are known is the Balanced Fair rate allocation [3] which generalizes the notion of ‘insensitivity’ of the processor sharing discipline in an M / G / 1 queuing system. Under balanced fairness, an explicit expression for mean delay was obtained in [5, 6] for a class of wireline networks, namely, those with line and tree topologies. Also, a performance bound for arbitrary polytope capacity region and arbitrary load was provided in [1]. Similarly, [11] developed bounds for stochastic networks where flows can be split over multiple paths. These bounds and expressions are either too specific or too loose. Recently, [23] developed an expression for the mean delay for systems with polymatroid capacity and arbitrary loads under balanced fair rate allocations. Unfortunately the result has exponential computational complexity in general. However, the symmetric case has low complexity, a fact we use in the sequel.
Balanced fair rate allocation is defined recursively and is difficult to implement. \(\alpha \)-fair rate allocations [13, 19] which are based on maximizing a concave sum utility function over the system’s capacity region (this includes proportional and max-min fair allocations) are more amenable to implementation [12, 15]. However, the only known explicit performance results for stochastic networks under such fairness criteria are for systems where proportional fair is equivalent to balanced fair [3, 17]. In [2], performance relationship under balanced and proportional fairness for several systems where they are not equivalent was studied through numerical computations, and were found to be relatively close in several scenarios.
In this paper we focus on a class of stochastic networks that can be characterized by a polymatroid capacity region. Such systems have also been considered in [23, 26]. For example, the work in [26] shows that when such systems are symmetric with respect to load and capacity, a greedy rate allocation is delay optimal. However, the result is brittle to asymmetries. We provide more details on greedy and other rate allocations in Sect. 3.
In summary, when it comes to fairness criteria and stochastic network performance there is a gap between what is implementable and what is analyzable. One of the goals of this paper is to provide comparison results which address this gap, with a particular focus on addressing user-performance in a large-scale content delivery system which leverages server diversity, i.e., availability of multiple copies of a file to serve a download request.
From a content delivery perspective, the two works closest to this paper are [24] and [23]. Both adopt a natural model for a content delivery system based on a bipartite graph which captures the availability of files at servers to support the file-download requests. They show that if the graph is chosen at random and scaled appropriately then user-performance is robust to load heterogeneity. The authors in [24] consider a service model where each request can be served by a single server—recall we consider systems allowing parallel download of a file from multiple servers. Resource pooling in our service model leads to a significantly improved mean delay bound. For example, upon availability of \(c_n\) servers for each class, our delays scale as \(O\left( \frac{1}{c_n}\right) \). Also in our work we are able to address the role of fairness criteria and robustness to heterogeneity in server capacities.
Our service model via resource pooling is same as in [23]. However, our work here is different in several respects. Firstly, in [23] the focus is on mean delays under balanced fair resource allocation, whereas here we directly study the impact of fairness criteria on users delays. Secondly, the system considered was by design symmetric, whereas here we establish the asymptotic symmetry. Thirdly, in this paper we establish new results on robustness to limited heterogeneity in file demands, server capacity and \(\alpha \)-fairness criteria by providing a uniform bound on delays.
2 System model
Our system consists of a set F of n classes. Jobs for class \(i \in F\) arrive as an independent Poisson process of rate \(\lambda _i\). Let \({\varvec{\lambda }}= (\lambda _i:i\in F)\). Service requirements of jobs are i.i.d. exponential with mean \(\nu \). Let \({\varvec{\rho }}= (\rho _i: i \in F)\), where \(\rho _i = \lambda _i\nu \) is the load associated with class i. For example, if the service requirement of a job is measured in bits then the load for each class is measured in bits per second.
Jobs arrive to the system at total rate \(\sum _{i\in F} \lambda _i\). Let \(u_k\) denote the job corresponding to the kth arrival after time \(t=0\). Let \(q_i(t)\) denote the set of ongoing jobs of class i at time t, i.e., jobs which have arrived but have not completed service, and \(\mathbf{q}(t) = (q_i(t): i \in F).\) For each \(A \subset F\), let \(q_A(t) = \cup _{i\in A} q_i(t)\), i.e., the set of all active jobs whose class is in A. Let \(\mathbf{x}(t) = (x_i(t): i \in F)\), where \(x_i(t) \triangleq |q_i(t)|\), i.e., \(\mathbf{x}(t)\) captures the number of ongoing jobs in each class.
We refer to \(\mathbf{x}(t)\) as the state of the system at time t. Let \(\mathbf{X}(t)\) correspond to the random vector describing the state of the system at time t. We refer to the random process \((\mathbf{X}(t):t\ge 0)\) as the state process. For any \(\mathbf{x}(t)\), let \(A_{\mathbf{x}(t)}\) denote the set of active classes, i.e., the classes with at least one ongoing job.
Service model For any \(v \in q_i(t)\), let \(b_v(t)\) be the rate at which job v is served at time t. The vector \(\mathbf{b}(t) = (b_v(t): v \in q_F(t))\) represents the rates assigned to ongoing jobs at time t. Within each class we assume that each job is allocated equal rate, i.e., \(b_v(t) = b_u(t)\) for each \(u,v \in q_i(t)\). If job v arrives at time \(t_v^a\) and has service requirement \(\eta _v\), then it departs at time \(t_v^d\) such that \(\eta _v = \int _{t_v^a}^{t_v^d} b_v(t) dt\). Thus, \(t_v^d - t_v^a\) is the delay for job v.
Further, let \(r_i(\mathbf{x}')\) be the total rate at which class i jobs are served at time t when \(\mathbf{x}(t) = \mathbf{x}'\), i.e., at any time t, \(r_i(\mathbf{x}(t)) = \sum _{ v\in q_i(t)} b_v(t)\). Let \(\mathbf{r}(\mathbf{x}')= (r_i(\mathbf{x}'): i\in F)\). We call the vector function \(\mathbf{r}(.)\) the rate allocation. Note that the rate allocation at any time t depends only on the \(\mathbf{x}(t)\) and thus can not depend on the residual file sizes of ongoing jobs.
Polymatroid capacity region We shall consider systems where rate allocation \(\mathbf{r}(\mathbf{x})\) for each \(\mathbf{x}\) are constrained to be within a polymatroid capacity region \({\mathcal {C}}\).
Definition 1
We say that \({\mathcal {C}}\) is a polymatroid if it takes the following form:
where \(\mu (.)\) is a set function which satisfies the following properties:
-
(1)
Normalized: \(\mu (\emptyset ) = 0\).
-
(2)
Monotonic: if \(A \subset B\), \(\mu (A) \le \mu (B)\).
-
(3)
Submodular: for all \( A,B \subset F\),
$$\begin{aligned} \mu (A ) + \mu (B) \ge \mu (A \cup B) + \mu (A \cap B). \end{aligned}$$
The function \(\mu (.)\) is called a rank function.
Polymatroids and submodular functions are well-studied in literature, see for example, [9, 21].
Definition 2
A polymatroid \({\mathcal {C}}\) is a symmetric polymatroid if its rank function \(\mu (.)\) satisfies the following property: for each \(A \subset F\), we have \(\mu (A) = h(|A|)\), where \(h : {\mathbb {Z}}_+ \rightarrow {\mathbb {R}}_+\) is a non-decreasing concave function; see Fig. 1.
For a given \(\mathbf{x}\), we say \(\mathbf{r}(\mathbf{x})\) is feasible if \(\mathbf{r}(\mathbf{x}) \in {\mathcal {C}}\); when this is true for all \(\mathbf{x}\), we say that the rate allocation \(\mathbf{r}(.)\) is feasible. We call \({\mathcal {C}}\) the capacity region of the system. Symmetric polymatroid capacity regions appear in several systems, for example Gaussian symmetric multiaccess channels [26]. Further, we will see in Sect. 5 that certain types of large content delivery systems have approximately symmetric polymatroid capacity regions.
Polymatroid capacity regions \({\mathcal {C}}\) have a special property that for any \(\mathbf{r}\in {\mathcal {C}}\), there exists \(\mathbf{r}' \ge \mathbf{r}\) such that \(\mathbf{r}' \in \mathcal {D} \triangleq \{\mathbf{r}\in {\mathcal {C}}: \sum _{i \in F} r_i = \mu (F)\}\) [9, 21]. Also, as evident from the definition, for any \(A \subset F\) the set \(\{\mathbf{r}\in {\mathcal {C}}: r_i = 0, \forall i \notin A\}\) is also a polymatroid, with a rank function which is the restriction of \(\mu (.)\) to subsets of A.
Further, we let
and will see that \({\hat{{\mathcal {C}}}}\) is the set of loads which are stabilizable for appropriate rate allocation policies.
Notation for ordering and majorization In the sequel we will rely on notation for ordering and majorization which we introduce below.
Let I be a finite arbitrary index set. Consider an arbitrary vector \(\mathbf{z}=(z_i:i\in I)\). We let \(z_{[1]} \ge z_{[2]} \ge \ldots \ge z_{[|I|]}\) denote the components of \(\mathbf{z}\) in decreasing order. We let \(|\mathbf{z}|\) denote \( \sum _{i\in I} |z_i|\). We let \(\mathbf{e}_i\) denote a vector with 1 at the ith coordinate and 0 elsewhere.
For vectors \(\mathbf{z}\) and \(\mathbf{z'}\) such that \(z_i \le z'_i\) for each \(i \in I\), we write \(\mathbf{z} \le \mathbf{z'}\) and say that \(\mathbf{z}\) is dominated by \(\mathbf{z'}\).
Below we define majorization (\(\prec \)) which describes how ‘balanced’ a vector is as compared to another vector. In words, by \(\mathbf{z} \prec \mathbf{z'}\) we mean that \(\mathbf{z}\) is ‘more balanced’ than \(\mathbf{z'}\) but they have the same sum. By \(\mathbf{z} \prec _w \mathbf{z'}\) we mean that \(\mathbf{z}\) is ‘more balanced’ and has lower sum than \(\mathbf{z'}\). Similarly, by \(\mathbf{z} \prec ^w \mathbf{z'}\) we mean that \(\mathbf{z}\) is ‘more balanced’ and has larger sum than \(\mathbf{z'}\).
Definition 3
For vectors \(\mathbf{z}\) and \(\mathbf{z'}\) such that \(|\mathbf{z}| = |\mathbf{z'}|\) and \(\sum _{l=1}^k z_{[l]} \le \sum _{l=1}^k z'_{[l]}\) for each \(k \in \{1,2,\ldots ,|I|\}\), we say \(\mathbf{z}\) is majorized by \(\mathbf{z'}\), and denote this by \(\mathbf{z} \prec \mathbf{z'}\).
If we have \(\sum _{l=1}^k z_{[l]} \le \sum _{l=1}^k z'_{[l]}\) for each \(k \in \{1,2,\ldots ,|I|\}\), we say \(\mathbf{z}\) is weak-majorized from below by \(\mathbf{z'}\), and denote this by \(\mathbf{z} \prec _w \mathbf{z'}\).
Similarly, if we have \(\sum _{l=0}^k z_{[|I|-l]} \ge \sum _{l=1}^k z'_{[|I|-l]}\) for each \(k \in \{0,1,\ldots ,|I|-1\}\), we say \(\mathbf{z}\) is weak-majorized from above by \(\mathbf{z'}\), and denote this by \(\mathbf{z} \prec ^w \mathbf{z'}\).
Dominance and majorization have an associated stochastic version, defined below.
Definition 4
Consider random vectors \(\mathbf{Z}\) and \(\mathbf{Z'}\). If there exist random vectors \({\tilde{\mathbf{Z}}}\) and \({\tilde{\mathbf{Z}}'}\) such that \(\mathbf{Z}\) and \({\tilde{\mathbf{Z}}}\) are identically distributed, \(\mathbf{Z'}\) and \({\tilde{\mathbf{Z}}'}\) are identically distributed, and \({\tilde{\mathbf{Z}}'} \le {\tilde{\mathbf{Z}}'}\) almost surely, then we say that \(\mathbf{Z}\) is stochastically dominated by \(\mathbf{Z'}\), and denote this by \({\tilde{\mathbf{Z}}} \le ^{st} {\tilde{\mathbf{Z}}'}\).
Instead, if \({\tilde{\mathbf{Z}}'} \prec _w {\tilde{\mathbf{Z}}'}\), then we say that \(\mathbf{Z}\) is stochastically weak-majorized from below by \(\mathbf{Z'}\), and denote this by \({\tilde{\mathbf{Z}}} \prec _w^{st} {\tilde{\mathbf{Z}}'}\).
In the sequel it will be useful to introduce following notation. Recall, \(\mathbf{r}(\mathbf{x}) = (r_i(\mathbf{x}): i\in F)\) is the vector of rates allocated to various classes. We define \(r_{(k)}(.)\) for each \(k\in \{1,\ldots ,n\}\) as follows: For a given state \(\mathbf{x}\), let \(i_k\) be the class corresponding to \(x_{[k]}\). Then \(r_{(k)}(\mathbf{x}) = r_{i_k}(\mathbf{x})\). In words, \(r_{(k)}(\mathbf{x})\) is the rate allocated to the class with the kth largest number of ongoing jobs.
Notation for scaling Consider sequences of numbers \((f_n: n \in {\mathbb {N}})\) and \((g_n: n \in {\mathbb {N}})\). We say that \(f_n = O(g_n)\) if there exists a constant \(k>0\) and an integer \(n_0\) such that for each \(n\ge n_0\) we have \(f_n \le k g_n\). We say that \(f_n = \Omega (g_n)\) if there exists a constant \(k>0\) and an integer \(n_0\) such that for each \(n\ge n_0\) we have \(f_n \ge k g_n\).
We say that \(f_n = o(g_n)\) if \(\lim _{n\rightarrow \infty } \frac{f_n}{g_n} = 0\). Similarly, we say that \(f_n = \omega (g_n)\) if \(\lim _{n\rightarrow \infty } \frac{g_n}{f_n} = 0\).
We say an event A happens with high probability (denoted as w.h.p.) if P(A) is \(1-o(1)\).
Several parts of the notation above are borrowed from [16, 26] and [22].
3 Rate allocation policies: background
There are several possible rate allocation policies, each resulting in potentially different user-perceived delays. Below, we introduce three different policies studied in the literature, each with its own merits.
(1) Greedy rate allocation Roughly, the greedy rate allocation policy on a polymatroid capacity region \({\mathcal {C}}\) assigns the maximum possible rate to the largest queues subject to the capacity constraints. We denote the greedy rate allocation by \(\mathbf{r}^G(.)\) and define it as follows: for each state \(\mathbf{x}\), we let
Equivalently, the sum rate assigned to the k largest queues, namely \(\sum _{l=1}^k r^G_{(l)}(\mathbf{x})\), is equal to \(\mu \left( \{[1],[2],\ldots ,[k]\}\right) \). Using a quadratic Lyapunov function, one can show that greedy rate allocation results in a stationary state process if \({\varvec{\rho }}\in {\hat{{\mathcal {C}}}}\), where \( {\hat{{\mathcal {C}}}}\) is defined in (1). The greedy rate allocation for symmetric polymatroid capacity regions was first studied in [26] where the following result was shown.
Proposition 1
([26]) Suppose the capacity region \({{\mathcal {C}}}\) is a symmetric polymatroid and the load \({\varvec{\rho }}\in {\hat{{\mathcal {C}}}}\) is homogeneous, i.e., \(\rho _i=\rho \) for each \(i \in F\). Then the following statements hold:
-
1.
Let \((\mathbf{X}^{G}(t): t\ge 0)\) and \(({\tilde{\mathbf{X}}}(t):t\ge 0)\) be state processes under the greedy and an arbitrary feasible rate allocation, respectively. If \(\mathbf{X}^{G}(0) \prec _w^{st} {\tilde{\mathbf{X}}}(0)\) then \(\mathbf{X}^{G}(t) \prec _w^{st} {\tilde{\mathbf{X}}}(t)\) for each \(t\ge 0\).
-
2.
The mean job delay under greedy rate allocation is less than or equal to that under any feasible rate allocation.
Unfortunately, this optimality result for symmetric systems does not provide any explicit performance characterization or bound. Further, the result is brittle to heterogeneity in load or capacity.
(2) \({\alpha }\) -fair rate allocation As introduced in [19], this policy allocates rates based on maximizing a concave sum utility function subject to the system’s capacity region. Formally, for a given \(\alpha > 0\), the \(\alpha \)-fair (\(\alpha \)F) rate allocation \(\mathbf{r}^{\alpha }(.)\) can be defined as follows: for each state \(\mathbf{x}\), let
This generalizes various notions of fairness across jobs, for example, proportional fair and max-min fair allocations are equivalent to the \(\alpha \)-fair policy for \(\alpha =1\) and \(\alpha \rightarrow \infty \), respectively [19]. However, for polymatroid capacity regions the following result has been established.
Proposition 2
([23]) All \(\alpha \)-fair rate allocations are equivalent for polymatroid capacity regions.
Further, the stability result in [7] implies that the \(\alpha \)F rate allocation results in a stationary state process when \({\varvec{\rho }}\in {\hat{{\mathcal {C}}}}\). The \(\alpha \)-fair rate allocation is attractive in that it is amenable to distributed implementation [12, 15] and satisfies natural axioms for fairness [13]. Unfortunately, little is known regarding their performance under stochastic arrivals. What has been shown is that for \(\alpha \)-fair allocations, the performance is sensitive to the distribution of service requirements [3]. Thus, it will be hard to make general claims. This leads us to the balanced fair rate allocation below.
(3) Balanced fair rate allocation As introduced in [3], the balanced fair (BF) rate allocation is ‘insensitive’, i.e., performance depends on the job service distribution only through its mean. Further, as we will see, it is more amenable to mean delay analysis. Formally, the balanced fair rate allocation \(\mathbf{r}^{B}(.)\) for a polymatroid capacity region \({\mathcal {C}}\) can be defined as follows, see [3]: for each state \(\mathbf{x}\), we have
where the function \(\varPhi \) is called a balance function and is defined recursively as follows: \(\varPhi (\mathbf{{0}}) = 1\), and \(\varPhi (\mathbf{x}) = 0 \ \forall \mathbf{x}\hbox { s.t. }x_i < 0\) for some i, otherwise
As shown in [3], (3) ensures the property of insensitivity, while (4) ensures that \(\mathbf{r}(\mathbf{x})\) for each \(\mathbf{x}\) lies in the capacity region, i.e., the constraints \(\sum _{i\in A} r_i(\mathbf{x}) \le \mu (A)\) are satisfied for each A. It also ensures that there exists a set \(B \subset A_\mathbf{x}\) for which \(\sum _{i\in B} r_i(\mathbf{x}) = \mu (B)\). In fact, the BF allocation is the unique policy satisfying the above properties.
It was shown in [2, 3] that if \({\varvec{\rho }}\in {\hat{{\mathcal {C}}}}\), the state process \((\mathbf{X}^B(t):t\ge 0)\) is asymptotically stationary. Further, under this condition, its stationary distribution is given by
The existence of such an expression for the stationary distribution makes balanced fairness amenable to time-averaged performance analysis, a property which we will use extensively in the sequel. While, in general, BF may result in wasteful resource allocation, for example, BF is not Pareto efficient for certain triangle networks studied in [3], for polymatroid capacity regions, BF has been shown to be Pareto efficient:
Proposition 3
([23]) For polymatroid capacity regions \({\mathcal {C}}\), BF rate allocation is Pareto efficient, i.e., \(\sum _{i \in A_\mathbf{x}} r_i^B(\mathbf{x}) = \mu (A_\mathbf{x})\) for each \(\mathbf{x}\).
Using Pareto optimality, a recursive expression for mean delay was provided in [23] for arbitrary polymatroid capacity region and load. The expression can be significantly simplified under symmetry, as also shown below. First, let
i.e., \(\pi _k\) is the stationary probability that there are k active classes in the system. Then, under symmetry, the following expression was shown to hold for \(\pi _k\) in [23]. We provide a (slightly different) proof below for the sake of completion.
Proposition 4
([23]) For a system with symmetric polymatroid capacity region, with load \(\rho _i = \rho \) for each class \(i\in F\), and with balanced fair rate allocation, we have
and for \(k=1,\ldots , n\) we have
Equivalently, for \(k=1,\ldots , n\), we have
Proof
It is enough to show that for each \(k \ge 1\) we have
There are two ways to argue that the above expression holds: (1) using PASTA and time reversibility, and (2) using the stationary distribution expression via the balance function. We summarize both approaches below.
Note that \(\pi _k h(k) = \sum _{|\mathbf{x}|: |A_\mathbf{x}| = k} \pi (\mathbf{x}) h(k)\) is the total rate of departures from states with k active classes. In reverse time these departures correspond either to (1) the arrivals to the system which see \(k-1\) active classes and cause an increase in the number of active classes, or to (2) arrivals which see k active classes and do not cause an increase the number of active classes. Since arrivals in the reverse time form a Poisson process, PASTA holds, and the rates of above transitions is equal to \((n-k+1) \rho \pi _{k-1}\) and \(k \rho \pi _k\), respectively. Thus, we get (8).
Alternatively, from the definition and Proposition 3, we have
This can be shown to simplify to the following:
Upon simplification, we get (8). \(\square \)
Now, let \(\beta _k = E\left[ |\mathbf{X}| \big | |A_\mathbf{X}|=k\right] \), i.e., \(\beta _k = \frac{\sum _{\mathbf{x}:|A_\mathbf{x}| = k} |\mathbf{x}| \pi (\mathbf{x}) }{\pi _k}\). There exists a surprisingly simple expression for \(\beta _k\) using which an explicit expression for the mean delay can be obtained, as given by the following theorem.
Theorem 1
Consider a system with symmetric polymatroid capacity region, and with load \(\rho _i = \rho \) for each class \(i\in F\). Under balanced fair rate allocation, let \(\beta _k = E\left[ |\mathbf{X}| \big | |A_\mathbf{X}| = k\right] \). Then, for \(k=1,\ldots ,n\) we have
Further, if the arrival rate for each class is equal to \(\lambda \) then the mean delay for jobs under balanced fairness is given by
where \(\pi _k\) can be computed using (5) and (7).
Proof
We provide a proof for the expression for \(\beta _k\). The expression for the mean delay then follows from Little’s law. From the definition and Proposition 3 we have
This can be shown to simplify to the following:
which in turn gives
Upon further simplification, one obtains
where the last equality follows from (6). From this (9) follows.
Paralleling the discussion for expression (8), (11) can also be argued directly using PASTA and time reversibility. In this case, \(\beta _k-1\) can be interpreted as the mean number of jobs a departure leaves behind it when the system has k active classes. Recalling the argument for (8), in reverse time, \(\frac{(n-k+1) \rho \pi _{k-1} }{ \pi _k h(k)} \) is the fraction of arrivals which result in k active classes by increasing the number of active classes by 1. Note that the rate of such arrivals does not depend on the precise state of the system. Thus, using a ‘ratio of rates’ argument, see [25], the mean number of customers seen by these arrivals is \(\beta _{k-1}\). Similarly, one can argue that the remaining fraction \(\frac{k \rho \pi _k}{ \pi _k h(k)}\) of arrivals which see k active classes see a mean number of jobs as \(\beta _{k}\). Thus, the expression (11) follows. \(\square \)
In the sequel we use several other properties of balanced fairness and also of other rate allocation policies, some of which are provided in the Appendix (Relative greediness and other rate allocation properties).
4 Performance bounds
Recall that for each rate allocation policy considered in Sect. 3, namely greedy, \(\alpha \)F, and BF, the underlying state process is asymptotically stationary if the load \({\varvec{\rho }}\in {\hat{{\mathcal {C}}}}\). Thus, the corresponding mean delays of the system’s jobs are finite. In this section, we assume that the capacity region \({\mathcal {C}}\) is symmetric, and develop explicit and easily computable bounds on the mean delay of jobs in systems with greedy or \(\alpha \)F rate allocation under potentially heterogeneous load \({\varvec{\rho }}\) within a subset of the stability region \( {\hat{{\mathcal {C}}}}\).
Our goal here is to enable performance analysis for a general enough class of systems so as to allow us to develop quantitative and qualitative insights for large-scale systems prevalent today. For example, the bounds developed below will enable us to later characterize user-performance in downloading files from heterogeneous (in loads and service capacities) large-scale content delivery systems supporting resource pooling.
Below we develop upper bounds for mean delay for the following three cases:
-
(i)
Homogeneous loads: We provide an upper bound for mean delay for loads \({\varvec{\rho }}\in {\hat{{\mathcal {C}}}}\) which are homogeneous across classes with non-zero entries, i.e., if A is the set of classes such that \(\rho _i > 0\) for each \(i \in A\), then \(\rho _i = \rho _j\) for each \(i,j \in A\).
-
(ii)
Dominance bound: Consider loads \({\varvec{\rho }}, {\varvec{\rho }}' \in {\hat{{\mathcal {C}}}}\) such that \({\varvec{\rho }}\le {\varvec{\rho }}'\) and \({\varvec{\rho }}'\) is homogeneous across non-zero entries as described above. Then, we show that the system with load \({\varvec{\rho }}\) has lower mean delay than that with load \({\varvec{\rho }}'\), even if \({\varvec{\rho }}\) is heterogeneous.
-
(iii)
Majorization bound: Consider loads \({\varvec{\rho }}, {\varvec{\rho }}' \in {\hat{{\mathcal {C}}}}\) such that \({\varvec{\rho }}\prec {\varvec{\rho }}'\). Further, suppose that \({\varvec{\rho }}'\) is homogeneous across non-zero entries as described above. Then, we show that the system with load \({\varvec{\rho }}\) has lower mean delay than that with load \({\varvec{\rho }}'\).
Throughout this section we will assume that the mean service requirements for jobs \(\nu \) is same for each system. The bound for homogeneous loads and the majorization bound are provided below for both \(\alpha \)F and greedy, whereas the dominance bound is provided for \(\alpha \)F. Next we will also develop a lower bound for mean delay for each rate allocation policy under arbitrary loads.
Note that using the majorization bound we can bound mean delay for a larger subset of heterogeneous loads as compared to the dominance bound. For example, consider \({\varvec{\rho }}= (\rho ,\frac{1}{2}\rho ,\frac{1}{2}\rho )\). Recall, for symmetric rank functions we have \(\mu (A) = h(|A|)\) for each \(A\subset F\), where h(.) is concave. Now, if \(\frac{1}{3}h(3)< \rho < \frac{1}{2}h(2)\), then \({\varvec{\rho }}' = (\rho ,\rho , 0)\) is in \({\hat{{\mathcal {C}}}}\) but \({\varvec{\rho }}'' = (\rho ,\rho ,\rho )\) is not. Then the majorization bound holds for \({\varvec{\rho }}\) but the dominance bound does not. Further, even if \({\varvec{\rho }}''\) is in \({\hat{{\mathcal {C}}}}\), the upper bound obtained through \({\varvec{\rho }}'\) may be tighter.
The bounds for each case will be obtained through coupling arguments on the corresponding state processes, followed by an application of Little’s law.
4.1 Homogeneous loads
Consider the following set of loads:
Since, by Proposition 1, the greedy rate allocation is delay optimal for homogeneous loads, for each \({\varvec{\rho }}\in {\mathcal {B}}_H\) one can immediately conclude that the performance of BF as obtained in Theorem 1 is an upper bound for that of greedy. Below we show that this performance upper bound via BF also holds for \(\alpha \)F rate allocation.
To this end, we show a coupling result for systems under \(\alpha \)F and BF rate allocations. In the process, we prove and use the property that \(\alpha \)F is more greedy than BF in the following sense: if the state process corresponding to \(\alpha \)F is the same as or more balanced than that of BF, then \(\alpha \)F assigns a larger rate to bigger queues than BF. This in turn keeps the state process for \(\alpha \)F more balanced in the future. For a proof of the theorem below, see Sect. 4.5.
Theorem 2
Consider a system with symmetric polymatroid capacity region and load \({\varvec{\rho }}\in {\mathcal {B}}_H\), i.e., \({\varvec{\rho }}\) is homogeneous across classes with non-zero entries. Then the following statements hold:
-
1.
Let \((\mathbf{X}^{\alpha }(t): t\ge 0)\) and \((\mathbf{X}^{B}(t):t\ge 0)\) be state processes under \(\alpha \)F and BF rate allocation. If \(\mathbf{X}^{\alpha }(0) \prec _w \mathbf{X}^{B}(0)\) then we have \(\mathbf{X}^{\alpha }(t) \prec _w^{st} \mathbf{X}^{B}(t)\) for each \(t\ge 0\).
-
2.
The mean delays for systems with \(\alpha \)F and BF rate allocation for load \({\varvec{\rho }}\in {\mathcal {B}}_H\) satisfy the following:
$$\begin{aligned} E[D^{\alpha }_{\varvec{\rho }}] \le E[D^{B}_{{\varvec{\rho }}}]. \end{aligned}$$
4.2 Dominance bound
Consider the following rate allocation property. Recall, \(\frac{r_i(\mathbf{x})}{x_i}\) is the rate allocated to each job in class i when the system is in state \(\mathbf{x}\).
Definition 5
(Per-job rate monotonicity) We say that a rate allocation \(\mathbf{r}(.)\) satisfies per-job rate monotonicity if the following holds for all states \(\mathbf{x}\) and \(\mathbf{x}'\) such that \(\mathbf{x}\ge \mathbf{x}'\): for each class i, we have \(\frac{r_i(\mathbf{x})}{x_i} \le \frac{r_i(\mathbf{x}')}{x'_i} \). In words, adding jobs into the system only decreases the rate allocated to each job.
From the definition of \(\alpha \)F, one can check that \(\alpha \)F rate allocation satisfies per-job rate monotonicity. This property was used in [4] to provide a comparison result for systems where the rate allocation in one system dominates that in another system for each state \(\mathbf{x}\). In contrast, we provide below a comparison result for systems with the same rate allocation policy and capacity region, but with different loads. For such systems, we show that the larger loads result in worse delays if the rate allocation satisfies per-job rate monotonicity. For a proof of the theorem below, see Sect. 4.5.
Theorem 3
Consider a system with symmetric polymatroid capacity region \({\mathcal {C}}\). Suppose that the rate allocation \(\mathbf{r}(.)\) satisfies per-job rate monotonicity. Let \({\varvec{\rho }},{\varvec{\rho }}' \in \hat{{\mathcal {C}}}\) (recall, \( {\hat{{\mathcal {C}}}}\) is the stability region) be such that \({\varvec{\rho }}\le {\varvec{\rho }}'\). Then the following statements hold:
-
1.
Let \((\mathbf{X}(t): t\ge 0)\) and \((\mathbf{X}'(t):t\ge 0)\) be state processes under loads \({\varvec{\rho }}\) and \({\varvec{\rho }}'\). If \(\mathbf{X}(0) \le \mathbf{X}'(0)\), then we have \(\mathbf{X}(t) \le ^{st} \mathbf{X}'(t)\) for each \(t\ge 0\).
-
2.
For systems with loads \({\varvec{\rho }}\) and \({\varvec{\rho }}'\), the mean delays for jobs for each class \(i \in F\) satisfy the following:
$$\begin{aligned} E\left[ D_i^{({\varvec{\rho }})}\right] \le E\left[ D_i^{({\varvec{\rho }}')}\right] . \end{aligned}$$
The above result holds for \(\alpha \)F since it satisfies per-job rate monotonicity. However, one can check that the greedy rate allocation does not satisfy per-job rate monotonicity in general. Thus, it is not clear if such a bound holds for greedy rate allocation.
Now, if \({\varvec{\rho }}'\) is homogeneous, then under \(\alpha \)F rate allocation we have an explicit bound for mean delays via Theorem 2. Thus, consider the following region:
or equivalently,
Theorem 3 implies that the mean delay under \(\alpha \)F rate allocation for each load \({\varvec{\rho }}\in {\mathcal {B}}_D\) can be bounded by that for a corresponding symmetric load \({\varvec{\rho }}' \in {\mathcal {B}}_H\), which in turn has an easily computable bound. Thus, we get the following corollary.
Corollary 1
Consider a system with symmetric polymatroid capacity region and load \({\varvec{\rho }}\in {\mathcal {B}}_D\). Let \(\rho ' = \max _i \rho _i\). Let \({\varvec{\rho }}'\) be such that for each \(i\in F\) we have \(\rho '_i = \rho '\) if \(\rho _i >0\) and \(\rho '_i=0\) if \(\rho _i = 0\). Then, mean delay for a system with \(\alpha \)F rate allocation for load \({\varvec{\rho }}\) satisfies the following:
4.3 Majorization bound
The theorem below generalizes the dominance bound to provide a mean delay bound for a system with load \({\varvec{\rho }}\) such that there exists \({\varvec{\rho }}' \in {\mathcal {B}}_H\) which satisfies \({\varvec{\rho }}\prec {\varvec{\rho }}'\).
Its proof is similar to that of Theorem 2, where instead of relative greediness between rate allocations, we use the following balancing property satisfied by both \(\alpha \)F and greedy: if state \(\mathbf{x}\) is more balanced than state \(\mathbf{x}'\), then the rate allocation \(\mathbf{r}(.)\) would provide larger rates to longer queues in state \(\mathbf{x}\) as compared to \(\mathbf{x}'\), and thus balancing it even further. For a proof of the theorem below, see Sect. 4.5.
Theorem 4
Consider a system with symmetric polymatroid capacity region \({\mathcal {C}}\). The rate allocation \(\mathbf{r}(.)\) is either \(\alpha \)F or greedy. Let \({\varvec{\rho }}, {\varvec{\rho }}' \in {\hat{{\mathcal {C}}}}\) be such that \({\varvec{\rho }}\prec {\varvec{\rho }}'\) and \({\varvec{\rho }}' \in {\mathcal {B}}_H\), i.e., \({\varvec{\rho }}'\) is homogeneous across classes with non-zero entries. Then the following statements hold:
-
1.
Let \((\mathbf{X}(t): t\ge 0)\) and \((\mathbf{X}'(t):t\ge 0)\) be state processes under loads \({\varvec{\rho }}\) and \({\varvec{\rho }}'\). If \(\mathbf{X}(0) \prec _w \mathbf{X}'(0)\), then we have \(\mathbf{X}(t) \prec _w^{st} \mathbf{X}'(t)\) for each \(t\ge 0\).
-
2.
The mean delays for systems with loads \({\varvec{\rho }}\) and \({\varvec{\rho }}'\) satisfy the following:
$$\begin{aligned} E[D_{\varvec{\rho }}] \le E[D_{{\varvec{\rho }}'}]. \end{aligned}$$
Theorem 4 above is stronger than Theorem 3 in the sense that it only requires the condition \({\varvec{\rho }}\prec _w {\varvec{\rho }}'\) instead of \({\varvec{\rho }}\le {\varvec{\rho }}'\). However, it is weaker in the sense that it requires \({\varvec{\rho }}'\) to be in \({\mathcal {B}}_H\) and that it gives stochastic weak-majorization of the corresponding state processes instead of stochastic dominance.
For both \(\mathbf{r}^G(.)\) and \(\mathbf{r}^\alpha (.)\), Theorem 4, along with Theorem 2 and Proposition 1, allows us to bound the mean delay for any load in the following region:
or equivalently,
Theorem 4 implies that for \(\alpha \)F and greedy rate allocation, the mean delay for each load \({\varvec{\rho }}\in {\mathcal {B}}_M\) can be bounded by that for a corresponding load \({\varvec{\rho }}' \in {\mathcal {B}}_H\), which in turn has an easily computable bound through Theorem 2. Thus, we get the following corollary.
Corollary 2
Consider a system with symmetric polymatroid capacity region and load \({\varvec{\rho }}\in {\mathcal {B}}_M\). Let \(\rho ' = \max _{i \in F} \rho _i\). Let \(k = \min \{l: \rho ' \le \frac{h(l)}{l} \text { and } |{\varvec{\rho }}| \le h(l) \}.\) Let A be an arbitrary subset of F of size k and \({\varvec{\rho }}'\) be such that \(\rho '_i = \rho ' \;\; \forall i\in A\) and \(\rho '_i=0\) otherwise. Then, the mean delays for systems with greedy and \(\alpha \)F rate allocations for load \({\varvec{\rho }}\) satisfy the following:
It is easy to check that for each \({\varvec{\rho }}\in {\mathcal {B}}_M\) the computation of the mean delay upper bound as given by Corollary 2 has complexity O(n) when computed using Theorem 1.
4.4 Lower bound
The following proposition provides a lower bound on the mean delay for any system with symmetric polymatroid capacity region, a feasible rate allocation policy, and with arbitrary loads. See Sect. 4.5 for a proof.
Proposition 5
Consider a system with a symmetric polymatroid capacity region \({\mathcal {C}}\) with rank function \(\mu (A) = h(|A|)\) for each \(A \subset F\), an arbitrary feasible rate allocation policy, and with load \({\varvec{\rho }}\in {\hat{{\mathcal {C}}}}\), i.e., the system is stabilizable. Let the total arrival rate for jobs, i.e. \(\sum _{i\in F} \lambda _i\), be equal to \(\lambda n\). Then, the following lower bound on the mean delay holds:
4.5 Proofs of coupling results
Proof of Theorem 2
Consider the following lemma regarding relative greediness of \(\alpha \)F and BF.
Lemma 1
Consider states \(\mathbf{x}\) and \(\mathbf{y}\) such that \(\mathbf{x}\prec _w \mathbf{y}\). For each k such that \(\sum _{l=1}^{k} x_{[l]} = \sum _{l=1}^{k} y_{[l]}\), we have \(\sum _{l=1}^{k} r^{\alpha }_{(l)}(\mathbf{x}) \ge \sum _{l=1}^{k} r^{B}_{(l)}(\mathbf{y})\).
Roughly, this asserts that if state \(\mathbf{x}\) is the same or more balanced than state \(\mathbf{y}\), then the sum rate assigned to larger queues by \(\alpha \)F to state \(\mathbf{x}\) is greater than that by BF to state \(\mathbf{y}\). The proof of this lemma is given in the Appendix (Relative greediness and other rate allocation properties). Below we provide a detailed coupling argument showing stochastic weak-majorization using this lemma.
Coupling argument Without loss of generality, assume \(\nu =1\). Suppose \(\mathbf{X}^{\alpha }(0) \prec _w \mathbf{X}^{B}(0)\). Below, we couple the arrivals and departures of the processes \((\mathbf{X}^{\alpha }(t):t\ge 0)\) and \((\mathbf{X}^{B}(t): t\ge 0)\) such that their marginal distributions remain intact and \(\mathbf{X}^{\alpha }(t) \prec _w \mathbf{X}^{B}(t)\) almost surely for each \(t\ge 0\).
Let \(\Pi _a\) be a Poisson point process with rate \(\sum _{i\in F} \lambda _i\), and let \(\Pi _d\) be Poisson point process with rate \(\mu (F)\). The points in these processes are the times of ‘potential events’ in \((\mathbf{X}^{B}(t): t\ge 0)\) and \((\mathbf{X}^{\alpha }(t): t\ge 0)\). We use \(\Pi _a\) to couple arrivals and \(\Pi _d\) to couple departures. For each time \(t'\) when a potential event occurs, let \(\epsilon _{t'}\) be a small enough number such that no potential event occurred in the time interval \([t'-\epsilon _{t'}, t')\).
Coupling of arrivals For each point \(t'\) in \(\Pi _a\), do the following: Choose a random variable \(Z_{t'}\) independently and uniformly from \(\{1,\ldots , n\}\). Let an arrival occur in \((\mathbf{X}^{\alpha }(t):t\ge 0)\) at time \(t'\) in the \(Z_{t'}^{{\mathrm {th}}}\) largest queue of \(\mathbf{X}^{\alpha }(t'-\epsilon _{t'})\). Ties are broken uniformly at random. Similarly, let an arrival occur in \((\mathbf{X}^{\alpha }(t):t\ge 0)\) at time \(t'\) in the \(Z_{t'}^{{\mathrm {th}}}\) largest queue of \(\mathbf{X}^{\alpha }(t'-\epsilon _{t'})\). Again, ties are broken uniformly at random.
Coupling of departures For each point \(t'\) of increment in \(\Pi _d\), do the following: Choose a random variable \(Z_{t'}\) independently and uniformly from the interval \((0,\mu (F)]\). For k such that
let a departure occur in \((\mathbf{X}^{\alpha }(t):t\ge 0)\) at time \(t'\) in the kth largest queue of \(\mathbf{X}^{\alpha }(t'-\epsilon _{t'})\), with ties broken uniformly and independently at random.
Similarly, for k such that
let a departure occur in \((\mathbf{X}^{B}(t):t\ge 0)\) at time \(t'\) in the kth largest queue of \(\mathbf{X}^{B}(t'-\epsilon _{t'})\), with ties broken uniformly and independently at random. Note that in both cases it is possible that no such k exists since some classes may not be active and the total service rate may be less than \(\mu (F)\). In that case, no departure occurs.
It can be checked that the marginal distributions of \((\mathbf{X}^{\alpha }(t):t\ge 0)\) and \((\mathbf{X}^{B}(t): t\ge 0)\) remain intact. We now show that \(\mathbf{X}^{\alpha }(t) \prec _w \mathbf{X}^{B}(t)\) almost surely for each t.
It is easy to check that if an arrival occurred at time \(t'\) and if \(\mathbf{X}^{\alpha }(t) \prec _w \mathbf{X}^{B}(t)\) for each \(t < t'\), then \(\mathbf{X}^{\alpha }(t') \prec _w \mathbf{X}^{B}(t')\) as well. We now show that the same holds for points of \(\Pi _d\) as well.
Suppose a potential departure occurred at \(t'\), and \(\mathbf{X}^{\alpha }(t) \prec _w \mathbf{X}^{B}(t)\) for each \(t < t'\). We show below that \(\sum _{l=1}^k X_{[l]}^\alpha (t') \le \sum _{l=1}^k X_{[l]}^B(t')\) for each k. Here we use Lemma 1. The following two cases arise.
Case 1 \(\sum _{l=1}^k X_{[l]}^\alpha (t'-\epsilon _{t'}) < \sum _{l=1}^k X_{[l]}^B(t'-\epsilon _{t'})\). Since a maximum of one departure occurs at time \(t'\) in either processes, we clearly have \(\sum _{l=1}^k X_{[l]}^\alpha (t') \le \sum _{l=1}^k X_{[l]}^B(t')\).
Case 2 \(\sum _{l=1}^k X_{[l]}^\alpha (t'-\epsilon _{t'}) = \sum _{l=1}^k X_{[l]}^B(t'-\epsilon _{t'})\). By using \(\mathbf{X}^{\alpha }(t-\epsilon _{t'}) \prec _w \mathbf{X}^{B}(t-\epsilon _{t'})\) in Lemma 1 and from the definition of the coupling at time \(t'\), it can be shown that if a departure occurs from any of the k largest queues in \(\mathbf{X}^{B}(t'-\epsilon _{t'})\), then it also occurs in one of the k largest queues in \(\mathbf{X}^{\alpha }(t'-\epsilon _{t'})\). Thus, \(\sum _{l=1}^k X_{[l]}^\alpha (t') \le \sum _{l=1}^k X_{[l]}^B(t')\).
Hence, the first part of the theorem follows. The second part follows by application of Little’s law to \((|\mathbf{X}^{\alpha }(t)|: t\ge 0)\) and \((|\mathbf{X}^{B}(t)|:t\ge 0)\). \(\square \)
Proof of Theorem 3
Suppose \(\mathbf{X}(0) \le \mathbf{X}'(0)\). Below we couple the arrivals and departures of jobs in \((\mathbf{X}(t):t\ge 0)\) and \((\mathbf{X}'(t): t\ge 0)\) such that their marginal distributions remain intact and \(\mathbf{X}(t) \le \mathbf{X}'(t)\) almost surely for each \(t\ge 0\).
Since the mean service requirement of jobs \(\nu \) is same for both the systems, the corresponding arrival rates satisfy \({\varvec{\lambda }}\le {\varvec{\lambda }}'\). For each i let \(\Pi _i\) and \(\Pi '_i\) be the Poisson arrival processes for class i in the respective systems. Let \(\Pi _i\) be obtained by sampling \(\Pi '_i\). For each class i, the arrivals in \((\mathbf{X}'(t): t\ge 0)\) at the sampled points, i.e., points in \(\Pi _i\), see the average delay which is equal to the overall average delay of jobs in \(\Pi '_i\) for this system. Thus, the theorem follows if we couple the departures of jobs in both the systems such that for each point in \(\Pi _i\), the corresponding job departure in \((\mathbf{X}(t): t\ge 0)\) is no later than that in \((\mathbf{X}'(t): t\ge 0)\). By using the per-flow rate monotonicity property, one can couple the service rate of these jobs at each time t so that if such a job departs from \((\mathbf{X}'(t): t\ge 0)\) than the corresponding job departs from \((\mathbf{X}(t): t\ge 0)\) as well, if it has not already. \(\square \)
Proof of Theorem 4
The theorem can be proved in a fashion similar to that of Theorem 2, except for the following changes. For notational convenience, for each time t let \(\lambda _{(k)}(t)\) and \(\lambda _{(k)}'(t)\) be the arrival rates of the kth largest queues in \(\mathbf{X}(t)\) and \(\mathbf{X}'(t)\), respectively, with ties broken arbitrarily.
-
1.
Coupling of arrivals For each point \(t'\) in \(\Pi _a\), we choose a random variable \(Z_{t'}\) independently and uniformly from the interval \((0,|{\varvec{\lambda }}|]\). For each k such that
$$\begin{aligned} Z_{t'} \in \left( \sum _{l=1}^{k-1} \lambda _{(l)}(t'-\epsilon _{t'}), \sum _{l=1}^{k}\lambda _{(l)}(t'-\epsilon _{t'})\right] , \end{aligned}$$let an arrival occur in \((\mathbf{X}(t):t\ge 0)\) at time \(t'\) in the kth largest queue of \(\mathbf{X}(t'-\epsilon _{t'})\). Similarly, for each k such that
$$\begin{aligned} Z_{t'} \in \left( \sum _{l=1}^{k-1} \lambda _{(l)}'(t'-\epsilon _{t'}), \sum _{l=1}^{k}\lambda _{(l)}'(t'-\epsilon _{t'})\right] , \end{aligned}$$let an arrival occur in \((\mathbf{X}'(t):t\ge 0)\) at time \(t'\) in the kth largest queue of \(\mathbf{X}'(t'-\epsilon _{t'})\).
-
2.
Coupling of departures Similar to that of Theorem 2, except that instead of Lemma 1 for a proof of weak-majorization upon a potential departure, we use the following lemma which asserts that \(\alpha \)F and greedy provide a larger rate to longer queues in more balanced states.
Lemma 2
Consider states \(\mathbf{x}\) and \(\mathbf{y}\) such that \(\mathbf{x}\prec _w \mathbf{y}\). For each k such that \(\sum _{l=1}^{k} x_{[l]} = \sum _{l=1}^{k} y_{[l]}\), we have \(\sum _{l=1}^{k} r^{\alpha }_{(l)}(\mathbf{x}) \ge \sum _{l=1}^{k} r^{\alpha }_{(l)}(\mathbf{y})\), and also \(\sum _{l=1}^{k} r^{G}_{(l)}(\mathbf{x}) \ge \sum _{l=1}^{k} r^{G}_{(l)}(\mathbf{y})\).
For \(\mathbf{r}^{G}(.)\), it is easy to verify that the lemma holds. For \(\mathbf{r}^{\alpha }(.)\), it follows from Lemma 9 in the Appendix (Relative greediness and other rate allocation properties).
Hence, the result follows. \(\square \)
Proof of Proposition 5
Consider a queue where the jobs arrive as a Poisson point process with rate \(\lambda n\). The buffer size is finite and equal to n. Thus, an arrival is blocked if there are already n ongoing jobs in the queue. Service requirements of jobs are i.i.d. exponential with rate \(\nu \). The total service rate of jobs at each time is state dependent, as follows: if there are \({\tilde{x}}(t)\) ongoing jobs in the queue at time t then the total service rate at time t is equal to \(h({\tilde{x}}(t))\). One can check that the mean number of jobs in a stationary regime for this system is given by
It is easy to check that for a given total number of ongoing jobs, the overall service rate in the above queue is greater than or equal to that in the original system with symmetric polymatroid capacity region. Thus, one can couple the arrivals and departures of the two systems such that the above queue has a lower than or equal number of active jobs at each time as compared to the original system. The result then follows by applying Little’s law to the original system. \(\square \)
5 Large system has approximately symmetric capacity
In this section we consider a large content delivery system employing resource pooling and show that such a system not only has polymatroid capacity, but under appropriate assumptions becomes approximately symmetric.
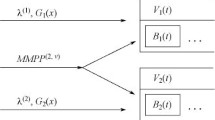
Consider a sequence of bipartite graphs \(G^{(n)} = (F^{(n)}\cup S^{(n)};E^{(n)})\) where \(F^{(n)}\) is a set of n files, \(S^{(n)}\) is a set of \(m= \left\lceil {b n} \right\rceil \) servers for some constant b, and each edge \(e\in E^{(n)}\) connecting a file \(i\in F^{(n)}\) and server \(s \in S^{(n)}\) implies that a copy of file i is available at server s (see Fig. 2). For each node \(s \in S^{(n)}\), let \(N_s^{(n)}\) denote the set of neighbors of server s, i.e., the set of files it stores and can serve. Henceforth, wherever possible, we will avoid the use of ceiling and floor notation to avoid clutter.
We associate each file in \(F^{(n)}\) to a class of jobs where the job corresponds to a download request for that file. The arrival processes and service requirements for the jobs are as described in Sect. 2, with \({\varvec{\lambda }}^{(n)}\) and \({\varvec{\rho }}^{(n)}\) representing the corresponding arrival rates and loads. Further, we let the service capacity of each server \(s\in S^{(n)}\) be \(\mu _s\) bits per second.
We allow each server \(s\in S^{(n)}\) to concurrently serve the jobs with classes \(N_s^{(n)}\) as long as the total service rate does not exceed \(\mu _s\). The service rate for each job is the sum of the rates it receives from different servers. For any \(A\subset F^{(n)}\), let \(\mu ^{(n)}(A)\) be the maximum sum rate at which jobs with file-class in A could be served, i.e.,
Clearly any rate allocation \(\mathbf{r}(.)\) for such a system must satisfy the following constraints for each state \(\mathbf{x}\): \(\forall A \subset F^{(n)},\)
It was shown in [22] that \(\mu ^{(n)}(.)\) is submodular and that the corresponding polymatroid
is indeed the capacity region for such a system, i.e., each \(\mathbf{r}\in {\mathcal {C}}^{(n)}\) is achievable.
Note that \({\mathcal {C}}^{(n)}\) will, in general, be an asymmetric polymatroid depending upon edges \(E^{(n)}\) and service capacities \(\mu _s\) for each \(s \in S^{(n)}\). However, we show below that if copies of files are stored across servers at random and scaled appropriately with n then, as n increases, a uniform law of large numbers holds where \({\mathcal {C}}^{(n)}\) gets uniformly close to a symmetric polymatroid, subject to the following assumptions:
Assumption 1
(Heterogeneous server capacities) \(S^{(n)}\) is partitioned into a finite number of groups where each group has \(\Omega (n)\) number of servers. Within each group, the server capacities are homogeneous. The server capacities across groups may be heterogeneous such that average of service capacity across servers
is independent of n.
Assumption 2
(Randomized file placement) Let \((c_n: n\in {\mathbb {N}})\) be a sequence such that
For each file \(i\in F^{(n)}\), store a copy in \(c_n\) different servers chosen uniformly and independently at random.
A randomized placement of file copies implies a random system configuration, i.e., a random graph which we denote by \({\mathcal {G}}^{(n)} = (F^{(n)}\cup S^{(n)};{\mathcal {E}}^{(n)})\). Similarly, for each \(s \in S^{(n)}\), let \({\mathcal {N}}^{(n)}_s\) denote the random set of neighbors of s, i.e., the random set of files stored in server s. Let \(M^{(n)}(.)\) denote the corresponding random rank function, and \(\mu ^{(n)}(.)\) a possible realization. Then, for each \(A \subset F^{(n)}\), we have
where \(\mathbf {1}_{\left\{ {A\cap \mathcal {N}^{(n)}_s \ne \emptyset }\right\} }\) is now a Bernoulli random variable indicating if a copy of at least one of the files in A is placed in s. In fact, for each \(A\subset F^{(n)}\) such that \(|A|=k\), the set \(\left\{ \mathbf {1}_{\left\{ {A\cap \mathcal {N}^{(n)}_s \ne \emptyset }\right\} }: s \in S^{(n)}\right\} \) is a set of m negatively associated Bernoulli(\(p_k^{(n)})\) random variables [8] where \(p_k^{(n)}\) is the probability that a given server is assigned at least one of the \(kc_n\) copies of files in A. Since the probability that a server does not have a copy of a file is equal to \(1-\frac{c_n}{m}\), we have
By linearity of expectation, for each \(A \subset F^{(n)}\) we have
Note that \({\bar{\mu }}^{(n)}(A)\) depends on A only through |A| and is thus symmetric. The theorem below shows that with high probability we can bound the random rank function \(M^{(n)}(.)\) uniformly over all \(A \subset F^{(n)}\), from above as well as from below, with a symmetric rank function which is close to \({\bar{\mu }}^{(n)}(A)\). See Section 5.1 for a proof.
Theorem 5
Fix \(\epsilon \) independent of n such that \(0<\epsilon <1\). Consider a sequence of systems with n files and \(m = \left\lceil {bn} \right\rceil \) servers, where \(b>0\) is a constant. Under Assumptions 1 and 2, let \(M^{(n)}(.)\) be the corresponding random rank function. Then, there exists a sequence \((g_n: n\in {\mathbb {N}})\) such that \(g_n = \omega (\log n)\), and
and
This result gives us the following corollary on the random capacity region associated with \(M^{(n)}(.)\) generated by random file placement. Recall, \({\bar{\mu }}^{(n)}(A) = E[M^{(n)}(A)]\) for all \(A \subset F^{(n)}\), and let
Thus, \({\bar{{\mathcal {C}}}}^{(n)}\) is the (symmetric) capacity region associated with the average rank function \({\bar{\mu }}(.)\). Then, the following holds:
Corollary 3
Fix \(\epsilon \) independent of n such that \(0<\epsilon <1\). Under Assumptions 1 and 2, the random capacity region associated with \({\mathcal {G}}^{(n)}\) is a subset of \((1+\epsilon ){\bar{{\mathcal {C}}}}^{(n)}\) and a superset of \((1-\epsilon ){\bar{{\mathcal {C}}}}^{(n)}\) with high probability.
Further, under Assumption 1, there exists a deterministic file placement where \(c_n= \omega (\log n)\) copies of each file are stored across servers such that the corresponding capacity region \({\mathcal {C}}^{(n)}\) is a subset of \((1+\epsilon ){\bar{{\mathcal {C}}}}^{(n)}\) and a superset of \((1-\epsilon ){\bar{{\mathcal {C}}}}^{(n)}\).
5.1 Proof of Theorem 5
Here we will only show
the other bound follows in similar fashion.
For now, suppose \(\mu _s =\xi \) for each \(s \in S^{(n)}\). We relax this assumption later.
We first provide a bound for \( P\left( M^{(n)}(A) \le (1-\epsilon ) {\bar{\mu }}^{(n)}(A) \right) \) for each \(A \subset F^{(n)}\). Then, for each \(k = 1,2,\ldots ,n\), we use the union bound to obtain a uniform bound over all sets \(A \subset F^{(n)}\) such that \(|A|=k\). The bound we provide for \( P\left( M^{(n)}(A) \le (1-\epsilon ) {\bar{\mu }}^{(n)}(A) \right) \) is small enough so that the above union bound is small too. Then, yet another use of the union bound would give us the uniform result over all sets \(A \subset F^{(n)}\).
Now, if the random variables \(\left\{ \mathbf {1}_{\left\{ {A\cap \mathcal {N}^{(n)}_s \ne \emptyset }\right\} }: s \in S^{(n)}\right\} \) were independent Bernoulli\((p_k^{(n)})\), then the following two concentration results would hold [18]: Fix \(k \in \{1,\ldots ,n\}\). For each set \(A\subset F^{(n)}\) such that \(|A| = k\), we have
and,
where H(p||q) is the KL divergence between Bernoulli(p) and Bernoulli(q) random variables, given by
However, in reality, since \(\left\{ \mathbf {1}_{\left\{ {A\cap \mathcal {N}^{(n)}_s \ne \emptyset }\right\} }: s \in S^{(n)}\right\} \) are negatively associated Bernoulli\((p_k^{(n)})\) random variables, the above Chernoff bounds still apply [8].
In the sequel, we will use the following two technical lemmas. Their proofs are provided in the Appendix (Technical lemmas for proof of Theorem 5).
Lemma 3
Let a sequence \((g_n: n\in {\mathbb {N}})\) be such that \( g_n = o(c_n).\) Let \(\delta _1<1\) be a positive constant independent of k and n. Then, for large enough n, we have
Lemma 4
There exists a positive constant \(\delta \), independent of k and n, such that \(H\left( p_k^{(n)}(1-\epsilon )||p_k^{(n)}\right) \ge - \delta + \epsilon \frac{ k c_n}{m} \).
Now, let \((g_n: n\in {\mathbb {N}})\) be a sequence such that \(g_n \triangleq ( c_ n \log n)^{1/2}\) for each n. The following properties of \(g_n\) can be easily checked:
We now provide a uniform bound over all sets \(A \subset F^{(n)}\) such that \(|A|=k\) for each \(k \in \{1,\ldots ,n\}\), under the following two cases.
Case 1 \(0 \le k \le \frac{n}{g_n}\): From Lemma 3, for each k we have
for a suitably chosen positive constant \(\delta _1\) independent of n. In the sequel, \(\delta _i\) for any \(i \ge 1\) will be a suitably chosen positive constant independent of n.
Using the concentration result (12), for \(|A|=k\) we get
and using the union bound, we get
for a constant \(\delta _2\) less than \(\frac{\epsilon ^2}{2} \delta _1 b\).
Case 2 \(\frac{n}{g_n} < k \le n\): In this case, we use the concentration result (13). From Lemma 4, there exists a constant \(\delta _6\) such that
Since \(g_n = o(c_n)\), for n large enough we get \(\delta _6 m \le (\epsilon /2) \frac{ n c_n}{ g_n}\). Also, for each \(k> \frac{n}{g_n}\), we have \( (\epsilon /2)\frac{ n c_n}{ g_n} \le (\epsilon /2) k c_n \). Thus, for large enough n, \( \delta _6 m - \epsilon k c_n \le -(\epsilon /2) k c_n\) for each k such that \( \frac{n}{g_n} < k \le n\), and consequently there exists a constant \(\delta _7\) such that
By using the union bound, for large enough n we get
for a constant \(\delta _8\) less than \(\delta _7\). Combining the above two cases, we can show that for large enough n there exists a positive constant \(\delta _9\) such that for each \(k\in \{1,\ldots ,n\}\) we have
Using the union bound again, we get
for a constant \(\delta _{10}\) less than \(\delta _9\). Now, we relax the assumption \(\mu _s =\xi \) for each \(s \in S^{(n)}\) with Assumption 1. The above proof can then be used to show a similar concentration result for individual groups. The overall result follows by linearity of expectation and yet another use of the union bound. \(\square \)
6 Performance robustness
We now combine results from Sects. 4 and 5 to exhibit performance robustness in large-scale content delivery systems. In Sect. 5 we showed that large systems support symmetric polymatroid capacity regions. This allows us to apply the performance bounds developed in Sect. 4 for symmetric polymatroid capacity regions.
However, there is one more hurdle to overcome before we can apply our bounds from Sect. 4. Recall, from Corollary 3, under Assumptions 1 and 2 the random capacity region for a content delivery system contains and is contained by approximate symmetric polymatroids with high probability. A realization of the random capacity region may still not be symmetric. We thus need to show that if the capacity region is bigger then the corresponding mean delay is smaller when subject to the same load.
Intuitively, larger capacity regions may imply larger service rates for each class, and may thus provide better performance. Although intuitively obvious, such results are not always straightforward. We show below that such a comparison result indeed holds under certain monotonicity conditions for rate allocations. Consider the following monotonicity condition.
Definition 6
(Monotonicity w.r.t. capacity region) We say that a rate allocation satisfies monotonicity w.r.t. capacity region if, for any state \(\mathbf{x}\), the rate allocation per class for a system with a larger capacity region dominates that with a smaller one.
Further, recall per-job rate monotonicity defined in Sect. 4.2, where the rate allocated to each job ( viz., \(\frac{r_i(\mathbf{x})}{x_i}\) for jobs in class i) only decreases when an additional job is added into the system. The following lemma can be shown to hold through a simple coupling argument across jobs for arbitrary polymatroid capacity regions.
Lemma 5
Consider systems with arbitrary polymatroid capacity regions \({\mathcal {C}}\) and \({\tilde{{\mathcal {C}}}}\) such that \({\mathcal {C}} \subset {\tilde{{\mathcal {C}}}}\). Consider a rate allocation which satisfies monotonicity w.r.t. capacity region as well as per-job rate monotonicity. Then, the mean delay for capacity region \({\mathcal {C}}\) under arbitrary load \({\varvec{\rho }}\) upper bounds that for capacity region \({\tilde{{\mathcal {C}}}}\) under the same load.
It is easy to check that \(\alpha \)-fair rate allocation satisfies per-job rate monotonicity as well as monotonicity w.r.t. capacity region. Thus, Lemma 5 holds for \(\alpha \)-fair rate allocation. However, one can show that greedy rate allocation may not satisfy either property for arbitrary polymatroid capacity regions. This further highlights the brittleness of greedy rate allocation to asymmetries. Even for balanced fair rate allocation it is not directly clear if the lemma holds. Thus, henceforth we will only consider \(\alpha \)-fair rate allocation.
Now we are indeed ready with all the tools required to exhibit robustness in large scale systems.
Assumption 3
(Load Heterogeneity) We consider a sequence of systems where load \({\varvec{\rho }}^{(n)}\) for each n is allowed to be within a set \({\mathcal {B}}^{(n)}\) defined as follows: Consider a sequence \((\theta _n: n \in {\mathbb {N}})\) such that \(\theta _n = \omega (1)\), \(\theta _n = o(\frac{n}{\log n})\), and \(\theta _n = o(c_n)\). Also, fix a constant \(\gamma <1\) independent of n. For each n
The condition \( |{\varvec{\rho }}| \le \gamma \xi m\) implies that we allow load to increase linearly with system size. Also, since \(\theta _n = \omega (1)\), the condition \(\max _i\rho _i \le \theta _n\) implies that we allow load across servers to be increasingly heterogeneous. However, the condition \(\theta _n = o\left( \min (\frac{n}{\log n}, c_n)\right) \) implies that peak per-class load is limited, i.e., it constrains the heterogeneity in load allowed in the system. Further, the condition \(\theta _n = o(c_n)\) would allow us to claim stability, and to show that the mean delay of the system tends to 0 as n increases.
The following is the main result of this section. For a proof, see Sect. 6.2.
Theorem 6
Consider a sequence of systems with n files \(F^{(n)}\) and \(m=\left\lceil {bn} \right\rceil \) servers \(S^{(n)}\), where b is a constant. For each n, let the total service capacity of servers be \(\xi m\), where \(\xi \) is independent of n. \(S^{(n)}\) is partitioned into a finite number of heterogeneous groups, each with \(\Omega (n)\) servers and equal per-server capacity. Suppose \(c_n = \omega (\log n)\) copies for each file are stored across servers at random. Let \({\mathcal {G}}^{(n)} = (F^{(n)}\cup S^{(n)};{\mathcal {E}}^{(n)})\) represent the associated random bipartite graph representing file placement across servers.
Given a realization of \({\mathcal {G}}^{(n)}\), let jobs for each file-class \(i\in F^{(n)}\) arrive at rate \(\lambda _i\). Let \({\varvec{\lambda }}^{(n)} = (\lambda _i: i \in F^{(n)})\). Let the mean service requirement of jobs be \(\nu \), where \(\nu \) is independent of n. Let \({\varvec{\rho }}^{(n)} = \nu {\varvec{\lambda }}^{(n)}\). Suppose that the jobs are served as per \(\alpha \)-fair rate allocation.
Let \((\theta _n: n \in {\mathbb {N}})\) be a sequence such that \(\theta _n = o\left( \min (\frac{n}{\log n}, c_n)\right) \). Fix a constant \(\gamma <1\). Let \({\mathcal {B}}^{(n)}= \left\{ {\varvec{\rho }}: \max _{i} \rho _i \le \theta _n \text { and } |{\varvec{\rho }}| \le \gamma \xi m \right\} \). Suppose that for each n we have \({\varvec{\rho }}^{(n)} \in {\mathcal {B}}^{(n)}\). Fix a constant \(\delta > 1\). Let \(E[D^{(n)}|{\mathcal {G}}^{(n)}]\) be the conditional expectation of delay of a typical job with respect to the \(\sigma \)-algebra generated by \({\mathcal {G}}^{(n)}\). Then, we have
6.1 Numerical validation and robustness of Theorem 6
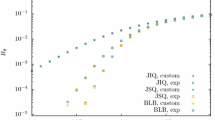
The mean delay bound in Theorem 6 holds with high probability when the system size n is large, and when the load heterogeneity \(\theta _n\) is small as compared to \(c_n\). Below, we numerically explore the impact of the system size and these parameters on performance and our bounds. The motivation for our work is, in part, that simulation of large systems is difficult and it is desirable to reach a rough understanding of how performance scales. To this end, we consider systems using randomized file placement, and assume that the capacity region is essentially symmetric—in our scaling regime, this is known to happen with high probability, see Theorem 5. Symmetry of the capacity region allows us to numerically compute the mean delay, and compare exact results to our asymptotic bounds, for large systems.
We first consider a large system with both symmetric capacity and symmetric load across classes. Theorem 1, along with Theorem 2, provides an upper bound for mean delay under \(\alpha \)-fair rate allocation. Further, Proposition 5 provides a lower bound for the same. Figure 3 exhibits these bounds as a function of load per class for several systems with large n, and \(c_n = \left\lceil {\log _2 n} \right\rceil \), and compares it with the asymptotic expression for expected delay given in Theorem 6 (i.e., \(\delta \frac{ \nu }{ \xi c_n} \frac{1}{\gamma }\log \left( \frac{1}{1-\gamma }\right) \)) for \(\delta =1\). As can be seen, as n increases, both bounds converge to the asymptotic expression, for example, the relative error of upper bound for \(n=1000\) and \(\gamma = 0.6\) is less than \(10 \%\). Recall that the expression in Theorem 6 is an asymptotic upper bound for \(\delta > 1\) (thus the asymptotic expression shown in the figure for \(\delta = 1\) is the most aggressive bound one could hope for). Thus, n needs to be as large as 1000 or more for the asymptotic upper bound to be meaningful at medium loads.
Next we study the impact of load heterogeneity. Recall that in our model for constrained heterogeneity we allow the peak per-class load to be at most \(\theta _n\) while maintaining the total system load to be less than or equal to \(\gamma \xi m\). Thus, the ‘worst case’ load heterogeneity is when the total system load is equal to \(\gamma \xi m\) and there is a subset of classes which have load equal to \(\theta _n\), with the remaining classes having a load equal to 0. An upper bound for mean delay for a system with such a worst case load and with \(\alpha \)-fair rate allocation can again be obtained via the expression in Theorem 1, with load per class equal to \(\theta _n\) but with a smaller total number of classes.
Figure 4 exhibits our mean delay upper bound obtained as above as a function of \(\theta _n\), and compares it with the asymptotic bound obtained via Theorem 6 for \(\delta = 2\). For \(n = 10000\), the asymptotic bound holds as \(\theta _n\) varies from 0.6 to up to 3.7. Note that \(\theta _n =0.6\) corresponds to a system with homogeneous load across classes. Thus, for a large system the asymptotic bound is good as long as the peak per-class load \(\theta _n\) is no more than six times the per-class load of the homogeneous system.
6.2 Proof of Theorem 6
In light of Corollary 3, we consider a symmetric capacity region which, with high probability, contains the capacity region resulting from randomized file placement. Further, to obtain an upper bound on the mean delay for heterogeneous loads, we consider a system with extremely unbalanced arrivals in that the arrival rate is maximum for a subset of classes and negligible for others. The bound is obtained via the mean delay expression under balanced fairness for the extremely unbalanced system.
Without loss of generality, assume \(\delta < \frac{1}{\gamma }\). From Corollary 3 and the definitions of \({\bar{{\mathcal {C}}}}^{(n)}\) and \({\bar{\mu }}^{(n)}(.)\), with high probability the capacity region contains the following symmetric polymatroid:
where
Thus, from Lemma 5 and Corollary 3, the theorem follows if we show that for a system with (deterministic) capacity region \({\tilde{{\mathcal {C}}}}^{(n)}\) and with \(\alpha \)-fair rate allocation the mean delay is upper bounded by \( \delta \frac{ \nu }{ \xi c_n} \frac{1}{\gamma }\log \left( \frac{1}{1-\gamma }\right) \) for large enough n. Thus, for the rest of the proof we will assume that the system has capacity region \({\tilde{{\mathcal {C}}}}^{(n)}\) and \(\alpha \)-fair rate allocation, and eventually establish the mean delay bound.
Note that since \({\tilde{{\mathcal {C}}}}^{(n)}\) is monotonic in \(c_n\), it is sufficient to assume that \(c_n = o(\frac{n}{\log n})\) since, if it is not, we can set \(c_n\) to be equal to \( \sqrt{\frac{n}{\log n}\theta _n }\) and all the assumptions still hold. Thus, henceforth we assume that
Let \(\xi ' \triangleq \xi /\delta . \) Also let \(\gamma ' \triangleq \delta \gamma \). Thus, we get
Since \(\gamma \xi m< \xi ' m\) and \(\theta _n = o(c_n)\), one can check that \(B^{(n)}\) is a subset of \({\tilde{{\mathcal {C}}}}^{(n)}\) for large enough n, and we get stability.
Now we consider a case where certain classes have maximum load (i.e., \(\theta _n\)) and the rest have load 0, while ensuring that the overall system load is still approximately \(\gamma m\).
Let \(t_n \triangleq \left\lceil {\frac{\gamma ' \xi ' m}{\theta _n}} \right\rceil \). Let \(A^{(n)}\) be an arbitrary subset of \(F^{(n)}\) such that \(|A^{(n)}| = t_n\). Let \(\hat{{\varvec{\rho }}}^{(n)} = (\hat{\rho }_i^{(n)}: i\in F^{(n)})\) where \(\hat{\rho }_i^{(n)} = \theta _n\) if \(i\in A^{(n)}\) and 0 otherwise. Then, it is easy to show that for each n we have
Thus, from Theorem 4, it is sufficient to show that the bound on mean delay holds for balanced fair rate allocation under the load \( {\varvec{\rho }}^{(n)} = \hat{{\varvec{\rho }}}^{(n)}\).
Henceforth, we assume BF rate allocation and let the load \( {\varvec{\rho }}^{(n)}= \hat{{\varvec{\rho }}}^{(n)}\). For each n, we invoke Proposition 4 and Theorem 1 with \(\rho \) replaced by \(\theta _n\) and n replaced by \(t_n\), to obtain an expression for \(\pi _k^{(n)}\) and \(\beta _k^{(n)}\), and eventually mean delay. We first show below concentration for \(\pi _k^{(n)}\) using Proposition 4.
Below we refrain from using ceiling and floor to avoid cluttering.
Theorem 7
Consider a system with capacity region \({\tilde{{\mathcal {C}}}}^{(n)}\) and with the load vector \(\hat{{\varvec{\rho }}}^{(n)}\). Under balanced fair rate allocation, \(\pi _k^{(n)}\), which represents the stationary probability that k classes are active in the system, satisfies the following concentration result. For any positive constants \(\epsilon >1\) and \(\epsilon '<1\) independent of n, there exists a constant \({\tilde{\delta }} < 1\) such that for large enough n we have
Proof
From Proposition 4 for \(k = 1, \ldots , t_n\) we have
Fix a constant \(\delta _{11}\) independent of n such that \(0<\delta _{11}<1\). Let
Then, one can check that \(h^{(n)}(k^{(n)}_{\downarrow }) \le \gamma ' \delta _{11} \xi ' m .\)
In fact, we have \(h^{(n)}(k) \le \gamma ' \delta _{11} \xi ' m, \;\;\forall k \le k_{\downarrow }^{(n)}.\) Using (16), for each \(k \le k_{\downarrow }^{(n)}\) we have
for a positive constant \(\delta _{12}\) such that \(\delta _{11}< \delta _{12} < 1\), and large enough n.
Equivalently, \(\pi _k^{(n)} \le \delta _{12} \pi _{k+1}^{(n)} \;\; \forall k < k_{\downarrow }^{(n)}.\)
Fix a positive constant \(\epsilon _{1}<1\). Then, for all \(k < \epsilon _1 k_{\downarrow }^{(n)}\) we have
Now, fix a constant \(\delta _{13}\) independent of n such that \(\gamma '<\delta _{13}<1\) and let
Then, one can check that \( \frac{h^{(n)}(k_{\uparrow }^{(n)}) }{\xi 'm} \rightarrow \gamma '/\delta _{13}\) as \(n \rightarrow \infty \). Thus, for some constant \(\delta '_{13}\) such that \(\delta _{13}< \delta '_{13}<1\), we have \( h^{(n)}(k_{\uparrow }^{(n)}) \ge \gamma ' \xi ' m /\delta '_{13}\). In fact, for all \( k\ge k_{\uparrow }^{(n)} \) we have \(h^{(n)}(k) \ge \gamma ' \xi ' m /\delta '_{13} .\)
Now, for large enough n, \( \gamma ' \xi ' m /\delta '_{13} \ge \gamma ' \xi ' m + \theta _n \ge ( t_n + 1) \theta _n\).
Thus, for large enough n, we have \(h^{(n)}(k) - k \theta _n \ge (t_n - k + 1) \theta _n \;\; \forall k\ge k_{\uparrow }^{(n)},\) or equivalently from (16),
In fact, for a fixed positive constant \(\epsilon _{2}>1\), for all k such that \( k_{\uparrow }^{(n)} \le k \le \epsilon _2 k_{\uparrow }^{(n)}\) we have
for a positive constant \(\delta _{14}\) such that \(\delta '_{13}<\delta _{14} < 1\), and for large enough n. Thus, \(\pi _{\epsilon _2 k_{\uparrow }^{(n)}}^{(n)} \le \delta _{14}^{(\epsilon _2-1)k_{\uparrow }^{(n)}} \pi _{k_{\uparrow }^{(n)}}^{(n)}\) for large enough n. Further, using (17) we get
Thus, we get
for suitably chosen positive constants \(\delta _{15}\) and \(\delta _{17}\). Thus, the concentration follows by noting that \(\epsilon _1, \epsilon _2, \delta _{11},\) and \(\delta _{13}\) can be chosen arbitrarily close to 1. \(\square \)
We now provide a bound for \(\beta _k^{(n)}\). From (9), for \(k=1,\ldots ,t_n\) we have
Using \(g_n = \frac{\theta _n}{\gamma ' \xi ' b}\) in Lemma 3, we get \(h^{(n)}(k) = \xi ' b n p_k^{(n)} \ge \frac{\delta _{18}}{\gamma '} k \theta _n\) for large enough n and some constant \(\delta _{18}\) such that \(\gamma '< \delta _{18} <1\). From (18), for each \(k=1, \ldots , t_n\), for large enough n we have
for some constant \(\delta _{19}\) which is greater than 1.
The above bound for \(\beta _k^{(n)}\) is somewhat loose, especially for lower values of k. Recall, the concentration result, namely Theorem 7, implies that the number of active classes is smaller than \(\epsilon b \log (\frac{1}{1-\gamma '})\frac{n}{c_n}\) with high probability. The bound on \(\beta _k^{(n)}\) can be further improved for the smaller values of k as follows.
Suppose \(h^{(n)}(.)\) is a continuous function, i.e., \(h^{(n)}(t) = \xi ' m\left( 1-e^{-\frac{tc_n}{m}}\right) \) for each \(t\in {\mathbb {R}}^+\). Then, by concavity of \(h^{(n)}(t)\) and noting that \(h^{(n)}(0) = 0\), we get \(\frac{h^{(n)}(t)}{t} \ge \frac{d}{dt} h^{(n)}(t)\). Further, by concavity, for each \(k \le \epsilon b \log (\frac{1}{1-\gamma '})\frac{n}{c_n}\) we have \(\frac{h^{(n)}(k)}{k} \ge \frac{d}{dt} h^{(n)}(t)\Big |_{t=k} \ge \frac{d}{dt} h^{(n)}(t) \Big |_{t= b \log (\frac{1}{1-\gamma '})\frac{n}{c_n}} = \xi ' c_n (1-\gamma ')^{-\epsilon }\).
From (18), for \(k=1, \ldots , \epsilon b \log (\frac{1}{1-\gamma '})\frac{n}{c_n}\), we have
We are now ready to bound mean delay. For large enough n, we have
The theorem thus follows from the definition of \(t_n\), \(\gamma '\) and \(\xi '\), and the fact that \(\epsilon \), \(\delta \), and \({\tilde{\delta }}\) were chosen arbitrarily. \(\square \)
7 Conclusions
Our main conclusions address both practical and theoretical aspects associated with such systems. We show that an infrastructure which allows a user to download in parallel from a pool of servers can achieve scalable performance under limited heterogeneity in file demands. Some elements of content delivery infrastructure such as a centralized back end which handles cache misses at distributed sites may see less pronounced heterogeneity in demands. Our results suggest that pooling of server resources is a scalable approach towards delivering content for such centralized systems without requiring complex caching strategies internally.
On the theoretical side we have established: (1) basic new results linking fairness in resource allocation to delays and (2) the asymptotic symmetry of randomly configured large-scale systems with heterogenous components. Together these results suggest large systems might eventually be robust to heterogeneity and fairness criterion.
8 Appendix
8.1 Relative greediness and other rate allocation properties
Below, we provide a proof of Lemma 1 which asserts that \(\alpha \)F is more greedy than BF. Along the way, we develop several other properties of the rate allocation policies.
The proof of Lemma 1 stems from the properties (1) and (2) below on per-job rate assignment for \(\alpha \)F and BF.
-
(1.)
\(\alpha \) F gives the most balanced per-job rate allocation This property follows from the fact that \(\alpha \)F is equivalent to max-min fair rate allocation; see Proposition 2. Formally,
Lemma 6
Let \(\mathbf{b}^{\alpha }\) represent a vector of rates assigned to a set of flows under \(\alpha \)F rate allocation. Let \({\tilde{\mathbf{b}}}\) be the rates assigned to the same set of flows under any other feasible rate allocation. Then, \(\mathbf{b}^{\alpha } \prec ^{w} {\tilde{\mathbf{b}}}\), i.e., weak majorization from above.
Proof
Let the set of flows be \(q_{A_\mathbf{x}}\). It is easy to show that \(\mathbf{b}^{\alpha }\) is the unique solution to the following optimization problem:
Also, since \( {\tilde{\mathbf{b}}}\) is feasible, it satisfies the constraints of the above problem. The result then follows by noting that the objective function of the above problem is monotonic and Schur-concave in \((\hat{b}_u: u \in q_{A_\mathbf{x}})\) [13, 16]. \(\square \)
-
(2.)
In \(\alpha \) F and BF, longest queues have smallest per-job rates For \(\alpha \)F, this property again follows from the fact that it is equivalent to max-min fair, and that the capacity region is convex and symmetric. For BF, the proof for this property is given in Appendix (In BF, longest queues have smallest per-job rates). Formally,
Lemma 7
\(\alpha \)F and BF rate allocations satisfy the following property for any state \(\mathbf{x}\): if \(x_i > x_j\) then \( \frac{r_i(\mathbf{x})}{x_i} \le \frac{r_j(\mathbf{x})}{x_j} \).
Proof
Below we prove the lemma for \(\alpha \)F rate allocation. For a proof of this lemma for BF rate allocation, see the Appendix (In BF, longest queues have smallest per-job rates).
Let \(\mathbf{b}^{\alpha } = (b^\alpha _u:u\in q_{A_\mathbf{x}})\) represent the rates assigned to ongoing flows under \(\alpha \)F rate allocation in state \(\mathbf{x}\). Suppose \(x_i > x_j\), but \(\frac{r_i^\alpha (\mathbf{x})}{x_i} > \frac{r_j^\alpha (\mathbf{x})}{x_j}\). Then, for each \(u'\in q_i\) and \(v' \in q_j\), we have \(b^\alpha _{u'} > b^\alpha _{v'}\). Let \({\tilde{\mathbf{b}}}= (\tilde{b}_u:u\in q_{A_\mathbf{x}})\), where \({\tilde{b}}_u = b^\alpha _u\) for each \(u \in q_{A_\mathbf{x}\backslash \{i,j\}}\) and \({\tilde{b}}_u = \frac{r_i^\alpha (\mathbf{x})+r_j^\alpha (\mathbf{x})}{x_i+x_j}\) for each \(u\in q_{\{i,j\}}\). It can be checked that \({\tilde{b}}_u \) is feasible and that \({\tilde{\mathbf{b}}} \prec ^{w} \mathbf{b}^{\alpha } \). This contradicts Lemma 6. Hence the result. \(\square \)
Now, let us study what the above properties imply for per-class rate allocation. Consider a state \(\mathbf{x}\). Lemma 7 above implies that the most disadvantaged jobs are the ones which belong to longest queues for both BF and \(\alpha \)F. This, along with Lemma 7, implies that \(\alpha \)F provides larger rate to longest queues. Thus, we get the following property:
-
(3.)
\(\alpha \) F provides a larger rate to longest queues compared to BF Formally, this property can be stated as follows:
Lemma 8
For any state \(\mathbf{x}\), we have \( \sum _{l=1}^{k} r^{\alpha }_{(l)}(\mathbf{x})\ge \sum _{l=1}^{k} r^{B}_{(l)}(\mathbf{x})\) for each \(k \in \{1,2,\ldots ,n\}\).
Proof
Let \(u_1, u_2,\ldots , u_{x_{[1]}}\) be the flows in the class corresponding to \(x_{[1]}\). Similarly, for each \(k\in \{2,\ldots ,n\}\), let \(u_{\sum _{l=1}^{k-1}x_{[l]}+1},\ldots , u_{\sum _{l=1}^{k}x_{[l]}}\) be the flows in the class corresponding to \(x_{[k]}\). From Lemma 7, under both BF and \(\alpha \)F rate allocation we have \(b_{u_1} \le b_{u_2} \le \ldots \le b_{u_{|x|}}\). Thus, it is enough to show that \(\mathbf{b}^{\alpha } \prec ^w \mathbf{b}^{B}\). However, this follows from Lemma 6. \(\square \)
Now, we focus on \(\alpha \)F and study how it allocates rates across classes for states \(\mathbf{x}\) and \(\mathbf{y}\) such that \(\mathbf{x}\prec \mathbf{y}\). Intuitively, jobs in longer queues in state \(\mathbf{y}\) are more constrained than those in \(\mathbf{x}\). Again using the fact that \(\alpha \)F is equivalent to max-min fair, the most constrained jobs in state \(\mathbf{y}\) have smaller rate than those in state \(\mathbf{x}\). By monotonicity of \(\alpha \)F, this holds even when \(\mathbf{x}\prec _w \mathbf{y}\). When translated to per-class rate allocation in states \(\mathbf{x}\) and \(\mathbf{y}\), this argument leads us to the following property:
-
(4.)
\(\alpha \) F provides a larger rate to longer queues in more balanced states Formally, this property can be stated as follows:
Lemma 9
Consider states \(\mathbf{x}\) and \(\mathbf{y}\) such that \(\mathbf{x}\prec _w \mathbf{y}\). For each k such that \(\sum _{l=1}^{k} x_{[l]} = \sum _{l=1}^{k} y_{[l]}\), we have \(\sum _{l=1}^{k} r^{\alpha }_{(l)}(\mathbf{x}) \ge \sum _{l=1}^{k} r^{\alpha }_{(l)}(\mathbf{y})\).
Proof
Due to monotonicity of \(\mathbf{r}^{\alpha }(\mathbf{y})\) with respect to components of \(\mathbf{y}\), it is enough to show the result for the case where \(\mathbf{x}\prec \mathbf{y}\). Assume \(\mathbf{x}\prec \mathbf{y}\). Let \(u_1, u_2,\ldots , u_{x_{[1]}}\) be the flows in the class corresponding to \(x_{[1]}\). Similarly, let \(u_{\sum _{l=1}^{k-1}x_{[l]}+1},\ldots , u_{\sum _{l=1}^{k}x_{[l]}}\) be the flows in the class corresponding to \(x_{[k]}\) for each \(k\in \{2,\ldots ,n\}\). Let the corresponding rates assigned to flows under \(\alpha \)F rate allocation be given by \(\mathbf{b}^{(\mathbf{x})}\). Using Lemma 7, we have \(b_{u_1} \le b_{u_2} \le \ldots \le b_{u_{|\mathbf{x}|}}\). Similarly, let \(v_1,v_2, \ldots , v_{|\mathbf{y}|}\) be the flows corresponding to state \(\mathbf{y}\) and construct the corresponding \(\mathbf{b}^{(\mathbf{y})}\).
One can check that \({\tilde{\mathbf{b}}}^{(\mathbf{x})} = ({\tilde{b}}^{(\mathbf{x})}_{u_k}: k \in \{1,2,\ldots ,|\mathbf{x}|\})\), where \({\tilde{b}}^{(\mathbf{x})}_{u_k} = b_{v_k}^{(\mathbf{y})}\) for each \(k \le |\mathbf{x}|\), is feasible under state \(\mathbf{x}\) as well. Thus, from Lemma 6, we have \(\mathbf{b}^{(\mathbf{x})} \prec ^w {\tilde{\mathbf{b}}}^{(\mathbf{x})}\). From this, the result follows. \(\square \)
Finally, we are ready to study relative greediness of \(\alpha \)F and BF.
-
(5.)
\(\alpha \) F is more greedy than BF We now prove Lemma 1. Consider states \(\mathbf{x}\) and \(\mathbf{y}\) such that \(\mathbf{x}\prec _w \mathbf{y}\). From Lemma 9 we have \(\sum _{l=1}^{k} r^{\alpha }_{(l)}(\mathbf{x}) \ge \sum _{l=1}^{k} r^{\alpha }_{(l)}(\mathbf{y})\), and from Lemma 8 we have \(\sum _{l=1}^{k} r^{\alpha }_{(l)}(\mathbf{y}) \ge \sum _{l=1}^{k} r^{B}_{(l)}(\mathbf{y})\). Hence, Lemma 1 holds.
8.2 In BF, longest queues have smallest per-job rates
Lemma 10
For any state \(\mathbf{x}\), if \(x_i > x_j\) then \( \frac{r_i^B(\mathbf{x})}{x_i} \le \frac{r_j^B(\mathbf{x})}{x_j} \).
Proof
Using the definition of balanced fairness, we have \(\frac{r_i^B(\mathbf{x})}{r^B_j(\mathbf{x})} = \frac{\varPhi (\mathbf{x}-\mathbf{e}_i)}{\varPhi (\mathbf{x}-\mathbf{e}_j)}\). Thus, we need to show that \( \frac{\varPhi (\mathbf{x}-\mathbf{e}_i)}{\varPhi (\mathbf{x}-\mathbf{e}_j)} \le \frac{x_i}{x_j}\). It is thus sufficient to prove that \(\frac{\varPhi (\mathbf{x}+\mathbf{e}_i)}{\varPhi (\mathbf{x}+\mathbf{e}_j)} \ge \frac{x_j+1}{x_i + 1}\) holds for each \(\mathbf{x}\) since the result follows when \(\mathbf{x}\) is replaced with \(\mathbf{x}-\mathbf{e}_i-\mathbf{e}_j\).
We show below that \(\frac{\varPhi (\mathbf{x}+\mathbf{e}_i)}{\varPhi (\mathbf{x}+\mathbf{e}_j)} \ge \frac{x_j+1}{x_i + 1}\) holds for each \(\mathbf{x}\).
Fix \(i,j \in F\). By symmetry of balanced fairness and the capacity region, the result holds for each \(\mathbf{x}\) such that \(x_i = x_j\). We show that the result holds for each \(\mathbf{x}\) such that \(x_i \ge x_j\) using induction on \(|\mathbf{x}|\). We will use the following recursive expression for \(\varPhi (.)\) which we get from the definition of balanced fair and Proposition 3: For each state \(\mathbf{x}\), we have
The result clearly holds for the base case of \(|\mathbf{x}|=0\). Assume that the result holds for all states \(\mathbf{x}'\) such that \(|\mathbf{x}'| < |\mathbf{x}|\). We prove that the result holds for the state \(\mathbf{x}\) under each of the following two possible cases for \(\mathbf{x}\):
Case 1 \(A_{\mathbf{x}+\mathbf{e}_i} \subsetneq A_{\mathbf{x}+\mathbf{e}_j}\): This case is possible only if \(x_i > 0\) and \(x_j=0\). Thus, \(\mu (A_{\mathbf{x}+\mathbf{e}_i}) \le \mu (A_{\mathbf{x}+\mathbf{e}_j})\). Using (19), we get
Using the induction hypothesis, we have \(\frac{\varPhi (\mathbf{x}+\mathbf{e}_i-\mathbf{e}_{i'})}{\varPhi (\mathbf{x}+\mathbf{e}_j-\mathbf{e}_{i'})} \ge \frac{x_j+1}{x_i + 1}\) for each \(i' \in A_\mathbf{x}\backslash \{i\}\). Thus, using the fact that \(\frac{a_1+a_2}{b_1+b_2} \ge \frac{x}{y}\) if \( \frac{a_k}{b_k} \ge \frac{x}{y}\) for each \(k\in \{1,2\}\), the result follows if we show that \(\frac{\varPhi (\mathbf{x})}{\varPhi (\mathbf{x})+\varPhi (\mathbf{x}+\mathbf{e}_j-\mathbf{e}_i) } \ge \frac{x_j+1}{x_i + 1}\). This in turn follows since \(x_j=0\) and \(\frac{\varPhi (\mathbf{x})}{\varPhi (\mathbf{x}+\mathbf{e}_j-\mathbf{e}_i)} \ge \frac{1}{x_i}\) holds by the induction hypothesis.
Case 2 \(A_{\mathbf{x}+\mathbf{e}_i} = A_{\mathbf{x}+\mathbf{e}_j}\): Again using (19), we get
Again, using the induction hypothesis we have \(\frac{\varPhi (\mathbf{x}+\mathbf{e}_i-\mathbf{e}_{i'})}{\varPhi (\mathbf{x}+\mathbf{e}_j-\mathbf{e}_{i'})} \ge \frac{x_j+1}{x_i + 1}\) for each \(i' \in A_\mathbf{x}\backslash \{i,j\}\). Thus, we only need to show that \( \frac{\varPhi (\mathbf{x})+ \varPhi (\mathbf{x}+\mathbf{e}_i-\mathbf{e}_j)}{\varPhi (\mathbf{x})+\varPhi (\mathbf{x}+\mathbf{e}_j-\mathbf{e}_i)} \ge \frac{x_j+1}{x_i+1}\). We show this below.
By the induction hypothesis, we have \(\frac{ \varPhi (\mathbf{x}+\mathbf{e}_i-\mathbf{e}_j)}{\varPhi (\mathbf{x})} \ge \frac{x_j}{x_i+1}\) and \(\frac{\varPhi (\mathbf{x})}{\varPhi (\mathbf{x}+\mathbf{e}_j-\mathbf{e}_i)} \ge \frac{x_j+1}{x_i}\). Thus, we get
Hence, the result. \(\square \)
8.3 Technical lemmas for proof of Theorem 5
Lemma 3 Let a sequence \((g_n: n\in {\mathbb {N}})\) be such that \( g_n = o(c_n).\) Let \(\delta _1<1\) be a positive constant independent of k and n. Then, for large enough n, we have
Proof
Consider a sequence of functions \(\left( f^{(n)}(.)\right) _{n\ge 1}\) where, for each n, \(f^{(n)}(t) = 1- (1-c_n/(bn))^{t}\) for each \(t \in {\mathbb {R}}_+\). Then,
Thus, there exists an integer \(n'\) such that \(f^{(n)}\left( n/g_n \right) \ge \delta _1\) for all \(n \ge n'\). Also, \(f^{(n)}(0) = 0\) for each n. Using concavity of \(f^{(n)}(.)\), for each \(n\ge n'\) we have
Hence, the lemma. \(\square \)
Lemma 4 There exists a positive constant \(\delta \), independent of k and n, such that \(H\left( p_k^{(n)}(1-\epsilon )||p_k^{(n)}\right) \ge - \delta + \epsilon \frac{ k c_n}{m} \).
Proof
From the definition,
Here, the term \(p_k^{(n)}(1-\epsilon )\log (1-\epsilon )\), while negative, is greater than \((1-\epsilon )\log (1-\epsilon )\), a constant. Similarly, the term \((1-p_k^{(n)}(1-\epsilon ))\log \left( 1-p_k^{(n)}(1-\epsilon )\right) \) is negative, but can be upper-bounded by a constant as follows:
Thus, we have
where in the last inequality we used the fact that \(1 - p_k^{(n)} \le e^{ -\frac{kc_n}{m} } \). \(\square \)
References
Bonald, T.: Throughput performance in networks with linear capacity contraints. In: Proceedings of CISS, pp. 644 –649 (2006)
Bonald, T., Massoulié, L., Proutière, A., Virtamo, J.: A queueing analysis of max-min fairness, proportional fairness and balanced fairness. Queueing Syst. 53, 65–84 (2006)
Bonald, T., Proutière, A.: Insensitive bandwidth sharing in data networks. Queueing Syst. 44, 69–100 (2003)
Bonald, T., Proutière, A.: On stochastic bounds for monotonic processor sharing networks. Queueing Syst. 47, 81–106 (2004)
Bonald, T., Proutière, A., Roberts, J., Virtamo, J.: Computational aspects of balanced fairness. In: Proceedings of ITC (2003)
Bonald, T., Virtamo, J.: Calculating the flow level performance of balanced fairness in tree networks. Perform. Eval. 58(1), 1–14 (2004)
de Veciana, G., Lee, T.J., Konstantopoulos, T.: Stability and performance analysis of networks supporting elastic services. IEEE/ACM Trans. Netw. 9(1), 2–14 (2001)
Dubhashi, D., Ranjan, D.: Balls and bins: A study in negative dependence. Random Struct. Algorithms 13(2), 99–124 (1998)
Edmonds, J.: Submodular functions, matroids, and certain polyhedra. In: Proceedings of Calgary International Conference on Combinatorial Structures and Applications, pp. 69–87. Gordon and Breach, New York (1969)
Frank, B., Poese, I., Smaragdakis, G., Feldmann, A., Maggs, B.M., Uhlig, S., Aggarwal, V., Schneider, F.: Collaboration opportunities for content delivery and network infrastructures. In: H. Haddadi, O. Bonaventure (eds.) Recent Advances in Networking, pp. 305–377 (2013)
Joseph, V., de Veciana, G.: Stochastic networks with multipath flow control: Impact of resource pools on flow-level performance and network congestion. In: Proceedings of the ACM Sigmetrics, pp. 61–72 (2011)
Kelly, F.P., Maulloo, A.K., Tan, D.K.H.: Rate control for communication networks: shadow prices, proportional fairness and stability. J. Oper. Res. Soc. 49(3), 237–252 (1998)
Lan, T., Kao, D., Chiang, M., Sabharwal, A.: An axiomatic theory of fairness in network resource allocation. In: Proceedings of IEEE Infocom, pp. 1–9 (2010)
Leconte, M., Lelarge, M., Massoulié, L.: Adaptive replication in distributed content delivery networks. arXiv preprint arXiv:1401.1770 (2014)
Lin, X., Shroff, N.: Utility maximization for communication networks with multipath routing. IEEE Trans. Autom. Control 51(5), 766–781 (2006)
Marshall, A.W., Olkin, I., Arnold, B.C.: Inequalities: Theory of Majorization and Its Applications, 2nd edn. Springer, New York (2011)
Massoulié, L., Roberts, J.: Bandwidth sharing and admission control for elastic traffic. Telecommun. Syst. 15(1–2), 185–201 (2000)
Mitzenmacher, M., Upfal, E.: Probability and Computing: Randomized Algorithms and Probabilistic Analysis. Cambridge University Press, Cambridge (2005)
Mo, J., Walrand, J.: Fair end-to-end window-based congestion control. IEEE/ACM Trans. Netw. 8(5), 556–567 (2000)
Moharir, S., Ghaderi, J., Sanghavi, S., Shakkottai, S.: Serving content with unknown demand: The high-dimensional regime. In: Proceedings of ACM Sigmetrics, pp. 435–447 (2014)
Nemhauser, G.L., Wolsey, L.A.: Integer and combinatorial optimization, vol. 18. Wiley, New York (1988)
Shah, V., de Veciana, G.: Performance evaluation and asymptotics for content delivery networks. In: IEEE Infocom, pp. 2607–2615 (2014)
Shah, V., de Veciana, G.: High performance centralized content delivery infrastructure: models and asymptotics. IEEE/ACM Trans. Netw. 23, 1674 (2015)
Tsitsiklis, J.N., Xu, K.: Flexible queueing architectures. arXiv preprint arXiv:1505.07648 (2015)
Walrand, J.: An Introduction to Queueing Networks. Prentice Hall, Englewood Cliffs (1988)
Yeh, E.: Multiaccess and fading in communication networks. Ph.D. thesis, Massachusetts Institute of Technology (2001)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Shah, V., de Veciana, G. Impact of fairness and heterogeneity on delays in large-scale centralized content delivery systems. Queueing Syst 83, 361–397 (2016). https://doi.org/10.1007/s11134-016-9491-0
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11134-016-9491-0