Abstract
We study a load balancing system in the many-server heavy-traffic regime. We consider a system with N servers, where jobs arrive to the system according to a Poisson process and have an exponentially distributed size with mean 1. We parametrize the arrival rate so that the arrival rate per server is \(1-N^{-\alpha }\), where \(\alpha >0\) is a parameter that represents how fast the load grows with respect to the number of servers. The many-server heavy-traffic regime corresponds to the limit as \(N\rightarrow \infty \), and subsumes several regimes, such as the Halfin–Whitt regime (\(\alpha =1/2\)), the NDS regime (\(\alpha =1\)), as \(\alpha \downarrow 0\) it approximates mean field and as \(\alpha \rightarrow \infty \) it approximates the classical heavy-traffic regime. Most of the prior work focuses on regimes with \(\alpha \in [0,1]\). In this paper, we focus on the case when \(\alpha >1\) and the routing algorithm is power-of-d choices with \(d=\lceil cN^\beta \rceil \) for some constants \(c>0\) and \(\beta \ge 0\). We prove that \(\alpha +\beta >3\) is sufficient to observe that the average queue length scaled by \(N^{1-\alpha }\) converges to an exponential random variable. In other words, if \(\alpha +\beta >3\), the scaled average queue length behaves similarly to the classical heavy-traffic regime. In particular, this result implies that if d is constant, we require \(\alpha >3\) and if routing occurs according to JSQ we require \(\alpha >2\). We provide two proofs to our result: one based on the Transform method introduced in Hurtado-Lange and Maguluri (Stoch Syst 10(4):275–309, 2020) and one based on Stein’s method. In the second proof, we also compute the rate of convergence in Wasserstein’s distance. In both cases, we additionally compute the rate of convergence in expected value. All of our proofs are powered by state space collapse.
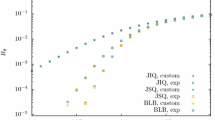
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
We study a load balancing system also known as supermarket checkout system, that is, a single-hop stochastic processing network (SPN) where each server has its own queue. There is a single stream of arrivals and, right after arriving, the jobs are routed to one of the queues by a dispatcher. Popular routing algorithms are join the shortest queue (JSQ) and power-of-d choices. Under JSQ, the new arrival is immediately sent to the shortest queue. Under power-of-d choices, d queues are sampled uniformly at random and the job is routed to the shortest queue among these d.
Exact analysis of many SPNs (including load balancing systems) usually becomes intractable. Hence, a common practice is to study the SPNs in some asymptotic regime to gain insights about their behavior. A popular regime is heavy traffic, where the number of servers is constant and the load is increased to the maximum capacity. One of the advantages of studying systems in heavy traffic is that, in the limit, many systems behave as lower-dimensional systems, a phenomenon known as state space collapse (SSC). In other words, if an SPN experiences SSC in the heavy-traffic limit, it behaves as if the number of queues was smaller.
Another popular asymptotic regime is mean field, where the load is kept constant and the number of servers is increased to infinity. In this regime, the main idea is that, as the number of servers increases, one can isolate one queue and study its interactions with the rest of the system. Then, since all the queues are equivalent, one uses the analysis of this single queue to understand the behavior of the entire system.
In this paper we work with the many-server heavy-traffic regime, where both, the load and the number of servers, increase together. Specifically, we let N be the number of servers and we parametrize the arrival process so that the mean arrival rate per server is \(1-N^{-\alpha }\), where \(\alpha >0\). Then, the total arrival rate to the system is \(N(1-N^{-\alpha })\). In the many-server heavy-traffic regime, there are different phases depending on the value of \(\alpha \). As \(\alpha \downarrow 0\), we approximately approach the mean-field regime, \(\alpha =\frac{1}{2}\) represents the Halfin–Whitt regime [24], \(\alpha =1\) represents the nondegenerate-slowdown regime (NDS) [2], and \(\alpha \rightarrow \infty \) can be thought of as the classical heavy-traffic regime. In this paper, we look at all super-NDS regimes, i.e., the regimes with \(\alpha >1\). Hence, we study regimes where the systems are more heavily loaded than NDS. The main contributions of this paper are summarized below:
-
(i)
We show that the total queue length scaled by \(N^{-\alpha }\) (or, equivalently, the average queue length scaled by \(N^{1-\alpha }\)) converges in distribution to an exponential random variable if the load grows ‘fast enough’ with respect to the number of servers. In particular, under power-of-d choices with constant d, we show that this result is valid if \(\alpha >3\) (see Corollary 1); and under JSQ the same result holds for \(\alpha >2\) (see Corollary 2). Further, we show the condition that \(\alpha \) must satisfy under power-of-d choices when d is a function of the number of servers. Specifically, we show that if \(d{\mathop {=}\limits ^{\triangle }}\lceil cN^\beta \rceil \) for some \(c>0\) and \(\beta \ge 0\) such that \(d\in [N]\), the convergence to the exponential random variable is valid if \(\alpha +\beta >3\) (see Theorem 1). We provide two proofs to our result, which we explain in the next two contributions.
-
(ii)
We first show the result using one-sided Laplace transform (see Sect. 3). Specifically, we generalize the Transform method introduced in [30] for discrete-time systems, to a continuous-time model. We briefly describe the Transform method below, and we provide more details in Sect. 3.1.
-
(iii)
We compute the rate of convergence of the scaled total queue length to the exponential random variable in Wasserstein’s distance (see Theorem 3). This is a stronger version of Theorem 1, where we actually obtain the convergence in distribution as a consequence of the error bound. To show this result, we use Stein’s method (see Sect. 4).
-
(iv)
All these proofs are powered by a multiplicative SSC result that we show in Proposition 1. We show SSC to the line generated by the vector \({\varvec{1}}\), i.e., we show that all the queue lengths are similar in the limit. Specifically, we compute bounds for the moments of the norm of the difference between the queue length vector and its projection on the line generated by the vector \({\varvec{1}}\). Further, we compute a bound for the moment generating function (MGF) of its norm. These bounds grow to infinity as the number of servers increase. However, after scaling the total queue length by \(N^{-\alpha }\) they become negligible (see Sect. 2.1), hence the name multiplicative.
-
(v)
We compute the rate of convergence in expected value of the total average queue length scaled by \(N^{-\alpha }\). Specifically, we show that the rate of convergence is of order \(\log (N)N^{3-\beta }\). As a consequence, we prove the convergence of the expectation under the same conditions established in Theorem 1 (see Theorem 2). Similarly to Theorem 1, we explicitly show that the power-of-d choices algorithm with constant d and the JSQ algorithm are immediate consequences of Theorem 2. To prove this result, we use the Drift method (see 3.3), which we briefly explain in Sect. 1.1, and Stein’s method (see Sect. 4).
Before discussing the related work, we briefly summarize the Transform method and Stein’s method. The Transform method introduced in [30] is a two-step procedure to compute the distribution of the queue lengths in classical heavy-traffic regime, and it can be used for queueing systems that experience SSC to a one-dimensional subspace. The method is introduced in the context of a load balancing system and a generalized switch. Before using the method, positive recurrence and SSC to a one-dimensional subspace must be proved. The main idea is to consider an exponential test function such that, after setting its drift to zero, yields the MGF of the projection of the vector of queue lengths on the subspace where SSC occurs. Then, an implicit expression that is valid for all traffic is obtained. The last step is to take the heavy-traffic limit and prove that the terms depending on the queue lengths vanish, so that we obtain an explicit expression for the limiting MGF.
Stein’s method is based on the approach introduced by [46]. The main idea is to bound the Wasserstein’s distance between the pre-limit random variable and the limiting random variable. In the definition of Wasserstein’s distance, all the Lipschitz functions with constant 1 are considered (see Definition 3). Hence, one needs to compute a bound that is valid for a family of functions.
In both methods, the use of test functions is essential. In the Transform method, this function is exponential and part of the merit of [30] was to realize the right exponential test function. In fact, the entire proof depends on this specific test function. In Stein’s method, instead, one simultaneously considers a whole family of test functions. Then, by studying their drift we can get the bounds on the Wasserstein’s distance.
The rest of the paper is organized as follows. In the rest of this section, we discuss related work (Sect. 1.1) and we establish the notation (Sect. 1.2). In Sect. 2 we present the model, the main result and some essential results to our proofs (including SSC). In Sect. 3 we present our proof based on the Transform technique and we additionally show the rate of convergence of the expected queue length using the Drift method. In Sect. 4 we compute the rate of convergence in Wasserstein’s distance using Stein’s method, and we obtain a proof of the main result as a consequence. We additionally obtain the rate of convergence in mean as a consequence of the main theorem of Sect. 4. Finally, in Sect. 6 we present concluding remarks and future work.
1.1 Related work
JSQ was first proposed in [59], and since then, it has received plenty of attention [1, 3, 14, 15, 17, 30, 42, 54]. It is particularly interesting in the heavy-traffic regime, because it experiences SSC to a one-dimensional subspace. Hence, its queue length vector behaves as a single-server queue and the distribution of the queue lengths is known to be exponential. Specifically, it has been proven that the scaled vector of queue lengths converges in distribution to a vector of the form \(\Upsilon {\varvec{1}}\), where \(\Upsilon \) is an exponential random variable and \({\varvec{1}}\) is the vector of ones. This proof has been performed using the diffusion limits approach [17], the Drift method [15] and the Transform method [30].
A drawback of this policy is that it requires a large communication overhead and, hence, it is not practical in large-scale systems (assuming that the dispatcher does not use any state-information stored in its memory to make the routing decision). On the other extreme is random routing, where all the arriving jobs are routed to a queue selected uniformly at random and, hence, no communication overhead is required. Power-of-d choices can be considered in between these two, since it only requires scanning d queues before routing. It has been proven that, even if \(d=2\), the queue lengths decrease considerably when compared to random routing. This result has been shown in the mean-field regime [39, 40, 51] and in the classical heavy-traffic regime [29, 37]. An extensive list of the literature on these policies is presented in [50].
The mean-field regime has become popular after it was used to show that the power-of-2 choices algorithm yields queue lengths that are considerably smaller than random routing [39, 40, 51]. It was later proved that the JSQ system behaves as an \(M/M/\infty \) system in the mean-field regime [3]. In [42], it was shown that under power-of-d choices with d growing with N, the fluid limit does not depend on the growth rate and, hence, power-of-d and JSQ have the same fluid limit. More recently, it has been shown that, in this regime, there must always be a proportion of empty queues and, hence, any routing policy that prioritizes empty queues yields queue lengths of at most one job [21]. Under the same logic, the join the idle queue (JIQ) policy has become popular. It was proposed in [34] and the idea is that, whenever a server idles, it communicates its status to the dispatcher. Then, the arrivals are routed randomly to one of the empty queues. If none of the queues is empty, then a server is selected uniformly at random. This policy has been rigorously analyzed in [49] under exponential job sizes, and in [18] for general job-size distributions. In both cases, the authors show that the steady-state probability that an arriving job waits in line vanishes as the number of servers grows to infinity.
Among the many-server heavy-traffic regimes, one of the most popular is the Halfin-Whit regime, where the difference between the service and arrival rate per server is \(N^{-1/2}\), i.e., \(\alpha =\frac{1}{2}\). This regime was introduced in [24], where the authors present the classical analysis of the M/M/N queue. More recently, [16] shows that the number of empty queues and the number of queues with one customer in line are of order \(O(\sqrt{N})\). The authors use the diffusion limits approach, but interchange of limits is not proved. This step is completed in [7]. In [4, 5] the work of [16] is continued. Specifically, in [4] the authors study tail asymptotics of the stationary distribution, and in [5] they study the moments of the stationary distribution. In [43], the authors show that JIQ routing yields diffusion-level optimality in the Halfin–Whitt regime.
In [33], load balancing systems under several routing policies in the sub-Halfin–Whitt regime are studied, and in [32] the analysis is extended to the case when \(\alpha \in \left[ \frac{1}{2},1\right) \). In [55] a load balancing system operating under power-of-d, where jobs are batches of tasks, is analyzed. Specifically, the authors find conditions on the value of d (as a function of the number of servers, the load and the number of tasks per job) such that power-of-d choices achieves zero delay in sub-Halfin–Whitt regime.
The NDS regime was introduced in [2] in the context of an M/M/N queue, and the author shows that the regime yields new diffusion processes. More recently, it has been used to compare routing policies in load balancing systems [21]. Specifically, the authors in [21] characterize the diffusion approximation of JSQ and propose a new policy with less communication overhead, and that achieves JSQ optimality. This policy is called idle-one-first and prioritizes routing to servers that are idling or have one job.
The heavy-traffic asymptotics of several systems have been studied in the literature. Most of the work is on systems that satisfy the complete resource pooling (CRP) condition, i.e., that satisfy SSC into a one-dimensional subspace. For a formal definition of the CRP condition, the reader is referred to [12, 27, 58]. The vast majority of the work has been performed using the diffusion limits approach [19, 25,26,27, 47, 57, 58]. In this approach, the scaled queue lengths are shown to converge to a reflected Brownian motion (RBM) process, and then the steady-state behavior of this RBM is studied using SSC. The last step is to show interchange of limits, which is usually challenging.
Recently, three ‘direct methods’ have been proposed to perform heavy-traffic analysis [11]. In these approaches, there is no need to show interchange of limits, as one directly works with the queue length process instead of working with an RBM. The methods are: (i) the BAR approach, (ii) the Drift method and (iii) Stein’s method. BAR stands for basic adjoint relationship, and the main idea of the method is to use carefully chosen exponential functions to handle the jumps of a continuous-time process [10, 41].
In the Drift method, the main idea is to choose the right test function and set its drift to zero in steady state. Then, using SSC, one gets error bounds on a function of the queue lengths that are tight in heavy traffic. If we use polynomial test functions, we obtain moments of the queue lengths [15, 28, 35, 36, 53]. The Transform method introduced in [30] is based on the Drift method and uses exponential test functions along with SSC to obtain the limiting MGF of the scaled queue lengths. Both, the Transform method and the BAR approach use exponential test functions, but the Transform method is focused on using SSC to obtain a closed-form distribution for the scaled queue lengths in the limit.
Stein’s method for analyzing SPNs was first introduced in [22], and it has now emerged as a simple yet powerful method that can be used not only to show asymptotic convergence, but also to bound the rate of convergence in Wasserstein’s distance. It has become a popular approach for both, the mean-field, the classical heavy-traffic and the many-server heavy-traffic regimes [7,8,9, 33, 48, 60, 61]. A key component of our proof that is novel relative to prior literature, is the use of Stein’s method in the presence of a multiplicative SSC.
Multiplicative SSC has been used in a variety of contexts in the literature [6, 13, 31, 45, 52, 53, 57]. The most relevant work in our context are the results in [13, 53]. In [13] the authors study a parallel-server system in the Halfin–Whitt regime, and they propose a framework for establishing SSC in queueing systems with multiple server pools in parallel and different customer classes. They use the fluid dynamics to establish their result. In [53] the multiplicative SSC result is used in the context of the heavy-traffic analysis of a bandwidth sharing network, and they use the Drift method to analyze it. Their proof is based on bounding the drift of the error of approximating the actual vector of flows by its projection on the subspace where SSC occurs, which is traditional in the Drift method [15, 35, 36]. In the traditional Drift method technique, the SSC bounds are independent of the heavy-traffic parameter. However, in [53], the bounds depend on the heavy-traffic parameter and the authors show that they become negligible after scaling. In this paper, we adopt their technique to show SSC and we use it in the context of a load balancing system in the many-server heavy-traffic regime.
In Table 1 we show a summary of the related work presented above, classified according to the value of \(\alpha \).
1.2 Notation
We use \({\mathbb {R}}\) and \({\mathbb {Z}}\) to denote the sets of real and integer numbers, respectively. We add a subscript \(+\) when we refer to nonnegative numbers, and a superscript \(n\in {\mathbb {Z}}_+\) when we mean vector spaces. We use bold letters to denote vectors. Given a vector \({\varvec{x}}\in {\mathbb {R}}^N\), we use \(x_{(i)}\) to its \(i{}^{\text {th}}\) smallest element.
For \({\varvec{x}}\in {\mathbb {R}}^n\), and \(p\in {\mathbb {Z}}_+\) with \(p\ge 1\) we use \(\Vert {\varvec{x}}\Vert _p\) to denote the p-norm of \({\varvec{x}}\), and we omit the index when we refer to Euclidean norm (i.e., when \(p=2\)). We use \({\varvec{1}}\) and \({\varvec{0}}\) to denote the vectors of all-one and all-zero elements, respectively. We use \({\varvec{e}}_n^{(i)}\) to denote the n-dimensional \(i{}^{\text {th}}\) canonical vector, i.e., an n-dimensional vector with a 1 in the \(i{}^{\text {th}}\) position and 0’s everywhere else. When the dimension is clear from the context, we may omit the subscript n.
Given a random variable X, we use \({\mathbb {E}}\left[ X \right] \) to denote its expected value and \(\text {Var}\left[ X \right] \) for its variance. For an event A we use \(\mathbbm {1}_{\left\{ A \right\} }\) to denote the indicator function of A. We use \(\Rightarrow \) to denote convergence in distribution.
Given two integers \(k,n\in {\mathbb {Z}}_+\), we use \(\left( {\begin{array}{c}n\\ k\end{array}}\right) \) for the binomial coefficient and we use the convention \(\left( {\begin{array}{c}n\\ k\end{array}}\right) =0\) if \(n<k\). We use [n] to the denote the set of positive integers that are smaller than or equal to n, i.e., \([n]{\mathop {=}\limits ^{\triangle }}\{1,\ldots ,n\}\).
For a function f with domain Dom(f), we denote \(\Vert f\Vert {\mathop {=}\limits ^{\triangle }}\sup _{x\in Dom(f)}|f(x)|\), and we use \(f'\), \(f''\) and \(f'''\) for its first, second and third derivative, respectively (provided their existence).
2 Model and asymptotic result
Consider a load balancing system operating in continuous time. Specifically, there are N parallel servers, and each of them has an infinite buffer. Arrivals to the system occur according to a Poisson process at rate \(\lambda N\), where \(\lambda \in (0,1)\). Upon arrival, a dispatcher immediately routes the new job to one of the servers, where they wait in line until the server can process them. All the servers are identical, and all the arriving jobs have exponential size with mean 1. Routing occurs according to power-of-d choices, where \(d\in {\mathbb {Z}}_+\) is of the form \(d{\mathop {=}\limits ^{\triangle }}\lceil cN^\beta \rceil \) for constants \(c>0\) and \(\beta \in [0,1]\). Specifically, upon arrival of a job, d servers are sampled uniformly at random and the new job is routed to the server with the shortest queue among those d. Ties are broken with the minimum index rule. Observe that if \(c=\beta =1\), then \(d=N\) and power-of-d choices is equivalent to JSQ.
For each \(t\in {\mathbb {R}}_+\) and each \(i\in [N]\), let \(q_i(t)\) be the number of jobs in queue i at time t, including the job in service (if any). Then, the queue length process \(\left\{ {\varvec{q}}(t):t\in {\mathbb {R}}_+ \right\} \) is a continuous-time Markov chain (CTMC) with the generator matrix G defined in (1). Let \({\varvec{q}}\in {\mathbb {Z}}_+^N\), and for each \(i\in [N]\) let \(\psi _{{\varvec{q}}}(i)\) be the index of the \(i{}^{\text {th}}\) smallest element of \({\varvec{q}}\), breaking ties by minimum index rule. Then, for any \({\varvec{q}}'\in {\mathbb {Z}}_+^N\) we have that the transition rate from state \({\varvec{q}}\) to state \({\varvec{q}}'\) is
The first case is the additive inverse of the sum of the other cases; the second case corresponds to a departure from queue i, which occurs at rate 1 and it can only happen if the queue is nonempty; and the third case corresponds to an arrival to the \(i{}^{\text {th}}\) shortest queue. Arrivals occur at rate \(\lambda N\), and \(\frac{\left( {\begin{array}{c}N-i\\ d-1\end{array}}\right) }{\left( {\begin{array}{c}N\\ d\end{array}}\right) }\) represents the probability that the new arrival is routed to the \(i{}^{\text {th}}\) shortest queue under power-of-d choices, for the following reason. Since the dispatcher samples d queues uniformly at random, there are \(\left( {\begin{array}{c}N\\ d\end{array}}\right) \) possible groups of d servers. One of the sampled servers needs to be the one labeled as \(\psi _{{\varvec{q}}}(i)\), and the other \(d-1\) servers need to have longer queues. Since \(\psi _{{\varvec{q}}}(i)\) represents the index of the \(i{}^{\text {th}}\) shortest queue, there are \(N-i\) queues that are longer and, hence, we there are \(\left( {\begin{array}{c}N-i\\ d-1\end{array}}\right) \) possible groups of servers that ensure that routing occurs to the server labeled as \(\psi _{{\varvec{q}}}(i)\). Hence, the probability of sending the new arrival to the \(i{}^{\text {th}}\) shortest queue is \(\frac{\left( {\begin{array}{c}N-i\\ d-1\end{array}}\right) }{\left( {\begin{array}{c}N\\ d\end{array}}\right) }\).
Remark 1
For ease of exposition, in this paper we assume that ties for the \(i{}^{\text {th}}\) shortest queue are broken deterministically, with the minimum index rule. However, all our results are valid for Markovian tie-breaking rules. It is true that the transition rate matrix G changes according to this rule. However, as the reader will notice later in this paper, we work with the total queue length and this object does not change if we change the deterministic tie-breaking rule described above by Markovian rules.
We are interested in the steady-state analysis of the load balancing system described above. First observe that the Markov chain is irreducible and nonexplosive. Additionally, the total arrival rate to the system \((\lambda N)\) is strictly smaller than the total service rate (N) for any \(\lambda \in (0,1)\). Then, the queue length process is also positive recurrent. Hence, stationary distribution exists and it is unique [23, Proposition 6.9b]. Let \({\overline{{\varvec{q}}}}\) be a steady-state random vector which is limit in distribution of \(\left\{ {\varvec{q}}(t):t\in {\mathbb {R}}_+ \right\} \), and define \({\overline{q}}_\Sigma {\mathop {=}\limits ^{\triangle }}\sum _{i=1}^N {\overline{q}}_i\).
We parametrize the system as follows. Consider \(\alpha >0\) and let \(\lambda ^{(N)}{\mathop {=}\limits ^{\triangle }}1-N^{-\alpha }\) be the arrival rate per server to the system. Then, the total arrival rate is \(\lambda ^{(N)}N\). Let \(\left\{ {\varvec{q}}^{(N)}(t):t\in {\mathbb {R}}_+ \right\} \) be the queue length process of the \(N{}^{\text {th}}\) system and \({\overline{{\varvec{q}}}}^{(N)}\) a steady-state random vector which is limit in distribution of \(\left\{ {\varvec{q}}^{(N)}(t):t\in {\mathbb {R}}_+ \right\} \). In the next theorem we present the main result of this paper.
Theorem 1
Consider a sequence of load balancing systems operating under power-of-d, parametrized by N as described above. If \(\alpha +\beta >3\), then \(N^{1-\alpha }\left( \frac{{\overline{q}}_\Sigma ^{(N)}}{N}\right) \Rightarrow \Upsilon \) as \(N\rightarrow \infty \), where \(\Upsilon \) is an exponential random variable with mean 1.
Immediate corollaries of Theorem 1 are the cases of power-of-d with constant d, and JSQ (which corresponds to \(d=N\)). We formally present these results below.
Corollary 1
Consider a sequence of load balancing systems operating under power-of-d choices, parametrized by N as described in Theorem 1. Suppose \(d=c\), where \(c\in {\mathbb {Z}}_+\) is a fixed parameter. If \(\alpha >3\), then \(N^{-\alpha }{\overline{q}}_\Sigma ^{(N)}\Rightarrow \Upsilon \) as \(N\rightarrow \infty \), where \(\Upsilon \) is an exponential random variable with mean 1.
The proof of Corollary 1 holds easily after setting \(\beta =0\) in Theorem 1. Now we present a result for the load balancing system under JSQ.
Corollary 2
Consider a sequence of load balancing systems operating under JSQ, parametrized by N as described in Theorem 1. If \(\alpha >2\), then \(N^{-\alpha }{\overline{q}}_\Sigma ^{(N)}\Rightarrow \Upsilon \) as \(N\rightarrow \infty \), where \(\Upsilon \) is an exponential random variable with mean 1.
The proof of Corollary 2 holds after letting \(c=\beta =1\) in Theorem 1.
Before proceeding with the proof of Theorem 1, we introduce the definition of the drift of a function, which is essential in our proofs. We use the definition provided in [53, Equation (14)].
Definition 1
Let \(\left\{ X(t): t\in {\mathbb {R}}_+ \right\} \) be a CTMC with countable state space \({\mathcal {X}}\) and transition rate matrix \(G^X\). For a function \(Z:{\mathcal {X}}\rightarrow {\mathbb {R}}_+\) and any \(x\in {\mathcal {X}}\), we define the drift of Z at x as
We write that we set the drift of Z to zero in steady state when we use the property \({\mathbb {E}}\left[ \Delta Z(X(t)) \right] =0\) under stationary distribution, provided that \({\mathbb {E}}\left[ Z(X(t)) \right] <\infty \) in steady state and \(\sup _{x\in {\mathcal {X}}} |G^X_{x,x}|<\infty \).
The drift of a function Z is also known as the generator applied to Z in the context of CTMCs. Here, we refer to it as drift, for consistency with [30, 53].
2.1 Essential results
The main difficulties in the proof of Theorem 1 are the dependency among queues, and handling the reflections due to the queue lengths being nonnegative. The latter is represented by the indicator functions in the transition rate matrix G. Both of these difficulties are handled with appropriate bounds, that are contributions by themselves.
We first present the SSC result, which establishes that all the queue lengths are approximately equal in the limit as \(N\rightarrow \infty \). Before stating the result formally, we introduce some notation. Given a vector \({\varvec{x}}\in {\mathbb {R}}_+^N\), define
Then, \({\varvec{x}}_\parallel \) is the projection of \({\varvec{x}}\) to the line generated by \({\varvec{1}}\), and \({\varvec{x}}_\perp \) represents the error of approximating \({\varvec{x}}\) by \({\varvec{x}}_\parallel \).
Our goal is to show that the queue lengths are similar in the limit. Using the notation above, we intuitively need to show that \({\overline{{\varvec{q}}}}^{(N)}\approx {\overline{{\varvec{q}}}}^{(N)}_\parallel \) asymptotically. We accomplish this goal by showing that \({\overline{{\varvec{q}}}}_\perp ^{(N)}\) is negligible as \(N\rightarrow \infty \), with the following result.
Proposition 1
Consider a load balancing system operating under power-of-d choices, as described in Sect. 2, and let \(\lambda _0\in (0,1)\). If c and \(\beta \) are such that \(d= \lceil c N^\beta \rceil \ge 2\), then for any \(\lambda \in (\lambda _0,1)\):
-
1.
There exists a finite constant C, which is independent of \(\lambda \), \(\beta \), c and N, such that for any positive integer r we have
$$\begin{aligned} {\mathbb {E}}\left[ \left\| {\overline{{\varvec{q}}}}_\perp \right\| ^r \right] \le C^r \left( \dfrac{N^2}{d-1}\right) ^r r^{r+\frac{1}{2}}. \end{aligned}$$(3) -
2.
Let e be Euler’s constant and \({\overline{C}}{\mathop {=}\limits ^{\triangle }}C \exp \left( {\scriptstyle \frac{1}{2e}}\right) \). Then, for any positive integer r we have
$$\begin{aligned} {\mathbb {E}}\left[ \left\| {\overline{{\varvec{q}}}}_\perp \right\| ^r \right] ^{\frac{1}{r}}\le {\overline{C}}r \left( \dfrac{N^2}{d-1}\right) . \end{aligned}$$(4) -
3.
Let \(\theta ^*\in {\mathbb {R}}\) be such that \(|\theta ^*|<\frac{1}{2}\log \left( 1 + \frac{\lambda _0(d-1)}{2N^2} \right) \). Then,
$$\begin{aligned} {\mathbb {E}}\left[ \exp \left( {\scriptstyle \theta ^* \left\| {\overline{{\varvec{q}}}}_\perp \right\| }\right) \right] \le \dfrac{\lambda _0 (d-1) \exp \left( {\scriptstyle \frac{2\theta ^* N^2}{\lambda _0(d-1)}}\right) }{\lambda _0(d-1) + 2N^2 \left( 1- \exp \left( {\scriptstyle 2\theta ^*}\right) \right) }. \end{aligned}$$(5)
We prove Proposition 1 in Sect. 5. Before ending this section, we discuss the result and prove a preliminary result that is essential for the rest of this paper.
The bounds (3), (4) and (5) clearly increase to infinity as \(N\rightarrow \infty \), unless \(\beta >2\). However, we are interested in a result that is valid for constant d as well as \(d=N\) (i.e., where \(\beta \in [0,1]\)), so we do not want to add conditions on \(\beta \). Instead, we must consider the scaling of the vector of queue lengths to argue that the bounds (3), (4) and (5) imply SSC. Indeed, Proposition 1 provides a multiplicative SSC result, which means collapse of the scaled vector of queue lengths. Observe that Theorem 1 provides convergence in distribution of the average queue length scaled by \(N^{1-\alpha }\). Therefore, the SSC result should imply that \(N^{1-\alpha }{\overline{{\varvec{q}}}}_\perp ^{(N)}\) is asymptotically negligible. In fact, using the bounds from Proposition 1 we obtain that \(N^{1-\alpha }{\overline{{\varvec{q}}}}_\perp ^{(N)}\) is negligible when \(\alpha +\beta >3\), which is the same condition from Theorem 1 and can be satisfied for constant d or \(d=N\).
We end this section with the result we use to handle the indicator function from the generator matrix G. When one computes the drift of any function, we get a term of the form \(\mathbbm {1}_{\left\{ q_i>0 \right\} }\) for each \(i\in [N]\). As mentioned above, this term represents that service cannot occur at empty queues and, therefore, the queue lengths cannot be negative. In this paper, we handle this indicator function using the property \(\mathbbm {1}_{\left\{ q_i>0 \right\} }=1-\mathbbm {1}_{\left\{ q_i=0 \right\} }\) for every \(i\in [N]\) and the following lemma. In fact, Lemma 1 is repeatedly used in the proof of SSC, in the two proofs that we provide for Theorem 1 and in the proof of Theorem 2.
The result presented in Lemma 1 is more general than the load balancing system described in Sect. 2, and holds for a variety of routing algorithms. All we need is throughput optimality, which we define below for clarity.
Definition 2
We say that a routing algorithm \({\mathcal {A}}\) is throughput optimal for the load balancing system described in Sect. 2 if the Markov chain \(\{{\varvec{q}}(t):t\in {\mathbb {R}}_+ \}\) operating under \({\mathcal {A}}\) is positive recurrent for all \(\lambda \in (0,1)\).
Now we present the result.
Lemma 1
Consider a load balancing system as described in Sect. 2, where the routing policy is throughput optimal. Let \(\lambda \in (0,1)\) be the arrival rate per server, and let \({\overline{{\varvec{q}}}}\) be a steady-state random vector which is limit in distribution of \(\left\{ {\varvec{q}}(t):t\in {\mathbb {R}}_+ \right\} \). Then,
Note that if we use \(\lambda ^{(N)}\) in this lemma, we obtain
Now we prove the result.
Proof
(of Lemma 1) Take \(M\in {\mathbb {Z}}_+\), and consider the test function \(V_M({\varvec{q}})=\min \left\{ \sum _{i=1}^N q_i,\, M\right\} \). The proof follows after setting its drift to zero in steady state and letting \(M\rightarrow \infty \).
We first compute the drift, considering the three cases: (i) \(\sum _{i=1}^N q_i<M\), (ii) \(\sum _{i=1}^N q_i=M\), and (iii) \(\sum _{i=1}^N q_i>M\). Observing that \(\Delta V_M({\varvec{q}})\mathbbm {1}_{\left\{ \sum _{i=1}^N q_i>M \right\} }=0\), we obtain
where (a) holds because \(\mathbbm {1}_{\left\{ \sum _{i=1}^N q_i=M \right\} }+\mathbbm {1}_{\left\{ \sum _{i=1}^N q_i<M \right\} } = \mathbbm {1}_{\left\{ \sum _{i=1}^N q_i\le M \right\} }\) by properties of indicator functions, and reorganizing terms.
Observe that \({\mathbb {E}}\left[ |V_M({\varvec{q}}(t))| \right] <\infty \) by definition of the test function \(V_M({\varvec{q}})\), and \(\sup _{{\varvec{q}}\in {\mathbb {Z}}_+^N}|G_{{\varvec{q}},{\varvec{q}}}| =N(\lambda +1)<\infty \) by definition of G in (1). Hence, \({\mathbb {E}}\left[ \Delta V_M({\overline{{\varvec{q}}}}) \right] =0\) in steady state. Applying this property to (6) and reorganizing terms, we obtain
Now we take the limit as \(M\rightarrow \infty \). Observe that \(\{{\varvec{q}}(t):t\in {\mathbb {R}}_+ \}\) is positive recurrent and, therefore, \( {\mathbb {P}}\left( \sum _{i=1}^N {\overline{q}}_i<\infty \right) =1\). Hence, we obtain
The result holds after reorganizing terms. \(\square \)
Observe that in Lemma 1 we do not need to assume that routing occurs according to power-of-d choices. Even though the drift is defined in terms of the generator matrix G, and this matrix changes with the routing algorithm, the proof of Lemma 1 does not use the details of G. We only use that, if there is an arrival, the total queue length increases by 1 and, if there is a departure (when the system is not empty), the total queue length decreases by 1.
Remark 2
An alternative proof of Lemma 1 is using Little’s law as follows. The expected number of busy servers \({\mathbb {E}}\left[ \sum _{i=1}^N \mathbbm {1}_{\left\{ {\overline{q}}_i>0 \right\} } \right] \) equals the expected arrival rate \(\lambda N\) multiplied by the expected time a job is processed, which is 1. We presented a proof using the Drift method above to highlight the similarities between the method in continuous and discrete-time systems.
Remark 3
In the proof of Lemma 1, we use the test function \(V_M({\varvec{q}})\), which is bounded by M with probability 1, even if the expected total queue length is infinite. If we additionally assume that \({\mathbb {E}}\left[ {\overline{q}}_\Sigma \right] <\infty \), we can instead use the linear test function \(V_\ell ({\varvec{q}})=\sum _{i=1}^N q_i\) to prove the result. Whether \({\mathbb {E}}\left[ {\overline{q}}_\Sigma \right] <\infty \) or not depends on the routing policy. For example, random routing, power-of-d choices and JSQ ensure that the expected total queue length is finite in steady state for any finite N.
In the last remark we claim that three routing policies yield finite expected total queue length for the load balancing system. The first observation for this proof is that it suffices to show that the expected total queue length is finite under random routing. Among the three routing policies, random routing results in the longest expected number of jobs in the system because it does not optimize the choice of the server where the new job goes.
To prove that random routing yields finite total expected queue length, there are several options. For brevity, we only discuss two methods here. One option is the Foster-Lyapunov approach, as indicated in [23, Corollaries 6.15 and 6.18]. In this approach we bound the drift of the test function \(V_2({\varvec{q}})=\Vert {\varvec{q}}\Vert ^2\) to obtain the result.
Another option is using the simplicity of random routing to compute the its total expected queue length. Since the arrivals to the system follow a Poisson process and routing is random (and independent of the arrival process), the splitting property of the Poisson process implies that arrivals to each queue also follow a Poisson process. Hence, random routing results in N M/M/1 queues, and the mean queue length of an M/M/1 queue is known (see [23, Section 6.6], for example).
Remark 4
In the classical heavy-traffic regime, one defines the heavy-traffic parameter as \(\epsilon {\mathop {=}\limits ^{\triangle }}\mu _\Sigma -\lambda _\Sigma \), where \(\mu _\Sigma \) is the total service rate (the sum of the mean service rate of each server) and \(\lambda _\Sigma \) is the total arrival rate. Then, one parametrizes the vector of queue lengths by \(\epsilon \) and can show that \(\epsilon \frac{1}{N}\sum _{i=1}^N {\overline{q}}^{(\epsilon )}_i\Rightarrow {\tilde{\Upsilon }}\), where \({\tilde{\Upsilon }}\) is an exponential random variable whose mean depends on the variance of the arrival and service processes. Further, one can show that \(\epsilon {\overline{{\varvec{q}}}}^{(\epsilon )}\Rightarrow {\varvec{1}}{\tilde{\Upsilon }}\) [15, 17, 30].
In this paper we study the many-server heavy-traffic regime, and our goal is to find the value of \(\alpha \) such that the scaled average queue length converges in distribution to an exponential random variable. In Theorem 1 we show convergence in distribution of the total queue length scaled by \(N^{-\alpha }\), which is equivalent to the average queue length scaled by \(N^{1-\alpha }\). Additionally, observe that the difference between the total service and arrival rate in this paper is \(N^{1-\alpha }\). In other words, in the many-server heavy-traffic regime, \(N^{1-\alpha }\) plays the role of the heavy-traffic parameter \(\epsilon \). Further, in the classical heavy-traffic regime there is an analogous result to Lemma 1, which is key to bound the so-called unused service.
Remark 5
As mentioned above, Lemma 1 is essential in the analysis. In discrete-time systems, there is an analogous of the indicator functions, known as unused service. In simple words, one models the number of jobs that each server processes in one time slot with the potential service, which is a random variable independent of the queue lengths and arrival processes. Then, the number of processed jobs is the minimum between the potential service and the number of jobs in the queue. The difference between the potential and actual service is the unused service. Hence, similarly to the indicator functions, the unused service prevents the queue lengths to go negative. The key property of the unused service is that, whenever it’s positive, the queue is empty in the next time slot. This property is analogous to the indicator function \(\mathbbm {1}_{\left\{ q_i=0 \right\} }\), which is positive only when the queues are empty and, hence, the server cannot process a job. This property of the unused service is key in the analysis of discrete-time systems, as it greatly facilitates the computation of performance measures such as the moments of the queue lengths and their distribution [15, 28, 30, 35, 36]. We will show that handling the indicator function \(\mathbbm {1}_{\left\{ q_i=0 \right\} }\) is key in the proofs we provide of Theorem 1.
3 Transform method: Proof of Theorem 1
The first proof of Theorem 1 that we present is motivated by the Transform method introduced in [30]. Before providing the proof, we briefly summarize the main idea and the steps of the method.
3.1 Review of the Transform method introduced in [30]
In [30] the authors introduce a Transform method based on the Drift method [15, 28, 35, 36], to compute the heavy-traffic distribution of the vector of queue lengths of SPNs that satisfy the CRP condition, i.e., that behave as a single-server queue in the limit.
3.1.1 Overview
The Transform method introduced in [30] uses an exponential transformation of the queue lengths to compute their heavy-traffic distribution. This exponential transformation can be the characteristic function, the MGF or the one-sided Laplace transform. In [30] the focus is on using the MGF. The authors propose a two-step procedure that yields the limiting MGF of the vector of queue lengths. In the first step, the goal is to obtain an implicit equation for the MGF of the queue lengths that is valid for all traffic. Then, in the second step, the heavy-traffic limit is taken and one needs to bound some terms to obtain an explicit limiting MGF. In the case of the SPNs studied in [30], this limit corresponds to the MGF of an exponential random variable.
3.1.2 Prerequisites for the MGF method
The two prerequisites of the MGF method are positive recurrence of the vector of queue lengths and SSC to a one-dimensional subspace. In the first step of the MGF method, the idea is to use the key unused service property described in Remark 5 to obtain an equation that is valid for all traffic. In this step, using SSC is key to obtain an expression that yields the exact MGF in the heavy-traffic limit. Then, one sets to zero the drift of the MGF and obtains an implicit equation, which depends on the MGF of the arrivals, the potential service and the unused service. In the second step of the MGF method, the goal is to bound the MGF of the unused service and compute the heavy-traffic limit of the MGF of the scaled queue lengths.
In Sect. 3.2 we use the key ideas of the MGF method described above, and we extend them to be used for the load balancing system modeled in continuous time in the many-server heavy-traffic regime (as described in Sect. 2). In this case, the role of the unused service is played by the indicator functions \(\mathbbm {1}_{\left\{ q_i(t)=0 \right\} }\) for \(i\in [N]\), since no job can be served from the \(i{}^{\text {th}}\) queue if \(q_i(t)=0\). In fact, this indicator function satisfies the key property \(\mathbbm {1}_{\left\{ q_i=0 \right\} }q_i=0\) with probability 1 for all \(i\in [N]\), which written in ‘exponential form’ yields \(\mathbbm {1}_{\left\{ q_i=0 \right\} }=\mathbbm {1}_{\left\{ q_i=0 \right\} }\exp \left( {\scriptstyle {\tilde{\theta }}q_i}\right) \), where \({\tilde{\theta }}\) is any real number. We present the details of the proof in Sect. 3.2.
3.2 Proof of Theorem 1 using the Transform method
In this proof we use one-sided Laplace transform to illustrate a different transform that falls in the scope of the work of [30]. The exponential equation required for Step 1 is accomplished by the following lemma.
Lemma 2
Consider a load balancing system operating under power-of-d choices, with \(d=\lceil cN^\beta \rceil \), as described in Theorem 1. Given a vector \({\varvec{q}}\in {\mathbb {Z}}_+^N\) and \(N\in {\mathbb {Z}}_+\), define
where \(q_\Sigma {\mathop {=}\limits ^{\triangle }}\sum _{i=1}^N q_i\). For every \(N\in {\mathbb {Z}}_+\), if
then,
This implies that, if \(\alpha +\beta >3\), then \({\mathbb {E}}\left[ \phi \left( {\overline{{\varvec{q}}}}^{(N)},N\right) \right] \) is \(o(N^{1-\alpha })\).
The proof of Lemma 2 is presented in Appendix A.1, and heavily uses the SSC result presented in Proposition 1. Now we prove the theorem.
Proof
(of Theorem 1 using Transform method) We omit the dependence on N of the variables, and we work with d instead of \(\lceil cN^\beta \rceil \) for ease of exposition. This proof is based on the use of the test function \(V_{\exp }({\varvec{q}}){\mathop {=}\limits ^{\triangle }}\exp \left( {\scriptstyle \theta N^{-\alpha }q_\Sigma }\right) \), where \(\theta <0\). Using the definition of drift, we obtain that for any \({\varvec{q}}\in {\mathbb {Z}}_+^N\)
where (a) holds because \(\sum _{i=1}^N \left( {\begin{array}{c}N-i\\ d-1\end{array}}\right) = \left( {\begin{array}{c}N\\ d\end{array}}\right) \); (b) holds by factorizing the term \((\exp \left( {\scriptstyle -\theta N^{-\alpha }}\right) -1)\) and rearranging terms; and (c) holds for the function \(\phi ({\varvec{q}},N)\) defined in Lemma 2.
Now we set the drift of \(V_{\exp }({\varvec{q}})\) to zero in steady state. Observe that, since \(\theta <0\), we have \({\mathbb {E}}\left[ \exp \left( {\scriptstyle \theta N^{-\alpha }{\overline{q}}_\Sigma }\right) \right] \le 1\). Additionally, \(G_{{\varvec{q}},{\varvec{q}}}\le N(\lambda +1)<\infty \). Then, we know \({\mathbb {E}}\left[ \Delta V_{\exp }({\overline{{\varvec{q}}}}) \right] =0\). Therefore, taking expected value with respect to stationary distribution in the expression above, replacing \(\lambda =1-N^{-\alpha }\), using Lemma 1 and rearranging terms we obtain
This completes Step 1. Observe that (7) gives an expression for the one-sided Laplace transform of \(N^{-\alpha }{\overline{q}}_\Sigma \) that is valid for all N. However, the numerator depends on \({\mathbb {E}}\left[ \phi ({\overline{{\varvec{q}}}},N) \right] \), which depends on the queue lengths.
Now we move to the second step, where the goal is to take the many-server heavy-traffic limit. The fraction (7) is of the form \(\frac{0}{0}\) in the limit as \(N\rightarrow \infty \), so we take Taylor expansion of the exponential function in the denominator. Expanding up to second order and canceling the factor \(N^{1-\alpha }\) from the numerator and the denominator we obtain
Finally, taking the limit as \(N\rightarrow \infty \) we obtain
which is the one-sided Laplace transform of an exponential random variable with mean 1. \(\square \)
Observe that (7) is valid for all N. Hence, it can be used to obtain an error bound and rate of convergence between \({\mathbb {E}}\left[ \exp \left( {\scriptstyle \theta N^{-\alpha }{\overline{q}}_\Sigma }\right) \right] \) and \(\frac{1}{1-\theta }\), which is the limiting one-sided Laplace transform. In this paper we do not perform this step for brevity.
3.3 Rate of convergence of the first moment
In Theorem 1 we showed convergence in distribution of the average queue length scaled by \(N^{1-\alpha }\) (or, equivalently, the total queue length scaled by \(N^{-\alpha }\)). However, convergence in distribution is not a sufficient condition to conclude convergence of the expected value. In other words, in Theorem 1 we showed \(N^{-\alpha }{\overline{q}}_\Sigma ^{(N)}\Rightarrow \Upsilon \), where \(\Upsilon \) is an exponential random variable with mean 1. However, from this statement we cannot directly conclude that \(\lim _{N\rightarrow \infty }{\mathbb {E}}\left[ N^{-\alpha }{\overline{q}}_\Sigma ^{(N)} \right] =1\). In this section we show that the last result holds using the Drift method [15, 35, 36, 53]. We first state the result formally.
Theorem 2
Consider a sequence of load balancing systems operating under power-of-d with \(d=\lceil cN^\beta \rceil \), parametrized by N as described in Sect. 2. If \(d\ge 2\), then
where \({\overline{C}}\) is the constant from Proposition 1. Additionally, if \(\alpha +\beta >3\), then
Note that the second part of the theorem is an immediate consequence of the error bound because, after multiplying everything by \(N^{-\alpha }\), the right-hand side of (8) converges to zero as \(N\rightarrow \infty \).
Similarly to Theorem 1, the case of power-of-d choices and JSQ are immediate consequences of Theorem 2. We formally state them below.
Corollary 3
Consider a sequence of load balancing systems operating under power-of-d choices with constant d, parametrized by N as described in Sect. 2. If \(d\ge 2\) and \(\alpha >3\), then
The proof of Corollary 3 holds easily after letting \(\beta =0\) in Theorem 2. Now we present the formal result for JSQ routing.
Corollary 4
Consider a sequence of load balancing systems operating under JSQ, parametrized by N as described in Sect. 2. If \(\alpha >2\), then
The proof of Corollary 4 holds after realizing that JSQ is equivalent to power-of-d choices with \(d=N\). Hence, it suffices to replace \(c=\beta =1\) in Theorem 2.
In the rest of this section, we prove Theorem 2 using the Drift method. In the Drift method there are two main steps. First, one shows SSC (which we did in Proposition 1), and secondly, one sets to zero the drift of \(V_\parallel ({\varvec{q}})=\Vert {\varvec{q}}_\parallel \Vert ^2\) in steady state (provided that its expectation is finite). To perform the second step, we first compute the drift of the test function \(V_\parallel ({\varvec{q}}){\mathop {=}\limits ^{\triangle }}\left\| {\varvec{q}}_\parallel \right\| ^2\). We provide the result in the following auxiliary lemma.
Lemma 3
Consider a load balancing system as described in Sect. 2. Let \(V_\parallel ({\varvec{q}}){\mathop {=}\limits ^{\triangle }}\left\| {\varvec{q}}_\parallel \right\| ^2\). Then,
We present the proof of Lemma 3 in Appendix A.2.
Proof
(of Theorem 2) Similarly to our previous proofs, we omit the dependence on N of the variables and we work with d instead of \(\lceil cN^\beta \rceil \) for ease of exposition. We start computing the drift of \(V_\parallel ({\varvec{q}})=\Vert {\varvec{q}}_\parallel \Vert ^2\). By Lemma 3, and since \(\sum _{i=1}^N \left( {\begin{array}{c}N-i\\ d-1\end{array}}\right) =\left( {\begin{array}{c}N\\ d\end{array}}\right) \), we obtain
Now we set the drift of \(V_\parallel ({\varvec{q}})\) to zero. We skip the proof of \({\mathbb {E}}\left[ V_\parallel ({\overline{{\varvec{q}}}}) \right] <\infty \) for ease of exposition. Taking expectation with respect to the stationary distribution, replacing \(\lambda =1-N^{-\alpha }\), using Lemma 1 to replace \({\mathbb {E}}\left[ \sum _{i=1}^N \mathbbm {1}_{\left\{ {\overline{q}}_i=0 \right\} } \right] =N^{1-\alpha }\) and reorganizing terms, we obtain:
We bound the last term of (9) using SSC. Specifically, we use (4), which establishes that for any positive integer r we have
where \({\overline{C}}\) is a constant.
First, note \(\mathbbm {1}_{\left\{ {\overline{q}}_i=0 \right\} }{\overline{q}}_i=0\) with probability 1 for all \(i\in [N]\). Then,
where \({\overline{q}}_{\perp i}\) is the \(i{}^{\text {th}}\) element of \({\overline{{\varvec{q}}}}_\perp \) and (a) holds by the definition of \({\overline{{\varvec{q}}}}_\perp \) in (2). Then,
where r is a positive integer. Here, (a) holds by Hölder’s inequality; (b) holds by Lemma 1 and by Proposition 1 for \(r\ge 2\) because of the inequalities of norms; and (c) holds by setting \(r=\left\lceil \alpha -1\right\rceil \left\lceil \log (N)\right\rceil \), because \(N^{\frac{\alpha -1}{\left\lceil \alpha -1\right\rceil \left\lceil \log (N)\right\rceil }}\le e\), and because \(cN^\beta \le \lceil cN^\beta \rceil \) by definition of the ceiling function. Using this result in (9), we obtain
This proves the theorem. \(\square \)
As we show in Sect. 4, using Stein’s method one immediately obtains both: convergence of the queue lengths in distribution and in expected value. However, the Transform method we used in Sect. 3.2 only provides convergence in distribution. For completeness, we provided the proof of convergence in mean in the last subsection, and we used the Drift method for consistency. An alternate path to prove both types of convergence using Transform methods would be to consider \(\theta \in {\mathbb {R}}\), as opposed to \(\theta <0\), and obtain convergence of the MGF (also known as two-sided Laplace transform). The proof is essentially the same as we developed in this section, with the exception that, to set the drift to zero, one needs to show that \({\mathbb {E}}\left[ \exp \left( {\scriptstyle \theta N^{-\alpha }{\overline{q}}_\Sigma ^{(N)}}\right) \right] <\infty \) for \(|\theta |<\Theta \), where \(\Theta \) is a constant independent of N. This step might be challenging in some systems.
4 Rate of convergence in Wasserstein’s distance
The proof we provide in this section is based on bounding the Wasserstein’s distance between the scaled total queue length and an exponential random variable. We start with the definition of this metric as presented in [44].
Definition 3
For two probability measures \(\nu _1\) and \(\nu _2\), the Wasserstein’s distance between them is
where Lip(1)\({\mathop {=}\limits ^{\triangle }}\left\{ h:{\mathbb {R}}\rightarrow {\mathbb {R}}\text { such that } |h(x)-h(y)|\le |x-y| \right\} \) is the set of Lipschitz functions with constant 1.
For random variables X and Y with laws \(\nu _1\) and \(\nu _2\), respectively, we write \(d_W(X,Y)\) instead of \(d_W(\nu _1,\nu _2)\), and when the measures are clear from the context we write
In the rest of this section we prove the following theorem.
Theorem 3
Consider a load balancing system operating under power-of-d choices with \(d=\lceil cN^\beta \rceil \), as described in Theorem 1. Let \(\Upsilon \) be an exponential random variable with mean 1. Then,
where \({\overline{C}}\) is the constant from Proposition 1.
Note that if we let \(\lambda =1-N^{-\alpha }\) and \(\alpha +\beta >3\), the right-hand side of (10) converges to zero as \(N\rightarrow \infty \). It is known that convergence to zero of the Wasserstein’s distance implies convergence in distribution [20, Theorem 2]. Therefore, since one of the assumptions of Theorem 1 is that \(\alpha +\beta >3\), we can prove Theorem 1 as a consequence of Theorem 3.
The Wasserstein’s distance considers the family of all Lipschitz-1 functions. Then, one can use specific functions to obtain the rate of convergence of a variety of functions of \((1-\lambda ){\overline{q}}_\Sigma \) and \(\Upsilon \). In the next corollary, we show how to obtain the rate of convergence of the mean as a consequence of Theorem 3.
Corollary 5
Consider a load balancing system as described in Theorem 3. Then,
The proof of Corollary 5 holds by noticing that \(f(x)=x\) is a Lipschitz-1 function and, hence,
This approach is an alternate proof to Theorem 2, and shows the power of Stein’s method.
Now we prove Theorem 3. We start with a result presented in [44, Theorem 5.4 part 1].
Lemma 4
Let Y be a random variable with \({\mathbb {E}}\left[ Y \right] <\infty \), and let \(\Upsilon \) be an exponential random variable with mean 1. Define
Then,
Now we prove the theorem.
Proof
(of Theorem 3) Similarly to all our previous proofs, for ease of exposition we omit the dependence on N of the variables and we use d instead of \(\lceil cN^\beta \rceil \). We use Lemma 4 with \(Y=(1-\lambda ){\overline{q}}_\Sigma \). Let f be a differentiable function such that \(g=f'\in {\mathcal {F}}_W\). By assuming differentiability we do not lose generality, for the following reason. Observe that \(f'\in {\mathcal {F}}_W\) implies that \(f\in \text {Lip(1)}\) and, hence, it implies that f is integrable. Therefore, if \(f'\in {\mathcal {F}}_W\), then f is well defined [56, Theorem 7.2].
By definition of drift, for any vector \({\varvec{q}}\in {\mathbb {Z}}_+^N\), we have
where \(\xi _1\) is between \((1-\lambda )q_\Sigma \) and \((1-\lambda )\left( q_\Sigma +1\right) \), and \(\xi _2,\xi _3\) are between \((1-\lambda )\) and \((1-\lambda )\left( q_\Sigma -1\right) \) Here, (a) holds because \(\sum _{i=1}^N \left( {\begin{array}{c}N-i\\ d-1\end{array}}\right) =\left( {\begin{array}{c}N\\ d\end{array}}\right) \); and (b) holds by taking Taylor approximation.
Since \(f'\in {\mathcal {F}}_W\), we know that f is integrable. Then, we can set its drift to zero in steady state. Taking expectation with respect to stationary distribution and reorganizing terms, we obtain
Using the last expression and the triangle inequality, we have
We bound term by term. For the first term we expand \(f'\big ((1-\lambda ){\overline{q}}_\Sigma \big )\) in Taylor series up to first order, around 0. Since \(f'\in {\mathcal {F}}_W\), we know that \(f'(0)=0\). Then, \(f'\big (1-\lambda ){\overline{q}}_\Sigma \big ) = (1-\lambda ){\overline{q}}_\Sigma f''(\xi _4)\), where \(|\xi _4|\in \left( 0,{\overline{q}}_\Sigma \right) \). Therefore, we obtain
where \(r>1\). Here, (a) holds because \(f'\in {\mathcal {F}}_W\) and, hence, \(\left| f''(\xi _4)\right| \le 1\); (b) holds because \(\mathbbm {1}_{\left\{ {\overline{q}}_i=0 \right\} }{\overline{q}}_i=0\) for all \(i\in [N]\); (c) holds by definition of \({\overline{{\varvec{q}}}}_\perp \) in (2); (d) holds by Hölder’s inequality; (e) holds because for any \(r\ge 2\) the \(r{}^{\text {th}}\) norm lower bounds Euclidean norm, and because \({\mathbb {E}}\left[ \sum _{i=1}^N \mathbbm {1}_{\left\{ {\overline{q}}_i=0 \right\} } \right] =N^{1-\alpha }=N(1-\lambda )\) by Lemma 1; and (f) holds because, by SSC in Proposition 1, we have \({\mathbb {E}}\left[ \left\| {\overline{{\varvec{q}}}}_\perp \right\| ^r \right] ^{\frac{1}{r}}\le {\overline{C}}r \left( \frac{N^2}{d-1}\right) \).
Taking \(r=\left\lceil \log \left( \frac{1}{N(1-\lambda )}\right) \right\rceil \), we obtain
For the second term, since \(f'\in {\mathcal {F}}_W\) we obtain
For the third term we obtain
where (a) holds because \(f'\in {\mathcal {F}}_W\); and (b) holds by Lemma 1.
For the fourth term, since \(f'\in {\mathcal {F}}_W\), we obtain
Similarly, for the fifth term we have
For the last term, we obtain
where (a) holds because \(f'\in {\mathcal {F}}_W\); and (b) holds by Lemma 1.
Using (12)–(17) in (11) and rearranging terms, we obtain
This proves the result. \(\square \)
5 Proof of state space collapse
Before ending this paper, we prove the SSC result presented in Proposition 1. The proof is based on [53, Lemma 10 in Appendix A], which we state below for completeness.
Lemma 5
Let \(\left\{ X(t):t\in {\mathbb {R}}_+ \right\} \) be a CTMC over a countable state space \({\mathcal {X}}\), with transition rate matrix \(G^X\). Suppose that it is irreducible, nonexplosive and positive recurrent, and it converges in distribution to a random variable \({\overline{X}}\) as \(t\rightarrow \infty \). Consider a Lyapunov function \(Z:{\mathcal {X}}\rightarrow {\mathbb {R}}_+\) and suppose its drift satisfies the following conditions:
-
(C1)
There exist constants \(\gamma >0\) and \(B>0\) such that \(\Delta Z(x)\le -\gamma \) for any \(x\in {\mathcal {X}}\) with \(Z(x)>B\)
-
(C2)
\(\nu _{\max }{\mathop {=}\limits ^{\triangle }}\sup \left\{ |Z(x')-Z(x)|: x,x'\in {\mathcal {X}}\text { and }G^X_{x,x'}>0 \right\} <\infty \).
-
(C3)
\({\overline{G}}{\mathop {=}\limits ^{\triangle }}\sup \left\{ -G^X_{x,x}: x\in {\mathcal {X}}\right\} <\infty \).
Then, for any nonnegative integer j, we have
where
As a result, for any positive integer r, the \(r{}^{\text {th}}\) moment of \(Z({\overline{X}})\) can be bounded as follows:
In the proof of Proposition 1, we additionally use a bound on the moment generating function of \(Z({\overline{X}})\), which we present below.
Lemma 6
Let \(\left\{ X(t):t\in {\mathbb {R}}_+ \right\} \) be a CTMC as described in Lemma 5, and suppose it satisfies the three conditions therein. Let \(\theta \in {\mathbb {R}}\) be such that \(|\theta |<\frac{1}{2\nu _{\max }}\log \left( 1+\tfrac{\gamma }{G_{\max }\nu _{\max }}\right) \). Then,
The proof of Lemma 6 is presented in Appendix B.1.
In the next subsection we present a series of auxiliary lemmas that we use in the proof of Proposition 1 and we prove in the appendix.
5.1 Auxiliary lemmas to prove Proposition 1
In the proof of Proposition 1, we use Lemmas 5 and 6 with \(Z({\varvec{q}})=\Vert {\varvec{q}}_\perp \Vert \). To show that condition (C1) is satisfied, we need to bound the drift of \(Z({\varvec{q}})\) outside a bounded set. On this step of the proof, we use the definition of \({\varvec{q}}_\perp {\mathop {=}\limits ^{\triangle }}{\varvec{q}}-{\varvec{q}}_\parallel \) and compute a bound based on the properties of \({\varvec{q}}\) and \({\varvec{q}}_\parallel \). Before stating the result with these bounds, we introduce the following notation.
Given a vector \({\varvec{q}}\in {\mathbb {Z}}_+^N\), define the following functions:
Lemma 7
Given a vector \({\varvec{q}}\in {\mathbb {Z}}_+^{(N)}\), consider the functions \(V({\varvec{q}}),\, V_\parallel ({\varvec{q}})\) and \(W_\perp ({\varvec{q}})\) defined in (20). Then,
We prove Lemma 7 in Appendix B.2. Using Lemma 7, the proof of (C1) reduces to computing an upper bound on \(\Delta V({\varvec{q}})\) and a lower bound on \(\Delta V_\parallel ({\varvec{q}})\), which we provide in the following lemmas.
Lemma 8
Consider a load balancing system operating under power-of-d choices, as described in Proposition 1. Let \(V({\varvec{q}})\) be as defined in (20). Then, for any vector of queue lengths \({\varvec{q}}\in {\mathbb {Z}}_+^{(N)}\) we have
The proof of Lemma 8 is presented in Appendix B.3. In the next lemma we provide a lower bound to \(\Delta V_\parallel ({\varvec{q}})\).
Lemma 9
Consider a load balancing system as described in Sect. 2. Let \(V_\parallel ({\varvec{q}})\) be as defined in (20). Then, for any vector of queue lengths \({\varvec{q}}\in {\mathbb {Z}}^{(N)}_+\) we have
Observe that we do not use the routing algorithm in the proof of Lemma 9. Indeed, the proof is based on the definition of the drift, properties of the Euclidean norm and the definition of indicator function. We present the proof of Lemma 9 in Appendix B.4.
5.2 Proof of Proposition 1
Using the lemmas proved in the previous subsection, we prove the SSC result stated in Proposition 1.
Proof
(of Proposition 1) We prove the proposition using d instead of \(\lceil cN^\beta \rceil \), for ease of exposition.
We show that each of the three conditions of Lemma 5 are satisfied. To show (C1), we use Lemmas 7, 8 and 9. Specifically, using the bounds from Lemmas 8 and 9 in Lemma 7 and canceling the term \(2(1-\lambda )\sum _{i=1}^N q_i\), we obtain
where (a) holds because \(\lambda \in (\lambda _0,1)\). Therefore, (C1) is satisfied with
Now we verify the (C2). Recall the definition of \(\nu _{\max }\):
From the definition of the transition rate matrix G in (1), observe that if \({\varvec{q}},{\varvec{q}}'\in {\mathbb {Z}}_+^N\) are such that \(G_{{\varvec{q}},{\varvec{q}}'}>0\), then there are only two options: either \({\varvec{q}}'={\varvec{q}}+{\varvec{e}}^{(i)}\) or \({\varvec{q}}'={\varvec{q}}-{\varvec{e}}^{(i)}\) for some \(i\in [N]\). Then, by definition of \({\varvec{q}}_\perp \) and linearity of projection, we have, \({\varvec{q}}'_\perp = {\varvec{q}}_\perp \pm \left( {\varvec{e}}^{(i)} - \frac{1}{N}{\varvec{1}}\right) \). Then, by triangle inequality, we obtain
which implies
where (a) holds by definition of the Euclidean norm; (b) holds after reorganizing terms; and (c) holds because if \(0\le x\le 1\) we have \(\sqrt{x}\le 1\). Since the inequality above holds for every pair of \({\varvec{q}},{\varvec{q}}'\in {\mathbb {Z}}_+^N\) such that \(G_{{\varvec{q}},{\varvec{q}}'}>0\), we obtain
To verify condition (C3), observe from (1) that
where the maximum is attained when none of the queues is empty. Finally, observe that \(G_{\max }\le {\overline{G}}\) by definition, and the upper bound is indeed attained when \({\varvec{q}}={\varvec{q}}_\parallel \ne {\varvec{0}}\). Therefore,
We verified that all the conditions are satisfied. Then, using (21), (22) and (24) in (19) we obtain that for any positive integer r
where (a) holds for some constant \(C\ge 16\) which is independent of \(\lambda \), d, N, c, and r; and (b) holds by Stirling’s approximation and because \(e^{1-r}\le 1\). This proves (3).
From (3), observe that \(r^{\frac{1}{2r}}\) is maximized at \(r=e\), so \(r^{\frac{1}{2r}}\le \exp \left( {\scriptstyle \frac{1}{2e}}\right) \). This completes the proof of (4).
To prove (5) we use Lemma 6 and that \(\lambda \in (0,1)\). Then, replacing \(d=\lceil cN^\beta \rceil \) we obtain the results. \(\square \)
6 Conclusion and future work
In this paper we study a supermarket checkout system in the many-server heavy-traffic regime. We parametrize the arrival rate so that the arrival rate per server is \(N^{-\alpha }\), for \(\alpha >0\) where N is the number of servers. Specifically, we answer the question: how fast should the number of servers grow with respect to the load to observe the classical heavy-traffic behavior of the scaled average queue lengths? We show that under power-of-d choices, where \(d=\lceil c N^\beta \rceil \), we need \(\alpha +\beta >3\). Then, the cases of constant d and JSQ routing are immediate consequences of our result, and we obtain \(\alpha >3\) and \(\alpha >2\), respectively. We use two proof techniques: one based on the Transform method proposed in [30] and the other one based on Stein’s method. We additionally show the rate of convergence of the expected value.
The case of \(\alpha \le 1\) is well studied in the literature. Then, there is a gap between our results and the literature. Future work is to explore how the system behaves if \(\alpha \in (1,3]\) for power-of-d choices and if \(\alpha \in (1,2]\) JSQ. We believe that there are only two phase transitions for \(\alpha \in (0,\infty )\): one at \(\alpha =\frac{1}{2}\) which corresponds to the Halfin–Whitt regime; and one at \(\alpha =1\) which corresponds to the NDS regime. Hence, we need to develop new proof techniques to close the gap.
Another line of future work is to create a unifying framework for all \(\alpha \in (0,\infty )\). As mentioned in Sect. 1, the cases of \(\alpha \in (0,1]\) are well-studied in the literature. However, the proof techniques are different for every phase of \(\alpha \). We believe there is a framework which gives a generic result, where we can obtain the results from the literature by simply plugging in the desired value of \(\alpha \).
References
Adan, I., van Houtum, G.J., van der Wal, J.: Upper and lower bounds for the waiting time in the symmetric shortest queue system. Ann. Oper. Res. 48(2), 197–217 (1994)
Atar, R.: A diffusion regime with nondegenerate slowdown. Oper. Res. 60(2), 490–500 (2012)
Badonnel, R., Burgess, M.: Dynamic pull-based load balancing for autonomic servers. In: NOMS 2008-2008 IEEE Network Operations and Management Symposium, pp. 751–754. IEEE (2008)
Banerjee, S., Mukherjee, D.: Join-the-shortest queue diffusion limit in Halfin–Whitt regime: tail asymptotics and scaling of extrema. Ann. Appl. Probab. 29(2), 1262–1309 (2019)
Banerjee, S., Mukherjee, D.: Join-the-shortest queue diffusion limit in Halfin–Whitt regime: sensitivity on the heavy-traffic parameter. Ann. Appl. Probab. 30(1), 80–144 (2020)
Bramson, M.: State space collapse with application to heavy-traffic limits for multiclass queueing networks. Queueing Syst. Theory Appl., 89 – 148 (1998)
Braverman, A.: Steady-state analysis of the join-the-shortest-queue model in the Halfin–Whitt regime. Math. Oper. Res. (2020)
Braverman, A., Dai, J.: Stein’s method for steady-state diffusion approximations of M/Ph/n+ M systems. Ann. Appl. Probab. 27(1), 550–581 (2017)
Braverman, A., Dai, J., Feng, J.: Stein’s method for steady-state diffusion approximations: an introduction through the Erlang-A and Erlang-C models. Stoch. Syst. 6(2), 301–366 (2017)
Braverman, A., Dai, J., Miyazawa, M.: Heavy traffic approximation for the stationary distribution of a Generalized Jackson Network: The BAR approach. Stoch. Syst. 7(1), 143–196 (2017)
Dai, J.: Steady-state approximations: achievement lecture. In: Abstracts of the 2018 ACM International Conference on Measurement and Modeling of Computer Systems, pp. 1–1. ACM (2018)
Dai, J., Lin, W.: Asymptotic optimality of maximum pressure policies in stochastic processing networks. Ann. Appl. Probab. 18(6), 2239–2299 (2008)
Dai, J., Tezcan, T.: State space collapse in many-server diffusion limits of parallel server systems. Math. Oper. Res. 36(2), 271–320 (2011)
Ephremides, A., Varaiya, P., Walrand, J.: A simple dynamic routing problem. IEEE Trans. Autom. Control 25(4), 690–693 (1980)
Eryilmaz, A., Srikant, R.: Asymptotically tight steady-state queue length bounds implied by drift conditions. Queueing Syst. 72(3–4), 311–359 (2012)
Eschenfeldt, P., Gamarnik, D.: Join the Shortest Queue with many servers. The heavy-traffic asymptotics. Math. Oper. Res. 43(3), 867–886 (2018)
Foschini, G., Salz, J.: A basic dynamic routing problem and diffusion. IEEE Trans. Commun. 26(3), 320–327 (1978)
Foss, S., Stolyar, A.L.: Large-scale join-idle-queue system with general service times. J. Appl. Probab. 995–1007 (2017)
Gamarnik, D., Zeevi, A.: Validity of heavy traffic steady-state approximations in Generalized Jackson Networks. Ann. Appl. Probab. 56–90 (2006)
Gibbs, A.L., Su, F.E.: On choosing and bounding probability metrics. Int. Stat. Rev. 70(3), 419–435 (2002)
Gupta, V., Walton, N.: Load balancing in the nondegenerate slowdown regime. Oper. Res. 67(1), 281–294 (2019)
Gurvich, I.: Diffusion models and steady-state approximations for exponentially ergodic Markovian queues. Ann. Appl. Probab. 24(6), 2527–2559 (2014)
Hajek, B.: Random Processes for Engineers. Cambridge University Press (2015)
Halfin, S., Whitt, W.: Heavy-traffic limits for queues with many exponential servers. Oper. Res. 29(3), 567–588 (1981)
Harrison, J.: Brownian models of queueing networks with heterogeneous customer populations. In: Stochastic Differential Systems, Stochastic Control Theory and Applications, pp. 147–186. Springer (1988)
Harrison, J.: Heavy traffic analysis of a system with parallel servers: asymptotic optimality of discrete review policies. Ann. App. Probab. 822–848 (1998)
Harrison, J., López, M.: Heavy traffic resource pooling in parallel-server systems. Queueing Syst. 339–368 (1999)
Hurtado-Lange, D., Maguluri, S.T.: Heavy-traffic analysis of queueing systems with no complete resource pooling. arXiv preprint arXiv:1904.10096 (2019)
Hurtado-Lange, D., Maguluri, S.T.: Throughput and delay optimality of power-of-d choices in inhomogeneous load balancing systems. arXiv preprint arXiv:2004.00538 (2020)
Hurtado-Lange, D., Maguluri, S.T.: Transform methods for heavy-traffic analysis. Stoch. Syst. 10(4), 275–309 (2020)
Kang, W., Kelly, F., Lee, N., Williams, R.: State space collapse and diffusion approximation for a network operating under a fair bandwidth sharing policy. Ann. Appl. Probab. 1719–1780 (2009)
Liu, X., Ying, L.: In: On universal scaling of distributed queues under load balancing (2019). ArXiv preprint arXiv:1912.11904
Liu, X., Ying, L.: A simple steady-state analysis of load balancing algorithms in the sub-Halfin–Whitt regime. ACM SIGMETRICS Perform. Eval. Rev. 46(2), 15–17 (2019)
Lu, Y., Xie, Q., Kliot, G., Geller, A., Larus, J., Greenberg, A.: Join-Idle-Queue: a novel load balancing algorithm for dynamically scalable web services. Perform. Eval. 68(11), 1056–1071 (2011)
Maguluri, S.T., Burle, S., Srikant, R.: Optimal heavy-traffic queue length scaling in an incompletely saturated switch. Queueing Syst. 88(3–4), 279–309 (2018)
Maguluri, S.T., Srikant, R.: Heavy traffic queue length behavior in a switch under the MaxWeight algorithm. Stoch. Syst. 6(1), 211–250 (2016). https://doi.org/10.1214/15-SSY193
Maguluri, S.T., Srikant, R., Ying, L.: Heavy traffic optimal resource allocation algorithms for cloud computing clusters. Perform. Eval. 81, 20–39 (2014)
Marshall, A.W., Olkin, I., Arnold, B.C.: Inequalities: theory of majorization and its applications, vol. 143. Springer (1979)
Mitzenmacher, M.: Load balancing and density dependent jump Markov processes. In: FOCS, p. 213. IEEE (1996)
Mitzenmacher, M.: The power of two choices in randomized load balancing. IEEE Trans. Parallel Distrib. Syst. 12(10), 1094–1104 (2001)
Miyazawa, M.: Diffusion approximation for stationary analysis of queues and their networks: a review. J. Oper. Res. Soc. Jpn. 58(1), 104–148 (2015)
Mukherjee, D., Borst, S.C., Van Leeuwaarden, J.S., Whiting, P.A.: Universality of power-of-d load balancing in many-server systems. Stoch. Syst. 8(4), 265–292 (2018)
Mukherjee, D., Borst, S.C., Van Leeuwaarden, J.S., Whiting, P.A., et al.: Universality of load balancing schemes on the diffusion scale. J. Appl. Probab. 53(4), 1111–1124 (2016)
Ross, N.: Fundamentals of Stein’s method. Probab. Surv. 8, 210–293 (2011)
Shah, D., Wischik, D.: Switched networks with maximum weight policies: fluid approximation and multiplicative state space collapse. Ann. Appl. Probab. 22(1), 70–127 (2012)
Stein, C.: A bound for the error in the normal approximation to the distribution of a sum of dependent random variables. In: Proceedings of the Sixth Berkeley Symposium on Mathematical Statistics and Probability, Volume 2: Probability Theory. The Regents of the University of California (1972)
Stolyar, A.: MaxWeight scheduling in a generalized switch: state space collapse and workload minimization in heavy traffic. Ann. Appl. Probab., 1–53 (2004)
Stolyar, A.: Tightness of stationary distributions of a flexible-server system in the Halfin–Whitt asymptotic regime. Stoch. Syst. 5(2), 239–267 (2015)
Stolyar, A.: Pull-based load distribution among heterogeneous parallel servers: the case of multiple routers. Queueing Syst. 85(1–2), 31–65 (2017)
van der Boor, M., Borst, S., van Leeuwaarden, J., Mukherjee, D.: Scalable load balancing in networked systems: a survey of recent advances. arXiv preprint arXiv:1806.05444 (2018)
Vvedenskaya, N., Dobrushin, R., Karpelevich, F.: Queueing system with selection of the shortest of two queues: an asymptotic approach. Probl. Inf. Transm. 32(1), 15–27 (1996)
Wang, C.H., Maguluri, S.T., Javidi, T.: Heavy traffic queue length behavior in switches with reconfiguration delay. In: INFOCOM 2017-IEEE Conference on Computer Communications, IEEE, pp. 1–9. IEEE (2017)
Wang, W., Maguluri, S.T., Srikant, R., Ying, L.: Heavy-traffic insensitive bounds for weighted proportionally fair bandwidth sharing policies. Math. Oper. Res. (2022)
Weber, R.: On the optimal assignment of customers to parallel servers. J. Appl. Probab. 15(2), 406–413 (1978)
Weng, W., Wang, W.: Dispatching parallel jobs to achieve zero queuing delay. arXiv preprint arXiv:2004.02081 (2020)
Wheeden, R.L.: Measure and Integral: An Introduction to Real Analysis, vol. 308. CRC Press (2015)
Williams, R.: Diffusion approximations for open multiclass queueing networks: sufficient conditions involving state space collapse. Queueing Syst. Theory Appl. pp. 27 – 88 (1998)
Williams, R.: On dynamic scheduling of a parallel server system with complete resource pooling. Fields Inst. Commun. 28(49–71), 5–1 (2000)
Winston, W.: Optimality of the shortest line discipline. J. Appl. Probab. 14(1), 181–189 (1977). https://doi.org/10.1017/S0021900200104772
Ying, L.: On the approximation error of mean-field models. In: Proceedings of the 2016 ACM SIGMETRICS International Conference on Measurement and Modeling of Computer Science, SIGMETRICS ’16, pp. 285–297. ACM, New York, NY, USA (2016). https://doi.org/10.1145/2896377.2901463
Ying, L.: Stein’s method for mean field approximations in light and heavy traffic regimes. Proc. ACM Meas. Anal. Comput. Syst. 1(1), 12:1–12:27 (2017). https://doi.org/10.1145/3084449
Acknowledgements
We would like to thank the anonymous reviewers for carefully checking the correctness of our arguments and their meaningful feedback to improve the presentation of our paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix
Details of proofs using Transform method
1.1 Proof of Lemma 2
Proof
(of Lemma 2) We omit the dependence on N and t of the variables, for ease of exposition. By definition of indicator function, for any \(i\in [N]\) we have
where \(q_{\perp i}\) is the \(i{}^{\text {th}}\) component of \({\varvec{q}}_\perp \). Here, (a) holds by definition of \({\varvec{q}}_\perp \) according to (2), and after adding and subtracting \(\mathbbm {1}_{\left\{ q_i=0 \right\} }\). Then, recalling the definition of \(\phi ({\varvec{q}},N)\) and reorganizing terms we obtain
We now compute the desired bound. We have
where \(r>1\). Here, (a) holds by triangle inequality; (b) holds because \(|\exp \left( {\scriptstyle x}\right) -1|\le |x|\exp \left( {\scriptstyle |x|}\right) \) for all \(x\in {\mathbb {R}}\); (c) hods by Hölder’s inequality for the vectors \({\varvec{X}}\) and \({\varvec{Y}}\) with elements \(X_i=\mathbbm {1}_{\left\{ {\overline{q}}_i=0 \right\} }\) and \(Y_i=|{\overline{q}}_{\perp i}| \exp \left( {\scriptstyle |\theta | N^{1-\alpha } |{\overline{q}}_{\perp i}|}\right) \) for \(i\in [N]\), and noticing that \(X_i^r = X_i\) because it is an indicator function; and (d) holds by Lemma 1.
Now we bound the expectation in (25) using properties of norms, Cauchy-Schwarz inequality and SSC. For \(r\ge 2\) we have
where (a) holds using that \(|{\overline{q}}_{\perp i}|\le \Vert {\overline{{\varvec{q}}}}_\perp \Vert \) in the exponent and by definition of the r-norm; (b) holds because the r-norm is smaller than the Euclidean norm for all \(r\ge 2\); and (c) holds by Cauchy-Schwarz inequality.
Now we bound each of the terms in (26) using SSC. From Proposition 1, recall that for every positive integer k we have
and for every \(\theta ^*\) satisfying \(|\theta ^*| < \frac{1}{2}\log \left( 1 + \tfrac{\lambda _0(d-1)}{2N^2}\right) \) we have
Using these results in (26) with \(k=2r\) and \(\theta ^*=2|\theta |rN^{1-\alpha }\), we obtain
Using this result in (25), we obtain
Since this upper bound holds for every \(r\ge 2\), we minimize the bound with respect to r and we obtain that \(r = \lceil \alpha -1\rceil \lceil \log (N)\rceil \) gives the tightest bound. Replacing this value we obtain the result. \(\square \)
1.2 Proof of Lemma 3
In this proof we use the definition of drift and we reorganize terms appropriately.
Proof
(of Lemma 3) We have:
where (a) holds by the definition of \({\varvec{x}}_\parallel \) given a vector \({\varvec{x}}\) in (2), and computing the norms. This completes the proof. \(\square \)
Details of the Proof of Proposition 1
1.1 Proof of Lemma 6
In the proof of Lemma 6, we use the bound (18) to compute an upper bound on the moment generating function of \(Z({\overline{X}})\).
Proof
(of Lemma 6) First observe that \(Z({\overline{X}})\ge 0\) by assumption of Lemma 5. Then,
We compute an upper bound for \({\mathbb {E}}\left[ \exp \left( {\scriptstyle |\theta | Z({\overline{X}})}\right) \right] \). Let \(F_Z(x)\) be the cumulative distribution function of \(Z({\overline{X}})\). Then,
where (a) holds integrating by parts; (b) holds because probabilities are upper bounded by 1, solving \(\int _0^B \exp \left( {\scriptstyle |\theta | x}\right) \,dx\), and breaking the last integral into intervals; (c) holds because \(f(x)=1-F_Z(x)={\mathbb {P}}\left( Z({\overline{X}})>x\right) \) is a nonincreasing function; (d) holds by (18) and solving the integral; and (e) holds after solving the geometric summation and reorganizing terms, because \(|\theta |<\frac{1}{2\nu _{\max }}\log \left( 1+\tfrac{\gamma }{G_{\max }\nu _{\max }}\right) \) by assumption and, hence, the geometric sum converges. \(\square \)
1.2 Proof of Lemma 7
In this proof we use the definition of drift and properties of concave functions.
Proof
(of Lemma 7) First observe that if g(x) is a differentiable concave function on \({\mathbb {R}}_+\), we have that for any \(x,y\in {\mathbb {R}}_+\)
Now, observe that \(W_\perp ({\varvec{q}})=\left\| {\varvec{q}}_\perp \right\| =\sqrt{\left\| {\varvec{q}}_\perp \right\| ^2}\) and \(g(x)=\sqrt{x}\) is a concave function. Therefore, by definition of drift in Definition 1, and the generator matrix in (1), we have
where (a) holds by (27) applied in the first and the second term in the following way. In the first term we use \(x=\left\| \left( {\varvec{q}}+{\varvec{e}}^{(\psi _{{\varvec{q}}}(i))} \right) _\perp \right\| ^2\) and \(y=\left\| {\varvec{q}}_\perp \right\| ^2\), and in the second term we use \(x=\left\| \left( {\varvec{q}}- {\varvec{e}}^{(i)}\right) _\perp \right\| ^2\) and \(y=\left\| {\varvec{q}}_\perp \right\| ^2\). Equality (b) holds by the definition of \(V(\cdot )\) and \(V_\parallel (\cdot )\) in (20) and because for any vector \({\varvec{x}}\in {\mathbb {R}}^N\), we have \(\left\| {\varvec{x}}_\perp \right\| ^2=\left\| {\varvec{x}}\right\| ^2 - \left\| {\varvec{x}}_\parallel \right\| ^2\); and (c) holds by reorganizing terms and by definition of drift. \(\square \)
1.3 Proof of Lemma 8
In this proof we use properties of the order statistics \(q_{(i)}\) for \(i\in [N]\). Recall that \(q_{(i)}\) represents the \(i{}^{\text {th}}\) shortest element of \({\varvec{q}}\), with ties broken by the minimum index.
Proof
(of Lemma 8) We have
where (a) holds because, by definition of \(\psi _{{\varvec{q}}}(i)\), we have \(q_{\psi _{{\varvec{q}}}(i)}=q_{(i)}\); and (b) holds because \(\mathbbm {1}_{\left\{ q_i=0 \right\} }q_i=0\) for all \(i\in [N]\), because \(\sum _{i=1}^N \mathbbm {1}_{\left\{ q_i=0 \right\} }\ge 0\) and reorganizing terms.
The last step of the proof is to show that
which we do at the end of this section. Using the bound (29), we obtain the result. \(\square \)
In the proof of (29), we use properties of the order statistics and majorization. Specifically, we use the following lemma, which is proved in [38, Section 16.A.2.a].
Lemma 10
Consider three vectors \({\varvec{a}},{\varvec{b}},{\varvec{x}}\in {\mathbb {R}}^N\). The inequality
holds if and only if
-
(C1)
The total sum satisfies
$$\begin{aligned} \sum _{i=1}^N a_i = \sum _{i=1}^N b_i. \end{aligned}$$ -
(C2)
For every \(k\in [N]\), the partial sums satisfy
$$\begin{aligned} \sum _{i=k}^N a_i \le \sum _{i=k}^N b_i. \end{aligned}$$
Now we show (29).
Proof
(of (29)) For each \(i\in [N]\) define
and observe that \(\eta _i=0\) for \(i\ge N-d+1\). Then,
Observe that \(\eta _1=d\). Then,
where (a) holds after reorganizing terms. We bound each of the terms of (31). For the first term we have
where (a) holds because \(q_{(1)}=\min _{i\in [N]}q_i\); (b) holds because norm-1 upper bounds the Euclidean norm; and (c) holds because, by definition of projection, the function \(g(x)=\left\| {\varvec{q}}-x{\varvec{1}}\right\| \) is minimized at \(x=\dfrac{1}{N}\sum _{i=1}^N q_i\), which equals the elements of \({\varvec{q}}_\parallel \). Then, the inequality holds by definition of \({\varvec{q}}_\perp {\mathop {=}\limits ^{\triangle }}{\varvec{q}}-{\varvec{q}}_\parallel \).
Now we only need to show that
We use Lemma 10 with \({\varvec{a}}\) and \({\varvec{b}}\) defined as follows:
We first show that condition (C1) is satisfied. To do so, we compute the sum of the elements of \({\varvec{a}}\) and \({\varvec{b}}\). For the vector \({\varvec{a}}\) we obtain
where (a) holds after solving the summation; and (b) holds after simplifying the last term.
For the vector \({\varvec{b}}\) we obtain
where the last equality holds because the general term of the summation does not depend on the index i. Hence, condition (C1) is satisfied.
To prove condition (C2), we consider three cases: (i) \(k\ge N-d+2\), (ii) \(2\le k\le N-d+1\), and (iii) \(k=1\). First observe that in case (iii) the inequality trivially holds after proving (C1). Now we prove the other two cases.
We start with case (i). Since \(k\ge N-d+2\), we have \(\left( {\begin{array}{c}N-k\\ d-1\end{array}}\right) =0\) for all k. Additionally, \(b_i\ge 0\) for all \(i\in [N]\) by definition. Therefore, condition (C2) is satisfied for \(k\ge N-d+2\).
For case (i) we compute the partial sums. We obtain
where (a) holds after solving the summation; (b) holds after reorganizing terms; (c) holds because \(k\ge 2\). Then, it suffices to show that
which is satisfied if and only if
Reorganizing terms in (33) we see that the condition is equivalent to \(d\ge 1\), which holds by assumption. This completes the proof. \(\square \)
1.4 Proof of Lemma 9
The goal of this section is to compute a lower bound on \(\Delta V_\parallel ({\varvec{q}})\). We use Lemma 3 (where we computed \(\Delta V_\parallel ({\varvec{q}})\)), properties of the Euclidean norm and of indicator functions.
Proof
(of Lemma 9) From Lemma 3 we have
where (a) holds after reorganizing terms; and (b) holds because \(\lambda \ge 0\), \(1-\mathbbm {1}_{\left\{ q_i=0 \right\} }\ge 0\) for all \(i\in [N]\), and \(\left( \sum _{i=1}^N \mathbbm {1}_{\left\{ q_i=0 \right\} }\right) \left( \sum _{i=1}^N q_i \right) \ge 0\) since every term is nonnegative. This completes the proof. \(\square \)
Rights and permissions
About this article
Cite this article
Hurtado-Lange, D., Maguluri, S.T. A load balancing system in the many-server heavy-traffic asymptotics. Queueing Syst 101, 353–391 (2022). https://doi.org/10.1007/s11134-022-09847-7
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11134-022-09847-7
Keywords
- Many-server heavy-traffic
- Load balancing system
- Stein’s method
- Transform method
- State space collapse
- Join the shortest queue
- Power-of-d choices
- Drift method
- Lyapunov drift