1 Introduction

Quantum entanglement is widely used as a very important resource in quantum information processing [1,2,3,4]. With the emergence of quantum information theory, quantum entanglement plays a very important role in quantum cryptography, quantum teleportation and measurement-based quantum computing. An important issue related to the entanglement metric is the limited shareability of the two-part entanglement in a multipartite entangled qubit system, that is, the single duality of entanglement [5]. Monogamy of entanglement (MoE) plays a very important role in many quantum information and communication processing tasks, such as security proof of quantum cryptography schemes and security analysis of quantum key distribution [6, 7].

For a tripartite quantum state \(\rho _{ABC}\), MoE can be described as \(E(\rho _{A|BC})\ge E(\rho _{AB})+E(\rho _{AC})\), where \(\rho _{AB}=\hbox {tr}_C(\rho _{ABC})\), \(\rho _{AC}=\hbox {tr}_B(\rho _{ABC})\), \(E(\rho _{A|BC})\) denotes the entanglement between systems A and BC. A remarkable result was established by Coffman, Kundu and Wootters (CKW) [8] for three qubits that was the simultaneous squares satisfy monogamy inequality. Then, the so-called CKW inequality was generalized to any N-qubit system [9]. Interestingly, it is further proved that similar inequalities of polyqubit monogamy can be established for negativity and convex-roof extended negativity (CREN) [10,11,12], the entanglement of formation (EoF) [13, 14], Rényi-\(\alpha \) entanglement [15, 16] and Tsallis-q entanglement [17].

Our paper is organized as follows. In Sect. 2, we present and prove two monogamy inequalities for the \(\beta \)th (\( \beta \ge 2\)) power of concurrence in N-qubit system. In Sect. 3, we give a tighter monogamy relation for the \(\beta \)th (\( \beta \ge \sqrt{2}\)) power of EoF in \(2\otimes 2\otimes 2^{N-2}\) system. Then, we extend the result to N-qubit system. In Sect. 4, the monogamy relation for the \(\beta \)th (\( \beta \ge 2\)) power of CREN in N-qubit system is discussed. In addition, detailed examples are given to illustrate the tightness. In Sect. 5, we summarize our results.

2 Tighter monogamy relations using concurrence

Given a bipartite pure state \(|\phi \rangle _{AB}\) on Hilbert space \({ H_A\otimes H_B}\), the concurrence is given by [18,19,20]

$$\begin{aligned} C(|\phi \rangle _{AB})=\sqrt{2(1-{\hbox {Tr}}(\rho ^2_A))} , \end{aligned}$$
(1)

where \(\rho _{A}\) is the reduced density matrix by tracing over the subsystem B, \(\rho _A={\hbox {Tr}}_B(|\phi \rangle _{AB}\langle \phi |)\). For a bipartite mixed state \(\rho _{AB}\), the concurrence is defined by the convex-roof,

$$\begin{aligned} C(\rho _{AB})=\min _{\{p_i,|\phi _i\rangle \}} \sum _ip_iC(|\phi _i\rangle _{AB}) , \end{aligned}$$
(2)

where the minimum is taken over all possible pure state decompositions of \(\rho _{AB}=\sum _ip_i|\phi _i\rangle \langle \phi _i|\), with \(\sum _ip_i=1\) and \(p_i\ge 0\).

For any N-qubit mixed state \(\rho _{AB_1\cdots B_{N-1}}\), the concurrence \(C(\rho _{A|B_1\cdots B_{N-1}})\) of the state \(\rho _{AB_1\cdots B_{N-1}}\) under bipartite partition A and \(B_1\cdots B_{N-1}\) satisfies [21]

$$\begin{aligned} \begin{array}{rl}&C^\beta (\rho _{A|B_1\cdots B_{N-1}})\ \ \ge C^\beta (\rho _{AB_1})+C^\beta (\rho _{AB_2})+\cdots +C^\beta (\rho _{AB_{N-1}}), \end{array} \end{aligned}$$
(3)

for \(\beta \ge 2\). Furthermore, for an N-qubit mixed state, if \(C_{AB_i}\ge C_{A|B_{i+1}\cdots B_{N-1}}\) for \(i=1,2,\ldots , m\), and \(C_{AB_j}\le C_{A|B_{j+1}\cdots B_{N-1}}\) for \(j={m+1},\ldots , {N-2}\), a generalized monogamy relation for \(\beta \ge 2\) was presented as [22]:

$$\begin{aligned} \begin{array}{rl} &{}C^\beta (\rho _{A|B_1\cdots B_{N-1}})\\ &{}\ \ge C^\beta (\rho _{AB_1})+(2^{\frac{\beta }{2}}-1)C^\beta (\rho _{AB_2})+\cdots +\big (2^{\frac{\beta }{2}}-1)^{m-1}C^\beta (\rho _{AB_{m}})\\ &{}\ \ \ +\big (2^{\frac{\beta }{2}}-1)^{m+1}[C^\beta (\rho _{AB_{m+1}})+\cdots + C^\beta (\rho _{AB_{N-2}})]+\big (2^{\frac{\beta }{2}}-1)^m C^\beta (\rho _{AB_{N-1}}), \end{array} \end{aligned}$$
(4)

where \( 1\le m\le N-3\), \(N\ge 4\).

In the following, we will show that these monogamy relations for concurrence can be further tightened under some conditions. Before that, we first introduce two lemmas as follows.

Lemma 1

For any \(x\in [0,1]\) and \(t\ge 1\), we have

$$\begin{aligned} (1+x)^t\ge & {} 1+\frac{t}{2}x+\frac{(t-1)^2}{4}x^2+(2^t-\frac{t}{2}+\frac{(t-1)^2}{4}-1)x^t-{\frac{(t-1)^2}{2}}x^{t+1}\nonumber \\\ge & {} 1+\frac{t}{2}x+(2^t-\frac{t}{2}-1)x^t\ge 1+(2^t-1)x^t. \end{aligned}$$
(5)

Proof

Let us consider the function \(f(t,x)=\frac{(1+x)^t-1-\frac{t}{2}x-\frac{(t-1)^2}{4}x^2+\frac{(t-1)^2}{2}x^{t+1}}{x^t}\). Then, \(\frac{\partial f(t,x)}{\partial x}=\frac{tx^{t-1}[1+\frac{t-1}{2}x+\frac{(t-1)^2(t-2)}{4t}x^2+\frac{(t-1)^2}{2t}x^{t+1}-(1+x)^{t-1}]}{x^{2t}}\). Next, we will prove that

$$\begin{aligned} 1+\frac{t-1}{2}x+\frac{(t-1)^2(t-2)}{4t}x^2+\frac{(t-1)^2}{2t}x^{t+1}\le (1+x)^{t-1}, \end{aligned}$$
(6)

thus \(\frac{\partial f(t,x)}{\partial x}\le 0\), f(t, x) is a decreasing function of x, i.e., \(f(t,x)\ge f(t,1)=2^t-\frac{t}{2}+\frac{(t-1)^2}{4}-1\). It follows that \((1+x)^t\ge 1+\frac{t}{2}x+\frac{(t-1)^2}{4}x^2+(2^t-\frac{t}{2}+\frac{(t-1)^2}{4}-1)x^t-\frac{(t-1)^2}{2}x^{t+1}\).

For the case \(1\le t\le 2\), it is obvious that \((1+x)^{t-1}\ge 1+(t-1)x+\frac{(t-1)(t-2)}{2}x^2\). Besides, we have

$$\begin{aligned} \frac{(t-1)(t-2)}{2}x^2= & {} \frac{t-1}{4t} 2t(t-2)x^{2}\\= & {} \frac{t-1}{4t}[(t-1)(t-2)x^{2}+(t^2+t-2)x^{2}-2tx^{2}]\\\ge & {} \frac{t-1}{4t}[(t-1)(t-2)x^{2}+(2t-2)x^{t+1}-2tx]. \end{aligned}$$

Thus, Eq. (6) is hold.

For the case \(t\ge 2\), it is obvious that \((1+x)^{t-1}\ge 1+(t-1)x+\frac{(t-1)(t-2)}{4}x^2\). Besides, we have

$$\begin{aligned} \frac{(t-1)(t-2)}{4}x^2= & {} \frac{t-1}{4t} t(t-2)x^{2} = \frac{t-1}{4t}[(t-1)(t-2)x^{2}+(2t-2)x^{2}-tx^2]\\\ge & {} \frac{t-1}{4t}[(t-1)(t-2)x^{2}+2(t-1)x^{t+1}-2tx]. \end{aligned}$$

Thus, Eq. (6) is hold.

On the other hand, since \(x^2-2x^{t+1}+x^t\ge 0\) and \(\frac{(t-1)^2}{4}\ge 0\), for \(t\ge 1\) and \(x\in [0,1]\), we can get \((1+x)^t\ge 1+\frac{t}{2}x+\frac{(t-1)^2}{4}x^2+(2^t-\frac{t}{2}+\frac{(t-1)^2}{4}-1)x^t-\frac{(t-1)^2}{2}x^{t+1} \ge 1+\frac{t}{2}x+(2^t-\frac{t}{2}-1)x^t\ge 1+(2^t-1)x^t\). \(\square \)

Lemma 2

For any mixed state \(\rho _{ABC}\) in a \(2\otimes 2\otimes 2^{N-2}\) system, suppose that \(C_{AB}\ge C_{AC}\), we have

$$\begin{aligned} C_{A|BC}^\beta\ge & {} C_{AB}^\beta +hC_{AC}^\beta +\frac{\beta }{4}C_{AC}^2\left( C_{AB}^{\beta -2}-C_{AC}^{\beta -2}\right) \nonumber \\&+\frac{(\beta -2)^2}{16}C_{AC}^4\left( C_{AB}^{\beta -4}+C_{AC}^{\beta -4}-2C_{AC}^{\beta -2}C_{AB}^{-2}\right) , \end{aligned}$$
(7)

for all \(\beta \ge 2\), where \(h=2^{\frac{\beta }{2}}-1\), \(C_{A|BC}=C(\rho _{A|BC})\), analogously for \(C_{AB}\) and \(C_{AC}\).

Proof

Since \(C_{AB}\ge C_{AC}\), we obtain

$$\begin{aligned} C_{A|BC}^\beta\ge & {} (C_{AB}^2+C_{AC}^2)^{\frac{\beta }{2}}= C_{AB}^\beta \left( 1+\frac{C_{AC}^2}{C_{AB}^2}\right) ^{\frac{\beta }{2}}\nonumber \\\ge & {} C_{AB}^\beta \left[ 1+\frac{\beta }{4}\frac{C_{AC}^2}{C_{AB}^2}+\frac{(\beta -2)^2}{16}\frac{C_{AC}^4}{C_{AB}^4}+\left( 2^{\frac{\beta }{2}}-\frac{\beta }{4} +\frac{(\beta -2)^2}{16}-1\right) \frac{C_{AC}^\beta }{C_{AB}^\beta }\right. \nonumber \\&\left. -\frac{(\beta -2)^2}{8}\frac{C_{AC}^{\beta +2}}{C_{AB}^{\beta +2}}\right] \nonumber \\= & {} C_{AB}^\beta +hC_{AC}^\beta +\frac{\beta }{4}C_{AC}^2\left( C_{AB}^{\beta -2}-C_{AC}^{\beta -2}\right) \nonumber \\&+\frac{(\beta -2)^2}{16}C_{AC}^4\left( C_{AB}^{\beta -4}+C_{AC}^{\beta -4} -2C_{AC}^{\beta -2}C_{AB}^{-2}\right) , \end{aligned}$$
(8)

where the first inequality is due to the fact that \(C_{A|BC}^2\ge C_{AB}^2+C_{AC}^2\) for any \(2\otimes 2\otimes 2^{N-2}\) tripartite state \(\rho _{A|BC}\) [9, 23] and the second inequality is due to Lemma 1. \(\square \)

Theorem 1

For any N-qubit mixed state \(\rho _{AB_1\cdots B_{N-1}}\), if \(C_{AB_i}\ge C_{A|B_{i+1}\cdots B_{N-1}}\), for \(i=1,2,\ldots , N-2\), we have

$$\begin{aligned} C_{A|B_1\cdots B_{N-1}}^\beta \ge \sum \limits _{i=1}^{N-2}h^{i-1}\left( C_{AB_i}^\beta +P_{AB_i}\right) +h^{N-2} C_{AB_{N-1}}^\beta , \end{aligned}$$
(9)

for all \(N\ge 3\), \(\beta \ge 2\), where \(h=2^{\frac{\beta }{2}}-1\), \(P_{AB_i}=\frac{\beta }{4}C_{A|B_{i+1}\cdots B_{N-1}}^2(C_{AB_i}^{\beta -2}-C_{A|B_{i+1}\cdots B_{N-1}}^{\beta -2})+ \frac{(\beta -2)^2}{16}C_{A|B_{i+1}\cdots B_{N-1}}^4(C_{AB_i}^{\beta -4}+C_{A|B_{i+1}\cdots B_{N-1}}^{\beta -4}-2C_{A|B_{i+1}\cdots B_{N-1}}^{\beta -2}C_{AB_i}^{-2})\).

Proof

Due to Eq. (7), we obtain

$$\begin{aligned}&C_{A|B_1\cdots B_{N-1}}^\beta \nonumber \\&\quad \ge C_{AB_1}^\beta +hC_{A|B_2\cdots B_{N-1}}^\beta +\frac{\beta }{4}C_{A|B_2\cdots B_{N-1}}^2\left( C_{AB_1}^{\beta -2}-C_{A|B_2\cdots B_{N-1}}^{\beta -2}\right) \nonumber \\&\qquad +\frac{(\beta -2)^2}{16}C_{A|B_2\cdots B_{N-1}}^4\left( C_{AB_1}^{\beta -4}+C_{A|B_2\cdots B_{N-1}}^{\beta -4}-2C_{A|B_{2}\cdots B_{N-1}}^{\beta -2}C_{AB_1}^{-2}\right) \nonumber \\&\quad \ge C_{AB_1}^\beta +h\left[ C_{AB_2}^\beta +hC_{A|B_3\cdots B_{N-1}}^\beta +\frac{\beta }{4}C_{A|B_3\cdots B_{N-1}}^2(C_{AB_2}^{\beta -2}-C_{A|B_3\cdots B_{N-1}}^{\beta -2})\right. \nonumber \\&\qquad \left. +\frac{(\beta -2)^2}{16}C_{A|B_3\cdots B_{N-1}}^4\left( C_{AB_2}^{\beta -4}+C_{A|B_3\cdots B_{N-1}}^{\beta -4}-2C_{A|B_{3}\cdots B_{N-1}}^{\beta -2}C_{AB_2}^{-2}\right) \right] \nonumber \\&\qquad +\frac{\beta }{4}C_{A|B_2\cdots B_{N-1}}^2\left( C_{AB_1}^{\beta -2}-C_{A|B_2\cdots B_{N-1}}^{\beta -2}\right) \nonumber \\&\qquad +\frac{(\beta -2)^2}{16}C_{A|B_2\cdots B_{N-1}}^4\left( C_{AB_1}^{\beta -4}+C_{A|B_2\cdots B_{N-1}}^{\beta -4}-2C_{A|B_{2}\cdots B_{N-1}}^{\beta -2}C_{AB_1}^{-2}\right) \nonumber \\&\quad \ge \cdots \nonumber \\&\quad \ge C_{AB_1}^\beta +hC_{AB_2}^\beta {+}\cdots +h^{N-2}C_{AB_{N-1}}^\beta {+}h^{N-3}\left[ \frac{\beta }{4}C_{AB_{N-1}}^2\left( C_{AB_{N-2}}^{\beta -2}{-}C_{AB_{N-1}}^{\beta -2}\right) \right. \nonumber \\&\qquad \left. +\frac{(\beta -2)^2}{16}C_{AB_{N-1}}^4\left( C_{AB_{N-2}}^{\beta -4}+C_{AB_{N-1}}^{\beta -4}-2C_{AB_{N-1}}^{\beta -2}C_{AB_{N-2}}^{-2}\right) \right] \nonumber \\&\qquad +\cdots +h\left[ \frac{\beta }{4}C_{A|B_3\cdots B_{N-1}}^2\left( C_{AB_2}^{\beta -2}-C_{A|B_3\cdots B_{N-1}}^{\beta -2}\right) \right. \nonumber \\&\qquad \left. +\frac{(\beta -2)^2}{16}C_{A|B_3\cdots B_{N-1}}^4\left( C_{AB_2}^{\beta -4}+C_{A|B_3\cdots B_{N-1}}^{\beta -4}-2C_{A|B_3\cdots B_{N-1}}^{\beta -2}C_{AB_{2}}^{-2}\right) \right] \nonumber \\&\qquad +\frac{\beta }{4}C_{A|B_2\cdots B_{N-1}}^2\left( C_{AB_1}^{\beta -2}-C_{A|B_2\cdots B_{N-1}}^{\beta -2}\right) \nonumber \\&\qquad +\frac{(\beta -2)^2}{16}C_{A|B_2\cdots B_{N-1}}^4\left( C_{AB_1}^{\beta -4}+C_{A|B_2\cdots B_{N-1}}^{\beta -4}-2C_{A|B_2\cdots B_{N-1}}^{\beta -2}C_{AB_{1}}^{-2}\right) . \end{aligned}$$
(10)

By the denotation of \(P_{AB_i}\), we complete the proof. \(\square \)

Theorem 2

For any N-qubit mixed state \(\rho _{AB_1\cdots B_{N-1}}\), if \(C_{AB_i}\ge C_{A|B_{i+1}\cdots B_{N-1}}\) for \(i=1,2,\ldots ,m\), and \(C_{AB_j}\le C_{A|B_{j+1}\cdots B_{N-1}}\) for \(j=m+1,\ldots ,N-2\), \(\forall ~ 1\le m\le N-3\), we have

$$\begin{aligned} C_{A|B_1\cdots B_{N-1}}^\beta\ge & {} \sum \limits _{i=1}^{m}h^{i-1}\left( C_{AB_i}^\beta +P_{AB_i}\right) \nonumber \\&+h^m\sum \limits _{j=m+1}^{N-2}\left( hC_{AB_j}^\beta +P_{AB_j}^1\right) +h^m C_{AB_{N-1}}^\beta , \end{aligned}$$
(11)

for all \(N\ge 4\), \(\beta \ge 2\), where \(h=2^{\frac{\beta }{2}}-1\), \(P_{AB_i}=\frac{\beta }{4}C_{A|B_{i+1}\cdots B_{N-1}}^2(C_{AB_i}^{\beta -2}-C_{A|B_{i+1}\cdots B_{N-1}}^{\beta -2})+ \frac{(\beta -2)^2}{16}C_{A|B_{i+1}\cdots B_{N-1}}^4(C_{AB_i}^{\beta -4}+C_{A|B_{i+1}\cdots B_{N-1}}^{\beta -4}-2C_{A|B_{i+1}\cdots B_{N-1}}^{\beta -2}C_{AB_i}^{-2})\), \(P_{AB_j}^1=\frac{\beta }{4}C_{AB_j}^2(C_{A|B_{j+1}\cdots B_{N-1}}^{\beta -2}-C_{AB_j}^{\beta -2}) +\frac{(\beta -2)^2}{16}C_{AB_j}^4(C_{A|B_{j+1}\cdots B_{N-1}}^{\beta -4}+C_{AB_j}^{\beta -4}-2C_{AB_j}^{\beta -2}C_{A|B_{j+1}\cdots B_{N-1}}^{-2})\).

Proof

Due to the proof process of Theorem 1, we can get that

$$\begin{aligned} C_{A|B_1\cdots B_{N-1}}^\beta \ge \sum \limits _{i=1}^{m}h^{i-1}\left( C_{AB_i}^\beta +P_{AB_i}\right) +h^{m}C_{A|B_{m+1}\cdots B_{N-1}}^\beta . \end{aligned}$$
(12)

In addition, since \(C_{AB_j}\le C_{A|B_{j+1}\cdots B_{N-1}}\) for \(j=m+1,\ldots ,N-2\), hence

$$\begin{aligned}&C_{A|B_{m+1}\cdots B_{N-1}}^\beta \nonumber \\&\quad \ge C_{A|B_{m+2}\cdots B_{N-1}}^\beta +hC_{AB_{m+1}}^\beta +\frac{\beta }{4}C_{AB_{m+1}}^2\left( C_{A|B_{m+2}\cdots B_{N-1}}^{\beta -2}-C_{AB_{m+1}}^{\beta -2}\right) \nonumber \\&\qquad +\frac{(\beta -2)^2}{16}C_{AB_{m+1}}^4\left( C_{A|B_{m+2}\cdots B_{N-1}}^{\beta -4}+C_{AB_{m+1}}^{\beta -4}-2C_{AB_{m+1}}^{\beta -2}C_{A|B_{m+2}\cdots B_{N-1}}^{-2}\right) \nonumber \\&\quad \ge \sum \limits _{j=m+1}^{N-2}\left( hC_{AB_j}^\beta +P_{AB_j}^1\right) +C_{AB_{N-1}}^\beta . \end{aligned}$$
(13)

Combing Eqs. (12) and (13), we can get the inequality (11). \(\square \)

Example 1

Consider the three-qubit state \(|\psi \rangle _{ABC}\) in generalized Schmidt decomposition form [25, 26]:

$$\begin{aligned} |\psi \rangle _{ABC}=\lambda _0|000\rangle +\lambda _1e^{i\varphi }|100\rangle +\lambda _2|101\rangle +\lambda _3|110\rangle +\lambda _4|111\rangle , \end{aligned}$$
(14)

where \(\lambda _i\ge 0\), \(i=0,1,2,3,4\), and \(\sum \limits _{i=0}^4\lambda _i^2=1\). A direct calculation shows that \(C_{A|BC}=2\lambda _0\sqrt{\lambda _2^2+\lambda _3^2+\lambda _4^2}\), \(C_{AB}=2\lambda _0\lambda _2\) and \(C_{AC}=2\lambda _0\lambda _3\).

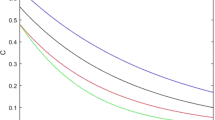
Set \(\lambda _0=\frac{\sqrt{2}}{3},\lambda _1=0,\lambda _2=\frac{\sqrt{5}}{3},\lambda _3=\frac{\sqrt{2}}{3},\lambda _4=0\). We have \(C_{A|BC}=\frac{2\sqrt{14}}{9}\), \(C_{AB}=\frac{2\sqrt{10}}{9}\) and \(C_{AC}=\frac{4}{9}\). Then, \(C_{A|BC}^\beta =(\frac{2\sqrt{14}}{9})^\beta \ge C_{AB}^\beta +hC_{AC}^\beta +\frac{\beta }{4}C_{AC}^2(C_{AB}^{\beta -2}-C_{AC}^{\beta -2})+\frac{(\beta -2)^2}{16}C_{AC}^4(C_{AB}^{\beta -4}+C_{AC}^{\beta -4} -2C_{AC}^{\beta -2}C_{AB}^{-2}) =(\frac{2\sqrt{10}}{9})^\beta +h(\frac{4}{9})^\beta +\frac{\beta }{4}(\frac{4}{9})^2\Big [(\frac{2\sqrt{10}}{9})^{\beta -2}-(\frac{4}{9})^{\beta -2}\Big ]+\frac{(\beta -2)^2}{16}(\frac{4}{9})^4\Big [(\frac{2\sqrt{10}}{9})^{\beta -4}+(\frac{4}{9})^{\beta -4}-2(\frac{4}{9})^{\beta -2}(\frac{2\sqrt{10}}{9})^{-2}\Big ]\). However, the result in [24] is \(C_{AB}^\beta +hC_{AC}^\beta +\frac{\beta }{4}C_{AC}^2(C_{AB}^{\beta -2}-C_{AC}^{\beta -2})=(\frac{2\sqrt{10}}{9})^\beta +h(\frac{4}{9})^\beta +\frac{\beta }{4}(\frac{4}{9})^2\Big [(\frac{2\sqrt{10}}{9})^{\beta -2}-(\frac{4}{9})^{\beta -2}\Big ]\). We can see that our results are better than the ones in [24] for \(\beta \ge 2\), see Fig. 1.

Fig. 1
figure 1

Dash dotted line, \(C^\beta _{A|BC}\) as a function of \(\beta \) (\(2\le \beta \le 10\)); solid line, the lower bound of \(C^\beta _{A|BC}\) as a function of \(\beta \) (\(2\le \beta \le 10\)) in Eq. (11); dash line, the lower bound of \(C^\beta _{A|BC}\) as a function of \(\beta \) (\(2\le \beta \le 10\)) in [24]

Full size image

3 Tighter monogamy relations using EoF

Let \(H_A\) and \(H_B\) be two Hilbert spaces with dimension m and n \((m\le n)\). The entanglement of formation (EoF) of a pure state \(|\phi \rangle _{AB}\) on Hilbert space \({H_A\otimes H_B}\), is defined as [27, 28]

$$\begin{aligned} E(|\phi \rangle _{AB})=S(\rho _A)=-{\hbox {Tr}}(\rho _A\log _2\rho _A), \end{aligned}$$
(15)

where \(S(\rho )=-\hbox {Tr}(\rho \log _2\rho )\) and \(\rho _A={\hbox {Tr}}_B(|\phi \rangle _{AB}\langle \phi |)\). For a bipartite mixed state \(|\phi \rangle _{AB}\) on Hilbert space \({H_A\otimes H_B}\), the EoF is given by

$$\begin{aligned} E(\rho _{AB})=\inf _{\{p_i,|\phi _i\rangle \}}\sum _ip_iE(|\phi _i\rangle ), \end{aligned}$$
(16)

where the infimum is taken over all possible pure state decompositions of \(\rho _{AB}\).

Let \(g(x)=H\big (\frac{1+\sqrt{1-x}}{2}\big )\) and \(H(x)=-x\log _2x-(1-x)\log _2(1-x)\), it is obvious that g(x) is a monotonically increasing function for \(0\le x\le 1\), and satisfies

$$\begin{aligned} g^{\sqrt{2}}(x^2+y^2)\ge g^{\sqrt{2}}(x^2)+g^{\sqrt{2}}(y^2), \end{aligned}$$
(17)

where \(g^{\sqrt{2}}(x^2+y^2)=[g(x^2+y^2)]^{\sqrt{2}}\).

From Eqs. (15) and (16), we have \(E(|\phi \rangle )=g(\mathcal {C}^2(|\phi \rangle ))\) for \(2\otimes d \ (d\ge 2)\) pure state \(|\phi \rangle \). And \(E(\rho )=g(\mathcal {C}^2(\rho ))\) for arbitrary two-qubit mixed state \(\rho \) [29].

Wootters [8] shows that the EoF does not satisfy the monogamy inequality \(E_{AB}+E_{AC}\le E_{A|BC}\). In [30], the authors shows that EoF is a monotonic function satisfying \(E^2(C_{A|B_1B_2\cdots B_{N-1}}^2)\ge E^2 \sum _{i=1}^{N-1}(C_{AB_i}^2)\). For N-qubit systems, one has [21]

$$\begin{aligned} E^\beta _{A|B_1B_2\cdots B_{N-1}}\ge E^\beta _{AB_1}+E^\beta _{AB_2}+\cdots +E^\beta _{AB_{N-1}}, \end{aligned}$$
(18)

for \(\beta \ge \sqrt{2}\), where \(E_{A|B_1B_2\cdots B_{N-1}}\) is the EoF of \(\rho \) under bipartite partition \(A|B_1B_2\cdots B_{N-1}\), \(E_{AB_i}\) is the EoF of the mixed state \(\rho _{AB_i}={\hbox {Tr}}_{B_1\cdots B_{i-1},B_{i+1}\cdots B_{N-1}}(\rho )\) for \(i=1,2,\ldots ,N-1\).

Lemma 3

For any mixed state \(\rho _{ABC}\) in a \(2\otimes 2\otimes 2^{N-2}\) system, \(\beta \ge \sqrt{2}\), if \(C_{AB}\ge C_{AC}\), then we have

$$\begin{aligned} E_{A|BC}^\beta\ge & {} E_{AB}^\beta +hE_{AC}^\beta +\frac{t}{2}E_{AC}^{\sqrt{2}}\left( E_{AB}^{\beta -{\sqrt{2}}}-E_{AC}^{\beta -{\sqrt{2}}}\right) \nonumber \\&+\frac{(t-1)^2}{4}E_{AC}^{2\sqrt{2}}\left( E_{AB}^{\beta -2\sqrt{2}}+E_{AC}^{\beta -2\sqrt{2}}-2E_{AC}^{\beta -\sqrt{2}}E_{AB}^{-\sqrt{2}}\right) , \end{aligned}$$
(19)

where \(t=\frac{\beta }{\sqrt{2}}, h=2^t-1\).

Proof

The proof is similar to the proof of Lemma 2. \(\square \)

In fact, the result can be generalized to N-qubit mixed state \(\rho _{AB_1\cdots B_{N-1}}\). The following theorem holds for \(\rho _{AB_1\cdots B_{N-1}}\).

Theorem 3

For any N-qubit mixed state \(\rho _{AB_1\cdots B_{N-1}}\), if \(C_{AB_i}\ge C_{A|B_{i+1}\cdots B_{N-1}}\) for \(i=1,2,\ldots ,N-2\), we have

$$\begin{aligned} E_{A|B_1\cdots B_{N-1}}^\beta \ge \sum \limits _{i=1}^{N-2}h^{i-1}\left( E_{AB_i}^\beta +Q_{AB_i}\right) +h^{N-2} E_{AB_{N-1}}^\beta , \end{aligned}$$
(20)

for \(\beta \ge \sqrt{2}\), where \(h=2^{t}-1\), \(t=\frac{\beta }{\sqrt{2}}\), \(Q_{AB_i}=\frac{t}{2}(E_{AB_{i+1}}^{\sqrt{2}}+\cdots +E_{AB_{N-1}}^{\sqrt{2}})(E_{AB_i}^{\beta -{\sqrt{2}}}-E_{A|{B_{i+1}\cdots B_{N-1}}}^{\beta -{\sqrt{2}}})+\frac{(t-1)^2}{4}(E_{AB_{i+1}}^{2\sqrt{2}}+\cdots +E_{AB_{N-1}}^{2\sqrt{2}}) [E_{AB_i}^{\beta -{2\sqrt{2}}}+\cdots +E_{AB_{N-1}}^{\beta -{2\sqrt{2}}}-2(E_{A|{B_{i+1}\cdots B_{N-1}}}^{\beta -\sqrt{2}})E_{AB_i}^{-\sqrt{2}}]\).

Proof

Let \(\rho =\sum _ip_i|\psi _i\rangle \langle \psi _i|\in H_A\otimes H_{B_1}\otimes \cdots H_{B_{N-1}}\) be the optimal decomposition of \(E_{A|B_1B_2\cdots B_{N-1}}(\rho )\) for the N-qubit mixed state \(\rho \), we have [22]

$$\begin{aligned} E_{A|B_1B_2\cdots B_{N-1}}\ge g\left( C^2_{A|B_1B_2\cdots B_{N-1}}\right) . \end{aligned}$$
(21)

In addition, for \(\beta \ge \sqrt{2}\), we have

$$\begin{aligned} g^{\beta }(x^2+y^2)= & {} \left[ g^{\sqrt{2}}(x^2+y^2)\right] ^t\ge \left[ g^{\sqrt{2}}(x^2)+g^{\sqrt{2}}(y^2)\right] ^t\nonumber \\\ge & {} g^{\beta }(x^2)+(2^t-1)g^{\beta }(y^2)+\frac{t}{2}g^{\sqrt{2}}(y^2)\nonumber \\&\left[ g^{\beta -{\sqrt{2}}}(x^2)-g^{\beta -{\sqrt{2}}}(y^2)\right] +\frac{(t-1)^2}{4}g^{2\sqrt{2}}(y^2)\nonumber \\&\left[ g^{\beta -2\sqrt{2}}(x^2)+g^{\beta -2\sqrt{2}}(y^2) -2g^{\beta -\sqrt{2}}(y^2)g^{-\sqrt{2}}(x^2)\right] , \end{aligned}$$
(22)

where the first inequality is due to Eq. (17), and without loss of generality, we can assume \(x^2\ge y^2\), then the second inequality is obtained from the monotonicity of g(x) and Eq. (5).

Thus, combining Eqs. (21) and (22), we obtain

$$\begin{aligned}&E^\beta _{A|B_1B_2\cdots B_{N-1}}\nonumber \\&\quad \ge g^\beta \left( C^2_{AB_1}+C^2_{AB_2}+\cdots +C^2_{AB_{N-1}}\right) \nonumber \\&\quad \ge g^\beta \left( C^2_{AB_1}\right) +hg^\beta \left( C^2_{AB_2}+\cdots +C^2_{AB_{N-1}}\right) +\frac{t}{2}g^{\sqrt{2}}\left( C^2_{AB_2}+\cdots +C^2_{AB_{N-1}}\right) \nonumber \\&\qquad \left[ g^{\beta -{\sqrt{2}}}\left( C^2_{AB_1}\right) -g^{\beta -{\sqrt{2}}}\left( C^2_{AB_2}+\cdots +C^2_{AB_{N-1}}\right) \right] \nonumber \\&\qquad +\frac{(t-1)^2}{4}g^{2\sqrt{2}}\left( C^2_{AB_2}+\cdots +C^2_{AB_{N-1}}\right) \nonumber \\&\qquad \left[ g^{\beta -2\sqrt{2}}\left( C^2_{AB_1}\right) +g^{\beta -2\sqrt{2}}\left( C^2_{AB_2}+\cdots +C^2_{AB_{N-1}}\right) \right. \nonumber \\&\qquad \left. -2g^{\beta -\sqrt{2}}\left( C^2_{AB_2}+\cdots +C^2_{AB_{N-1}}\right) g^{-\sqrt{2}}(C^2_{AB_1})\right] \nonumber \\&\quad \ge g^\beta \left( C^2_{AB_1}\right) +hg^\beta \left( C^2_{AB_2}+\cdots +C^2_{AB_{N-1}}\right) \nonumber \\&\qquad +\frac{t}{2}\left[ g^{\sqrt{2}}\left( C^2_{AB_2}\right) +\cdots +g^{\sqrt{2}}\left( C^2_{AB_{N-1}}\right) \right] \nonumber \\&\qquad \cdot \left[ g^{\beta -{\sqrt{2}}}\left( C^2_{AB_1}\right) -g^{\beta -{\sqrt{2}}}\left( C^2_{A|B_2\cdots B_{N-1}}\right) \right] \nonumber \\&\qquad +\frac{(t-1)^2}{4}\left[ g^{2\sqrt{2}}(C^2_{AB_2})+\cdots +g^{2\sqrt{2}}\left( C^2_{AB_{N-1}}\right) \right] \nonumber \\&\qquad \cdot \left[ g^{\beta -{2\sqrt{2}}}(C^2_{AB_1})+\cdots +g^{\beta -{2\sqrt{2}}}\left( C^2_{AB_{N-1}}\right) \right. \nonumber \\&\qquad \left. -2g^{\beta -\sqrt{2}}(C^2_{A|B_2\cdots B_{N-1}})g^{-\sqrt{2}}\left( C^2_{AB_1}\right) \right] \nonumber \\&\quad \ge g^\beta \left( C^2_{AB_1}\right) +hg^\beta \left( C^2_{AB_2}\right) +\cdots +h^{N-2}g^\beta \left( C^2_{AB_{N-1}}\right) \nonumber \\&\qquad +h^{N-3}\cdot \frac{t}{2}\cdot g^{\sqrt{2}}\left( C^2_{AB_{N-1}}\right) \left[ g^{\beta -{\sqrt{2}}}\left( C^2_{AB_{N-2}}\right) -g^{\beta -{\sqrt{2}}}\left( C^2_{AB_{N-1}}\right) \right] +\cdots \nonumber \\&\qquad +\frac{t}{2}\left[ g^{\sqrt{2}}\left( C^2_{AB_2}\right) +\cdots +g^{\sqrt{2}}\left( C^2_{AB_{N-1}}\right) \right] \nonumber \\&\qquad \cdot \left[ g^{\beta -{\sqrt{2}}}\left( C^2_{AB_1}\right) -g^{\beta -{\sqrt{2}}}\left( C^2_{A|B_2\cdots B_{N-1}}\right) \right] \nonumber \\&\qquad +h^{N-3}\cdot \frac{(t-1)^2}{4}\cdot g^{2\sqrt{2}}\left( C^2_{AB_{N-1}}\right) \left[ g^{\beta -{2\sqrt{2}}}\left( C^2_{AB_{N-2}}\right) +g^{\beta -{2\sqrt{2}}}\left( C^2_{AB_{N-1}}\right) \right. \nonumber \\&\qquad \left. -2g^{\beta -{\sqrt{2}}}\left( C^2_{AB_{N-1}}\right) g^{-\sqrt{2}}\left( C^2_{AB_{N-2}}\right) \right] +\cdots \nonumber \\&\qquad +\frac{(t-1)^2}{4}\left[ g^{2\sqrt{2}}\left( C^2_{AB_2}\right) +\cdots +g^{2\sqrt{2}}\left( C^2_{AB_{N-1}}\right) \right] \nonumber \\&\qquad \cdot \left[ g^{\beta -{2\sqrt{2}}}\left( C^2_{AB_1}\right) +\cdots +g^{\beta -{2\sqrt{2}}}\left( C^2_{AB_{N-1}}\right) \right. \nonumber \\&\qquad \left. -2g^{\beta -{\sqrt{2}}}\left( C^2_{A|B_2\cdots B_{N-1}}\right) g^{-\sqrt{2}}\left( C^2_{AB_1}\right) \right] , \end{aligned}$$
(23)

where we have utilized Eq. (3) and the monotonicity of g(x) to obtain the first inequality, the third and the forth inequalities are due to Eq. (17) and the monotonicity of the function g(x).

According to Eq. (21) and the fact that \(g(\mathcal {C}^2(\rho ))=E(\rho )\) for arbitrary two-qubit mixed state \(\rho \), we obtain Eq. (20). \(\square \)

Example 2

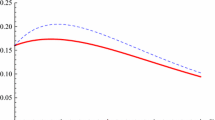
Let us consider the state in (14) given in Example 1. Set \(\lambda _0=\frac{\sqrt{6}}{3},\lambda _1=0,\lambda _2=\frac{\sqrt{2}}{3},\lambda _3=\frac{1}{3},\lambda _4=0\), we have \(E_{A|BC}=0.91829\), \(E_{AB}=0.68193\), \(E_{AC}=0.40416\). Then, \(E_{A|BC}^\beta =(0.91829)^\beta \ge E_{AB}^\beta +hE_{AC}^\beta +\frac{\beta }{2\sqrt{2}}E_{AC}^{\sqrt{2}}(E_{AB}^{\beta -{\sqrt{2}}}-E_{AC}^{\beta -{\sqrt{2}}})+ \frac{(\beta -\sqrt{2})^2}{8}E_{AC}^{2\sqrt{2}}(E_{AB}^{\beta -2\sqrt{2}}+E_{AC}^{\beta -2\sqrt{2}}-2E_{AC}^{\beta -\sqrt{2}}E_{AB}^{-\sqrt{2}}) =(0.68193)^\beta +h(0.40416)^\beta +\frac{\beta }{2\sqrt{2}}(0.40416)^{\sqrt{2}}\Big [(0.68193)^{\beta -{\sqrt{2}}}-(0.40416)^{\beta -{\sqrt{2}}}\Big ]+\frac{(\beta -\sqrt{2})^2}{8}(0.40416)^{2\sqrt{2}}\Big [(0.68193)^{\beta -2\sqrt{2}}+(0.40416)^{\beta -2\sqrt{2}}-2 (0.40416)^{\beta -\sqrt{2}}(0.68193)^{-\sqrt{2}}\Big ]\). While the result in [24] is \(E_{AB}^\beta +hE_{AC}^\beta +\frac{\beta }{2\sqrt{2}}E_{AC}^{\sqrt{2}}(E_{AB}^{\beta -{\sqrt{2}}}-E_{AC}^{\beta -{\sqrt{2}}})=(0.68193)^\beta +h(0.40416)^\beta +\frac{\beta }{2\sqrt{2}}(0.40416)^{\sqrt{2}}\Big [(0.68193)^{\beta -{\sqrt{2}}}-(0.40416)^{\beta -{\sqrt{2}}}\Big ]\). We can see that our results are better than the ones in [24], see Fig. 2.

Fig. 2
figure 2

Dash dotted line, \(E^\beta _{A|BC}\) as a function of \(\beta \) (\(\sqrt{2}\le \beta \le 10\)); solid line, the lower bound of \(E^\beta _{A|BC}\) as a function of \(\beta \) (\(\sqrt{2}\le \beta \le 10\)) in Eq. (20); dash line, the lower bound of \(E^\beta _{A|BC}\) as a function of \(\beta \) (\(\sqrt{2}\le \beta \le 10\)) in [24]

Full size image

4 Tighter monogamy relations using negativity

The negativity is a well-known quantifier of bipartite entanglement. Given a bipartite state \(\rho _{AB}\) in Hilbert space \(H_A\otimes H_B\), the negativity is defined as [31]:

$$\begin{aligned} \mathcal {N}(\rho _{AB})=\frac{\Vert \rho _{AB}^{T_A}\Vert -1}{2}, \end{aligned}$$
(24)

where \(\rho _{AB}^{T_A}\) is the partial transposed matrix of \(\rho _{AB}\) with respect to the subsystem A and \(\Vert X\Vert \) denotes the trace norm of X, i.e., \(\Vert X\Vert =\hbox {Tr}\sqrt{XX^{\dag }}\). For convenience, we use the definition of negativity as: \(\Vert \rho _{AB}^{T_A}\Vert -1\) [10].

If a bipartite pure state \(|\phi \rangle _{AB}\) with the Schmidt decomposition, \(|\phi \rangle _{AB} = \sum _{i}\sqrt{\lambda _i}|ii\rangle \), \(\lambda _i\ge 0\), \(\sum _{i}\lambda _i = 1\), then [10]

$$\begin{aligned} \mathcal {N}(|\phi \rangle _{AB}) = 2\sum _{i< j}\sqrt{\lambda _i\lambda _j}. \end{aligned}$$
(25)

From the definition of concurrence (1), we have

$$\begin{aligned} C(|\phi \rangle _{AB}) = 2\sqrt{\sum _{i< j}\lambda _i\lambda _j}. \end{aligned}$$
(26)

As a consequence, for any bipartite pure state \(|\phi \rangle _{AB}\) with Schmidt rank 2, one has \(\mathcal {N}(|\phi \rangle _{AB})=C(|\phi \rangle _{AB})\).

For a mixed state \(\rho _{AB}\), the convex-roof extended negativity (CREN) is given by

$$\begin{aligned} \mathcal {N}_c(\rho _{AB})=\min \limits _{\{p_i,|\phi _i\rangle \}}\sum _{i}p_i\mathcal {N}(|\phi _i\rangle ), \end{aligned}$$
(27)

where the minimum is taken over all possible pure state decomposition of \(\rho _{AB}\). CREN gives a perfect discrimination between PPT bound entangled states and separable states in any bipartite quantum system [32]. It follows that for any \(2\otimes d ~(d\ge 2)\) mixed state \(\rho _{AB}\), we have

$$\begin{aligned} \mathcal {N}_c(\rho _{AB})=\min \limits _{\{p_i,|\phi _i\rangle \}}\sum _{i}p_i\mathcal {N}(|\phi _i\rangle )=\min \limits _{\{p_i,|\phi _i\rangle \}} \sum _{i}p_iC(|\phi _i\rangle )=C(\rho _{AB}). \end{aligned}$$
(28)

According to the relation between CREN and concurrence, we have the following results for the lower bound of \(\mathcal {N}_{c{A|B_1\cdots B_{N-1}}}^{\beta }\).

Theorem 4

For any N-qubit mixed state \(\rho _{AB_1\cdots B_{N-1}}\), if \(\mathcal {N}_{c{AB_i}}\ge \mathcal {N}_{c{AB_{i+1}\cdots B_{N-1}}}\) for \(i=1,2,\ldots ,m\), and \(\mathcal {N}_{c{AB_j}}\le \mathcal {N}_{c{A|B_{j+1}\cdots B_{N-1}}}\) for \(j=m+1,\ldots ,N-2\), \(\forall 1\le m\le N-3\), then we have

$$\begin{aligned} \mathcal {N}_{c{A|B_1\cdots B_{N-1}}}^\beta\ge & {} \sum \limits _{i=1}^{m}h^{i-1}(\mathcal {N}_{c{AB_i}}^\beta +R_{AB_i})\nonumber \\&+h^m\sum \limits _{j=m+1}^{N-2}(h\mathcal {N}_{c{AB_j}}^\beta +R_{AB_j}^1)+h^m \mathcal {N}_{c{AB_{N-1}}}^\beta , \end{aligned}$$
(29)

for all \(N\ge 4\), \(\beta \ge 2\), where \(h=2^{\frac{\beta }{2}}-1\), \(R_{AB_i}=\frac{\beta }{4}\mathcal {N}_{c{A|B_{i+1}\cdots B_{N-1}}}^2(\mathcal {N}_{c{AB_i}}^{\beta -2}-\mathcal {N}_{c{A|B_{i+1}\cdots B_{N-1}}}^{\beta -2})+ \frac{(\beta -2)^2}{16}\mathcal {N}_{c{A|B_{i+1}\cdots B_{N-1}}}^4(\mathcal {N}_{c{AB_i}}^{\beta -4}+\mathcal {N}_{c{A|B_{i+1}}\cdots B_{N-1}}^{\beta -4}-2\mathcal {N}_{c{A|B_{i+1}\cdots B_{N-1}}}^{\beta -2}\mathcal {N}_{c{AB_i}}^{-2})\), \(R_{AB_j}^1=\frac{\beta }{4}\mathcal {N}_{c{AB_j}}^2 (\mathcal {N}_{c{A|B_{j+1}\cdots B_{N-1}}}^{\beta -2}-\mathcal {N}_{c{AB_j}}^{\beta -2})+\frac{(\beta -2)^2}{16}\mathcal {N}_{c{AB_j}}^4(\mathcal {N}_{c{A|B_{j+1}\cdots B_{N-1}}}^{\beta -4}+\mathcal {N}_{c{AB_j}}^{\beta -4}-2\mathcal {N}_{c{AB_j}}^{\beta -2}\mathcal {N}_{c{A|B_{j+1}\cdots B_{N-1}}}^{-2})\).

Fig. 3
figure 3

Dash dotted line, \(\mathcal {N}^\beta _{cA|BC}\) as a function of \(\beta \) (\(2\le \beta \le 10\)); solid line, the lower bound of \(\mathcal {N}^\beta _{cA|BC}\) as a function of \(\beta \) (\(2\le \beta \le 10\)) in Eq. (30); dash line, the lower bound of \(\mathcal {N}^\beta _{cA|BC}\) as a function of \(\beta \) (\(2\le \beta \le 10\)) in [24]

Full size image

Theorem 5

For any N-qubit mixed state \(\rho _{AB_1\cdots B_{N-1}}\), if \(\mathcal {N}_{c{AB_i}}\ge \mathcal {N}_{c{A|B_{i+1}\cdots B_{N-1}}}\) for \(i=1,2,\ldots ,N-2\), then we can obtain

$$\begin{aligned} \mathcal {N}_{c{A|B_1\cdots B_{N-1}}}^\beta \ge \sum \limits _{i=1}^{N-2}h^{i-1}\left( \mathcal {N}_{c{AB_i}}^\beta +R_{AB_i}\right) +h^{N-2} \mathcal {N}_{c{AB_{N-1}}}^\beta , \end{aligned}$$
(30)

for all \(N\ge 3\), \(\beta \ge 2\), where \(h=2^{\frac{\beta }{2}}-1\), \(R_{AB_i}=\frac{\beta }{4}\mathcal {N}_{c{A|B_{i+1}\cdots B_{N-1}}}^2(\mathcal {N}_{c{AB_i}}^{\beta -2}-\mathcal {N}_{c{A|B_{i+1}\cdots B_{N-1}}}^{\beta -2})+ \frac{(\beta -2)^2}{16}\mathcal {N}_{c{A|B_{i+1}\cdots B_{N-1}}}^4(N_{c{AB_i}}^{\beta -4}+\mathcal {N}_{c{A|B_{i+1}\cdots B_{N-1}}}^{\beta -4}-2\mathcal {N}_{c{A|B_{i+1}\cdots B_{N-1}}}^{\beta -2}\mathcal {N}_{c{AB_i}}^{-2})\).

Example 3

Let us consider the state in (14) given in Example 1. We have \(\mathcal {N}_{cA|BC}=2\lambda _0\sqrt{\lambda _2^2+\lambda _3^2+\lambda _4^2}\), \(\mathcal {N}_{cAB}=2\lambda _0\lambda _2\) and \(\mathcal {N}_{cAC}=2\lambda _0\lambda _3\). Set \(\lambda _0=\frac{\sqrt{2}}{3},\lambda _1=0,\lambda _2=\frac{\sqrt{5}}{3},\lambda _3=\frac{\sqrt{2}}{3},\lambda _4=0\). We have \(\mathcal {N}_{c{A|BC}}^\beta \ge \mathcal {N}_{c{AB}}^\beta +h\mathcal {N}_{c{AC}}^\beta +\frac{\beta }{4}\mathcal {N}_{c{AC}}^2(\mathcal {N}_{c{AB}}^{\beta -2}-\mathcal {N}_{c{AC}}^{\beta -2})+\frac{(\beta -2)^2}{16}\mathcal {N}_{c{AC}}^4(\mathcal {N}_{c{AB}}^{\beta -4}+\mathcal {N}_{c{AC}}^{\beta -4} -2\mathcal {N}_{c{AC}}^{\beta -2}\mathcal {N}_{c{AB}}^{-2}) =(\frac{2\sqrt{10}}{9})^\beta +h(\frac{4}{9})^\beta +\frac{\beta }{4}(\frac{4}{9})^2\Big [(\frac{2\sqrt{10}}{9})^{\beta -2}-(\frac{4}{9})^{\beta -2}\Big ]+\frac{(\beta -2)^2}{16}(\frac{4}{9})^4\Big [(\frac{2\sqrt{10}}{9})^{\beta -4}+(\frac{4}{9})^{\beta -4}-2(\frac{4}{9})^{\beta -2}(\frac{2\sqrt{10}}{9})^{-2})\). While the result in[24] is \(\mathcal {N}_{cAB}^\beta +h\mathcal {N}_{cAC}^\beta +\frac{\beta }{4}\mathcal {N}_{cAC}^2(\mathcal {N}_{cAB}^{\beta -2}-\mathcal {N}_{cAC}^{\beta -2})=(\frac{2\sqrt{10}}{9})^\beta +h(\frac{4}{9})^\beta +\frac{\beta }{4}(\frac{4}{9})^2\Big [(\frac{2\sqrt{10}}{9})^{\beta -2}-(\frac{4}{9})^{\beta -2}\Big ]\). We can see that our result is better than the one in [24] for \(\beta \ge 2\), see Fig. 3.

5 Conclusion

Entanglement monogamy relations are fundamental properties of multipartite entangled states. In this paper, we have provided the multipartite entanglement based on the monogamy relations for \(\beta \)th power of concurrence \(C_{A|B_1\cdots B_{N-1}}^{\beta }\) (\(\beta \ge 2\)), entanglement of formation \(E_{A|B_1\cdots B_{N-1}}^{\beta }\) (\(\beta \ge \sqrt{2}\)) and convex-roof extended negativity \(\mathcal {N}_{cA|B_1\cdots B_{N-1}}^{\beta }\) (\(\beta \ge 2\)). Our monogamy relations have larger lower bounds and are tighter than the existing results [24]. These tighter monogamy inequalities can also provide a finer description of the entanglement distribution. In multi-qubit system, our research results provide a rich reference for future research on multi-party quantum entanglement. Our method can also be applied to the study of other properties of monogamy related to quantum correlations.