1 Introduction

The resource theory of quantum coherence [1,2,3,4,5,6,7,8] plays an important role in characterizing the intrinsic feature of quantum mechanics. Over the past decades, the properties of a resource have been extensively investigated under a suitable set of allowed free operations [9,10,11,12,13,14]. In this setting, quantum coherence is regarded as a useful quantum resource allowing us to do many tasks more efficiently. The free states, i.e., the incoherent states are defined as the diagonal density matrices under a fixed reference basis. Free operations are the ones that transform the free states to free states. To single out a unique class of free operations under which the operational features of coherence should be investigated, many definitions of free operations are proposed, such as the maximally incoherent operations (MIOs) [1], the incoherent operations (IOs) [2], the dephasing-covariant incoherent operations (DIOs) [9, 15], and the strictly incoherent operations (SIOs) [16,17,18,19,20,21].

One of the most fundamental operational problems within a resource theory is how to manipulate the resource by using free operations. Among such manipulations, the coherence distillation stands out as one of the most important problems in the resource theory of quantum coherence [19, 22,23,24,25,26,27]. It focuses on the conversion of copies of a given d-dimensional state \(\rho \) into the canonical unit resource \(|\Phi _q\rangle \) (q-dimensional maximally coherent state). In a realistic setting, only finite supply of states is available. Thus, it is of significance to consider the one-shot version of coherence distillation [29,30,31,32].

In Ref. [26], the authors proposed a method to transform a pure state to a maximally coherent state with certain probability via SIOs. They presented an optimal probabilistic protocol to distill quantum coherence with reduced waste of resources. The protocol was expanded to possibly avert a complete waste of resources by exploiting an additional transformation into a suitable intermediate state.

In this paper, we give specific conditions when a d-dimensional pure state can be transformed to a maximally coherent state \(|\Psi _d\rangle =\frac{1}{\sqrt{d}}\sum \nolimits _i|i\rangle \) without complete waste of resource with the maximal probability for a given protocol proposed in Ref. [26]. We also give a protocol to transform a mixed state \(\rho \) to a maximally coherent state via a series of SIOs with probability based on the pure state decomposition of \(\rho \). Moreover, we show that the probability to get a maximally coherent state is independent of the pure state decomposition.

2 Preliminary

For a given d-dimensional Hilbert space \({\mathcal {H}}\) with an orthonormal basis \(\{|i\rangle \}_{i=1}^d\), the incoherent states are defined as: \(\sigma =\sum \nolimits _{i=1}^d p_i|i\rangle \langle i|\), with \(p_i\ge 0\), and \(\sum \nolimits _{i=1}^dp_i=1\). The set of all the incoherent states is denoted as \({\mathcal {I}}\). Without loss of generality, any d-dimensional pure coherent state can be expressed as

$$\begin{aligned} |\psi \rangle =\sum \limits _{i=1}^d\psi _i|i\rangle , \end{aligned}$$
(1)

where \(\{\psi _i\}\) are nonnegative real numbers in nonincreasing ordering, i.e., \(\psi _i\ge \psi _{i+1}\ge 0\), and \(\sum \nolimits _{i=1}^d\psi _i^2=1\). Here, one should note that not every pure state can be expressed in this form, but it can be brought into this form by using an SIO unitary in a reversible manner.

The one-shot coherence distillation is the process of transforming a given state \(\rho \) into a maximally coherent pure state under different classes of free operations [28, 29]. For a given state \(\rho \) and \(\epsilon \ge 0\), the one-shot coherence distillation rate with error \(\epsilon \) under free operation \({\mathcal {O}}\) is defined as

$$\begin{aligned} C_{d,{\mathcal {O}}}^{(1),\epsilon }(\rho ):=\log \max \{m\in \mathbb {N},F_{{\mathcal {O}}}(\rho ,\psi _m)\geqslant 1-\epsilon \}, \end{aligned}$$

where \(F_{{\mathcal {O}}}(\rho ,\psi _m)=\max \limits _{\Lambda \in {\mathcal {O}}}\langle \Lambda (\rho ),\psi _m\rangle \) is the fidelity. Such one-shot distillable rates can be quantified by the relative entropy of coherence [28].

A completely positive trace-preserving map \(\Phi \) is called a strictly incoherent operation (SIO) if \(\Phi (\rho )=\sum \nolimits _iK_i\rho K_i^{\dag }\), with the Kraus operators \(\{K_i\}\) satisfying \(K_i{\mathcal {I}}K_i^{\dag }\subseteq {\mathcal {I}}\), \(K_i^{\dag }{\mathcal {I}}K_i\subseteq {\mathcal {I}}\), and \(\sum \nolimits _{i}K_i^{\dag }K_i=I\). In this paper, by using a class of particular SIOs, we focus on transforming a single copy of the input state \(\rho \) given in Eq. (1) to a maximally coherent state with certain probability under incoherent operations. A class of SIOs \(\Phi \) for the coherence distillation from \(|\psi \rangle \) defined in Eq. (1) has been presented in [26],

$$\begin{aligned} \Phi (\rho )=\sum \limits _{q=1}^dK_q\rho K_q^{\dag }, \end{aligned}$$
(2)

with the Kraus operators \(K_q\) satisfying

$$\begin{aligned} K_q|\psi \rangle =\sqrt{p_q}|\Psi _q\rangle , \end{aligned}$$
(3)

where

$$\begin{aligned} K_q= & {} \sqrt{p_q}\left( \frac{1}{\sqrt{q}}\sum \limits _{i=1}^q\frac{|i\rangle \langle i|}{\psi _i}\right) , \end{aligned}$$
(4)
$$\begin{aligned} p_d= & {} d\psi _d^2, \ \ p_q=q(\psi _q^2-\psi _{q+1}^2), \ \ q=1,2,\ldots ,d-1, \end{aligned}$$
(5)

and \(|\Psi _q\rangle =\frac{1}{\sqrt{q}}\sum \nolimits _{j=1}^q|i\rangle \) \((1\le q\le d)\) is the q-dimensional maximally coherent state. From Eqs. (3), (4), and (5), one can see that the expression of SIO depends on the pure state from which we want to distillate the maximally coherent states.

As the coherence cannot be increased under SIOs, one may want to know how much coherence is lost on average during the protocol. Here, we adopt the \(l_1\)-norm as the measure of coherence [2]. The \(l_1\)-norm of coherence is defined as

$$\begin{aligned} {\mathcal {C}}_{l_1}(\rho )=\sum \limits _{i\ne j}|\rho _{ij}|, \end{aligned}$$

where \(\rho _{ij}=\langle i|\rho |j\rangle \). Thus, the average coherence for the output ensemble \(\{p_q,|\Psi _q\rangle \}_{q=1,2,\ldots ,d}\) of \(|\psi \rangle _{out}\) can be given by [26]

$$\begin{aligned} \mathcal {\bar{C}}_{l_1}(|\psi \rangle _{out})=\sum \limits _{j=2}^d(2j-2)\psi _j^2. \end{aligned}$$
(6)

3 The extreme value of \(\mathcal {\bar{C}}_{l_1}(|\psi \rangle _{out})\) without complete waste of resources

In this section, for a given initial pure state \(|\psi \rangle \), we give a specific method to avoid a complete waste of resources with the maximal probability to get \(|\Psi _d\rangle \), and calculate the range of the average coherence of \(|\psi \rangle _{out}\) via SIOs defined in Eq. (2).

We first recall the concept of majorization introduced in [33, 34]. For two d-dimensional real vectors \(x=(x_1,x_2,\ldots ,x_d)^t\) and \((y_1,y_2,\ldots ,y_d)^t\), we say that x is majorized by y if \(\sum \nolimits _{j=1}^kx_j^{\downarrow }\le \sum \nolimits _{j=1}^ky_j^{\downarrow }\), where \(x_j^{\downarrow }\) (\(y_j^{\downarrow }\)) denotes the components of x (y) arranged in decreasing order. We denote \(x\prec y\) if x is majorized by y.

Without a complete waste of resources means that the probability of transforming the given pure state \(|\psi \rangle \) to the incoherent state \(|\Psi _1\rangle \) is zero via SIO defined in Eq. (2), namely \(p_1=0\) in Eq. (3) [26]. By different IOs, a pure state \(|\psi \rangle \) can be transformed into different pure states \(|\phi \rangle \), \(|\psi \rangle {\mathop {\longrightarrow }\limits ^{IO}}|\phi \rangle \) iff \(|\psi \rangle \prec |\phi \rangle \) [35]. Thus, for the case \(p_1\ne 0\), there may exit many IOs to make \(p_1=0\) while keep \(p_d\) unchanged if we first transform \(|\psi \rangle \) to \(|\phi \rangle \) via a proper IO. Specifically, when we say that \(|\Psi _d\rangle \) can be distilled from a pure state \(|\psi \rangle \) given in Eq. (1) with maximal probability via SIOs defined in Eq. (2) and avoid a complete waste of resources, we mean the following two cases: if \(\psi _1=\psi _2\), then \(p_d=d\psi _d^2\) is the maximal probability to transform \(|\psi \rangle \) to \(|\Psi _d\rangle \), and \(p_1=0\) via the SIOs defined in Eq. (2); if \(\psi _1>\psi _2\), and there exists at least one incoherent operation such that \(|\psi \rangle {\mathop {\longrightarrow }\limits ^{IO}}|\phi \rangle =\sum \nolimits _{i=1}^d\phi _i|i\rangle \), where \(\{\phi _i\}\) are nonnegative real numbers in nonincreasing ordering with \(\phi _1=\phi _2\) and \(\phi _d=\psi _d\), one gets that \(p_1^{\prime }=0\), and \(p_d^{\prime }=d\psi _d^2\) is the maximal probability, with \(p_1^{\prime }\) and \(p_{d}^{\prime }\) similarly defined in Eq. (5). One can see that if such IOs exist, \(|\phi \rangle \) can be always transformed into a maximally coherent one via SIOs defined in Eq. (2) with \(p_1^{\prime }=0\), and \(p_d^{\prime }=d\psi _d^2\), although \(p_1\) may be larger than 0 for \(|\psi \rangle \).

For the case \(d=2\), if \(\psi _1>\psi _2\), there are no IOs to change the value of \(\psi _1\) while keep \(\psi _2\) unchanged. Thus, \(|\Psi _2\rangle \) cannot be distilled from a pure state \(|\psi \rangle \) given in Eq. (1) for the case \(\psi _1>\psi _2\), with maximal probability via SIOs defined in Eq. (2) and avoid a complete waste of resources. For the case \(d=3\), if \(\psi _1>\psi _2\), there are no IOs that transform \(|\psi \rangle \) to \(|\phi \rangle \) such that \(\phi _1=\phi _2\ge \psi _1\) and \(\phi _3=\psi _3\). In other words, \(|\Psi _3\rangle \) cannot be distilled from a pure state \(|\psi \rangle \) given in Eq. (1) for the case \(\psi _1>\psi _2\), with maximal probability via SIOs defined in Eq. (2) and avoid a complete waste of resources. Nevertheless, for the cases \(d\ge 4\), we have

Theorem 1

For a pure state \(|\psi \rangle \) given in (1), we can obtain the maximally coherent state \(|\Psi _d\rangle \) with the maximal probability via SIOs defined in Eq. (2), and avoid a complete waste of resources at the same time if and only if \(\sum \nolimits _{j=2}^{d-1}\psi _j^2\ge \psi _1^2+(d-3)\psi _{d}^2\).

Proof

Suppose \(\sum \nolimits _{j=2}^{d-1}\psi _j^2\ge \psi _1^2+(d-3)\psi _{d}^2\). Let \(|\phi \rangle =\sum \nolimits _j\phi _j|j\rangle \) with \(\phi _1=\phi _2=\sqrt{\frac{1-(d-2)\psi _d^2}{2}}\), and \(\phi _j=\psi _d, \ j=3,4,\ldots ,d\). Obviously, \(\{\phi _j\}\) is in a nonincreasing order. We prove now there indeed exists an incoherent operation which transforms \(|\psi \rangle \) to \(|\phi \rangle \). In other words, we need to prove \(\sum \nolimits _{j=1}^s\psi _j^2\le \sum \nolimits _{j=1}^s\phi _j^2\) for \(s=1,2,\ldots ,d\). From \(\sum \nolimits _{j=2}^{d-1}\psi _j^2\ge \psi _1^2+(d-3)\psi _{d}^2\), we see that \(2\psi _1^2+(d-2)\psi _{d}^2\le \sum \nolimits _{j=2}^{d-1}\psi _j^2+\psi _1^2+\psi _d^2=1\). Thus, \(\psi _1^2\le \frac{1-(d-2)\psi _d^2}{2}=\phi _1^2\). Then, one can also find that \(\psi _1^2+\psi _2^2\le 2\psi _1^2\le 2\phi _1^2=\phi _1^2+\phi _2^2\). For any \(s\ge 3\), we have \(\sum \nolimits _{j=1}^s\psi _j^2=1-\sum \nolimits _{j=s+1}^d\psi _j^2\le 1-(d-s)\psi _d^2=\sum \nolimits _{j=1}^s\phi _i^2\).

Now suppose that one wants to obtain the maximally coherent state \(|\Psi _d\rangle \) with the maximal probability, and avoid a complete waste of resources at the same time via SIOs defined in Eq. (2), i.e., \(p_1=0\) and \(p_d=d\psi _d^2\). Assume there exists an incoherent operation which transforms \(|\psi \rangle \) to \(|\phi \rangle =\sum \nolimits _i\phi _i|i\rangle \). Then, \(\phi _1=\phi _2\ge \psi _1\), \(\phi _d=\psi _d\), and \(\phi _i\ge \phi _{i+1}\) for \(i=1,2,\ldots ,d-1\). Thus,

$$\begin{aligned} \begin{array}{rl} \sum \limits _{j=2}^{d-1}\psi _j^2&{}=1-(\psi _1^2+\psi _d^2)\\ &{}=\sum \limits _{j=1}^d\phi _d^2-(\psi _1^2+\psi _d^2)\\ &{}\ge 2\psi _1^2+(d-2)\psi _d^2-(\psi _1^2+\psi _d^2)\\ &{}=\psi _1^2+(d-3)\psi _d^2. \end{array} \end{aligned}$$
(7)

\(\square \)

In fact, for a given \(|\psi \rangle \), there may exist many IOs satisfying \(|\psi \rangle {\mathop {\longrightarrow }\limits ^{IO}}|\phi \rangle \), such that one obtains \(|\Psi _d\rangle \) with maximal probability and avoid a complete waste of resource at the same time. Different \(|\phi \rangle \) given in \(|\psi \rangle {\mathop {\longrightarrow }\limits ^{IO}}|\phi \rangle \) gives rise to different values of \(\mathcal {\overline{C}}_{l_1}(|\phi \rangle _{out})\) via the corresponding SIOs defined in Eq. (2). Then, for a given pure state \(|\psi \rangle \), we can get a range of \(\mathcal {\overline{C}}_{l_1}(|\phi \rangle _{out})\) over all \(|\phi \rangle \) satisfying \(\phi _1=\phi _2\) and \(\phi _d=\psi _d\). In the following, \(\mathcal {\overline{C}}_{l_1}(|\psi \rangle _{out})\) also stands for \(\mathcal {\overline{C}}_{l_1}(|\phi \rangle _{out})\) with \(|\psi \rangle {\mathop {\longrightarrow }\limits ^{IO}}|\phi \rangle \) satisfying \(\phi _1=\phi _2\), \(\phi _d=\psi _d\) and \(\psi _1\ge \psi _2\).

Next, we study the lower and upper bounds of \(\mathcal {\overline{C}}_{l_1}(|\psi \rangle _{out})\) at the conditions of obtaining the maximally coherent state \(|\Psi _d\rangle \) with maximal probability and avoiding a complete waste of resource at the same time via SIOs defined in Eq. (2).

Our approach can be summarized as follows. For remain the condition \(p_1=0\) and \(p_d=d\psi _d^2\), we should always fix \(\phi _1=\phi _2\) and \(\phi _d=\psi _d\) while we transform \(|\psi \rangle \) into \(|\phi \rangle \) under IOs. From Eq. (6), one can see that the value of \(\mathcal {\bar{C}}_{l_1}(|\psi \rangle _{out})\) depends on the values of \(\{\psi _j\}\). Specifically, the value of \(\psi _j\) is related to its coefficient \(2j-2\) and \(\sum \nolimits _{j=1}^d\psi _j^2=1\). Thus, for an arbitrary pure state \(|\psi \rangle \) defined in Eq. (1), if we want to get the maximal value \(\mathcal {\overline{C}}_{l_1}(|\psi \rangle _{out})_{\max }\) of \(\mathcal {\overline{C}}_{l_1}(|\psi \rangle _{out})\), from Eq. (6), we should keep \(\phi _i\) as large as possible under the condition \(|\psi \rangle {\mathop {\longrightarrow }\limits ^{IO}}|\phi \rangle \) when i increases. Similarly, if we want to get the minimal value \(\mathcal {\overline{C}}_{l_1}(|\psi \rangle _{out})_{\min }\) of \(\mathcal {\overline{C}}_{l_1}(|\psi \rangle _{out})\), we should keep \(\phi _i\) as small as possible under the condition \(|\psi \rangle {\mathop {\longrightarrow }\limits ^{IO}}|\phi \rangle \) when i increases.

For \(d=4\), from Theorem 1 we obtain the maximal probability of getting \(|\Psi _4\rangle \) and avoid a complete waste of resource at the same time if and only if \(\psi _1^2+\psi _4^2\le \psi _2^2+\psi _3^2\). Hence, to get the \(\mathcal {\overline{C}}_{l_1}(|\psi \rangle _{out})_{\max }\), one should keep \(\phi _1=\phi _2\) as small as possible under the condition \(|\psi \rangle {\mathop {\longrightarrow }\limits ^{IO}}|\phi \rangle \). Thus, \(\phi _1=\phi _2=\psi _1\). In this case, \(\phi _3=\sqrt{\psi _2^2+\psi _3^2-\psi _1^2}\) and \(\mathcal {\overline{C}}_{l_1}(|\psi \rangle _{out})_{\max }=4+2\psi _4^2-6\psi _1^2\). To get \(\mathcal {\overline{C}}_{l_1}(|\psi \rangle _{out})_{\min }\), one should keep \(\phi _1=\phi _2\) as large as possible and \(\phi _3\) as small as possible under the condition \(|\psi \rangle {\mathop {\longrightarrow }\limits ^{IO}}|\phi \rangle \). Thus, \(\phi _3=\phi _4=\psi _4\), \(\phi _1=\phi _2=\sqrt{\frac{1-2\psi _4^2}{2}}\), and \(\mathcal {\overline{C}}_{l_1}(|\psi \rangle _{out})_{\min }=1+8\psi _4^2\). Easily, one can see that for both cases, \(|\psi \rangle \prec |\phi \rangle \). Therefore, we have

Theorem 2

For \(d=4\) and \(|\psi \rangle \) given in (1) with \(\psi _1^2+\psi _4^2\le \psi _2^2+\psi _3^2\), we have

$$\begin{aligned} 1+8\psi _4^2\le \mathcal {\bar{C}}_{l_1}(|\psi \rangle _{out})\le 4+2\psi _4^2-6\psi _1^2, \end{aligned}$$
(8)

if the maximally coherent state \(|\Psi _4\rangle \) is obtained with the maximal probability via SIOs defined in Eq. (2) without a complete waste of resources. Moreover, the left equality holds if \(\phi _1=\phi _2=\sqrt{\frac{1-2\psi _4^2}{2}}\) and \(\phi _3=\phi _4=\psi _4\). The right equality holds if \(\phi _1=\phi _2=\psi _1\), \(\phi _3=\sqrt{\psi _2^2+\psi _3^2-\psi _1^2}\) and \(\phi _4=\psi _4\).

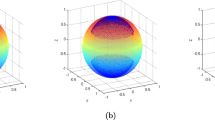
To illustrate Theorem 2, we show the lower and upper bounds of \(\mathcal {\bar{C}}_{l_1}(|\psi \rangle _{out})\) in Fig. 1, where the intersecting line of the green and blue surfaces stands for the case \(\psi _1^2+\psi _4^2=\frac{1}{2}\), and from the nonincreasing order of \(\{\psi _j\}_{j=1}^4\) and \(\sum \nolimits _{j=1}^4\psi _j^2=1\), we have \(0\le \psi _4\le \frac{1}{2}\) and \(\sqrt{\frac{1-\psi _4^2}{3}}\le \psi _1\le \sqrt{\frac{1}{2}-\psi _4^2}\). Specially, for \(\psi _4=0\), see Fig. 2.

Fig. 1
figure 1

The green surface corresponds to the maximal value of \(\mathcal {\bar{C}}_{l_1}(|\psi \rangle _{out})\), and the blue one corresponds to the minimal value of \(\mathcal {\bar{C}}_{l_1}(|\psi \rangle _{out})\). From the relations \(\sum \nolimits _{i=1}^4\psi _i^2=1\),\(\psi _1\ge \psi _2\ge \psi _3\ge \psi _4\), and \(\psi _1^2+\psi _4^2\le \psi _2^2+\psi _3^2\), one can see \(0\le \psi _4\le \frac{1}{2}\), and \(\sqrt{\frac{1-\psi _4^2}{3}}\le \psi _1\le \sqrt{\frac{1-2\psi _4^2}{2}}\). Particularly, from Fig. 1, one can see that for the case \(\psi _1=\psi _4=\frac{1}{2}\), \(\mathcal {\bar{C}}_{l_1}(|\psi \rangle _{out})_{\max }=\mathcal {\bar{C}}_{l_1}(|\psi \rangle _{out})_{\min }\). This is in consistent with the fact that for the case \(|\psi \rangle =\frac{1}{2}\sum \nolimits _{j=1}^4|j\rangle \) and \(p_4=1\), \(\mathcal {\bar{C}}_{l_1}(|\psi \rangle _{out})_{\max }=\mathcal {\bar{C}}_{l_1}(|\psi \rangle _{out})_{\min }=3\)

Full size image
Fig. 2
figure 2

The case of \(\psi _4=0\). Blue line and green line correspond to the minimal and maximal value of \(\mathcal {\bar{C}}_{l_1}(|\psi \rangle _{out})\), respectively

Full size image

For \(d=5\), from (6) one gets \(\mathcal {\overline{C}}_{l_1}(|\psi \rangle _{out})_{\max }\) when \(\phi _1=\phi _2=\psi _1\), \(\phi _3=\sqrt{\psi _2^2+\psi _3^2-\psi _1^2}\), \(\phi _4=\psi _4\) and \(\phi _5=\psi _5\) under the condition \(|\psi \rangle {\mathop {\longrightarrow }\limits ^{IO}}|\phi \rangle \) when \(\psi _1^2+\psi _4^2\le \psi _2^2+\psi _3^2\) via SIOs defined in Eq. (2). In this case, \(\mathcal {\overline{C}}_{l_1}(|\psi \rangle _{out})_{\max }=4\psi _2^2+4\psi _3^2+6\psi _4^2+8\psi _5^2-2\psi _1^2\). Similar to the discussions on the case of \(d=4\), we have \(\mathcal {\overline{C}}_{l_1}(|\psi \rangle _{out})_{\min }=1+15\psi _5^2\). However, for \(\psi _1^2+\psi _4^2> \psi _2^2+\psi _3^2\), there exist no incoherent operations such that \(|\psi \rangle {\mathop {\longrightarrow }\limits ^{IO}}|\phi \rangle \) with \(\phi _1=\phi _2=\psi _1\), \(\phi _3=\sqrt{\psi _2^2+\psi _3^2-\psi _1^2}\), \(\phi _4=\psi _4\) and \(\phi _5=\psi _5\), since one can find that \(\phi _3<\phi _4\). Thus, one needs to change \(\phi _3\) and \(\phi _4\) while keeps \(\phi _1=\phi _2=\psi _1\). From Eq. (6), we have \(\phi _3=\phi _4=\sqrt{\frac{\psi _2^2+\psi _3^2+\psi _4^2-\psi _1^2}{2}}\). However, the condition \(|\psi \rangle {\mathop {\longrightarrow }\limits ^{IO}}|\phi \rangle \) requires that \(\phi _4\ge \phi _5\), i.e., \(\psi _2^2+\psi _3^2+\psi _4^2\ge \psi _1^2+2\psi _5^2\). In this case, \(\mathcal {\overline{C}}_{l_1}(|\psi \rangle _{out})_{\max }=5\psi _2^2+5\psi _3^2+5\psi _4^2+8\psi _5^2-3\psi _1^2\). Similarly, \(\mathcal {\overline{C}}_{l_1}(|\psi \rangle _{out})_{\min }=1+15\psi _5^2\). By Theorem 1, one cannot obtain the maximal probability with respect to \(|\Psi _5\rangle \) without a complete waste of resource when \(\psi _2^2+\psi _3^2+\psi _4^2<\psi _1^2+2\psi _5^2\) via SIOs defined in Eq. (2).

Following the discussions above, for a general d-dimension pure state \(|\psi \rangle \) with \(d\ge 5\), one can deal with the problem via SIOs defined in Eq. (2) according to the following \(d-3\) cases.

Case 1: \(\psi _2^2+\psi _3^2\ge \psi _1^2+\psi _4^2\)

From Eq. (6), if \(\phi _1=\phi _2=\psi _1\), \(\phi _3=\sqrt{\psi _2^2+\psi _3^2-\psi _1^2}\) and \(\phi _j=\psi _j, \ j=4,5,\ldots ,d\), we have the maximal value, \(\mathcal {\bar{C}}_{l_1}(|\psi \rangle _{out})_{\max } =4\sum \nolimits _{j=2}^3\psi _j^2+2\sum \nolimits _{j=4}^d(j-1)\psi _j^2-2\psi _1^2\).

Conversely, we can get the minimal value of \(\mathcal {\bar{C}}_{l_1}(|\psi \rangle _{out})\) if \(\phi _1=\phi _2=\sqrt{\frac{1-(d-2)\psi _d^2}{2}}\), and \(\phi _j=\psi _d, \ j=3,4,\ldots ,d\), \(\mathcal {\bar{C}}_{l_1}(|\psi \rangle _{out})_{\min }=1+d(d-2)\psi _d^2\).

Case 2: \(\psi _2^2+\psi _3^2<\psi _1^2+\psi _4^2\) and \(\psi _2^2+\psi _3^2+\psi _4^2\ge \psi _1^2+2\psi _5^2\)

From Eq. (6), if \(\phi _1=\phi _2=\psi _1\), \(\phi _3=\phi _4=\sqrt{\frac{\psi _2^2+\psi _3^2+\psi _4^2-\psi _1^2}{2}}\) and \(\phi _j=\psi _j, \ j=5,6,\ldots ,d\), we get the maximal value \(\mathcal {\bar{C}}_{l_1}(|\psi \rangle _{out})_{\max }=5\sum \nolimits _{j=2}^4\psi _j^2+2\sum \nolimits _{j=5}^d(j-1)\psi _j^2-3\psi _1^2\). If \(\phi _1=\phi _2=\sqrt{\frac{1-(d-2)\psi _d^2}{2}}\) and \(\phi _j=\psi _d, \ j=3,4,\ldots ,d\), we get the minimal value of \(\mathcal {\bar{C}}_{l_1}(|\psi \rangle _{out})\), \(\mathcal {\bar{C}}_{l_1}(|\psi \rangle _{out})_{\min }=1+d(d-2)\psi _d^2\).

\(\cdots \cdots \)

Case k: \(\sum \nolimits _{j=2}^{k+1}\psi _j^2<\psi _1^2+(k-1)\psi _{2+k}^2\) and \(\sum \nolimits _{j=2}^{k+2}\psi _j^2\ge \psi _1^2+k\psi _{3+k}^2\)

From Eq. (6), if \(\phi _1=\phi _2=\psi _1\), \(\phi _3=\phi _4=\cdots =\phi _{2+k}=\sqrt{\frac{\Sigma _{j=2}^{k+2}\psi _j^2-\psi _1^2}{k}}\) and \(\phi _j=\psi _j, \ j=3+k,4+k,\ldots ,d\), we get the maximal value

$$\begin{aligned} \mathcal {\bar{C}}_{l_1}(|\psi \rangle _{out})_{\max }=(k+3)\sum \nolimits _{j=2}^{k+2}\psi _j^2+2\sum \nolimits _{j=k+3}^d(j-1)\psi _j^2-(k+1)\psi _1^2. \end{aligned}$$

If \(\phi _1=\phi _2=\sqrt{\frac{1-(d-2)\psi _d^2}{2}}\) and \(\phi _j=\psi _d, \ j=3,4,\ldots ,d\), we obtain the minimal value of \(\mathcal {\bar{C}}_{l_1}(|\psi \rangle _{out})\), \(\mathcal {\bar{C}}_{l_1}(|\psi \rangle _{out})_{\min }=1+d(d-2)\psi _d^2\).

\(\cdots \cdots \)

Case \(d-3\): \(\sum \nolimits _{j=2}^{d-2}\psi _j^2<\psi _1^2+(d-4)\psi _{d-1}^2\) and \(\sum \nolimits _{j=2}^{d-1}\psi _j^2\ge \psi _1^2+(d-3)\psi _{d}^2\)

From Eq. (6), if \(\phi _1=\phi _2=\psi _1\), \(\phi _3=\phi _4=\cdots =\phi _{d-1}=\sqrt{\frac{\Sigma _{j=2}^{d-1}\psi _j^2-\psi _1^2}{d-3}}\) and \(\phi _d=\psi _d\), we have the maximal value,

$$\begin{aligned} \mathcal {\bar{C}}_{l_1}(|\psi \rangle _{out})_{\max } =d\sum \limits _{j=2}^{d-1}\psi _j^2+2(d-1)\psi _d^2-(d-2)\psi _1^2. \end{aligned}$$

If \(\phi _1=\phi _2=\sqrt{\frac{1-(d-2)\psi _d^2}{2}}\) and \(\phi _j=\psi _d, \ j=3,4,\ldots ,d\), we get the minimal value of \(\mathcal {\bar{C}}_{l_1}(|\psi \rangle _{out})\), \(\mathcal {\bar{C}}_{l_1}(|\psi \rangle _{out})_{\min }=1+d(d-2)\psi _d^2\).

One can see that the \(d-3\) cases together are just the condition \(\sum \nolimits _{j=2}^{d-1}\psi _j^2\ge \psi _1^2+(d-3)\psi _{d}^2\) in Theorem 1 to realize the one-shot coherence distillation via SIOs defined in Eq. (2). Thus, we can just discuss the \(d-3\) cases above based on the SIOs defined in Eq. (2). Here, in the discussions of the \(d-3\) cases above, we have assumed that \(|\psi \rangle {\mathop {\longrightarrow }\limits ^{IO}}|\phi \rangle \), i.e., \(\sum \nolimits _{m=1}^j\psi _m^2\le \sum \nolimits _{m=1}^j\phi _m^2\), and \(\phi _m\ge \phi _{m+1}\) for \(m=1,2,\ldots ,d-1\) and \(j=1,2,\ldots ,d\), which needs to be proved further.

For case k (\(1\le k\le d-3\)), concerning the maximal value of \(\mathcal {\bar{C}}_{l_1}(|\psi \rangle _{out})\), as \(\phi _1=\phi _2=\psi _1\) and \(\phi _j=\psi _j\) for \(j=3+k,4+k,\ldots ,d\), for the proof of \(\sum \nolimits _{m=1}^j\psi _m^2\le \sum \nolimits _{m=1}^j\phi _m^2\), we only need to prove \(\sum \nolimits _{m=1}^j\psi _m^2\le \sum \nolimits _{m=1}^j\phi _m^2\) for \(j=3,4,\ldots ,k+2\). We have

$$\begin{aligned} \begin{array}{rl} \sum \nolimits _{m=1}^j\phi _m^2-\sum \nolimits _{m=1}^j\psi _m^2&{}= \frac{(k+2-j)\psi _1^2+k(\psi _{j+1}^2+\cdots +\psi _{k+1}^2)+(j-2)\psi _{k+2}^2-(k+2-j)(\psi _2^2+\cdots +\psi _{k+1}^2)}{k}\\ &{}\ge \frac{(k+2-j)\psi _1^2+[k(k-j+1)+j-2]\psi _{k+2}^2-(k+2-j)(\psi _2^2+\cdots +\psi _{k+1}^2)}{k}\\ &{}=\frac{(k+2-j)[\psi _1^2+(k-1)\psi _{k+2}^2-(\psi _2^2+\cdots +\psi _{k+1}^2)}{k}]\\ &{}\ge 0 \end{array} \end{aligned}$$
(9)

for \(j=3,4,\ldots ,k+2\). The last inequality is due to the condition \(\sum \nolimits _{j=2}^{k+1}\psi _j^2<\psi _1^2+(k-1)\psi _{2+k}^2\).

For the proof of \(\phi _m\ge \phi _{m+1}\) for \(m=1,2,\ldots ,d-1\), we only need to prove \(\phi _2\ge \phi _3\) and \(\phi _{2+k}\ge \phi _{3+k}\). Obviously,

$$\begin{aligned} \begin{array}{rl} \phi _{2}\ge \phi _{3}&\Leftrightarrow \phi _{2}^2\ge \phi _{3}^2 \Leftrightarrow \psi _1^2\ge \frac{\sum _{j=2}^{k+2}\psi _j^2-\psi _1^2}{k} \Leftrightarrow (k+1)\psi _1^2\ge \sum \nolimits _{j=2}^{k+2}\psi _j^2, \end{array} \end{aligned}$$
(10)

and

$$\begin{aligned} \begin{array}{rl} \phi _{2+k}\ge \phi _{k+3}&\Leftrightarrow \phi _{2+k}^2\ge \phi _{k+3}^2 \Leftrightarrow \frac{\sum _{j=2}^{k+2}-\psi _1^2}{k}\ge \phi _{3+k}^2 \Leftrightarrow \sum \nolimits _{j=2}^{k+2}\psi _j^2\ge \psi _1^2+k\psi _{3+k}^2. \end{array}\nonumber \\ \end{aligned}$$
(11)

Thus, we get \(\phi _m\ge \phi _{m+1}\) for \(m=1,2,\ldots ,d-1\). Concerning the minimal value of \(\mathcal {\bar{C}}_{l_1}(|\psi \rangle _{out})\), similarly, one can also prove that \(|\psi \rangle {\mathop {\longrightarrow }\limits ^{IO}}|\phi \rangle \). Altogether, we have the following theorem for the general Case k.

Theorem 3

For the pure state \(|\psi \rangle \) given in Eq. (1) with \(\sum \nolimits _{j=2}^{k+1}\psi _j^2<\psi _1^2+(k-1)\psi _{2+k}^2\) and \(\sum \nolimits _{j=2}^{k+2}\psi _j^2\ge \psi _1^2+k\psi _{3+k}^2\) \((1\le k\le d-3)\), \(\mathcal {\bar{C}}_{l_1}(|\psi \rangle _{out})\) satisfies the following relations,

$$\begin{aligned} 1+d(d-2)\psi _d^2\le \mathcal {\bar{C}}_{l_1}(|\psi \rangle _{out})\le (k+3)\sum \limits _{j=2}^{k+2}\psi _j^2+2\sum \limits _{j=k+3}^d(j-1)\psi _j^2-(k+1)\psi _1^2,\nonumber \\ \end{aligned}$$
(12)

if the maximal probability of getting \(|\Psi _d\rangle \) is attained without a complete waste of resources via SIOs defined in Eq. (2). The left equality holds when \(\phi _1=\phi _2=\sqrt{\frac{1-(d-2)\psi _d^2}{2}}\) and \(\phi _j=\psi _d, \ j=3,4,\ldots ,d\). The right equality holds when \(\phi _1=\phi _2=\psi _1\), \(\phi _3=\phi _4=\cdots =\phi _{2+k}=\sqrt{\frac{\Sigma _{j=2}^{k+2}\psi _j^2-\psi _1^2}{k}}\) and \(\phi _j=\psi _j, \ j=3+k,4+k,\ldots ,d\).

From Theorem 3, we know that the average coherence of output ensemble depends on the dimensional d. To illustrate this, we show the lower bound of \(\mathcal {\bar{C}}_{l_1}(|\psi \rangle _{out})\) in Fig. 3.

Fig. 3
figure 3

The dependence of the average coherence \(\mathcal {\bar{C}}_{l_1}\) on the dimension d as well as on the value of \(\psi _d\)

Full size image

From Theorems 2 and 3, for a given initial pure state, one can judge which method one can use to get \(|\Psi _d\rangle \) with the maximal probability, and avoid a complete waste of resources at the same time via SIOs defined in Eq. (2). One can also obtain the range of the corresponding average loss of coherence. From the inequality (12), one can see that \(\mathcal {\bar{C}}_{l_1}(|\psi \rangle _{out})_{\min }\) only depends on the value of \(\psi _d\), while \(\mathcal {\bar{C}}_{l_1}(|\psi \rangle _{out})_{\max }\) depends on \(\{\psi _i\}\). Since the lower and upper bounds of \(\mathcal {\bar{C}}_{l_1}(|\psi \rangle _{out})\) depend on the initially given pure states, one can only estimate \(\mathcal {\bar{C}}_{l_1}(|\psi \rangle _{out})_{\max }\) or \(\mathcal {\bar{C}}_{l_1}(|\psi \rangle _{out})_{\min }\) for given pure states. In other words, if one does not know the specific expressions of two initial pure states \(|\psi \rangle \) and \(|{\widetilde{\psi }}\rangle \) which belong to different cases, one cannot say which one of \(\mathcal {\bar{C}}_{l_1}(|\psi \rangle _{out})_{\min }\) and \(\mathcal {\bar{C}}_{l_1}(|{\widetilde{\psi }}\rangle _{out})_{\min }\) is larger, as one cannot assure which one of \(\psi _d\) and \({\widetilde{\psi }}_d\) is larger. The same is for case of \(\mathcal {\bar{C}}_{l_1}(|\psi \rangle _{out})_{\max }\). What is more, if we want to get the maximal value of \(\mathcal {\bar{C}}_{l_1}(|\psi \rangle _{out})_{\max }\) over all pure states, \(\psi _1\) should be as small as possible. Thus, the maximal value of \(\mathcal {\bar{C}}_{l_1}(|\psi \rangle _{out})_{\max }\) over all pure states can be attained at \(\psi _1=\frac{1}{\sqrt{d}}\), i.e., \(|\psi \rangle =|\Psi _d\rangle \).

To illustrate our results, let us consider an example for the case \(d=4\).

Example 1

Let

$$\begin{aligned} |\psi \rangle =\sqrt{0.28}|1\rangle +\sqrt{0.25}|2\rangle +\sqrt{0.22}|3\rangle +\sqrt{0.15}|4\rangle +\sqrt{0.1}|5\rangle , \\ |{\widetilde{\psi }}\rangle =\sqrt{0.305}|1\rangle +\sqrt{0.25}|2\rangle +\sqrt{0.2}|3\rangle +\sqrt{0.13}|4\rangle +\sqrt{0.115}|5\rangle \end{aligned}$$

and

$$\begin{aligned} |\psi ^{\prime }\rangle =\sqrt{0.3}|1\rangle +\sqrt{0.25}|2\rangle +\sqrt{0.2}|3\rangle +\sqrt{0.14}|4\rangle +\sqrt{0.11}|5\rangle . \end{aligned}$$

For the pure state \(|\psi \rangle \), one finds that \(\psi _1^2+\psi _4^2=0.43\le \psi _2^2+\psi _3^2=0.47\). Thus, \(|\psi \rangle \) is a pure state of the Case 1. By Theorem 3, we have

$$\begin{aligned} \mathcal {\bar{C}}_{l_1}(|\psi \rangle _{out})_{\max } =\mathcal {\bar{C}}_{l_1}((|\phi \rangle _{\max })_{out})=3.02, \end{aligned}$$

with \(|\psi \rangle {\mathop {\longrightarrow }\limits ^{IO}}|\phi \rangle _{\max }= \sqrt{0.28}|1\rangle +\sqrt{0.28}|2\rangle +\sqrt{0.19}|3\rangle +\sqrt{0.15}|4\rangle +\sqrt{0.1}|5\rangle \), and

$$\begin{aligned} \mathcal {\bar{C}}_{l_1}(|\psi \rangle _{out})_{\min }=\mathcal {\bar{C}}_{l_1}((|\phi \rangle _{\min })_{out})=2.5 \end{aligned}$$

with \(|\psi \rangle {\mathop {\longrightarrow }\limits ^{IO}}|\phi \rangle _{\min }= \sqrt{0.35}|1\rangle +\sqrt{0.35}|2\rangle +\sqrt{0.1}|3\rangle +\sqrt{0.1}|4\rangle +\sqrt{0.1}|5\rangle \).

Let \(|\phi \rangle _{\max }\), \(|{\widetilde{\phi }}\rangle _{\max }\) and \(|\phi ^{\prime }\rangle _{\max }\) be the corresponding pure states satisfying \(|\psi \rangle {\mathop {\longrightarrow }\limits ^{IO}}|\phi \rangle _{\max }\), \(|{\widetilde{\psi }}\rangle {\mathop {\longrightarrow }\limits ^{IO}}|{\widetilde{\phi }}\rangle _{\max }\) and \(|\psi ^{\prime }\rangle {\mathop {\longrightarrow }\limits ^{IO}}|\phi ^{\prime }\rangle _{\max }\), respectively. Similarly, one finds that \(|{\widetilde{\psi }}\rangle \) belongs to the Case 1 with \(\mathcal {\bar{C}}_{l_1}(|{\widetilde{\psi }}\rangle _{out})_{\max }=2.89\) and \(\mathcal {\bar{C}}_{l_1}(|\psi \rangle _{out})_{\min }=2.725\). \(|\psi ^{\prime }\rangle \) belongs to the Case 2 with \(\mathcal {\bar{C}}_{l_1}(|\psi ^{\prime }\rangle _{out})_{\max }=2.93\) and \(\mathcal {\bar{C}}_{l_1}(|\psi \rangle _{out})_{\min }=2.65\).

4 Coherence loss related to mixed states

In Ref. [27], Lami et.al showed that one may have a very limited coherence distillation power via SIOs when mixed input states are concerned. In Ref. [36], the authors showed that no mixed qubit state can be distilled to a maximally coherent qubit state with nonzero probability using a SIO. In fact, we can generally prove the following.

Lemma 1

No d-dimensional mixed states \(\rho \) can be distilled to any d-dimensional pure states via a SIO with nonzero probability.

Proof

First, a \(\rho \) is pure if and only if \(\rho _{jj}\rho _{kk}=|\rho _{jk}|^2\), since

$$\begin{aligned} \begin{array}{rl} {{\,\mathrm{tr}\,}}\rho ^2&{}=\sum \limits _{jk}|\rho _{jk}|^2\\ &{}=\sum \limits _{j}|\rho _{jj}|^2+2\sum \limits _{j<k}|\rho _{jk}|^2\\ &{}=\sum \limits _{j}|\rho _{jj}|^2+2\sum \limits _{j<k}\rho _{jj}\rho _{kk}\\ &{}=\left( \sum \limits _{j}\rho _{jj}\right) ^2\\ &{}=1. \end{array} \end{aligned}$$
(13)

Let \(\Phi \) be a SIO. Then, the Kraus operators \(\{K_n\}\) of \(\Phi \) can be the form of \(K_n=\sum \nolimits _{j}K_{nj}|f(j)\rangle \langle j|\) with f a bijection. One has

$$\begin{aligned} K_{n}\rho K_{n}^{\dag }=\sum \limits _{jk}K_{nj}K_{nk}^*\rho _{jk}|f(j)\rangle \langle f(k)|. \end{aligned}$$
(14)

If \(\rho \) can be distilled to a d-dimensional pure state via \(\Phi \) with nonzero probability, then \(|K_{nj}|^2|K_{nk}|^2\rho _{jj}\rho _{kk}=|K_{nj}K_{nk}^*|^2|\rho _{jk}|^2\), which give rise to \(\rho _{jj}\rho _{kk}=|\rho _{jk}|^2\), i.e., \(\rho \) is a pure state, which completes the proof. \(\square \)

Therefore, to find a method to transform a mixed state into a maximally coherent state via a series of SIOs is necessary, which also generalizes the results of coherence loss for pure states [26]. In the following, we present a way to transform a mixed state into maximally coherent states with probability via a series of SIOs on the pure states of the ensemble of the mixed state.

For a mixed state \(\rho \), without loss of generality, one can assume \(\rho _{ii}\ge \rho _{i+1,i+1}\) for \(i=1,2,\ldots ,d-1\). Let \(\rho =\sum \nolimits _{i}q_i|\varphi _i\rangle \langle \varphi _i|\) be a pure state decomposition of \(\rho \), where \(|\varphi _i\rangle =\sum \nolimits _{j=1}^d\varphi _{ij}|j\rangle \) with \(\varphi _{ij}\ge \varphi _{i,j+1}\ge 0\) for \(j=1,\ldots ,d-1\). Here, it should be noted that the coefficients of the pure states may be not in non-increasing order. Nevertheless, one can always apply unitary SIOs to let the corresponding pure states satisfy this condition. Define \(\Phi _i\) to be the SIO corresponding to \(|\varphi _i\rangle \),

$$\begin{aligned} \Phi _i(|\varphi _i\rangle )=\sum \limits _{j=1}^dK_{ij}|\varphi _i\rangle \langle \varphi _i|K_{ij}^{\dag }, \end{aligned}$$
(15)

where

$$\begin{aligned} K_{ij}=\sqrt{p_{ij}}\left( \frac{1}{\sqrt{j}}\sum \limits _{q=1}^j\frac{|q\rangle \langle q|}{\varphi _{iq}}\right) , \end{aligned}$$
(16)

with

$$\begin{aligned} p_{id}=d\varphi _{id}^2, \ \ p_{iq}=q(\varphi _{iq}^{2}-\varphi _{i,q+1}^2), \ \ q=1,2,\ldots ,d-1. \end{aligned}$$
(17)

First, we prepare a series of SIOs \(\{\Phi _i\}\) on \(|\varphi _i\rangle \), with \(\{p_i,|\varphi _i\rangle \}\) the pure state decomposition of \(\rho \) and \(\Phi _i\) defined in Eq. (15). Define \(\Phi \) as

$$\begin{aligned} \Phi (\rho )=\sum \limits _{i}p_i\Phi _i(|\varphi _i\rangle ). \end{aligned}$$
(18)

Theorem 4

Let \(\Phi \) defined in Eq. (18) with \(\Phi _i\) defined in Eq. (15). \(\Phi \) can transform \(\rho \) into a maximally coherent state \(|\Psi _{q}\rangle \) with the probability \(p_q=q(\rho _{qq}-\rho _{q+1,q+1})\), \(q=1,2,\ldots ,d-1\), and \(p_d=d\rho _{dd}\). Moreover, \(\Phi \) is independent of the pure decomposition of \(\rho \).

Proof

From Eq. (15) and the expression of \(|\varphi _i\rangle \), \(\Phi _i\) can transform \(|\varphi _i\rangle \) into a maximally coherent state \(|\Psi _{q}\rangle \) with the probability \(p_{iq}\). Then, \(\Phi \) can transform \(\rho \) to \(|\Psi _{q}\rangle \) with probability \(p_q=\sum \nolimits _{i}q_ip_{iq}\). Then, the conclusion follows from Eq. (17). \(\square \)

Corollary 1

For an arbitrary mixed state \(\rho \), we have

$$\begin{aligned} \mathcal {\bar{C}}_{l_1}(\rho _{out})=2\sum \nolimits _{q=2}^d(q-1)\rho _{qq} \end{aligned}$$
(19)

with \(\rho _{out}=\Phi (\rho )\) and \(\Phi \) defined in Eq. (18).

Similar to the pure state case, one can also get the conditions related to the no complete waste of resource for mixed states \(\rho \).

Theorem 5

For a given d-dimensional mixed state \(\rho \) with \(d\ge 4\), if one can avoid a complete waste of resource while \(p_d=d\rho _{dd}\) via \(\Phi \) defined in Eq. (18), then \(\sum \nolimits _{j=2}^{d-1}\rho _{jj}\ge \rho _{11}+(d-3)\rho _{dd}\), where \(p_q\) are defined in Theorem 4 for \(q=1,2,\ldots ,d\).

Proof

Let \(\rho =\sum \nolimits _iq_i|\varphi _i\rangle \langle \varphi _i|\) with \(|\varphi _i\rangle =\sum \nolimits _j\varphi _{ij}|j\rangle \), \(\varphi _{ij}\ge \varphi _{i,j+1}\ge 0\) for \(j=1,\ldots ,d-1\). Assuming \(p_1=0\) we have \(p_{i1}=0\), where \(p_{i1}\) is defined in Eq. (17). Thus, for each pure state \(|\varphi _i\rangle \), one has \(\sum \nolimits _{j=2}^{d-1}\varphi _{ij}^2\ge \varphi _{i1}^2+(d-3)\varphi _{id}^2\). Therefore, \(\sum \nolimits _{j=2}^{d-1}\rho _{jj}\ge \rho _{11}+(d-3)\rho _{dd}\). \(\square \)

From Theorem 5, one sees that via operations defined in Eq. (18), there is always possibility of a complete waste of resource while \(p_d\) remains nonzero if \(\sum \nolimits _{j=2}^{d-1}\rho _{jj}<\rho _{11}+(d-3)\rho _{dd}\).

5 Conclusion

We presented a protocol of one-shot coherence distillation with the maximal probability to transform a d-dimensional pure state \(|\psi \rangle \) into the maximally coherent state \(|\Psi _d\rangle \) without complete waste of resource. In this process, an incoherent operation may be used to transform \(|\psi \rangle \) to \(|\phi \rangle \). For mixed states \(\rho \), we also proposed a method to transform \(\rho \) into a maximally coherent state without complete waste of resource. Our method is independent of the pure decompositions of \(\rho \). These results may highlight further investigations on the theory of coherence manipulations.