1 Introduction

Quantifying the degree of quantumness of a channel has both theoretical and practical significance in quantum information science [1]. Quantum channels refer to completely positive and trace-preserving maps and can be practically applied to transfer quantum information in a given environment [2]. To this end, it is important that a channel should preserve the integrity of transmitted quantum states and resist classicalization of the states. Clearly, it is important to quantify such a degree of quantumness of a quantum channel [3]. Considering that classical states are usually identified as those whose correlations can be described in terms of classical probabilities, the quantumness of a channel will indicate how well nonclassical correlations such as entanglement, discord and related quantities [4] of a transmitted state are preserved by the channel. One particularly simple approach to quantifying the quantumness of a channel is to build it on the quantumness measure for a single system, essentially asking how well it preserves the non-commuting property of two states of the system that initially possess this property. This approach has the advantage that it makes no reference to the correlations and requires no complicated optimization procedures [5].

Channel noise is usually known for its detrimental role in reducing the degree of coherence in a system and thus tends to undermine the quantumness of a channel [6]. For example, the deteriorating effect of the environment on a quantum state has been studied in the context of coherence-breaking channels and coherence sudden death [7]. An interesting class of channels known as semi-classical channels \(\varLambda _{\mathrm{SC}}\) map all the input states \(\rho \) to \(\varLambda _{\mathrm{SC}}(\rho )\), such that the later are diagonal in the same basis. Such channels are realized by complete decoherence after which only diagonal elements of the density matrix are nonzero [8].

However, factors such as squeezing [9,10,11] or non-Markovianity [12,13,14] can counterbalance the effect of decoherence for some states and thus are conducive to the quantumness of the channel. Refs. [15,16,17] show that local environments can enhance the average fidelity of quantum teleportation for certain entangled states. Enhancement in quantum discord by local Markovian (i.e., memoryless) noise channels was reported in [18, 19]. In [20], it was shown that the quantum channels need not be decohering, but could also have cohering power [21], which is upper bounded by the corresponding unitary operation.

Unitary operations may be considered as noiseless channels, and they can give rise to a notion of quantumness based on their entangling power. The entangling capabilities of unitary operations acting on bipartite systems was reported in [22], with the maximum entanglement being created with product input states [23].

On the specific question of quantumness of channels, it may be worth noting that in [24,25,26], coherence of quantum channels was analyzed using Choi-Jamiolwski isomorphism. A coherence-based measure of quantumness of channel was proposed in [27], by defining the measure as the average quantum coherence of the state after the quantum channel acts on it, and minimized over all orthonormal basis sets of the state space. This measure was studied in the context of various (non-)Markovian channels [28]. Further, this measure connects different coherence and entanglement measures, and is also the upper bound for another important coherence measure called robustness of coherence for all qubit states [29].

A necessary and sufficient condition for the creation of quantum correlations via local channels in finite dimensions is that they should not be commutativity preserving [30]. Commutative quantum channels preserve the commutation relation of any two compatible states, i.e., if \([\rho , \sigma ] = 0\), then \([{\mathcal {E}}(\rho ), {\mathcal {E}}(\sigma )] = 0\). It is clear that the semiclassical channels, defined above, are commutativity preserving, implying that a departure from semiclassicality is necessary to create quantum correlations. In that spirit, here we propose a simple measure for the quantumness of channels, based on commutation properties of the states evolving under a given channel. The degree to which a quantum channel preserves the non-commutativity of two states can be attributed as the quantumness of the channel.

This paper is organized as follows: in Sect. 2, we introduce a measure of quantumness of channels. Section 3 is devoted to applying this measure to various well-known quantum channels. The experimental relevance of this measure is discussed in Sect. 4. Results and their discussion are presented in Sect. 5. We conclude in Sect. 6.

2 Quantumness of channels

Given two arbitrary states \(\rho \) and \(\sigma \), one can quantify their mutual incompatibility by the Hilbert-Schmidt (HS) norm of their commutator \({\mathcal {M}}(\rho , \sigma ) = 2 || {\text {C}}||^{2}_{HS} \equiv 2 {\text {Tr}}[{\text {C}}^\dagger {\text {C}}]\). The measure is defined in terms of the HS norm of their commutator \({\text {C}} = \rho \sigma - \sigma \rho \). This measure was motivated in [5] with the aim of identifying nonclassicality with the incompatibility of states. Consider two qubit states \(\rho _a = \frac{1}{2}(\mathbb {1} + \mathbf {a} \cdot \mathbf {\sigma })\) and \(\rho _b = \frac{1}{2}(\mathbb {1} + \mathbf {b} \cdot \mathbf {\sigma })\), with \(\mathbf {a}, \mathbf {b} \in {\mathbb {R}}^3\) and \(\mathbf {\sigma } = (\sigma _x, \sigma _y, \sigma _z)\) represents the three Pauli spin matrices. We have \( \rho _a \rho _b - \rho _b \rho _a = i \frac{1}{2} (\mathbf {a} \times \mathbf {b}) \cdot \mathbf {\sigma }\), and

$$\begin{aligned} {\mathcal {M}}(\rho _a, \rho _b) = 2 {\text {Tr}}\{( \rho _a \rho _b - \rho _b \rho _a)^\dagger ( \rho _a \rho _b - \rho _b \rho _a)\} = | \mathbf {a} \times \mathbf {b}|^2. \end{aligned}$$
(1)

This quantity attains its maximum value of one for orthogonal \(\mathbf {a}\) and \(\mathbf {b}\) and vanishes when \(\mathbf {a}\) and \(\mathbf {b}\) are parallel, \(0 \le {\mathcal {M}}(\rho , \sigma ) \le 1\).

Here we try to exploit this approach to probe the quantumness of a channel. Consider a channel described by a linear, completely positive and trace preserving map \(\varPhi : L({\mathcal {H}}_A) \rightarrow L({\mathcal {H}}_B)\) [31, 32]. The action of this map on an input state \(\rho \) leads to an output state \(\rho ^\prime \) and can be summarized as

$$\begin{aligned} \rho ^\prime = \varPhi [\rho ]. \end{aligned}$$
(2)

In the context of quantum channels, we start with two states \(\rho _a\) and \(\rho _b\) which are maximally noncommuting in the sense that \({\mathcal {M}}(\rho _a, \rho _b) = 1\). By subjecting these states to a quantum channel, the quantumness of the channel can be attributed to the extent to which \(\rho _a^\prime \) and \(\rho _b^\prime \) (the outputs) are incompatible

$$\begin{aligned} {\mathcal {M}}(\rho _a^\prime , \rho _b^\prime ) = 2 {\text {Tr}}[{\text {C}}^\dagger {\text {C}}], \end{aligned}$$
(3)

with \({\text {C}} = \rho _a^\prime \rho _b^\prime - \rho _b^\prime \rho _a^\prime \). This quantity when maximized over all input states serves as a measure for the quantumness of the channel

$$\begin{aligned} \mu = \max _{\rho _a, \rho _b} {\mathcal {M}}(\rho _a^\prime = \varPhi [\rho _a], \rho _b^\prime = \varPhi [\rho _b]). \end{aligned}$$
(4)

As an example, consider the states \(|a\rangle = \cos (x/2) |0\rangle + e^{-i \phi } \sin (x/2) |1\rangle \) and \(|b\rangle = \cos (y/2) |0\rangle + e^{-i \xi } \sin (y/2) |1\rangle \), with the respective density matrix representations

$$\begin{aligned} \rho _a&=\frac{1}{2} (\mathbb {1} + \mathbf {a}\cdot \mathbf {\sigma }) = \begin{pmatrix} \cos ^2(x/2) &{} \quad e^{i \phi } \frac{\sin (x)}{2}\\ e^{-i \phi }\frac{\sin (x)}{2} &{} \quad \sin ^2(x/2) \end{pmatrix}, \nonumber \\ \rho _b&=\frac{1}{2} (\mathbb {1} + \mathbf {b}\cdot \mathbf {\sigma }) = \begin{pmatrix} \cos ^2(y/2) &{} \quad e^{i \phi } \frac{\sin (y)}{2}\\ e^{-i \xi }\frac{\sin (y)}{2} &{} \quad \sin ^2(y/2) \end{pmatrix}. \end{aligned}$$
(5)

The states \(\rho _a\) and \(\rho _b\) are maximally non-commuting for \(y = x + \pi /2\) and \(\xi = \phi \), as can be seen by calculating the commutator

$$\begin{aligned} {\text {C}} = \rho _a \rho _b - \rho _b \rho _a = \begin{pmatrix} 0 &{} \quad \frac{e^{i \phi }}{2}\\ - \frac{e^{-i \phi }}{2} &{}\quad 0 \end{pmatrix}. \end{aligned}$$
(6)

Therefore \({\mathcal {M}}(\rho _a, \rho _b) = 2 {\text {Tr}}[{\text {C}}^\dagger {\text {C}}] = 1\). Thus the states are maximally noncommuting and in this sense share maximum nonclassicality. In this example, no optimization is required since the quantity \({\mathcal {M}}(\rho _a, \rho _b)\) is independent of input state parameters. However, as discussed ahead, subjecting these states to quantum channels can make \({\mathcal {M}}(\rho _a, \rho _b)\) dependent on input state parameters. In such cases, we need to maximize over all such parameters to compute the degree of incompatibility of the output states.

3 Application to quantum channels

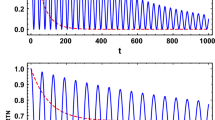
We will now apply the above definition to some well-known quantum channels. We consider the dephasing channels like random telegraph noise (RTN) [33], non-Markovian dephasing (NMD) [34], phase damping (PD) [35] and generalized depolarizing channel (GDC) [36]. The generalized amplitude damping channel (GAD) [9, 37], which represents a dissipative channel is also studied. The Kraus operators for these channels are given in Table 1.

Random Telegraph Noise (RTN): The dynamical map is represented by the Kraus operators \(K_0(t) = k_+ ~ {\mathbf {I}}\) and \(K_1(t) = k_{-} ~ \sigma _z\), where \(k_{\pm } = \sqrt{ \frac{1 \pm \varLambda (t)}{2}}\), such that the action on a general qubit state

$$\begin{aligned} \rho = \begin{pmatrix} 1-p &{} \quad x\\ x^* &{} \quad p \end{pmatrix}, \end{aligned}$$
(7)

is given by

$$\begin{aligned} \rho ^\prime = \varPhi ^{RTN} \begin{pmatrix} 1-p &{}\quad x\\ x^* &{}\quad p \end{pmatrix} = \begin{pmatrix} 1-p &{} \quad x \varLambda (t) \\ x^* \varLambda (t) &{}\quad p \end{pmatrix}. \end{aligned}$$
(8)

Let us use the maximally nonclassical pair of states given in Eq. (5), subject to the constraints enunciated below it. The states \(\rho _a\) and \(\rho _b\), defined in Eq. (5) are subjected to RTN evolution

$$\begin{aligned} \rho ^\prime _a&=\left( \begin{array}{cc} \cos ^2\left( \frac{x}{2}\right) &{} \quad \frac{1}{2} e^{i \phi } \sin (x) \varLambda (t) \\ \frac{1}{2} e^{-i \phi } \sin (x) \varLambda (t) &{}\quad \sin ^2\left( \frac{x}{2}\right) \\ \end{array} \right) ,\nonumber \\ \rho ^\prime _b&= \left( \begin{array}{cc} \cos ^2\left( \frac{1}{4} (2 x+\pi )\right) &{}\quad \frac{1}{2} e^{i \phi } \cos (x) \varLambda (t) \\ \frac{1}{2} e^{-i \phi } \cos (x) \varLambda (t) &{} \quad \sin ^2\left( \frac{1}{4} (2 x+\pi )\right) \\ \end{array} \right) . \end{aligned}$$
(9)

The pertinent commutator in this case becomes

$$\begin{aligned} {\text {C}} =\left( \begin{array}{cc} 0 &{} \quad \frac{1}{2} e^{i \phi } \varLambda (t) \\ -\frac{1}{2} e^{-i \phi } \varLambda (t) &{}\quad 0 \\ \end{array} \right) . \end{aligned}$$
(10)

Therefore, the quantumness measure for the RTN channel turns out to be \(\mu = \max _{\rho _a, \rho _b} {\mathcal {M}}(\rho _a^\prime , \rho _b^\prime ) = 2 {\text {Tr}}[{\text {C}}^\dagger {\text {C}}] = [\varLambda (t)]^2\). Similarly, for non-Markovian dephasing (NMD) and phase damping (PD) channels, characterized by the Kraus operators in Table 1, the quantumness measure turns out to be

$$\begin{aligned} NMD: ~ \mu&= \max _{\rho _a, \rho _b} {\mathcal {M}}(\rho _a^\prime , \rho _b^\prime ) = [\varOmega (p)]^2, \end{aligned}$$
(11)
$$\begin{aligned} PD: ~ \mu&= \max _{\rho _a, \rho _b} {\mathcal {M}}(\rho _a^\prime , \rho _b^\prime ) = 1-\gamma . \end{aligned}$$
(12)

It may be pointed out that the channels RTN, NMD and PD are all types of dephasing channels, and hence they are not expected to show dissimilar behavior. However, they are all included, partly for two reasons: (a) comparison with previous literature reporting on the quantumness of these channels; (b) they illustrate different specific principles of decoherence, and thus indicate distinct underlying physics. Specifically, RTN is a non-Markovian (P-indivisible) channel having infinitely many singularities, and NMD is a non-Markovian (also, P-indivisible) channel with a single singularity, whereas PD can be Markovian.

Next, we consider an example of non-dephasing class of quantum channel, namely the amplitude damping (AD) channel. This channel models the processes like spontaneous emission and is characterized by Kraus operators \(A_0\), \(A_1\) given in Table 1. Here \(\gamma \in [0,1]\). The action of AD channel on a qubit state can be described as

$$\begin{aligned} \begin{pmatrix} 1-p ~&{} \quad q\\ \\ q^* ~ &{}\quad p \end{pmatrix} \rightarrow \begin{pmatrix} 1-p(1-\gamma ) ~&{} \quad q \sqrt{1-\gamma }\\ \\ q^* \sqrt{1-\gamma } ~&{} \quad p(1-\gamma ) \end{pmatrix} \end{aligned}$$
(13)

Following the recipe given above, the quantumness in this case turns out to be

$$\begin{aligned} \mu = \max _{\rho _a, \rho _b} {\mathcal {M}}(\rho _a^\prime , \rho _b^\prime ) = 1 - \gamma . \end{aligned}$$
(14)

It follows that as \(\gamma \rightarrow 1\), the quantumness parameters becomes zero, and the state loses coherence in the given basis, see Eq. (13).

We next consider the example of the Unruh channel. The Unruh effect is the emergence of finite temperature recorded by an observer undergoing acceleration a in a vacuum bath. Yet, paradoxically, it is a rank 2 (rather than full rank) noise effect and in that sense is similar to the AD channel, which represents the effect of a zero temperature thermal bath. The parameter r appearing in Kraus operators is related to acceleration by \(\cos (r) = (1 + e^{-2 \pi \omega c/a})^{-1/2}\), where \(\omega \) is the Dirac particle frequency and c is speed of light in vacuum. The quantumness parameter for this channel is given by

$$\begin{aligned} \mu = \cos ^2(r) = (1 + e^{-2 \pi \omega c/a})^{-1}, \end{aligned}$$
(15)

and approaches one in the limit \(a \ll 2\pi c~ \omega \).

Our final example is the generalized depolarizing channel (GDC), represented by the following Kraus operators \(M_i = \sqrt{p_i} \sigma _i\) with \(i = 0,1,2,3\), where \(\sigma _i\) are the Pauli matrices. The states \(\rho _a\) and \(\rho _b\) given by Eq. (5) evolve under the action of this channel such that the new Bloch vectors are given by

$$\begin{aligned} \mathbf {a}&= \begin{pmatrix} (p_0 + p_1 - p_2 - p_3) \sin x \cos \phi \\ (-p_0 + p_1 - p_2 + p_3) \sin x \sin \phi \\ (p_0 - p_1 - p_2 + p_3) \cos x \end{pmatrix}, \nonumber \\ \mathbf {b}&= \begin{pmatrix} (p_0 + p_1 - p_2 - p_3) \cos x \cos \phi \\ (-p_0 + p_1 - p_2 + p_3) \cos x \sin \phi \\ (-p_0+p_1+p_2-p_3) \sin x \end{pmatrix}. \end{aligned}$$
(16)

Therefore,

$$\begin{aligned} {\mathcal {M}}(\rho _a^\prime , \rho _b^\prime )&= |\mathbf {a} \times \mathbf {b}|, \nonumber \\&\quad = (p_0 - p_1 - p_2 + p_3)^2 [2 (p_0 - p_3) (p_1 - p_2) \cos (2\phi )\nonumber \\&\quad + (p_0 - p_3)^2 + (p_1 - p_2)^2]. \end{aligned}$$
(17)

This is maximum for \(\phi = 0\), i.e., \(\mu = {\mathcal {M}}(\rho _a^\prime , \rho _b^\prime )|_{\phi = 0} = (p_0 + p_1 -p_2 -p_3)^2 (p_0 - p_1 - p_2 + p_3)^2\). The various results discussed above are summarized in Table 1, and compared with the prediction of a coherence-based measure of the quantumness of channels.

4 Experimental relevance of the measure

It is important to note that the quantity \({\mathcal {M}}(\rho _a^\prime , \rho _b^\prime )\) can be given an experimental interpretation using an interferometric setup [38]. This useful technique can be easily incorporated to our purpose of quantifying quantumness of channels. One can write

$$\begin{aligned} \mu = \max _{\rho _a, \rho _b} {\mathcal {M}}(\rho _a^\prime , \rho _b^\prime ) = 4 \max _{\rho _a, \rho _b} {\text {Tr}}[(\rho _a^\prime )^2 (\rho _b^\prime )^2 - (\rho _a^\prime \rho _b^\prime )^2 ]. \end{aligned}$$
(18)

The two quantities \({\text {Tr}}[(\rho _a^\prime )^2 (\rho _b^\prime )^2]\) and \({\text {Tr}}[(\rho _a^\prime \rho _b^\prime )^2]\) can be obtained from two separate measurements. The input state \(\rho = |0\rangle \langle 0 | \otimes \rho _a^\prime \otimes \rho _a^\prime \otimes \rho _b^\prime \otimes \rho _b^\prime \), where \(|0\rangle \) is the control qubit, is subjected to the controlled unitary gate U. This modifies the interference of the controlled qubit by the factor \({\text {Tr}}[\rho U] = v e^{i \alpha }\), with v and \(\alpha \) being the visibility and phase shift of the interference fringes, respectively [39,40,41,42]. Two such schemes (corresponding to \({\text {Tr}}[(\rho _a^\prime )^2 (\rho _b^\prime )^2]\) and \({\text {Tr}}[(\rho _a^\prime \rho _b^\prime )^2]\) ) lead to the quantumness \({\mathcal {M}}(\rho _a^\prime , \rho _b^\prime ) = 4 (v_1 - v_2)\), where \(v_1\) and \(v_2\) correspond to the respective visibilities obtained by the action of relevant unitary gates. We motivate the present discussion by illustrating this notion on some of the channels discussed above.

  1. (a)

    For RTN, the two visibilities (with \(x=\phi =0\)) correspond to

    $$\begin{aligned} {\text {Tr}}[(\rho _a^\prime \rho _b^\prime )^2] = \frac{1}{4}, \quad {\text {Tr}}[(\rho _a^\prime )^2 (\rho _b^\prime )^2 ] = \frac{1}{4}(1 + [\varLambda (t)]^2). \end{aligned}$$
    (19)

    Making use of these in Eq. (18), we obtain \({\mathcal {M}}(\rho _a^\prime , \rho _b^\prime ) = [\varLambda (t)]^2\), consistent with the definition in Eq. (3), see Eq. (10).

  2. (b)

    For GDC, the two visibilities (with \(x=\phi =0\)) turn out to be

    $$\begin{aligned} {\text {Tr}}[(\rho _a \rho _b^\prime )^2]&= 1/4 - 2 (-1 + p_1 + p_2) (p_1 + p_2) (-1 + p_2 + p_3) (p_2 + p_3),\nonumber \\ {\text {Tr}}[(\rho _a^\prime )^2 (\rho _b^\prime )^2 ]&= 1/2 (1 + 2 p_1^2 + 2 (-1 + p_2) p_2+ p_1 (-2 + 4 p_2)) (1 + 2 p_2^2 \nonumber \\ {}&\quad + 2 (-1 + p_3) p_3 + p_2 (-2 + 4 p_3)). \end{aligned}$$
    (20)

    These lead to the expression \(\mu = {\mathcal {M}}(\rho _a^\prime , \rho _b^\prime )|_{\phi =0} = (p_0 + p_1 -p_2 -p_3)^2 (p_0 - p_1 - p_2 + p_3)^2\) in accord with the definition in Eq. (3), see Eq. (17).

What makes this approach particularly attractive is that here the quantumness of the channel can be experimentally determined.

Table 1 Various quantum channels, introduced at the beginning of Sect. 3, with their Kraus operators and the quantumness using commutation-based measure \(\mu = \max _{\rho _a, \rho _b} {\mathcal {M}}(\rho _a^\prime , \rho _b^\prime )\)
Full size table

5 Results and discussion

The quantumness of two arbitrary states \(\rho \) and \(\sigma \) can be identified with their incompatibility and quantified by \(\mu = \max _{\rho , \sigma } {\mathcal {M}}(\rho , \sigma )\) as defined in Sect. 2. For a mixed initial diagonal state \(\rho _0 = \sum _{i} \lambda _i | i \rangle \langle i |\), which evolves to \(\rho _t\) under some dynamics, the following inequality holds [43]

$$\begin{aligned} \frac{{\mathcal {M}}(\rho _0, \rho _t) }{4} \le F(\rho _0, \rho _t) \le \frac{C_{l_1}(\rho _0, \rho _t)}{2}. \end{aligned}$$
(21)

Here, \(F(\rho _0, \rho _t)\) is the quantum Fisher information and \(C_{l_1}(\rho _0, \rho _t)\) is the \(l_1\)-norm coherence of \(\rho _t\), defined as \(\sum _{i\ne j} |\rho _t^{ij}|\); both well known measures of quantumness. The commutator-based measure provides a lower bound and a reliable witness of quantumness.

In this work, we extend the approach of quantifying the quantumness of states, in terms of their incompatibility, to explore the quantumness of channels. This method involves starting with two states which are maximally non-commuting and subjecting them to a quantum channel. The incompatibility of the resulting output states can be attributed to the degree of quantumness of the channel. We have computed the quantumness of various well-known channels and compared them with the analogous estimation of quantumness from a coherence based measure [27]. These are listed in Table 1. Specifically, we investigated the quantumness of the dephasing channels such as RTN, non-Markovian dephasing (NMD), phase damping (PD), and Unruh channels. These channels model the phenomenon of decoherence without dissipation. The dissipative channels considered here are amplitude damping (AD) and generalized amplitude damping (GAD) channels. The quantumness is given in terms of the channel parameters. In particular, for the channels with memory, the quantumness turns out to be a function of the memory kernel, which, in turn, decides the Markovian and non-Markovian nature of the dynamics. As reported in [28], the non-Markovian dynamics helps to sustain the quantumness over longer time as compared to Markovian case. It is interesting to note that quantumness from the proposed measure is in good agreement with that with the coherence-based measure [28]. This is consistent with our intuition as coherence is related to the off-diagonal elements of the density matrix as would be the cause for noncommutativity between the states. It should be noted that in the case of GDC, the coherence-based measure leads to quantumness \((p_0 -p_1)^2 + (p_2 - p_3)^2\), different from that obtained by the commutation-based measure adapted here. This is consistent with Eq. (21).

The attractive feature here is that the measure proposed can be calculated easily and is also amenable to experimental determination. Further, from the cases of the RTN and NMD channels, it is evident that quantumness reflects the non-Markovian nature of the channel under consideration.

6 Conclusion

The quantum channels provide a way to describe the processes where pure states go over to mixed ones. Therefore, it is natural to ask how well a quantum channel preserves the quantumness of the states which are subjected to it. Recently, a measure based on the \(l_1\)-norm coherence was introduced to quantify the quantumness of channels. In this work, we have addressed the problem by using an intuitive approach based on the incompatibility of the states. The quantumness of a system is identified with the mutual non-commutation of all its accessible states. We illustrated the approach developed here by considering various examples of quantum channels, both Markovian and as non-Markovian, and found that our results are in good agreement with the coherence-based measure. An added attraction of this method is that it is easy to compute and can be probed experimentally.