Precision localization of single atom via spontaneous emission in three dimensions

Abstract

We present a new scheme for high-efficiency three-dimensional (3D) atom localization in a three-level atomic system via spontaneous emission. Owing to the space-dependent atom–field interaction, the position probability distribution of the atom can be directly determined by measuring the spontaneous emission. It is found that, by properly varying the parameters of the system, the probability of finding the atom at a particular position can be almost 100 %. Our scheme opens a promising way to achieve high-precision and high-efficiency 3D atom localization, which provides some potential applications to spatially selective single-qubit phase gate, entangling gates, and quantum error correction for quantum information processing.

1 Introduction

In the past few years, the precision position measurement of an atom has been the subject of many recent studies because of its potential applications in laser cooling and trapping of neutral atoms [1], atom nano-lithography [2], Bose–Einstein condensation [3], and quantum information science [4]. In some pioneering works, Thomas and colleagues have suggested and experimentally demonstrated subwavelength position localization of atoms using spatially varying energy shifts [5, 6]. Walls and coworkers have discussed subwavelength atom localization using the measurement of the phase shift [7] after the passage of the atom through an off-resonant standing-wave field.

On the other hand, it is well known that atomic coherence can give rise to some interesting phenomena [8–12]. Based on atomic coherence, a variety of schemes for the precise localization of the atom in one dimension have been proposed. For example, Paspalakis and Knight proposed a quantum-interference-induced subwavelength atomic localization, a three-level $\Lambda$-type atom, and they found that the atomic position with high precision can be achieved via the measurement of the upper-state population of the atom [13]. Zubairy and coworkers have discussed atom localization using resonance fluorescence and phase and amplitude control of the absorption spectrum [14–16], and Agarwal and Kapale presented a scheme [17] based on coherent population trapping (CPT). Also, one-dimensional (1D) atom localization can be realized via dual measurement of the field and the atomic internal state [18], double-dark resonance effects [19], phase and amplitude control of the driving field [20, 21], coherent manipulation of the Raman gain process [22], or spontaneous emission [23, 24]. Recently, atom localization has been demonstrated in a proof-of-principle experiment using the technique of electromagnetically induced transparency (EIT) [25]. Apart from the above-mentioned 1D atom localization, some schemes have been put forward for two-dimensional (2D) atom localization by applying two orthogonal standing-wave laser fields. For instance, a scheme for 2D atom localization was proposed by Ivanov and Rozhdestvensky using the measurement of the population in the upper state or in any ground state in a four-level tripod system [26]. Subsequently, related 2D localization schemes [27–33] have been studied by Wan, Ding, Qamar, and their coworkers via controlled spontaneous emission, probe absorption and gain, and interacting double-dark resonances, and Raman-driven coherence. In addition, atom nano-lithography based on 2D atom localization has been achieved by Jin et al. in [34].

More recently, two schemes [35, 36] have also been discussed about the three-dimensional (3D) atom localization in five-level and four-level atomic systems, respectively. However, to the best of our knowledge, the maximum probability of finding an atom at a particular position in a wavelength domain is very low in these schemes; see, e.g., in the recent work [34], the maximum probability of finding an atom at a particular position in a wavelength domain is 1/8. In order to deal with the above problem, here we put forward a scheme to realize efficient 3D atom localization based on the measurement of spontaneous emission in a three-level atomic system. The work is mainly based on [35, 36]; however, our scheme shows more advantages that the two schemes do not have. First, we show that efficient 3D localization is realistically possible with only three atomic levels, and that one obtains interesting patterns around points of localization by a simple tuning of the parameters of the system. Second, owing to the space-dependent atom–field interaction, the atom can be localized at a particular position, and the maximal probability of finding the atom in one period of the standing-wave fields reaches 100 %, which is the main advantage compared with the previous schemes [35, 36]. Third, we can improve the localization precision and spatial resolution of the atom under certain conditions, which provide a possibility of making the atom localized at a given position by varying the system parameters in 3D space.

2 The model and dynamic equations

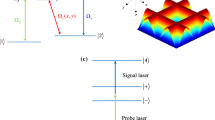
We consider a three-level atomic system as shown in Fig. 1a, which has one ground state $\left| 0\right\rangle$, and two excited states $\left| 1\right\rangle$ and $\left| 2\right\rangle$. The transition from the $\left| 1\right\rangle$ to $\left| 0\right\rangle$ is assumed to be coupled by the vacuum modes in the free space, while a composite field E with Rabi frequency $2\varOmega$ is applied to couple transition $\left| 1\right\rangle \leftrightarrow \left| 2\right\rangle$. In our scheme, the composite field E is the superposition of a controlling field $\varOmega _{c}$ and three standing waves with the same frequency, and its Rabi frequency is

$$\begin{aligned} 2\varOmega =2\varOmega _{1}\sin (kx)+2\varOmega _{2}\sin (ky)+2\varOmega _{3}\sin (kz)+2\varOmega _{c}. \end{aligned}$$

(1)

We assume that the center-of-mass position of the atom is nearly constant along the directions of the laser waves and neglect the kinetic part of the atom from the Hamiltonian in the Raman–Nath approximation. Then, under electric–dipole and rotating-wave approximations, the Hamiltonian for the system can be written as

$$\begin{aligned} H=\varOmega [\exp (i\varDelta t)\left| 2\right\rangle \left\langle 1\right| +H.c.]+\sum _{m}[g_{m}\exp (i\delta _{m}t)\left| 1\right\rangle \left\langle 0\right| b_{m}+H.c.], \end{aligned}$$

(2)

where $\varDelta =\omega _{21}-\omega$ and $\delta _{m}=\omega _{10}-\omega _{m}$ are the detunings of the composite field and the vacuum mode, respectively. $b_{m}$ is the annihilation operator for the mth vacuum mode with frequency $\omega _{m}$. $g_{m}$ stands for the coupling constant between the mth vacuum mode and the atomic transition $\left| 1\right\rangle \leftrightarrow \left| 0\right\rangle$.

Fig. 1

Schematic diagram of a three-level atomic system

The dynamics of this system can be described by using the probability amplitude equations. Then, the wave function of the system at time t can be expressed in terms of the state vectors as

$$\begin{aligned} \left| \Psi (t)\right\rangle =&\int \mathrm{d}x\mathrm{d}y\mathrm{d}zf(x,y,z)\left| x\right\rangle \left| y\right\rangle \left| z\right\rangle \left[ A_{1,0_{m}}(x,y,z;t)\left| 1,0_{m}\right\rangle \nonumber \right. \\&\left. + A_{2,0_{m}}(x,y,z;t)\left| 2,0_{m}\right\rangle +\sum _{m}A_{0,1_{m}}(x,y,z;t)\left| 0,1_{m}\right\rangle \right] , \end{aligned}$$

(3)

where the probability amplitude $A_{i,0_{m}}(x,y,z;t)$ $(i=1,2)$ represents the state of atom at time t when there is no spontaneously emitted photon in the mth vacuum mode, $A_{0,1_{m}}(x,y,z;t)$ is the probability amplitude that the atom is in level $\left| 0\right\rangle$ with one photon emitted spontaneously in the mth vacuum mode, and f(x, y, z) is the center-of-mass wave function of the atom.

The atom localization in our scheme is based on the fact that the spontaneously emitted photon carries information about the position of atom in 3D space as a result of the spatial position-dependent atom–field interaction. When we have detected at time t a spontaneously emitted photon in the vacuum mode of wave vector m, the atom is in its internal state $\left| 0\right\rangle$ and the state vector of the system, after making appropriate projection over $\left| \Psi (t)\right\rangle$, is reduced to

$$\begin{aligned} \left| \psi _{0,1_{m}}\right\rangle = \mathbb {N} \left\langle 0,1_{m}|\Psi (t)\right\rangle = \mathbb {N} \int \mathrm{d}x\mathrm{d}y\mathrm{d}zf(x,y,z)A_{0,1_{m}}(x,y,z;t)\left| x\right\rangle \left| y\right\rangle \left| z\right\rangle , \end{aligned}$$

(4)

where $\mathbb {N}$ is a normalization factor. Thus, the conditional position probability distribution, i.e., the probability of finding the atom in the (x, y) position at time t, is

$$\begin{aligned} W(x,y,z;t|0,1_{m})=\left| \mathbb {N} \right| ^{2}\left| \left\langle x\right| \left\langle y\right| \left\langle z|\psi _{0,1_{m}}\right\rangle \right| ^{2}=\left| \mathbb {N} \right| ^{2}\left| f(x,y,z)\right| ^{2}\left| A_{0,1_{m}}(x,y,z;t)\right| ^{2}, \end{aligned}$$

(5)

which follows from the probability amplitude $A_{0,1_{m}}(x,y,z;t)$.

We now derive an analytical expression for the probability amplitude $A_{0,1_{m}}(x,y,z;t)$ by solving the time-dependent Schrödinger wave equation $i\left| \dot{\Psi }(t)\right\rangle =H\left| \Psi (t)\right\rangle$ with the interaction Hamiltonian [Eq. (2)] and the atom–field state vector [Eq. (3)]. With the Weisskopf–Wigner theory, the dynamical equations for the atomic probability amplitudes are given by

$$\begin{aligned} i\frac{\partial A_{1,0_{m}}(x,y,z;t)}{\partial t}&=-i\frac{\varGamma }{2} A_{1,0_{m}}(x,y,z;t)+\varOmega \exp (-i\varDelta t)A_{2,0_{m}}(x,y,z;t), \end{aligned}$$

(6)

$$\begin{aligned} i\frac{\partial A_{2,0_{m}}(x,y,z;t)}{\partial t}&=\varOmega \exp (i\varDelta t)A_{1,0_{m}}(x,y,z;t), \end{aligned}$$

(7)

$$\begin{aligned} i\frac{\partial A_{0,1_{m}}(x,y,z;t)}{\partial t}&=g_{m}^{*}\exp (-i\delta _{m}t)A_{3,0_{m}}(x,y,z;t), \end{aligned}$$

(8)

where $\varGamma =2\pi |g_{m}|^{2}D(\omega _{m})$ is the spontaneous decay rate from level $\left| 1\right\rangle$ to level $\left| 0\right\rangle$, and $D(\omega _{m})$ is the density of mode at frequency $\omega _{m}$ in the vacuum.

By utilizing the Laplace transformation $\tilde{A}(x,y,z;s)=\int _{0}^{\infty }\exp (-st)A(x,y,z;t)\mathrm{d}t$ (s is the time Laplace transform variable) and the final value theorem, we obtain the probability amplitude $A_{0,1_{m}}(x,y,z;t)$ in the long time limit, i.e., $\varGamma t>>1$, as

$$\begin{aligned} A_{0,1_{m}}(x,y,z;t\rightarrow & {} \infty )=-ig_{m}^{*}\tilde{A} _{0,1_{m}}(s=-i\delta _{m}) \nonumber \\= & {} g_{m}^{*}\frac{\varDelta +\delta _{m}}{\varOmega ^{2}-\delta _{m}^{2}-\varDelta \delta _{m}+i\frac{\varGamma }{2}(\varDelta +\delta _{m})}, \end{aligned}$$

(9)

where $\tilde{A}_{0,1_{m}}(s=-i\delta _{m})$ is the Laplace transformation of $A_{0,1_{m}}(x,y,z;t)$ with $s=-i\delta _{m}$. Finally, the conditional probability of finding the atom in level $\left| 0\right\rangle$ with a spontaneously emitted photon of frequency $\omega _{m}$ in the vacuum mode m is then given by

$$\begin{aligned} W(x,y,z;t&\rightarrow \infty |0,1_{m})=\left| \mathbb {N} \right| ^{2}\left| f(x,y,z)\right| ^{2}\left| A_{0,1_{m}}(x,y,z;t\rightarrow \infty )\right| ^{2} \nonumber \\&=\left| \mathbb {N} \right| ^{2}\left| f(x,y,z)\right| ^{2}\left| g_{m}\right| ^{2}\left| \tilde{A}_{0,1_{m}}(x,y,z;s=-i\delta _{m})\right| ^{2} \nonumber \\&=\left| \mathbb {N} \right| ^{2}\left| f(x,y,z)\right| ^{2}\left| g_{m}\right| ^{2}\times \frac{(\varDelta +\delta _{m})^{2}}{(\varOmega ^{2}-\delta _{m}^{2}-\varDelta \delta _{m})^{2}+\frac{\varGamma ^{2}}{4}(\varDelta +\delta _{m})^{2}}\text {.} \end{aligned}$$

(10)

As the center-of-mass wave function of the atom f(x, y, z) is assumed to be nearly constant over many wavelengths of the standing-wave fields, the conditional position probability distribution $W(x,y,z;t\rightarrow \infty |0,1_{m})$ is determined by the filter function defined as

$$\begin{aligned} F(x,y,z)=\frac{(\varDelta +\delta _{m})^{2}}{(\varOmega ^{2}-\delta _{m}^{2}-\varDelta \delta _{m})^{2}+\frac{\varGamma ^{2}}{4}(\varDelta +\delta _{m})^{2}}\text {.} \end{aligned}$$

(11)

3 Results

In this section, we analyze the conditional position probability distribution of the atom via a few numerical calculations based on the filter function F(x, y, z) in the Eq. (11) and then address how the system parameters can be used to achieve 3D atom localization by measuring spontaneous emission. In the following numerical calculations, the spontaneous decay rate from level $\left| 1\right\rangle$ to level $\left| 0\right\rangle$ is set as $\varGamma =2\gamma$. All the parameters used in this paper are in units of $\gamma$, which should be in the order of MHz for rubidium atoms.

The isosurfaces for the filter function $F(x,y,z)=0.1$ versus positions $(-1\leqslant kx/\pi \leqslant 1$, $-1\leqslant ky/\pi \leqslant 1$, $-1\leqslant kz/\pi \leqslant 1$) for different values of the detuning of spontaneously emitted photon are plotted in Fig. 2. When the $\delta _{m}=10\gamma$, it can be seen that the filter function F(x, y, z) exhibits two big spheres in the subspaces ($-1\leqslant kx/\pi \leqslant 0$, $-1\leqslant ky/\pi \leqslant 0$, $-1\leqslant kz/\pi \leqslant 0$) and ($0\leqslant kx/\pi \leqslant 1$, $0\leqslant ky/\pi \leqslant 1$, $0\leqslant kz/\pi \leqslant 1$), respectively, as shown in Fig. 2a. For the case that $\delta _{m}=12\gamma$, the filter function F(x, y, z) is also situated in two subspaces of the 3D space (see Fig. 2b), but the volume of sphere in each subspace becomes small. Furthermore, when the detuning is detected at an appropriate value (i.e., $\delta _{m}=13\gamma$ in Fig. 2c or $\delta _{m}=13.5\gamma$ in Fig. 2d), the volume of sphere in each subspace becomes more and more small. In such a case, we can achieve high-precision and high-resolution 3D atom localization by measuring the frequency of the spontaneously emitted photon under corresponding conditions.

Fig. 2

Isosurfaces for the filter function $F(x,y,z)=0.1$ versus positions $(-1\leqslant kx/\pi \leqslant 1$, $-1\leqslant ky/\pi \leqslant 1$, $-1\leqslant kz/\pi \leqslant 1$) for different values of $\delta _{m}$. a $\delta _{m}=10\gamma$, b $\delta _{m}=12\gamma$, c $\delta _{m}=13\gamma$ and d $\delta _{m}=13.5\gamma$. The other parameters are $\varDelta =0$, $\varOmega _{1}=\varOmega _{2}=\varOmega _{3}=4\gamma$, $\varOmega _{c}=0$, and $\varGamma =2\gamma$

In order to understand the physical mechanisms of the above results in Fig. 2, we will turn our attention to the dressed-state picture, generated by the composite field E, namely the $\left| 1\right\rangle \rightarrow \left| 2\right\rangle$ transition together with the composite field are treated as a whole “atom + field” system and the energy levels of the dressed states as shown in Fig. 1b. It is obvious that the bare-state level $\left| 1\right\rangle$ should be split into two dressed-state sublevels $\left| +\right\rangle$ and $\left| -\right\rangle$. The energy eigenvalues of the two dressed states read

$$\begin{aligned} \epsilon _{\pm }=\frac{1}{2}(\varDelta \pm \sqrt{4\varOmega ^{2}+\varDelta ^{2}}) \text {.} \end{aligned}$$

(12)

The corresponding energy eigenstates are written as

$$\begin{aligned} \left| +\right\rangle&=\sin \theta \left| 2\right\rangle +\cos \theta \left| 1\right\rangle , \end{aligned}$$

(13)

$$\begin{aligned} \left| -\right\rangle&=-\cos \theta \left| 2\right\rangle +\sin \theta \left| 1\right\rangle , \end{aligned}$$

(14)

with $\sin \theta =\epsilon _{+}/\sqrt{\varOmega ^{2}+\epsilon _{+}^{2} }$ and $\cos \theta =-\epsilon _{-}/\sqrt{\varOmega ^{2}+\epsilon _{-}^{2}}$.

From Eqs. 13 and 14, it is straightforward to show that there exists quantum interference between two different spontaneous emission pathways (see Fig. 1b) $\left| +\right\rangle \leftrightarrow \left| 0\right\rangle$ and $\left| -\right\rangle \leftrightarrow \left| 0\right\rangle$. Quantum interference among these two pathways results in the spectral-line narrowing and the quenching of spontaneous emission. Consequently, we can observe different localization structures in the 3D space in Fig. 2.

In Fig. 3, we study the effect of the intensity of the controlling field $\varOmega _{c}$ on the 3D atom localization. In the case of $\varOmega _{c}=0.2\gamma$, the maxima of the filter function are distributed in the subspaces ($-1\leqslant kx/\pi \leqslant 0$, $-1\leqslant ky/\pi \leqslant 0$, $-1\leqslant kz/\pi \leqslant 0$) and ($0\leqslant kx/\pi \leqslant 1$, $0\leqslant ky/\pi \leqslant 1$, $0\leqslant kz/\pi \leqslant 1$) with different localization precisions, in which the filter function in the subspace ($-1\leqslant kx/\pi \leqslant 0$, $-1\leqslant ky/\pi \leqslant 0$, $-1\leqslant kz/\pi \leqslant 0$) displays a small-diameter sphere-like pattern with a high precision, and the filter function in the subspace ($0\leqslant kx/\pi \leqslant 1$, $0\leqslant ky/\pi \leqslant 1$, $0\leqslant kz/\pi \leqslant 1$) exhibits a large-diameter sphere-like pattern with a low precision, which leads to the localization of the atom at these spheres (see Fig. 3a). Under the condition of $\varOmega _{c}=0.5\gamma$, as shown in Fig. 3b, it is easy to see that the volume of sphere in the subspace ($-1\leqslant kx/\pi \leqslant 0$, $-1\leqslant ky/\pi \leqslant 0$, $-1\leqslant kz/\pi \leqslant 0$) becomes small, while the sphere in the subspace ($0\leqslant kx/\pi \leqslant 1$, $0\leqslant ky/\pi \leqslant 1$, $0\leqslant kz/\pi \leqslant 1$) becomes big. Most interestingly, as we further increase the coupling field $\varOmega _{c}$ to $\gamma$, the sphere ( $-1\leqslant kx/\pi \leqslant 0$, $-1\leqslant ky/\pi \leqslant 0$, $-1\leqslant kz/\pi \leqslant 0$) is completely disappeared, and the maxima of the filter function only situated in the subspace ($0\leqslant kx/\pi \leqslant 1$, $0\leqslant ky/\pi \leqslant 1$, $0\leqslant kz/\pi \leqslant 1$) with a sphere-like pattern (see Fig. 3c). In such a condition, the probability of finding the atom in one period of the standing-wave fields is increased to 100 %, that is to say, the atom can be localized at a particular position and the 3D atom localization is indeed achieved efficiently. This is a significant advantage of our proposed scheme. Of course, on the condition of $\varOmega _{c}=3\gamma$, the sphere in the subspace ($0\leqslant kx/\pi \leqslant 1$, $0\leqslant ky/\pi \leqslant 1$, $0\leqslant kz/\pi \leqslant 1$) becomes bigger (see Fig. 3d), which implies that the increasing controlling field will bring a destructive effect to the precision of 3D atom localization when large detuning of spontaneously emitted photon is considered.

Fig. 3

Isosurfaces for the filter function $F(x,y,z)=0.1$ versus positions $(-1\leqslant kx/\pi \leqslant 1$, $-1\leqslant ky/\pi \leqslant 1$ , $-1\leqslant kz/\pi \leqslant 1$) for different intensities of the controlling field. a $\varOmega _{c}=0.2\gamma$, b $\varOmega _{c}=0.5\gamma$, c $\varOmega _{c}=\gamma$ and d $\varOmega _{c}=3\gamma$. The other parameters are $\varDelta =0$, $\delta _{m}=13\gamma$, $\varOmega _{1}=\varOmega _{2}=\varOmega _{3}=4\gamma$, and $\varGamma =2\gamma$

Finally, a new way for realizing the efficient 3D atom localization is shown in Fig. 4. Here, we investigate the influence of detuning $\varDelta$ on the 3D atom localization when small intensity of the controlling field $\varOmega _{c}$ is considered. For the detuning $\varDelta$, i.e., $\varDelta =-3.5\gamma$ or $-2\gamma$ , the filter function F(x, y, z) exhibits two big spheres in the subspaces ($-1\leqslant kx/\pi \leqslant 0$, $-1\leqslant ky/\pi \leqslant 0$, $-1\leqslant kz/\pi \leqslant 0$) and ($0\leqslant kx/\pi \leqslant 1$, $0\leqslant ky/\pi \leqslant 1$, $0\leqslant kz/\pi \leqslant 1$), respectively, as shown in Fig. 4a, b. In the case that $\varDelta =2\gamma$, the filter function F(x, y, z) is also situated in two subspaces with different localization precision (see Fig. 4c), and the volume of sphere in each subspace becomes small. Interestingly, when the detuning $\varDelta$ is increased to $\varDelta =3.8\gamma$, the atom is localized in only the subspace ($0\leqslant kx/\pi \leqslant 1$, $0\leqslant ky/\pi \leqslant 1$, $0\leqslant kz/\pi \leqslant 1$ ), and the position information of the atom in the 3D space is clear (see Fig. 4d). Obviously, the precision of 3D atom localization can be enhanced via the detuning $\varDelta$. In fact, in the presence of the strong perturbation of the controlling field, quantum interference among these two pathways bring a constructive effect to the precision of 3D atom localization. Therefore, this fact can be exploited to atom localization in three dimensions.

Fig. 4

Isosurfaces for the filter function $F(x,y,z)=0.1$ versus positions $(-1\leqslant kx/\pi \leqslant 1$, $-1\leqslant ky/\pi \leqslant 1$, $-1\leqslant kz/\pi \leqslant 1$) for different values of $\varDelta$. a $\varDelta =-3.5\gamma$, b $\varDelta =-2\gamma$, c $\varDelta =2\gamma$ and d $\varDelta =3.8\gamma$. The other parameters are $\varOmega _{c}=0.2\gamma$, $\delta _{m}=12\gamma$, $\varOmega _{1}=\varOmega _{2}=\varOmega _{3}=4\gamma$, and $\varGamma =2\gamma$

4 Conclusions

To sum up, we have investigated the three-dimensional atom localization via spontaneous emission in a three-level atomic system. It is found that the precision and resolution of the 3D atom localization can be significantly improved due to the space-dependent atom–field interaction. More importantly, the 3D atom localization patterns reveal that the maximal probability of finding an atom within the sub-half-wavelength domain of the standing waves can reach 100 %, which is increased by a factor of 4 or 8 compared with the previous proposed schemes [35, 36]. As a result, our scheme may be helpful in realizing spatially selective single-qubit phase gate, entangling gates between cold atoms, and error budget for the single-qubit phase gate in three dimensions.