Decoherence dynamics of geometric measure of quantum discord and measurement induced nonlocality for noninertial observers at finite temperature

Abstract

Quantum discord quantifies the total non-classical correlations in mixed states. It is the difference between total correlation, measured by quantum mutual information, and the classical correlation. Another step forward towards the quantification of quantum discord was by Dakić et al. (Phys Rev Lett 105:190502, 2010) who introduced the geometric measure of quantum discord (GMQD) and derived an explicit formula for a two-qubit state. Recently, Luo and Fu (Phys Rev Lett 106:120401, 2011) introduced measurement-induced nonlocality (MIN) as a measure of nonlocality for a bipartite quantum system. The dynamics of GMQD is recently considered by Song et al. (arXiv: quant/ph.1203.3356) and Zhang et al. (Eur Phys J D 66:34, 2012) for inertial observers. However, the topic requires due attention in noninertial frames, particularly, from the perspective of MIN. Here I consider $X$-structured bipartite quantum system in noninertial frames and analyze the decoherence dynamics of GMQD and MIN at finite temperature. The dynamics under the influence of amplitude damping, depolarizing and phase flip channels is discussed. It is worth-noting that initial state entanglement plays an important role in bipartite states. It is possible to distinguish the Bell, Werner and general type initial quantum states using GMQD. Sudden transition in the behaviour of GMQD and MIN occurs depending upon the mean photon number of the local environment. The transition behaviour disappears for larger values of $\bar{n},$ i.e. $\bar{n}>0.3.$ It becomes more prominent, when environmental noise is introduced in the system. In the presence of environmental noise, as we increase the value of acceleration $r$, GMQD and MIN decay due to Unruh effect. The effect is prominent for the phase flip and amplitude damping channels. However, in case of depolarizing channel, no sudden change in the behaviour of GMQD and MIN is observed. The environmental noise has stronger affect on the dynamics of GMQD and MIN as compared to the Unruh effect. Furthermore, Werner like states are more robust than General type initial states at finite temperature.

1 Introduction

Quantum entanglement, a special quantum correlation, has attracted considerable attention during recent years because many quantum information processes depend on entanglement [1]. Main difficulty with entanglement is its quantification. Different entanglement measures have been proposed [2, 3]. Quantum correlation, one of the key features in quantum information theory, has become an important tool to study quantum many-body systems, for example, quantum phase transition in different correlated systems. However, the quantitative and qualitative evaluation of such correlations remains an open problem. So far, several quantifiers of non-classicality of correlations have been introduced in literature [4–10], but still there is no clear criteria for the faithfulness of them. Moreover, for the multipartite states, the geometric measure of entanglement (GME) has been proposed [11–16]. The topic attracted due respect in short span of time and bounds on several entanglement measures like von Neumann Entropy [17], Negativity [18], Concurrence [19] and GME [20, 21] were obtained.

Recent investigations reveal that there exist quantum correlations other than entanglement. Quantum discord [22, 23] quantifies the total non-classical correlations in a quantum state. It was suggested that the quantum discord, rather than entanglement, is responsible for the efficiency of a quantum computer, which is confirmed both theoretically [24] and experimentally [25]. A systematical analysis of quantum and classical correlations for bipartite and multipartite quantum systems have been proposed by Okrasa and Walczak [26]. Quantum discord for the subclass of so-called $X$-states [27–30], a qubit-qutrit [31] and qubit-qudit [32] systems have also been proposed. Huang et al. [33] have proposed a new criterion for judging zero quantum discord for arbitrary bipartite states. Yao et al. [34] have proposed the geometric interpretation of the geometric discord. The dynamics of quantum discord for a two-qubit system in a quantum spin environment have been proposed by Guo et al. [35]. Recently, discord for multipartite quantum states has been investigated [36, 37] and its dynamics under decoherence [38].

However, the quantum discord for a general two qubit state remains a nontrivial task and only the lower and upper bounds were investigated [39, 40]. Motivated from the difficultly in computing the quantum discord, the geometric measure of quantum discord (GMQD) was proposed [6], which quantifies the amount of non-classical correlations of a state in terms of its minimal distance from the set of genuinely classical states. It can be defined as the nearest distance between the given state and the set of zero-discord states. Recently, Luo and Fu [41, 42] have introduced a geometric measure of nonlocality which they termed as measurement-induced nonlocality (MIN). It can be defined as the maximum distance between the bipartite state and its post-measurement state, where the maximum is taken over all the von Neumann local measurements which do not disturb the local state. Recent investigations in this direction includes [43–60], where the behaviour of the dynamics of the system is discussed under different scenarios. Furthermore, the dynamics of entanglement at zero and finite temperature has been studied by many authors, for example [61–63].

The most difficult problem in realizing the quantum information technology is that the quantum system can never be isolated from the surrounding environment completely. Interactions with the environment deteriorate the purity of the quantum states. This general phenomenon, known as decoherence [64], is a serious obstacle against the preservation of quantum super-positions over long periods of time. Decoherence entails non-unitary evolutions, with serious consequences, like a loss of information and probable leakage toward the environment. Therefore, in a realistic and practical situation, decoherence caused by an external environment is inevitable and the influence of an external environmental system on the entanglement cannot be ignored. However in some cases it can create quantum correlations in the system [65]. Understanding the dynamics of open quantum systems is of considerable importance. The Schrodinger equation, which describes the evolution of closed systems, is generally inapplicable to open systems, unless one includes the environment in the description. This is, however, generally difficult, due to the large number of environment degrees of freedom. An alternative is to develop a description for the evolution of only the subsystem of interest. Much attention has been given to the phenomenon of decoherence that causes an irreversible transfer of information from the system to the environment [66, 67] with the special attention to the degradation of entanglement [68–73]. On the other hand, the behaviour of entanglement in noninertial frames was investigated for the first time by Alsing et al. [74]. The subject have attracted much attention during recent years [75–93]. It has also been investigated under decoherence for qubit-qubit [94–97], qubit-qutrit system [98] and multipartite systems [99]. The entanglement dynamics for noninertial observers in a correlated environment is considered in Ref. [100], where it is shown that correlated noise compensates the loss of entanglement caused by the Unruh effect. Recently, Oliveira et al. [101] have studied the entanglement measure for pure six-qubit quantum states. Whereas Zehua and Jiliang [102] have studied how the Unruh effect affects the transition between classical and quantum decoherence for a general class of initial states.

In this paper, I have investigated the decoherence dynamics of geometric measure of quantum discord and measurement-induced nonlocality at finite temperature for $X$-type initial states in relativistic frames. The two observers Alice and Bob share an $X$-type state in noninertial frames. Alice is considered to be stationary whereas Bob moves with a uniform acceleration $r$. It is shown that initial state entanglement plays an important role in bipartite quantum states. Different decoherence channels are considered parameterized by decoherence parameter $p$ such that $p\in [0,1]$. The lower and upper limits of decoherence parameter represent the fully coherent and fully decohered system, respectively. Whereas, the lower and upper limits of parameter $X$ correspond to $t=\infty , \,0$, respectively. It is seen that different initial states can be distinguished using GMQD such as the Bell diagonal, Werner and general type initial states. It is also seen that the depolarizing channels heavily influences the dynamics of GMQD and MIN as compared to the amplitude damping channel. Furthermore, no GMQD and MIN sudden death is seen at finite temperature even in the presence of decoherence.

2 Decoherence dynamics of accelerated observers

The evolution of a system and its environment can be described by

$$\begin{aligned} U_{SE}(\rho _{S}\otimes |0\rangle _{E}\left\langle 0\right| )U_{SE}^{\dag } \end{aligned}$$

(1)

where $U_{SE}$ represents the evolution operator for the combined system and $|0\rangle _{E}$ corresponds to the initial state of the environment. By taking trace over the environmental degrees of freedom, the evolution of the system can be obtained as

$$\begin{aligned} L(\rho _{S})&= \text{ Tr }_{E}\{U_{SE}(\rho _{S}\otimes |0\rangle _{E}\left\langle 0\right| )U_{SE}^{\dag }\} \nonumber \\&= \sum \nolimits _{\mu }\ _{E}\left\langle \mu \right| U_{SE}|0\rangle _{E}\rho _{SE}\left\langle 0\right| )U_{SE}^{\dag }|\mu \rangle _{E} \end{aligned}$$

(2)

where $|\mu \rangle _{E}$ represents the orthogonal basis of the environment and $L$ is the operator describing the evolution of the system. The above equation can also be written as

$$\begin{aligned} L(\rho _{S})=\sum \nolimits _{\mu }M_{\mu }\rho _{S}M_{\mu }^{\dag } \end{aligned}$$

(3)

where $M_{\mu }=\ _{E}\left\langle \mu \right| U_{SE}|0\rangle _{E}$ are the Kraus operators as given in Ref. [103]. The Kraus operators satisfy the completeness relation

$$\begin{aligned} \sum \nolimits _{\mu }M_{\mu }^{\dag }M_{\mu }=1 \end{aligned}$$

(4)

The decoherence process can also be represented by a map in terms of the complete system-environment state. The dynamics of a $d$-dimensional quantum system can be represented by the following map [104]

$$\begin{aligned} U_{SE}|\xi _{l}\rangle _{S}\otimes |0\rangle _{E}=\sum \nolimits _{k}M_{k}|\xi _{l}\rangle _{S}\otimes |k\rangle _{E} \end{aligned}$$

(5)

where $\{|\xi _{l}\rangle _{S}\} \,(l=1,\ldots ,d)$ is the complete basis for the system and

$$\begin{aligned} |\xi _{1}\rangle _{S}\otimes |0\rangle _{E}&\rightarrow M_{0}|\xi _{1}\rangle _{S}\otimes |0\rangle _{E}+\cdots +M_{d^{2}-1}|\xi _{1}\rangle _{S}\otimes |d^{2}-1\rangle _{E} \nonumber \\ |\xi _{2}\rangle _{S}\otimes |0\rangle _{E}&\rightarrow M_{0}|\xi _{2}\rangle _{S}\otimes |0\rangle _{E}+\cdots +M_{d^{2}-1}|\xi _{2}\rangle _{S}\otimes |d^{2}-1\rangle _{E} \nonumber \\ \cdot&\nonumber \\ \cdot&\nonumber \\ \cdot&\nonumber \\ |\xi _{d}\rangle _{S}\otimes |0\rangle _{E}&\rightarrow M_{0}|\xi _{d}\rangle _{S}\otimes |0\rangle _{E}+\cdots +M_{d^{2}-1}|\xi _{d}\rangle _{S}\otimes |d^{2}-1\rangle _{E} \end{aligned}$$

(6)

Let Alice and Bob (the accelerated observer) share the following $X$-type initial state [105]

$$\begin{aligned} \rho _{AB}=\frac{1}{4}\left( I_{AB}+\sum \limits _{i=1}^{3}c_{i}\sigma _{i}^{(A)}\otimes \sigma _{i}^{(B)}\right) \end{aligned}$$

(7)

where $I_{AB}$ is the identity operator in a two-qubit Hilbert space, $\sigma _{i}^{(A)}$ and $\sigma _{i}^{(B)}$ are the Pauli operators of the Alice’s and Bob’s qubit and $c_{i} \,(0\le |c_{i}|\le 1)$ are real numbers satisfying the unit trace and positivity conditions of the density operator $\rho _{AB}.$ In order to study the entanglement dynamics, different cases for initial state are considered, for example, the general initial state $(|c_{1}|=0.7,|c_{2}|=0.9,|c_{3}|=0.4)$, the Werner initial state $(|c_{1}|=|c_{2}|=|c_{3}|=0.8)$, and Bell basis state $(|c_{1}|=|c_{2}|=|c_{3}|=1)$.

Let the Dirac fields, as shown in Refs. [83, 84], from an inertial perspective, can be described by a superposition of Unruh monochromatic modes $|0_{U}\rangle =\otimes _{\omega }|0_{\omega }\rangle _{U}$ and $|1_{U}\rangle =\otimes _{\omega }|1_{\omega }\rangle _{U}$ with

$$\begin{aligned} |0_{\omega }\rangle _{U}=\cos r|0_{\omega }\rangle _{I}|0_{\omega }\rangle _{II}+\sin r|1_{\omega }\rangle _{I}|1_{\omega }\rangle _{II} \end{aligned}$$

(8)

and

$$\begin{aligned} |1_{\omega }\rangle _{M}=|1_{\omega }\rangle _{I}|0_{\omega }\rangle _{II} \end{aligned}$$

(9)

where $\cos r=(e^{-2\pi \omega c/a}+1)^{-1/2}, \,a$ is the acceleration of the observer, $\omega$ is frequency of the Dirac particle and $c$ is the speed of light in vacuum. The subscripts $I$ and $II$ of the kets represent the Rindler modes in region $I$ and $II$, respectively, as shown in the Rindler spacetime diagram (see Ref. [92], Fig. (1)). By using Eqs. (8) and (9), Eq. (7) can be re-written in terms of Minkowski modes for Alice ($A$) and Rindler modes for Bob $(\tilde{B})$. The single-mode approximation is used in this study, i.e. a plane wave Minkowski mode is assumed to be the same as a plane wave Unruh mode (superposition of Minkowski plane waves with single-mode transformation to Rindler modes). Therefore, Alice being an inertial observer while her partner Bob who is in uniform acceleration, are considered to carry their detectors sensitive to the $\omega$ mode. To study the entanglement in the state from their perspective one must transform the Unruh modes to Rindler modes. Hence, Unruh states must be transformed into the Rindler basis. Let Bob detects a single Unruh mode and Alice detects a monochromatic Minkowski mode of the Dirac field. Considering that an accelerated observer in Rindler region $I$ has no access to the field modes in the causally disconnected region $II$ and by taking the trace over the inaccessible modes, one obtains the following density matrix

$$\begin{aligned} \rho _{A\tilde{B}}&\!=\!&\frac{1}{4}\left( \begin{array}{l@{\quad }l@{\quad }l@{\quad }l} (1\!+\!c_{3})\cos ^{2}r &{}\quad 0 &{}0 &{}\quad c^{\!-\!}\cos r \\ 0 &{}\quad (1\!+\!c_{3})\sin ^{2}r+(1-c_{3}) &{} c^{\!+\!}\cos r &{}\quad 0 \\ 0 &{}\quad c^{\!+\!}\cos r &{} (1\!-\!c_{3})\cos ^{2}r &{}\quad 0 \\ c^{\!-\!}\cos r &{}\quad 0 &{}0 &{}\quad (1\!+\!c_{3})\!+\!(1\!-\!c_{3})\sin ^{2}r \end{array} \right) \end{aligned}$$

(10)

where $c^{+}=c_{1}+c_{2}$ and $c^{-}=c_{1}-c_{2}.$

Fig. 1

(Color online). Geometric measure of quantum discord (GMQD) and measurement-induced nonlocality (MIN) are plotted as a function of acceleration $r$ for Bell, Werner and General type initial states

Since noise is a major hurdle while transmitting quantum information from one party to other through classical and quantum channels. This noise causes a distortion of the information sent through the channel. It is considered that the system is strongly correlated quantum system, the correlation of which results from the memory of the channel itself. The action of a two qubit Pauli channel when both the qubits of Alice and Bob are streamed through it, can be described in operator sum representation as [1]

$$\begin{aligned} \rho _{f}=\sum \limits _{k_{1}, k_{2}=0}^{1}(A_{k_{2}}\otimes A_{k_{1}})\rho _{in}(A_{k_{1}}^{\dagger }\otimes A_{k_{2}}^{\dagger }) \end{aligned}$$

(11)

where $\rho _{in}$ represents the initial density matrix for quantum state and $A_{k_{i}}$ are the Kraus operators. A detailed list of single qubit Kraus operators for different quantum channels under consideration is given in Table 1. In order to quantify the quantum correlations, the dynamics of the system-environment interaction is investigated and only the reduced matrices are considered. It is assumed that both Alice and Bob’s qubits are influenced by the environment. The reduced-density matrix of the inertial subsystem $A$ and the noninertial subsystem $\tilde{B}$, can be obtained by taking the partial trace of $\rho _{A\tilde{B}E_{A}E_{\tilde{R}}}=\rho _{A \tilde{B}}\otimes \rho _{A\tilde{B}E_{A}E_{\tilde{B}}}$ over the degrees of freedom of the environment i.e.

$$\begin{aligned} \rho _{A\tilde{B}}=\text{ Tr }_{E_{A}E_{\tilde{B}}}\{\rho _{A\tilde{B}E_{A}E_{ \tilde{B}}}\}. \end{aligned}$$

(12)

Table 1 Single qubit Kraus operators for amplitude damping, depolarizing, and phase flip channels where $p$ represents the decoherence parameter.

3 GMQD and MIN at finite temperature

Let us consider a two-qubit system (two two-level atoms) is interacting with a thermal reservoir. Unlike the Ref. [103], where the authors studied the system at $T=0$, in the present scheme, the effect of heat is included. The dynamics of the density matrix $\hat{\rho }$ describing the two qubit system is given by [106]

$$\begin{aligned} \frac{d\rho }{dt}&= \frac{1}{2}(\bar{n}+1)\Gamma \sum \limits _{i=1}^{2}\left\{ \left[ \sigma _{-}^{i},\rho \sigma _{+}^{i}\right] +\left[ \sigma _{-}^{i}\rho , \sigma _{+}^{i}\right] \right\} \nonumber \\&\quad +\frac{1}{2}\bar{n}\Gamma \sum \limits _{i=1}^{2}\left\{ \left[ \sigma _{+}^{i},\rho \sigma _{-}^{i} \right] +\left[ \sigma _{+}^{i}\rho , \sigma _{-}^{i}\right] \right\} \end{aligned}$$

(13)

where $\Gamma$ is the spontaneous emission rate, $\sigma _{\pm }^{i} \, (i=1;2)$ are the rasing $(+)$ and lowering $(-)$ operators of atom $i$ defined as $\sigma _{+}^{i}=\left| 1\right\rangle \left\langle 0\right| _{i}, \,\sigma _{-}^{i}=\left| 0\right\rangle \left\langle 1\right| _{i}, \,\bar{n}$ is the mean occupation number of the reservoir (assumed to be the same for both qubits) that can be related to the parameter $X=\exp ^{-\Gamma (2\bar{n}+1)t}.$ Here, the quantity $X$ is the time-dependent parameter which can be used to monitor the evolution of GMQD and MIN for the the two-qubit system. Notice that at $t=0, \,X=1$, and that at $t=\infty , \,X=0$. Therefore, physically meaningful values for $X$ are between $0$ and $1$. On the right hand side of Eq. (13), the first term describes the depopulation of the atoms due to stimulated and spontaneous emission, while the second term corresponds to the re-excitations caused by the finite temperature. The final state of the system (for the initial state of the form Eq. (10)) keeps its $X$-form at any time during its evolution and leads to

$$\begin{aligned} \left[ \begin{array}{llll} \rho _{11}[t] &{}\quad 0 &{}\quad 0 &{}\quad \rho _{141}[t] \\ 0 &{}\quad \rho _{22}[t] &{}\quad \rho _{23}[t] &{}\quad 0 \\ 0 &{}\quad \rho _{32}[t] &{}\quad \rho _{33}[t] &{}\quad 0 \\ \rho _{41}[t] &{}\quad 0 &{}\quad 0 &{}\quad \rho _{44}[t] \end{array} \right] \end{aligned}$$

(14)

The master equation of the system, governed by the first-order coupled differential equations, can be solved to yield the expressions of the final density matrix as given in Appendix [107]. The quantum discord, a measure of the minimal loss of correlation in the sense of quantum mutual information, can be defined for a bipartite quantum state as [22]

$$\begin{aligned} D_{A}(\rho ):=\underset{\Pi ^{A}}{\min }\{I(\rho )-I(\rho |\Pi ^{A})\} \end{aligned}$$

(15)

where minimum is taken over all local von Neumann measurements $\Pi ^{A}.$

$$\begin{aligned} I(\rho ):=S(\rho _{A})+S(\rho _{B})-S(\rho ) \end{aligned}$$

(16)

can be interpreted as the quantum mutual information,

$$\begin{aligned} S(\rho ):=-\text{ Tr }(\rho \log \rho ) \end{aligned}$$

(17)

is the von Neumann entropy,

$$\begin{aligned} I(\rho |\Pi ^{A})&:&= S(\rho _{B})-S(\rho |\Pi ^{A}) \nonumber \\ S(\rho |\Pi ^{A})&:&= \sum \limits _{k}p_{k}S(\rho _{k}) \end{aligned}$$

(18)

and

$$\begin{aligned} \rho _{k}=\frac{1}{p_{k}}(\Pi _{k}^{A}\otimes I_{B})\rho (\Pi _{k}^{A}\otimes I_{B}) \end{aligned}$$

(19)

with

$$\begin{aligned} p_{k}=\text{ Tr }[(\Pi _{k}^{A}\otimes I_{B})\rho (\Pi _{k}^{A}\otimes I_{B})], k=1,2 \end{aligned}$$

(20)

Measurement-induced nonlocality can be viewed as a kind of quantum correlation from a geometric perspective based on the local von Neumann measurements from which one of the reduced states is left invariant. The MIN of $\rho$, denoted by $MIN(\rho )$, can be defined as [42]

$$\begin{aligned} MIN_{A}(\rho ):=\underset{\Pi ^{A}}{\max }\left\| \rho -|\Pi ^{A}(\rho )\right\| ^{2} \end{aligned}$$

(21)

where $\left\| . \right\|$ stands for the Hilbert-Schmidt norm ($\left\| A\right\| =[Tr(A^{\dagger }A)]^{1/2}$) and the maximum is taken over all local von Neumann measurement $\Pi ^{A}=\{\Pi _{k}^{A}\}$ with $\sum \limits _{k}\Pi _{k}^{A}\rho _{A}\Pi _{k}^{A}=\rho _{A}$,

$$\begin{aligned} \Pi ^{A}(\rho )=\sum \limits _{k}(\Pi _{k}^{A}\otimes I_{B})\rho (\Pi _{k}^{A}\otimes I_{B}). \end{aligned}$$

(22)

Whereas the geometric measure of quantum discord for the class of $X$-states can be defined as [108]

$$\begin{aligned} D_{G}(\rho ):=\underset{\Pi ^{A}}{\min }\left\| \rho -\chi \right\| ^{2} \end{aligned}$$

(23)

where the minimum is over the set of zero-discord states $\chi$. The square of Hilbert-Schmidt norm of Hermitian operators, $\left\| \rho -\chi \right\| ^{2}=\text{ Tr }[(\rho -\chi )^{2}]$. This quantity have been evaluated by Dakić et al. [6] for an arbitrary two-qubit state.

4 Results and discussions

Instead of presenting analytical expressions for the geometric measure of quantum discord and measurement-induced nonlocality, these quantities are interpreted in terms of their corresponding graphs for various situations as illustrated in the figures captions. Influence of different decoherence channels such as amplitude damping, depolarizing and phase flip channels is investigated for $X$-type initial states in accelerated frames at finite temperature. The results consist of three parts (1) the effect of acceleration $r$ on the GMQD and MIN of $X$-type initial states (2) the effect of decoherence on the GMQD and MIN (3) the effect of finite temperature $X$ on the GMQD and MIN influenced by the decoherence channels.

In Fig. 1, the geometric measure of quantum discord (GMQD) and measurement-induced nonlocality (MIN) are plotted as a function of acceleration $r$ for Bell, Werner and General type initial states. It is seen that GMQD can be used to distinguish initial quantum states, whereas in case of MIN, all the three states overlap. In Fig. 2, GMQD and MIN are plotted as a function of decoherence parameter $p$ for Bell, Werner and General type initial states for $r=0$ (upper panel) and $r=\pi /4$ (lower panel) for the case of amplitude damping channel. Here $r=\pi /4$ corresponds to infinite acceleration limit. It can be seen that the depolarizing channels heavily influences the geometric quantum discord and MIN as compared to amplitude damping channel. In Fig. 3, GMQD and MIN are plotted as a function of decoherence parameter $p$ (upper panel) for Bell, Werner and General type initial states for $r=\pi /4$ (lower panel) as a function of decoherence parameter $p$ and acceleration $r$ for Werner type initial states, for phase flip channel. It is seen that the behaviour of phase flip channel is symmetrical around 50 % decoherence. It is also seen that for lower level range of decoherence, different initial states can be distinguished. Furthermore, GMQD sudden birth appears for higher level of decoherence for which the initial states become distinguishable. Whereas, for the intermediate range of decoherence, it is difficult to distinguish different initial states.

Fig. 2

(Color online). GMQD and MIN are plotted as a function of decoherence parameter $p$ for Bell, Werner and General type initial states for $r=0$ (upper panel) amplitude damping channel and $r=\pi /4$ (lower panel) for the case of amplitude damping channel

Fig. 3

(Color online). GMQD and MIN are plotted as a function of decoherence parameter $p$ (upper panel) for Bell, Werner and General type initial states for $r=\pi /4$ (lower panel) as a function of decoherence parameter $p$ and acceleration $r$ for Werner type initial states, for phase flip channel

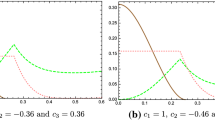
In Fig. 4, GMQD and MIN are plotted as a function of the parameter $X$ for General type initial state for $\bar{n}=0.01, \,\bar{n}=0.1$ and $\bar{n} =0.3$ for $r=0$ (upper panel) and for $r=\pi /4$ (lower panel) respectively. It is seen that a sudden change in the behaviour (rise and then fall) of GMQD occurs depending upon the mean photon number of the local environment. Whereas, MIN suddenly falls down at finite $\bar{n}$ (i.e. very small mean photon number) for higher values of the parameter $X$. In Fig. 5, GMQD is plotted for depolarizing, amplitude damping and phase flip channels for $\bar{n}=0.01$ (upper graph) and $\bar{n}=0.1$ (lower graph) for the Werner like states. A sudden change in the behaviour of GMQD is seen depending upon the choice of the parameter $c$ and the mean photon number $\bar{n}$. It is also seen that the mean number of photons plays a crucial role in the dynamics of GMQD as we increase the value of $\bar{n},$ the changing behaviour of GMQD saturates for $\bar{n}>0.3.$ The sudden change in the behaviour of GMQD and MIN become more prominent, when we introduce the environmental noise in the system.

Fig. 4

(Color online). GMQD and MIN are plotted as a function of the parameter $X$ for General type initial state ($c_{1}=0.2, \,c_{2}=-0.3, \,c_{3}=0.3$) for $\bar{n}=0.01, \,\bar{n}=0.1$ and $\bar{n}=0.3$ for $r=0$ (upper panel) and for $r=\pi /4$ (lower panel) respectively

Fig. 5

(Color online). GMQD is plotted as a function of parameter $c$ for depolarizing, amplitude damping and phase flip channels for $\bar{n}=0.01$ (upper graph) and $\bar{n}=0.1$ (lower graph) for the Werner like states ($\left| c_{1}\right| =\left| c_{2}\right| =\left| c_{3}\right| =c$)

In Fig. 6, GMQD (upper panel, with $p=0.5$) and MIN (lower panel, with $r=\pi /4$) are plotted as a function of acceleration $r, \,p$ respectively, and parameter $X$ for General initial state for $\bar{n}=0.01$ and $\bar{n} =0.1$ (a) amplitude damping (b) depolarizing (c) phase flip channels. Here upper graph corresponds to lower value of the mean number of photons of the local reservoir. It is seen from the figure that as the value of acceleration $r$ increases, the GMQD and MIN are degraded, the effect is more prominent in case of phase flip channel. The sudden transition in the behaviour of GMQD and MIN can be seen for amplitude damping and phase flip channels. This sudden change is dependent on the mean number of photons of the local environment. Similarly, sudden change in the behaviour of MIN is also seen in the finite temperature regime (i.e. at finite $\bar{n}$). It is noticeable that in case of depolarizing channel, no sudden change in the behaviour of GMQD and MIN is observed. It means that the depolarizing channel has destructive interference effect on the local environment. Furthermore, the environmental noise has stronger affect on the dynamics of GMQD and MIN as compared to the Unruh effect. It is also seen that Werner like states are more robust than General type initial states at finite temperature.

Fig. 6

(Color online). GMQD (upper panel, with $p=0.5$) and MIN (lower panel, with $r=\pi /4$) are plotted as a function of acceleration $r, \,p$ respectively, and parameter $X$ for General initial state ($c_{1}=0.2, \, c_{2}=-0.3, \,c_{3}=0.3$) with $\bar{n}=0.01$  (upper graph) and $\bar{n} =0.1$ (lower graph) for amplitude damping, depolarizing and phase flip channels

5 Conclusions

Decoherence dynamics of geometric measure of quantum discord (GMQD) and measurement-induced nonlocality (MIN) is investigated for noninertial observers at finite temperature. A two-qubit $X$-state is considered in noninertial frames and the effect of acceleration $r$, decoherence and finite temperature is analyzed. Evolution of GMQD and MIN is studied influenced by different environments such as amplitude damping, depolarizing and phase flip channels. It is shown that initial state entanglement plays an important role in bipartite quantum states. It is possible to distinguish the Bell diagonal, Werner and general type initial states using the GMQD. A sudden transition in the behaviour of GMQD and MIN occurs depending upon the mean photon number of the local environment at finite $\bar{n}$ (i.e. for small mean photon number). Therefore, mean photon number plays an important role in the dynamics of GMQD and MIN. The transition behaviour disappears for larger values of $\bar{n}$, i.e. $\bar{n}>0.3.$ This transition behaviour become more prominent, when environmental noise is introduced in the system. In the presence of environmental noise, as we increase the value of acceleration $r$, GMQD and MIN decay due to Unruh effect which is more prominent for the phase flip noise. This sudden change is dependent on the mean number of photons of the local environment. It is notable that for the depolarizing channel, no sudden change in the behaviour of GMQD and MIN is observed means that the depolarizing channel has destructive interference effect on the local environment. Furthermore, the environmental noise has stronger affect on the dynamics of GMQD and MIN as compared to the Unruh effect. It is also seen that Werner like states are more robust than General type initial states at finite temperature.

Appendix

$$\begin{aligned} \rho _{11}[t]&= \frac{1}{^{(2\bar{n}+1)^{2}}}\{\bar{n}^{2}+[2(\rho _{11}-\rho _{44})\bar{n}^{2}+(\rho _{11}-\rho _{44}+1)\bar{n}]X \\&+[(2\rho _{11}+2\rho _{44}-1)\bar{n}^{2}+(3\rho _{11}+\rho _{44}-1)\bar{n} +\rho _{11}]X^{2}\} \\ \rho _{22}[t]&= \frac{1}{^{^{(2\bar{n}+1)^{2}}}}\{\bar{n}(\bar{n} +1)-[2(\rho _{11}+2\rho _{33}+\rho _{44}-1)\bar{n}^{2} \\&+(\rho _{11}+4\rho _{33}+3\rho _{44}-2)\bar{n}+(\rho _{33}+\rho _{44}-1)]X\\&-[(2\rho _{11}+2\rho _{44}-1)\bar{n}^{2}+(3\rho _{11}+\rho _{44}-1)\bar{n} +\rho _{11}]X^{2}\} \\ \rho _{33}[t]&= \frac{1}{^{^{(2\bar{n}+1)^{2}}}}\{\bar{n}(\bar{n} +1)+[2(\rho _{11}+2\rho _{33}+\rho _{44}-1)\bar{n}^{2}\\&+(3\rho _{11}+4\rho _{33}+\rho _{44}-2)\bar{n}]X -[(2\rho _{11}+2\rho _{44}-1)\bar{n}^{2}\\&+(3\rho _{11}+\rho _{44}-1)\bar{n} +\rho _{11}]X^{2}\} \\ \rho _{44}[t]&= \frac{1}{^{^{(2\bar{n}+1)^{2}}}}\{(\bar{n}+1)^{2}-(\bar{n} +1)[2\bar{n}(\rho _{11}-\rho _{44})+(\rho _{11}-\rho _{44}-+)]X \\&+[(2\rho _{11}+2\rho _{44}-1)\bar{n}^{2}+(3\rho _{11}+\rho _{44}-1)\bar{n} +\rho _{11}]X^{2}\} \\ \rho _{14}[t]&= \rho _{44}X, \rho _{23}[t]=\rho _{23}X \end{aligned}$$

where $X=\exp ^{-\Gamma (2\bar{n}+1)t}$ and $\Gamma$ is the spontaneous decay rate of the qubits.