Genuine correlations of tripartite system

Abstract

We define genuine total, classical and quantum correlations in tripartite systems. The genuine tripartite quantum discord can be interpreted as ‘quantum advantage’ in tripartite superdense coding. We find in a symmetrical tripartite state, for total correlation and classical correlation, the genuine tripartite correlations are no less than the pair-wise correlations. However, the genuine quantum tripartite correlation can be surpassed by the pair-wise quantum correlations. Analytical expressions for genuine tripartite correlations are obtained for pure states and rank-2 symmetrical states. The genuine correlations in both entangled and separable states are calculated.

1 Introduction

It is believed that various quantum correlations are resources in quantum information processing. Such quantum correlations include entanglement and quantum discord, they are closely related but different from each other. Much progress has been made in studying quantum entanglement [1], it is also found that theories of entanglement may be applied in quantum phase transitions and adiabatic quantum computation [2]. Quantum discord, introduced and studied in Refs. [3–7], has recently drawn much attention as well. There is nonzero quantum discord in general separable states in comparison the entanglement vanishes in this case. Additionally, entanglement may disappear at a finite time [8], while quantum discord decays asymptotically even at a finite temperature, which is known as the robustness of quantum discord [9]. In general, it seems that quantum discord is more common than entanglement in quantum states. For specific applications of quantum discord in quantum information protocols, the deterministic quantum computation with one qubit (DQC1) [10] and state discrimination [11, 12] can be realized using states with zero entanglement but positive quantum correlation. The importance of quantum discord is also presented in quantum communication [13]. The operational significance of discord consumption has been discussed theoretically and experimentally [14]. Generally, numerical methods is required for calculating quantum discord. By far, analytical evaluation of quantum discord are developed for some special two-qubit states, e. g. X states [15, 16]. A simple method is pointed out to get the analytical quantum discord of a rank-two bipartite state by relationship with entanglement of formation (EOF) [17].

Despite the great potential advantages of multipartite quantum correlations, the problem of quantifying and characterizing the correlation contained in the multipartite quantum systems is still open. Recently, much effort has been devoted in classifying multipartite states and measuring the quantum correlations contained in these states. There exist two kinds of tripartite states according to the behavior of states under the action of LOCC (local operations and classical communication) [18]. Moreover, in Ref. [19], basing on the action of SLOCC (stochastic local quantum operations assisted by classical communication), the complete classification of all different classes of four qubits has been discussed. For more general case, since of nine different ways of entangling four qubits, there should exist nine families of states. A global measure is proposed for quantum correlations of multipartite systems [20]. The quantum dissension which measures the quantum correlations in a tripartite state is introduced in Ref. [21]. Moreover in Ref. [22], the genuine total, quantum and classical correlations in multipartite system are defined by employing relative entropy as a distance measure of correlations [23]. Some general criteria about the definition of genuine $n$-partite correlations has been given by Bennett et al. [24].

In this paper, we try to provide some new definitions of genuine tripartite correlations. The genuine total or quantum correlation goes to zero if and only if there is a bipartition of the tripartite system such that no total or quantum correlation exist between the two parts. The operational significance of genuine tripartite quantum discord is discussed. We also obtain the analytical expressions of the genuine tripartite correlations in pure and rank-two states. Genuine total, quantum and classical correlations are compared with their pairwise counterparts. We find that the genuine total and classical correlations are greater than their pairwise counterparts in symmetrical states, but this quantitative relation does not hold for quantum correlations. Our definition of genuine tripartite quantum correlation is no greater than the one defined in [22], but the two definitions coincide for pure states.

The remainder of this paper is arranged as follows. In Sect. 2, we give our new definitions of genuine tripartite correlations and investigate the case of pure and symmetrical tripartite states, and then discuss the operational significance of genuine tripartite quantum discord. In Sect. 3, we will illustrate by examples the tripartite genuine quantum discord and classical correlations in symmetrical systems. Section 4 is devoted to the conclusion.

2 An optimal genuine tripartite correlations

Let us briefly recall the definition of two-particle quantum discord [3]:

$$\begin{aligned} D(\rho _{a:b})\equiv I(\rho _{a,b})-J(\rho _{a:b}), \end{aligned}$$

(1)

where the mutual information $I(\rho _{a,b})=S(\rho _{a})+S(\rho _{b})-S(\rho _{ab})$, with $S(\rho )=-tr(\rho \log _2\rho )$, characterizes the total correlations, and $J(\rho _{a:b})=S(\rho _{a})-\min _{\{{E}^b_l\}} S(\rho _{a|{\{{E}^b_l}\}})$ is called the classical correlation. Here $\{{E}^b_l\}$ is positive operator valued measures (POVM) performed on system $b$ and $S(\rho _{a|{\{{E}^b_l}\}})=\sum \limits _l p_lS(\rho _{a|{E^b_l}})$, where $\rho _{a|{E^b_l}}=Tr_b(E^b_l\rho _{ab})/p_l$ and $p_l=Tr_{ab}(E^b_l\rho _{ab})$.

The operational significance of discord consumption has been discussed [14]. Quantum discord quantifies a resource which can be consumed during encoding to give coherent interactions an operationally meaningful advantage. Under the assumption that $D(\rho _{a:b})\le D(\rho _{b:a})$, Bob possesses particle $b$ while Alice owns particle $a$ and encodes information within it. His aim is to get the encoded data. The encoded state which resulted from that Alice encodes a random variable $K$ with probability $P(P=K)=p_k$ by applying a corresponding unitary operator $U_k$ is:

$$\begin{aligned} \widetilde{\rho }_{ab}=\sum \limits _kp_kU_k\rho _{ab}U_k^{\dag }. \end{aligned}$$

(2)

The amount of discord consumed in encoding is the difference between $D(\rho _{a:b})$ and $D(\widetilde{\rho }_{a:b})$:

$$\begin{aligned} \triangle D(\rho _{a:b})=D(\rho _{a:b})-D(\widetilde{\rho }_{a:b}). \end{aligned}$$

(3)

Then, Alice gives particle $a$ to Bob. When bob is only allowed to a single local measurement on each of $a$ and $b$, his best possible performance, the maximal information he can get, is $I_c$. When he can operate arbitrary operations on system $a$ and $b$ even the joint system $ab$, his maximum performance is $I_q$. The extra quantum advantage that coherent interactions can potentially deliver is defined as the difference $\triangle I=I_q-I_c$. From Ref. [14]:

$$\begin{aligned} \triangle D(\rho _{a:b})-\widetilde{J}(\rho _{a:b})\le \triangle I \le \triangle D(\rho _{a:b}). \end{aligned}$$

(4)

Specially, $\triangle I =\triangle D=D(\rho _{a:b})$ in case of maximal encoding when $D(\widetilde{\rho }_{a:b})= J(\widetilde{\rho }_{a:b})=0$. It is noticed that there always exists maximal encoding [14].

A state of $n$ particles is said to possess genuine $n$-partite correlations when it is nonproduct in every bipartite cut [24]. From this point of view, we can define genuine tripartite correlations in tripartite states $\rho _{abc}\equiv \rho$ as

$$\begin{aligned} T^{(3)}(\rho )\equiv \min [I(\rho _{a,bc}),I(\rho _{b,ac}),I(\rho _{c,ab})], \end{aligned}$$

(5)

where $I(\rho _{i,jk})=S(\rho _{i})+S(\rho _{jk})-S(\rho )$ is the mutual information between one-qubit part and the left two-qubit part, which goes to zero if and only if $\rho =\rho _i\otimes \rho _{jk}$. This definition of genuine total correlation coincides with which defined in Ref. [22].

Consistent with the definition of $T^{(3)}$, and taking the operational significance of discord consumption into consideration, we define genuine tripartite quantum discord as:

$$\begin{aligned} D^{(3)}(\rho )=\min [D(\rho _{a:bc}),D(\rho _{b:ac}),D(\rho _{c:ab})], \end{aligned}$$

(6)

where $D(\rho _{i:jk})=S(\rho _{jk})+S(\rho _{i|jk})-S(\rho ), \,S(\rho _{k|ij})=\min _{\{{E}^{ij}_m\}}[S(\rho _{k|\{{E}^{ij}_m\}})]$, and $\{{E}^{ij}_m\}$ is a two-particle POVM operating on $i$ and $j$. It must be the form that X(i)-C(jk) (X: quantum or classical states, C: classical states ) when the genuine tripartite quantum discord $D^{(3)}(\rho )=D(\rho _{i:jk})$ of a state is null. Therefore, the tripartite states can be divided into two groups: X(i)-C(jk) and X(i)-Q(jk) (Q: quantum states), according to the null or non-zero genuine tripartite quantum discord.

Then, we define genuine tripartite classical correlations as:

$$\begin{aligned} J^{(3)}(\rho )=\min [J(\rho _{a:bc}),J(\rho _{b:ac}),J(\rho _{c:ab})], \end{aligned}$$

(7)

where $J(\rho _{i:jk})=S(\rho _{i})-S(\rho _{i|jk})$.

Now, we explain the operational significance of genuine tripartite quantum consumption in our definition. We assume that $\min [D(\rho _{a:bc}),D(\rho _{b:ac}),D(\rho _{c:ab})]=D(\rho _{a:bc})$. Alice owns particle $a$ and encodes information within it. Bob possesses particle $b$ and Chris owns particle $c$. The aim of Bob and Chris is to get the encoded data. They must cooperate with each other, so that they can get the most information. The encoded state which resulted from that Alice encodes a random variable $K$ with probability $P(P=K)=p_k$ by applying a corresponding unitary operator $U_k$ is:

$$\begin{aligned} \widetilde{\rho }_{abc}=\sum \limits _kp_kU_k\rho _{abc}U_k^{\dag }. \end{aligned}$$

(8)

The amount of discord consumed in encoding is the difference between $D(\rho _{a:bc})$ and $D(\widetilde{\rho }_{a:bc})$:

$$\begin{aligned} \triangle D(\rho _{a:bc})=D(\rho _{a:bc})-D(\widetilde{\rho }_{a:bc}). \end{aligned}$$

(9)

Then, Alice gives particle $a$ to Bob and Chris. There are two situations when Bob and Chris decode the information. For the first situation, Bob and Chris can not store their qubits until they receive Alice’s qubit, so they must operate their own qubits first, and then operate Alice’s qubit. Therefore, they must operate qubit $a$ and the system of qubits $b$,$c$ separately. When Bob and Chris are only allowed to a single local measurement on each of $a$ and $bc$, their best possible performance, the maximal information they can get, is $I_c$. For the second situation, they can operate arbitrary operations on system $a$ and $bc$ even the joint system $abc$, their maximum performance is $I_q$. The extra quantum advantage that coherent interactions can potentially deliver is the difference $\triangle I=I_q-I_c$. According to Ref. [14], we can get that:

$$\begin{aligned} \triangle D(\rho _{a:bc})-\widetilde{J}(\rho _{a:bc})\le \triangle I \le \triangle D(\rho _{a:bc}). \end{aligned}$$

(10)

Specially, like the bipartite case, $\triangle I =\triangle D=D(\rho _{a:bc})$ in case of maximal encoding when $D(\widetilde{\rho }_{a:bc})= J(\widetilde{\rho }_{a:bc})=0$. It is noticed that there always exists maximal encoding [14]. The genuine tripartite correlations is greater than the bipartite counterpart sometimes, so that the upper bound of $\triangle I$ is greater as well.

We discuss some properties of genuine tripartite correlations below. Without loss of generality, we make the following assumption:

$$\begin{aligned} I(\rho _{c,ab})\le I(\rho _{a,bc})\le I(\rho _{b,ac}). \end{aligned}$$

(11)

The left discussion about pure and symmetrical states in this section is based on it. According to Schmidt decomposition, $S(\rho _{c|ab})=0$ and $S(\rho _{i})=S(\rho _{jk})$ in the tripartite pure states. By assumption (11), we have $S(\rho _{c})=S(\rho _{ab})\le S(\rho _{a})=S(\rho _{bc}) \le S(\rho _{b})=S(\rho _{ac})$. Therefore, we can obtain the genuine tripartite total, classical correlations and quantum discord:

$$\begin{aligned} T^{(3)}(\rho )&= 2S(\rho _{c})=2S(\rho _{ab}),\nonumber \\ D^{(3)}(\rho )&= J^{(3)}(\rho )=S(\rho _{ab})=S(\rho _{c}). \end{aligned}$$

(12)

It means that genuine tripartite classical correlations and quantum discord are both equal to half of the genuine tripartite total correlations and satisfy $T^{(3)}(\rho )=D^{(3)}(\rho )+J^{(3)}(\rho )$ in a pure state, which coincide with the genuine correlations defined in Ref [22].

When the tripartite quantum system is symmetrical, i. e., the state of the whole system is invariant under the permutations of the three parties, the genuine tripartite total, classical and quantum correlations can be regarded as:

$$\begin{aligned} T^{(3)}(\rho )&= S(\rho _{c})+S(\rho _{ab})-S(\rho ),\nonumber \\ J^{(3)}(\rho )&= S(\rho _{c})-S(\rho _{c|ab}),\nonumber \\ D^{(3)}(\rho )&= S(\rho _{ab})+S(\rho _{c|ab})-S(\rho ). \end{aligned}$$

(13)

We can see that the genuine total correlation is the sum of genuine classical and quantum correlations in a symmetrical tripartite state. Now, we derive some properties of the genuine correlations.

Theorem

For a symmetrical tripartite quantum state, the genuine tripartite total and classical correlations is no less than the any pairwise counterpart, respectively

$$\begin{aligned} T^{(3)}(\rho )&\ge T^{(2)}(\rho ),\nonumber \\ J^{(3)}(\rho )&\ge J^{(2)}(\rho ), \end{aligned}$$

(14)

where the $T^{(2)}$ and $J^{(2)}$ are pairwise total and classical correlations respectively.

Proof of Theory

The mutual information does not increase when discards quantum subsystem: $I(\rho _{c,a}) \le I(\rho _{c,ab})$ [25], it is obvious that genuine tripartite correlations is no less than pairwise correlations of symmetrical tripartite systems. For classical correlations, we have $J^{(3)}(\rho )=J(\rho _{c:ab})$ and $J^{(2)}(\rho )=J(\rho _{c:a})$. Direct calculations lead to $J^{(3)}(\rho )-J^{(2)}(\rho )=S(\rho _{c|a})-S(\rho _{c|ab})$. Notice that $S(\rho _{c|a})=\min _{\{{E}^a\otimes I^b\}}S(\rho _{c|\{{E}^a_l\otimes I^b\}})$, and that $\{{E}^a_l\otimes I^b\}$ may not be the optimal POVM $\{{E}^{ab}_l\}$ in the definition of $S(\rho _{c|ab})$. Therefore, we have $J^{(3)}(\rho )\ge J^{(2)}(\rho )$. This completes the proof.

For quantum correlations, there are no fixed quantitative relation between genuine and pairwise quantum correlations, which we will illustrate in the next section by some concrete examples.

3 Analytic expression of genuine tripartite quantum discord for rank-two symmetrical states

We now consider genuine quantum discord of rank-two symmetrical states of three qubits, which we can get the analytic results. A rank-two symmetrical tripartite system can be written as

$$\begin{aligned} \rho =p|\varphi _1\rangle \langle \varphi _1|_{abc}+(1-p)|\varphi _2\rangle \langle \varphi _2|_{abc}, \end{aligned}$$

(15)

where $|\varphi _i\rangle _{abc}$ is a three-qubit symmetrical state. The state in Eq. (15) can be purified to a four-qubit pure state by attaching an auxiliary system $d$:

$$\begin{aligned} |\Psi _{abcd}\rangle =\sqrt{p}|\varphi _1,0\rangle +\sqrt{1-p}|\varphi _2,1\rangle . \end{aligned}$$

(16)

According to the Koashi–Winter relation in Ref. [17], we can obtain $E(\rho _{cd})=S(\rho _{c|ab})$ and deduce the genuine tripartite discord in Eq. (13) as:

$$\begin{aligned} D^{(3)}(\rho )=S(\rho _{ab})+E(\rho _{cd})-S(\rho ). \end{aligned}$$

(17)

Here $E(\rho _{cd})$ is the EOF between qubits $c$ and $d$, which is defined as

$$\begin{aligned} E(\rho _{cd})=\min _{\{{p}_i,|\phi _i\rangle _{cd}\}}\sum \limits _ip_iS(Tr_c(|\phi _i\rangle \langle \phi _i|)), \end{aligned}$$

(18)

and can be calculated as follows: $E(\rho _{cd})=-h\log _2h-(1-h)\log _2(1-h)$, where $h=\frac{1+\sqrt{1-C_{cd}^2}}{2}, \,C_{cd}$ being the concurrence of $\rho _{cd}$ [26, 27]. Optimal POVM $\{{E}_i^{ab}\}$ in the definition of $D^{(3)}$ related to the optimal pure state decomposition $\{{p}_i,|\phi _i\rangle _{cd}\}$ for EOF as follows [17]:

$$\begin{aligned} \rho ^i_{c|ab}=Tr_{ab}\{{E}_i^{ab}\rho \}/p_i=Tr_{d}\{|\phi _i\rangle \langle \phi _i|\}. \end{aligned}$$

(19)

Obviously, we can obtain the genuine tripartite correlations even in general rank-two states.

We study two concrete examples to investigate more closely the properties of genuine tripartite correlations. Firstly, consider a symmetric tripartite system as the form:

$$\begin{aligned} \rho =p|000\rangle \langle 000|+(1-p)|\phi \phi \phi \rangle \langle \phi \phi \phi | \end{aligned}$$

(20)

where $|\phi \rangle =\cos \theta |0\rangle +\sin \theta |1\rangle$. This is a three-qubit separated state with no entanglement of any type. We calculate nonzero eigenvalues of $\rho$ and $\rho _{ab}$ as well as the analytical formula of $h$:

$$\begin{aligned} \lambda _1^{abc}&= \frac{1}{8} (4-\sqrt{2} \sqrt{8-pq(22-15 \cos 2\theta -6\cos 4\theta -\cos 6\theta }),\nonumber \\ \lambda _2^{abc}&= \frac{1}{8} (4+\sqrt{2}\sqrt{8-pq(22-15\cos 2\theta -6\cos 4\theta -\cos 6\theta }),\nonumber \\ \lambda _1^{ab}&= \frac{1}{4}(2-\sqrt{2} \sqrt{2-pq(5-4\cos 2\theta -\cos 4\theta }),\nonumber \\ \lambda _2^{ab}&= \frac{1}{4}(2+\sqrt{2} \sqrt{2-pq(5-4\cos 2\theta -\cos 4\theta }),\nonumber \\ h&= \frac{1}{8}\Big (4+\Big (16+15pq(\cos 2\theta -18+2\cos 4\theta +\cos 6\theta )\nonumber \\&+\,8\sqrt{pq (\sin \theta )^6\sqrt{pq(5 \sin \theta +\sin 3\theta )^2}}\Big )^{\frac{1}{2}}\Big ), \end{aligned}$$

(21)

where $q=1-p$. Then from Eq. (17), we obtain the the analytic expression for the genuine tripartite quantum discord:

$$\begin{aligned} D^{(3)}(\rho )&= -\lambda _1^{ab}\log _2\lambda _1^{ab}-\lambda _2^{ab}\log _2\lambda _2^{ab}\nonumber \\&-(1-h)\log _2(1-h)\nonumber \\&-h\log _2h+\lambda _1^{abc}\log _2\lambda _1^{abc}\nonumber \\&+\lambda _2^{abc}\log _2\lambda _2^{abc}. \end{aligned}$$

(22)

The analytical results are plotted in Fig. 1. Figure 1a is $D^{(3)}(\rho )$ as a function of $p$ and $\theta$. We see that the $D^{(3)}(\rho )$ is equal to zero when $p=0$ or $p=1$, and it takes the maximal value for $p=\frac{1}{2}$ when $\theta$ is fixed. It is not difficult to find that $D^{(3)}(\rho )$ is symmetric with $p=\frac{1}{2}$ when $\theta$ is fixed. This can be understood as follows. The state in Eq. (20) can be transformed into $\rho ^\prime =(1-p)|000\rangle \langle 000|+p|\phi \phi \phi \rangle \langle \phi \phi \phi |$ by the unitary operator $U^\prime =U\otimes U \otimes U$, where $U=\{\cos \theta ,\sin \theta ;\sin \theta ,-\cos \theta \}$. Genuine correlations are preserved under local unitary operations, that is $D^{(3)}(\rho )=D^{(3)}(\rho ^\prime )$. Hence, $D^{(3)}(\rho )$ is invariant when $p$ and $1-p$ are interchanged. Then, we find that $D^{(3)}(\rho )$ takes the maximal value when $p=\frac{1}{2}$ and $\theta =0.688$. In Fig. 1b plots the difference between $D^{(3)}$ and $D^{(2)}$ as a function of $p$ and $\theta$. The cases that $D^{(3)}(\rho )$ is less than, equal to or greater than $D^{(2)}(\rho )$ are all possible. Therefore, in superdense coding, the ‘quantum advantage’ when Bob and Chris possess particle $b$ and $c$ may be greater than, equal to or less than the case when only Bob owns particle $b$.

Fig. 1

a $D^{(3)}(\rho )$ as a function of $\theta$ and $p$. b $D^{(3)}(\rho )-D^{(2)}(\rho )$ as function of $\theta$ and $p$

We then turn to find out the corresponding optimal measurements by which we get the genuine tripartite quantum discord. The case for $p=\frac{1}{2}$ is discussed in here. Firstly, we achieve the optimal pure state decomposition of $\rho _{cd}$ which minimized the EOF of the state using the method in Ref. [27]:

$$\begin{aligned} |\phi _1\rangle&= \frac{1}{2}\left(\sqrt{1+{\cos }^2\theta }+{\sin }\theta \right)|00\rangle \nonumber \\&+\frac{1}{2} {\cos }\theta \left(\sqrt{1+{\cos }^2\theta }-{\sin }\theta \right)|01\rangle \nonumber \\&+\frac{1}{2} \left(\sqrt{1+{\cos }\theta ^2}-{\sin }\theta \right) {\sin }\theta |11\rangle ,\nonumber \\ |\phi _2\rangle&= \frac{1}{2} \left(\sqrt{1+{\cos }^2\theta }-{\sin }\theta \right)|00\rangle \nonumber \\&+\frac{1}{2}\left({\cos }\theta \sqrt{1+{\cos }^2\theta }+{\cos }\theta {\sin }\theta \right)|01\rangle \nonumber \\&+\frac{1}{2} \left(\sqrt{1+{\cos }^2\theta } {\sin }\theta +{\sin }^2\theta \right)|11\rangle . \end{aligned}$$

(23)

Then from Eq. (19), we have the optimal measurement bases for $D^{(3)}$ as

$$\begin{aligned} |E^{ab}_1\rangle&= \frac{\sqrt{3+\cos 2\theta }+\sqrt{2}\sin \theta }{2\sqrt{2}}|00\rangle \nonumber \\&-\frac{{\sin }\theta \left(\sqrt{3+\cos 2\theta }-\sqrt{2}{\sin }\theta \right)}{2\sqrt{3+\cos 2\theta }}|11\rangle \nonumber \\&-\frac{{\cos }\theta \left(\sqrt{3+\cos 2\theta }-\sqrt{2}{\sin }\theta \right)}{2 \sqrt{3+\cos 2\theta }}(|01\rangle +|10\rangle ), \end{aligned}$$

(24)

$$\begin{aligned} |E^{ab}_2\rangle&= \frac{\sqrt{3+\cos 2\theta }-\sqrt{2}\sin \theta }{2\sqrt{2}}|00\rangle \nonumber \\&+\frac{{\sin }\theta \left(\sqrt{3+\cos 2\theta }+\sqrt{2}{\sin }\theta \right)}{2\sqrt{3+\cos 2\theta }}|11\rangle \nonumber \\&+\frac{{\cos }\theta \left(\sqrt{3+\cos 2\theta }+\sqrt{2}{\sin }\theta \right)}{2\sqrt{3+\cos 2\theta }}(|01\rangle +|10\rangle ). \end{aligned}$$

(25)

The other two measurements with above two measurements constitute a set of orthogonal basis which satisfy that $\sum \nolimits _{k=1}^4|E^{ab}_k\rangle \langle E^{ab}_k|=I$. It must be noticed that $|E^{ab}_k\rangle$ can not always be written as $|E^{a}_l\rangle \otimes |E^{b}_m\rangle$.

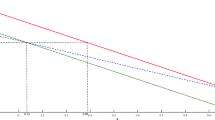
The genuine tripartite classical and quantum correlations we defined are different with which defined in Ref. [22]. Here we compare our measure for genuine correlations with those defined in Ref. [22], where $J^{\prime (3)}(\rho )=S(\rho _{c})-S^{\prime }(\rho _{c|ab})$ and $D^{\prime (3)}(\rho )=S(\rho _{ab})+S^{\prime }(\rho _{c|ab})-S(\rho _{abc})$ with $S^{\prime }(\rho _{c|ab})=\min _{\{{E}^a_l,E^b_m\}}[S(\rho _{c|\{{E}^a_l,E^b_m\}})]$ are the genuine quantum and classical correlations. Since $\{{E}^a_l\otimes E^b_m\}$ may not be the optimal POVM $\{{E}^{ab}_m\}$ in the definition of $D^{(3)}$, we have $D^{(3)}(\rho )\le D^{\prime (3)}(\rho )$ and $J^{(3)}(\rho )\ge J^{\prime (3)}(\rho )$. The comparison is shown in Fig. 2 which is the $\theta$-dependent correlations variation curves when $p=\frac{1}{2}$. From Fig. 2, we can see that $D^{(3)}(\rho )$ and $D^{\prime (3)}(\rho )$ are quite close to each other. However, the two measures of genuine quantum correlation do not coincide for $\theta \ne 0$ or $\pi /2$. It means that even for separable state in Eq. (20), the optimal measurement $\{{E}^{ab}_m\}$ in the definition of genuine quantum correlation $D^{(3)}$ can not be written as $E^{ab}_m=E^a_l\otimes E^b_m$. Another interesting phenomenon is that the genuine quantum correlation $D^{(3)}(\rho )$ may surpass the genuine classical correlation $J^{(3)}(\rho )$ even for separable states.

Fig. 2

Correlations for the state, $\rho =p|000\rangle \langle 000|+(1-p)|\phi \phi \phi \rangle \langle \phi \phi \phi |$, vary with $\theta$ when $p=1/2$ : $D^{(3)}(\rho )$(blue solid line), $J^{(3)}(\rho )$ (black dashed line), $D^{\prime (3)}(\rho )$ (red dot-dashed line), $J^{\prime (3)}(\rho )$ (orange dotted line) (Color figure online)

Now, we consider a state of this form

$$\begin{aligned} \rho =p|GHZ\rangle \langle GHZ|+(1-p)|W\rangle \langle W|, \end{aligned}$$

(26)

where $|GHZ\rangle =\frac{1}{\sqrt{2}}(|000\rangle +|111\rangle )$ and $|W\rangle =\frac{1}{\sqrt{3}}(|100\rangle +|010\rangle +|001\rangle )$. The genuine tripartite discord of the state as in Eq. (26) can be calculated using the same method as above state. Therefore,

$$\begin{aligned} D^{(3)}(\rho )&= -\left(\frac{1-p}{3}+\frac{p}{2}\right)\log _2\left(\frac{1-p}{3}+\frac{p}{2}\right)\nonumber \\&-\left(\frac{2}{3}\left(1-p\right)\right)\log _2\left(\frac{2}{3}\left(1-p\right)\right)-\left(\frac{p}{2}\right)\log _2\left(\frac{p}{2}\right)\nonumber \\&+p\log _2p+(1-p)\log _2(1-p). \end{aligned}$$

(27)

Figure 3a shows $D^{(3)}(\rho )$ is greater than $D^{(2)}(\rho )$. There is a transition point at $p=0.51$ for $D^{(2)}(\rho )$ because of the sudden change of the measurement basis. The three-tangle $\tau _3$ [29] of the state (26) which we showed in the Fig. 3a has been obtained in ref [28]. We can see that the genuine quantum discord is no less than the three-tangle $\tau _3$. Figure 3b shows $D^{\prime (3)}(\rho ), \,D^{(3)}(\rho ), \,J^{(3)}(\rho )$ and $J^{\prime (3)}(\rho )$ as functions of $p$. The four quantities coincide only for $p=0$ or $p=1$, where the state in Eq. (26) is just the $|W\rangle$ state or $|GHZ\rangle$ state. For $p\in (0,1)$, we can see that in this state, the gap between $D^{\prime (3)}(\rho )$ and $D^{(3)}(\rho )$, as well as that between $J^{(3)}(\rho )$ and $J^{\prime (3)}(\rho )$ can be very large. Moreover, the ordering is different, i.e., $J^{(3)}$ is greater than $D^{(3)}$ while $J^{\prime (3)}$ is less than $D^{\prime (3)}$.

Fig. 3

Correlations for the state, $\rho _{abc}=p|GHZ\rangle \langle GHZ|+(1-p)|W\rangle \langle W|$, vary with p. a $D^{(3)}(\rho )$ (solid line), $D^{(2)}(\rho )$ (dashed line), $\tau _3$ (dot-dashed line). b $D^{(3)}(\rho )$ (solid line), $J^{(3)}(\rho )$ (dashed line), $D^{\prime (3)}(\rho )$ (dot-dashed line), $J^{\prime (3)}(\rho )$ (dotted line)

4 Conclusion and discussion

In summary, we have investigated the genuine correlations in tripartite quantum states. We proposed the definitions for genuine tripartite quantum and classical correlations, and obtained the analytical expression of them for rank-two symmetrical states of three qubits, as well as the operational significance of tripartite genuine quantum discord. The tripartite genuine correlations can be regard as bipartite correlations between particle $a$ and joint system of particle $b,c$. The tripartite genuine quantum discord can be used to quantify ‘quantum advantage’ in superdense coding. We have shown that, genuine tripartite classical correlations and quantum discord are both equal to half of genuine tripartite total correlations in pure tripartite states, which coincide with the definition of genuine correlation given in [22]. For a symmetrical tripartite state, the quantitative relation between genuine tripartite quantum discord and its pairwise counterpart is not fixed, while the genuine tripartite total and classical correlations are no less than their any pairwise counterparts. Interestingly, the genuine quantum correlation can surpass the genuine classical correlation even in some separable states. The main results of this paper are illustrated in Table 1.

Table 1 Main results: the expressions of genuine tripartite correlations and properties of some particular states, where RTST (Rank-two symmetrical states) and RTS (Rank-two states)

We can extend the definitions of genuine tripartite correlations to symmetric $n$-particle systems. The genuine $n$-partite correlations of symmetric states can be defined as: $T^{(n)}(\rho )\equiv I(\rho _{(a_1),(a_2 \ldots a_n)})$. It is worthy to mention that $T^{(n)}(\rho )$ is the minimum mutual information of any bipartite-cut of the $n$-partite symmetric states. We first prove it in four-partite symmetric states by strong subadditively principal: $S(\rho _{abc})+S(\rho _{b})\le S(\rho _{ab})+S(\rho _{bc})$. We can induce that $S(\rho _{abc})+S(\rho _{d})\le S(\rho _{ab})+S(\rho _{cd})$ since $S(\rho _{b})=S(\rho _{d})$ and $S(\rho _{bc})=S(\rho _{cd})$ in symmetric states, then we get that $I(\rho _{(abc),d})\le I(\rho _{(ab),(cd)})$. It is easy to prove it in $n$-partite symmetric states. Like the tripartite case, the genuine $n$-partite quantum discord and classical correlations of symmetric states can be defined as follows:

$$\begin{aligned} D^{(n)}(\rho )&=D(\rho _{a_1:(a_2 \ldots a_n)}),\nonumber \\ J^{(n)}(\rho )&=J(\rho _{a_1:(a_2 \ldots a_n)}). \end{aligned}$$

(28)

The operational significance of $n$-particle genuine quantum discord consumption can be considered as this way: under the condition that $D^{(n)}(\rho )=D(\rho _{a_1:(a_2 \ldots a_n)})$, Alice owns particle $a_1$ and encodes information in it when the other $n-1$ person have particles $a_2 \ldots a_n$ respectively. Then Alice sends particle $a_1$ to them. Only the $n-1$ person collaborate with each other, can they decode the most of the information. Therefore, the inequality (10) is valid when it is extended into $n$-particle symmetric systems.

We also have discussed the difference between correlations we defined and which defined in Ref. [22]. The reason of the difference is the different measurement. The POVM’s on $i$ and $j$ in Ref. [22] is of the form that $\{{E}^{i}_l, E^{j}_m\}$ while we use $\{{E}^{ij}_{k}\}$. That is to say $i$ and $j$ are treated as two systems in Ref. [22] whereas we regard them as a whole system. It is noticeable that $\{{E}^{ij}_{k}\}$ can not always be expressed as $E^{ij}_k=E^i_l\otimes E^j_m$. If it can, the result of different definitions would be coincident. Moreover, it is possible that there exists null genuine tripartite discord by our definitions while genuine tripartite discord is nonzero with the definitions in Ref. [22].

The study of various correlations in multipartite states is of interests not only for quantum information science but also for many-body systems in condensed matter physics and statistical mechanics. However, no consensual measures of various correlations in multipartite case are found, even in the well-studied entanglement case. The correlation measures in tripartite states proposed in this paper should be a start point in completely quantifying the multipartite correlations. It will also be interesting to use the correlation measures presented in this paper in some real physical systems.