The denominator rule with unit ratio difference

Abstract

In this paper we extend the denominator rule for ratios given in different units of measurement and we explain how to derive the relevant aggregation shares, which are given in terms of the denominator variable and the constants converting the relevant variables into the same unit of measurement.

1 Introduction

This paper was motivated by a stimulating question raised by W.E. Diewert about the applicability of the denominator rule for ratios given in different units of measurement. As initially stated by Fӓre and Karagiannis (2017), the denominator rule, namely that aggregation of ratio-type variables should be based on weights given in terms of the denominator variable of the relevant quotient, is related to the theoretically consistent aggregation of ratios given in the same unit of measurement across decision-making units (DMUs). In this paper we undertake the task of extending the denominator rule for ratios given in different units of measurement.

In many empirical studies we are not only interested in individual performance but also on how well a group of DMUs performs. Consider, for example, the case of public hospitals: hospital managers are more interested on their specific units while health authority staff are more interested on the overall picture. Notice however that the vast majority of previous efficiency studies in health care delivery, with the exception of Pilayavsky and Staat (2008), Nguyen and Zelenyuk (2021) and Färe and Karagiannis (2022), analyzed the overall picture by means of a simple arithmetic average of individual efficiency scores. As it is explained in Karagiannis (2015a), this accurately reflects aggregate achievements only when performance and size are uncorrelated. Otherwise, a weighted average should be used and in this case, the choice of aggregation weights become crucial in order to ensure theoretical consistency, in the sense that the individual and the aggregate scores have the same form and the same intuitive interpretation.

Fӓre and Karagiannis (2017) have recently provided such an aggregation rule, i.e., the denominator rule, for ratios given in the same unit of measurement and explained how it can be used to aggregate, for example, individual (radial) technical, allocative and scale efficiency scores, measures of input congestion, and capacity utilization. It is important to note however that the applicability of the denominator rule is not limited to the above cases presupposing DMU’s optimizing behavior, where the denominator rule may be viewed as the practical counterpart of Koopmans (1957) theorem and its cost and revenue corollaries, but it may also be used to aggregate partial and total productivity indices¹ as well as other ratio-type measures of performance given in the same unit of measurement. The latter may include programmatic efficiency scores or metafrontier technology gap ratios (Karagiannis 2015b; Walheer 2018a), DEA-based composite indicators (Karagiannis 2017; Rogge 2018), cost efficiency scores with private and public inputs (Walheer 2019), and markup or Lerner market power indices (Basu 2019; deLoecker et al. 2020; Shaffer and Spierdijk 2020).

In this paper we extend the denominator rule for ratios given in different units of measurement and we explain how to derive the relevant aggregation shares. In this case, the aggregation weights are given in terms of the denominator variable and the constants that are used to convert the relevant variables into the same unit of measurement. This enlarges considerably the applicability of the denominator rule to include cases of aggregating (across DMUs) performance measures given in different units of measurement as well as cases of aggregating across commodities, inputs or outputs. In this direction, we provide a number of applications illustrating how the denominator rule with unit ratio difference can be used for (i) aggregating Fӓre efficiency indices, enhanced Russell efficiency indices, and Lerner’s indices of market power across DMUs and (ii) deriving a weighted Russell efficiency index, a weighted potential improvement efficiency index as well as the weighted average form of the Laspeyres, Paasche and Lowe price and quantity indices.

The rest of this paper unfolds as follows: in the next section we present the theoretical part and the main results. In the third section, we provide a number of applications of the denominator rule with unit ratio difference. Concluding remarks follow in the last section.

2 Problem setting and main results

Consider that our objective is to aggregate two ratios z₁/ξ₁ and z₂/ξ₂, given in different units of measurement, by means of an aggregator function $L:R_ + ^2 \to R_ +$ describing the type of aggregation, namely, arithmetic, harmonic, geometric, etc., in such a way to preserve theoretical consistency in the sense that z₁/ξ₁, z₂/ξ₂ and the resulting aggregate measure have the same (ratio) form and the same intuitive interpretation. The main result is stated as:²

2.1 Denominator rule with unit ratio difference

Let z=(z₁, z₂)>0, ξ=(ξ₁, ξ₂)>0 and c₁, c₂>0 are constants converting c₁z₁, c₁ξ₁, c₂z₂, and c₂ξ₂ into the same unit of measurement. Then, for arithmetic aggregation we have

$$L\left( {\frac{{z_1}}{{\xi _1}},\frac{{z_2}}{{\xi _2}}} \right) = \theta _1\left( {\frac{{z_1}}{{\xi _1}}} \right) + \theta _2\left( {\frac{{z_2}}{{\xi _2}}} \right) = \frac{{c_1z_1 + c_2z_2}}{{c_1\xi _1 + c_2\xi _2}}$$

(1)

where $\theta _1 = \frac{{c_1\xi _1}}{{c_1\xi _1 + c_2\xi _2}} \ge 0$, $\theta _2 = \frac{{c_2\xi _2}}{{c_1\xi _1 + c_2\xi _2}} \ge 0$ and θ₁ + θ₂ = 1.

If the ratios are given in the same unit of measurement c₁ = c₂ = 1 and the conventional denominator rule applies (see Fӓre and Karagiannis 2017). If, in addition to c₁ = c₂ = 1, we have ξ₁ = ξ₂ = ξ then

$$L\left( {\frac{{z_1}}{\xi },\frac{{z_2}}{\xi }} \right) = \left( {\frac{\xi }{{2\xi }}} \right)z_1 + \left( {\frac{\xi }{{2\xi }}} \right)z_2 = \frac{1}{2}\left( {z_1 + z_2} \right)$$

(2)

in which case, the average reflects accurately the aggregate. Two are the implications of this result: first, (2) provides one of the alternative ways to derive the simple (equally-weighted) arithmetic average form of the translation function–based Luenberger productivity indicator, introduced in Chambers (2002); for the other two see Fӓre and Zelenyuk (2019). Second, (2) provides the theoretically consistent way for aggregating (across DMUs) composite indicators by means of the Benefit-of-the-Doubt (BoD) model (see Karagiannis 2017), which essentially is an input-oriented DEA model with a single constant (unitary) input.

On the other hand, an alternative way to obtain the same aggregate value, namely c₁z₁+c₂z₂/(c₁ξ₁+c₂ξ₂), is to use harmonic aggregation and define the aggregation weights in terms of the numerator (instead of the denominator) of the relevant ratio–this is called the numerator rule by Fӓre and Karagiannis (2017):

$$L\left( {\frac{{z_1}}{{\xi _1}},\frac{{z_2}}{{\xi _2}}} \right) = \frac{{c_1z_1 + c_2z_2}}{{c_1\xi _1 + c_2\xi _2}} = \left[ {\delta _1\left( {\frac{{z_1}}{{\xi _1}}} \right)^{ - 1} + \delta _2\left( {\frac{{z_2}}{{\xi _2}}} \right)^{ - 1}} \right]^{ - 1}$$

(3)

where $\delta _1 = c_1z_1/\left( {c_1z_1 + c_2z_2} \right) \ge 0$, $\delta _2 = c_2z_2/\left( {c_1z_1 + c_2z_2} \right) \ge 0$ and δ₁+δ₂ = 1.

Next let us consider the relationship between the denominator rule with unit ratio difference and Aczél’s (1987, p. 150) geometric aggregation rule, namely:

$$\underline L \left( {\frac{{z_1}}{{\xi _1}},\frac{{z_2}}{{\xi _2}}} \right) = \left( {\frac{{z_1}}{{\xi _1}}} \right)^{g_1}\left( {\frac{{z_2}}{{\xi _2}}} \right)^{g_2} = \frac{{\mathop {\prod }\nolimits_{i = 1}^2 z_i^{g_i}}}{{\mathop {\prod }\nolimits_{i = 1}^2 \xi _i^{g_i}}}$$

(4)

where g₁≥0, g₂≥0 and g₁+g₂ = 1. In particular, we look for the values of g₁ and g₂ that make the aggregate value in (1) equal to the aggregate value in (4). For this purpose, we use Reinsdorf et al. (2002) result for the additive decomposition of geometric means, namely that

$$\underline L = \frac{{\pi _1z_1 + \pi _2z_2}}{{\pi _1\xi _1 + \pi _2\xi _2}} = \left( {\frac{{\pi _1\xi _1}}{{\pi _1\xi _1 + \pi _2\xi _2}}} \right)\frac{{z_1}}{{\xi _1}} + \left( {\frac{{\pi _2\xi _2}}{{\pi _1\xi _1 + \pi _2\xi _2}}} \right)\frac{{z_2}}{{\xi _2}}$$

(5)

where $\pi _1 = g_1/m\left( {z_1,\xi _1L} \right)$, $\pi _2 = g_2/m\left( {z_2,\xi _2L} \right)$ and m(.) denotes the logarithmic mean, i.e., $m\left( {z_1,\xi _1L} \right) = \left( {z_1 - \xi _1L} \right)/\left[ {\ln \left( {z_1} \right) - {{{\mathrm{ln}}}}\left( {\xi _1L} \right)} \right]$ and $m\left( {z_2,\xi _2L} \right) = \left( {z_2 - \xi _2L} \right)/\left[ {\ln \left( {z_2} \right) - {{{\mathrm{ln}}}}\left( {\xi _2L} \right)} \right]$.³ Then, from (1) and (5), we have $\theta _1 = \pi _1\xi _1/\left( {\pi _1\xi _1 + \pi _2\xi _2} \right)$ and $\theta _2 = \pi _2\xi _2/\left( {\pi _1\xi _1 + \pi _2\xi _2} \right)$. By substituting π₁ and π₂ into these and rearranging terms yields:

$$\theta _1 = \frac{{g_1\xi _1m\left( {z_2,\xi _2L} \right)}}{{g_1\xi _1m\left( {z_2,\xi _2L} \right) + g_2\xi _2m\left( {z_1,\xi _1L} \right)}}$$

(6)

$$\theta _2 = \frac{{g_2\xi _2m\left( {z_1,\xi _1L} \right)}}{{g_1\xi _1m\left( {z_2,\xi _2L} \right) + g_2\xi _2m\left( {z_1,\xi _1L} \right)}}$$

But from (1) we know that $\theta _1 = c_1\xi _1/\left( {c_1\xi _1 + c_2\xi _2} \right)$ and $\theta _2 = c_2\xi _2/\left( {c_1\xi _1 + c_2\xi _2} \right)$. Combining these with (6) and given that g₁+g₂ = 1, we obtain the values of g₁ and g₂ for which $L\,=\,{\underline{L}}$ as:

$$g_1 = \frac{{c_1m\left( {z_1,\xi _1L} \right)}}{{c_1m\left( {z_1,\xi _1L} \right) + c_2m\left( {z_2,\xi _2L} \right)}}$$

(7)

$$g_2 = \frac{{c_2m\left( {z_2,\xi _2L} \right)}}{{c_1m\left( {z_1,\xi _1L} \right) + c_2m\left( {z_2,\xi _2L} \right)}}$$

An alternative proof of (7), following Balk (2008, pp. 141-42), is:⁴ rewrite (1) as:

$$\theta _1\left( {L - \frac{{z_1}}{{\xi _1}}} \right) + \theta _2\left( {L - \frac{{z_2}}{{\xi _2}}} \right) = 0$$

(8)

and use the logarithmic mean to get:

$$\theta _1m\left( {L,z_1/\xi _1} \right){{{\mathrm{ln}}}}\left( {\frac{{L\xi _1}}{{z_1}}} \right) + \theta _2m\left( {L,z_2/\xi _2} \right){{{\mathrm{ln}}}}\left( {\frac{{L\xi _2}}{{z_2}}} \right) = 0$$

(9)

After few manipulations and rearrangement of terms, (9) results in:

$$lnL = \eta _1ln\left( {\frac{{z_1}}{{\xi _1}}} \right) + \eta _2ln\left( {\frac{{z_2}}{{\xi _2}}} \right)$$

(10)

where

$$\eta _1 = \frac{{\theta _1m\left( {L,z_1/\xi _1} \right)}}{{\theta _1m\left( {L,z_1/\xi _1} \right) + \theta _2m\left( {L,z_2/\xi _2} \right)}}$$

(11)

$$\eta _2 = \frac{{\theta _2m\left( {L,z_2/\xi _2} \right)}}{{\theta _1m\left( {L,z_1/\xi _1} \right) + \theta _2m\left( {L,z_2/\xi _2} \right)}}$$

By substituting $\theta _1 = c_1\xi _1/\left( {c_1\xi _1 + c_2\xi _2} \right)$ and $\theta _2 = c_2\xi _2/\left( {c_1\xi _1 + c_2\xi _2} \right)$ into (11) we can verify that η₁ = g₁ and η₂ = g₂.

If the ratios are given in the same units of measurement, then c₁ = c₂= 1 and the aggregation weights in (7) are simplified as follows:

$$g_1 = \frac{{m\left( {z_1,\xi _1L} \right)}}{{m\left( {z_1,\xi _1L} \right) + m\left( {z_2,\xi _2L} \right)}}$$

(12)

$$g_2 = \frac{{m\left( {z_2,\xi _2L} \right)}}{{m\left( {z_1,\xi _1L} \right) + m\left( {z_2,\xi _2L} \right)}}$$

This should be compared to the approximate solutions provided by Fӓre and Zelenyuk (2005) and Fӓre and Karagiannis (2020) for the arithmetic aggregation to result in the same aggregate value as the geometric aggregation. Here, thanks to the denominator rule with unit ratio difference, we are able to provide an exact solution to this problem.

As suggested by a referee, g₁ and g₂ in (7) may also be obtained by relating (3) and (4). In this case, a relation analogous to (5) is given as:

$$\underline L = \frac{{\pi _1^\prime z_1 + \pi _2^\prime z_2}}{{\pi _1^\prime \xi _1 + \pi _2^\prime \xi _2}} = \left[ {\left( {\frac{{\pi _2^\prime z_1}}{{\pi _1^\prime z_1 + \pi _2^\prime z_2}}} \right)\left( {\frac{{z_1}}{{\xi _1}}} \right)^{ - 1} + \left( {\frac{{\pi _2^\prime z_2}}{{\pi _1^\prime z_1 + \pi _2^\prime z_2}}} \right)\left( {\frac{{z_2}}{{\xi _2}}} \right)^{ - 1}} \right]^{ - 1}$$

(13)

where $\pi _1^\prime = g_1/m\left( {\xi _1,z_1L^{ - 1}} \right)$, $\pi _2^\prime = g_2/m\left( {\xi _2,z_2L^{ - 1}} \right)$, $m\left( {\xi _1,z_1L^{ - 1}} \right) = \left( {\xi _1 - z_1L^{ - 1}} \right)/\left[ {\ln \left( {\xi _1} \right) - {{{\mathrm{ln}}}}\left( {z_1L^{ - 1}} \right)} \right]$ and $m\left( {\xi _2,z_2L^{ - 1}} \right) = \left( {\xi _2 - z_2L^{ - 1}} \right)/\left[ {\ln \left( {\xi _2} \right) - {{{\mathrm{ln}}}}\left( {z_2L^{ - 1}} \right)} \right]$. Then, following the same steps as above, one can verify that

$$g_1 = \frac{{c_1m\left( {\xi _1,z_1L^{ - 1}} \right)}}{{c_1m\left( {\xi _1,z_1L^{ - 1}} \right) + c_2m\left( {\xi _2,z_2L^{ - 1}} \right)}}$$

(14)

$$g_2 = \frac{{c_2m\left( {\xi _2,z_2L^{ - 1}} \right)}}{{c_1m\left( {\xi _1,z_1L^{ - 1}} \right) + c_2m\left( {\xi _2,z_2L^{ - 1}} \right)}}$$

We have thus shown that there are four alternative ways to obtain the same aggregate value of $\left( {c_1z_1 + c_2z_2} \right)/\left( {c_1\xi _1 + c_2\xi _2} \right)$ by using either (1), (3), (4) with (7) or (4) with (14). The last two alternatives are less attractive than the first two, as the aggregate and the individual ratios (or their inverse) occur in the aggregation weights in (7) and (14). On the other hand, as aggregate data is published in the form of totals, aggregate performance ratios are better understood as arithmetic rather than geometric aggregates of the individual performance ratios (Färe and Karagiannis 2020). In addition, by comparing the first two alternatives, the denominator rule is intuitively more appealing and simpler than the numerator rule.

Notice that (1) and (4) with (7) rely on denominator-based weights while (3) and (4) with (14) on numerator-based weights. One may think that advantages would result by combining the two types of weights to obtain the aggregate ratio. This can be done, for example, by taking the geometric means of either (1) and (3) or (4) with (7) and (4) with (14). In such cases, however, the resulting relations are less useful for analytical purposes (e.g., for ascertaining the impact of individual ratios on the aggregate ratio) compared to those using either the denominator- or the numerator-based weights. Alternatively, one may follow a procedure analogous to that used for obtaining Montgomery and Sato-Vartia type of indices (see Balk 2008, pp. 85–87). In the former case, one can verify that the resulting aggregation weights do no add-up to 1 and this is a serious shortcoming when considering share weighted averages while in the latter the aggregation weights are given as:

$$g_1 = \frac{{m\left( {\frac{{c_1z_1}}{{c_1z_1 + c_2z_2}},\frac{{c_1\xi _1}}{{c_1\xi _1 + c_2\xi _2}}} \right)}}{{m\left( {\frac{{c_1z_1}}{{c_1z_1 + c_2z_2}},\frac{{c_1\xi _1}}{{c_1\xi _1 + c_2\xi _2}}} \right) + m\left( {\frac{{c_2z_2}}{{c_1z_1 + c_2z_2}},\frac{{c_2\xi _2}}{{c_1\xi _1 + c_2\xi _2}}} \right)}}$$

(15)

$$g_2 = \frac{{m\left( {\frac{{c_2z_2}}{{c_1z_1 + c_2z_2}},\frac{{c_2\xi _2}}{{c_1\xi _1 + c_2\xi _2}}} \right)}}{{m\left( {\frac{{c_1z_1}}{{c_1z_1 + c_2z_2}},\frac{{c_1\xi _1}}{{c_1\xi _1 + c_2\xi _2}}} \right) + m\left( {\frac{{c_2z_2}}{{c_1z_1 + c_2z_2}},\frac{{c_2\xi _2}}{{c_1\xi _1 + c_2\xi _2}}} \right)}}$$

which add-up to one but they are far less intuitively appealing compared to those of the denominator rule with unit ratio difference. In particular, the aggregation weights in (15) may be interpreted as the normalized logarithmic mean of the “value” shares of the numerator and denominator variables while the aggregation weights in (1) are simply the “value” shares of the denominator variable. For c₁= c₂ = 1, i.e., when the ratios are given in the same unit of measurement, (15) have been used by Balk (2021, ch. 9) for aggregating labor and total factor productivity indices across DMUs.

3 Some applications

In this section, we present several applications where the denominator rule with unit ratio difference may be used:

3.1 Price and quantity indices

We start by explaining how the denominator rule with unit ratio difference can be used to obtain the weighted average form of several well-known price and quantity indices.⁵First, consider the case where $c_1 = y_1^0$, $c_2 = y_2^0$, $z_1 = p_1^1$, $\xi _1 = p_1^0$, $z_2 = p_2^1$, and $\xi _2 = p_2^0$, with p_i and y_i being respectively the price and the quantity of the ith commodity (subscripts are used to index commodities and superscripts to index time periods). Then, the application of the denominator rule with unit ratio difference results in the Laspeyres price index:

$$P_L\left( {p^1,p^0,y^0} \right) = \frac{{p_1^1y_1^0 + p_2^1y_2^0}}{{p_1^0y_1^0 + p_2^0y_2^0}} = \frac{{p_1^0y_1^0}}{{p_1^0y_1^0 + p_2^0y_2^0}}\left( {\frac{{p_1^1}}{{p_1^0}}} \right) + \frac{{p_2^0y_2^0}}{{p_1^0y_1^0 + p_2^0y_2^0}}\left( {\frac{{p_2^1}}{{p_2^0}}} \right)$$

(16)

Similarly, if $c_1 = y_1^1$, $c_2 = y_2^1$, $z_1 = p_1^1$, $\xi _1 = p_1^0$, $z_2 = p_2^1$, and $\xi _2 = p_2^0$, then the application of the denominator rule with unit ratio difference results in the Paasche price index:

$$\begin{array}{l}P_P\left( {p^1,p^0,y^1} \right) = \frac{{p_1^1y_1^1 + p_2^1y_2^1}}{{p_1^0y_1^1 + p_2^0y_2^1}} = \frac{{p_1^0y_1^1}}{{p_1^0y_1^1 + p_2^0y_2^1}}\left( {\frac{{p_1^1}}{{p_1^0}}} \right) \\ \qquad\qquad\qquad\quad+ \frac{{p_2^0y_2^1}}{{p_1^0y_1^1 + p_2^0y_2^1}}\left( {\frac{{p_2^1}}{{p_2^0}}} \right)\end{array}$$

(17)

In addition, if $c_1 = y_1^b$, $c_2 = y_2^b$, $z_1 = p_1^1$, $\xi _1 = p_1^0$, $z_2 = p_2^1$, and $\xi _2 = p_2^0$, then the application of the denominator rule with unit ratio difference results in the Lowe price index:

$$\begin{array}{l}P_{Lo}\left( {p^1,p^0,y^1} \right) = \frac{{p_1^1y_1^b + p_2^1y_2^b}}{{p_1^0y_1^b + p_2^0y_2^b}} = \frac{{p_1^0y_1^b}}{{p_1^0y_1^b + p_2^0y_2^b}}\left( {\frac{{p_1^1}}{{p_1^0}}} \right) \\ \qquad\qquad\qquad\quad+ \frac{{p_2^0y_2^b}}{{p_1^0y_1^b + p_2^0y_2^b}}\left( {\frac{{p_2^1}}{{p_2^0}}} \right)\end{array}$$

(18)

where b refers to some third period.

Second, by interchanging the role of prices and quantities one can obtain the corresponding quantity indices: that is, (i) if $c_1 = p_1^0$, $c_2 = p_2^0$, $z_1 = y_1^1$, $\xi _1 = y_1^0$, $z_2 = y_2^1$, and $\xi _2 = y_2^0$, the application of the denominator rule with unit ratio difference results in the Laspeyres quantity index, (ii) if $c_1 = p_1^1$, $c_2 = p_2^1$, $z_1 = y_1^1$, $\xi _1 = y_1^0$, $z_2 = y_2^1$, and $\xi _2 = y_2^0$, one can obtain the Paasche quantity index, and (iii) if $c_1 = p_1^b$, $c_2 = p_2^b$, $z_1 = y_1^1$, $\xi _1 = y_1^0$, $z_2 = y_2^1$, and $\xi _2 = y_2^0$, we get the Lowe quantity index. These results clearly support Caves et al. (1982, p. 73) assertion that “numerous index number formulas can be explicitly derived from particular aggregator functions”. In the cases of the Laspeyres, Paasche and Lowe price and quantity indices, we have shown that this is given by the denominator rule with unit ratio difference.

3.2 Efficiency indices

Consider first the Fӓre (1975) input-oriented non-radial efficiency measure, which is defined as:

$$\begin{array}{*{20}{c}} {E^k\left( {x^k,y^k} \right) = \Big[ {\mathop {{\min }}\limits_i \Big\{ {\mathop {{\min }}\limits_{\lambda _i^k} \lambda _i^k:\left( {x_1^k, \ldots ,\lambda _i^kx_i^k, \ldots ,x_I^k} \right) \in L\left( {y^k} \right),} } } \\ { { {0 < \lambda _i^k \le 1\,\forall \,i} \Big\}} \Big]^{ - 1} \ge 1} \end{array}$$

(19)

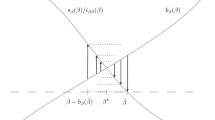
where x_i refers to input quantities, L(y) = {x:(x,y)∈T} is the input requirement set and T is the production possibility set. The input requirement set is assumed to be closed and non-empty for finite y, to satisfy strong (input and output) disposability, input convexity, continuity, and 0_I∉L(y) for y ≥ 0_J but 0_I∈L(0_J).⁶E^k (x^k, y^k) seeks the shortest, uni-dimensional distance to the frontier by scaling down each input in turn, holding output and other inputs fixed, and then takes the minimum over all these scalings. Let us assume that there are only two inputs and that we want to aggregate the efficiency scores of two firms or DMUs A and B (see Fig. 1). Then, according to the Fӓre (1975) efficiency measure, the score of firm A is determined by means of the first input while that of firm B by means of the second input; that is $E^A = 1/\lambda _1^A = x_1^A/\widetilde x_1^A$ and $E^B = 1/\lambda _2^B = x_2^B/\widetilde x_2^B$, where a tilde over a variable denotes its potential or technically efficient quantity. Applying the denominator rule with unit ratio difference to the optimal solution of (19) and let $z_1 = x_1^A$, $\xi _1 = \widetilde x_1^A = \lambda _1^Ax_1^A$, $z_2 = x_2^B$, and $\xi _2 = \widetilde x_2^B = \lambda _2^Bx_2^B$, we obtain:

$$\begin{array}{l}L\left( {\frac{{x_1^A}}{{\widetilde {x}}_1^A},\frac{{x_2^B}}{{\widetilde {x}}_2^B}} \right) = \frac{{c_1{\widetilde {x}}_1^A}}{{c_1{\widetilde {x}}_1^A + c_2{\widetilde {x}}_2^A}}\left( {\frac{{x_1^A}}{{\widetilde {x}}_1^A}} \right) + \frac{{c_2{\widetilde {x}}_2^A}}{{c_1{\widetilde {x}}_1^A + c_2{\widetilde {x}}_2^A}}\left( {\frac{{x_2^B}}{{\widetilde {x}}_2^B}} \right)\\ = \frac{{c_1x_1^A + c_2x_2^B}}{{c_1{\widetilde {x}}_1^A + c_2{\widetilde {x}}_2^A}}\end{array}$$

(20)

with input prices being potential candidates for c₁ and c₂.

Fig. 1

Fӓre input-oriented efficiency measure for a technology with two inputs and a single output

Second, consider the most widely used non-radial efficiency metric, namely the Russell measure, the input-oriented form of which is defined by Fӓre and Lovell (1978) as:

$$\begin{array}{*{20}{c}} {R^k\left( {x^k,y^k} \right) = \mathop {{\min }}\limits_{\lambda ^k} \left\{ {\frac{1}{I}\mathop {\sum}\nolimits_{i = 1}^I {\lambda _i^k:\left( {\lambda _1^kx_1^k, \ldots ,\lambda _i^kx_i^k, \ldots ,\lambda _I^kx_I^k} \right) \in L\left( {y^k} \right),} } \right.} & {} \\ {} & {\left. {0 < \lambda _i^k \le 1\,\forall \,i} \right\} \le 1} \end{array}$$

(21)

where $\lambda _i^k = \widetilde x_i^k/x_i^k$. $R^k\left( {x^k,y^k} \right)$ reduces all non-zero inputs by a set of individual factors that minimize the arithmetic mean of the reductions in such a way to ensure that the resulting input vector belongs to the efficient subset. The Russell measure has been often criticized (see e.g., Ruggiero and Bretschneider 1998) for implicitly assuming that all inputs equally affect the level of potential production, regardless of their importance in total cost as well as the extent of their input-specific inefficiency, i.e., the magnitude of the λ_i’s. To overcome this shortcoming, Zhu (1996) and Ruggiero and Bretschneider (1998) proposed a weighted Russell measure defined as:

$$\begin{array}{l}R_w^k\left( {x^k,y^k} \right) = \mathop {{\min }}\limits_{\lambda ^k} \left\{ {\mathop {\sum}\nolimits_{i = 1}^I {\phi _i^k\lambda _i^k:\left( {\lambda _1^kx_1^k, \ldots ,\lambda _i^kx_i^k, \ldots ,\lambda _I^kx_I^k} \right) \in L\left( {y^k} \right),} } \right.\\ \quad \quad \quad \quad \quad \quad 0 < \lambda _i^k \le 1\,\forall \,i = 1, \ldots ,I\left. {\phi _i^k \ge 0,\,\mathop {\sum}\nolimits_{i = 1}^I {\phi _i^k = 1} } \right\} \le 1\end{array}$$

(22)

In the literature, there are several different alternatives for determining the weights ϕ’s, ranging from expert opinion (Zhu 1996), to regression analysis (Ruggiero and Bretschneider 1998) and to Shannon entropy (Hsiao et al. 2011).

We may also use the denominator rule with unit ratio difference for determining the ϕ’s as the $\lambda _i^k = \widetilde x_i^k/x_i^k$ are in different units of measurement. By substituting $z_1 = \widetilde x_1^k$, $z_2 = \widetilde x_2^k$, $\xi _1 = x_1^k$ and $\xi _2 = x_2^k$, we have for the two-inputs case:

$$R_w^k\left( {x_1^k,x_2^k,y^k} \right) = \theta _1^k\lambda _1^k + \theta _2^k\lambda _2^k = \theta _1^k\left( {\frac{{\widetilde x_1^k}}{{x_1^k}}} \right) + \theta _2^k\left( {\frac{{\widetilde x_2^k}}{{x_2^k}}} \right) = \frac{{c_1^k\widetilde x_1^k + c_2^k\widetilde x_2^k}}{{c_1^kx_1^k + c_2^kx_2^k}}$$

(23)

where $\theta _1^k = c_1^kx_1^k/\left( {c_1^kx_1^k + c_2^kx_2^k} \right)$ and $\theta _2^k = c_2^kx_2^k/\left( {c_1^kx_1^k + c_2^kx_2^k} \right)$. There are several candidates for $c_1^k$ and $c_2^k$ but here we focus only on two that have been previously used in the literature. If we use input prices for $c_1^k$ and $c_2^k$, i.e., $c_1^k = w_1$ and $c_2^k = w_2$ where w refers to inputs prices, then (23) becomes what Fӓre et al. (1985, p. 148) referred to as the Russell input cost measure of technical efficiency. Alternatively, one may use output elasticities obtained from a production function regression model for $c_1^k$ and $c_2^k$, as Ruggiero and Bretschneider (1998) suggested, but this choice is less intuitively appealing.

Notice that if θ₁= θ₂ in (23) then we are back to the conventional Russell measure with $c_1^kx_1^k = c_2^kx_2^k$ or alternatively, $c_1^k/c_2^k = x_2^k/x_1^k$, which determines the slope of the implicit isocost line. The latter is essentially related to de Borger et al. (1998) interpretation of the conventional Russell measure’s projection point: for DMU A in Fig. 2, the projection point A₁ reflects the cost minimizing input choice when the relative factor price equals the (negative) ratio of actual input quantities, i.e., $- x_2^A/x_1^A$.⁷ Given that cost at point A₁ is equal to that at point A₃, i.e., the point of intersection between the implicit isocost line and the ray through DMU A’s actual input bundle, the ratio OA₃/OA renders to the conventional Russell measure of technical efficiency a (shadow) cost-saving interpretation (see Dervaux et al. 1998).⁸ On the other hand, as actual cost at point A₁ equals that at point A₂, i.e., the point of intersection between the market isocost line and the ray through DMU A’s actual input bundle, the ratio OA₂/OA renders to the Russell input cost measure of technical efficiency a clear cost saving interpretation.

Fig. 2

Russell input-oriented efficiency measure for a technology with two inputs and a single output

Third, a similar issue, namely that input excesses are considered as equally important, arises in the case of the potential improvement inefficiency index, which in its input-oriented form is given as (see Bogetoft and Hougaard 1998):

$$P^k\left( {x^k,y^k} \right) = \mathop {\sum}\nolimits_{i = 1}^I {\beta ^k\left( {\frac{{x_i^k - \widehat x_i^k}}{{x_i^k}}} \right)} = \mathop {\sum}\nolimits_{i = 1}^I {\left( {\frac{{x_i^k - \tilde x_i^k}}{{x_i^k}}} \right) \ge 0}$$

(24)

where $\widehat x_i^k$ is the ith coordinate of the ideal reference point corresponding to the largest possible reduction in the ith input such that $\widehat x_i^k = min\left\{ {x_i^k:\left( {x_1^k, \ldots ,\widehat x_i^k, \ldots ,x_I^k} \right) \in L\left( y \right)} \right\}$, and $\beta ^k = \left( {x_i^k - \widetilde x_i^k} \right)/\left( {x_i^k - \widehat x_i^k} \right)$ is constant for all inputs.⁹ For the two-inputs case depicted in Fig. 3, the projection point of P^A (x^A, y^A) is A₁ and its coordinates are given by a “weighted” average of actual and ideal reference point coordinates, i.e., $\widetilde x_i^k = \left( {1 - \beta ^k} \right)x_i^k + \beta ^k\widehat x_i^k$ for i = 1, 2. Both the potential improvement inefficiency index in (24), which is equal to the sum of the (normalized) input-specific potential improvement indices, and that of Wang et al. (2013), which is equal to the simple average of the (normalized) input-specific potential improvement indices, weight the excess of each input equally even if their prices or their cost shares differ significantly. Based on the denominator rule with unit ratio difference and by substituting $z_1^k = x_1^k - \widehat x_1^k$, $z_2^k = x_2^k - \widehat x_2^k$, $\xi _1^k = x_1^k$ and $\xi _2^k = x_2^k$ we can obtain a weighted potential improvement inefficiency index $P_w^k\left( {x^k,y^k} \right)$, which overcomes the above criticism:

$$\begin{array}{*{20}{c}} {P_w^k\left( {x^k,y^k} \right) = \theta _1^k\left( {\frac{{x_1^k - \widetilde x_1^k}}{{x_1^k}}} \right) + \theta _2^k\left( {\frac{{x_2^k - \widetilde x_2^k}}{{x_2^k}}} \right)} & {} \\ {} & { = \frac{{\left( {c_1^kx_1^k + c_2^kx_2^k} \right) - \left( {c_1^k\widetilde x_1^k + c_2^k\widetilde x_2^k} \right)}}{{c_1^kx_1^k + c_2^kx_2^k}}} \end{array}$$

(25)

where $\theta _1^k = c_1^kx_1^k/\left( {c_1^kx_1^k + c_2^kx_2^k} \right)$ and $\theta _2^k = c_2^kx_2^k/\left( {c_1^kx_1^k + c_2^kx_2^k} \right)$. If $c_1^k$ and $c_2^k$ are set equal to input prices then $P_w^k\left( {x^k,y^k} \right)$ has a nice cost-saving interpretation: let the slope of the iso-cost line passing through point A in Fig. 3 reflect the actual relative input prices, then $P_w^A\left( {x^A,y^A} \right)$ = (cost at point A – cost at point A₁)/cost at point A.

Fig. 3

Potential improvement inefficiency measure for a technology with two inputs and a single output

Fourth, consider the enhanced Russell efficiency measure and its aggregation across DMUs. The enhanced Russell measure is defined as (Pastor et al. 1999):¹⁰

$$\begin{array}{*{20}{c}} {R_E^k = \mathop {{\min }}\limits_{\lambda ^k,\delta ^k} \left\{ {\frac{{\left( {\frac{1}{I}} \right)\mathop {\sum}\nolimits_{i = 1}^I {\lambda _i^k} }}{{\left( {\frac{1}{J}} \right)\mathop {\sum}\nolimits_{j = 1}^J {\delta _j^k} }}:\left( {\lambda _1^kx_1^k, \ldots ,\lambda _I^kx_I^k,\delta _1^ky_1^k, \ldots ,\delta _J^ky_J^k} \right) \in T,} \right.} & {} \\ {} & {\left. {0 < \lambda _i^k \le 1\,\forall i,\,\delta _j^k \ge 1\,\forall j} \right\} \le 1} \end{array}$$

(26)

Cooper et al. (2007), using essentially the conventional denominator rule suitable for ratios given in the same unit of measurement, derived a “system” efficiency measure for each input and output as:

$$\lambda _i^T = \mathop {\sum}\nolimits_{k = 1}^K {\lambda _i^k\left( {\frac{{x_i^k}}{{x_i^T}}} \right)} = \mathop {\sum}\nolimits_{k = 1}^K {\left( {\frac{{\tilde x_i^k}}{{x_i^k}}} \right)\left( {\frac{{x_i^k}}{{x_i^T}}} \right)} = \frac{{\mathop {\sum}\nolimits_{k = 1}^K {\widetilde x_i^k} }}{{x_i^T}} = \frac{{\widetilde x_i^T}}{{x_i^T}}$$

(27)

$$\delta _j^T = \mathop {\sum}\nolimits_{k = 1}^K {\delta _j^k\left( {\frac{{y_j^k}}{{y_j^T}}} \right)} = \mathop {\sum}\nolimits_{k = 1}^K {\left( {\frac{{\widetilde y_j^k}}{{y_j^k}}} \right)\left( {\frac{{y_j^k}}{{y_j^T}}} \right)} = \frac{{\mathop {\sum}\nolimits_{k = 1}^K {\widetilde y_j^k} }}{{y_j^T}} = \frac{{\widetilde y_j^T}}{{y_j^T}}$$

where $x_i^T = \mathop {\sum}\nolimits_{k = 1}^K {x_i^k}$ and $y_j^T = \mathop {\sum}\nolimits_{k = 1}^K {y_j^k}$. Then, in an attempt to obtain an overall “system” efficiency measure they used the following relationship:¹¹

$$R_E = \frac{{\left( {\frac{1}{I}} \right)\mathop {\sum }\nolimits_{i = 1}^I \lambda _i^T}}{{\left( {\frac{1}{J}} \right)\mathop {\sum }\nolimits_{j = 1}^J \delta _j^T}} = \frac{{\left( {\frac{1}{I}} \right)\mathop {\sum }\nolimits_{k = 1}^K \mathop {\sum }\nolimits_{i = 1}^I \left( {\frac{{x_i^k}}{{x_i^T}}} \right)\lambda _i^k}}{{\left( {\frac{1}{J}} \right)\mathop {\sum }\nolimits_{k = 1}^K \mathop {\sum }\nolimits_{j = 1}^J \left( {\frac{{y_j^k}}{{y_j^T}}} \right)\delta _j^k}}$$

(28)

which however implicitly assumes that every input (output) has the same effect on cost-saving (revenue-enhancing). A more intuitively appealing overall “system” efficiency measure can be obtained by relying on the denominator rule with unit ratio difference. By setting $z_i = \widetilde x_i^T$ and $\xi _i = x_i^T$ for inputs and $z_j = \tilde y_j^T$ and $\xi _j = y_j^T$ for outputs we get:

$$\begin{array}{l}R_E = \frac{{\mathop {\sum}\nolimits_{i = 1}^I {\theta _i\lambda _i^T} }}{{\mathop {\sum}\nolimits_{j = 1}^J {\theta _j\delta _j^T} }} = \frac{{\mathop {\sum}\nolimits_{i = 1}^I {\left( {\frac{{c_ix_i^T}}{{\mathop {\sum}\nolimits_{i = 1}^I {c_ix_i^T} }}} \right)\left( {\frac{{\widetilde x_i^T}}{{x_i^T}}} \right)} }}{{\mathop {\sum}\nolimits_{j = 1}^J {\left( {\frac{{c_jy_j^T}}{{\mathop {\sum}\nolimits_{j = 1}^J {c_jy_j^T} }}} \right)\left( {\frac{{\widetilde y_j^T}}{{y_j^T}}} \right)} }} = \frac{{\mathop {\sum}\nolimits_{k = 1}^K {\mathop {\sum}\nolimits_{i = 1}^I {\left( {\frac{{c_ix_i^k}}{{\mathop {\sum}\nolimits_{i = 1}^I {c_ix_i^T} }}} \right)\lambda _i^k} } }}{{\mathop {\sum}\nolimits_{k = 1}^K {\mathop {\sum}\nolimits_{j = 1}^I {\left( {\frac{{c_jy_j^k}}{{\mathop {\sum}\nolimits_{j = 1}^J {c_jy_j^T} }}} \right)\delta _j^k} } }}\\ \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \, = \frac{{\mathop {\sum}\nolimits_{k = 1}^K {\mathop {\sum}\nolimits_{i = 1}^I {\theta _i^k\lambda _i^k} } }}{{\mathop {\sum}\nolimits_{k = 1}^K {\mathop {\sum}\nolimits_{j = 1}^I {\theta _j^k\delta _j^k} } }}\end{array}$$

(29)

with the most obvious candidates for c_i and c_j being the input and output prices.

3.3 Market Power Index

If we set c₁ = y₁, z₁= p₁−MC₁, ξ₁= p₁, c₂= y₂, z₂= p₂−MC₂, and ξ₂= p₂ then we can use the denominator rule with unit ratio difference to aggregate price-cost margins or Lerner (1934) indices of market power:

$$\begin{array}{l}L\left( {\frac{{p_1 - MC_1}}{{p_1}},\frac{{p_2 - MC_2}}{{p_2}}} \right) = \frac{{p_1y_1}}{{p_1y_1 + p_2y_2}}\left( {\frac{{p_1 - MC_1}}{{p_1}}} \right) + \frac{{p_2y_2}}{{p_1y_1 + p_2y_2}}\left( {\frac{{p_2 - MC_2}}{{p_2}}} \right)\\ \qquad \quad \quad \quad \quad \quad \quad \quad \; = \frac{{\left( {p_1y_1 + p_2y_2} \right) - \left( {MC_1y_1 + MC_2y_2} \right)}}{{p_1y_1 + p_2y_2}}\end{array}$$

(30)

where MC refers to marginal cost. That is, the aggregate Lerner index is obtained by aggregating the individual measures with revenue shares as weights. Without any formal reasoning or any further explanation, Dickson (1979) used these weights to relate the aggregate Lerner index of market power with the Herfindahl index, the conjectural variation, and the industry demand elasticity.

4 Concluding remarks

In this paper we have provided a rule for consistent (arithmetic) aggregation of ratio-type variables with different units of measurement. This consists an extension of the denominator rule and the implied aggregation shares are given in terms of the denominator variable of the relevant ratio and the constants converting the relevant variables into the same unit of measurement. The denominator rule with unit ratio difference is a necessary and sufficient condition for consistent aggregation of ratio-type variables with different units of measurement. Its main advantage is that it can be used to aggregate ratio-type variables not only across DMUs but also across commodities, outputs or inputs.

The applicability of the conventional denominator rule is mainly limited to aggregation across DMUs and it is thus particular helpful for working with ratio-type performance measures, including a quite large number of efficiency and productivity indices. For some other performance measures though such as the non-radial technical efficiency indices, e.g., Fӓre efficiency measure and the enhanced Russell efficiency measure, and the Lerner index of market power that we considered in this paper, the denominator rule with unit ratio difference should be used to obtain a theoretically consistent aggregate (across DMUs) measure. By doing so, we have shown that (23) provides an alternative set of weights for aggregate Russell efficiency measure compared to that of Zhu (1996) based on expert opinion, and that of Hsiao et al. (2011) based on Shannon entropy. In addition, the denominator rule with unit ratio difference provides a justification for the weights used by Dickson (1979) to obtain the aggregate Lerner index of market power.

However, the applicability of the denominator rule with unit ratio difference goes beyond aggregation across DMUs as it can be used to aggregate price and/or quantities across commodities, outputs or inputs. As an illustration in Section 3, we have shown how Laspayres, Paasche and Lowe price and quantity indices can be obtained by applying the denominator rule with unit ratio difference. In addition, we have used it to derive a weighted Russell efficiency index and a weighted potential improvement efficiency index. In particular, (24) provides an alternative set of weights for the weighted potential improvement inefficiency index compared to equal weights used by Wang et al. (2013) while (29) provides an alternative set of weights for the enhanced Russell efficiency measure compared to those of Cooper et al. (2007) and Lozano (2009). The denominator rule with unit ratio difference could also be found useful in several other aggregation problems in economics, management and operation research.