Abstract
A detailed analysis of joint-contribution of premises and conclusions in classically valid sequents is presented in terms of hypergraphs. In (Saint-Germier, P., Verdée, P., & Villalonga, P. T. (2024). Relevant entailment and logical ground. Philosophical Studies (pp. 1–43). https://doi.org/10.1007/s11098-024-02101-1), this idea of joint-contribution is introduced and motivated as a method for characterizing four kinds of relevant validity, in the sense of selecting the relevantly valid sequents among the classically valid sequents. The account in (Saint-Germier, P., Verdée, P., & Villalonga, P. T. (2024). Relevant entailment and logical ground. Philosophical Studies (pp. 1–43). https://doi.org/10.1007/s11098-024-02101-1) is built on a calculus, called \(\textsf{GLK}^{\hbox {a}}\), which proves grounding claims for (enthymematically) valid sequents. In the present paper an adequate representation of \(\textsf{GLK}^{\hbox {a}}\) is given in terms of hypergraphs. The hypergraphs are a kind of diagrammatic proofs for Classical Propositional Logic, entirely based on the grounds of premises and conclusions. The hypergraphs and their visualization provide insights into the relations between premises and conclusions and into the way validity is produced by the binding of premises and conclusions via their partial grounds. They visualize the network of elements of the sequent that contribute to its logical validity. Non-contributing (i.e. irrelevant) premises and conclusions are then specified to be those that are disconnected from the network, however one constructs the graphs.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In this paper we deal with formally representing how exactly certain premises and conclusions of classically valid arguments contribute to the validity of the sequent and others do not. We will conceive of arguments as multiple-conclusion sequents. As is fairly common, let SET-SET sequents be pairs of sets of formulas separated by the  -symbol. In the sequent
-symbol. In the sequent  , the members of \(\Gamma\) represent the premises of the argument and the members of \(\Delta\) its conclusions. A multiple-conclusion argument is valid if, whenever all the premises hold, some of the conclusions hold, whence
, the members of \(\Gamma\) represent the premises of the argument and the members of \(\Delta\) its conclusions. A multiple-conclusion argument is valid if, whenever all the premises hold, some of the conclusions hold, whence  is defined to be valid if, in all interpretations, either at least one member of \(\Gamma\) is false or at least one member of \(\Delta\) is true,Footnote 1
is defined to be valid if, in all interpretations, either at least one member of \(\Gamma\) is false or at least one member of \(\Delta\) is true,Footnote 1
Validity in this sense by definition admits Weakening for premises and conclusions, i.e. if  is valid then so is
is valid then so is  , whenever \(\Gamma \subseteq \Gamma '\) and \(\Delta \subseteq \Delta '\). This means that, when one already has a valid sequent, one can arbitrarily add random formulas as premises or as conclusions. Qua random formulas, they do no work for establishing the validity of the sequent; they are so to say mere harmless bystanders.Footnote 2
, whenever \(\Gamma \subseteq \Gamma '\) and \(\Delta \subseteq \Delta '\). This means that, when one already has a valid sequent, one can arbitrarily add random formulas as premises or as conclusions. Qua random formulas, they do no work for establishing the validity of the sequent; they are so to say mere harmless bystanders.Footnote 2
Consider for example the valid sequents  and
and  . In both cases q is present in a non-contributing way; the other premises and conclusions are intuitively doing all the work for the validity and q could have been any other formula. We assume these to be non-controversial and straightforward cases of non-contributing premises or conclusions. But other cases are more interesting. In the equally valid
. In both cases q is present in a non-contributing way; the other premises and conclusions are intuitively doing all the work for the validity and q could have been any other formula. We assume these to be non-controversial and straightforward cases of non-contributing premises or conclusions. But other cases are more interesting. In the equally valid  , conclusion q is non-contributing in exactly the same sense as before, but it seems that also one of the premises \(p\wedge r\) and \(r\wedge p\) plays no role at all. We only need one of the two for the validity, the other could again have been any other formula. However, there is no good reason to mark one of them as non-contributing and not the other. In this case we need the notion of ‘joint contribution’. While all of the premises and the first conclusion contribute, \(p\wedge r\) and p form a jointly contributing set of premises and conclusions, and so do \(r\wedge p\) and p. The set containing all three of them does not form a jointly contributing set. A similar phenomenon occurs in
, conclusion q is non-contributing in exactly the same sense as before, but it seems that also one of the premises \(p\wedge r\) and \(r\wedge p\) plays no role at all. We only need one of the two for the validity, the other could again have been any other formula. However, there is no good reason to mark one of them as non-contributing and not the other. In this case we need the notion of ‘joint contribution’. While all of the premises and the first conclusion contribute, \(p\wedge r\) and p form a jointly contributing set of premises and conclusions, and so do \(r\wedge p\) and p. The set containing all three of them does not form a jointly contributing set. A similar phenomenon occurs in  and in
and in  : merely a subset of the premises and conclusions are jointly contributing (in the first case either the two p-formulas or the two q formulas and in the second case either the premise on its own or the conclusion on its own), but there is no good reason to choose one of the jointly contributing subsets over the others. As a last example, consider
: merely a subset of the premises and conclusions are jointly contributing (in the first case either the two p-formulas or the two q formulas and in the second case either the premise on its own or the conclusion on its own), but there is no good reason to choose one of the jointly contributing subsets over the others. As a last example, consider  : while the conclusion p could have been any other formula without affecting the validity, one can nevertheless consider both the premise and the conclusion as jointly contributing to the validity, in the sense that the sequent is an instance of the valid schema
: while the conclusion p could have been any other formula without affecting the validity, one can nevertheless consider both the premise and the conclusion as jointly contributing to the validity, in the sense that the sequent is an instance of the valid schema  , in which all elements jointly contribute to the validity. One of the reasons why the sequent is valid, i.e. that it is an instance of that valid schema, involves this specific conclusion p.
, in which all elements jointly contribute to the validity. One of the reasons why the sequent is valid, i.e. that it is an instance of that valid schema, involves this specific conclusion p.
So there is an intuitive sense in which some subsets of premises and conclusions of a valid sequent jointly contribute to the validity and others may not. But the natural question to ask is: if they indeed contribute, how exactly do they contribute and what is it that they contribute? A partial possible answer to this question is proposed and defended in (Saint-Germier et al., 2024). The basic idea there is that premises and conclusions contribute part of their meaning to the validity. In  the first premise contributes by offering itself entirely to the conclusion and the conclusion contributes by receiving the p-part of its meaning. The second premise does not contribute anything. One could say that the two contributing elements of the sequent are bound by a part of their meaning, namely p, and that this binding makes the sequent valid.
the first premise contributes by offering itself entirely to the conclusion and the conclusion contributes by receiving the p-part of its meaning. The second premise does not contribute anything. One could say that the two contributing elements of the sequent are bound by a part of their meaning, namely p, and that this binding makes the sequent valid.
Saint-Germier et al. (2024) uses the notion of grounding (in the spirit of (Correia, 2013) and (Fine, 2012), but then conceived in a bilateral fashion) as the more precise way to capture what we here intuitively introduced in terms of parthood of meaning. More specifically, it introduces a notion of bilateral logical grounding, i.e. the idea that the truth or falsity of complex sentences can be explained by the truth or falsity of other, less complex sentences. This way of explaining is found in the common practice of giving recursive clauses when defining truth and falsity of formulas in a model. We say that the truth or falsity of a complex sentence is grounded in the truth or falsity of simpler sentences if, whenever the simpler sentences have those truth values, the truth value of the complex formula can be explained by those truth values (in virtue of the usual semantic clauses). For example, we say that the truth of p grounds the truth of \(p\vee q\). The truth of p also grounds the falsity of \(\lnot p\) and, together with the falsity of q, it moreover grounds the falsity of \(\lnot p\vee q\). Reading this kind of grounding as articulating one aspect of parthood of meaning, one could say that p is a positive part of the positive meaning of \(p\wedge q\), of the negative meaning of \(\lnot p\), and of the negative meaning of \(\lnot p\vee q\). q is a negative part of the latter. Jointly-contributing sets of premises and conclusions contribute to the validity of sequents by those premises and conclusions being bound together by these kinds of grounds.
Remember that we defined validity of sequents as a property involving the falsity of some premises and the truth of some conclusions. It is then natural to expect that premises contribute partial grounds for their falsity to the validity of the sequent, while conclusions contribute partial grounds for their truth. In  , the first premise contributes the falsity of p and the conclusion contributes the truth of p. Because p is always either true or false, because the falsity of p trivially grounds the falsity of the first premise, and because the truth of p grounds the truth of the conclusion, in all possible interpretations at least the falsity of premise p or the truth of conclusion \(p\vee r\) is grounded, which is enough to establish validity. In the sequent
, the first premise contributes the falsity of p and the conclusion contributes the truth of p. Because p is always either true or false, because the falsity of p trivially grounds the falsity of the first premise, and because the truth of p grounds the truth of the conclusion, in all possible interpretations at least the falsity of premise p or the truth of conclusion \(p\vee r\) is grounded, which is enough to establish validity. In the sequent  , the falsity of p grounds the first premise, that of q the second and the truth of p, together with the truth of q, ground the conclusion. Because every interpretation supports either the truth or falsity of p and either the truth or falsity of q, at least one of the premises is grounded in those models in which either p or q are false, while in the models where they are both true, the conclusion is grounded. Consequently, the validity is established by binding the first premise via its only partial ground to the conclusion accounting for one of its two partial grounds in combination with binding the second premise via its only partial ground to the conclusion, accounting for its other partial ground. In general, this process shows that validity can be obtained by premises and conclusions being bound by their opposite partial grounds.
, the falsity of p grounds the first premise, that of q the second and the truth of p, together with the truth of q, ground the conclusion. Because every interpretation supports either the truth or falsity of p and either the truth or falsity of q, at least one of the premises is grounded in those models in which either p or q are false, while in the models where they are both true, the conclusion is grounded. Consequently, the validity is established by binding the first premise via its only partial ground to the conclusion accounting for one of its two partial grounds in combination with binding the second premise via its only partial ground to the conclusion, accounting for its other partial ground. In general, this process shows that validity can be obtained by premises and conclusions being bound by their opposite partial grounds.
In (Saint-Germier et al., 2024) a sequent calculus called \(\textsf{GLK}^{\hbox {a}}\) is given that specifies how one can derive the validity of sequents from mere claims about grounding of the falsity of premises and the truth of conclusions, by repeatedly binding jointly contributing elements of a sequent via their opposite partial groundsFootnote 3. The binding metaphor is intuitively clear and simple for basic cases like the aforementioned sequents: anybody who knows basic propositional logic, sees which premises and conclusion can be bound in this way.
It might then seem that reducing contribution to such binding relations is a mere matter of realizing that a premise or conclusion contributes if and only if it is able to bind with some other premise or conclusion. However, the notion of contribution considered here is much more subtle: for there to be contribution, exactly those binding relations between contributing premises or conclusions need to make the sequent valid, not other bindings that do not sufficiently establish validity. For example, in the valid sequent  only the premise contributes to the validity (by the fact that two copies of it can be bound through the truth/falsity of q), although the premise and conclusion have opposed partial grounds and can be bound by those partial grounds.
only the premise contributes to the validity (by the fact that two copies of it can be bound through the truth/falsity of q), although the premise and conclusion have opposed partial grounds and can be bound by those partial grounds.
In fact, the way \(\textsf{GLK}^{\hbox {a}}\) explicates contribution gives rise to a structurally rather complex binding relation between premises and conclusions. This interesting structure is not immediately transparent in \(\textsf{GLK}^{\hbox {a}}\)-derivations. Understanding how the (joint) contribution really works by ground-binding requires explicitly mapping the network of interactions between premises and conclusions in detail.
This is the main objective of the present paper. We provide insight into the ways in which parts of valid sequents relate to each other by mapping and visualizing this complicated relation of establishing sequent validity by means of ground binding. We completely stick to the formalism presented in (Saint-Germier et al., 2024) for the basic notion of joint-contribution and grounding, but, by means of hypergraphs consisting of vertices labeled by formulas–premises, conclusions and their partial grounds– and their sign (positive/true or negative/false), we are able to represent the detailed network of binding interactions between all the different premises and conclusions of sequents. The crucial factor for joint-contribution will be the connectedness of parts of the networks. Only if there is some connected subnetwork (i.e. one in which all elements are indirectly connected to each other) involving a set of premises and conclusions in some correct network representation of the sequent, the network will prove validity, and only the premises and conclusions in such a subnetwork will be seen as jointly contributing to the validity. In this way one obtains clear and visual insight into the precise way in which several elements of sequents interact by matching opposite partial grounds.
Like in (Saint-Germier et al., 2024), the aim behind all of this is to explicate relevance intuitions in a natural and insightful way, without going beyond or against classical logic. In (Saint-Germier et al., 2024), the ground-theoretical joint-contribution idea is used for the definition of four types of relevant validity, three of which have before been discussed in the literature (cf. Brauer, 2020; Smiley, 1996; Tennant, 2017; Verdée et al., 2019), ultimately based on a negative account of contribution as a form of indispensability. The main contribution of (Saint-Germier et al., 2024) is to provide a positive account of the four kinds of relevance by means of joint-contribution cashed out in terms of grounding. It is that account that is further analysed here. Unlike (Saint-Germier et al., 2024), the current paper will not directly discuss relevant validity or relevant entailment. It is straightforward for the reader of both papers to see how the hypergraphs can also be seen as providing a proof theory and visualization for each of the four kinds of relevant validity.
This paper does not aim or claim to offer deep mathematical results about the concepts that are introduced or used. The whole text is written in such a way that the metatheoretical propositions we formulate are easily seen to hold, once the definitions are well understood. The definition of the hypergraphs and the associated joint-contribution idea is supposed to be a new way of thinking visually and structurally about relevant and irrelevant arguments. It is an invitation to use this new language for pedagogical purposes and for proving substantial mathematical results about proofs conceptualized as networks or hypergraphs.
2 The calculus \(\textsf{GLK}^{\hbox {a}}\) for bilateral grounding
We start by rehearsing the \(\textsf{GLK}^{\hbox {a}}\)-calculus from (Saint-Germier et al., 2024).
Fix the language of propositional logic with connectivesFootnote 4\(\lnot\), \(\vee\), \(\wedge\), and sentential letters p, q, r, \(\ldots\), possibly with subscripts. \(A, B, A_1, \ldots\) will be used as metavariables for formulas. A signed formula \(A^+\) or \(A^-\) is a formula A with a sign ‘\(+\)’ or ‘−’ added to it. They represent formulas with their truth value (\(A^+\) means ‘A is true’, while \(A^-\) means ‘A is false’).
We will represent sequents by means of multisets of signed formulas with their truth value, namely the falsity of the premises together with the truth of the conclusions. A multiset is a set, combined with the information how often each member occurs in the multiset. We represent them by enumerating each copy of each member between double braces \(\{ \! \{\) and \(\} \! \}\) (we omit the braces if there is no confusion). Sequents will be represented as expressions of the form \([[\Phi ]]\), where \(\Phi\) is a multiset of signed formulas, such that \([[\{ \! \{A_1^+, \ldots , A_n^+, B^-_1,\ldots B^-_m\} \! \}]]\) denotes the sequent  . We use multisets instead of sets because premises and conclusions can play multiple different roles for establishing validity. Take for example
. We use multisets instead of sets because premises and conclusions can play multiple different roles for establishing validity. Take for example  , in which the first premise is used once together with the second premise to give q and once with the third premise to give r. We need both the truth of q and that of r to ground the conclusion, so one could say that, in the multiset \(\{ \! \{p^-, p^-, \lnot p\vee q^-, \lnot p\vee r^-, q\wedge r^+\} \! \}\) used for representing the sequent, all elements jointly contribute to the validity. This would not hold if we had added a (useless) third copy of \(p^-\) to the multiset. We call the members of \(\Phi\) the s-elements (abbreviation of ‘sequent elements’) of the sequent \([[\Phi ]]\).
, in which the first premise is used once together with the second premise to give q and once with the third premise to give r. We need both the truth of q and that of r to ground the conclusion, so one could say that, in the multiset \(\{ \! \{p^-, p^-, \lnot p\vee q^-, \lnot p\vee r^-, q\wedge r^+\} \! \}\) used for representing the sequent, all elements jointly contribute to the validity. This would not hold if we had added a (useless) third copy of \(p^-\) to the multiset. We call the members of \(\Phi\) the s-elements (abbreviation of ‘sequent elements’) of the sequent \([[\Phi ]]\).
Sequents can be valid absolutely/simpliciter as stipulated before, but they can also be enthymematically valid given a set of fixed truths and falsities (certain formulas with determined truth values) if either the premises are false or the conclusions are true in all interpretations respecting the given set of fixed truths and falsities. For example: \([[\lnot p \vee q^-, q^+]]\) is enthymematically valid given the truth of p, because either \(\lnot p\vee q\) is false or q is true in all interpretations in which p is true.
Capital letters \(X, Y, Z, X_1, \ldots\) are used as metavariables for signed formulas, and Greek capital letters \(\Phi , \Phi , \Sigma , \Sigma _1, \ldots\) as metavariables for multisets of signed formulas. \([[\Phi ]], [[\Phi _1]], [[\Sigma ]], [[\Sigma _1]], \ldots\) are then metavariables for sequents. We use \(\textsf{X}, \textsf{Y}, \textsf{Z}, \mathsf {X_1}, \ldots\) as metavariables for signed formulas or sequents.Footnote 5
In the grounding calculus, grounding statements are constructs of the form \(\Phi < \textsf{X}\), i.e. of the form \(\Phi < X\) or \(\Phi < [[\Psi ]]\).
Let us discuss one of the ways to read and understand such claims.
and
mean that, if all \(A_i\) were true and all \(B_i\) were false, the falsity of C, resp. the truth of D, would be grounded in the the truth of the \(A_i\) and the falsity of the \(B_i\).
means that, assuming that we fix all \(A_i\) as true and all the \(B_i\) as false, the fact that either one of the \(C_i\) is true or one of the \(D_i\) is false in all thus selected interpretations can be grounded by the truth of the \(A_i\) in combination with the falsity of the \(B_i\). The sequents that can be \(\textsf{GLK}^{\hbox {a}}\)-derived with an empty ground slot to the left of < (we say that they are zero-grounded) are all and only the ones that are classically valid. For philosophical interpretation and justification of this grounding relation and its calculus, we refer to (Saint-Germier et al., 2024).
Definition 1
\(\Psi < \textsf{X}\) holds if it can be derived from the rules in Table 1.
For this paper it will suffice to restrict ourselves to, so called, analytic derivations. They are, informally put, the ones in which the structural rules are applied separately by type, not intermingled, and in a specific order; in a first phase axioms, then only (Trans\(_<\)), in the third phase only (Bind), in the fourth only (Amalg), and in the final phase only (<W), with the nuance that (SCon) and (GCon) are possible everywhere.Footnote 6 Formally we can represent this with the rules in Table 2, in which a grounding claim of the form \(\Phi <_i \textsf{X}\) means that \(\Phi < \textsf{X}\) can be derived in phase i of a derivation.
Here is an example of an analytic derivation in the grounding calculus \(\textsf{GLK}^{\hbox {a}}\) divided into the aforementioned phases. We omit applications of the (Ph)-rule. We start with derivations \({\mathcal{D}}_1\) for \(p^+,q^-<_2 [[\lnot p \vee q^-]]\), \({\mathcal {D}}_2\) for \(r^- <_2 [[\lnot r^+]]\), and \({\mathcal {D}}_3\) for \(q^+,r^+ <_1 [[q \wedge r^+]]\).



In derivation \({\mathcal {D}}_4\) and \({\mathcal {D}}_5\) we resp. show that \(p^+ <_3 [[\lnot p \vee q^-, \lnot r^+,q \wedge r^+]]\) and that \(<_3 [[p^-,\lnot p \vee q^-, \lnot r^+,q \wedge r^+]]\), now also utilizing the (Bind)-rule:


In the last derivation we finally add the missing premise by means of (<W):

3 From \(\textsf{GLK}^{\hbox {a}}\)-derivations to logical hypergraphs
In this section, we introduce a graph-theoretic representation of the grounding calculus \(\textsf{GLK}^{\hbox {a}}\) by means of a special kind of graphs. The logical hypergraphs, as we shall call them, will have exactly the same proving power as that calculus, but by associating graphs to every sequent, we are able to show whether and how the partial grounds of the contributing premises and conclusions relate to each other. In this way, we obtain a clear and visual insight into and a precise mathematical characterization of joint-contribution and the relevance and irrelevance of parts of valid sequents.
Technically, the graph-theoretical objects we shall employ are hypergraphs, a generalization of ordinary graphs allowing edges to connect multiple vertices (instead of just two in ordinary graphs). This is, admittedly, a rather unfamiliar notion, but it can simply be seen as a totality of nodes that can be connected by edges that can relate a multitude of nodes at once (instead of always two in ordinary graph theory).
Definition 2
[Hypergraph] A hypergraph is a pair \(\langle X, E\rangle\) such that X is some set (called the vertices) and E is a set of non-empty subsets of X (called the edges).
Accordingly, several usual notions of graph theory (e.g., path, cycle, etc.) need to be generalized to apply to hypergraphs. While, in the literature, these notions are sometimes given alternative names (such as e.g. Berge path), we use the ordinary graph-theoretical names. This is possible without causing confusion because we do not need to and will not speak about ordinary graphs at all in this paper. Even the word graph will always denote a hypergraph in the remainder of the paper. The reader does not need to be acquainted with hypergraphs to understand our very basic usage of them. The following definitions suffice to comprehend what follows.
Definition 3
We use the following fairly standard notions from hypergraph theory:
-
A vertex v and an edge e are adjacent iff \(v\in e\).
-
A path consists of a sequence of k distinct vertices \(v_1, v_2,\dots ,v_k\) and \(k-1\) distinct edges \(e_1\), e2, ..., \(e_{k-1}\) such that \(v_i, v_{i+1} \in e_i\) for all \(i \in \{1, 2, \dots , k-1 \}\).
-
A cycle is a path containing at least two vertices and such that \(v_1\,=\,v_k\).
-
A set V of vertices in a hypergraph are connected iff there is a path between every two distinct vertices \(u, v\in V\).
-
A hypergraph \({\mathcal {G}}_1\) is a subgraph of another hypergraph \({\mathcal {G}}_2\) if the vertices of \({\mathcal {G}}_1\) are vertices of \({\mathcal {G}}_2\) and the edges of \({\mathcal {G}}_1\) are edges of \({\mathcal {G}}_2\).
-
A connected set is moreover non-trivially connected iff it is has at least two members.
-
A hypergraph is connected if the totality of its vertices is.
-
A component of a hypergraph \({\mathcal {G}}\) is a connected subgraph of \({\mathcal {G}}\) that is not a proper subgraph of another connected subgraph of \({\mathcal {G}}\). A component is non-trivial if it contains at least two vertices.
-
The disjoint union of two hypergraphs is the hypergraph created by taking the union of the vertices of the two hypergraphs as the set of vertices and the union of the edges of two hypergraphs as the set of edges, under the assumption that the two hypergraphs share no vertices (otherwise the operation is undefined).
The kind of hypergraphs we are interested in have vertices that are labeled by signed formulas X or by single element sequents, i.e. expressions of the form [[X]]. There are two kinds of vertices: groundee vertices (denoted by an arrowhead) and ground vertices (denoted by an arrowtail). The visualization is specified in Table 3.
There are three kinds of edges, closing edges, disjunctive grounding edges and conjunctive grounding edges Footnote 7 (if we speak of grounding edges simpliciter, we just mean either kind of grounding edge). Closing edges contain exactly two vertices, a ground vertex and a groundee vertex with the same signed formulas as their labels. We represent them by drawing the groundee vertex’s arrowhead inside the ground vertex’s Y-shape, and by mentioning the common label only once (see Table 4). Vertices adjacent to a closing edge are called closed and the others open.
Grounding edges will be represented by stars of straight lines, as illustrated in Table 5. In the generic visualizations of graphs and their rules, the diamond-shaped nodes are used to represent vertices (open or closed) and the boxes represent hypergraphs. The lines are dashed in the case of disjunctive grounding edges and full in the conjunctive case. A star is a bold point from which a line leaves to each member of the edge; if the edge has just two vertices as members, the star will look like an ordinary straight line between the two vertices, often utilized to visualize an edge in ordinary (non-hyper) graph theory. Singleton edges will not occur in our graphs. Grounding edges express a grounding relation between the labels of the ground vertices adjacent to them on the one hand and the labels of the adjacent groundee vertices on the other. In case there are multiple groundee vertices with a label of the form [[X]], the groundee is the sequent made up out of the combination of all those labels.
Definition 4
[S-element, justified vertex, justified hypergraph] An s-element vertex is an open groundee vertex of the form [[X]]. An s-element is justified if it is adjacent to a grounding edge and fully justified if there is moreover no path to an open ground vertex. A hypergraph is fully justified if all its s-element vertices are fully justified.
Definition 5
[Flat and sequent hypergraphs] A hypergraph with at least one s-element vertex is called a sequent hypergraph and one that has one open groundee vertex labeled by a signed formula is called flat.
Sequent hypergraphs are very different from flat hypergraphs if it comes to their purpose and interpretation. Flat ones express ways in which sentences having truth values can be grounded (corresponding to gounding sequents like \(X_1, \dots , X_n < Y\)) while sequent hypergraphs express ways in which the validity or enthymematic validity of sequents can be grounded (corresponding to grounding sequent like \(X_1, \dots , X_n < [[ Y_1, \dots , Y_m ]]\)). Every open groundee vertex of a flat one is labeled by a signed formula, while in a sequent one they are labeled by signed formulas enclosed by double square brackets, expressing the formula qua premise or conclusion. It makes no sense to have multiple open groundee vertices in a flat hypergraph: one want to ground one fact (that a sentence has a truth value), no a multitude of them.
Closed vertices can be seen as vertices that are no longer of interest when one wants to extract the basic grounding and validity information from the labeled hypergraph. They have fulfilled their duty as intermediates, and are only represented in the graph to be able to trace back how we found the connections. The open groundee vertices are grounded in all the other open vertices that are (directly or indirectly) connected to them.
We introduce the notion of a logical hypergraph, a hypergraph that has the right structure to represent grounding and entailment relations. This will give us the means to define a graph-theoretic version of the (relevant) grounding calculus. First consider some useful visualization machinery in Table 6.
Definition 6
[Logical hypergraph] A logical hypergraph is a hypergraph in the above sense, constructed according to the operational axioms in Table 7 and the structural rules in Table 8.
Some structural rules are restricted to sequent hypergraphs as they simply make no sense when applied to flat hypergraphs. If a rule can multiply the number of open groundee vertices and we allow it to apply it to flat hypergraphs, we risk the meaningless outcome that a graph would express a grounding claim for two or more formulas each having some specific truth value, which makes no sense in our interpretation. Either we have multiple groundees, in which case we deal with sequents, who can have multiple premises and conclusions, represented by signed formulas between double square brackets, or we have a simple claim about what grounds a single formula having a truth value. Hybrids of this make no sense and have no purpose in our framework. The contraction rule for grounds (GCon) applies to any graph that expresses a grounding relation, whether it is a sequent graph or not, as soon as there are two same-labeled open ground vertices. The other contraction rule expresses that two copies of a same premise or conclusion may be reduced to just one. This does not make any sense for flat graphs, as they do not have premises or conclusions.
Definition 7
[Analytic logical hypergraph] A logical hypergraph is recursively defined to be in stage 1 if its construction only involves (GCon) and axioms, in stage 2 if it is in stage 1 or it is the result of applying (Trans\(_<\)) or (GCon) to stage 2-graphs, in stage 3 if it is in stage 2 or the result of applying (Bind), (GCon), or (SCon) to stage 2-graphs, in stage 4 if it is in stage 3 or the result of applying (Amalg) to stage 3-graphs and, finally in stage 5 if it is in stage 4 or the result of applying (<W) to stage 4-graphs. An analytic logical hypergraph is a logical hypergraph which is in one of the five stages mentioned above (or, equivalently, in stage five).
In what follows we will only consider analytic logical hypergraphs. Whenever we speak of logical hypergraphs, we only refer to the ones that are analytic. It is quite plausible that the specificity of the analytic kind only concerns the construction process and that the two categories are therefore extensionally equivalent. We have not proven this conjecture. In any case, the analytic graphs have the same proving power as the more general kind of graphs in view of the parallels with the (analytic) \(\textsf{GLK}^{\hbox {a}}\)-derivations, so this restriction (if it really is one at all) is logically innocent.
Proposition 1
Each logical hypergraph is either a sequent hypergraph or a flat hypergraph, and never both.
Proof
By induction.
The base case. All hypergraphs introduced by the operational axioms are flat and those introduced by (Ent) are always sequent hypergraphs.
Induction step. Assume that the premise graphs of each rule are flat or sequent but not both. We prove that the same holds for the conclusion graphs of each rule. (Trans\(_<\)). By the induction hypothesis the second premise graph is flat and so it has only one groundee vertex. In the conclusion graph this groundee vertex is closed, so the groundee vertices of the conclusion graph are identical to those of the first premise graph, which is flat or sequent but not both by the induction hypothesis. (Bind). The premise graphs need to be sequent graphs, so all the groundee vertices are sequent-labeled. The groundee vertices of the conclusion graph are a subset of the groundee vertices of the two premise graphs combined and, consequently, also the conclusion graph is a sequent graph and not flat. (GCon). This rule does not change the groundee vertices so the induction hypothesis justifies that the conclusion graph is also either sequent or flat but not both. (SCon). Both premise and conclusion graph are sequent and the conclusion is not flat because the premise is not by the induction hypothesis and no new open groundee vertex emerges in the rule-application. (<W) and (Amalg). Both rules transform sequent graphs into other sequent graphs. The premise graphs cannot be flat in view of the induction hypothesis, and so the conclusion graphs are not flat either because no new signed-formula-labeled groundee vertices can be introduced by these rules. \(\square\)
Verifying whether a given hypergraph is indeed a logical hypergraph can go as follows. One breaks down the graph step by step, by applying the structural rules, phase by phase in reverse, until no further structural rules can be applied in reverse to any of the hypergraphs that result from this decomposition procedure. To see that this method can be transformed into a deterministic procedure, consider that all hypergraphs are finite and that there are only a finite number of rules such that the hypergraph can be the result of its application. Because each rule makes the hypergraphs strictly more complex, the application in reverse results in ever simpler graphs. We can thus exhaustively try out every way in which the hypergraph can be broken down into simpler graphs (in an arbitrary predetermined orderFootnote 8) and, if the current full breakdown does not result in axiomatic basic hypergraphs, we backtrack the process and try the other ways to break it down (the fact that we apply the rules in phases does not make a difference here, given that we do an exhaustive breakdown). The original hypergraph was then a logical hypergraph iff all the obtained hypergraphs after decomposition are of the form of one of the hypergraphs that can be obtained by applying the axioms.
Just like the \(\textsf{GLK}^{\hbox {a}}\)-calculus, the logical hypergraphs constitute a calculus for proving grounding claims.
Definition 8
[Proving grounding claims] A flat logical hypergraph is said to prove \(\Phi < X\) if (i) the members of \(\Phi\) are the labels of the open ground vertices and (ii) X is the label of its open groundee vertex. A sequent logical hypergraph proves \(\Phi < [[\Psi ]]\) if (i) the members of \(\Phi\) are the labels of the open ground vertices and (ii) the members of \(\Psi\) are the labels of the s-element vertices of the hypergraph, put inside double square brackets. We also say that it is a logical hypergraph for \(\Phi < X\) resp. \(\Phi < [[\Psi ]]\).
Proposition 2
[Adequacy] There is a \(\textsf{GLK}^{\hbox {a}}\)-derivation for \(\Phi <\textsf{X}\) iff there is a logical hypergraph that proves \(\Phi <\textsf{X}\).
Proof
Definition 8 allows finding the grounding claim proven by a hypergraph solely based on the labels of open vertices in logical hypergraphs. If one merely focuses on the open vertices, the rules for forming logical hypergraphs out of other hypergraphs are identical to those for deriving correct grounding claims out of other correct grounding claims in analytic \(\textsf{GLK}^{\hbox {a}}\)-derivations.
We will only discuss this process for the (Bind)-rule in the two calculi. The reader can easily verify that the other rules also match perfectly with their \(\textsf{GLK}^{\hbox {a}}\)-counterparts. In \(\textsf{GLK}^{\hbox {a}}\), (Bind) allows for removing \(A^-\) as a partial ground from one grounding claim and \(A^+\) as a partial ground from another before merging those two claims into one. This is also done by the graph rule (Bind): the resulting hypergraph contains the very same open vertices as \({\mathcal {G}}_1\) and \({\mathcal {G}}_2\) taken together, except that an open \(A^+\)-labeled ground vertex from \({\mathcal {G}}_1\) and an open \(A^-\)-labeled ground vertex from \({\mathcal {G}}_2\) are closed in the resulting graph. \(\square\)
It is important to realize that, despite the fact that the rules for constructing logical hypergraphs resemble the rules to go from correct grounding sequents to other correct grounding sequents, logical hypergraphs contain much more information; they constitute entire proofs for the grounding sequent they prove. There are no logical hypergraphs for incorrect grounding sequents, and so, if we can construct a logical hypergraph, the grounding sequent for which it is a logical hypergraph is correct.
Logical hypergraphs do not only serve to prove grounding claims. They are also ways to represent (possibly unfinished or failed) attempts of proving sequents.
Definition 9
[Logical hypergraph for sequents] A logical hypergraph \({\mathcal {G}}\) is a logical hypergraph for a sequent if the s-elements of the sequent, put inside double square brackets, are the labels of the s-element vertices of \({\mathcal {G}}\). Any number of open ground vertices is allowed here.
It is perfectly possible that a logical hypergraph for a sequent does not prove the sequent in question (consider that a logical hypergraph for \(p^-<[[p^+]]\) is also a logical hypergraph for the sequent \([[p^+]]\), which is obviously not valid). Only valid hypergraphs prove the sequent for which they are logical hypergraphs. What validity means for a logical hypergraph is developed in Sect. 5.
4 Some examples of logical hypergraphs
As a first example, we construct a logical hypergraph that corresponds to the \(\textsf{GLK}^{\hbox {a}}\)-derivation given in Sect. 2, which showed how \(<[[p\vee s^-, p^-, \lnot p \vee q^-, q\wedge r^+,\lnot r^+]]\) can be obtained from basic grounding principles.
To represent this proof as a logical hypergraph, we first create, by means of the axioms of the system, the stage 1-logical hypergraphs consisting of one grounding edge that corresponds to an axiom in the \(\textsf{GLK}^{\hbox {a}}\)-derivation. The result is represented in Fig. 1.
Next we connect the stage 1-logical hypergraphs step by step by first applying the (Trans\(_<\))-rule resulting in stage 2-logical hypergraphs. Here we need to do this four times by connecting two disjoint hypergraphs by means of a closing edge. We obtain 4 stage 2-hypergraphs. These steps correspond to the applications of (Trans\(_<\)) in the \(\textsf{GLK}^{\hbox {a}}\)-derivation. In the third stage we apply the (Bind)-rule three times, reducing the number of stage 3-logical hypergraphs from 4 to 3, from 3 to 2, from 2 to 1, in the end creating one connected stage 3-logical hypergraph. Afterwards the (<W)-rule allows us to add the isolated \([[p\vee s^-]]\)-labeled groundee vertex to the graph. This corresponds to the application of Weakening in the last step of the \(\textsf{GLK}^{\hbox {a}}\)-derivation. The result is a logical hypergraph in which the labels of the s-element vertices correspond exactly to the s-elements of the sequent whose zero-groundedness is proved by the \(\textbf{GLK}\)-proof. It is visualized in Fig. 2.
A second and somewhat more complex example is visualized in Fig. 3. The complexity lies here in the fact that we here have at three points in the graph construction two grounds or groundees with the same label that need to be contracted into one new ground/groundee vertex connected to both. Concretely, premise \([[r\vee s^-]]\) occurs as the label of two s-element vertices before the last (SCon)-application, but it is then reduced to only one by (SCon). In an earlier stage of the construction, we also twice need a case of ground contraction, dealt with by (GCon). First the two copies of the partial ground \(p^+\) are contracted into only one and then the same is done for the two copies of \(q^+\). In the visualization, the dashed lines (indicating disjunctive grounding edges) show where these contractions are situated.
5 Graphs and validity
Logical hypergraphs are, just like \(\textsf{GLK}^{\hbox {a}}\)-derivations, interesting tools to prove and represent grounding relations, but here we are mostly interested in their capacity to represent ground-connections between s-elements in a valid sequent. We aim to capture what it is that makes sequents valid, i.e. what makes the difference between a graph that does not establish the validity of its sequent and a graph that does.
A logical hypergraph for a sequent only becomes a proof for that sequent if it has a non-trivial component without open ground vertices. Such a component makes the hypergraph valid.
Definition 10
[Validity-maker, basis] A logical hypergraph \({\mathcal {G}}_1\) is a validity-maker of a logical hypergraph \({\mathcal {G}}_2\) if \({\mathcal {G}}_1\) is a fully justified component of \({\mathcal {G}}_2\). A set V of s-element vertices in \({\mathcal {G}}\) is a basis for \({\mathcal {G}}\) if there is a validity-maker \({\mathcal {G}}'\) of \({\mathcal {G}}\) such that V exactly contains the s-element vertices in \({\mathcal {G}}'\).
Definition 11
[Validity of a graph] A logical hypergraph is valid if it has a validity-maker.
Proposition 3
There is a valid logical hypergraph for all and only the classically valid sequents.
Proof
Valid sequent \(\Rightarrow\) valid graph. Proposition 2 and the fact the classically valid sequents are exactly those that are zero-grounded according to \(\textsf{GLK}^{\hbox {a}}\) entail that there is a graph without open ground vertices for each classically valid sequent. Given that the construction of that graph must have started with an axiom, and because edges are never removed, it has at least one non-trivial component. Because this component has no open ground vertices it is fully justified and therefore a validity-maker.
Valid graph \(\Rightarrow\) valid sequent. A valid graph has a validity-maker. This validity-maker has no open ground vertices and is therefore on its own a hypergraph for the zero-groundedness of a subsequent of the sequent for which the graph is a logical hypergraph. Because the zero-grounded sequents are the classically valid ones, that subsequent will be classically valid. Hence the entire sequent for which the graph is a logical hypergraph is a Weakening thereof and so it is equally valid. \(\square\)
Given the notion of a validity-maker and a basis, we can directly see which s-element vertices actually contribute to the validity.
Definition 12
[Contribution in a hypergraph] An s-element vertex contributes to the validity of a logical hypergraph \({\mathcal {G}}\) iff it is a member of a basis for \({\mathcal {G}}\). A set V of s-element vertices jointly contributes to the validity if it is a subset of a basis for \({\mathcal {G}}\) and sufficiently contributes to the validity if V is the union of some set of bases for \({\mathcal {G}}\).
Figure 4 illustrates these notions. It represents a single logical hypergraph divided into its components in frames 1–6. To know for which sequent it is a logical hypergraph, we just need to gather the labels of all the s-element vertices, i.e. \([[p^-]], [[q^-]], [[p^-]], [[q^-]], [[p\vee q^-]], [[p\wedge q^+]], [[p^+]], [[q^+]], [[q\wedge r^+]], [[r\vee \lnot r^+]],\) and \([[r^+]]\), which gives the sequent \([[p^-, q^-, p^-, q^-, p\vee q^-, p\wedge q^+, p^+, q^+, q\wedge r^+, r\vee \lnot r^+, r^+]]\). Components 1, 2, 3, and 5 are validity-makers. In each of them the set of their s-element vertices jointly and sufficiently contributes to the validity. Each of their proper subsets contributes jointly but not sufficiently. All the s-element vertices in any of these validity-makers contribute. Components 4 and 6 are not validity-makers because 4 contains open ground vertices and 6 lacks a grounding edge. Their s-element vertices do not contribute at all. Because there is at least one validity-maker, the graph is valid, which means that it can count as a proof for the main sequent, but also for the sequents corresponding to subgraphs that also contain a validity-maker, such as the valid combination of components 2 and 6 (hypergraph for \(<[[p^-, p^+, r^+]]\)) and the valid hypergraph consisting only of component 1 (hypergraph for \(<[[r\vee \lnot ^+]]\)). The hypergraph consisting of hypergraphs 4 and 6 has no validity-maker whence it is not valid and therefore it does not count as a proof for the (invalidFootnote 9) sequent \([[p\vee q^-, q\wedge r^+, r^+]]\). The combination of components 1 and 5, which is a logical hypergraph for \([[p^-,q^-, p\wedge q^+, r\vee \lnot r^+]]\) only contains validity-makers. All its s-element vertices therefore sufficiently contribute to the validity, but they do not contribute jointly as a whole. Component 1 is nothing but a validity-maker for its sequent \([[r\vee \lnot r^+]]\).
6 Joint-contribution visualized
Now that we have represented \(\textsf{GLK}^{\hbox {a}}\) in graph-theoretic terms, we have everything at our disposal to finally explicate and visualize how exactly premises and conclusions contribute to the validity. The basic idea is that an s-element contributes to the validity of a sequent by establishing a certain kind of connection between its partial grounds and the partial grounds of other s-elements within a validity-maker; we will say that such s-elements are bound by their partial grounds.
For what follows, to obtain the most interesting structure for the remainder of the analysis, it is best to undo the applications of the (SCon)-rule at the end of the logical hypergraph construction, which means that distinct s-element vertices with the same label that play a distinct role are always individually analyzed.
The relevant sort of binding connection essentially involves what we call bridges.Footnote 10
Definition 13
A bridge is a subgraph of a logical hypergraph consisting of nothing but two groundee vertices with labels \(A^+\) and \(A^-\), for some formula A, and a conjunctive grounding edge containing exactly those two vertices. A path that includes a bridge will be said to cross that bridge. A path from \(v_1\) to \(v_2\) is said to cross an X-Y-bridge if it crosses a bridge with vertices labeled X and Y, in order of occurrence in the path.
Note that bridges are always introduced in logical hypergraphs by the (Bind)-rule and every (Bind)-rule introduces a new bridge in the graph. They are always of the form  .
.
As an illustration, the graph depicted in Fig. 4 contains 6 bridges. In component 2 of that graph there is only one bridge; the central edge with its two adjacent groundee vertices labeled \(p^-\) and \(p^+\).
Definition 14
[Partial ground-reception] An s-element vertex \(v_1\) receives partial ground X from another s-element vertex \(v_2\) (in symbols: \(\textsf{Rec}_X(v_1,v_2)\)) if there is a path from \(v_1\) to \(v_2\) that crosses exactly one bridge, an X-Y bridge.Footnote 11
Definition 15
[Binding] We say that two s-element vertices \(v_1\) and \(v_2\) are bound, i.e. \(\textsf{Bound}(v_1,v_2)\), if there is some X such that \(\textsf{Rec}_X(v_1,v_2)\). Two sets of s-element vertices \(V_1\) and \(V_2\) are bound if a member of \(V_1\) is bound with a member of \(V_2\). We also say that two s-element vertices or two sets of s-element vertices are bound by partial ground (\(A^x/A^{-x}\)) if they are bound and the X that is received is either \(A^x\) or \(A^{-x}\).
The following proposition explains why we speak of partial grounds when we say what binds s-element vertices.
Proposition 4
If an s-element vertex labeled \([[X_1]]\) receives partial ground \(A^x\) from an s-element vertex labeled \([[X_2]]\) then \(A^x\) is a partial ground of \([[X_1]]\) (i.e. there is a \(\Phi\) such that \(\Phi , A^x < [[X_1]]\)) and \(A^{-x}\) is a partial ground of \([[X_2]]\) (i.e. there is a \(\Phi\) such that \(\Phi , A^{-x} < [[X_2]]\)).
Proof
If an s-element vertex \(v_1\) labeled \([[X_1]]\) receives partial ground \(A^x\) from an s-element vertex \(v_2\) labeled \([[X_2]]\), then there is a single bridge between the two vertices. This bridge must have been introduced by an application of the (Bind)-rule in the construction of the graph. Because there is only one bridge in between \(v_1\) and \(v_2\), we can reconstruct the graph construction in such a way that the (Bind)-rule application was such that the premise graph \({\mathcal {G}}'\) containing \(v_1\) itself contains no bridges, whence it is in Phase 2. Because Phase 2-graphs never have more than one groundee, the \({\mathcal {G}}'\) premise graph of that (Bind)-rule application must have had \([[X_1]]\) as the label of its only open groundee vertex and \(A^x\) as the label of one of its ground vertices. This premise graph therefore proves some grounding claim of the form \(A^x, \Psi < [[X_1]]\). By Proposition 2 this grounding claim is correct and so \(A^x\) is a partial ground of \([[X_1]]\). \(\square\)
With the conceptual machinery now at our disposal, we can characterize an interesting notion of strong joint-contribution of a set of fully justified s-element vertices as the property of being binding-interwoven, i.e. the property that each two exclusive and exhaustive subsets of a strongly jointly contributing set are bound. The difference between joint-contribution simpliciter and strong joint-contribution is that a set of s-element vertices V that are together in a validity-maker, but in which a pair of subsets of V are only indirectly bound via other s-element vertices that are not in V count as jointly contributing to the validity but not strongly so. The intuition here is that, while they are part of the team that is responsible for the validity, some subsets are divided without direct bridge; so they cannot do work together to obtain validity. One could say that they do not form a contributing fraction of the validity-maker.
Definition 16
[Interwoven by a binary relation] Let R be a binary relation over a set a. We say that a is R-interwoven iff, for each two non-empty mutually exclusive and together exhaustive subsets \(a_1\) and \(a_2\) of a, R(x, y) holds for some \(x\in a_1\) and \(y\in a_2\).
As an example: the set of natural numbers is \(\textsf{Succ}\)-interwoven where \(\textsf{Succ}(x,y)\) iff \(x=y+1\) or \(y=x+1\). Note that this does not mean that each subset of the natural numbers would be \(\textsf{Succ}\)-interwoven: as a counterexample take the set \(\{1,2,4,5\}\) of which the two mutually exclusive and together exhaustive subsets \(\{1,2\}\) and \(\{4,5\}\) fail to have members (one from each set) that stand in the \(\textsf{Succ}\)-relation.
Definition 17
[Strong joint-contribution] A set of fully justified s-element vertices strongly jointly contributes to the validity of a logical hypergraph iff it is \(\textsf{Bound}\)-interwoven.Footnote 12
Proposition 5
A set V of s-element vertices is a basis of the hypergraph iff it contributes sufficiently and (strongly) jointly to the validity of \({\mathcal {G}}\).
Proof
A basis of a hypergraph contains exactly the s-elements in a validity-maker. According to Definition 12, s-elements of a sequent contribute sufficiently iff it is the union of multiple bases, so a sufficiently contributing set is always a (proper or improper) superset of a basis. Definition 12 also stipulates that s-elements of sequents contribute jointly iff they constitute a (proper or improper) subset of a basis. Consequently, a set of s-elements that contributes both sufficiently and jointly is both a superset and a subset of a basis, and so it is a basis for the hypergraph. For strong joint-contribution (cf. Definition 17) just consider that the difference between strong and normal joint contribution evaporates when the set of s-element vertices is sufficiently contributing, because, in that case, there cannot be a divide in the subsets of a set of s-element vertices. \(\square\)
To visualize all this, we will simplify the logical hypergraphs and their visualization a bit. First we will introduce the admissible rules given in Table 9, which allow for the omission of the closing edges and streamlining combinations of many applications of (SCon) and (GCon). The aspects that are skipped over with such shortcut rules are important for reconstructing the proof that it is a correct logical hypergraph and therefore this simplification takes away the quality of simplified logical hypergraphs as full-blown proofs from the axioms, but it visualizes more economically the binding connections of interest. All this information is also present in the original hypergraphs we just presented, but at this point it may be useful to focus only on how premises and conclusions are interconnected by their ultimate grounds.
The first rule in Table 9 is a way to apply several axioms and instances of the (Trans\(_<\))-rule together at the same time without keeping the vertices that were closed off at intermediate stages. We thus compress graphs in such way that we no longer see why certain signed formulas are indirect grounds of others, but immediately go down to the level of (indirect) grounding at which we can bind s-elements. If we only want to visualize the way in which s-elements are bound together, it is not useful to, for example, know that \(p^-\) is a ground of \(\lnot p^+\) and that \(\lnot p^+\) and \(q^+\) are grounds of \(\lnot p\wedge q^+\), when all we need to know is that some conclusion \(\lnot p\wedge q\) is bound to some premise by means of its ground \(p^-\). To avoid the unnecessary information about intermediate direct grounding steps, we draw a grounding edge directly connecting \(\lnot p\wedge q^+\) to its indirect grounds \(p^-\) and \(q^+\).
In the simplification we maximally apply these admissible rules to obtain simpler graphs. Once this is done we also visualize bridges and the adjacent vertices, cutting edges and disjunctive grounding edges more efficiently by abbreviating a recurring pattern by a triangle notation as specified in Table 10. A triangle with label A expresses that its pointy end contributes \(A^+\) and its flat basis contributes \(A^-\) to the graph. If the triangle (seen as an arrow) goes from a premise to a conclusion, it expresses that the premise offers the information A to enable the derivation of the conclusion.
Figure 5 illustrates how the graph from Fig. 2 can be simplified. We can read a lot of useful information off of this graph. We directly see the grounding relations: \([[p^-]]\) is fully grounded by \(p^-\), \([[\lnot p\vee q^-]]\) is fully grounded by \(p^+\) and \(q^-\), \([[q\wedge r^+]]\) is fully grounded by \(q^+\) and \(r^+\) and finally \([[\lnot r^+]]\) is fully grounded by \(r^-\). But, more importantly, we see what each s-element in the sequent contributes to the validity: \(p\vee s^-\) contributes nothing, premise p contributes \(p^+\) to allow the third premise to contribute \(q^+\) to the conclusion \(q\wedge r\). This conclusion is moreover only possible thanks to the contribution of \(r^+\) by the other conclusion. We also observe that the different s-element vertices are bound by the truth/falsity of the formulas that figure in the triangles to which they are connected.
Efficiently drawing the arrow paths in Fig. 2 by means of triangles
In Fig. 6 the simplified version of the hypergraph in Fig. 3 is represented.
Efficiently drawing the arrow paths in Fig. 3 by means of triangles
7 From graphs back to sequents
We have now said a lot about graphs having validity-makers and about how their s-element vertices contribute to the validity of the graph. But we were first and foremost interested in the contribution of premises and conclusions to valid sequents. Although the translation is rather straightforward, we here list the most important ways in which the talk of graphs and their s-element vertices can be translated into talk of sequents and their s-elements.
Definition 18
The following properties of (multisets of) s-elements of sequents are direct counterparts of the corresponding properties of (sets of) s-element vertices in logical hypergraphs.
-
A multiset \(\Sigma\) of s-elements of a sequent is a validity-maker of the sequent if there is a logical hypergraph for the sequent and \(\Sigma\) is the multiset of labels of a basis of the graph.
-
A multiset \(\Sigma\) of s-elements of a sequent (strongly) jointly contributes to the validity of the sequent if they are the labels of s-element vertices (strongly) jointly contributing to the validity of a logical hypergraph for the sequent.
-
A multiset of s-elements sufficiently contributes to the validity of a sequent if it is the union of some set of validity-makers of the sequent.
-
An s-element \([[X_1]]\) of some sequent receives its partial ground Y from s-element \([[X_2]]\) in the same sequent if there is a logical hypergraph for the sequent in which an \([[X_1]]\)-labeled s-element vertex receives Y from an \([[X_2]]\)-labeled s-element vertex. We say that \(X_1\) and \(X_2\) are bound and write \(\textsf{Bind}(X_1,X_2)\).
-
An s-element [[X]] contributes Y to a valid sequent if it is the label of an s-element vertex v in the basis of a logical hypergraph for that sequent and v receives Y from another s-element vertex.
Let us go back to our sequent  . Its s-elements are \([[p\vee s^-]]\), \([[p^-]]\), \([[\lnot p \vee q^-]]\), \([[q\wedge r^+]]\), and \([[\lnot r^+]]\). Its only validity-maker is \(\{ \! \{[[p^-]], [[\lnot p \vee q^-]], [[q\wedge r^+]],[[\lnot r^+]]\} \! \}\). This set and some of its non-singleton subsets strongly jointly contribute to the validity: \(s_1=\{[[p^-]], [[\lnot p \vee q^-]]\}\), \(s_2=\{ \! \{[[\lnot p \vee q^-]], [[q\wedge r^+]]\} \! \}\), \(s_3=\{ \! \{[[q\wedge r^+]],[[\lnot r^+]]\} \! \}\), \(s_4= s_1\cup s_2\), \(s_5= s_2\cup s_3\), \(s_6=s_3\cup s_4\), \(s_7=s_4\cup s_5\), \(s_8= s_6\cup s_7\). Only the entire validity-maker (strongly) jointly and sufficiently contributes to the sequent’s validity. \([[p^-]]\) and \([[\lnot p\vee q^-]]\) are bound by their partial ground (\(p^-/p^+\)). The sets of s-elements \(\{ \! \{[[p^-]], [[\lnot p\vee q^-]]\} \! \}\) and \(\{ \! \{[[q\wedge r^+]],[[\lnot r^+]]\} \! \}\) are bound by their partial ground (\(q^-/q^+\)). \(\{ \! \{[[\lnot p \vee q^-]]\} \! \}\) and \(\{ \! \{[[p^-]], [[q\wedge r^+ ]], [[\lnot r^+]]\} \! \}\) are bound by their partial grounds (\(p^+/p^-\) and \(q^-/q^+\)). \([[\lnot p \vee q^-]]\) receives its partial grounds \(p^+\) and \(q^-\) from \([[p^-]]\) and \([[q\wedge r^+]]\). Together these partial grounds form a full ground for that premise. \([[p\vee s^-]]\) contributes nothing to the validity of the sequent. \([[p^-]]\) contributes \(p^-\), \([[\lnot p\vee q^-]]\) contributes \(p^+\) and \(q^-\), \([[q\wedge r^+]]\) contributes \(q^+\) and \(r^+\), and \([[\lnot r^+]]\) contributes \(r^-\).
. Its s-elements are \([[p\vee s^-]]\), \([[p^-]]\), \([[\lnot p \vee q^-]]\), \([[q\wedge r^+]]\), and \([[\lnot r^+]]\). Its only validity-maker is \(\{ \! \{[[p^-]], [[\lnot p \vee q^-]], [[q\wedge r^+]],[[\lnot r^+]]\} \! \}\). This set and some of its non-singleton subsets strongly jointly contribute to the validity: \(s_1=\{[[p^-]], [[\lnot p \vee q^-]]\}\), \(s_2=\{ \! \{[[\lnot p \vee q^-]], [[q\wedge r^+]]\} \! \}\), \(s_3=\{ \! \{[[q\wedge r^+]],[[\lnot r^+]]\} \! \}\), \(s_4= s_1\cup s_2\), \(s_5= s_2\cup s_3\), \(s_6=s_3\cup s_4\), \(s_7=s_4\cup s_5\), \(s_8= s_6\cup s_7\). Only the entire validity-maker (strongly) jointly and sufficiently contributes to the sequent’s validity. \([[p^-]]\) and \([[\lnot p\vee q^-]]\) are bound by their partial ground (\(p^-/p^+\)). The sets of s-elements \(\{ \! \{[[p^-]], [[\lnot p\vee q^-]]\} \! \}\) and \(\{ \! \{[[q\wedge r^+]],[[\lnot r^+]]\} \! \}\) are bound by their partial ground (\(q^-/q^+\)). \(\{ \! \{[[\lnot p \vee q^-]]\} \! \}\) and \(\{ \! \{[[p^-]], [[q\wedge r^+ ]], [[\lnot r^+]]\} \! \}\) are bound by their partial grounds (\(p^+/p^-\) and \(q^-/q^+\)). \([[\lnot p \vee q^-]]\) receives its partial grounds \(p^+\) and \(q^-\) from \([[p^-]]\) and \([[q\wedge r^+]]\). Together these partial grounds form a full ground for that premise. \([[p\vee s^-]]\) contributes nothing to the validity of the sequent. \([[p^-]]\) contributes \(p^-\), \([[\lnot p\vee q^-]]\) contributes \(p^+\) and \(q^-\), \([[q\wedge r^+]]\) contributes \(q^+\) and \(r^+\), and \([[\lnot r^+]]\) contributes \(r^-\).
8 Conclusion
In this paper we have presented a graph-theoretic representation of joint-contribution based on partial-ground binding, as presented in (Saint-Germier et al., 2024). The logical hypergraphs and their visualization nicely clarify how exactly premises and conclusions together contribute (or not) to making the sequent they occur in valid. We showed how they do this by being bound by their partial grounds. We explained that certain graphs are fully connected (in the sense that there is a path from each vertex to each other), while others have (connected) components that are logical graphs themselves, but also contain vertices that are not connected to such a component. Some of these components are validity-makers, in the sense that they, on their own, suffice for validity. We concluded that the s-element vertices in such a validity-maker are jointly and sufficiently contributing vertices. Their labels together form a subset of the sequent that is responsible for its validity. Parts of the sequent that are not contained in such a validity-maker do not contribute to the validity and are mere bystanders.
We believe that the graphical/diagrammatic system we presented could be of pedagogical and explanatory value for logic teaching. In virtue of their visual elegance, the graphs may provide an easy and insightful method for proving classical logic validity. The only thing that needs to be done for establishing the validity of a given argument is matching the right kind of atomic hypergraphs as much as needed in such a way that the only s-elements that can be found are among the premises and the conclusions of the argument. Besides a proof method for classical logic, it also provides a visual explanation of why certain arguments appear counterintuitive (such as explosion and other cases where parts of the argument do no work) although they are valid.
Finally, it is worth mentioning that the graphs provide visual guidance for the theorem-proving process, in the sense that the open ground vertices of an unfinished logical hypergraph suggest ways in which the user can continue with the proof. Open ground vertices could be seen as open problems whose resolution may lead to finding a proof.
Notes
The terms interpretation, false, and true can be formalized as in one’s preferred formulation of standard classical logic model-theory.
The added formulas may happen to constitute parts of other ways of establishing the validity and in that specific case we would consider them as doing work, as will become clear later. But the fact that they are introduced by Weakening means that a proof in which they are so introduced would contain no evidence that they play any role in making the sequent valid.
As an intermediate between grounding the truth values of premises and conclusion and proving the validity of sequents, the calculus also produces grounding claims for enthymematic validity. Enthymematic validity is the idea that even invalid sequents may be enthymematically valid implicitly assuming the truth or falsity of specific sentences. If those sentences are more basic than the sequent, we then say that the sentences having those truth values grounds the sequent’s enthymematic validity. An example: assuming the truth of q, the sequent
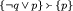 is enthymatically valid and, because q’s truth is more basic than the sequent, we say that the sequent can be grounded by the truth of q. Properly valid sequents will then be a special case of the enthymematically valid sequents, namely those that can be grounded by the empty set, those that do not require supplementary assumptions about the world.
is enthymatically valid and, because q’s truth is more basic than the sequent, we say that the sequent can be grounded by the truth of q. Properly valid sequents will then be a special case of the enthymematically valid sequents, namely those that can be grounded by the empty set, those that do not require supplementary assumptions about the world.In (Saint-Germier et al., 2024), the term sequent term is used for constructs of the form \([[\Sigma ]]\). Here we conflate sequents and their formulation as enthymeme-terms.
In (Saint-Germier et al., 2024) there are only four phases, because the first phase is not distinguished from the second. This slight modification is useful for explanatory purposes and has no impact on any of the formal definitions or results.
To avoid confusion, it may be useful to clarify that the conjunctive/disjunctive grounding edges have nothing to do with ways of grounding the conjunction/disjunction connective in the object language. Conjunctive here refers to the fact that partial grounds form a full ground by conjoining them, while disjunctive refers to the fact that, in cases where such edges are applied, we ground an open ground vertex by means of multiple open groundee vertices of a same connected graph. We will see that multiple groundee vertices in one connected graph will together represent (parts of) sequents, which are understood here in a disjunctive way. So the kind of grounding involved in this special case is not conjunctive but disjunctive. If the disjunctive notion does not become more transparent throughout the paper, this is not a problem, because this kind of edges will here only be introduced by the contraction rules (GCon) and (SCon), in which case they are rather easily understood. One might even plainly call them contraction edges for the purpose of this paper. However, if one also wants to design graphs for non-classical logics with intensional connectives, like intuitionistic or linear logic, a more operational notion of disjunctive grounding, represented by disjunctive grounding edges, becomes very useful.
The only thing that matters is that all rules are tried out (in reverse) until the graph is broken down into a set of primitive graphs, if this is indeed possible.
Here the invalid hypergraph is a logical hypergraph for an invalid sequent, but of course we can also have invalid hypergraphs for valid sequents. In such cases, however, there will be another hypergraph for that sequent that is valid. To be sure that the sequent is invalid, we need to have tried out every possible hypergraph for that sequent. This may seem intractable, but given the analytic nature of the hypergraphs, it is doable in a finite time.
The term ‘bridge’ is sometimes used in graph theory to denote an edge between two subgraphs, that would be separate components if the edge were removed. While the notion here is somewhat related (at the moment right after the application of the (Bind)-rule, removing it creates two new components in the graph), it should not be confused with our usage.
Note that, by the definition of a bridge, \(Y=A^{-x}\) when \(X=A^x\).
Incidentally, this idea of the interwovenness of a set of s-vertices via binding can be used as inspiration to propose an improved criterion of variable-sharing for MSET-MSET sequents. Variable-sharing is broadly accepted as a good necessary condition for something to count as relevant: a premise relevantly entails a conclusion only if they at least share some variable. It is not trivial how to generalize this to MSET-MSET format, but one of the ways to do this is saying that each subset of premises and conclusions should share a variable with the rest of the sequent. This is defined as the property that it has only one s-element or it is \(\textsf{Share}\)-interwoven, where \(\textsf{Share}\) is the property of sharing a variable. \(\textsf{Share}\)-interwovenness basically means that each subsequent shares a variable with the rest of the sequent. One of the advantages is that cases of mere sufficient contribution of all s-elements, like in \([[p^-, q^-, p^+, q^+]]\) are excluded as candidates for relevance.
References
Brauer, E. (2020). Relevance for the classical logician. Review of Symbolic Logic, 13(2), 436–457. https://doi.org/10.1017/s1755020318000382
Correia, F. (2013). Logical grounds. Review of Symbolic Logic, 7(1), 1–29. https://doi.org/10.1017/s1755020313000300
Fine, K. (2012). Guide to ground. In F. Correia & B. Schnieder (Eds.), Metaphysical grounding (pp. 37–80). Cambridge University Press.
Saint-Germier, P., Verdée, P., & Villalonga, P. T. (2024). Relevant entailment and logical ground. Philosophical Studies (pp. 1–43). https://doi.org/10.1007/s11098-024-02101-1.
Smiley, T. (1996). Rejection. Analysis, 56(1), 1–9. https://doi.org/10.1111/j.0003-2638.1996.00001.x
Tennant, N. (2017). Core logic. Oxford: Oxford University Press.
Verdée, P., Bal, I. D., & Samonek, A. (2019). A non-transitive relevant implication corresponding to classical logic consequence. Australasian Journal of Logic 16(2), 10–40. https://doi.org/10.26686/ajl.v16i2.5273
Acknowledgements
Funding for this research was provided by an FNRS BelgiumWIP grant with identifier PGY F.4540.20. All authors contributed equally to the ideas expressed in the paper. The order of the authors reflects their involvement in the writing process. We thank João Daniel Dantas who greatly contributed to many brainstorming sessions about these ideas. We are also indebted to the audiences of many workshops and conferences in Hamburg, Louvain-la-Neuve, Berlin, Campinas, Leuven, Pamplona, Salamanca, Bochum, and Paris, where we presented preliminary versions of the results in this paper. Our final words are for the two anonymous reviewers who had the patience to carefully examine previous versions of this paper and provided many insightful comments that lead to enormous improvements.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Verdée, P., Saint-Germier, P. & Villalonga, P.T. Connecting the dots: hypergraphs to analyze and visualize the joint-contribution of premises and conclusions to the validity of arguments. Philos Stud 181, 2361–2390 (2024). https://doi.org/10.1007/s11098-024-02141-7
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11098-024-02141-7


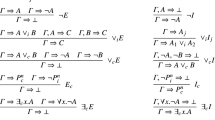







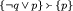 is enthymatically valid and, because q’s truth is more basic than the sequent, we say that the sequent can be grounded by the truth of q. Properly valid sequents will then be a special case of the enthymematically valid sequents, namely those that can be grounded by the empty set, those that do not require supplementary assumptions about the world.
is enthymatically valid and, because q’s truth is more basic than the sequent, we say that the sequent can be grounded by the truth of q. Properly valid sequents will then be a special case of the enthymematically valid sequents, namely those that can be grounded by the empty set, those that do not require supplementary assumptions about the world.