A variety of optical soliton solutions in closed-form of the nonlinear cubic quintic Schrödinger equations with beta derivative

Abstract

In the field of nonlinear optics, both fractional and classical-order nonlinear Schrödinger (NS) equations are investigated. However, the fractional-order NS equation has gained widespread acceptance due to its higher compatibility. The space-time fractional nonlinear Schrödinger equation enfolding beta derivative has a wide range of applications in nonlinear optics, quantum computing, Bose-Einstein condensates, wave propagation in complex media, quantum mechanics, and engineering, where understanding wave propagation and nonlinear interactions are diametrical. In this article, the improved Bernoulli sub-equation function (IBSEF) procedure has been used to establish optical soliton solutions in the form of trigonometric, exponential, and hyperbolic functions comprising substantive parameters. These soliton solutions have different shapes, including kink, periodic soliton, singular kink, breathing soliton, and other types. The physical features of the solitons are revealed through three-, two-, contour, and density graphs. The research findings confirm that the IBSEF scheme is effective, straightforward, and applicable for ascertaining soliton solutions in various nonlinear fractional-order models in the fields of physics and communication engineering.

1 Introduction

In mathematical physics, many real and rational problems in the world are modeled through fractional evolution equations. Fractional nonlinear evolution equations (FNLEEs) have broad acceptability across numerous fields, notably optics, control theory, signal processing, plasma physics, electrochemistry, system identification, image processing, medicine, probability, and others to control systems (Bilal et al. 2021; Alquran et al. 2021). Indeed, FNLEEs are significant tools for defining problems further precisely. Accordingly, FNLEEs and their analytical soliton solutions including dark and bright solitons are significant for decoding the obscurity of intricate physical events and nonlinear features (Sharma et al. 2013; Sharma and Goyal 2014). Thus, several powerful techniques, for example the modified extended tanh-function (Yalçınkaya et al. 2021; Arnous et al. 2021; Mamun et al. 2020, 2021a, b, c, 2022a, b, c, d), $(G^{\prime }/{G}^{2})$-expansion procedure (Akram et al. 2022; Mamun et al. 2021a, b, c; Ananna et al. 2021), the modified auxiliary expansion technique (Ismael et al. 2021), the generalized Kudryashov scheme (Demiray 2020; Malik et al. 2022), the multiple exp-function process (Nisar et al. 2021; Gepreel and Zayed 2021), the unified approach (Raza et al. 2021), the dynamical approach (Tripathy et al. 2023), sine-Gordon expansion mode (Yıldırım 2021; Mamun et al. 2022a, b, c, d), extended sinh-Gordon equation expansion method (Bezgabadi and Bolorizadeh 2021), the solitary wave ansatz approach (Mathanaranjan 2021), the $({G}^{{\prime }}/G, 1/G)$-expansion scheme (Alam et al. 2021; Mamun et al. 2021a, b, c), the tanh–coth approach (Mamun et al. 2022a, b, c, d), the new auxiliary scheme (Mamun et al. 2023), the advanced $\text{e}\text{x}\text{p}(-\varphi \left(\psi \right)$-expansion approach (Mamun et al. 2022a, b, c, d; Shahen et al. 2020), etc. have been established and well-designed by physicists, engineers, and applied mathematicians in the literature to assess soliton solutions to the FNLEEs. Although the classical cubic quintic nonlinear Schrödinger equations (NLSEs), as well as the nonlinear cubic Schrödinger equation are employed in the disciplines of optics, concurrently the fractional-order NLSE is widely used owing to their higher compatibility. However, only a small amount of study has been done on the fractional-order cubic quintic nonlinear Schrödinger equation (NLSE) to date, namely, Arshad et al. (2017) examined this equation through the modified extended auxiliary equation approach, Chen et al. used the mapping technique and the Jacobian elliptic function approach (Chen 2020) and double function (Chen and Xiao 2021) technique. Islam et al. (2017), etc. Further, various ansatz methods (Wu et al. 2020; Hashemi and Akgül 2018; Yousif et al. 2018; Inc et al. 2018) were employed to study the cubic nonlinear Schrödinger (NS) equation. These methods include the fractional Riccati method (Wu et al. 2020), the simplest equation approach (Hashemi and Akgül 2018), the fractional mapping expansion method (Yousif et al. 2018), the generalized tanh and the Bernoulli sub-ODE method (Inc et al. 2018), and others (Zhao et al. 2020, 2022a, b; Zhang et al. 2021; Kong and Liu 2021; Li et al. 2021; Cao et al. 2021; Chung et al. 2022; Cai et al. 2023; Meng et al. 2023; Guo et al. 2023).

The IBSEF approach is a powerful mathematical technique and used for unraveling nonlinear fractional models in physics and applied mathematics. By providing soliton solutions and uncovering the underlying physical features, the IBSEF method contributes to the development of nonlinear dynamics, present valuable insights of complex phenomena and facilitating applications in areas such as communication engineering and physics. This approach is used to obtain traveling wave solutions (Buryak et al. 2002) for several equations, for instance the nonlinear Lindau–Ginzburg–Higgs model (Islam et al. 2022), Mathanaranjan et al. (2023) explored chirped optical soliton solutions within the context of the nonlinear Schrödinger equation. They specifically focus on situations involving nonlinear chromatic dispersion and a refractive index governed by a quadratic-cubic law. Bo et al. (2023) investigated the multiple soliton solutions in the context of the saturable nonlinear Schrödinger equation, taking into account the existence of a PT-symmetric potential. Wang and Liu (2023) focused on investigating the nonlinear Schrödinger equation which describe the propagation of pulses in optical fibers. It is important to note that the kink, breather, and periodic solitons play critical roles in various fields of science and engineering, ranging from describing wave phenomena and complex dynamics to understanding phase transitions, topological defects, and nonlinear optics applications. Their study helps us better comprehend the rich behavior of nonlinear systems and harness it for practical purposes. However, these particular soliton types have not been examined in the previously mentioned studies (Mathanaranjan et al. 2023; Bo et al. 2023; Wang and Liu 2023). Therefore, this study aims to develop specific optical soliton solutions for the cubic quintic nonlinear Schrödinger equation with parabolic nonlinearity and the cubic nonlinear Schrödinger equation with Kerr law nonlinearity by using the IBSEF approach and fractional wave transformation in the sense of fractional beta-derivative. Various types of solitons, including periodic, kink, breather, and singular kink-type solitons, have been extracted from the obtained solutions.

The organization of this article is as follows: Sect. 2 provides a description of the beta derivative. Section 3 outlines the methodology used in the study. In Sect. 3.4, the mathematical analysis of the optical soliton solutions is presented. The results and discussion are presented in Sect. 5, and finally, Sect. 6 contains the conclusions.

2 The beta derivative

Many academicians have attempted to establish an appropriate definition of fractional-order derivative (FD). The Riemann-Liouville FD (Agarwal et al. 2009), modified Riemann-Liouville FD (Jumarie 2006), Caputo FD (Almeida 2017), conformable FD (Khalil et al. 2014), etc. are some of the vastly used definitions. However, each definition has some limitations. For instance, the Leibnitz and chain rules are not followed by the Riemann-Liouville and Caputo fractional derivatives. The Riemann-Liouville fractional derivative does not provide zero for the derivative of a constant, while Caputo does. The conformable fractional derivative also does not comply with the derivative rule at the origin. Atangana et al. (2016) developed a new definition of fractional derivative known as the beta derivative to overcome these problems. This concept is well-behaved, adheres to both Leibnitz and chain principles, and interacts effectively with the classical derivative (Atangana and Alqahtani 2016).

Definition

Let, where, and let be a function such that. According to the definition provided in Atangana et al. (2016), the beta derivative of a function is defined as follows:

$${D}_{y}^{\beta }f\left(y\right)=\left\{\begin{array}{l}\begin{array}{l}lim\\ \epsilon \to 0\end{array}\frac{f\left(y+\epsilon {\left(y+\frac{1}{{\Gamma }\beta }\right)}^{1-\beta }\right)-f\left(y\right)}{\epsilon }, \quad y\ge 0, 0<\beta \le 1\\ f\left(y\right), y\ge 0, \beta =0\end{array}\right.$$

For $\beta =1$, from the definition, we have ${D}_{t}^{\beta }f\left(y\right)=\frac{d}{d y}f\left(y\right)$.

The beta derivative has emerged as a promising tool to the researchers across various fields, owing to its remarkable simplicity, ease of use, and potential to enhance the accuracy and applicability of mathematical models in physical applications. Its growing popularity is evidence of the increasing recognition of its efficiency in constructing analytical solutions as well as its ability to simplify complex mathematical equations. The adoption of this novel definition of the fractional derivative has led to significant improvements in the quality and accuracy of research in various fields, providing researchers with a powerful tool to drive invention forward (Akram et al. 2022; Ismael et al. 2021).

3 The method

The Bernoulli sub-equation function method (Islam et al. 2022), which is widely used in solving nonlinear differential equations, has been further developed to establish the improved Bernoulli sub-equation function (IBSEF) scheme. This enhanced approach includes a series of steps that have been refined and optimized to provide further useful and efficient solutions. The IBSEF method has been shown to be mostly effective in solving complex nonlinear equations in physics, engineering, and other fields. The steps involved in the IBSEF method are documented in various studies (Buryak et al. 2002; Islam et al. 2022):

3.1 1st step

The fractional nonlinear equation is assumed in the ensuing form:

$$M{(u,D}_{t}^{\beta }u,{D}_{x}^{\beta }u,{D}_{tt}^{2\beta }u,{D}_{xt}^{2\beta }u,{D}_{xx}^{2\beta }u,\dots)=0.$$

(1)

In above equation, $M$ refers to a polynomial of $u$, while ${D}_{t}^{\beta }$ denotes the fractional derivative of $\beta$-order. Moreover, $u(x,t)$ represents an implicit function of $x$ and $t$. We convert Eq. (1) into a nonlinear differential equation with the aid of an appropriate fractional wave transformation. The subsequent form of the wave transformation is supposed to convert (1) into an integer-order equation:

$$u\left(x,t\right)=\chi \left(\zeta \right), \zeta =\frac{s}{\beta }{\left(x+\frac{1}{\varGamma \left(\beta \right)}\right)}^{\beta }+\frac{\omega }{\beta }{\left(t+\frac{1}{\varGamma \left(\beta \right)}\right)}^{\beta },$$

(2)

where $\omega$ represents the velocity of traveling wave, $s$ stands for the wave number, $\zeta$ denotes the wave variable, and $\beta$ refers to the order of the fractional derivative. The wave alteration (2) turns the Eq. (1) to the subsequent equation:

$$N\left(\chi ,{\chi }^{{\prime }},{\chi }^{{\prime \prime }},{\chi }^{{\prime \prime \prime }},\dots\right)=0.$$

(3)

3.2 2nd step

According to the IBSEF approach, it is possible to consider the interim solution of Eq. (3) as:

$$\chi \left(\zeta \right)=\frac{\sum _{i=0}^{m}{a}_{i}{F}^{i}\left(\zeta \right)}{\sum _{j=0}^{l}{b}_{j}{F}^{j}\left(\zeta \right)}=\frac{{a}_{0}+{a}_{1}F\left(\zeta \right)+{a}_{2}{F}^{2}\left(\zeta \right)+\dots +{a}_{m}{F}^{m}\left(\zeta \right)}{{b}_{0}+{b}_{1}F\left(\zeta \right)+{b}_{2}{F}^{2}\left(\zeta \right)+\dots +{b}_{l}{F}^{l}\left(\zeta \right)}.$$

(4)

here $F=F\left(\zeta \right)$ satisfies the improved Bernoulli equation, where a set of coefficients ${a}_{0}$, ${a}_{1}$, ${a}_{2}$, ${a}_{3}$, $\dots$, ${a}_{m}$ and another set of coefficients ${b}_{0}$, ${b}_{1}$, ${b}_{2}$, $\dots$, ${b}_{l}$ are determined subsequently. The values of $l$ and $m$, which are non-zero constants, can be established using the balancing principle. The improved Bernoulli equation can be represented in a general form as follows:

$${F}^{{\prime }}\left(\zeta \right)=\lambda F\left(\zeta \right)+\theta {F}^{r}\left(\zeta \right), \lambda \ne 0, \theta \ne 0, r\in R-\left\{0,1,2\right\}.$$

(5)

The highest-order linear term in Eq. (4) can be equated with the highest-order nonlinear term by using the theory of homogeneous balance. This technique helps determine the values of the unknown parameters $l$ and $m$. Following this procedure, the values of $l$ and $m$ can be obtained. When the solution (4) is inserted into Eq. (3), taking the assistance of Eq. (5), it yields a polynomial equation $\mathcal{B}\left(F\right(\zeta )$ of $F\left(\zeta \right):$

$$\mathcal{B}(F\left(\zeta \right)={\alpha }_{s}{F\left(\zeta \right)}^{s}+{\alpha }_{s-1}{F\left(\zeta \right)}^{s-1}+\dots +{\alpha }_{1}F\left(\zeta \right)+{\alpha }_{0}=0.$$

(6)

3.3 3rd step

By setting all coefficients of $\mathcal{B}(F\left(\zeta \right)$ to zero, we obtain an algebraic system of equations as:

$${\alpha }_{k}=0, k=0,\dots ,s.$$

The system can be estimated to obtain the respective values of ${a}_{0}$, ${a}_{1}$, $\dots$, ${a}_{m}$ and ${b}_{0}$, ${b}_{1}$, $\dots$, ${b}_{l}$.

3.4 4th step

The solution of Eq. (5) depends on $\lambda$ and $\theta$, and the subsequent two conditions are met:

$$F\left(\zeta \right)={\left[-\frac{\theta }{\lambda }+\frac{\alpha }{{e}^{\lambda \left(r-1\right)\zeta }}\right]}^{\frac{1}{1-r}}, \quad \lambda \ne \theta ,$$

(7)

$$F\left(\zeta \right)={\left[\frac{\left(\alpha -1\right)+\left(\alpha +1\right)\text{tanh}\left(\frac{\lambda \left(1-r\right)\zeta }{2}\right)}{1-\text{tanh}\left(\frac{\lambda \left(1-r\right)\zeta }{2}\right)}\right]}^{\frac{1}{1-r}}, \quad \lambda =\theta ,$$

(8)

where $\alpha$ as a constant of integration and $\alpha \in \mathbb{R}$.

The process of obtaining the analytical solutions for Eq. (1) involves substituting the solutions derived from Eq. (3) into Eq. (1) with the aid of transformation (2). This substitution allows us to determine the explicit mathematical expressions that satisfy Eq. (1). Consequently, through this approach, the investigation aimed at finding the analytical solution for Eq. (1) is successfully completed, providing a comprehensive understanding of its solutions.

4 Analysis of the solutions

In this subsection, our objective is to develop stable and comprehensive solutions that cover a wide range of spectral properties for the space–time fractional cubic quintic nonlinear Schrödinger (NS) equation and the cubic nonlinear Schrödinger equation. We achieve this by employing the IBSEF approach, which enables us to restore certain known solutions existing in the literature and derive some new closed-form wave solutions.

4.1 The weakly nonlocal space–time fractional cubic quintic Schrödinger equation

In the case of nonlocal nonlinear media, the optical pulse intensity changed by the refractive index (Yousif et al. 2018) is given by

$$ \Delta n\left( I \right)\left( {x,t} \right) = \rho \int\limits_{{ - \propto }}^{ \propto } {Q\left( {x - x^{\prime } } \right)I\left( {x^{\prime } ,t} \right)dx^{\prime } } , $$

(9)

where $\int Q\left(x\right)dx=1$ i.e., $Q\left(x\right)$ is normalized, a rationally symmetric and positive real localized function, $\rho$ represents self-focusing ($\rho >0$) and self-defocusing ($\rho <0$) nonlinearities. The space–time fractional NS equation with nonlocal nonlinearities (Chen and Xiao 2021) can be expressed as

$$i{D}_{t}^{\beta }u+b{D}_{xx}^{2\beta }u+kG\left({\left|u\right|}^{2}\right)u+\varDelta n\left(I\right)u=0,$$

(10)

where $u(x,t)$ be the function of complex envelope and intensity of optical pulse $I={\left|v\right|}^{2}$, $0<\beta \le 1$, $t$ and $x$ represent the temporal and spatial variables respectively. All quantities are taken as non-dimensional form. $k$ and $b$ are constants which represent the non-linearity and the diffraction’s coefficient respectively, the real valued algebraic function is differentiable and $kG\left({\left|u\right|}^{2}\right)u$ is a $k$ times differentiable in complex plane $C$.

For weakly nonlocal nonlinear medium, using the condition on $\varDelta n\left(I\right)$ and considering parabolic nonlinearity, $G\left(u\right)=u+\delta {u}^{2}$, Eq. (10) becomes

$$i{D}_{t}^{\beta }u+b{D}_{xx}^{2\beta }u+{k}_{3}{\left|u\right|}^{2}u+{k}_{5}{\left|u\right|}^{4}u+\gamma \left({D}_{xx}^{2\beta }{\left|u\right|}^{2}\right)u=0,$$

(11)

where $\gamma$, ${k}_{3}$ and ${k}_{5}$ represent the weakly non-local nonlinearities, cubic, quintic coefficients.

Consider the fractional wave transformation

$$u\left(x,t\right)=U\left(\zeta \right), \zeta =\frac{p}{\beta }{\left(x+\frac{1}{\varGamma \left(\beta \right)}\right)}^{\beta }+\frac{q}{\beta }{\left(t+\frac{1}{\varGamma \left(\beta \right)}\right)}^{\beta },$$

(12)

where $p$ is the wave number, $q$ is the wave velocity and $0<\beta \le 1$. Setting transformation (12) into the Eq. (11), it is obtained

$$iq\delta {U}^{{\prime }}+b{p}^{2}{U}^{{\prime \prime }}+{k}_{3}{\left|U\right|}^{2}U+{k}_{5}{\left|U\right|}^{4}U+\gamma {{(\left|U\right|}^{2})}^{{\prime }{\prime }}U=0.$$

(13)

The complex envelope can be considered as

$$U\left(\zeta \right)=V\left(\zeta \right){e}^{is\zeta },$$

(14)

whereas $s$ be the phase shift of the complex envelope.

By means of (14) and its derivatives with respect to $\zeta$ into the Eq. (13), obtaining an equation and equating real and imaginary parts, we attain

$$b{p}^{2}{V}^{{\prime \prime }}-qs\delta V-b{p}^{2}{s}^{2}V+2\gamma V\left({{(V}^{{\prime }})}^{2}+{VV}^{{\prime \prime }}\right)+{k}_{3}{V}^{3}+{k}_{5}{V}^{5}=0,$$

(15)

$$\text{and} \quad \left(q\delta +2sb{p}^{2}\right)V=0$$

(16)

Since $V\ne 0$, from Eq. (16), it can be found

$$q=-\frac{2bs{p}^{2}}{\delta }.$$

(17)

Setting the value of $q$ from (17) into Eq. (15), we obtain

$$b{p}^{2}{s}^{2}V+b{p}^{2}{V}^{{\prime \prime }}+2\gamma {p}^{2}\left(V{{V}^{{\prime }}}^{2}+{V}^{2}{V}^{{\prime }{\prime }}\right)+{k}_{3}{V}^{3}+{k}_{5}{V}^{5}=0,$$

(18)

Balancing ${V}^{2}V^{\prime\prime }$ and ${V}^{5}$, we found a relationship among $l$, $r$ and $m$ as

$$l+r=m+1.$$

For $l=1$, $r=3$, we found $m=3$.

Therefore, the following is the trial solution of Eq. (18):

$$V\left(\zeta \right)=\frac{{a}_{0}+{a}_{1}F\left(\zeta \right)+{a}_{2}{F}^{2}\left(\zeta \right)+{a}_{3}{F}^{3}\left(\zeta \right)}{{b}_{0}+{b}_{1}F\left(\zeta \right)},$$

(19)

where ${F}^{{\prime }}\left(\zeta \right)=\lambda F\left(\zeta \right)+\theta {F}^{3}\left(\zeta \right), {a}_{3}\ne 0, \lambda \ne 0, \theta \ne 0.$

By introducing the solution (19) along with (5) into Eq. (18), we obtain a polynomial equation involving $F$. Setting each coefficient of this polynomial equation to zero leads to a system of equations that is over-determined. Using Maple software, we analyze and solve this algebraic system of equations, resulting in the following estimated values for the coefficients:

$${a}_{0}=\pm \frac{\sqrt{2\gamma b(2{\lambda }^{2}-{s}^{2})}}{2\gamma \lambda }{b}_{0}, \quad {a}_{1}=\pm \frac{\sqrt{2\gamma b(2{\lambda }^{2}-{s}^{2})}}{2\gamma \lambda }{b}_{1}, \quad {a}_{2}=\pm \frac{\sqrt{2\gamma b(2{\lambda }^{2}-{s}^{2})}}{\gamma {\lambda }^{2}}\theta {b}_{0},$$

$${a}_{3}=\pm \frac{\sqrt{2\gamma b\left(2{\lambda }^{2}-{s}^{2}\right)}}{\gamma {\lambda }^{2}}\theta {b}_{1}, \quad {k}_{3}=\frac{4{p}^{2}\gamma {\lambda }^{2}(3{\lambda }^{2}-{s}^{2})}{2{\lambda }^{2}-{s}^{2}}, \quad {k}_{5}=-\frac{12\gamma {p}^{2}{\lambda }^{4}}{b(2{\lambda }^{2}-{s}^{2})},$$

(20)

where ${b}_{0}$ and ${b}_{1}$ are arbitrary parameters.

Case 1

For $\lambda \neq 0,$ 

The resultant solution for the space–time fractional cubic quintic NS equation is obtained by substituting the parameter values given in (20) into the solution (19) and combining it with the solution (7) of the modified Bernoulli equation, along with the establishment of transformation (12) and complex envelope (14):

$$u\left(x,t\right)=\pm \frac{\sqrt{2\gamma b\left(2{\lambda }^{2}-{s}^{2}\right)}}{2\gamma \lambda }\left(1+\frac{2\theta {e}^{\lambda \zeta }}{-\theta {e}^{\lambda \zeta }+\lambda \alpha {e}^{-\lambda \zeta }}\right){e}^{is\zeta },$$

(21)

where $s$, $\theta$, $\lambda$, $\alpha$, $p$, $q$, $\gamma$ and $b$ are free parameters and $\zeta =\frac{p}{\beta }{\left(x+\frac{1}{\varGamma \left(\beta \right)}\right)}^{\beta }+\frac{q}{\beta }{\left(t+\frac{1}{\varGamma \left(\beta \right)}\right)}^{\beta }$.

By simplifying the solution (21), we obtain the solution in the form of a hyperbolic function:

$${u}_{1}\left(x,t\right)=\pm \frac{\sqrt{2\gamma b\left(2{\lambda }^{2}-{s}^{2}\right)}}{2\gamma \lambda }\left(1+\frac{2\theta (\text{cosh}\left(\lambda \zeta \right)+\text{sinh}\left(\lambda \zeta \right))}{\left(\lambda \alpha -\theta \right)\text{cosh}\left(\lambda \zeta \right)-\left(\lambda \alpha +\theta \right)\text{sinh}\left(\lambda \zeta \right)}\right){e}^{is\zeta },$$

(22)

Since $\alpha$ is an arbitrary parameter, we have the freedom to intuitively assign its values in terms of $\lambda$ and $\theta$, which are parameters of the improved Bernoulli equation. This approach enables us to obtain a more simplified expression for the solution, which will be extensively explained in the subsequent:

When $\alpha =18\lambda /\theta$, we ascertain the following solution from solution (22):

$${u}_{11}\left(x,t\right)=\pm \frac{\sqrt{2\gamma b\left(2{\lambda }^{2}-{s}^{2}\right)}}{2\gamma \lambda }\left(\frac{19\text{cosh}\left(\lambda \zeta \right)-17\text{sinh}\left(\lambda \zeta \right)}{17\text{c}\text{o}\text{s}\text{h}\left(\lambda \zeta \right))-19\text{s}\text{i}\text{n}\text{h}(\lambda \zeta )}\right){e}^{is\zeta },$$

(23)

where $\zeta =\frac{p}{\beta }{\left(x+\frac{1}{\varGamma \left(\beta \right)}\right)}^{\beta }+\frac{q}{\beta }{\left(t+\frac{1}{\varGamma \left(\beta \right)}\right)}^{\beta }$.

Moreover, for $\alpha =-\lambda /\theta$, solution (22) yields the dark soliton shape solution

$${u}_{12}\left(x,t\right)=\pm \frac{\sqrt{2\gamma b\left(2{\lambda }^{2}-{s}^{2}\right)}}{2\gamma \lambda }\text{t}\text{a}\text{n}\text{h}\left(\lambda \zeta \right){e}^{is\zeta }.$$

(24)

When $\alpha =\lambda /\theta$, we accomplish the singular kink shape solution

$${u}_{13}\left(x,t\right)=\pm \frac{\sqrt{2\gamma b\left(2{\lambda }^{2}-{s}^{2}\right)}}{2\gamma \lambda }\text{c}\text{o}\text{t}\text{h}\left(\lambda \zeta \right){e}^{is\zeta },$$

(25)

Likewise, by varying the value of the integral constant $\alpha$, we can discover different solution geometries. However, for the sake of simplicity, these alternative solutions are not presented in this context.

Case 2

When $\lambda = 0.$

Setting the scores of the parameters gathered in (20), we obtain the following solution from (19), using the transformation (12) and complex envelope (14) along solution (8).

$${u}_{2}\left(x,t\right)=\pm \frac{\sqrt{2\gamma b\left(2{\lambda }^{2}-{s}^{2}\right)}}{2\gamma \lambda }\left(1+\frac{2(1+\text{tanh}\left(\lambda \zeta \right))}{\left(\alpha -1\right)-\left(\alpha +1\right)\text{tanh}\left(\lambda \zeta \right)}\right){e}^{is\zeta },$$

(26)

where $p$, $q$, $s$, $\alpha$, $\lambda$ are arbitrary parameters and $\zeta =\frac{p}{\beta }{\left(x+\frac{1}{\varGamma \left(\beta \right)}\right)}^{\beta }+\frac{q}{\beta }{\left(t+\frac{1}{\varGamma \left(\beta \right)}\right)}^{\beta }$.

Simplifying solution (26), we perceive the subsequent solution

$${u}_{21}\left(x,t\right)=\pm \frac{\sqrt{2\gamma b\left(2{\lambda }^{2}-{s}^{2}\right)}}{2\gamma \lambda }\left(\frac{\left(\alpha +1\right)-\left(\alpha -1\right)\text{t}\text{a}\text{n}\text{h}\left(\lambda \zeta \right)}{\left(\alpha -1\right)-\left(\alpha +1\right)\text{t}\text{a}\text{n}\text{h}\left(\lambda \zeta \right)}\right){e}^{is\zeta },$$

(27)

As $\alpha$ is an integrating constant, we choose $\alpha =\sqrt{3}+1$, thus we found from solution (27)

$${u}_{22}\left(x,t\right)=\pm \frac{\sqrt{2\gamma b\left(2{\lambda }^{2}-{s}^{2}\right)}}{2\gamma \lambda }\left(\frac{\left(\sqrt{3}+2\right)-\sqrt{3}\text{t}\text{a}\text{n}\text{h}\left(\lambda \zeta \right)}{\sqrt{3}-\left(\sqrt{3}+2\right)\text{t}\text{a}\text{n}\text{h}\left(\lambda \zeta \right)}\right){e}^{is\zeta },$$

(28)

When $\alpha =0$, solution (27) converts to

$${u}_{23}\left(x,t\right)=\pm \frac{\sqrt{2\gamma b\left(2{\lambda }^{2}-{s}^{2}\right)}}{2\gamma \lambda }{e}^{is\left(\frac{p}{\beta }{\left(x+\frac{1}{\varGamma \left(\beta \right)}\right)}^{\beta }+\frac{q}{\beta }{\left(t+\frac{1}{\varGamma \left(\beta \right)}\right)}^{\beta }\right)},$$

(29)

Since $\alpha$ is an arbitrary constant, we can obtain infinite number of solutions to this equation by choosing the values of $\alpha$ instinctively. For conciseness, only a few solutions are taken here.

4.2 The space–time fractional cubic nonlinear Schrödinger equation

The equation designated as Yousif et al. (2018) is the cubic nonlinear Schrödinger (NS) equation with Kerr nonlinearity effects, which is considered within the framework of space-time fractional dynamics:

$$i{D}_{t}^{\mu }p+r{D}_{t}^{\mu }{D}_{x}^{\beta }p+s{D}_{xx}^{2\beta }p+q{\left|p\right|}^{2}p=0,$$

(30)

where $r$, $s$, $q$ are three real parameters with $0<\beta$, $\mu \le 1$, $i=\sqrt{-1}$ and the function $p$ represents a complex-valued function that is associated with both the spatial coordinate $x$ and the temporal variable $t$. The operators ${D}_{t}^{\mu }p$, ${D}_{x}^{\beta }p$ and ${D}_{xx}^{2\beta }p$ represent the beta derivative with respect to $t$ of order $\mu$ and $x$ of order $\beta$ and $2\beta$ respectively.

The fractional wave transformation is assumed as

$$p(x,t)=P\left(\zeta \right){e}^{i\psi }.$$

(31)

The wave variable $\zeta$ and $\psi$ of the transformation (31) can be defined as

$$\begin{aligned} & \zeta =\frac{1}{\beta }{\left(x+\frac{1}{\varGamma \left(\beta \right)}\right)}^{\beta }-\frac{\omega }{\mu }{\left(t+\frac{1}{\varGamma \left(\mu \right)}\right)}^{\mu }, \\ & \quad \text{and} \quad \psi =-\frac{k}{\beta }{\left(x+\frac{1}{\varGamma \left(\beta \right)}\right)}^{\beta }+\frac{\gamma }{\mu }{(t+\frac{1}{\varGamma \left(\mu \right)})}^{\mu } \end{aligned}$$

where $\omega$, $k$ and $\gamma$ represent wave velocity, wave frequency and wave number respectively.

Introducing transformation (31) into Eq. (30) and extrication real and imaginary parts, it is found

$$\left(rk\gamma -s{k}^{2}-\gamma \right)P+\left(s-r\omega \right){P}^{{\prime }{\prime }}+q{P}^{3}=0,$$

(32)

$$\text{and} \quad \omega =\frac{2ks-r\gamma }{rk-1}$$

(33)

Setting the estimation of $\omega$ into Eq. (32), we obtain

$$\left(rk\gamma -s{k}^{2}-\gamma \right)P+\left(s-r\frac{2ks-r\gamma }{rk-1}\right){P}^{{\prime }{\prime }}+q{P}^{3}=0.$$

(34)

Balancing ${P}^{{\prime }{\prime }}$ and ${P}^{3}$, the relationship among $l$, $r$ and $m$ is obtained as

$$m-r=l-1.$$

If we choose $r=3$, $l=1$, it is obtained $m=3$.

Therefore, the trial solution of (35) can be assumed to

$$P\left(\zeta \right)=\frac{{a}_{0}+{a}_{1}F\left(\zeta \right)+{a}_{2}{F}^{2}\left(\zeta \right)+{a}_{3}{F}^{3}\left(\zeta \right)}{{b}_{0}+{b}_{1}F\left(\zeta \right)},$$

(35)

where ${F}^{{\prime }}\left(\zeta \right)=\lambda F\left(\zeta \right)+\theta {F}^{3}\left(\zeta \right), \quad {a}_{3}\ne 0, \;\; \lambda \ne 0, \;\; \theta \ne 0$.

Combining solution (36) with Eq. (5) in Eq. (34) leads to the formation of a polynomial expression involving the variable $F$. To obtain a system of equations, we set each coefficient of the polynomial to zero, resulting in an over-determined system. Using Maple, we successfully solved the algebraic system of equations and derived the corresponding values for the coefficients.

$$\begin{aligned} \gamma & =\frac{s({k}^{2}-{k}^{3}r+2rk{\lambda }^{2}+2{\lambda }^{2})}{2rk-{r}^{2}{k}^{2}+2{r}^{2}{\lambda }^{2}-1}, {a}_{0} \pm \frac{\sqrt{2s}\lambda {b}_{0}}{\sqrt{q(2rk-{r}^{2}{k}^{2}+2{r}^{2}{\lambda }^{2}-1)}}, {a}_{1}=\pm \frac{\sqrt{2s}\lambda {b}_{1}}{\sqrt{q(2rk-{r}^{2}{k}^{2}+2{r}^{2}{\lambda }^{2}-1)}},\\{a}_{2} & =\pm \frac{2\sqrt{2s}\theta {b}_{0}}{\sqrt{q(2rk-{r}^{2}{k}^{2}+2{r}^{2}{\lambda }^{2}-1)}}, {a}_{3}=\pm \frac{\sqrt{2s}\theta {b}_{1}}{\sqrt{q(2rk-{r}^{2}{k}^{2}+2{r}^{2}{\lambda }^{2}-1)}}, \end{aligned} $$

(36)

where ${b}_{0}$ and ${b}_{1}$ are arbitrary parameters.

Case 1

As the solutions derived from the improved Bernoulli’s equation depend on the specific values of and, we make the assumption that is not equal to. By substituting the values given in (37) and incorporating solution (7) of the improved Bernoulli equation into (36), we derive the resulting rational exponential function:

$$P\left(\zeta \right)=\mp \frac{\sqrt{2s}\lambda }{\sqrt{q\left(2rk-{r}^{2}{k}^{2}+2{r}^{2}{\lambda }^{2}-1\right)}}\left(\frac{\theta {e}^{2\lambda \zeta }+\lambda \alpha }{\lambda {e}^{2\lambda \zeta }-\lambda \alpha }\right).$$

(37)

By introducing the solution (38) into transformation (31), we find the following broad-ranging solution of Eq. (30):

$$p(x,t)=\mp \frac{\sqrt{2s}\lambda }{\sqrt{q\left(2rk-{r}^{2}{k}^{2}+2{r}^{2}{\lambda }^{2}-1\right)}}\left(\frac{\theta {e}^{2\lambda \zeta }+\lambda \alpha }{\theta -\lambda \alpha }\right){e}^{i\psi },$$

(38)

where $\zeta =\frac{1}{\beta }{\left(x+\frac{1}{\varGamma \left(\beta \right)}\right)}^{\beta }-\frac{\omega }{\mu }{\left(t+\frac{1}{\varGamma \left(\mu \right)}\right)}^{\mu }, \;\; \gamma =\frac{s\left({k}^{2}-{k}^{3}r+2rk{\lambda }^{2}+2{\lambda }^{2}\right)}{2rk-{r}^{2}{k}^{2}+2{r}^{2}{\lambda }^{2}-1}, \;\; \omega =\frac{2ks-r \gamma }{rk-1}$ and $\psi =-\frac{k}{\beta }{\left(x+\frac{1}{\varGamma \left(\beta \right)}\right)}^{\beta }+\frac{\gamma }{\mu }{\left(t+\frac{1}{\varGamma \left(\mu \right)}\right)}^{\mu }$ 

By restructuring the solution (39), we can obtain the solution in the hyperbolic form given below:

$${p}_{1}\left(x,t\right)=\pm \frac{\sqrt{2s}\lambda }{\sqrt{q\left(2rk-{r}^{2}{k}^{2}+2{r}^{2}{\lambda }^{2}-1\right)}}\left(\frac{\left(\theta +\lambda \alpha \right)\text{c}\text{o}\text{s}\text{h}\left(\lambda \zeta \right)+(\theta -\lambda \alpha )\text{s}\text{i}\text{n}\text{h}\left(\lambda \zeta \right)}{\left(\theta -\lambda \alpha \right)\text{c}\text{o}\text{s}\text{h}\left(\lambda \zeta \right)+(\theta +\lambda \alpha )\text{s}\text{i}\text{n}\text{h}\left(\lambda \zeta \right)}\right){e}^{i\psi },$$

(39)

The integral constant $\alpha$ can be intuitively determined in relation to the parameters $\lambda$ and $\theta$ of the Bernoulli’s equation to ascertain other solutions. Considering $\alpha =\lambda /4\theta$, from (40), we achieve the next solution

$${p}_{11}\left(x,t\right)=\mp \frac{\sqrt{2s}\lambda }{\sqrt{q\left(2rk-{r}^{2}{k}^{2}+2{r}^{2}{\lambda }^{2}-1\right)}}\left(\frac{5\text{c}\text{o}\text{s}\text{h}\left(\lambda \zeta \right)+3\text{s}\text{i}\text{n}\text{h}\left(\lambda \zeta \right)}{3\text{c}\text{o}\text{s}\text{h}\left(\lambda \zeta \right)+5\text{s}\text{i}\text{n}\text{h}\left(\lambda \zeta \right)}\right){e}^{i\psi }.$$

(40)

In an alternative approach, when we select $\alpha =\lambda /\theta$, we attain the resulting given in the next:

$${p}_{12}\left(x,t\right)=\pm \frac{\sqrt{2s}\lambda }{\sqrt{q\left(2rk-{r}^{2}{k}^{2}+2{r}^{2}{\lambda }^{2}-1\right)}}\text{coth}\left(\lambda \zeta \right){e}^{i\psi },$$

(41)

Again, when $\alpha =-\lambda /\theta$, we ascertain dark soliton solution from (41) in the following:

$${p}_{13}\left(x,t\right)=\pm \frac{\sqrt{2s}\lambda }{\sqrt{q\left(2rk-{r}^{2}{k}^{2}+2{r}^{2}{\lambda }^{2}-1\right)}}\text{tanh}\left(\lambda \zeta \right){e}^{i\psi },$$

(42)

where $\zeta =\frac{1}{\beta }{\left(x+\frac{1}{\varGamma \left(\beta \right)}\right)}^{\beta }-\frac{\omega }{\mu }{\left(t+\frac{1}{\varGamma \left(\mu \right)}\right)}^{\mu },\psi =-\frac{k}{\beta }{\left(x+\frac{1}{\varGamma \left(\beta \right)}\right)}^{\beta }+\frac{\gamma }{\mu }{\left(t+\frac{1}{\varGamma \left(\mu \right)}\right)}^{\mu },$   wave velocity $\omega =\frac{2ks-r\gamma }{rk-1}$ and wave number$\gamma =\frac{s({k}^{2}-{k}^{3}r+2rk{\lambda }^{2}+2{\lambda }^{2})}{2rk-{r}^{2}{k}^{2}+2{r}^{2}{\lambda }^{2}-1}$.For the sake of brevity, we have not mentioned other pertinent solutions that can be derived from the same general solution (40) by varying the values of the parameter $\alpha$.

Case 2

We assume $\lambda = 0$:

By substituting the values of the parameters gathered in (37), combined with (31) and (8), into the solution (36), we obtain the solution to the fractional cubic NS equation in the form of hyperbolic and exponential functions, as presented below.

$${p}_{2}(x,t)=\pm \frac{\sqrt{2s}\lambda }{\sqrt{q\left(2rk-{r}^{2}{k}^{2}+2{r}^{2}{\lambda }^{2}-1\right)}}\left(\frac{\left(\alpha -1\right)\text{t}\text{a}\text{n}\text{h}\left(\lambda \zeta \right)-(\alpha +1)}{\left(\alpha +1\right)\text{t}\text{a}\text{n}\text{h}\left(\lambda \zeta \right)-(\alpha -1)}\right){e}^{i\psi },$$

(43)

where $\zeta =\frac{1}{\beta }{\left(x+\frac{1}{\varGamma \left(\beta \right)}\right)}^{\beta }-\frac{\omega }{\mu }{\left(t+\frac{1}{\varGamma \left(\mu \right)}\right)}^{\mu } \quad \text{and} \quad \psi =-\frac{k}{\beta }{\left(x+\frac{1}{\varGamma \left(\beta \right)}\right)}^{\beta }+\frac{\gamma }{\mu }{\left(t+\frac{1}{\varGamma \left(\mu \right)}\right)}^{\mu }.$ 

Since $\alpha$ is an integrating constant, so we can choose several values of $\alpha$. When $\alpha =\sqrt{3}$, we acquire the ensuing solution from (44):

$${p}_{21}(x,t)=\pm \frac{\sqrt{2s}\lambda }{\sqrt{q\left(2rk-{r}^{2}{k}^{2}+2{r}^{2}{\lambda }^{2}-1\right)}}\left(\frac{\left(\sqrt{3}-1\right)\text{t}\text{a}\text{n}\text{h}\left(\lambda \zeta \right)-\left(\sqrt{3}+1\right)}{\left(\sqrt{3}+1\right)\text{t}\text{a}\text{n}\text{h}\left(\lambda \zeta \right)-\left(\sqrt{3}-1\right)}\right){e}^{i\psi }.$$

(44)

 where $\zeta =\frac{1}{\beta }{(x+\frac{1}{\varGamma \left(\beta \right)})}^{\beta }-\frac{\omega }{\mu }{(t+\frac{1}{\varGamma \left(\mu \right)})}^{\mu } \quad \text{and} \quad \psi =-\frac{k}{\beta }{\left(x+\frac{1}{\varGamma \left(\beta \right)}\right)}^{\beta }+\frac{\gamma }{\mu }{\left(t+\frac{1}{\varGamma \left(\mu \right)}\right)}^{\mu }.$ 

We can obtain several solutions to the fractional cubic NS equation by choosing the values of arbitrary parameter $r$ instinctively. For brevity, only a few solutions are shown.

5 Results and discussion

The acquired soliton solutions are portrayed in the diagrams in this section, and the profiles of these wave solutions for various parametric values are discussed using the symbolic computational program Mathematica.

5.1 The fractional cubic quintic NS equation

In this module, we analyze the graphical representations of the solutions derived for the fractional cubic quintic NS equation, considering various parametric values. The obtained solutions consist of two components: the real part and the imaginary part.

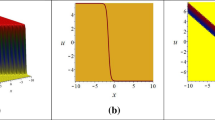
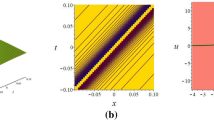
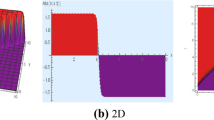
The kink soliton is obtained for the modulus of the solution (22) for the values $b=-5$, $\lambda =-5$, $\gamma =-5$, $\theta =-1$, $\alpha =-1$, $p=1.45$,$\beta =0.81$ with wave velocity $q=-2.59$ within the intervals $0\le x\le 10$, $0\le t\le 5$, is displayed in the three-dimensional plot in Fig. 1a, b displays the two-dimensional plot for $t = 1.5$, while Fig. 1c shows the contour plot. Additionally, by varying the values of α from − 1 to 2, a singular kink-type soliton is obtained for the modulus of the solution (22), as depicted in Fig. 2. The 3D plot in Fig. 3a demonstrates that the real part of the solution (22) exhibits a periodic soliton with varying amplitudes for the values $b=-4.23$, $d=1.66$, $\gamma =-2.52$, $h=-2.745$, $s=0.21$, $\alpha =-0.3$, $p=4.5$, $\beta =0.5$ with wave velocity $q=4.28$ within the intervals $0\le x,t\le 30$; the 2D plot for $t = 10$ is depicted in Fig. 3b, the contour graph in Fig. 3c. By keeping all the parameters constant except for the fractional order $\beta$, the two-, three-dimensional and contour plots of the real part of the solution (22) depict a multi-periodic soliton with identical amplitudes. This is illustrated in Fig. 4 for $\beta =0.95$. When considering the parametric values $b=0.42$, $\lambda =0.24$, $\gamma =-1.94$, $\theta =-2.1$, $s=-0.52$, $\alpha =2$, $p=1.55$, $\beta =0.7$ with wave velocity $q=1.67$ within the intervals $0\le x,t\le 30$ the imaginary part of the solution (22) exhibits a periodic bell-shaped soliton, outlined 3D plot in Fig. 5a; the 2D plot for $t = 30$ is shown in Fig. 5b and the contour graph in Fig. 5c. Figure 6 displays the multi-periodic soliton obtained for the real part of the solution (23) using the following parameter values: $b=-10$, $\lambda =-10$, $\gamma =0.35$, $s=0.5$, $p=4.14$, $\beta =0.7$, and a wave velocity of $q=1.52$. The plot covers the intervals $0\le x,t\le 30$. On the other hand, Fig. 7 displays the imaginary part of the solution (23) depicting a periodic bell-shaped soliton. This soliton is obtained using the parameter values: $b=-2.98$, $\lambda =-2.25$, $s=-0.17$, $\gamma =-2.98$, $p=3.54$, $\mu =0.64$, and a travelling wave velocity of $q=2.6$. Figure 8 illustrates breather soliton generated from the solution (24) for $b=-2.06$, $\lambda =-3.4$, $s=-4.74$, $\gamma =-0.35$, $p=4.06$, $q=2.47$, $\beta =0.94$ within the range $-1\le x,t\le 15$. Breathing solitons are a kind of dissipative Kerr soliton with periodic oscillations in pulse duration and peak intensity (Mamun et al. 2022a, b, c, d). Further, both 2D graphs are drawn for $t=1$. Also, the periodic soliton is obtained for $p=2.81$, $q=0.36$, $\beta =0.9$, $\lambda =2.26$, $s=0.52$, $\gamma =-1.92$, $\alpha =3.23$, $p=4.7$, $q=4.35$, from the solution (26) and represented in Fig. 9.

For conciseness, other soliton solutions obtained for different values of the free parameters are not depicted here. Based on the previous illustrations of soliton profiles, it can be concluded that the shape of the soliton mainly depends on the fractional order $\beta$, phase shift, wave number, and velocity. The coefficients $b$ and $\gamma$ in the equation do not have a significant impact on the wave speed. However, the Bernoulli parameters $\lambda$ and $\theta$, as well as the integrating constants, do considerably contribute to the soliton characteristics.

Fig. 1

Graph of the modulus part of the solution (22) for a 3D, b 2D and c contour graphs

Fig. 2

Graph of the modulus part of the solution (22) for a 3D, b 2D plot and c contour graphs

Fig. 3

Graph of real part of the solution (22) for a 3D, b 2D and c contour graphs

Fig. 4

Graph of real part of the solution (22) for a 3D, b 2D and c contour graphs

Fig. 5

Graph of imaginary part of the solution (22) for a 3D, b 2D and c contour graphs

Fig. 6

Plot of real part of the solution (23) for a 3D, b 2D for $t=1$ and c contour graphs

Fig. 7

Plot of imaginary part of the solution (23) for a 3D, b 2D for $t=1$ and c contour graphs

Fig. 8

Breather soliton obtained from solution (24) for a 3D, b 2D and c density graphs

Fig. 9

Plot of of the solution (26) for a 3D, b 2D and c contour graphs

5.2 The fractional cubic NS equation

For a specific value, $\lambda =-5$, $q=-5$, $s=-5$, $k=-5$, $r=-3.02$, $\alpha =-5$, $\theta =-0.62$, $\omega =1.1$, $\beta =0.4$, $\mu =0.31$, the modulus of the solution ${p}_{1}(x,t)$ exhibits the kink shaped soliton. The contour and three-dimensional graphs are drawn for the interval $0\le x,t\le 20$ as shown in Fig. 10a, c. Further, Fig. 10b is obtained for $t=1$. The solution ${p}_{1}(x,t)$, shown in Fig. 11, represents periodic soliton with different amplitudes for $\lambda =-5.7$, $q=-2.52$, $s=-8.2$, $k=-0.66$, $r=2.76$, $\alpha =-3.6$, $\theta =-3.6$, $\omega =1.1$, $\beta =0.4$, $\mu =0.31$ inside the intervals $0\le x\le 10$, $0\le t\le 5$. Increasing only the value $k$ from $-0.66$ to $1.75$, the wave frequency increases with similar amplitudes and an identical wave profile that is obtained from the real part of the solution ${p}_{1}(x,t)$, which is shown in Fig. 12.

For certain parameter values $\beta =0.99$ and $\mu =0.99$, while keeping other parameters constant, the imaginary part of the solution ${p}_{1}(x,t)$ represents a breathing soliton. The 3D and density graphs are plotted for the interval $0\le x,t\le 20$. Additionally, Fig. 13 displays the 2D graph of this solution specifically for $t=1$ within the interval $0\le x\le 20$. In the limiting case, as $\mu \to 1$ and $\beta \to 1$, the fractional form of the solution ${p}_{1}(x,t)$ closely matches the classical form of the solution.

The solution ${p}_{2}(x,t)$ represents breathing soliton for the certain values of $\lambda =-5$, $q=-5$, $s=-5$, $k=20.6$, $r=0.13$, $\alpha =-0.31$, $\omega =-0.33$, $\beta =0.716$, $\mu =0.82$. The 3D and density graphs are attained for the region $0\le x,t\le 20$. Also, 2D graphs are drawn for $t=1$ as shown in Fig. 14.

Keeping the values of $\lambda$, $q$, $s$ as constant, the breathing soliton is accomplished for $k=-5$, $r=-1.64$, $\alpha =-4.02$, $\omega =0.65$, $\beta =0.75$, $\mu =0.7$ for the imaginary part of the solution ${p}_{2}(x,t)$ throughout the intervals $0\le x,t\le 20$ and illustrated in Fig. 15.

The other solutions obtained for this equation that exhibit analogous soliton shapes, such as kink, breathing, and periodic solitons, are not presented here for conciseness. Based on the previous illustration of soliton profiles, it can be observed that the shape of the solitons primarily depends on the values of the fractional order, wave frequency, wave number, and velocity. The coefficients $k$, $r$, $q$, and $s$ in the equation do not affect the wave speed. However, the Bernoulli parameters $\lambda$ and $\theta$, as well as the integrating constants, do play a role in determining the soliton characteristics.

Fig. 10

The modulus plot of the solution ${p}_{1}(x,t)$ for a 3D, b 2D and c contour graphs

Fig. 11

Plot of solution ${p}_{1}(x,t)$ for a 3D, b 2D for $t=1$ and c contour graphs

Fig. 12

Plot of real part of the solution ${p}_{1}(x,t)$ for a 3D, b 2D and c contour graphs

Fig. 13

Plot of imaginary part of the solution ${p}_{1}(x,t)$ for a 3D, b 2D and c density graphs

Fig. 14

Plot of real part of the solution ${p}_{2}(x,t)$ for a 3D, b 2D and c density graphs

Fig. 15

Plot of imaginary part of the solution ${p}_{2}(x,t)$ for a 3D, b 2D and c density graphs

From the preceding discussion, we can conclude that variability of the solution is determined by parameter values, such as singular kink, breather soliton, kink, periodic, and other soliton shapes.

6 Conclusion

In this article, we have competently extracted wide-ranging optical soliton solutions of the space-time fractional cubic quintic NS equation and the space–time fractional cubic NS equation comprising assorted subjective constraints by putting in use of the IBSEF approach that could be useful for analyzing optical solitons in communication engineering. The obtained solutions cover a wide range of soliton types, including kink, periodic solitons, breathing solitons, singular kink-type solitons, and other distinct solitons. These diverse solitons have implications in plasmas, condensed matter physics, photonics, nonlinear optics, and some other physical domains. The computations necessary for this study were accomplished using the symbolic computation software Maple, while Wolfram Mathematica was employed to visualize the 3D, density, and 2D surfaces of all the solutions with appropriate parametric values. This visualization is crucial in understanding the underlying physical characteristics of the solitons. The research findings affirm that the IBSEF approach is straightforward, effective, powerful, and rational. It has the ability to generate stable soliton solutions for a wide range of other fractional nonlinear evolution equations (FNLEEs) in the fields of quantum physics, optics, and applied mathematics.