1 Introduction

The most generally optical models for electromagnetic energy introduce electromagnetic flux, thermal drift energy, extrusion modeling. Optical thermal energy engages numerical design and macroscopic applications with thermal energy photonics. Optical thermal energy applications have conducted electroosmotic illustrations with different multi optical optimistic energy. Thermal energy applications associate photonic geometric phase, optoelectronic geometric phase, piezoelectric phase, photodiode phase. Semirecursional optical flux is constructed in optical microscale sensing methods (Yamada et al. 2011; Amjadi et al. 2016; Yan et al. 2018; Tao et al. 2012; Abouraddy et al. 2007; Fink et al. 1998; Korpinar and Körpınar 2021; Körpınar 2021; Körpınar and Korpinar 2021a, b).

Optical energy improvement of quasi electronics and spherical designs with energy modeling machinery is inflation important optical applications. Optical hybrid flux is decisive significance in mathematical energy physics, geometric applications, optical geometry in optical energy (Garcia de Andrade 2006c, a, b; Vieira and Horley 2012; Guo and Ding 2008; Hasimoto 1972; Jones 1941; Biener et al. 2002; Berry and Klein 1996; Zygelman 1987; Son and Yamamoto 2012; Smit 1955; Körpınar and Demirkol 2019; Körpınar et al. 2019, 2019a, b; Cao et al. 2018; Körpınar and Demirkol 2020; Cao et al. 2017; Erb et al. 2016; Körpınar et al. 2020).

Microfluidic optical energy with recursional sensing phases are regularly experienced in optical spherical applications, optical design, PDT, optical signal theory, PTT. Modeling of spherical flux systems are associated by diverse optical and physical systems with antiferromagnetic Heisenberg optical model, Landau–Lifshitz optical model, Schrödinger optical model, binormal optical model, Da Rios optical model, localized induction optical model, etc. (Furlani and Ng 2006; Tomita and Chiao 1986; Körpınar et al. 2020; Balakrishnan et al. 1990; Wassmann and Ankiewicz 1998; Balakrishnan et al. 1993; Balakrishnan and Dandoloff 1999; Körpinar and Demirkol 2018a, b; Körpinar 2020; Dandoloff and Zakrzewski 1989; Kugler and Shtrikman 1988; Yamashita 2012; Satija and Balakrishan 2009; Lamb 1977; Yamashita 2012; Murugesh and Balakrishnan 2001; Gürbüz 2005; Körpınar et al. 2021a; Körpınar and Körpınar 2021a; Körpınar et al. 2021b; Körpınar and Körpınar 2021b; Körpınar et al. 2022).

The establishment of our paper is as follows. First, we obtain optical angular momentum of \(\phi \left( \varvec{\alpha }\right) ,\phi \left( {\textbf{t}}\right) ,\phi \left( {\textbf{s}}\right)\) by using optical spherical frame. Also, we construct magnitude of optical angular momentum and spherical magnetic moment of \(\phi \left( \varvec{\alpha }\right) ,\phi \left( {\textbf{t}}\right) ,\phi \left( {\textbf{s}}\right)\). Thus, we illustrate optical \(\tau _{\phi \left( \varvec{\alpha }\right) },\tau _{\phi \left( {\textbf{t}}\right) },\tau _{\phi \left( {\textbf{s}}\right) }\) magnetic torque phase microscale. Moreover, we have electroosmotic microfluidic \(\tau _{\phi \left( \varvec{\alpha }\right) },\tau _{\phi \left( {\textbf{t}}\right) },\tau _{\phi \left( {\textbf{s}}\right) }\) magnetic torque density. Finally, we design electroosmotic magnetic torque density with antiferromagnetic model.

2 Spherical optical magnetic torque

Spherical frame of \(\alpha :{\mathbb {I}}\rightarrow {\mathbb {S}}^{2}\) is given by

$$\begin{aligned} \nabla _{\sigma }\alpha&={\textbf{t}} \\ \nabla _{\sigma }{\textbf{t}}&=-\alpha +\varepsilon {\textbf{s}} \\ \nabla _{\sigma }{\textbf{s}}&=-\varepsilon \textbf{t}, \end{aligned}$$

and

$$\begin{aligned} \begin{array}{ccc} \alpha =\textbf{t}\times \textbf{s},&{\textbf{t}}=\textbf{s}\times \varvec{\alpha },&{\textbf{s}}=\varvec{\alpha } \times \textbf{t}. \end{array} \end{aligned}$$

  • Lorentz forces and magnetic field are given

    $$\begin{aligned} \phi \left( \varvec{\alpha }\right)&=\textbf{t}+\rho \textbf{s},\\ \phi \left( {\textbf{t}}\right)&=-\varvec{\alpha }+\varepsilon \textbf{s}, \\ \phi \left( {\textbf{s}}\right)&=-\rho \varvec{\alpha }-\varepsilon \textbf{t}, \\ {\mathcal {B}}&=\varepsilon \varvec{\alpha }-\rho \textbf{t}+\textbf{s}. \end{aligned}$$

    Optical angular momentum is obtained by

    $$\begin{aligned} \otimes = f\times m^{f}\Psi (f). \end{aligned}$$

    Optical magnitude of angular momentum is

    $$\begin{aligned} \left\| \otimes \right\| =\left\| f\times m^{f}\Psi (f)\right\| . \end{aligned}$$

    Optical magnetic moment is given

    $$\begin{aligned} \theta _{\phi \left( f\right) }=\frac{\omega ^{f}}{2m^{f}} \otimes . \end{aligned}$$

    Optical magnetic torque given by

    $$\begin{aligned} \tau _{\phi \left( f\right) }=\theta \times {\mathcal {B}}. \end{aligned}$$

    Also, we have

    $$\begin{aligned} \theta _{\phi \left( \varvec{\alpha }\right) }&=\frac{1}{2}\rho \omega ^{\varvec{\alpha }}\varvec{\alpha }, \\ \theta _{\phi \left( {\textbf{t}}\right) }&=\frac{1}{2}\varepsilon \omega ^{{\textbf{t}}}\varvec{\alpha }+\frac{1}{2}\omega ^{{\textbf{t}}}\textbf{s}, \\ \theta _{\phi \left( {\textbf{s}}\right) }&=\frac{1}{2}\rho \omega ^{{\textbf{s}}}\textbf{s}. \end{aligned}$$

    Putting

    $$\begin{aligned} \dfrac{\partial \alpha }{\partial t}={\mathcal {L}}{\textbf{t}}+{\mathcal {F}}\mathbf {s.} \end{aligned}$$

  • Flows of forces are obtained by

    $$\begin{aligned} \nabla _{t}\phi \left( \varvec{\alpha }\right)&=-({\mathcal {L}}+\rho {\mathcal {F}})\varvec{\alpha }-\rho \left( {\mathcal {L}}\varepsilon +\dfrac{\partial {\mathcal {F}}}{\partial \sigma }\right) {\textbf{t}}+\left( \frac{\partial \rho }{\partial t} +\left( {\mathcal {L}}\varepsilon +\dfrac{\partial {\mathcal {F}}}{\partial \sigma }\right) \right) \textbf{s}, \\ \nabla _{t}\phi \left( {\textbf{t}}\right)&=-{\mathcal {F}}\varepsilon \varvec{\alpha }-\left( {\mathcal {L}}+\left( {\mathcal {L}}\varepsilon +\dfrac{\partial {\mathcal {F}}}{\partial \sigma }\right) \varepsilon +\right) {\textbf{t}}+\left( -{\mathcal {F}}+\dfrac{\partial \varepsilon }{\partial t}\right) \textbf{s}, \\ \nabla _{t}\phi \left( {\textbf{s}}\right)&=\left( -\frac{\partial \rho }{\partial t}+{\mathcal {L}}\right) \varvec{\alpha }-\left( \rho {\mathcal {L}}+\frac{\partial \varepsilon }{\partial t}\right) {\textbf{t}}-\left( \varepsilon \left( {\mathcal {L}}\varepsilon + \dfrac{\partial {\mathcal {F}}}{\partial \sigma }\right) +\rho {\mathcal {F}}\right) \mathbf {s.} \end{aligned}$$

  • Flows of magnetic moments are

    $$\begin{aligned} \nabla _{t}\theta _{\phi \left( \varvec{\alpha }\right) }&=\frac{1}{2} \frac{\partial \rho }{\partial t}\omega ^{\varvec{\alpha }}\varvec{\alpha }+ \frac{1}{2}\rho {\mathcal {L}}\omega ^{\varvec{\alpha }}\textbf{t}+\frac{\rho }{2}\omega ^{\varvec{\alpha }}{\mathcal {F}}\textbf{s}, \\ \nabla _{t}\theta _{\phi \left( {\textbf{t}}\right) }&=\left( \frac{1}{2}\omega ^{ {\textbf{t}}}\frac{\partial \varepsilon }{\partial t}-\frac{{\mathcal {F}}}{2} \omega ^{{\textbf{t}}}\right) \varvec{\alpha }+\left( \frac{1}{2}\varepsilon \omega ^{ {\textbf{t}}}{\mathcal {L}}-\frac{1}{2}\left( \dfrac{\partial {\mathcal {F}}}{\partial \sigma }+{\mathcal {L}}\varepsilon \right) \omega ^{{\textbf{t}}}\right) {\textbf{t}}+\frac{ \varepsilon }{2}\omega ^{{\textbf{t}}}{\mathcal {F}}\textbf{s}, \\ \nabla _{t}\theta _{\phi \left( {\textbf{s}}\right) }&=-\frac{1}{2} {\mathcal {F}}\rho \omega ^{{\textbf{s}}}\varvec{\alpha }-\frac{1}{2}\omega ^{ {\textbf{s}}}\rho \left( \dfrac{\partial {\mathcal {F}}}{\partial \sigma }+{\mathcal {L}}\varepsilon \right) {\textbf{t}}+\frac{1}{2}\frac{\partial }{\partial t}\rho \omega ^{ {\textbf{s}}}\textbf{s}. \end{aligned}$$

3 Spherical magnetic torque phase microscale

3.1 Microfluidic antiferromagnetic \(\tau _{\phi \left( \varvec{\alpha }\right) }\) magnetic torque phase

  • \(\tau _{\phi \left( \varvec{\alpha }\right) }\) magnetic torque phase microscale is

    $$\begin{aligned} ^{{\mathcal {B}}}{\mathcal {M}}_{\phi \left( {\textbf{t}}_{\varvec{\omega }}\right) }=\tau _{0}^{\varvec{\alpha }}\int \int _{{\mathcal {W}}}\nabla _{t}\phi \left( \varvec{\alpha }\right) \cdot\nabla _{t}\tau _{\phi \left( \varvec{\alpha }\right) }d{\mathcal {W}}. \end{aligned}$$

Optical angular momentum of \(\phi \left( \varvec{\alpha }\right)\) is given

$$\begin{aligned} \otimes _{\phi \left( \varvec{\alpha }\right) }=\rho m^{\varvec{\alpha }}\varvec{\alpha }. \end{aligned}$$

The magnitude of optical angular momentum is

$$\begin{aligned} \left\| \otimes _{\phi \left( \varvec{\alpha }\right) }\right\| =\rho m^{\varvec{\alpha }}. \end{aligned}$$

Spherical magnetic moment of \(\phi \left( \varvec{\alpha }\right)\) is

$$\begin{aligned} \theta _{\phi \left( \varvec{\alpha }\right) }=\frac{\omega ^{\varvec{\alpha }}}{2}\rho \varvec{\alpha }. \end{aligned}$$

\(\tau _{\phi \left( \varvec{\alpha }\right) }\) magnetic torque of \(\phi \left( \varvec{\alpha }\right)\) is constructed by

$$\begin{aligned} \tau _{\phi \left( \varvec{\alpha }\right) }=-\frac{1}{2}\rho \omega ^{\varvec{\alpha }}{{\textbf{t}}}-\frac{1}{2}\rho ^{2}\omega ^{ \varvec{\alpha }}\textbf{s}. \end{aligned}$$

Thus, fluid of \(\tau _{\phi \left( \varvec{\alpha }\right) }\) magnetic torque is

$$\begin{aligned} \nabla _{t}\tau _{\phi \left( \varvec{\alpha }\right) }&=\left( \frac{1 }{2}\rho {\mathcal {L}}\omega ^{\varvec{\alpha }}+\frac{1}{2} {\mathcal {F}}\omega ^{\varvec{\alpha }}\rho ^{2}\right) \varvec{\alpha }+\left( \frac{1}{2} \rho ^{2}\omega ^{\varvec{\alpha }}\left( \dfrac{\partial {\mathcal {F}}}{\partial \sigma }+{\mathcal {L}}\varepsilon \right) -\frac{1}{2}\frac{\partial \rho }{\partial t}\omega ^{\varvec{\alpha }}\right) {\textbf{t}}\\&\quad -\left( \frac{1}{2}\rho \omega ^{\varvec{\alpha }}\left( \dfrac{\partial {\mathcal {F}}}{\partial \sigma }+\varepsilon {\mathcal {L}}\right) +\rho \omega ^{ \varvec{\alpha }}\frac{\partial \rho }{\partial t}\right) \textbf{s}. \end{aligned}$$

  • Electroosmotic microfluidic \(\tau _{\phi \left( \varvec{\alpha }\right) }\) magnetic torque density is

    $$\begin{aligned} {\mathcal {V}}_{\tau _{\phi \left( \varvec{\alpha }\right) }}&= -({\mathcal {L}}+\rho {\mathcal {F}})\left( \frac{1}{2}\rho \omega ^{\varvec{\alpha } }{\mathcal {L}}+\frac{1}{2}{\mathcal {F}}\rho ^{2}\omega ^{\varvec{\alpha }}\right) \\&\quad -\rho \left( {\mathcal {L}}\varepsilon +\dfrac{\partial {\mathcal {F}}}{\partial \sigma }\right) \left( \frac{1}{2}\rho ^{2}\omega ^{\varvec{\alpha }}\left( \dfrac{\partial {\mathcal {F}}}{\partial \sigma } +{\mathcal {L}}\varepsilon \right) -\frac{1}{2}\omega ^{\varvec{\alpha }}\frac{ \partial \rho }{\partial t}\right) \\&\quad -\left( \frac{1}{2}\rho \omega ^{\varvec{\alpha }}\left( \dfrac{\partial {\mathcal {F}}}{\partial \sigma }+\varepsilon {\mathcal {L}}\right) +\rho \frac{\partial \rho }{\partial t}\omega ^{ \varvec{\alpha }}\right) \left( \left( {\mathcal {L}}\varepsilon +\dfrac{\partial {\mathcal {F}}}{ \partial \sigma }\right) +\frac{\partial \rho }{\partial t}\right) . \end{aligned}$$

  • Microfluidic \(\tau _{\phi \left( \varvec{\alpha } \right) }\) magnetic torque phase microscale is given

    $$\begin{aligned} {\mathcal {T}}_{\tau _{\phi \left( \varvec{\alpha }\right) }}&=\tau _{0}^{ \varvec{\alpha }}\int \int _{{\mathcal {W}}}\left( -\rho \left( {\mathcal {L}}\varepsilon + \dfrac{\partial {\mathcal {F}}}{\partial \sigma }\right) \left( \frac{1}{2}\rho ^{2}\omega ^{\varvec{\alpha }}\left( \dfrac{\partial {\mathcal {F}}}{\partial \sigma } +{\mathcal {L}}\varepsilon \right) -\frac{1}{2}\frac{\partial \rho }{\partial t}\omega ^{\varvec{\alpha } }\right) \right. \\&\quad -({\mathcal {L}}+\rho {\mathcal {F}})\left( \frac{1}{2}\rho \omega ^{\varvec{\alpha } }{\mathcal {L}}+\frac{1}{2}{\mathcal {F}}\rho ^{2}\omega ^{\varvec{\alpha }}\right) \\&\left. \quad -\left( \frac{1}{2}\rho \omega ^{\varvec{\alpha }}\left( \dfrac{\partial {\mathcal {F}}}{ \partial \sigma }+\varepsilon {\mathcal {L}}\right) +\rho \frac{\partial \rho }{ \partial t}\omega ^{\varvec{\alpha }}\right) \left( \left( {\mathcal {L}}\varepsilon +\dfrac{ \partial {\mathcal {F}}}{\partial \sigma }\right) +\frac{\partial \rho }{ \partial t}\right) \right) d{\mathcal {W}}, \end{aligned}$$

    where \(\tau _{0}^{\varvec{\alpha }}\) is magnetic torque constant for \(\phi \left( \varvec{\alpha }\right)\).

  • Microfluidic antiferromagnetic \(\tau _{\phi \left( \varvec{\alpha }\right) }\) magnetic torque phase microscale is given

    $$\begin{aligned} ^{{\mathcal {B}}}{\mathcal {M}}_{\tau _{\phi \left( \varvec{\alpha }\right) }}=\tau _{0}^{\varvec{\alpha }}\int \int _{{\mathcal {W}}}\nabla _{t}\phi \left( \varvec{\alpha }\right) \cdot \tau _{\phi \left( \varvec{\alpha } \right) }\times \nabla _{\sigma }\tau _{\phi \left( \varvec{\alpha }\right) }d{\mathcal {W}}. \end{aligned}$$

    From spherical frame, we have

    $$\begin{aligned} \tau _{\phi ( \varvec{\alpha }) }\times \nabla _{\sigma }\tau _{\phi \left( \varvec{\alpha }\right) }&=\left( \frac{1}{2}\rho \omega ^{ \varvec{\alpha }}\left( \rho \omega ^{\varvec{\alpha }}\dfrac{\partial \rho }{\partial \sigma }+\frac{\omega ^{\varvec{\alpha }}}{2}\varepsilon \right) +\left( \varepsilon \rho ^{2} -\dfrac{\partial \rho }{\partial \sigma }\right) \right. \\&\left. \quad \times \left( \frac{1}{2}\omega ^{\varvec{\alpha }}\right) ^{2}\rho ^{2}\right) \varvec{\alpha }-\left( \frac{1}{2}\omega ^{\varvec{\alpha }}\right) ^{2}\rho ^{2}\textbf{t}+\left( \frac{1}{2}\omega ^{\varvec{\alpha }}\right) ^{2}\rho \textbf{s}. \end{aligned}$$

  • Electroosmotic antiferromagnetic microfluidic \(\tau _{\phi \left( \varvec{\alpha }\right) }\) magnetic torque density is

    $$\begin{aligned} {\mathcal {V}}_{\tau _{\phi ( \varvec{\alpha }) }}^{{\mathcal {A}} }&=-({\mathcal {L}}+\rho {\mathcal {F}})\left( \frac{1}{2}\rho \left( \rho \omega ^{\varvec{\alpha }}\dfrac{\partial \rho }{\partial \sigma }+\frac{ \omega ^{\varvec{\alpha }}}{2}\varepsilon \right) \omega ^{\varvec{\alpha }} \right. \\&\left. \quad +\left( \varepsilon \rho ^{2}-\dfrac{\partial \rho }{\partial \sigma }\right) \left( \frac{1}{2} \omega ^{\varvec{\alpha }}\right) ^{2}\rho ^{2}\right) +\left( \frac{1}{2}\omega ^{\varvec{\alpha }}\right) ^{2}\rho ^{3}\left( {\mathcal {L}}\varepsilon +\dfrac{\partial {\mathcal {F}}}{\partial \sigma }\right) \\&\quad +\left( \frac{1}{2}\omega ^{ \varvec{\alpha }}\right) ^{2}\rho \left( \left( {\mathcal {L}}\varepsilon +\dfrac{\partial {\mathcal {F}}}{\partial \sigma }\right) +\frac{\partial \rho }{\partial t}\right) . \end{aligned}$$

  • Microfluidic antiferromagnetic \(\tau _{\phi \left( \varvec{\alpha }\right) }\) magnetic torque phase microscale is

    $$\begin{aligned} {\mathcal {T}}_{\tau _{\phi \left( \varvec{\alpha }\right) }}^{{\mathcal {A}} }&=\tau _{0}^{\varvec{\alpha }}\int \int _{{\mathcal {W}}}\left( \left( \frac{1}{2}\omega ^{ \varvec{\alpha }}\right) ^{2}\rho ^{3}\left( {\mathcal {L}}\varepsilon +\dfrac{\partial {\mathcal {F}}}{\partial \sigma }\right) -\left( \frac{1}{2}\omega ^{\varvec{\alpha }}\rho \left( \rho \omega ^{\varvec{\alpha }}\dfrac{\partial \rho }{\partial \sigma }+\frac{1}{2}\varepsilon \omega ^{\varvec{\alpha }}\right) \right. \right. \\&\left. \quad +\left( \varepsilon \rho ^{2}-\dfrac{\partial \rho }{\partial \sigma }\right) \left( \frac{1}{2} \omega ^{\varvec{\alpha }}\right) ^{2}\rho ^{2}\right) ({\mathcal {L}}+\rho {\mathcal {F}})\\&\left. \quad +\left( \frac{1}{2}\omega ^{\varvec{\alpha }}\right) ^{2}\rho \left( \left( {\mathcal {L}}\varepsilon + \dfrac{\partial {\mathcal {F}}}{\partial \sigma }\right) +\frac{\partial \rho }{\partial t}\right) \right) d{\mathcal {W}}, \end{aligned}$$

    where \(\tau _{0}^{\varvec{\alpha }}\) is magnetic torque constant for \(\phi \left( \varvec{\alpha }\right)\). Also, we easily get

    $$\begin{aligned} \phi \left( \varvec{\alpha }\right) \times \nabla _{\sigma }\phi \left( \varvec{\alpha }\right) =\left( \frac{\partial \rho }{\partial \sigma } +\rho ^{2}\varepsilon +\varepsilon \right) \varvec{\alpha }-\rho {\textbf{t}} +\textbf{s}. \end{aligned}$$

  • Electroosmotic \(\tau _{\phi \left( \varvec{\alpha }\right) }\) magnetic torque density with antiferromagnetic\(\phi \left( \varvec{\alpha }\right)\) is

    $$\begin{aligned} ^{\phi \left( \varvec{\alpha }\right) }{\mathcal {V}}_{\tau _{\phi \left( \varvec{\alpha }\right) }}^{{\mathcal {A}}}&=\left( \frac{\partial \rho }{ \partial \sigma }+\rho ^{2}\varepsilon +\varepsilon \right) \left( \frac{1}{2}\rho \left( \rho \omega ^{\varvec{\alpha }}\dfrac{\partial \rho }{\partial \sigma }+\frac{\omega ^{\varvec{\alpha }}}{2}\varepsilon \right) \omega ^{\phi \left( \varvec{\alpha }\right) } \right. \\&\left. \quad +\left( \varepsilon \rho ^{2}-\dfrac{\partial \rho }{\partial \sigma }\right) \left( \frac{1}{ 2}\omega ^{\varvec{\alpha }}\right) ^{2}\rho ^{2}\right) +\left( \frac{1}{2}\omega ^{ \varvec{\alpha }}\right) ^{2}\rho ^{3}+\left( \frac{1}{2}\omega ^{\varvec{\alpha }}\right) ^{2}\rho . \end{aligned}$$

  • Antiferromagnetic \(\tau _{\phi \left( \varvec{\alpha }\right) }\) magnetic torque phase microscale with antiferromagnetic \(\phi \left( \varvec{\alpha }\right)\) is

    $$\begin{aligned} ^{\phi \left( \varvec{\alpha }\right) }{\mathcal {T}}_{\tau _{\phi \left( \varvec{\alpha }\right) }}^{{\mathcal {A}}}&=\tau _{0}^{\varvec{\alpha }}\int \int _{{\mathcal {W}}}\left( \left( \frac{1}{2}\omega ^{\varvec{\alpha }}\right) ^{2}\rho ^{3}+ \left( \frac{\partial \rho }{\partial \sigma }+\rho ^{2}\varepsilon +\varepsilon \right) \left( \frac{1}{2}\rho \omega ^{\varvec{\alpha }}\left( \rho \omega ^{\varvec{\alpha }}\dfrac{\partial \rho }{ \partial \sigma }\right. \right. \right. \\&\left. \left. \left. \quad +\frac{1}{2}\varepsilon \omega ^{\varvec{\alpha }}\right) +\left( \varepsilon \rho ^{2}- \dfrac{\partial \rho }{\partial \sigma }\right) \left( \frac{1}{2}\omega ^{\varvec{\alpha }}\right) ^{2}\rho ^{2}\right) +\left( \frac{1}{2}\omega ^{\varvec{\alpha }}\right) ^{2}\rho \right) d {\mathcal {W}}, \end{aligned}$$

    where\(\tau _{0}^{\varvec{\alpha }}\) is magnetic torque constant for \(\phi \left( \varvec{\alpha }\right)\).

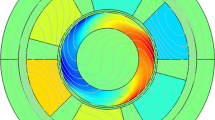
Optical effect of microfluidic antiferromagnetic \(\tau _{\phi \left( \varvec{\alpha }\right) }\) magnetic torque phase microscale is constructed vortex reactors in Fig. 1.

Fig. 1
figure 1

Microfluidic antiferromagnetic \(\tau _{\phi \left( \varvec{\alpha }\right) }\)

Full size image

3.2 Microfluidic antiferromagnetic \(\tau _{\phi \left( {\textbf{t}}\right) }\) magnetic torque phase

  • \(\tau _{\phi \left( {\textbf{t}}\right) }\) magnetic torque phase microscale is

    $$\begin{aligned} ^{{\mathcal {B}}}{\mathcal {M}}_{\phi \left( {\textbf{t}}\right) }=\tau _{0}^{ {\textbf{t}}}\int \int _{{\mathcal {W}}}\nabla _{t}\phi \left( {\textbf{t}}\right) \cdot\nabla _{t}\tau _{\phi \left( {\textbf{t}}\right) }d{\mathcal {W}}. \end{aligned}$$

    Optical angular momentum of \(\phi \left( {\textbf{t}}\right)\) is given

    $$\begin{aligned} \otimes _{\phi \left( {\textbf{t}}\right) }=m^{{\textbf{t}}}{\textbf{s}} +\varepsilon m^{{\textbf{t}}}\varvec{\alpha }. \end{aligned}$$

    The magnitude of optical angular momentum is

    $$\begin{aligned} \left\| \otimes _{\phi \left( {\textbf{t}}\right) }\right\| =m^{ {\textbf{t}}}(1+\varepsilon ^{2})^{\frac{1}{2}}. \end{aligned}$$

    Spherical magnetic moment of \(\phi \left( {\textbf{t}}\right)\) is

    $$\begin{aligned} \theta _{\phi \left( {\textbf{t}}\right) }=\frac{1}{2}\varepsilon \omega ^{ {\textbf{t}}}\varvec{\alpha }+\frac{1}{2}\omega ^{{\textbf{t}}}\textbf{s}. \end{aligned}$$

    \(\tau _{\phi \left( {\textbf{t}}\right) }\) magnetic torque of \(\phi \left( {\textbf{t}}\right)\) is constructed by

    $$\begin{aligned} \tau _{\phi \left( {\textbf{t}}\right) }=\frac{1}{2}\rho \omega ^{{\textbf{t}}} \varvec{\alpha }-\frac{1}{2}\varepsilon \omega ^{{\textbf{t}}}\rho \textbf{s}. \end{aligned}$$

    Thus, fluid of \(\tau _{\phi \left( {\textbf{t}}\right) }\) magnetic torque is

    $$\begin{aligned} \nabla _{t}\tau _{\phi \left( {\textbf{t}}\right) }&=\left( \frac{1}{2}\frac{\partial \rho }{\partial t}\omega ^{{\textbf{t}}}+\frac{1}{2}{\mathcal {F}}(\varepsilon \rho )\right) \omega ^{{\textbf{t}}}\varvec{\alpha }+\left( \frac{\omega ^{{\textbf{t}}}}{2} (\varepsilon \rho )\left( \dfrac{\partial {\mathcal {F}}}{\partial \sigma } +{\mathcal {L}}\varepsilon \right) \right. \\&\left. \quad +\frac{1}{2}\rho \omega ^{{\textbf{t}}}{\mathcal {L}}\right) {\textbf{t}}+\left( \frac{1}{2}\rho \omega ^{{\textbf{t}}}{\mathcal {F}}-\frac{1}{2} \frac{\partial }{\partial t}(\varepsilon \rho )\omega ^{{\textbf{t}}}\right) \textbf{s}. \end{aligned}$$

  • Electroosmotic microfluidic \(\tau _{\phi \left( {\textbf{t}}\right) }\) magnetic torque density is

    $$\begin{aligned} {\mathcal {V}}_{\tau _{\phi \left( {\textbf{t}}\right) }}&=-\varepsilon {\mathcal {F}}\left( \frac{1}{2}\frac{\partial \rho }{\partial t}\omega ^{\phi \left( {\textbf{t}}\right) }+\frac{1}{2}{\mathcal {F}}(\varepsilon \rho )\omega ^{\phi \left( {\textbf{t}}\right) }\right) \\&\quad -\left( \varepsilon \left( {\mathcal {L}}\varepsilon +\dfrac{\partial {\mathcal {F}}}{\partial \sigma }\right) +{\mathcal {L}}\right) \left( \frac{1}{2}(\varepsilon \rho )\omega ^{\phi \left( {\textbf{t}}\right) }\left( \dfrac{\partial {\mathcal {F}}}{\partial \sigma } +{\mathcal {L}}\varepsilon \right) \right. \\&\left. \quad +\frac{1}{2}\rho \omega ^{\phi \left( {\textbf{t}}\right) }{\mathcal {L}}\right) +\left( \frac{1}{2}\rho {\mathcal {F}}\omega ^{\phi \left( {\textbf{t}}\right) }-\frac{1 }{2}\frac{\partial }{\partial t}(\varepsilon \rho )\omega ^{\phi \left( {\textbf{t}}\right) }\right) \left( \dfrac{\partial \varepsilon }{\partial t}-{\mathcal {F}}\right) . \end{aligned}$$

  • Microfluidic \(\tau _{\phi \left( {\textbf{t}} \right) }\) magnetic torque phase microscale is given

    $$\begin{aligned} {\mathcal {T}}_{\tau _{\phi \left( {\textbf{t}}\right) }}&=\tau _{0}^{{\textbf{t}}} \int \int _{{\mathcal {W}}}\left( \left( \frac{1}{2}\rho \omega ^{{\textbf{t}}}{\mathcal {F}}- \frac{1}{2}\omega ^{{\textbf{t}}}\frac{\partial }{\partial t}(\varepsilon \rho )\right) \left( \dfrac{\partial \varepsilon }{\partial t}-{\mathcal {F}}\right) \right. \\&\quad -\varepsilon {\mathcal {F}}\left( \frac{1}{2}\omega ^{{\textbf{t}}}\frac{\partial \rho }{\partial t}+\frac{1}{2}{\mathcal {F}}(\varepsilon \rho )\omega ^{{\textbf{t}} }\right) -\left( \varepsilon \left( {\mathcal {L}}\varepsilon +\dfrac{\partial {\mathcal {F}}}{\partial \sigma }\right) +{\mathcal {L}}\right) \\&\left. \quad \times \left( \frac{1}{2}(\varepsilon \rho )\left( \dfrac{\partial {\mathcal {F}}}{\partial \sigma }+{\mathcal {L}}\varepsilon \right) \omega ^{{\textbf{t}}}+\frac{1}{2}\rho \omega ^{{\textbf{t}}}{\mathcal {L}}\right) \right) d{\mathcal {W}}, \end{aligned}$$

    where \(\tau _{0}^{{\textbf{t}}}\) is magnetic torque constant for \(\phi \left( {\textbf{t}}\right)\).

  • Microfluidic antiferromagnetic \(\tau _{\phi \left( {\textbf{t}}\right) }\) magnetic torque phase microscale is given

    $$\begin{aligned} ^{{\mathcal {B}}}{\mathcal {M}}_{\tau _{\phi \left( {\textbf{t}}\right) }}=\tau _{0}^{{\textbf{t}}}\int \int _{{\mathcal {W}}}\nabla _{t}\phi \left( {\textbf{t}} \right) \cdot\tau _{\phi \left( {\textbf{t}}\right) }\times \nabla _{\sigma }\tau _{\phi \left( {\textbf{t}}\right) }d{\mathcal {W}}. \end{aligned}$$

    From spherical frame, we have

    $$\begin{aligned} \tau _{\phi \left( {\textbf{t}}\right) }\times \nabla _{\sigma }\tau _{\phi \left( {\textbf{t}}\right) }&=\left( \frac{1}{2}(\varepsilon ^{2}\rho )\omega ^{ {\textbf{t}}}+\frac{1}{2}\omega ^{{\textbf{t}}}\rho \right) \frac{1}{2}\varepsilon \omega ^{{\textbf{t}}}\rho \varvec{\alpha }+\left( \rho \left( \frac{1}{2}\omega ^{{\textbf{t}}}\right) ^{2}\dfrac{\partial }{\partial \sigma }(\varepsilon \rho )\right. \\&\left. \quad -\varepsilon \rho \left( \frac{1}{2}\omega ^{{\textbf{t}}}\right) ^{2}\dfrac{\partial \rho }{\partial \sigma }\right) {\textbf{t}}+\frac{1}{2}\rho \omega ^{{\textbf{t}}}\left( \frac{1}{2}(\varepsilon ^{2}\rho )\omega ^{{\textbf{t}}}+\frac{1}{2}\rho \omega ^{{\textbf{t}}}\right) {\textbf{s}} \end{aligned}$$

  • Electroosmotic antiferromagnetic microfluidic \(\tau _{\phi \left( {\textbf{t}}\right) }\) magnetic torque density is

    $$\begin{aligned} {\mathcal {V}}_{\tau _{\phi \left( {\textbf{t}}\right) }}^{{\mathcal {A}}}&=-\left( \rho \left( \frac{1}{2}\omega ^{{\textbf{t}}}\right) ^{2}\dfrac{\partial }{\partial \sigma }(\varepsilon \rho )-\varepsilon \rho \left( \frac{1}{2}\omega ^{{\textbf{t}}}\right) ^{2} \dfrac{\partial \rho }{\partial \sigma }\right) \left( \varepsilon \left( {\mathcal {L}}\varepsilon +\dfrac{\partial {\mathcal {F}}}{\partial \sigma }\right) +{\mathcal {L}}\right) \\&\quad -\left( \frac{1}{2} (\varepsilon ^{2}\rho )\omega ^{{\textbf{t}}}+\frac{1}{2}\rho \omega ^{\textbf{ t}}\right) \frac{1}{2}\varepsilon ^{2}\rho \omega ^{{\textbf{t}}}{\mathcal {F}}\\&\quad +\left( \dfrac{\partial \varepsilon }{\partial t}-{\mathcal {F}}\right) \frac{1}{2}\rho \omega ^{{\textbf{t}}}\left( \frac{1}{2}(\varepsilon ^{2}\rho )\omega ^{{\textbf{t}}}+ \frac{1}{2}\omega ^{{\textbf{t}}}\rho \right) . \end{aligned}$$

  • Microfluidic antiferromagnetic \(\tau _{\phi \left( {\textbf{t}}\right) }\) magnetic torque phase microscale is

    $$\begin{aligned} {\mathcal {T}}_{\tau _{\phi \left( {\textbf{t}}\right) }}^{{\mathcal {A}}}&=\tau _{0}^{{\textbf{t}}}\int \int _{{\mathcal {W}}}\left( \left( \dfrac{\partial \varepsilon }{ \partial t}-{\mathcal {F}}\right) \frac{1}{2}\rho \omega ^{{\textbf{t}}}\left( \frac{1}{2} (\varepsilon ^{2}\omega ^{{\textbf{t}}}\rho )+\frac{1}{2}\omega ^{{\textbf{t}}}\rho \right) \right. \\&\quad -\left( \rho \left( \frac{1}{2}\omega ^{{\textbf{t}}}\right) ^{2}\dfrac{\partial }{ \partial \sigma }(\varepsilon \rho )-\varepsilon \rho \left( \frac{1}{2}\omega ^{ {\textbf{t}}}\right) ^{2}\dfrac{\partial \rho }{\partial \sigma }\right) \left( \varepsilon \left( {\mathcal {L}}\varepsilon +\dfrac{\partial {\mathcal {F}}}{\partial \sigma } \right) +{\mathcal {L}}\right) \\&\left. \quad -\left( \frac{1}{2}(\varepsilon ^{2}\rho )\omega ^{{\textbf{t}}}+\frac{1}{2}\rho \omega ^{{\textbf{t}}}\right) \frac{1}{2}\varepsilon ^{2}\omega ^{{\textbf{t}}}\rho {\mathcal {F}}\right) d{\mathcal {W}}, \end{aligned}$$

    where \(\tau _{0}^{{\textbf{t}}}\) is magnetic torque constant for \(\phi \left( {\textbf{t}}\right)\). Also, we easily get

    $$\begin{aligned} \phi \left( {\textbf{t}}\right) \times \nabla _{\sigma }\phi \left( {\textbf{t}} \right) =-\varepsilon (\varepsilon ^{2}+1)\varvec{\alpha }+\frac{ \partial \varepsilon }{\partial \sigma }{\textbf{t}}-(\varepsilon ^{2}+1) \textbf{s}. \end{aligned}$$

  • Electroosmotic \(\tau _{\phi \left( {\textbf{t}} \right) }\) magnetic torque density with antiferromagnetic \(\phi \left( {\textbf{t}}\right)\) is

    $$\begin{aligned} ^{\phi \left( {\textbf{t}}\right) }{\mathcal {V}}_{\tau _{\phi \left( {\textbf{t}} \right) }}^{{\mathcal {A}}}&=\frac{\partial \varepsilon }{\partial \sigma }\left( \rho \left( \frac{1}{2}\omega ^{{\textbf{t}}}\right) ^{2}\dfrac{\partial }{\partial \sigma } (\varepsilon \rho )-\varepsilon \rho \left( \frac{1}{2}\omega ^{{\textbf{t}}}\right) ^{2} \dfrac{\partial \rho }{\partial \sigma }\right) \\&\quad -\varepsilon (\varepsilon ^{2}+1)\left( \frac{1}{2}(\varepsilon ^{2}\rho )\omega ^{{\textbf{t}}}+\frac{1}{2}\rho \omega ^{{\textbf{t}}}\right) \frac{1}{2} \varepsilon \omega ^{{\textbf{t}}}\rho \\&\quad -(\varepsilon ^{2}+1)\frac{1}{2}\rho \omega ^{{\textbf{t}}}\left( \frac{1}{2}\omega ^{{\textbf{t}}}(\varepsilon ^{2}\rho )+\frac{1}{2}\rho \omega ^{{\textbf{t}}}\right) . \end{aligned}$$

  • Antiferromagnetic \(\tau _{\phi \left( {\textbf{t}} \right) }\) magnetic torque phase microscale with antiferromagnetic \(\phi \left( {\textbf{t}}\right)\) is

    $$\begin{aligned} ^{\phi \left( {\textbf{t}}\right) }{\mathcal {T}}_{\tau _{\phi \left( {\textbf{t}} \right) }}^{{\mathcal {A}}}&=\tau _{0}^{{\textbf{t}}}\int \int _{{\mathcal {W}}}\left( -\left( \frac{1}{2}(\varepsilon ^{2}\omega ^{{\textbf{t}}}\rho )+\frac{1}{2} \rho \omega ^{{\textbf{t}}}\right) \frac{1}{2}\varepsilon ^{2}(\varepsilon ^{2}+1)\omega ^{{\textbf{t}}}\rho \right. \\&\quad +\frac{\partial \varepsilon }{\partial \sigma }\left( \rho \left( \frac{1}{2}\omega ^{ {\textbf{t}}}\right) ^{2}\dfrac{\partial }{\partial \sigma }(\varepsilon \rho )-\varepsilon \rho \left( \frac{1}{2}\omega ^{{\textbf{t}}}\right) ^{2}\dfrac{\partial \rho }{\partial \sigma }\right) \\&\left. \quad -(\varepsilon ^{2}+1)\frac{1}{2}\rho \omega ^{{\textbf{t}}}\left( \frac{1}{2} (\varepsilon ^{2}\rho )\omega ^{{\textbf{t}}}+\frac{1}{2}\rho \omega ^{{\textbf{t}}}\right) \right) d{\mathcal {W}}, \end{aligned}$$

    where \(\tau _{0}^{{\textbf{t}}}\) is magnetic torque constant for \(\phi \left( {\textbf{t}}\right)\).

Optical effect of microfluidic antiferromagnetic \(\tau _{\phi \left( {\textbf{t}}\right) }\) magnetic torque phase microscale is constructed vortex reactors in Fig. 2.

Fig. 2
figure 2

Microfluidic antiferromagnetic \(\tau _{\phi \left( {\textbf{t}}\right) }\)

Full size image

3.3 Microfluidic antiferromagnetic \(\tau _{\phi \left( {\textbf{s}}\right) }\) magnetic torque phase

  • \(\tau _{\phi \left( {\textbf{s}}\right) }\) magnetic torque phase microscale is

    $$\begin{aligned} ^{{\mathcal {B}}}{\mathcal {M}}_{\phi \left( {\textbf{s}}\right) }=\tau _{0}^{ {\textbf{s}}}\int \int _{{\mathcal {W}}}\nabla _{t}\phi \left( {\textbf{s}}\right) \cdot \nabla _{t}\tau _{\phi \left( {\textbf{s}}\right) }d{\mathcal {W}}. \end{aligned}$$

    Optical angular momentum of \(\phi \left( {\textbf{s}}\right)\) is given

    $$\begin{aligned} \otimes _{\phi \left( {\textbf{s}}\right) }=\rho m^{{\textbf{s}}} \textbf{s}. \end{aligned}$$

    The magnitude of optical angular momentum is

    $$\begin{aligned} \left\| \otimes _{\phi \left( {\textbf{s}}\right) }\right\| =\rho m^{{\textbf{s}}}. \end{aligned}$$

    Spherical magnetic moment of \(\phi \left( {\textbf{s}}\right)\) is

    $$\begin{aligned} \theta _{\phi \left( {\textbf{s}}\right) }=\frac{1}{2}\rho \omega ^{{\textbf{s}}} \mathbf {s.} \end{aligned}$$

    \(\tau _{\phi \left( {\textbf{s}}\right) }\) magnetic torque of \(\phi \left( {\textbf{s}}\right)\) is constructed by

    $$\begin{aligned} \tau _{\phi \left( {\textbf{s}}\right) }=\frac{1}{2}\rho ^{2}\omega ^{ {\textbf{s}}}{\varvec{\alpha }}+\frac{1}{2}\rho \varepsilon \omega ^{ {\textbf{s}}}\textbf{t}. \end{aligned}$$

    Thus, fluid of \(\tau _{\phi \left( {\textbf{s}}\right) }\) magnetic torque is

    $$\begin{aligned} \nabla _{t}\tau _{\phi \left( {\textbf{s}}\right) }&=\left( \rho \omega ^{{\textbf{s}}}\frac{\partial \rho }{\partial t}-{\mathcal {L}}\frac{1}{2} (\rho \omega ^{{\textbf{s}}}\varepsilon )\right) \varvec{\alpha }+\left( \frac{1}{2 }\omega ^{{\textbf{s}}}\frac{\partial }{\partial t}(\rho \varepsilon ) \right. \\&\left. \quad +\frac{1}{2}\rho ^{2}\omega ^{{\textbf{s}}}{\mathcal {L}}\right) {\textbf{t}} +\left( {\mathcal {F}}\frac{1}{2}\rho ^{2}\omega ^{{\textbf{s}}}+\left( \dfrac{\partial {\mathcal {F}}}{\partial \sigma }+\varepsilon {\mathcal {L}}\right) \frac{1}{2} (\varepsilon \omega ^{{\textbf{s}}}\rho )\right) \mathbf {s.} \end{aligned}$$

  • Electroosmotic microfluidic \(\tau _{\phi \left( {\textbf{s}}\right) }\) magnetic torque density is

    $$\begin{aligned} {\mathcal {V}}_{\tau _{\phi \left( {\textbf{s}}\right) }}&=\left( {\mathcal {L}}- \frac{\partial \rho }{\partial t}\right) \left( \rho \omega ^{{\textbf{s}}}\frac{ \partial \rho }{\partial t}-{\mathcal {L}}\frac{1}{2}\varepsilon \omega ^{ {\textbf{s}}}(\rho )\right) \\&\quad -\left( \frac{1}{2}\frac{\partial }{\partial t}(\rho \varepsilon )\omega ^{{\textbf{s}}}+\frac{1}{2}\rho ^{2}\omega ^{{\textbf{s}}}{\mathcal {L}}\right) \left( \frac{ \partial \varepsilon }{\partial t}+\rho {\mathcal {L}}\right) -\left( \varepsilon \left( {\mathcal {L}}\varepsilon +\dfrac{\partial {\mathcal {F}}}{\partial \sigma }\right) +\rho {\mathcal {F}}\right) \\&\quad \times \left( {\mathcal {F}}\frac{1}{2}\rho ^{2}\omega ^{{\textbf{s}}}+\left( \dfrac{\partial {\mathcal {F}}}{\partial \sigma }+\varepsilon {\mathcal {L}}\right) \frac{1}{2} (\varepsilon \omega ^{{\textbf{s}}}\rho )\right) . \end{aligned}$$

  • Microfluidic\(\tau _{\phi \left( {\textbf{s}} \right) }\) magnetic torque phase microscale is given

    $$\begin{aligned} {\mathcal {T}}_{\tau _{\phi \left( {\textbf{s}}\right) }}&=\tau _{0}^{{\textbf{s}} }\int \int _{{\mathcal {W}}}\left( -\left( \frac{1}{2}\frac{\partial }{\partial t} (\rho \varepsilon )\omega ^{{\textbf{s}}}+\frac{1}{2}\rho ^{2}\omega ^{{\textbf{s}}}{\mathcal {L}}\right) \left( \frac{\partial \varepsilon }{\partial t}+\rho {\mathcal {L}}\right) \right. \\&\quad +\left( {\mathcal {L}}-\frac{\partial \rho }{\partial t}\right) \left( \rho \omega ^{{\textbf{s}}}\frac{\partial \rho }{\partial t}-{\mathcal {L}}\frac{1}{2} (\rho \varepsilon )\omega ^{{\textbf{s}}}\right) -\left( \varepsilon \left( {\mathcal {L}}\varepsilon +\dfrac{\partial {\mathcal {F}}}{\partial \sigma }\right) +\rho {\mathcal {F}}\right) \\&\left. \quad \times \left( {\mathcal {F}}\frac{1}{2}\rho ^{2}\omega ^{{\textbf{s}} }+\omega ^{{\textbf{s}}}\left( \dfrac{\partial {\mathcal {F}}}{\partial \sigma } +\varepsilon {\mathcal {L}}\right) \frac{1}{2}(\varepsilon \rho )\right) \right) d{\mathcal {W}}, \end{aligned}$$

    where \(\tau _{0}^{{\textbf{s}}}\) is magnetic torque constant for \(\phi \left( {\textbf{s}}\right)\) .

  • Microfluidic antiferromagnetic \(\tau _{\phi \left( {\textbf{s}}\right) }\) magnetic torque phase microscale is given

    $$\begin{aligned} ^{{\mathcal {B}}}{\mathcal {M}}_{\tau _{\phi \left( {\textbf{s}}\right) }}=\tau _{0}\int \int _{{\mathcal {W}}}\nabla _{t}\phi \left( {\textbf{s}}\right) \cdot \tau _{\phi \left( {\textbf{s}}\right) }\times \nabla _{\sigma }\tau _{\phi \left( {\textbf{s}}\right) }d{\mathcal {W}}. \end{aligned}$$

    From spherical frame, we have

    $$\begin{aligned} \tau _{\phi \left( {\textbf{s}}\right) }\times \nabla _{\sigma }\tau _{\phi \left( {\textbf{s}}\right) }&=\left( \frac{1}{2}\omega ^{{\textbf{s}} }\right) ^{2}(\rho ^{2}\varepsilon ^{3})\varvec{\alpha }-\rho ^{2}\left( \frac{1 }{2}\omega ^{{\textbf{s}}}\right) ^{2}(\rho \varepsilon ^{2})\textbf{t}\\&\quad +\left( \frac{1}{2} \omega ^{{\textbf{s}}}\rho ^{2}\left( \frac{1}{2}\omega ^{{\textbf{s}}}\dfrac{\partial }{\partial \sigma }(\rho \varepsilon )+\frac{1}{2}\rho ^{2}\omega ^{{\textbf{s}}}\right) \right. \\&\left. \quad -\frac{1}{2}\rho \omega ^{ {\textbf{s}}}\varepsilon \left( \omega ^{{\textbf{s}}}\rho \dfrac{\partial \rho }{\partial \sigma }-\frac{1}{2}(\rho \omega ^{{\textbf{s}}}\varepsilon )\right) \right) {\textbf{s}}. \end{aligned}$$

  • Electroosmotic antiferromagnetic microfluidic \(\tau _{\phi \left( {\textbf{s}}\right) }\) magnetic torque density is

    $$\begin{aligned} {\mathcal {V}}_{\tau _{\phi \left( {\textbf{s}}\right) }}^{{\mathcal {A}}}&= \rho ^{2}\left( \frac{1}{2}\omega ^{{\textbf{s}}}\right) ^{2}(\rho \varepsilon ^{2})\left( \frac{\partial \varepsilon }{\partial t}+\rho {\mathcal {L}}\right) +\left( \frac{1}{2}\omega ^{{\textbf{s}}}\right) ^{2}(\rho ^{2}\varepsilon ^{3})\left( {\mathcal {L}}-\frac{\partial \rho }{\partial t}\right) \\&\quad -\left( \varepsilon \left( {\mathcal {L}}\varepsilon +\dfrac{\partial {\mathcal {F}}}{\partial \sigma }\right) +\rho {\mathcal {F}}\right) \left( \frac{1}{2}\rho ^{2}\omega ^{{\textbf{s}}}\left( \frac{1}{2}\dfrac{\partial }{\partial \sigma }(\rho \varepsilon )\omega ^{{\textbf{s}}}+\frac{1}{2}\rho ^{2}\omega ^{{\textbf{s}}}\right) \right. \\&\left. \quad -\frac{1}{2}\omega ^{{\textbf{s}}}\rho \varepsilon \left( \omega ^{{\textbf{s}}}\rho \dfrac{\partial \rho }{\partial \sigma }-\frac{1}{2}(\rho \omega ^{{\textbf{s}}}\varepsilon )\right) \right) . \end{aligned}$$

  • Microfluidic antiferromagnetic \(\tau _{\phi \left( {\textbf{s}}\right) }\) magnetic torque phase microscale is

    $$\begin{aligned} {\mathcal {T}}_{\tau _{\phi \left( {\textbf{s}}\right) }}^{{\mathcal {A}}}&=\tau _{0}^{{\textbf{s}}}\int \int _{{\mathcal {W}}}\left( -\left( \varepsilon \left( {\mathcal {L}}\varepsilon +\dfrac{\partial {\mathcal {F}}}{\partial \sigma }\right) +\rho {\mathcal {F}}\right) \left( \frac{1}{2}\omega ^{{\textbf{s}}}\rho ^{2}\left( \frac{1}{2}\dfrac{\partial }{\partial \sigma }(\rho \varepsilon ) \omega ^{{\textbf{s}}}+\frac{1}{2}\rho ^{2}\omega ^{{\textbf{s}}}\right) \right. \right. \\&\left. \quad -\frac{1}{2}\rho \omega ^{{\textbf{s}}}\varepsilon \left( \omega ^{{\textbf{s}}}\rho \dfrac{\partial \rho }{\partial \sigma }-\frac{1}{2}(\rho \varepsilon )\omega ^{{\textbf{s}}}\right) \right) \\&\left. \quad +\rho ^{2}\left( \frac{1}{2}\omega ^{{\textbf{s}}}\right) ^{2}(\rho \varepsilon ^{2})\left( \frac{\partial \varepsilon }{\partial t}+\rho {\mathcal {L}}\right) +\left( \frac{1}{2}\omega ^{{\textbf{s}}}\right) ^{2}(\rho ^{2}\varepsilon ^{3})\left( {\mathcal {L}}-\frac{\partial \rho }{\partial t}\right) \right) d{\mathcal {W}}, \end{aligned}$$

    where \(\tau _{0}^{{\textbf{s}}}\) is magnetic torque constant for \(\phi \left( {\textbf{s}}\right)\).

Also, we easily get

$$\begin{aligned} \phi \left( {\textbf{s}}\right) \times \nabla _{\sigma }\phi \left( {\textbf{s}} \right) =\varepsilon ^{3}\varvec{\alpha }+\left( \rho \left( \frac{\partial \varepsilon }{\partial \sigma }+\rho \right) -\rho \varepsilon ^{2}\right) \textbf{t}+ \left( \varepsilon -\frac{\partial \rho }{\partial \sigma }\right) \varepsilon )\textbf{s}. \end{aligned}$$

  • Electroosmotic\(\tau _{\phi \left( {\textbf{s}} \right) }\) magnetic torque density with antiferromagnetic \(\phi \left( {\textbf{t}}\right)\) is

    $$\begin{aligned} ^{\phi \left( {\textbf{s}}\right) }{\mathcal {V}}_{\tau _{\phi \left( {\textbf{s}} \right) }}^{{\mathcal {A}}}&=\varepsilon ^{6}\rho ^{2}\left( \frac{1}{2} \omega ^{{\textbf{s}}}\right) ^{2}-\rho ^{2}\left( \rho \left( \frac{\partial \varepsilon }{\partial \sigma }+\rho \right) -\rho \varepsilon ^{2}\right) \left( \frac{\omega ^{{\textbf{s}}}}{2}\right) ^{2}(\rho \varepsilon ^{2}) +\left( \varepsilon -\frac{\partial \rho }{\partial \sigma }\right) \varepsilon )\\&\quad \times \left( \frac{\omega ^{{\textbf{s}}}}{2}\rho ^{2}\left( \frac{\omega ^{{\textbf{s}}}}{2} \dfrac{\partial }{\partial \sigma }(\rho \varepsilon )+\frac{\omega ^{{\textbf{s}}}}{2}\rho ^{2}\right) \right. \\&\left. \quad -\frac{\omega ^{{\textbf{s}}}}{2}\rho \varepsilon \left( \omega ^{{\textbf{s}}}\rho \dfrac{\partial \rho }{\partial \sigma }-\frac{\omega ^{{\textbf{s}}}}{2}(\rho \varepsilon )\right) \right) . \end{aligned}$$

  • Antiferromagnetic \(\tau _{\phi \left( {\textbf{s}} \right) }\) magnetic torque phase microscale with antiferromagnetic \(\phi \left( {\textbf{s}}\right)\) is

    $$\begin{aligned} ^{\phi \left( {\textbf{s}}\right) }{\mathcal {T}}_{\tau _{\phi \left( {\textbf{s}} \right) }}^{{\mathcal {A}}}&=\tau _{0}^{{\textbf{s}}}\int \int _{{\mathcal {W}}}\left( -\rho ^{2}\left( \rho \left( \frac{\partial \varepsilon }{\partial \sigma } +\rho \right) -\rho \varepsilon ^{2}\right) \left( \frac{\omega ^{{\textbf{s}}}}{2} \right) ^{2}(\rho \varepsilon ^{2}) \right. \\&\left. \quad +\varepsilon ^{6}\rho ^{2}\left( \frac{\omega ^{{\textbf{s}}}}{2}\right) ^{2} +\left( \varepsilon -\frac{\partial \rho }{\partial \sigma }\right) \varepsilon \right) \left( \frac{\omega ^{\phi \left( {\textbf{s}}\right) }}{2}\rho ^{2}\left( \frac{\omega ^{ {\textbf{s}}}}{2}\dfrac{\partial }{\partial \sigma }(\rho \varepsilon )+\frac{\omega ^{{\textbf{s}}}}{2}\rho ^{2}\right) \right. \\&\left.\left. \quad -\frac{\omega ^{{\textbf{s}}}}{2}\rho \varepsilon \left( \omega ^{\phi \left( {\textbf{s}}\right) }\rho \dfrac{\partial \rho }{\partial \sigma }-\frac{\omega ^{{\textbf{s}}}}{2}(\rho \varepsilon )\right) \right) \right)d{\mathcal {W}}, \end{aligned}$$

    where \(\tau _{0}^{{\textbf{s}}}\) is magnetic torque constant for \(\phi \left( {\textbf{s}}\right)\) .

Optical effect of microfluidic antiferromagnetic \(\tau _{\phi \left( {\textbf{s}}\right) }\) magnetic torque phase microscale is constructed vortex reactors in Fig. 3.

Fig. 3
figure 3

Microfluidic antiferromagnetic \(\tau _{\phi \left( {\textbf{s}}\right) }\)

Full size image

4 Conclusions

Quasi optical electromagnetic energy and flux are illustrated by flexible elastic curves, optical waves and biharmonic sonics. The results of optical modelling of biharmonic magnetic curves with optical applications are characterized (Körpınar 2020; Körpınar et al. 2020, 2021c, d; Körpınar and Körpınar 2021c, d; Ashkin et al. 1986; Ashkin 1970; Dholakia and Zemánek 2010; Schief and Rogers 2005; Dong et al. 2019; Seung 2015; Körpinar and Körpinar 2023d, b; Körpinar et al. 2023; Körpinar and Körpinar 2023d, a; Korpinar et al. 2023; Körpinar and Körpinar 2023c; Körpinar et al. 2023; Körpınar and Körpınar 2023e; Körpinar et al. 2023; Körpinar and Körpinar 2023).

In this paper, we illustrate optical \(\tau _{\phi \left( \varvec{\alpha } \right) },\tau _{\phi \left( {\textbf{t}}\right) },\tau _{\phi \left( {\textbf{s}}\right) }\) magnetic torque phase microscale. Moreover, we have electroosmotic microfluidic \(\tau _{\phi \left( \varvec{\alpha }\right) },\tau _{\phi \left( {\textbf{t}}\right) },\tau _{\phi \left( {\textbf{s}} \right) }\) magnetic torque density. Finally, we design electroosmotic magnetic torque density with antiferromagnetic model.