New optical quantum effects of ferromagnetic electroosmotic phase

Abstract

In this paper, we study electroosmotic microfluidic $\tau _{\nabla _{t}\phi \left( \mathbf {\alpha }\right) },$ $\tau _{\nabla _{t}\phi \left( {\textbf{t}}\right) },$ $\tau _{\nabla _{t}\phi \left( {\textbf{s}} \right) }$ magnetic torques density with spherical fields. Also, we obtain optical geometric microfluidic $\tau _{\nabla _{t}\phi \left( \mathbf {\alpha }\right) },$ $\tau _{\nabla _{t}\phi \left( {\textbf{t}}\right) },$ $\tau _{\nabla _{t}\phi \left( {\textbf{s}}\right) }$ magnetic torques phase microscale in wave phenomena. Then, we illustrate optical microfluidic ferromagnetic electroosmotic $\tau _{\nabla _{t}\phi \left( \mathbf {\alpha } \right) },$ $\tau _{\nabla _{t}\phi \left( {\textbf{t}}\right) },$ $\tau _{\nabla _{t}\phi \left( {\textbf{s}}\right) }$ magnetic torques density. Thus, we present microfluidic ferromagnetic $\tau _{\nabla _{t}\phi \left( \mathbf {\alpha }\right) },$ $\tau _{\nabla _{t}\phi \left( {\textbf{t}}\right) },$ $\tau _{\nabla _{t}\phi \left( {\textbf{s}}\right) }$ magnetic torques phase microscale in wave phenomena.

1 Introduction

The modeling of hybrid optical microfluid is an important dynamic analysis area in optical microfluidics and perspective of constructing optical models. Unique in flux devices with different views have been advanced by some directions geometric optics. Optical microfluidic is constructed by optophotonics, optoelectronics, environmental science, remote sensing, metamaterials, biemedicine and quantum geometric optics (Ashkin et al. 1986; Ashkin 1970; Dholakia and Zemánek 2010; Burns et al. 1989; Wang et al. 2005; Körpınar 2020; Körpınar et al. 2020, 2021a, b; Körpınar and Körpınar 2021a, b).

Optical modeling of spherical cooling, binding, trapping, sorting, optical forces, transporting has designed intensive physical applications. Optical modeling is important tool in optics, atomic physics, chemistry, biological science. Also, by a rapid progression of optical nanotechnology, geometric features have constructed diverse progress with microwave and nanometer phase (Chaumet and Nieto-Vesperinas 2001; Almaas and Brevik 2013; Moffitt et al. 2008; Chang et al. 2009; Fazal and Block 2011; Reiserer et al. 2013; Körpınar et al. 2021a, b; Körpınar and Körpınar 2021a, b; Neirameh 2021; de Azevedo et al. 1982; Chou and Qu 2001; Marí Beffa et al. 2002; Calini and Ivey 2005).

Optical electroosmotic microfluidic of quasi electromagnetic and spherical geometric design for flux modeling is numerically important optical illustrations. Optical microfluidic flux is important significance in mathematical solitons, optical applications, wave geometry with electromagnetic energy (Körpınar et al. 2019a, b, c; Balakrishnan et al. 1990; Bliokh 2009; Marí Beffa 2009; Marí Beffa and Olver 2010; Calini et al. 2009; Wo and Qu 2007; Li et al. 2010; Körpınar and Körpınar 2021; Arbind et al. 2019; Körpınar 2020; Körpınar et al. 2020, 2021a, b; Körpınar and Körpınar 2021; Gürbüz 2022a, b, 2021).

The establishment of our paper is as follows. First, we study electroosmotic microfluidic $\tau _{\nabla _{t}\phi \left( \mathbf {\alpha }\right) },$ $\tau _{\nabla _{t}\phi \left( {\textbf{t}}\right) },$ $\tau _{\nabla _{t}\phi \left( {\textbf{s}}\right) }$ magnetic torques density with spherical fields. Also, we obtain optical geometric microfluidic $\tau _{\nabla _{t}\phi \left( \mathbf {\alpha }\right) },\tau _{\nabla _{t}\phi \left( {\textbf{t}} \right) },$ $\tau _{\nabla _{t}\phi \left( {\textbf{s}}\right) }$ magnetic torques phase microscale. Then, we illustrate optical Microfluidic ferromagnetic electroosmotic $\tau _{\nabla _{t}\phi \left( \mathbf {\alpha } \right) },$ $\tau _{\nabla _{t}\phi \left( {\textbf{t}}\right) },$ $\tau _{\nabla _{t}\phi \left( {\textbf{s}}\right) }$ magnetic torques density. Thus, we present microfluidic ferromagnetic $\tau _{\nabla _{t}\phi \left( \mathbf {\alpha }\right) },$ $\tau _{\nabla _{t}\phi \left( {\textbf{t}}\right) },$ $\tau _{\nabla _{t}\phi \left( {\textbf{s}}\right) }$ magnetic torques phase microscale.

2 Spherical magnetic torque phase microscale

2.1 Microfluidic ferromagnetic $\tau _{\nabla _{t} \phi \left( \mathbf {\alpha }\right) }$ magnetic torque phase

$\tau _{\nabla _{t}\phi \left( \mathbf {\alpha }\right) }$ magnetic torque of $\nabla _{t}\phi \left( \mathbf {\alpha }\right)$ is constructed by

$$\begin{aligned} \tau _{\nabla _{t}\phi \left( \mathbf {\alpha }\right) }=\Lambda \left( \beta _{1} \mathbf {+}\left( \Upsilon \beta _{1}+\dfrac{\partial \beta _{2}}{\partial \sigma } \right) \omega \right) \mathbf {t.} \end{aligned}$$

Thus, fluid of $\tau _{\nabla _{t}\phi \left( \mathbf {\alpha }\right) }$ magnetic torque is

$$\begin{aligned} \nabla _{t}\tau _{\nabla _{t}\phi \left( \mathbf {\alpha }\right) }= & {} -\Lambda \beta _{1}\left( \beta _{1}\mathbf {+}\left( \Upsilon \beta _{1}+\dfrac{\partial \beta _{2}}{\partial \sigma }\right) \omega \right) \mathbf {\alpha }\\{} & {} +\Lambda \frac{\partial }{ \partial t}\left( \beta _{1}\mathbf {+}\left( \Upsilon \beta _{1} +\dfrac{\partial \beta _{2}}{\partial \sigma }\right) \omega \right) {\textbf{t}}+\Lambda \left( \beta _{1}\Upsilon +\dfrac{\partial \beta _{2}}{\partial \sigma }\right) \left( \beta _{1}\mathbf {+}\left( \Upsilon \beta _{1}+\dfrac{\partial \beta _{2}}{\partial \sigma }\right) \omega \right) \mathbf {s.} \end{aligned}$$

$\divideontimes$ Electroosmotic microfluidic $\tau _{\nabla _{t}\phi \left( \mathbf {\alpha }\right) }$ magnetic torque density is

$$\begin{aligned} {\mathcal {V}}_{\tau _{\phi \left( \mathbf {\alpha }\right) }}= & {} \Lambda \beta _{1}^{2}\left( \beta _{1}\mathbf {+}\left( \Upsilon \beta _{1}+\dfrac{\partial \beta _{2} }{\partial \sigma }\right) \omega \right) \\{} & {} +\left( \beta _{1}\Upsilon +\dfrac{\partial \beta _{2}}{\partial \sigma } \right) ^{2}\Lambda \left( \beta _{1}\mathbf {+}\left( \Upsilon \beta _{1}+\dfrac{\partial \beta _{2}}{\partial \sigma }\right) \omega \right) . \end{aligned}$$

$\divideontimes$ Microfluidic $\tau _{\nabla _{t}\phi \left( \mathbf {\alpha }\right) }$ magnetic torque phase microscale is given

$$\begin{aligned} {\mathcal {T}}_{\tau _{\phi \left( \mathbf {\alpha }\right) }}= & {} \tau _{\rho }^{ \mathbf {\alpha }}\int \int _{{\mathcal {W}}}\Bigg (\beta _{1}^{2}\Lambda \left( \beta _{1} \mathbf {+}\left( \Upsilon \beta _{1}+\dfrac{\partial \beta _{2}}{\partial \sigma } \right) \omega \right) \\{} & {} +\Lambda \left( \beta _{1}\Upsilon +\dfrac{\partial \beta _{2}}{\partial \sigma } \right) ^{2}\left( \beta _{1}\mathbf {+}\left( \Upsilon \beta _{1}+\dfrac{\partial \beta _{2}}{ \partial \sigma }\right) \omega \right) \Bigg )d{\mathcal {W}}, \end{aligned}$$

where $\tau _{0}^{\mathbf {\alpha }}$ is magnetic torque potential for $\nabla _{t}\phi \left( \mathbf {\alpha }\right)$.

Also, we easily get

$$\begin{aligned} \phi \left( \mathbf {\alpha }\right) \times \nabla _{\sigma }^{2}\phi \left( \mathbf {\alpha }\right) =\frac{\partial \Upsilon }{\partial \sigma }\mathbf { \alpha .} \end{aligned}$$

$\divideontimes$ Microfluidic ferromagnetic electroosmotic $\tau _{\nabla _{t}\phi \left( \mathbf {\alpha }\right) }$ magnetic torque density is

$$\begin{aligned} {\mathcal {V}}_{\tau _{\phi \left( \mathbf {\alpha }\right) }}^{{\mathcal {F}} }=-\Lambda \beta _{1}\frac{\partial \Upsilon }{\partial \sigma }\left( \beta _{1} \mathbf {+}\left( \Upsilon \beta _{1}+\dfrac{\partial \beta _{2}}{\partial \sigma } \right) \omega \right) . \end{aligned}$$

$\divideontimes$ Microfluidic ferromagnetic $\tau _{\nabla _{t}\phi \left( \mathbf {\alpha }\right) }$ magnetic torque phase microscale is

$$\begin{aligned} {\mathcal {T}}_{\tau _{\phi \left( \mathbf {\alpha }\right) }}^{{\mathcal {F}} }=\;\tau _{\rho }^{\mathbf {\alpha }}\int \int _{{\mathcal {W}}}\left( -\beta _{1}\frac{ \partial \Upsilon }{\partial \sigma }\Lambda \left( \beta _{1}\mathbf {+}\left( \Upsilon \beta _{1}+\dfrac{\partial \beta _{2}}{\partial \sigma }\right) \omega \right) \right) d\mathcal {W }, \end{aligned}$$

where $\tau _{\rho }^{\mathbf {\alpha }}$ is magnetic torque potential for $\nabla _{t}\phi \left( \mathbf {\alpha }\right)$ .

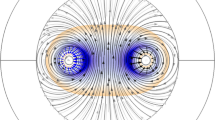
With the flexibility of microfluidic ferromagnetic $\tau _{\nabla _{t}\phi \left( \mathbf {\alpha }\right) }$ magnetic torque phase microscale, a variety of spherical effects can be illustrated for electroosmotic microfluidic $\tau _{\nabla _{t}\phi \left( \mathbf {\alpha }\right) }$ magnetic torque metasurfaces, with diverse potential optical applications in Fig. 1.

Fig. 1

Flexibility of microfluidic ferromagnetic $\tau _{\nabla _{t}\phi \left( \mathbf {\alpha }\right) }$

2.2 Microfluidic ferromagnetic $\tau _{\nabla _{t} \phi \left( {\textbf{t}}\right) }$ magnetic torque phase

$\tau _{\nabla _{t}\phi \left( {\textbf{t}}\right) }$ magnetic torque of $\nabla _{t}\phi \left( {\textbf{t}}\right)$ is presented by

$$\begin{aligned} \tau _{\nabla _{t}\phi \left( {\textbf{t}}\right) }=-\Lambda \left( \beta _{1}+\omega \left( \dfrac{\partial \beta _{2}}{\partial \sigma }+\beta _{1}\Upsilon \right) \right) \mathbf {\alpha }+\Lambda \frac{\partial \omega }{\partial t} \omega \mathbf {t+}\omega \left( \beta _{1}+\omega \left( \dfrac{\partial \beta _{2}}{ \partial \sigma }+\beta _{1}\Upsilon \right) \right) \Lambda \mathbf {s.} \end{aligned}$$

Flow of $\tau _{\nabla _{t}\phi \left( {\textbf{t}}\right) }$ magnetic torque is

$$\begin{aligned} \nabla _{t}\tau _{\nabla _{t}\phi \left( {\textbf{t}}\right) }= & {} -\Lambda \Bigg (\frac{ \partial }{\partial t}\left( \beta _{1}+\left( \dfrac{\partial \beta _{2}}{\partial \sigma }+\Upsilon \beta _{1}\right) \omega \right) +\beta _{1}\left( \frac{\partial \omega }{ \partial t}\omega \right) \\{} & {} +\left( \omega \left( \beta _{1}+\omega \left( \beta _{1}\Upsilon +\dfrac{\partial \beta _{2}}{\partial \sigma }\right) \right) \right) \beta _{2}\mathbf {\alpha }+\Lambda \Bigg (\frac{ \partial }{\partial t}\left( \frac{\partial \omega }{\partial t}\omega \right) -\beta _{1}\Bigg (\beta _{1} \\{} & {} +\left( \dfrac{\partial \beta _{2}}{\partial \sigma }+\Upsilon \beta _{1}\right) \omega \Bigg )-\left( \beta _{1}\Upsilon +\dfrac{\partial \beta _{2}}{\partial \sigma }\right) \Bigg (\omega \Bigg (\beta _{1}+\Bigg (\dfrac{\partial \beta _{2}}{\partial \sigma } \\{} & {} +\Upsilon \beta _{1}\Bigg )\omega \Bigg )\Bigg )\Bigg )\mathbf {t+\Lambda } \Bigg (\frac{\partial }{\partial t}\left( \omega \left( \beta _{1}+\left( \dfrac{\partial \beta _{2}}{\partial \sigma } +\Upsilon \beta _{1}\right) \omega \right) \right) -\beta _{2}\Bigg (\beta _{1} \\{} & {} +\left( \dfrac{\partial \beta _{2}}{\partial \sigma }+\Upsilon \beta _{1}\right) \omega \Bigg )+\left( \beta _{1}\Upsilon +\dfrac{\partial \beta _{2}}{\partial \sigma }\right) \left( \omega \frac{\partial \omega }{\partial t}\right) \Bigg )\mathbf {s.} \end{aligned}$$

$\divideontimes$ Electroosmotic microfluidic $\tau _{\nabla _{t}\phi \left( {\textbf{t}}\right) }$ magnetic torque density is

$$\begin{aligned} {\mathcal {V}}_{\tau _{\phi \left( {\textbf{t}}\right) }}= & {} \Lambda \omega \beta _{2}\Bigg (\frac{\partial }{\partial t}\left( \omega \left( \dfrac{\partial \beta _{2}}{ \partial \sigma }+\Upsilon \beta _{1}\right) +\beta _{1}\right) +\beta _{1}\left( \omega \frac{ \partial \omega }{\partial t}\right) \\{} & {} +\left( \omega \left( \beta _{1}+\left( \dfrac{\partial \beta _{2}}{\partial \sigma } +\Upsilon \beta _{1}\right) \omega \right) \right) \beta _{2}\Bigg )-\Lambda \Bigg (\beta _{1}+\Bigg (\dfrac{ \partial \beta _{2}}{\partial \sigma } \\{} & {} +\Upsilon \beta _{1}\Bigg )\omega \Bigg )\Bigg (\frac{\partial }{\partial t}\Bigg (\omega \frac{ \partial \omega }{\partial t}\Bigg )-\Bigg (\beta _{1}+\omega \Bigg (\dfrac{\partial \beta _{2} }{\partial \sigma }+\beta _{1}\Upsilon \Bigg )\Bigg )\beta _{1}-\Bigg (\Upsilon \beta _{1} \\{} & {} +\dfrac{\partial \beta _{2}}{\partial \sigma }\Bigg )\Bigg (\omega \Bigg (\beta _{1}+\omega \Bigg (\dfrac{\partial \beta _{2}}{\partial \sigma }+\beta _{1}\Upsilon \Bigg )\Bigg )\Bigg )\Bigg )+\Lambda \Bigg (-\beta _{2} \\{} & {} +\frac{\partial \omega }{\partial t}\Bigg )\Bigg (\frac{\partial }{\partial t}\Bigg ( (\beta _{1}+\omega \Bigg (\beta _{1}\Upsilon +\dfrac{\partial \beta _{2}}{\partial \sigma }\Bigg )\Bigg )\omega \Bigg )-\beta _{2}\Bigg (\beta _{1} \\{} & {} +\Bigg (\dfrac{\partial \beta _{2}}{\partial \sigma }+\Upsilon \beta _{1}\Bigg )\omega \Bigg )+\Bigg (\beta _{1}\Upsilon +\dfrac{\partial \beta _{2}}{\partial \sigma }\Bigg )\Bigg (\omega \frac{\partial \omega }{\partial t}\Bigg )\Bigg ). \end{aligned}$$

$\divideontimes$ Microfluidic $\tau _{\nabla _{t}\phi \left( {\textbf{t}}\right) }$magnetic torque phase microscale is given

$$\begin{aligned} {\mathcal {T}}_{\tau _{\phi \left( {\textbf{t}}\right) }}=\; & {} \tau _{\rho }^{\textbf{t }}\int \int _{{\mathcal {W}}}\Bigg (\Bigg (-\beta _{2}+\frac{\partial \omega }{\partial t} \Bigg )\Lambda \Bigg (\frac{\partial }{\partial t}\Bigg (\omega \Bigg (\beta _{1}+\Bigg (\dfrac{ \partial \beta _{2}}{\partial \sigma }+\Upsilon \beta _{1}\Bigg )\omega \Bigg )\Bigg ) \\{} & {} -\beta _{2}\Bigg (\beta _{1}+\Bigg (\dfrac{\partial \beta _{2}}{\partial \sigma } +\Upsilon \beta _{1}\Bigg )\omega \Bigg )+\Bigg (\beta _{1}\Upsilon +\dfrac{\partial \beta _{2} }{\partial \sigma }\Bigg )\Bigg (\omega \frac{\partial \omega }{\partial t}\Bigg )\Bigg )+\beta _{2}\omega \Lambda \Bigg (\frac{\partial }{\partial t}\Bigg (\beta _{1} \\{} & {} +\omega \Bigg (\dfrac{\partial \beta _{2}}{\partial \sigma }+\beta _{1}\Upsilon \Bigg )\Bigg )+\beta _{1}\Bigg (\omega \frac{\partial \omega }{\partial t}\Bigg )+\Bigg (\omega \Bigg (\beta _{1}+\omega \Bigg (\dfrac{\partial \beta _{2}}{\partial \sigma }+\beta _{1}\Upsilon \Bigg )\Bigg )\Bigg )\beta _{2}\Bigg ) \\{} & {} -\Bigg (\beta _{1}+\Bigg (\dfrac{\partial \beta _{2}}{\partial \sigma }+\Upsilon \beta _{1})\omega \Bigg )\Lambda \Bigg (\frac{\partial }{\partial t}\Bigg (\frac{\partial \omega }{ \partial t}\omega \Bigg )-\beta _{1}\Bigg (\beta _{1}+\Bigg (\dfrac{\partial \beta _{2}}{ \partial \sigma }+\Upsilon \beta _{1}\Bigg )\omega \Bigg ) \\{} & {} -\Bigg (\beta _{1}\Upsilon +\dfrac{\partial \beta _{2}}{\partial \sigma }\Bigg )\Bigg ( \omega \Bigg (\beta _{1}+\Bigg (\dfrac{\partial \beta _{2}}{\partial \sigma }+\Upsilon \beta _{1})\omega \Bigg )\Bigg )\Bigg )\Bigg )d{\mathcal {W}}, \end{aligned}$$

where $\tau _{\rho }^{{\textbf{t}}}$ is magnetic torque potential for $\nabla _{t}\phi \left( {\textbf{t}}\right)$.

Thus, we have

$$\begin{aligned} \phi \left( {\textbf{t}}\right) \times \nabla _{\sigma }^{2}\phi \left( {\textbf{t}}\right)=\; & {} \omega \left( \omega \frac{\partial \Upsilon }{\partial \sigma } +2\frac{\partial \omega }{\partial \sigma }\Upsilon \right) \mathbf {\alpha }+\Bigg (\frac{ \partial ^{2}\omega }{\partial \sigma ^{2}} \\{} & {} \mathbf {+}(\omega -\Upsilon )(\omega \Upsilon +1)\Bigg ){\textbf{t}}-\left( \frac{\partial \Upsilon }{\partial \sigma }\omega +2\Upsilon \frac{\partial \omega }{ \partial \sigma }\right) \mathbf {s.} \end{aligned}$$

$\divideontimes$ Ferromagnetic electroosmotic $\tau _{\nabla _{t}\phi \left( {\textbf{t}}\right) }$ magnetic torque density is

$$\begin{aligned} {\mathcal {V}}_{\tau _{\phi \left( {\textbf{t}}\right) }}^{{\mathcal {F}}}=\; & {} -\Lambda \Bigg ( \frac{\partial }{\partial t}\Bigg (\beta _{1}+\Bigg (\dfrac{\partial \beta _{2}}{ \partial \sigma }+\Upsilon \beta _{1}\Bigg )\omega \Bigg )+\beta _{1}\Bigg (\omega \frac{ \partial \omega }{\partial t}\Bigg )+\Bigg (\omega \Bigg (\beta _{1} \\{} & {} +\Bigg (\dfrac{\partial \beta _{2}}{\partial \sigma }+\Upsilon \beta _{1}\Bigg )\omega \Bigg )\Bigg )\beta _{2}\Bigg )\omega \Bigg (\omega \frac{\partial \Upsilon }{\partial \sigma } +2\Upsilon \frac{\partial \omega }{\partial \sigma }\Bigg )+\Lambda \Bigg (\frac{ \partial }{\partial t}\Bigg (\omega \frac{\partial \omega }{\partial t}\Bigg ) \\{} & {} -\beta _{1}\Bigg (\beta _{1}+\Bigg (\dfrac{\partial \beta _{2}}{\partial \sigma } +\Upsilon \beta _{1}\Bigg )\omega \Bigg )-\Bigg (\beta _{1}\Upsilon +\dfrac{\partial \beta _{2} }{\partial \sigma }\Bigg )\Bigg (\omega \Bigg (\beta _{1}+\Bigg (\dfrac{\partial \beta _{2} }{\partial \sigma } \\{} & {} +\Upsilon \beta _{1}\Bigg )\omega \Bigg )\Bigg )\Bigg (\frac{\partial ^{2}\omega }{\partial \sigma ^{2}}+\Bigg (\omega -\Upsilon \Bigg )\Bigg (\omega \Upsilon +1\Bigg )\Bigg )-\Lambda \Bigg ( \frac{\partial }{\partial t}\Bigg (\omega \Bigg (\beta _{1}+\Bigg (\dfrac{\partial \beta _{2}}{\partial \sigma }+\Upsilon \beta _{1}\Bigg )\omega \Bigg )\Bigg ) \\{} & {} -\beta _{2}\Bigg (\beta _{1}+\Bigg (\dfrac{\partial \beta _{2}}{\partial \sigma } +\Upsilon \beta _{1}\Bigg )\omega \Bigg )+\Bigg (\beta _{1}\Upsilon +\dfrac{\partial \beta _{2} }{\partial \sigma }\Bigg )\Bigg (\omega \frac{\partial \omega }{\partial t}\Bigg )\Bigg )\Bigg (\frac{ \partial \Upsilon }{\partial \sigma }\omega +2\Upsilon \frac{\partial \omega }{\partial \sigma }\Bigg ). \end{aligned}$$

$\divideontimes$Microfluidic ferromagnetic $\tau _{\nabla _{t}\phi \left( {\textbf{t}}\right) }$magnetic torque phase microscale is

$$\begin{aligned} {\mathcal {T}}_{\tau _{\phi \left( {\textbf{t}}\right) }}^{{\mathcal {F}}}= & {} \tau _{\rho }^{{\textbf{t}}}\int \int _{{\mathcal {W}}}\Bigg (\Bigg (\frac{\partial }{\partial t} \Bigg (\omega \frac{\partial \omega }{\partial t}\Bigg )-\beta _{1}\Bigg (\beta _{1}+\Bigg (\dfrac{ \partial \beta _{2}}{\partial \sigma }+\Upsilon \beta _{1}\Bigg )\omega \Bigg )-\Bigg (\beta _{1}\Upsilon \\{} & {} +\dfrac{\partial \beta _{2}}{\partial \sigma }\Bigg )\Bigg (\omega \Bigg (\beta _{1}+\Bigg ( \dfrac{\partial \beta _{2}}{\partial \sigma }+\Upsilon \beta _{1}\Bigg )\omega \Bigg )\Bigg )\Bigg ( \frac{\partial ^{2}\omega }{\partial \sigma ^{2}}+\Bigg (\omega -\Upsilon \Bigg )\Bigg (\omega \Upsilon +1\Bigg )\Bigg )\Lambda -\Bigg (\frac{\partial }{\partial t}\Bigg (\beta _{1} \\{} & {} +\Bigg (\dfrac{\partial \beta _{2}}{\partial \sigma }+\Upsilon \beta _{1}\Bigg )\omega \Bigg )+\beta _{1}\Bigg (\omega \frac{\partial \omega }{\partial t}\Bigg )+\Bigg (\omega \Bigg (\beta _{1}+\Bigg (\dfrac{\partial \beta _{2}}{\partial \sigma }+\Upsilon \beta _{1}\Bigg )\omega \Bigg )\Bigg )\beta _{2}\Bigg )\omega \Bigg (\omega \frac{\partial \Upsilon }{\partial \sigma } \\{} & {} +2\Upsilon \frac{\partial \omega }{\partial \sigma }\Bigg )\Lambda -\Bigg ( \frac{\partial }{\partial t}\Bigg (\omega \Bigg (\beta _{1}+\Bigg (\dfrac{\partial \beta _{2}}{\partial \sigma }+\Upsilon \beta _{1})\omega \Bigg )\Bigg )-\beta _{2}\Bigg (\beta _{1} \\{} & {} +\Bigg (\dfrac{\partial \beta _{2}}{\partial \sigma }+\Upsilon \beta _{1}\Bigg )\omega \Bigg )+\Bigg (\beta _{1}\Upsilon +\dfrac{\partial \beta _{2}}{\partial \sigma }\Bigg )\Bigg (\omega \frac{\partial \omega }{\partial t}\Bigg )\Bigg )\Bigg (\frac{\partial \Upsilon }{\partial \sigma }\omega +2\Upsilon \frac{\partial \omega }{\partial \sigma }\Bigg )\Lambda \Bigg )d{\mathcal {W}}, \end{aligned}$$

where $\tau _{\rho }^{{\textbf{t}}}$ is magnetic torque potential for $\nabla _{t}\phi \left( {\textbf{t}}\right)$.

With the flexibility of microfluidic ferromagnetic $\tau _{\nabla _{t}\phi \left( {\textbf{t}}\right) }$ magnetic torque phase microscale, a variety of spherical effects can be illustrated for electroosmotic microfluidic $\tau _{\nabla _{t}\phi \left( {\textbf{t}}\right) }$ magnetic torque metasurfaces, with diverse potential optical applications in Fig. 2.

Fig. 2

Flexibility of microfluidic antiferromagnetic $\tau _{\nabla _{t}\phi \left( {\textbf{t}}\right) }$

2.3 Microfluidic ferromagnetic $\tau _{\nabla _{t} \phi \left( {\textbf{s}}\right) }$ magnetic torque phase

$\tau _{\nabla _{t}\phi \left( {\textbf{s}}\right) }$magnetic torque microscale is

$$\begin{aligned} {}^{{\mathcal {B}}}{\mathcal {M}}_{\phi \left( {\textbf{s}}\right) }=\tau _{\rho }^{ {\textbf{s}}}\int \int _{{\mathcal {W}}}\nabla _{t}\phi \left( {\textbf{s}}\right) {\cdot }\nabla _{t}\tau _{\phi \left( {\textbf{s}}\right) }d{\mathcal {W}}. \end{aligned}$$

$\tau _{\nabla _{t}\phi \left( {\textbf{t}}\right) }$ magnetic torque of $\nabla _{t}\phi \left( {\textbf{t}}\right)$ is presented by

$$\begin{aligned} \tau _{\nabla _{t}\phi \left( {\textbf{s}}\right) }=-\Lambda \frac{\partial \omega }{\partial t}\mathbf {\alpha }-\Bigg (\Bigg (\dfrac{\partial \beta _{2}}{\partial \sigma }+\beta _{1}\Upsilon \Bigg )\omega ^{2}+\beta _{1}\omega \Bigg )\Lambda \mathbf {t+ }\frac{\partial \omega }{\partial t}\omega \Lambda \mathbf {s.} \end{aligned}$$

Thus, fluid of $\tau _{\nabla _{t}\phi \left( {\textbf{s}}\right) }$ magnetic torque is

$$\begin{aligned} \nabla _{t}\tau _{\nabla _{t}\phi \left( {\textbf{s}}\right) }= & {} \Bigg (\beta _{1}\Bigg (\Bigg ( \dfrac{\partial \beta _{2}}{\partial \sigma }+\beta _{1}\Upsilon \Bigg )\omega ^{2}+\beta _{1}\omega \Bigg )-\frac{\partial }{\partial t}\frac{\partial \omega }{ \partial t}-\beta _{2}\mathbf {\Bigg (}\frac{\partial \omega }{\partial t}\omega \Bigg )\Bigg )\Lambda \mathbf {\alpha } \\{} & {} -\Bigg (\frac{\partial }{\partial t}\Bigg (\Bigg (\dfrac{\partial \beta _{2}}{\partial \sigma } +\beta _{1}\Upsilon \Bigg )\omega ^{2}+\beta _{1}\omega \Bigg )+\frac{\partial \omega }{ \partial t}\beta _{1}+\Bigg (\beta _{1}\Upsilon +\dfrac{\partial \beta _{2}}{ \partial \sigma }\Bigg )\mathbf {\Bigg (}\frac{\partial \omega }{\partial t}\omega \Bigg )\Bigg )\Lambda {\textbf{t}} \\{} & {} \mathbf {+\Bigg (}\frac{\partial }{\partial t}\mathbf {\Bigg (}\frac{\partial \omega }{ \partial t}\omega \Bigg )-\Bigg (\Bigg (\dfrac{\partial \beta _{2}}{\partial \sigma }+\beta _{1}\Upsilon \Bigg )\omega ^{2}+\beta _{1}\omega \Bigg )\Bigg (\beta _{1}\Upsilon +\dfrac{ \partial \beta _{2}}{\partial \sigma }\Bigg )-\frac{\partial \omega }{\partial t} \beta _{2}\Bigg )\Lambda \mathbf {s.} \end{aligned}$$

$\divideontimes$ Electroosmotic microfluidic $\tau _{\nabla _{t}\phi \left( {\textbf{s}}\right) }$ magnetic torque density is

$$\begin{aligned} {\mathcal {V}}_{\tau _{\phi \left( {\textbf{s}}\right) }}= & {} \frac{\partial \omega }{ \partial t}\Lambda \Bigg (\frac{\partial }{\partial t}\Bigg (\Bigg (\dfrac{\partial \beta _{2} }{\partial \sigma }+\beta _{1}\Upsilon \Bigg )\omega ^{2}+\beta _{1}\omega \Bigg )+\frac{ \partial \omega }{\partial t}\beta _{1} \\{} & {} +\Bigg (\beta _{1}\Upsilon +\dfrac{\partial \beta _{2}}{\partial \sigma }\Bigg )\mathbf {\Bigg ( }\frac{\partial \omega }{\partial t}\omega \Bigg )\Bigg )+\Lambda \Bigg (\beta _{1}\Bigg (\Bigg (\dfrac{ \partial \beta _{2}}{\partial \sigma }+\beta _{1}\Upsilon \Bigg )\omega ^{2}+\beta _{1}\omega \Bigg ) \\{} & {} -\frac{\partial }{\partial t}\frac{\partial \omega }{\partial t}-\beta _{2} \Bigg (\frac{\partial \omega }{\partial t}\omega \Bigg )\Bigg )\beta _{1}\omega -\Bigg ( \dfrac{\partial \beta _{2}}{\partial \sigma }+\beta _{1}\Upsilon \Bigg )\omega \mathbf {\Bigg (}\frac{\partial }{\partial t}\Bigg (\frac{\partial \omega }{ \partial t}\omega \Bigg ) \\{} & {} -\Bigg (\Bigg (\dfrac{\partial \beta _{2}}{\partial \sigma }+\beta _{1}\Upsilon \Bigg )\omega ^{2}+\beta _{1}\omega \Bigg )\Bigg (\beta _{1}\Upsilon +\dfrac{\partial \beta _{2}}{ \partial \sigma }\Bigg )-\frac{\partial \omega }{\partial t}\beta _{2}\Bigg )\Lambda . \end{aligned}$$

$\divideontimes$ Microfluidic $\tau _{\nabla _{t}\phi \left( {\textbf{s}}\right) }$ magnetic torque phase microscale is given

$$\begin{aligned} {\mathcal {T}}_{\tau _{\phi \left( {\textbf{s}}\right) }}= & {} \tau _{\rho }^{\textbf{s }}\int \int _{{\mathcal {W}}}\Bigg (-\Bigg (\dfrac{\partial \beta _{2}}{\partial \sigma } +\beta _{1}\Upsilon \Bigg )\omega \Bigg (\frac{\partial }{\partial t}\Bigg ( \frac{\partial \omega }{\partial t}\omega \Bigg )-\Bigg (\Bigg (\dfrac{\partial \beta _{2}}{ \partial \sigma }+\beta _{1}\Upsilon \Bigg )\omega ^{2} \\{} & {} +\beta _{1}\omega \Bigg )\Bigg (\beta _{1}\Upsilon +\dfrac{\partial \beta _{2}}{\partial \sigma }\Bigg )-\frac{\partial \omega }{\partial t}\beta _{2}\Bigg )\Lambda +\Bigg (\beta _{1}\Bigg (\Bigg (\dfrac{\partial \beta _{2}}{\partial \sigma }+\beta _{1}\Upsilon \Bigg )\omega ^{2} \\{} & {} +\beta _{1}\omega \Bigg )-\frac{\partial }{\partial t}\frac{\partial \omega }{ \partial t}-\beta _{2}\Bigg (\frac{\partial \omega }{\partial t}\omega \Bigg )\Bigg )\beta _{1}\omega \Lambda +\Lambda \frac{\partial \omega }{\partial t}\Bigg ( \frac{\partial }{\partial t}\Bigg (\Bigg (\dfrac{\partial \beta _{2}}{\partial \sigma } \\{} & {} +\beta _{1}\Upsilon \Bigg )\omega ^{2}+\beta _{1}\omega \Bigg )+\frac{\partial \omega }{ \partial t}\beta _{1}+\Bigg (\beta _{1}\Upsilon +\dfrac{\partial \beta _{2}}{ \partial \sigma }\Bigg )\Bigg (\frac{\partial \omega }{\partial t}\omega \Bigg )\Bigg )\Bigg )d {\mathcal {W}}, \end{aligned}$$

where $\tau _{0}^{{\textbf{s}}}$ is magnetic torque potential for $\nabla _{t}\phi \left( {\textbf{s}}\right)$.

Also, we easily get

$$\begin{aligned} \phi \left( {\textbf{s}}\right) \times \nabla _{\sigma }^{2}\phi \left( {\textbf{s}}\right) =\omega \left( \omega \frac{\partial \Upsilon }{\partial \sigma } +2\frac{\partial \omega }{\partial \sigma }\Upsilon \right) \mathbf {\alpha }+2\frac{ \partial \omega }{\partial \sigma }\omega \mathbf {s.} \end{aligned}$$

$\divideontimes$ Microfluidic ferromagnetic electroosmotic $\tau _{\nabla _{t}\phi \left( {\textbf{s}}\right) }$magnetic torque density is

$$\begin{aligned} {\mathcal {V}}_{\tau _{\phi \left( {\textbf{s}}\right) }}^{{\mathcal {F}}}= & {} \Bigg (\beta _{1}\Bigg (\Bigg (\dfrac{\partial \beta _{2}}{\partial \sigma }+\beta _{1}\Upsilon \Bigg )\omega ^{2}+\beta _{1}\omega \Bigg )-\frac{\partial }{\partial t}\frac{\partial \omega }{\partial t} \\{} & {} -\beta _{2}\Bigg (\frac{\partial \omega }{\partial t}\omega \Bigg )\Bigg )\omega \Bigg (\omega \frac{\partial \Upsilon }{\partial \sigma }+2\frac{\partial \omega }{ \partial \sigma }\Upsilon \Bigg )\Lambda +\Bigg (\frac{\partial }{\partial t} \Bigg (\frac{\partial \omega }{\partial t}\omega \Bigg )-\Bigg (\Bigg (\dfrac{\partial \beta _{2}}{\partial \sigma } \\{} & {} +\beta _{1}\Upsilon \Bigg )\omega ^{2}+\beta _{1}\omega \Bigg )\Bigg (\beta _{1}\Upsilon + \dfrac{\partial \beta _{2}}{\partial \sigma }\Bigg )-\frac{\partial \omega }{ \partial t}\beta _{2}\Bigg )2\frac{\partial \omega }{\partial \sigma }\omega \Lambda . \end{aligned}$$

$\divideontimes$ Microfluidic ferromagnetic $\tau _{\nabla _{t}\phi \left( {\textbf{s}}\right) }$ magnetic torque phase microscale is

$$\begin{aligned} {\mathcal {T}}_{\tau _{\phi \left( {\textbf{s}}\right) }}^{{\mathcal {F}}}= & {} \tau _{\rho }^{{\textbf{s}}}\int \int _{{\mathcal {W}}}\Bigg (2\Lambda \frac{\partial \omega }{\partial \sigma }\omega \Bigg (\frac{\partial }{\partial t}\Bigg ( \frac{\partial \omega }{\partial t}\omega \Bigg )-\Bigg (\Bigg (\dfrac{\partial \beta _{2}}{ \partial \sigma }+\beta _{1}\Upsilon \Bigg )\omega ^{2} \\{} & {} +\beta _{1}\omega \Bigg )\Bigg (\beta _{1}\Upsilon +\dfrac{\partial \beta _{2}}{\partial \sigma }\Bigg )-\frac{\partial \omega }{\partial t}\beta _{2}\Bigg )\mathbf {+}\Lambda \Bigg (\beta _{1}\Bigg (\Bigg (\dfrac{\partial \beta _{2}}{\partial \sigma }+\beta _{1}\Upsilon \Bigg )\omega ^{2} \\{} & {} +\beta _{1}\omega \Bigg )-\frac{\partial }{\partial t}\frac{\partial \omega }{ \partial t}-\beta _{2}\Bigg (\frac{\partial \omega }{\partial t}\omega \Bigg )\Bigg )\omega \Bigg (\omega \frac{\partial \Upsilon }{\partial \sigma }+2\frac{\partial \omega }{\partial \sigma }\Upsilon \Bigg )\Bigg )d{\mathcal {W}}, \end{aligned}$$

where $\tau _{\rho }^{{\textbf{s}}}$is magnetic torque potential for $\nabla _{t}\phi \left( {\textbf{s}}\right)$.

With the flexibility of microfluidic ferromagnetic $\tau _{\nabla _{t}\phi \left( {\textbf{s}}\right) }$ magnetic torque phase microscale, a variety of spherical effects can be illustrated for electroosmotic microfluidic $\tau _{\nabla _{t}\phi \left( {\textbf{s}}\right) }$ magnetic torque metasurfaces, with diverse potential optical applications in Fig. 3.

Fig. 3

Flexibility of microfluidic ferromagnetic $\tau _{\nabla _{t}\phi \left( {\textbf{s}}\right) }$

3 Conclusions

The concept for geometric microfluidic is constructed by magnetic nano fluids, electromagnetic nanoparticles with optical heat transfer fluid and some optical applications (Ashkin et al. 1986; Ashkin 1970; Dholakia and Zemánek 2010; Burns et al. 1989; Chaumet and Nieto-Vesperinas 2001; Almaas and Brevik 2013; Körpınar and Körpınar 2021; Körpınar et al. 2021a, b; Yépez-Martínez et al. 2022; Rehman et al. 2022; Bhambere and Durge 2022; Zafar et al. 2023; Singh et al. 2023; Raza et al. 2023; Kang et al. 2022; Viscarra and Urzagasti 2022; Körpinar et al. 2023a; Körpinar and Körpinar 2023a, b, c; Körpinar et al. 2023b; Körpinar and Körpinar 2023d, e; Korpinar et al. 2023; Körpinar and Körpinar 2023f; Körpinar et al. 2023; Körpınar and Körpınar 2023).

In this paper, we obtain optical geometric microfluidic $\tau _{\nabla _{t}\phi \left( \mathbf {\alpha }\right) },$ $\tau _{\nabla _{t}\phi \left( {\textbf{t}}\right) },$ $\tau _{\nabla _{t}\phi \left( {\textbf{s}}\right) }$ magnetic torques phase microscale. Then, we illustrate optical microfluidic ferromagnetic electroosmotic $\tau _{\nabla _{t}\phi \left( \mathbf {\alpha } \right) },$ $\tau _{\nabla _{t}\phi \left( {\textbf{t}}\right) },$ $\tau _{\nabla _{t}\phi \left( {\textbf{s}}\right) }$ magnetic torques density. Thus, we present microfluidic ferromagnetic $\tau _{\nabla _{t}\phi \left( \mathbf {\alpha }\right) },$ $\tau _{\nabla _{t}\phi \left( {\textbf{t}}\right) },$ $\tau _{\nabla _{t}\phi \left( {\textbf{s}}\right) }$ magnetic torques phase microscale.