Characterizing the thermal quantum correlations in a two-qubit Heisenberg XXZ spin-$\frac{1}{2}$ chain under Dzyaloshinskii–Moriya and Kaplan–Shekhtman–Entin–Wohlman–Aharony interactions

Abstract

We considered the two-qubit Heisenberg XXZ spin chain in the presence of Dzyaloshinskii–Moriya and Kaplan–Shekhtman–Entin–Wohlman–Aharony interactions in thermal equilibrium. As discord-type quantifiers of thermal non-classical correlations, we used trace distance discord and local quantum uncertainty. Depending on the thermal state of the system considered, the explicit analytical expressions of the suggested quantifiers are derived and their behaviors with respect to the various parameters of the system are examined. The results obtained showed that the Dzyaloshinskii–Moriya and Kaplan–Shekhtman–Entin–Wohlman–Aharony interactions considerably improve the quantum correlations contained in the bipartite system while the temperature tends to decrease their quantity.

1 Introduction

Quantum entanglement, a significant property of quantum mechanics, is regarded as a basic resource for quantum information and quantum computation (Horodecki et al. 2009; Nielsen and Chuang 2000). It plays an important role in many fundamental aspects of quantum information processing tasks such as superdense coding (Bennett and Wiesner 1992), quantum teleportation (Bennett et al. 1993) and quantum states merging (Horodecki et al. 2005, 2007). One of the main problems heavily investigated in quantum information science is the characterization and quantification of correlations in quantum states. At first, it was believed that quantum correlation was synonymous with quantum entanglement and that quantum information protocols could only be implemented through entangled states (Horodecki et al. 2009). Nonetheless, non-trivial quantum correlations have been discovered in mixed separable states (Ferraro et al. 2010) which were later used in some useful quantum information protocols which cannot be achieved by classical means (Modi et al. 2012; Datta et al. 2008). It has been shown that this type of correlations can only be quantified by what is called quantum discord (Henderson and Vedral 2001; Ollivier and Zurek 2001). In this context, quantum discord goes beyond entanglement; because it does not only measure the quantum correlations in the entangled states but also in the separable states. But the analytical computation of quantum discord in its entropy form is usually not an easy task. To facilitate the computation of quantum discord, two different approaches have been adopted as an alternative way : the first approach is based on metric criteria in the state space (Dakić et al. 2010; Paula et al. 2013) while the second is based on the concept of uncertainty (Luo 2003; Girolami et al. 2013). One of the most important geometrical versions of discord is trace distance discord (TDD) (Ciccarello et al. 2014) which quantifies the amount of non-classical correlations through the measure of the distance between the probing state and its closest genuinely zero-discord states (Debarba et al. 2012; Montealegre et al. 2013; Rana and Parashar 2013). Concerning the second approach, the discord-like correlations between different parts of a composite system can also be quantified through what is called local quantum uncertainty (LQU) (Girolami et al. 2013). This reliable measure of quantum discord was inspired by the notion of skew information introduced by Wigner and Yanasse (1963) (Luo 2003) mainly to measure the uncertainty resulting from a single local observable action on a given state of the bipartite system. As with TDD, LQU can also be calculated simply and a closed formula for qubit-qudit system states is given in Wang et al. (2013). More precisely, a flexible formalism for the computation of LQU in a two-qubit X state has been established in Khedif and Daoud (2019), Habiballah et al. (2018), Khedif et al. (2019), Khedif and Daoud (2021) and Khedif et al. (2021a).

Recently, intensive interest has been devoted to the characterization and quantification of quantum correlations in condensed matter physics systems (Wang 2001; Sun et al. 2003; Park 2019; Yurischev 2020; Khedif and Daoud 2021; Khedif et al. 2019, 2021a, b). From a practical standpoint, the Heisenberg spin chain has been considered the most widely used quantum system for this purpose. In this context, several studies of thermal pairwise entanglement within different Heisenberg spin chain models have been investigated (Rigolin 2004; Sun et al. 2003; Sha et al. 2018; Asoudeh and Karimipour 2005; Zhang and Li 2005). In addition, thermal quantum correlation in such systems under the interplay of magnetic field have also been quantified particularly by quantum discord (Werlang and Rigolin 2010; Guo et al. 2011). It is worth mentioning that the spin-spin coupling was the most common interaction in the Heisenberg model spin chain. But in fact, the genuine interaction between two neighboring spins is the one that includes also the spin-orbit coupling. To characterise the antisymmetric contribution arising from this coupling, the Dzyaloshinskii–Moriya (DM) (Moriya 1960a, b) terms are incorporated in the Heisenberg model. This new model has been employed in several works to investigate the pairwise thermal quantum correlations via various quantifiers (Park 2019; Khedif and Daoud 2021; Khedif et al. 2021a). Furthermore, the quantum phase transition of a two-spin XYZ Heisenberg model with homogeneous external transverse magnetic field and DM interaction was variously discussed in Park (2019) and Najarbashi and Seifi (2017). Meanwhile, the Heisenberg spin models, without (Ming et al. 2018a; Shi et al. 2019) and with DM interactions (Ming et al. 2018b; Yang et al. 2019), have been used to characterise the thermal features of the bipartite entropy-based uncertainty. Further to DM interaction, it is shown that the spin-orbit coupling provides also a symmetric contribution termed Kaplan–Shekhtman–Entin–Wohlman–Aharony interaction (KSEA) (Shekhtman et al. 1992, 1993; Yurischev 2020; Khedif et al. 2021b; Abd-Rabboul et al. 2021). Within the intrinsic decoherence framework, the temporal evolution of quantum correlations in a two-qubit Heisenberg spin chain models with DM (Muthuganesan and Chandrasekar 2021; Guo et al. 2021; Ait Chlih et al. 2021; Essakhi et al. 2022) as well as the KSEA (Hashem et al. 2022) interactions has been also recently studied.

The main goal of this paper is the study of the effects of both contributions, antisymmetric (DM) and symmetric (KSEA), of spin-orbit coupling on the thermal non-classical correlations quantified by discord-like quantifiers. More specifically, we are interested in the characterization of non-classical thermal correlations in a two-dimensional XXZ Heisenberg spin chain in the presence of DM and KSEA interactions along the z direction using TDD and LQU. After the evaluation of the thermal state of the considered system, the relevant expressions of the quantum correlations are derived. For the sake of comparison, we study the effects of different system parameters on non-classical correlations in the spin chain and discuss the remarkable differences between them.

This paper is organized as follows. In Sect. 2, we present the Hamiltonian which describes the XXZ Heisenberg two-qubit model and the density matrix of the system. In Sect. 3, we review some preliminaries about the quantifiers that we use to quantify the quantum correlations in our system, namely TDD and LQU. The TDD and LQU analytical expressions corresponding to the investigated model are derived in Sect. 4. The effects of different parameters on the amounts of non-classical correlations are exploited and examined in detail in Sect. 5. To close this paper, concluding remarks are given in Sect. 6.

2 Two-qubit XXZ Heisenberg model with DM and KSEA coupling

In this section, we consider the XXZ Heisenberg two-qubit model under the effect of DM and KSEA interactions directed along the z-axis which we will now denote by z-DM and z-KSEA for simplicity. The Hamiltonian model is given by Khedif et al. (2019), Yurischev (2020)

$$\begin{aligned} H=J\left( \sigma _{1}^{x}\sigma _{2}^{x}+\sigma _{1}^{y}\sigma _{2}^{y}+ \gamma \sigma _{1}^{z}\sigma _{2}^{z}\right) +D\left( \sigma _{1}^{x}\sigma _{2}^{y}-\sigma _{1}^{y}\sigma _{2}^{x}\right) +\Gamma \left( \sigma _{1}^{x}\sigma _{2}^{y}+\sigma _{1}^{y}\sigma _{2}^{x}\right) \end{aligned}$$

(1)

where the $\sigma _{i}^{\alpha \in \left\{ x, y, z\right\} }$ denote the standard Pauli operators acting on the site $i=1,~2$, the dimensionless factor $\gamma \in \left[ 0,1\right]$ is the anisotropy parameter in the z direction, J denotes the exchange coupling constant between the spins, D and $\Gamma$ stand for the z-DM and z-KSEA components, respectively. $J>0$ corresponds to the antiferromagnetic chain while $J<0$ refers to the ferromagnetic chain case. We notice that we are working in units so that D, $\Gamma$ and J are dimensionless.

The Hamiltonian (1) can be rewritten, in the two-qubit standard computational basis is $\mathcal{B}=\{|00\rangle , |01\rangle , |10\rangle ,|11\rangle \}$ in the following matrix form

$$\begin{aligned} H=\left( \begin{array}{cccc} \gamma J &{} 0 &{} 0 &{} -2i\Gamma \\ 0 &{} -\gamma J\ &{} 2\left( J+iD\right) &{} 0 \\ 0 &{} 2\left( J-iD\right) &{} -\gamma J &{} 0 \\ 2i\Gamma &{} 0 &{} 0 &{} \gamma J \\ \end{array} \right) . \end{aligned}$$

(2)

In the basis $\mathcal{B}$, the eigenvalues $E_n$ and the corresponding eigenvectors $\vert \varphi _n\rangle$ of the Hamiltonian (2) can be easily obtained in the following forms

$$\begin{aligned} E_{1,2}= \gamma J\pm 2\Gamma ,&\qquad \vert \varphi _{1,2}\rangle = \frac{1}{\sqrt{2}}(\vert 00 \rangle \pm \vert 11 \rangle ), \end{aligned}$$

(3a)

$$\begin{aligned} E_{3,4}= -\gamma J\pm 2\xi ,&\qquad \vert \varphi _{3,4}\rangle = \frac{1}{\sqrt{2}}(\vert 01 \rangle \pm e^{i\theta }\vert 10 \rangle ), \end{aligned}$$

(3b)

where $\xi :=\sqrt{J^2+D^2}$ and $\displaystyle \cos \theta =\frac{J}{\xi }$. The kets $\vert 0 \rangle$ and $\vert 1 \rangle$ denote spin-up and spin-down states, respectively.

We propose to study the non-classical correlations, in the considered system, captured by LQU and TDD by taking into account the thermal fluctuations. To this end, we first evaluate the Gibbs density matrix describing the two-spin system at thermal equilibrium defined by

$$\begin{aligned} \rho (T)=\frac{e^{-H/T}}{\mathrm{Tr}(e^{-H/T})}, \end{aligned}$$

(4)

where T is the temperature in energy units. From the spectrum 3 of the Hamiltonian H, we can analytically derive the two-qubit thermal density matrix $\rho (T)$. After simple algebraic operations, the density matrix (4) is rewritten, in the basis $\mathcal{B}$ as

$$\begin{aligned} \rho (T)=\frac{1}{2\left( r+s\right) }\left( \begin{array}{llll} r &{} 0 &{} 0 &{} u \\ 0 &{} s &{} v &{} 0 \\ 0 &{} v^{*} &{} s &{} 0 \\ u^{*} &{} 0 &{} 0 &{} r \end{array}\right) . \end{aligned}$$

(5)

We find that $\rho (T)$ has an X form where its elements are expressed as following

$$\begin{aligned} r= & {} e^{-\frac{\gamma J}{T}} \cosh \left( \frac{2\Gamma }{T}\right) ,\nonumber \\ u= & {} ie^{-\frac{\gamma J}{T}} \sinh \left( \frac{2\Gamma }{T}\right) ,\nonumber \\ s= & {} e^{\frac{\gamma J}{T}} \cosh \left( \frac{2\xi }{T}\right) , \nonumber \\ v= & {} -e^{\frac{\gamma J}{T}} \sinh \left( \frac{2\xi }{T}\right) . \end{aligned}$$

(6)

3 Non-classical correlations quantifiers

3.1 Local quantum uncertainty

Local quantum uncertainty is a discord-like measure of non-classical correlations in multipartite systems. More precisely, it has been proposed to quantify the minimum quantum uncertainty produced in a quantum state due to a measurement of a single local observable (Girolami et al. 2013). Considering the density matrix $\rho _{AB}$ describing a bipartite quantum state shared between A and B parts, and let $K_{A}^{\Lambda }\otimes \mathbbm {1}_B$ be a local observable, where $K_{A}^{\Lambda }$ is a Hermitian operator on A of spectrum $\Lambda$ and $\mathbbm {1}_B$ is the identity operator acting on the subsystem B. The LQU, with respect to subsystem A, is defined as Girolami et al. (2013)

$$\begin{aligned} \mathscr {U}(\rho _{AB}) := \min _{K_{A}^{\Lambda } \otimes \mathbbm {1}_B} \mathscr {I}\Big (\rho _{AB}, K_{A}^{\Lambda }\otimes \mathbbm {1}_B\Big ), \end{aligned}$$

(7)

where the minimum is optimized over all local observables on subsystem A with a non-degenerate spectrum ${\Lambda }$ and the quantity

$$\begin{aligned} \mathscr {I}(\zeta , K_{A}^{\Lambda } \otimes \mathbbm {1}_B):=-\frac{1}{2}{\mathrm{Tr}}\left( \Big [\sqrt{\zeta }, K_{A}^{\Lambda } \otimes \mathbbm {1}_B\Big ]^{2}\right) \end{aligned}$$

(8)

refers to the Wigner–Yanase skew information (Wigner and Yanasse 1963; Luo 2003). It is used to measure the uncertainty produced in a given state $\zeta$ due to the observable K measurement. In particular, we can show that, for pure states$(\zeta ^2=\zeta )$, the skew information reduces to the conventional variance formula

$$\begin{aligned} {\mathrm{Var}}\left( \zeta , K\right) ={\mathrm{Tr}}\left( \zeta K^2\right) -\Big ({\mathrm{Tr}}\big (\zeta K\big )\Big )^2. \end{aligned}$$

(9)

The analytical evaluation of LQU is performed by a minimization procedure over all local observables acting on part A of the considered bipartite system. Accordingly, a closed formula for qubit-qudit systems is available (Wang et al. 2013). In particular, the LQU for qubits with respect to subsystem A reads as Girolami et al. (2013)

$$\begin{aligned} \mathscr {U}(\rho _{AB}) = 1 - \omega _{\max }, \end{aligned}$$

(10)

where $\omega _{\max }$ denotes the maximal eigenvalue of the $3\times 3$ symmetric matrix $\mathscr {W}_{AB}$ with the elements

$$\begin{aligned} \Big (\mathscr {W}_{AB}\Big )_{uv} \equiv {\text { Tr}}\left\{ \sqrt{\rho _{AB}}\Big (\sigma _{A}^{u}\otimes {\mathbbm {1}}_{B}\Big )\sqrt{\rho _{AB}}\Big (\sigma _{A}^{v}\otimes {\mathbbm {1}}_{B}\Big )\right\} \end{aligned}$$

(11)

and $\sigma _{A}^{u,v} (u, v = x, y, z)$ are the three Pauli operators of the subsystem A. The LQU has been shown to meet all the physical requirements of a measure of quantum correlations (Girolami et al. 2013). Indeed, it is invariant under any local unitary operations. Moreover, LQU provides a reliable discord-like measure (i.e. LQU vanishes for all states which have zero discord) and it has a geometrical significance in terms of Hellinger distance (Luo 2003; Girolami et al. 2013).

3.2 Trace distance discord

The trace distance discord (TDD) is a reliable geometric quantifier of discord-type correlations. It quantifies the quantum correlations by means of the Schatten 1-norm distance. More precisely, it measures the distance between a given state and its closest zero discord one. For a bipartite state $\rho _{AB}$ of the Hilbert space $\mathcal{H}_{A} \otimes \mathcal{H}_{B}$, the TDD is defined as Paula et al. (2013)

$$\begin{aligned} D_{\text {T}}(\rho _{AB})=\min _{\rho _{\text {cq}}\in \Omega _0}\Vert \rho _{AB}-\rho _{\text {cq}}\Vert _1. \end{aligned}$$

(12)

Here, $\rho _{\text {cq}}$ denotes a classical-quantum state with zero quantum discord, $\Omega _0$ is the set of states with vanishing quantum discord and $\Vert \mathscr {O}\Vert _1={\mathrm{Tr}} \left( \sqrt{\mathscr {O}^{\dagger } \mathscr {O}}\right)$ defines the trace norm of a generic operator $\mathscr {O}$. Note that, the set of classical-quantum states $\rho _{\text {cq}}$, with respect to local measurements on subsystem A, can be expressed as Luo (2008)

$$\begin{aligned} \rho _{\text {cq}}=\sum _{k=1}^{2}p_k|k\rangle \langle k|^A\otimes \rho _{k}^{B}, \end{aligned}$$

(13)

where $\{|k\rangle ^A\}$ is an orthonormal basis of A subsystem’s Hilbert space $\mathcal{H}_A$, $\rho _{k}^{B}$ a general reduced density operator of the subsystem B on its Hilbert space $\mathcal{H}_B$ and $\{p_k\}$ is a set of statistical probability distribution with a convex combination ($p_k \ge 0$ and ${\sum _{k=1}}p_k=1$).

4 Thermal non-classical correlations

In this section, we study LQU and TDD to quantify the non-classical correlations contained in the bipartite quantum state $\rho (T)$ (5). To compute LQU (10) with respect to the subsystem A, the elements of the matrix $\mathcal{{W}}_{AB}$ corresponding to the thermal state $\rho (T)$ should be identified. By inserting (5) into (11), we can straightforwardly check that the matrix elements of $\mathcal{{W}}_{AB}$ are given by Khedif et al. (2019), for more details

$$\begin{aligned} \omega _{11}= & {} \frac{1}{r+s} \left( \sqrt{r-\left| u\right| } \sqrt{s-\left| v\right| }+\sqrt{r+\left| u\right| } \sqrt{s +\left| v\right| }\right) , \nonumber \\ \omega _{22}= & {} \frac{1}{r+s} \left( \sqrt{r+\left| u\right| } \sqrt{s-\left| v\right| }+\sqrt{r-\left| u\right| } \sqrt{s +\left| v\right| }\right) , \nonumber \\ \omega _{33}= & {} \frac{1}{r+s} \left( \sqrt{r^2-\left| u\right| ^2}+\sqrt{s^2-\left| v\right| ^2 }\right) . \end{aligned}$$

(14)

So, the LQU is computed as

$$\begin{aligned} \mathscr {U}\left( \rho (T)\right) = 1-\max \left( \omega _{11},\omega _{22},\omega _{22}\right) . \end{aligned}$$

(15)

On the other hand, the explicit and compact expression of TDD for a generic two-qubit X state was derived and presented in Ciccarello et al. (2014). Following this, the TDD corresponding to the thermal state $\rho \left( T\right)$ is expressed as

$$\begin{aligned} \mathscr {D}\left( \rho (T)\right) =\sqrt{\frac{\varepsilon _{+}^{2} \max \left\{ \varepsilon _{-}^{2},\varepsilon ^2\right\} -\varepsilon _{-}^{2} \min \left\{ \varepsilon _{+}^{2},\varepsilon ^2\right\} }{\max \left\{ \varepsilon _{-}^{2},\varepsilon ^2\right\} -\min \left\{ \varepsilon _{+}^{2},\varepsilon ^2\right\} +\varepsilon _{+}^{2}-\varepsilon _{-}^{2}}} \end{aligned}$$

(16)

where $\varepsilon _{\pm }=\frac{\vert u\vert \pm \vert v\vert }{r+s}$ and $\varepsilon =\frac{r-s}{r+s}$ are the non vanished components of the correlation matrix appearing in the Fano-Bloch decomposition of the density matrix $\rho \left( T\right)$ (Bloch 1946; Fano 1983; Khedif et al. 2019).

5 Results and discussions

In what follows, we analyze TDD and LQU as functions of the temperature, spin-spin as well as spin-orbit exchanges couplings and the anisotropy parameters.

Fig. 1

a TDD and b LQU versus temperature T for various values of z-KSEA component in a two ferromagnetic isotropic XXX Heisenberg spin-$\frac{1}{2}$ system by taking $D=0.5$ and $J=-2$

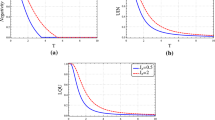
The changes in quantum correlations in terms of the temperature T in the ferromagnetic XXX Heisenberg spin-1/2 chain under the effect of z-DM and z-KSEA interactions are shown in Fig. 1. We observe that TDD (Fig. 1a) and LQU (Fig. 1b) exhibit an almost similar behaviour with respect to the temperature T. They have a maximum value (close to unity) when $T\rightarrow 0$. This happens because at very low temperatures, the bipartite system exists in the maximally entangled pure ground state $\vert \varphi _{2}\rangle = \frac{1}{\sqrt{2}}(\vert 00 \rangle -\vert 11 \rangle )$ 3. Then, due to thermal fluctuations, we observe that both quantifiers undergo asymptotic decay with increasing temperature. Remarkably, the thermal feature of TDD (Fig. 1a) manifests a local minimum when the value of the z-KSEA component is relatively small ($\Gamma =0.1$). Correspondingly, such an aspect disappears completely as the values of $\Gamma$ sufficiently increase. Hence, the increasing values of $\Gamma$ tend to suppress the local minimum for TDD quantifier Yurischev (2020). It should be mentioned that LQU disappears faster than TDD at higher temperatures. We also note that the larger $\Gamma$, the longer the system will survive in the ground state. Indeed, this behaviour is due to the dependence of the ground state relevant minimum energy $(E_{\min }= J-2\Gamma )$ by $\Gamma$ (see left side of (3a)). It follows that increasing the latter implies weakening the effect of temperature fluctuations on quantum correlations. It should be noted that in low temperature regime and for the ferromagnetic two-spin XXX isotropic system, the elements of the density matrix (6) can be simplified to $r=\vert u\vert \simeq e^{\frac{\Gamma -J}{T}}$, $s=\vert v\vert =0$ and therefore $\mathcal{D}(\rho (T\rightarrow 0))=\mathcal{U}(\rho (T\rightarrow 0))=1$.

In Fig. 2, we analyze the effect of the DM interaction on the quantum correlations for various values of temperature T, in the ferromagnetic two-qubit XXZ Heisenberg spin chain system in the absence of the z-KSEA interaction $({\Gamma }=0)$. As shown in Fig. 2a, b, respectively, the TDD and LQU behave in the same way with respect to the parameter D. They first increase from T-dependent initial values with D increasing to asymptotically reach the value 1 for a very sufficient value of D. Furthermore, it is observed that the temperature effect disappears completely for high values of D. This highlights that the antisymmetric contribution of spin-orbit coupling in the z-direction serves to improve and maintain the value of quantum correlations in two-spin XXZ ferromagnetic system. In addition, this makes the considered system more resistant against to the decoherence phenomenon produced by the fluctuations temperatures effects.

Fig. 2

The variations of a TDD and b LQU in terms of D for various temperatures in a two neighboring XXZ ferromagnetic spin-$\frac{1}{2}$system by considering $\gamma =0.8$, $J=-1$ and $\Gamma =0$

Now we study how the exchange coupling constant J affects the non-classical correlations measured by TDD (Fig. 3a) and LQU (Fig. 3b) for various temperature values T. The graphs in Fig. 3 show that the non-classical correlations captured by the considered quantifiers evolve in terms of J according to a similar behavior as that observed when the D effects were considered (Fig. 2). As a result, increasing J improves quantum correlations between antiferromagnetic spins and prevents the destructive effect of thermal fluctuations.

Next, we examine the effect of the KSEA interaction, as a symmetric contribution of spin-orbit coupling, along the z-axis ($\Gamma$) on quantum correlations for fixed values of temperature. The main results are illustrated in Fig. 4 for two ferromagnetic XXZ Heisenberg spin systems.

Fig. 3

a TDD and b LQU as a function of the exchange coupling constant J for various temperatures in a two-spin XXZ Heisenberg system under the effect of z-DM and z-KSEA interactions by considering $D=0.6$, $\Gamma =0.3$ and $\gamma =0.8$

As shown in this figure, the two quantifiers behave differently with respect to the parameter $\Gamma$. On the one hand, the variations of TDD (Fig. 4a) show two stages. It first decreases from a T-dependent maximum value when ${\Gamma }=0$ to reach a peaked minimum value corresponding to a critical value ${\Gamma _c}=\varepsilon -\gamma J\simeq 1.97$ which is also T-dependent (see inset of Fig. 4a). It is interesting to notice that the value of ${\Gamma _c}$ can be obtained analytically when the condition ${\varepsilon _{+}^{2}}={\varepsilon _{-}^{2}}={\varepsilon ^{2}}$ is fulfilled. After that, the quantum correlations quantified by the trace norm increase to asymptotically reach a maximal amount of correlations equal to unity. On the other hand, LQU (Fig. 4b) increases monotonically from a T-dependent value for ${\Gamma }=0$ to tend asymptotically towards unity. It is concluded that, like to z-DM interaction effects, the z-KSEA interaction clearly improves the thermal quantum correlations between the two neighboring XXZ ferromagnetic spins, and also limits the effect of thermal fluctuations on them.

Fig. 4

a TDD and b LQU versus $\Gamma$ for various temperatures in a two neighboring ferromagnetic spin-$\frac{1}{2}$ XXZ system under the effect of z-DM interaction by taking $J=-1.2$, $D=2.5$ and $\gamma =2/3$

Finally, we study the influence of the anisotropy parameter $\gamma$ on the thermal quantum correlations quantified by TDD and LQU in a two ferromagnetic XXZ Heisenberg spins under the effect of z-DM and z-KSEA interactions for different temperature values. In Fig. 5, it is observed that the considered quantifiers also provide different aspects in terms of $\gamma$. An almost linear decrease in TDD (Fig. 5a) with $\gamma$ increasing to reach a peaked minimum for $\gamma ^{*}=\frac{-\epsilon +\Gamma }{J}\simeq 0.77$ wherein a sudden change in behavior occurs. The non-classical correlations captured by LQU (Fig. 5b) in the system also show a linear decrease with respect to $\gamma$. The sudden change in behavior observed in the case of TDD (Fig. 5a) at $\gamma ^{*}\simeq 0.77$, which takes place only for ${\varepsilon _{+}^{2}}={\varepsilon _{-}^{2}}={\varepsilon ^{2}}$, does not reverse the changes in LQU as a function of $\gamma$. Interestingly, the two quantifiers reveal more quantum correlations in the bipartite isotropic XX Heisenberg system in comparing with the isotropic XXX system. That is to say, the presence of the DM and KSEA interactions along the z-axis make the two isotropic XX ferromagnetic spins system more correlated than that of the isotropic XXX Heisenberg bipartite system.

Fig. 5

a TDD and b LQU versus anisotropy parameter $\gamma$ for various temperatures in a two neighboring ferromagnetic spin-$\frac{1}{2}$ system under the effect of z-DM and z-KSEA interactions by considering $J=-2$, $D=1.2$, and ${\Gamma }=0.8$

6 Concluding remarks

In this study, thermal non-classical correlations quantified by TDD and LQU in a two-spin-$\frac{1}{2}$ XXZ Heisenberg model under the effect of DM and KSEA interactions both directed along the z-axis were investigated. The analytic expressions of the two quantifiers are derived from the Hamiltonian model. TDD and LQU dependencies according to model parameters are exploited and highlighted. It is observed that the thermal fluctuations act to dampen the quantum correlations, while the z components of the two interactions DM and KSEA serve maintain and improve these bipartite correlations, especially in the ferromagnetic system. For the influences of the anisotropy parameter $\gamma$, it is shown that the amounts of quantum correlations are more important in the isotropic XX Heisenberg model than in the isotropic XXX one. Given the observations and facts described above, an appropriate control parameter to decrease thermal fluctuations on the quantum correlations by varying the model parameters can be obtained. In general, except for the influences of the ${\Gamma }$ and ${\gamma }$ parameters, similar behavior of TDD and LQU with respect to other parameters of the model was confirmed.