1 Introduction

Organic solar cells (OSCs) exhibit a strong potential to be used in future solar cell technologies due to their low production costs, small weight, printability, solution processing, and the possibility of using flexible substrates (Ghosekar and Patil 2021). Their power conversion efficiencies have now surpassed 18% (Zhang et al. 2021). Still, the potential of OSCs has not been completely exploited due to the lack of an adequate physical model that describes their operation.

The standard van Roosbroeck model (Van Roosbroeck 1950) including the peculiarities of organic semiconductors through photogeneration and recombination terms is most often used for modeling the OSCs (Koster et al. 2005). This drift–diffusion model (DDM) is usually solved with Dirichlet’s boundary conditions (BCs) describing ideally conductive (Ohmic) contacts or applying homogenous Robin BCs (ideally blocking contact) for minority carriers (Schroeder 1994). It was shown that surface processes at electrode contacts in OSCs, such as surface recombination and thermionic emission, have a significant impact on their performance (Khalf et al. 2020a, b; Sandberg et al. 2014). To take into account these processes in DDM, full Robin type BCs need to be applied on both electrode contacts and for both types of carriers (Khalf et al. 2020a).

The DDM is usually numerically solved by either finite difference, finite volume, or finite element methods using Schaffeter-Gummel (SG) discretization (Farrell et al. 2020). The Voronoi finite volume method with SG numerical flux proved to be the most adequate approach (Farrell et al. 2017). In the one-dimensional case often used for OSCs modeling, this method reduces to the finite difference method (FDMSG).

In this paper, the standard DDM was simplified by decoupling the electron and hole continuity equations assuming that the recombination rate for one type of carriers is proportional to its concentration square and by taking the electric field in the device to be constant. Surface recombination and thermionic emission of holes and electrons on both electrode contacts were included through Robin-type BCs. When FDMSG numerical method was used for current density—voltage (J–V) calculations in a wide range of surface recombination velocities (SRVs), significant instabilities were observed. Trying to reduce these instabilities, a Discontinuous Galerkin (DG) method with Lax-Friedricks (LF) numerical flux (DGLF) was applied. The DGLF approach led to even more unstable calculations. Implementation of the Schaffeter-Gummel numerical flux (SG) in the DG method (DGSG) produced remarkable progress in the stability of J–V calculations. Each of three different numerical approaches considered in this paper was used to define the intervals of SRV values in which the electrode contacts act as (1) ideally blocking, (2) neither blocking nor conductive, and (3) ideally conductive. The SRV ranges for which the instabilities occur were determined for each numerical method. Finally, the J–V characteristic simulated by the DDM solved with the DGSG method was compared to the experimental ITO/PEDOT:PSS/P3HT:PCBM/Al solar cells J–V curves for model validation.

2 Modeling

The J–V characteristics of OSCs were calculated by using the steady-state DDM based on Poisson’s equation and continuity equations for electrons and holes. The surface recombination and thermionic emission were included through BCs of Robin type applied at the anode and cathode contacts, whereby the majority carrier injection barriers were assumed to be zero. The photogeneration and transport of charge carriers were taken to be the same as in (Khalf et al. 2020a).

In general case steady-state DDM (Khalf et al. 2020a) consists of three coupled second-order nonlinear and non-homogeneous differential equations. To avoid the complexities of the problem and to enable a separate analysis of the effect of electron and hole BCs on the steady-state solution certain simplifications were introduced. First, the electric field was assumed to be constant. Second, the electron and hole continuity equations were decoupled, by taking the holes bimolecular recombination velocity to be \({R}_{p}\left(x\right)=\gamma {p}^{2}\left(x\right)\), and analogously for electrons \({R}_{n}\left(x\right)=\gamma {n}^{2}\left(x\right)\), where \(\gamma\) is Langevin recombination constant, while n and p are electron and hole densities, respectively. In this way, the system is reduced to two separate second-order nonlinear and non-homogeneous DEs, one for holes, and the other for electrons:

$$\mu_{p} E_{f} \frac{\partial p\left( x \right)}{{\partial x}} - D_{p} \frac{{\partial^{2} p\left( x \right)}}{{\partial x^{2} }} = G - R_{p} \left( x \right), R_{p} \left( x \right) = \gamma p^{2} \left( x \right),$$
(1)
$$- \mu_{n} E_{f} \frac{\partial n\left( x \right)}{{\partial x}} + D_{n} \frac{{\partial^{2} n\left( x \right)}}{{\partial x^{2} }} = R_{n} \left( x \right) - G, \quad R_{n} \left( x \right) = \gamma n^{2} \left( x \right).$$
(2)

where \({E}_{f}=\left|U-{V}_{bi}\right|/d\) is the electric field intensity, \(U\) is the applied bias voltage, \({V}_{bi}\) is the built-in voltage, d is the OSCs active layer thickness, \({\mu }_{n(p)}\) is the electron or hole mobility, \({D}_{n(p)}\) is the diffusion constant of electrons or holes, \(G\) is the photogeneration rate calculated using the transfer matrix theory (Sievers et al. 2006). For \(n(x)\) calculation, the cathode is placed at \(x=0\) and the anode is positioned at \(x=d\), while for \(p(x)\) calculation, the electrodes were positioned oppositely as it can be seen from the Insets of Fig. 3a and b.

The BCs had the form:

$$J_{p} \left( 0 \right) = qS_{p0} \left( {p\left( 0 \right) - p_{th}^{a} } \right),\;J_{p} (d) = qS_{p} d(p(d) - p_{t} h^{c} )$$
(3)
$$J_{n} \left( 0 \right) = qS_{n0} \left( {n\left( 0 \right) - n_{th}^{c} } \right),\;J_{n} (d) = qS_{n} d(n(d) - n_{t} h^{a} )$$
(4)

where q is the elementary charge, \({J}_{n(p)}\) are the current densities of electrons and holes, \({S}_{n0(d)}\) and \({S}_{p0(d)}\) are the SRVs for electrons and holes, respectively, at the \(x=0\) and \(x=d\). The \({n}_{th}^{a}\) and \({p}_{th}^{a}\) are the thermionic electron and hole densities at the anode, respectively, and \({n}_{th}^{c}, {p}_{th}^{c}\) are the same for the cathode (Khalf et al. 2020a).

We only discuss the discretization of the decoupled equation system for electrons (Eqs. (2) and (4)) since the system for holes differs only by the values of physical parameters.

The first model for solving the decoupled equation systems was the finite difference method (FDM) with SG discretization to provide better convergence (Scharfetter and Gummel 1969), denoted by FDMSG. The OSCs active layer domain is discretized into \(N+1\) elements (subintervals) \({I}_{j}=[{x}_{j},{x}_{j+1}]\) with equidistant nodes. The obtained system of difference equations was then solved by the Newton algorithm.

The second and third models are based on the DG method (Chen and Bagci 2020) with the same discretization (number of elements) as in the FDMSG method. It is a hybrid method that combines the advantages of finite volume and finite element methods, using local high-order expansions to approximate the unknowns to be solved for. To solve the simplified model consisting of one nonlinear second-order electron continuity Eq. (2), we first decoupled the equation to obtain a system of two first-order equations. This was done by introducing the auxiliary function \(g(x)\), defined as the derivative of electron concentration. Each obtained equation is tested with Lagrange polynomials \({l}_{i}(x)\) of degree 8 at Legendre–Gauss-Lobatto nodes on each elementresulting in the weak formulation of the problem. We expand \({n}_{j}\) and \({g}_{j}\) with the same set of Lagrange polynomials \({l}_{i}\text{:}\)

$$n_{j} \left( x \right) \approx \mathop \sum \limits_{i = 1}^{{N_{p} }} n_{j}^{i} l_{i} \left( x \right), \quad g_{j} \left( x \right) \approx \mathop \sum \limits_{i = 1}^{{N_{p} }} g_{j}^{i} l_{i} \left( x \right)$$
(5)

where \({n}_{j}^{i}\) and \({g}_{j}^{i}, \quad i=1,\dots , {N}_{p}\), are the unknown coefficients to be solved for. The integral on the right-hand side is approximated with the Legendre–Gauss-Lobatto quadrature rule. The Gummel iterative method is applied and the value of recombination in the current iteration is computed using the values of \(n(x)\) from the previous iteration.

Each expansion is defined on a single element and is connected to other expansions defined on the neighboring elements, resulting in a piecewise continuous function with discontinuities at the interface. The numerical flux \({[f]}^{*}\) is a function that provides the unique value of \(f\) (\(f=f(n\left(x\right),g(x)\)) by combining information from both elements, to be used at the interface. The choice of the numerical flux should correspond to the physical model. At boundary interfaces, the numerical flux is replaced with the corresponding BCs. For more details see Hesthaven and Warburton (2008). Based on the choice of the numerical flux we created two DG models.

In the DGLF model the LF numerical flux was chosen for the drift term (Chen and Bagci 2020):

$$\left[ {\mu_{n} E_{f} n} \right]_{LF} = \mu_{n} E_{f} \frac{{n^{ + } + n^{ - } }}{2} + \alpha \vec{\user2{n}}\left( {n^{ - } - n^{ + } } \right),$$
$$\alpha = \frac{1}{2}\max \left\{ {\left| {\mu_{n} E_{f} n^{ - } \left| , \right|\mu_{n} E_{f} n^{ + } } \right|} \right\},$$
(6)

and for the diffusion term the local DG (LDG) flux was used, for both electron and hole models:

$$\left[ n \right]_{1} = \frac{{n^{ + } + n^{ - } }}{2} + \frac{1}{2}\left( {n^{ - } - n^{ + } } \right),$$
(7)
$$\left[ g \right]_{2} = \frac{{g^{ + } - g^{ - } }}{2} - \frac{1}{2}\left( {g^{ - } - g^{ + } } \right).$$
(8)

Here \({f}^{+} ({f}^{-})\) denotes the value of the function on the outside (inside) of the element \({I}_{j}\), and \(\overrightarrow{{\varvec{n}}}\) denotes outward unit vector normal to the boundary of the \({I}_{j}\). In one dimension it is \(\overrightarrow{{\varvec{n}}}=1\) or \(\overrightarrow{{\varvec{n}}}=-1\).

In the DGSG model the numerical flux in Eq. (7) was based on the exponentially fitted scheme, also known as the SG flux, based on (Kumar 2017):

$$\left[ {\mu_{n} E_{f} n\left( x \right) + D_{n} g\left( x \right)} \right]_{SG} = \frac{{D_{n} }}{h}\left( {B\left( { - \frac{{\mu_{n} E_{f} }}{{D_{n} }}h} \right)n\left( {x + \frac{h}{2}} \right) - B\left( {\frac{{\mu_{n} E_{f} }}{{D_{n} }}h} \right)n\left( {x - \frac{h}{2}} \right)} \right)$$
(9)

Here \(h\) is the length of the element \({I}_{j}\) and \(B\left(x\right)=\frac{x}{{e}^{x}-1}\) is the Bernoulli function. In Eq. (8) the LDG flux is chosen, as in the DGLF model.

3 Results and discussions

The Jn–V and Jp–V curves were calculated based on \(n(x)\) and \(p(x)\) obtained from the Eqs. (1) and (2) solved by FDMSG, DGLF, and DGSG numerical methods in the wide range of SRVs. The parameters used in calculations were the same as for P3HT:PCBM based solar cell given in (Khalf et al. 2020a). It was assumed that the drift current density is dominant at both electrode contacts so the SRVs were compared to the average drift velocity of electrons and holes \(\langle {v}_{drift}^{n\left(p\right)}\rangle ={\mu }_{n\left(p\right)}\langle E\rangle\), \(\langle E\rangle ={V}_{bi}/2d\). From this assumption, the — sign was attributed to \({S}_{p0}\) and \({S}_{pd}\) in Eq. (3) and the + sign to \({S}_{n0}\) and \({S}_{nd}\) in Eq. (4). The SRVs values varied from \(0.002\cdot \langle {v}_{drift}^{n\left(p\right)}\rangle\) to \(500\cdot \langle {v}_{drift}^{n\left(p\right)}\rangle\). We analyzed three different cases: (1) large SRV (\(500\cdot \langle {v}_{drift}^{n\left(p\right)}\rangle\)) applied at \(x=0\), while SRV at \(x=d\) was varied; (2) SRV at \(x=d\) large (\(500\cdot \langle {v}_{drift}^{n\left(p\right)}\rangle\)) and the SRV at \(x=0\) was varied; (3) SRVs at both contacts were assumed to be the same and they were varied simultaneously (see Table 1, for example).

Table 1 The instability SRV intervals (grey shaded areas) for the FDMSG, DGLF, and DGSG Jn–V calculations for electrons in three different cases
Full size table

In certain SRV intervals the FDMSG, DGLF, and DGSG calculations were unstable. The ranges of instability for three numerical models are presented in Table 1 for electrons and Table 2 for holes.

Table 2 The instability SRV intervals (grey shaded areas) for the FDMSG, DGLF, and DGSG Jp–V calculations for holes in three different cases
Full size table

In Figs. 1 and 2, respectively, the Jn–V and Jp–V curves obtained with FDMSG, DGLF, and DGSG for some characteristic SRV values indicated in Tables 1 and 2 are depicted. Based on Tables 1 and 2 it can be concluded that for any SRV value from the range in which SRVs were varied at least one numerical model provides a solution. It can be deduced from Figs. 1 (a3), (b2), (b3), (c3) and 2 (a3), (b2), (b3), (c3) that FDMSG and DGLF, when they converge, lead to almost the same Jn–V and Jp–V characteristics. On the contrary, the DGSG model in some cases gives a solution that deviates from the other two as shown in Fig. 1(b1) and (c1). The mathematical analysis of the accuracy of the applied numerical methods, which is planned to be done in the future, should indicate the right solution. It was noticed that for SRV values in the vicinity of the instability interval all numerical models give unreliable results. The example is shown in Fig. 1 (b2) and Fig. 2(b2) for the DGSG model.

Fig. 1
figure 1

The FDMSG, DGLF, and DGSG simulated Jn–V characteristics at three characteristic SRVs for the case when (a) \({S}_{n0}=500\cdot \langle {v}_{drift}^{n}\rangle\) and \({S}_{nd}\) is variable, (b) \({S}_{n0}\) is variable and \({S}_{nd}=500\cdot \langle {v}_{drift}^{n}\rangle\), and (c) \({S}_{n0}={S}_{nd}\) is variable

Full size image
Fig. 2
figure 2

The FDMSG, DGLF, and DGSG simulated Jp–V characteristics at three characteristic SRVs for the case when (a) \({S}_{p0}=500\cdot \langle {v}_{drift}^{p}\rangle\) and \({S}_{p0}\) is variable, (b) \({S}_{p0}\) is variable and \({S}_{pd}=500\cdot \langle {v}_{drift}^{p}\rangle\), and (c) \({S}_{p0}={S}_{pd}\) is variable

Full size image

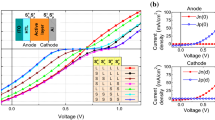
When large SRVs (\(500\cdot \langle {v}_{drift}^{n\left(p\right)}\rangle\)) were applied at both contacts electrodes behaved as ideally conductive (ideally Ohmic) (Sandberg et al. 2017) and all numerical methods showed good stability and give approximately the same solution (Fig. 3a and b). The DDM with DGSG numerical approach was used to calculate the J–V characteristics of ITO/PEDOT:PSS/P3HT:PCBM/Al solar cell. The overall current density was determined as \({J=J}_{n}+{J}_{p}\) and compared to the measured J–V curve (Jelić et al. 2014) in Fig. 3c. A very good agreement between theory and experiment was accomplished which validates the model and puts it in the physical context.

Fig. 3
figure 3

The FDMSG, DGLF, and DGSG simulated (a) Jn–V with \({S}_{n0}={S}_{nd}=500\cdot \langle {v}_{drift}^{n}\rangle\), and (b) Jp–V characteristics with \({S}_{p0}={S}_{pd}=500\cdot \langle {v}_{drift}^{p}\rangle\). (c) The DGSG simulated J–V characteristic where \(J={J}_{n}+{J}_{p}\) compared to the measured J–V curve of ITO/PEDOT:PSS/P3HT:PCBM/Al solar cell

Full size image

It should be mentioned that for several voltage values around open circuit voltage \({V}_{oc},\) even in the case of ideally conductive electrodes (large SRVs), numerical models didn’t give results (the calculation diverged). The number of voltage values in which it wasn’t possible to find a solution was greater when \(\mu {E}_{f}\) product was smaller (this product was an order of magnitude smaller for holes than for electrons in our calculations). Also, for the DGLF model number of critical voltage points was greater than for FDMSG and DGSG. The DGSG model for electrons was stable for all voltages. The Jn(p)–V curves could be unambiguously interpolated in this narrow zone near the voltage axis which was done for curves presented in Fig. 3. For each numerical model separately, the calculations that diverged at more voltage points than the calculations shown in Fig. 3 were considered unstable.

In further investigation, by detailed analysis of simulated Jn(p)–V data it was noticed that for each numerical approach there is an interval of low SRVs in which the obtained solution was always the same. A similar interval of high SRVs was also observed. This is very much in accord with OSCs contact physics (Khalf et al. 2020b; Sandberg et al. 2017) from which it is known that for \(SRV\ll {v}_{drift}^{n\left(p\right)}\) contact acts as ideally blocking and for \(SRV\gg {v}_{drift}^{n\left(p\right)}\) contact behaves as ideally conductive. The SRV ranges in which contacts exhibit (1) ideally blocking, (2) neither blocking nor conductive, and (3) ideally conductive behavior for FDMSG, DGLF, and DGSG are presented in Fig. 4. Instability ranges for each considered numerical method (the union of appropriate three rows from Tables 1 and 2 are shown as shaded areas in Fig. 4.

Fig. 4
figure 4

The SRV intervals obtained using FDMSG, DGLF, and DGSG numerical methods in which the contact act as ideally blocking, neither blocking nor conductive, and ideally conductive for (a) electrons, and (b) holes. Crisscrossed areas denote the SRV ranges in which calculations were unstable

Full size image

It is clear from Fig. 4 that the DGSG numerical approach showed the best stability, much better than the often-used FDMSG method. Also, it should be noticed that the SRV ranges for which instabilities occur in the DGSG and FDMSG cases nearly complement each other. It is very important to state that the DGSG method can be further improved by e. g. implementation of inhomogenous SG numerical flux (Kumar et al. 2017), but that the FDMSG numerical scheme does not provide an opportunity for further improvement. The DGLF method proved to be the worst in terms of stability. The DDM calculations of the Jn–V and Jp–V curves performed with the DGLF method when the — sign is attributed to \({S}_{p0},\) and the + sign to \({S}_{pd}\), along with the + sign taken for \({S}_{n0}\) and the — sign for \({S}_{nd}\), and showed a much greater stability (Ćirović et al. 2021). It was noticed that the SRV signs had a significant impact on the calculation stability for all three numerical methods considered in this paper which will be a topic of future research.

4 Conclusion

The simplified DDM model under the assumption of constant electric field and with decoupled hole and electron continuity equations was solved with three different numerical approaches: FDMSG, DGLF, and DGSG. The Robin-type BCs were applied accounting for surface recombination and thermal injection of holes and electrons at both electrodes. The most often used FDMSG method showed significant instabilities in the wide range of SRVs. Therefore, the DGLF method for stability improvement was proposed. Since this method showed even less stability, the DGSG numerical approach was introduced. The DGSG method proved to be much more stable compared to previous methods. The SRV intervals for which the contacts were acting as (1) ideally blocking, (2) neither blocking nor conductive, and (3) ideally conductive were defined with each of three numerical methods considered in this paper. Also, the SRV ranges in which instabilities occur were determined for the FDMSG, DGLF, and DGSG methods. The DDM simulated J-V characteristics using DGSG numerical approach very well reproduced the measured ones for the ITO/PEDOT:PSS/P3HT:PCBM/Al solar cell. It was shown that the SRVs signs had a significant impact on calculation stability regardless of the applied numerical method. This will be the subject of future investigations. Also, a further improvement of the DGSG method will be considered in the future.