1 Introduction

Surface plasmons (SPs) are the collective oscillation of free electrons at the metal–dielectric interface and evanescently confined in the perpendicular direction (Ritchie 1957; Raether 1988; Maier 2007). The coupling of electromagnetic field and propagation of coherent charge density oscillations along the boundary between metal and dielectric is a well-known physical effect, denoted as the surface plasmon resonance (SPR) (Homola 2006; Liedberg et al. 1983). Due to this reason, various techniques of coupling are always the interest of researchers. The commonly used coupling techniques are prism coupling (Kretschmann and Raether 1968; Chen and Chen 1981; Jha and Sharma 2009), grating coupling (Cai et al. 2008; Dhibi et al. 2015, 2016a, b), tapered film coupling (Tien and Martin 1971) and fiber-optic coupling (Sharma and Gupta 2007; Perrotton et al. 2011; Gentleman and Booksh 2006; Kort and Bernhard 2015).

The SPR phenomenon has many applications such as the sensors (Homola 2006; Liedberg et al. 1983; Jha and Sharma 2009; Cai et al. 2008; Dhibi et al. 2015, 2016a; Sharma and Gupta 2007; Perrotton et al. 2011; Gentleman and Booksh 2006; Kort and Bernhard 2015). Since the first application of SPR in gas sensing (Liedberg et al. 1983), many research articles have been reported, for example, on chemical, biochemical and organic sensing, real-time detection of the concentration and variety of biological molecules, biomedicine and accurate and precise detection of other biomedical agents (Homola 1997; Salamon et al. 1997; Jung et al. 1998; Homola et al. 1999; Peng et al. 2013; Hasan et al. 2018; Zhou et al. 2018; Islam et al. 2018; Bijalwan and Rastogi 2018). Peng et al. proposed an SPR sensor consists of metallic nanowire grating deposited on a substrate positioned upside down above a conventional Kretschmann configuration at a certain distance. The proposed design found for chemical gas detection (Peng et al. 2013). Recently, Hasan et al. (2018) employed a novel niobium nanofilm sensor. The proposed niobium nanofilm based sensor can be potentially implemented in biochemical and organic chemical sensing. Zhou et al. (2018) developed a photonic crystal fiber (PCF) sensor based on SPR. This sensor can be used for real-time detection of the concentration and variety of biological molecules. Bijalwan and Rastogi (2018) proposed an SPR sensor based on a bimetallic diffraction grating for the detection of hemoglobin concentration in human blood. Moreover, it has been known from a large number of publications that many physical and chemical factors affect the SPR phenomenon. One significant factor is the temperature of the sensing environment. Hence, the effects from temperature variation may affect the performance of SPR sensor. However, Chiang et al. (2001) presented a self-contained model of the effect of temperature on the sensitivity of a prism-based SPR sensor. Hence, he used Drude model for making the modeling feasible on a purely theoretical basis. Here, only the temperature dependence of the metal properties was considered. Sharma and Gupta (2006) studied theoretically the effect of temperature on the sensitivity and signal-to-noise ratio (SNR) of a fiber-optic-based SPR sensor. They used gold and silver fiber-optic sensors. Thus, both the temperature dependences of the dielectric and metal properties were considered. These sensors show almost the same variation in SNR and sensitivity with temperature.

In this work, we have theoretically studied the effect of temperature on the performance of an SPR sensor. We used gold and silver grating sensors based on SPR. We have analyzed the effect of temperature on the sensitivity, the detection accuracy (DA) and quality parameter (χ) using numerical simulations based on rigorous coupled wave analysis (RCWA) (Moharam et al. 1995). Further, the sensitivity, DA and χ are compared is carried out for the two most commonly used metals (silver and gold).

2 Rigorous coupled-wave analysis for one-dimensional grating

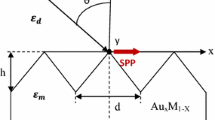
Figure 1 shows the schematic of grating-coupled surface plasmon resonance (GCSPR) sensors. The sensors consist of metal (gold or silver) grating of period d, depth h, width of the metal strip \(\Lambda\) and filling ratio f (\(= \frac{\Lambda }{d}\)) deposited on metal film (gold or silver) and a analyte of refractive index na placed on the top of the grating. Grating parameters chosen for numerical simulations are grating period d = 0.5 µm, grating depth h = 0.03 µm and filling ratio f = 0.5. As is well known, the most effective way to model the reflectivity (R) of the GCSPR is to use the RCWA method. In this approach, we start by analyze the magnetic wave propagation in the first region for p polarization. So, the normalized incident magnetic field in region I can be expressed as

$$H_{inc,y} = \exp ( - jk_{0} n_{a} (\sin (\theta )x + \cos (\theta )z),$$
(1)

where \(k_{0} = \frac{2\pi }{{\lambda_{0} }}\) with \(\lambda_{0}\) is the free-space wavelength, \(n_{a}\) is the refractive index of region I, \(\theta\) is the incidence angle and \(j = \sqrt { - 1}\).

Fig. 1
figure 1

Illustration of SPR sensors based on metallic diffraction grating

Full size image

In both homogeneous regions I (z < 0) and II (z > h), the normalized fields may be written as

$$H_{I,y} = H_{inc,y} + \sum\limits_{i} {R_{i} \exp \left( { - j\left( {k_{i}^{x} x - k_{i}^{Iz} z} \right)} \right),}$$
(2)
$$H_{II,y} = \sum\limits_{i} {T_{i} \exp \left( { - j\left( {k_{i}^{x} x - k_{i}^{IIz} (z - h)} \right)} \right),}$$
(3)

where the quantity \(k_{i}^{x}\) is the x component of the wave vectors. It is determined from the vector Floquet condition and is given by

$$k_{i}^{x} = k_{0} \left( {n_{a} \sin (\theta ) + i\left( {\frac{{\lambda_{0} }}{d}} \right)} \right),$$
(4)

and where the z components can be expressed as

$$k_{i}^{Lz} = \sqrt {\left( {(k_{0} n_{L} )^{2} - (k_{i}^{x} )^{2} } \right)} ,\;{\text{with}}\;L = I,II,$$
(5)

\((R_{i} )\) is the magnetic-field amplitude of the ith reflected (backward-diffracted) wave in region I, and \((T_{i} )\) is the magnetic-field amplitude of the ith transmitted (forward-diffracted) wave in region II.

In the grating region (0 < z < h) the periodic permittivity is represented in a Fourier series of the form

$$\varepsilon (x) = \varepsilon (x + d) = \sum\limits_{p} {\varepsilon_{p} \exp \left( {j\frac{2\pi px}{d}} \right)} ,$$
(6)

where \(\varepsilon_{p}\) is the pth Fourier component of the relative permittivity in the grating region.

In the modulated region (0 < z < h) the tangential magnetic (Hy) and electric (Ex) fields may be written as

$$H_{y} = \sum\limits_{i} {\Omega_{i}^{y} (z)\exp \left( { - jk_{i}^{x} x} \right)} ,$$
(7)
$$E_{x} = j\left( {\frac{{\mu_{0} }}{{\varepsilon_{0} }}} \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} \sum\limits_{i} {\Psi_{i}^{x} (z)\exp \left( { - jk_{i}^{x} x} \right)} ,$$
(8)

where \(\varepsilon_{0}\) and \(\mu_{0}\) are the permittivity and the permeability of free space. \(\Omega_{i}^{y} (z)\) and \(\Psi_{i}^{y} (z)\) are the normalized amplitudes of the ith space-harmonic fields.

Using Maxwell’s equations, we find that the set of coupled wave equations for the electromagnetic fields, in matrix form, is

$$\left[ \begin{aligned} {{\partial \Omega^{y} } \mathord{\left/ {\vphantom {{\partial \Omega^{y} } {\partial \left( {z^{\prime } } \right)}}} \right. \kern-0pt} {\partial \left( {z^{\prime } } \right)}} \hfill \\ {{\partial \Psi^{x} } \mathord{\left/ {\vphantom {{\partial \Psi^{x} } {\partial \left( {z^{\prime } } \right)}}} \right. \kern-0pt} {\partial \left( {z^{\prime } } \right)}} \hfill \\ \end{aligned} \right] = \left[ {\begin{array}{*{20}c} 0 & A \\ B & 0 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\Omega^{y} } \\ {\Psi^{x} } \\ \end{array} } \right],$$
(9)

where \(z^{\prime } = k_{0} z\), \(A\) is the matrix formed by the permittivity harmonic components and \(B\) is the matrix given by

$$B = K^{x} A^{ - 1} K^{x} - I,$$
(10)

where \(K^{x}\) is a diagonal matrix whose elements equal \({\raise0.7ex\hbox{${k_{i}^{x} }$} \!\mathord{\left/ {\vphantom {{k_{i}^{x} } {k_{0} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${k_{0} }$}}\) and \(I\) is the identity matrix. Noted that B, A, \(K^{x}\), and I are (n × n) matrices, where n is the number of harmonics retained in the field expansion. By eliminating \(\psi^{x}\), Eq. (9) can be reduced to

$$\left[ {{{\partial \Omega^{y} } \mathord{\left/ {\vphantom {{\partial \Omega^{y} } {\partial \left( {z^{\prime } } \right)}}} \right. \kern-0pt} {\partial \left( {z^{\prime } } \right)}}} \right] = \left[ {AB} \right]\left[ {\Omega^{y} } \right],$$
(11)

By diagonalizing AB, the decomposition of eigenvalues and the eigenvectors is able to be carried out more efficiently. Then the solution can be written as follows

$$\Omega_{i}^{y} (z) = \sum\limits_{m - 1}^{n} {w_{i,m} \left\{ {C_{m}^{ + } \exp ( - k_{0} q_{m} z) + C_{m}^{ - } \exp \left[ {k_{0} q_{m} (z - h)} \right]} \right\},}$$
(12)
$$\Psi_{i}^{x} (z) = \sum\limits_{m - 1}^{n} {v_{i,m} \left\{ { - C_{m}^{ + } \exp ( - k_{0} q_{m} z) + C_{m}^{ - } \exp \left[ {k_{0} q_{m} (z - h)} \right]} \right\}.}$$
(13)

where \(w_{i,m}\) is the (i, m)’th element of the eigenvector matrix W and \(q_{m}\) is the positive square root of the eigenvalues of the matrix AB. The quantities \(v_{i,m}\) are the (i, m)’th elements of the product matrix \(V = A^{ - 1} WQ\), with Q being a diagonal matrix with the diagonal elements \(q_{m}\). The quantities \(C_{m}^{ + }\) and \(C_{m}^{ - }\) are unknown constants to be determined from the boundary conditions

The coupled-wave equations can be solved by setting up boundary value conditions of the tangential electric and magnetic field components. With the normalized magnetic field amplitudes of the reflected wave, reflectivity in each diffraction order can be calculated.

3 Coupling of the incident field and the SP

When the grating is illuminated by a p-polarized plane wave of a wavelength λ = 632.8 nm, at some particular incident angle, the SP starts propagating at the metal–dielectric interface. It is due to the coupling of the incident field and the coherent charge density oscillations at the interface. When, the wave vector of the SP is coincident with the wave vector of the incident electromagnetic radiation, a sharp dip in the reflectance spectrum is shown Fig. 2a. This is an SPR condition. Therefore, the coupling condition is given by

$$k_{i}^{x} = k_{0} \left( {n_{a} \sin \left( {\theta_{res} } \right) + i\left( {\frac{{\lambda_{0} }}{d}} \right)} \right) = \pm \text{Re} \left( {\sqrt {\frac{{n_{I}^{2} \varepsilon_{m} }}{{n_{I}^{2} + \varepsilon_{m} }}} } \right),$$
(14)

where \(\varepsilon_{m}\) is the metal permittivity, \(\theta_{res}\) is the resonance angle at which coupling occurs and “\(i = 0, \pm 1 \ldots ..\)” is the diffraction order.

Fig. 2
figure 2

a Illustration of the angular SPR response of the sensor for na1 b for different analytes of refractive indices na1 and na2

Full size image

From Eq. (14), the resonance angle is defined as

$$\theta_{res} = \arcsin \left( {\frac{{ \pm \text{Re} \left( {\sqrt {\frac{{n_{a}^{2} \varepsilon_{m} }}{{n_{a}^{2} + \varepsilon_{m} }}} } \right) - ik_{0} \left( {\frac{{\lambda_{0} }}{d}} \right)}}{{n_{a} k_{0} }}} \right).$$
(15)

It is clear that \(\theta_{res}\) changes with refractive index \(n_{a}\), as shown in Fig. 2b.

4 Performance of grating-based SPR sensors

The SPR sensor’s performance is described by two very important features such as the sensitivity (S) and the detection accuracy (DA). Thus, if the resonance incidence angle is shifted by \(\Delta \theta_{res}\) due to increase in refractive index by \(\Delta n_{a}\) (Temperature by \(\Delta T\)), then the sensitivity is defined as (Roh et al. 2011)

$$S_{\theta } = \frac{{\Delta \theta_{res} }}{{\Delta n_{a} }},$$
(16)

On the other hand, the detection accuracy (DA) as given by Brahmachari and Ray (2014) is

$$DA = \frac{1}{FWHM},$$
(17)

Besides the sensitivity and the detection-accuracy, the sensor performance is quantified in other term such as the quality \((\chi )\). It is defined as (Homola et al. 1999)

$$\chi = \frac{{S_{\theta } }}{FWHM}.$$
(18)

5 Thermo-optical metals properties

The frequency-dependent dielectric function of any metal is represented by the Drude formula, i.e.

$$\varepsilon \left( \omega \right) = 1 - \frac{{\omega_{p}^{2} }}{{\omega \left( {\omega + i\omega_{c} } \right)}},$$
(19)

where \(\omega_{p}\) is the plasma frequency given by

$$\omega_{p} = \sqrt {\frac{{4\pi Ne^{2} }}{{m^{*} }}} ,$$
(20)

with \(N\) and \(m^{*}\) are the density and effective mass of the electrons, respectively. Here, assuming that the variation of these two parameters with temperature can be neglected. However, the temperature dependence of plasma frequency can be described by (Sharma and Gupta 2006; Chiang et al. 1998, 2000)

$$\omega_{p} = \omega_{p0} \left[ {1 + \gamma_{e} \left( {T - T_{0} } \right)} \right]^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} ,$$
(21)

where \(\gamma_{e}\) is the thermal linear expansion coefficient of the metal, \(T_{0}\) is the room temperature acting as the reference temperature and \(\omega_{p0}\) is the plasma frequency at \(T_{0}\).

On the other hand, \(\omega_{c}\) is collision frequency that comes from two factors: phonon–electron scattering \(\omega_{cp}\) and electron–electron scattering \(\omega_{ce}\). Hence, the combined effect of the two gives

$$\omega_{c} = \omega_{cp} + \omega_{ce} ,$$
(22)

The temperature dependence of phonon-electron scattering is accounted by the following Holstein’s model (Chiang et al. 1998, 2000; Holstein 1954):

$$\omega_{cp} \left( T \right) = \omega_{0} \left[ {\frac{2}{5} + 4\left( {\frac{T}{{T_{D} }}} \right)^{5} \int_{0}^{{{{T_{D} } \mathord{\left/ {\vphantom {{T_{D} } T}} \right. \kern-0pt} T}}} {\frac{{z^{4} dz}}{{e^{z} - 1}}} } \right],$$
(23)

where \(\omega_{0}\) is a constant that must be calculated with care and \(T_{D}\) is the Debye temperature.

In addition, the Lawrence’s model provides the temperature dependence of electron–electron scattering given by (Lawrence 1976)

$$\omega_{ce} \left( T \right) = \frac{1}{6}\pi^{4} \frac{\Gamma \Delta }{{hE_{F} }}\left[ {\left( {k_{B} T} \right)^{2} + \left( {\frac{h\omega }{{4\pi^{2} }}} \right)^{2} } \right].$$
(24)

where \(E_{F}\) is the Fermi energy, \(h\) is the Fermi constant, \(\Gamma\) is a constant giving the average over the Fermi surface of the scattering probability, \(\Delta\) is the fractional scattering and \(k_{B}\) is the Boltzmann constant. For gold and silver, the values of these parameters are summarized in Table 1 (Sharma and Gupta 2006; Chiang et al. 1998, 2000). The values of the real part and the imaginary part of the metal–dielectric function with temperature for gold and silver are given in Table 2.

Table 1 Gold and silver parameters used for the numerical simulation
Full size table
Table 2 The real part and the imaginary part of the metal–dielectric function with temperature for gold and silver
Full size table

6 Results and discussion

Figure 3 gives the SPR curves of reflectivity depending on the incident angle at room temperature T = 300 K. Two very important key features may be noted from these curves. The resonance angle and the full width at half maximum (FWHM) of the SPR curves. These two features are more susceptible to the value of the complex dielectric constant of the metal given by Eq. (19). The real part of the dielectric constant determines the SPR position and the imaginary part determines the bandwidth (Jha and Sharma 2009; Su et al. 2012; Yuk et al. 2014). We observe reflectance dips with close resonance angles. This is due to the similar values of the real part of Au and Ag at the room temperature. In the other hand, an important observation is that there is not much difference between the FWHM of SPR curves corresponding to Au and Ag. This is due to the small difference in the imaginary part of the dielectric constant of pure metals.

Fig. 3
figure 3

Variation of reflectivity with incidence angle at room temperature T = 300 K. Here, the refractive index of analyte na = 1.35

Full size image

Figure 4a, b, respectively, show how the SPR curve between reflectivity and incident angle varies with temperature. Two main factors may be noted from these curves. First, with an increase in temperature the resonance angle shifts to the higher side. The results are shown in Table 3. Second, the SPR curve broadens with the increase in temperature. This can be understood from the increase in plasma frequency and increase in collision frequency in the Drude model as the temperature increases (Sharma and Gupta 2006). The variations of these two parameters cause a variation of the metal–dielectric function with temperature according to Eq. (19). Hence, the combined effect of the above two factors on the real part and the imaginary part of the metal–dielectric function appears in the shifting of the resonance condition and the broadening of the SPR curve. For a good sensor, this shift should be large and FWHM should be small.

Fig. 4
figure 4

Effect of temperature on the surface plasmon resonance (SPR) phenomenon: a gold and b silver

Full size image
Table 3 Temperature effect on the resonance angle of gold and grating-based SPR sensor
Full size table

In Fig. 4, we see that the SPR spectra with bigger temperature have larger FWHM. For discussion, we have plotted the variation of FWHM with temperature for two different metal sensors: silver and gold as shown in Fig. 5a. We observe that FWHM increases with increasing temperature. This effect of temperature on FWHM can be explained in terms of the permittivity. Indeed, when we vary the temperature, the real part of the permittivity changes. This temperature dependent permittivity is the reason for increasing FWHM.

Fig. 5
figure 5

aFWHM and b detection accuracy versus different temperature of gold and silver

Full size image

The broadening of the SPR curve is very important feature within the context of detection accuracy (DA) of the SPR sensor. Figure 5b shows the variation of DA with temperature. It is very clear that the silver has a larger DA than gold. Also, the variation in DA with temperature is more evident in silver. As the temperature T varies from 300 to 800 K, DA decreases from 1.169 to 0.710 deg−1 in the case of gold grating-based SPR sensor, whereas for silver grating-based SPR sensor the DA decreases from 1.385 to 0.809 deg−1. This result allows one to understand that the increase of temperature can further deteriorate the detection accuracy of the sensor.

Figures 6 and 7 provide the reflectance spectra of the gold and silver grating-based SPR sensor for analyte refractive indexes between 1.35 and 1.40 with different temperature. The results show that the position of the resonant angle is affected by the varying of analyte RI. The resonance dips shift to the longer angles with the analyte RI increase. But the FWHM is unchanged when varying the analyte RI. Tables 4 and 5 describes the changes in the resonance peak positions (\(\Delta \theta_{res}\)) and variations of the analyte refractive indexes (\(\Delta n_{a}\)) for different temperature. As temperature increases, but the changes in the resonance peak positions does not change. Therefore \(\Delta \theta_{res}\) is independent of the temperature. This is due to the well-established fact that \(\varepsilon_{mr}\) varies relatively insignificantly with T compared to the imaginary part of the dielectric function for metals (Leung et al. 1996).

Fig. 6
figure 6

Angular SPR curves of gold with six different refractive indices of analyte

Full size image
Fig. 7
figure 7

Angular SPR curves of silver with six different refractive indices of analyte

Full size image
Table 4 Temperature effect on the performance of gold grating-based SPR sensor
Full size table
Table 5 Temperature effect on the performance of silver grating-based SPR sensor
Full size table

Besides the detection-accuracy (DA), the sensor performance is quantified in other terms; the sensitivity (S) and the quality (χ). Mathematically, the sensitivity is calculated by Eq. (16). From Eq. (16), and Figs. 6 and 7, the variation of sensitivity with temperature is listed in Tables 6 and 7. As is clear from the results, we find that the sensitivity of gold and silver grating-based SPR sensors is very stable with the change of temperature. It may be noted that the theoretical results are in reasonable agreement with the literature one (Chiang et al. 2001; Sharma and Gupta 2006). Further, increases of the temperature decreases the quality of proposed sensors, as expected from Eq. (18). It decreases to 37.55 RIU−1 and 43.04 RIU−1 for the case of gold grating-based SPR sensor and silver grating-based SPR sensor, respectively. So we cannot improve the sensitivity and the quality of grating-based SPR sensor by increases the temperature. On the other hand, the resonant angles were plotted as a function of the sensing refractive index for different temperature in Figs. 8 and 9. It could be observed from that the resonance angle increases linearly as analyte index increases. This is show a good linearity and stability of the gold and silver grating- based SPR sensors response, respectively.

Table 6 Temperature effect on the performance of gold grating-based SPR sensor
Full size table
Table 7 Temperature effect on the performance of silver grating-based SPR sensor
Full size table
Fig. 8
figure 8

Linear regression analysis between resonance angle and refractive index of analyte for gold

Full size image
Fig. 9
figure 9

Linear regression analysis between resonance angle and refractive index of analyte for silver

Full size image

7 Conclusions

In this paper, we have analyzed in detail the temperature dependence of the performance of a 1D grating sensor based on surface plasmon resonance. The sensor performance has been presented in terms of the detection accuracy (DA), the sensitivity S and the quality parameter (χ). We have used two sensors with different metals, namely gold and silver. Silver provides large values of DA, S and χ compared to gold. As far as the temperature dependence is concerned, there is not much difference in the sensor’s performance. Both metals show almost the same variation in DA, S and χ with temperature. However, best performance has been obtained for sensor consists of Ag at the room temperature T = 300 K.