1 Introduction

Glasses doped with nanosized inclusions of metals or semiconductors are known since a very long time. The first glasses containing metal nanoparticles were fabricated by Roman glassmakers in the fourth century A.D. Mediaval cathedral windows through several European countries witness the attention drawn by stained glasses containing metal aggregates as artistic work (Poole et al. 2003). They exhibit great varieties of beautiful colors owing to the nanosized metal particles which were embedded in the glass matrix.

Semiconductor-doped glasses were, however, not so widespread used. One very important application of semiconductor-doped glasses are sharp cut-off glass filters. In most cases, Cd (Sx,Sex) nanocrystals are used for this purpose. By varying × the position of the cut-off wavelength can be precisely tuned between ~ 400 and 1000 nm.

These glass filters are easily available from different glassmakers, such as Schott, Corning, Hoya, or Toshiba. This is an import point, as it allowed a great number of optics groups to study this kind of composite material without the need for skills in material preparation.

From technological perspective, CdSe nanoparticles are of significant interest because of their unique quantum confinement properties, bright photoluminescence, narrow emission band, and photostability (Srivastava and Singh 2012). CdSe-polymer nanocomposites find potential applications in the fabrication of devices like photovoltaic cells, laser, thin film transistors, light emitting diodes (Yu et al. 2006; Oertel et al. 2005), catalysis (Ahmadi et al. 1996) and biological fluorescence labels (Bruchez et al. 1998; Chan and Nie 1998). In particular, CdSe nanocrystals have been proposed as working elements for nanotransistors (Klein et al. 1997), electrohromic materials (Wang et al. 2001), and charge-coupling devices (Woo et al. 2002).

In the present paper we studied photoluminescence characteristics of CdSe quantum dots in glass matrix along with investigating surface morphology of the system using AFM measurements.

2 Experimental details

CdSe nanoparticles embedded in transparent silicate-based glasses was successfully fabricated by a novel technique consisting in joined utilization of the thermal annealing below glass crystalization temperature, and the UV continuous wave laser irradiation (Argon laser at 244 nm). This innovative fabrication method exploits adapted combination of thermal annealing and UV laser power density that allows controlling the spatial localization of the nanocrystals formation inside the glass sample. The originality of the technique is that the required thermal energy needed for the precipitation of CdSe into crystals is brought by thermal annealing in association to UV absorption, which leads to the control of the spatial crystallization. Further information about samples fabricating can be found elsewhere (Mekhlouf et al. 2007).

The surface morphology of our sample was investigated by atomic force microscopy (AFM). AFM imaging was done using the NTEGRA Prima system from NT MDT. AFM measurements were performed at room temperature and under ambient conditions.

The UV–VIS absorbance spectrum was recorded on the room temperature in the wavelength range 200–800 nm on a Shimadzu UV-2600 spectrophotometer equipped with an integrated sphere. The absorbance spectrum was measured relative to a reference sample of BaSO4.

Photoluminescence measurements on room temperature were obtained by Jobin-Yvon U1000 spectrometer equipped with RCA-C31034A photomultiplier with housing cooled by Peltier element, amplifiers and counters. As an excitation sources, the 488 and 514.5 nm lines of Argon laser were used.

3 Results and discussion

3.1 Results of AFM surface characterization

The surface morphology of our sample was investigated by atomic force microscopy, in order to determine the general cell wall structure, together with the assembly of particular components into the wall structure as a whole. Areas of 2 × 2 and 5 × 5 µm were investigated, and AFM images of our sample are presented in Fig. 1a, b. From Fig. 1 it is clear that the sample is packed and continuous without the presence of porosity and voids. The surface is rather smooth with no cracks observed. The small islands of several nm to several tenths of nm in diameter are distinguished, which corresponds to the nanoparticles of CdSe. According to the height bars at the right side of Fig. 1a, b, the surface height of our sample is up to 14 nm. Figure 1c, d show the histograms of the nanostructure height in 2 × 2 and 5 × 5 µm areas of AFM images, respectfully. The sample exhibits an ensemble of nanostructures with an average height of (4.9 ± 0.2) nm for chosen area of 2 × 2 µm, and (6.4 ± 0.2) nm for 5 × 5 µm area.

Fig. 1
figure 1

2D AFM images and histograms of CdSe nanoparticles embeded in transparent silicate-based glasses, a 2 × 2 µm image, b 5 × 5 µm image, c 2 × 2 µm histogram, d 5 × 5 µm histogram

Full size image

3.2 Optical characterization: photoluminescence and UV–VIS absorbance measurements

UV–VIS absorbance spectrum of our sample is presented in Fig. 2. The position of the first optical transition is at 520 nm. The position of a peak is related to the size of the absorbing nanocrystal and to the band gap. The average size of the nanocrystal of interest can be obtained using the relation (Yu et al. 2003):

Fig. 2
figure 2

UV–VIS absorbance spectrum of CdSe QDs

Full size image
$$D\; = \;1.6122 \, \times \, 10^{ - 9} \times \, \lambda^{4} - \, 2.6575 \, \times \, 10^{ - 6} \times \, \lambda^{3} + \, 1.6242 \, \times \, 10^{ - 3} \times \, \lambda^{2} - \, 0.4277 \, \times \, \lambda \, + \, 41.57$$
(1)

where λ (nm) is the first exciton peak of CdSe absorbance spectrum. From the λ = 520 nm the calculated size of our nanoparticles is 2.6 nm.

There are several approaches in literature to determine the band gap from the absorbance spectra. In the present study we employ the approach of Yu et al. (2003) and Hegazy and Abd (2014) where the Eg is calculated directly from the absorption maximum of the first exciton absorption peak. Using formula

$$E_{g} \; = \;h\nu \; = \;hc/\lambda ,$$
(2)

the obtained band gap is 2.39 eV.

Normally, the absorption of light by CdSe QDs increases with decreasing wavelength (Kongkanand et al. 2008; Debgupta et al. 2014). In present case, we must conclude that the glass matrix modify the spectrum of CdSe QDs—the absorption spectrum of glass matrix: CdSe QDs hybrid composite differ from those of individual components, as in Dayneko et al. (2016) where the CdSe QDs were incorporated in poly[N-9′-heptadecanyl-2,7-carbazole-alt-5,5-(4′,7′-di-2-thienyl-2′,1′,3′-benzothiadiazole)].

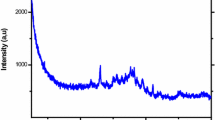
PL spectra of CdSe QDs in glass matrix are presented in Fig. 3. The dominant band in both spectra is very broad and has a maximum at ~ 2.14 eV. Such a broad band implies the existence of vast size distribution of CdSe QDs. We assigned this transition as direct band-to-band transition in CdSe. Due to the Stokes shift, this value is smaller than the band gap observed from absorption spectrum. However, the band gap of bulk CdSe is reported to be 1.75 eV. The observed blue shift of this band is ~ 0.39 eV, and its position can be explained in the following manner.

Fig. 3
figure 3

Photoluminescence spectra of CdSe QDs excited with 488 nm (blue) and 514.5 nm (green) lines of Ar–laser and recorded on the room temperature. (Color figure online)

Full size image

3.3 Model

The single quantum dot we consider is spherical CdSe core surrounded by transparent glass. R is the core radius and the dot center is center of coordinates (Schoss et al. 1994; Kostić and Stojanović 2011). Electron and hole i.e. carriers, in such a system are characterized by their effective masses. In this case m * e and m * h are electron and hole effective masses of CdSe. Rectangular potential through the structure, having in mind that CdSe is surrounded by glass, is assumed as:

$$\begin{array}{*{20}l} {V_{} \left( r \right) = \left\{ {\begin{array}{ll} 0 & \quad {r \le R} \\ \infty &\quad {r > R} \\ \end{array} } \right.} \end{array}$$
(3)

Considering that the carrier spectra are mainly formed by size quantization, the stationary Schrödinger equation for a single particle (electron or hole).

$$\left( { - \frac{{\hbar^{2} }}{{2m_{i}^{ * } }}\nabla^{2} + V(r)} \right)\varPsi (\overrightarrow {r} ) = E_{i} \varPsi_{i} (\overrightarrow {r} ),\;i\; = \;e,\;h$$
(4)

is solved in spherically symmetric potential V(r), described by (3). Separation of radial and angular coordinates leads to \(\varPsi_{lm} (r) = R_{l} (r)Y_{lm} (\theta ,\phi )\). \(R_{l} (r)\) is the radial wave function, and \(Y_{lm} (\theta ,\phi )\) is a spherical harmonic. l and m are orbital and magnetic quantum numbers. For a spherical potential with stepwise constant value 0, in the core, and ∞, outside the core, the radial function \(R_{l} (r)\) is given by:

$$R_{l} \left( r \right) = \left\{ {\begin{array}{ll} {A_{l}^{} j_{l} \left( {k_{} r} \right)} & {r \le R} \\ 0 & {r > R} \\ \end{array} } \right. ,$$
(5)

\(j_{l}\), are Bessel spherical functions. These solutions already satisfy conditions that the wave function is regular when r = 0. Each solution must satisfy boundary conditions. In case of infinitely high potential barrier, wave function does not penetrate into the surrounding medium and must satisfy trivial boundary condition: to be zero at r = R. This trivial boundary condition leads to equation characteristic for each l (l = 0, 1, 2,…). There is series of solutions (eigensolutions i.e. eigenenergies) characteristic for each l. Number n numerates eigenenergies Enl. For an electron Enl shows the energy above core conductive band, and for hole energy below valence band of core material.

As it is common, the lowest energy among solution for each l is numerated as n = 1. Among all states, state l = 0, n = 1 is the lowest energy solution i.e. it is the ground state.

Once the eigenvalues Enl are determined, the coefficients Anl in Eq. (5) are determined by using the normalization condition for Rnl(r), \(\int\nolimits_{0}^{\infty } {R_{nl}^{2} } \left( r \right) \cdot r^{2} dr\; = \;1\). Result of these calculations is the complete information about eigenenergies Enl and corresponding wave functions Rnl(r).

One state can be identified by characteristic energy, denoted as Enl and wave function, denoted as ψnl, or just (n, l). As it is usual all l = 0 states are assigned as s, l = 1 states as p and l = 2 states as d. In all papers l = 0 (s) states are assigned: (l = 0, n = 1) as 1s, (l = 0, n = 2) as 2s, (l = 0, n = 3) as 3s etc. For the l = 1 (p) states, some authors assigned states in the same manner as for l = 0, i.e. (l = 1 n = 1) as 1p, (l = 1, n = 2) as 2p, (l = 1, n = 3) as 3p etc. For the l = 2 (d) states, assignation is: (l = 2 n = 1) is 1d, (l = 2, n = 2) is 2d, (l = 2, n = 3) is 3d etc. In this assignation number in front s, p or d numerates if it is the first, second or higher order solution. It is possible, having in mind wave functions properties, to use hydrogen like assignation: (l = 1 n = 1) is 2p, (l = 1 n = 2) is 3p, (l = 1 n = 3) is 4p…; (l = 2 n = 1) is 3d, (l = 2 n = 2) is 4d, (l = 2 n = 3) is 5d… Hydrogen like assignation is even more desirable if we deal with charged impurities inside QD.

These calculations were performed for electrons and holes in similar procedure, giving the confinement energies \(E_{nl}^{e}\) and \(E_{nl}^{h}\), and wave functions \(R_{nl}^{e}\) and \(R_{nl}^{h}\). Once the electron and hole wave functions are known, radial probability in the system give an illustrative picture, especially in more complex structures, of electron and hole spatial localization.

We focused our analysis to transition between l = 0, n = 1 hole (1sh) and electron (1se) states, because this is the basic interband transition.

From the electron and hole wave functions, the Coulomb interaction of electron and hole can be calculated. In the frame of perturbation theory energy of Coulomb interaction is given by:

$$E_{C} = - e^{2} \int {\int {\frac{{\left| {R^{e} \left( {r_{e} } \right)} \right|^{2} \left| {R^{h} \left( {r_{r} } \right)} \right|^{2} }}{{4\pi \varepsilon \left| {r_{e} - r_{h} } \right|}}} } r_{e}^{2} r_{h}^{2} dr_{e} dr_{h}$$
(6)

ε is the high energy dielectric permittivity.

The transition electronic energy (E10) is sum of the core gap energy, corresponding electron and hole eigenvalues and the Coulomb energy:

$$E_{10} = E_{g} + E_{10}^{e} + E_{10}^{h} + E_{C}^{{}}$$
(7)

The parameters characteristic for CdSe bulk are presented in Table 1. Calculation parameters, effective masses of carriers and dielectric permittivity, are transferred from literature (Kostić and Stojanović 2011; Sahin et al. 2009). Calculated transition energy is presented in Fig. 4.

Table 1 The material parameters used in the calculations
Full size table
Fig. 4
figure 4

1sh–1se interband transition energy in CdSe QD as function on the dot radius

Full size image

Energy of basic interband transition (1sh–1se) in the quantum dots increases as the dimension of the dot decreases. Simple model based on effective mass approximation can estimate transition energy of QD. This energy depends on the dimension of the dot, and parameters of the bulk material like energy gap, dielectric permittivity, and electron and hole effective masses. Due to the very broad band, we consider that trere is an ensemble of quantum dots with a wide range of sizes. As a provisional borders, we used the energy values of FWHM of the band obtained by 514.5 nm laser line, which is less broad than the one obtained with 488 nm. These borders are 1.94–2.32 eV, and corresponding QD dimensions are 2.5–4.2 nm. The band maximum at 2.14 eV corresponds to the QD size of 3.1 nm. These results are in agreement with the calculations for UV–VIS absorbance.

4 Conclusions

The photoluminescence measurements along with AFM measurements of CdSe nanoparticles embedded in transparent glass are presented. The AFM measurements reveal the presence of small islands of several nm in diameter, which correspond to the nanoparticles of CdSe. The UV–VIS absorbance spectrum displayed the first exciton peak at 520 nm. Calculated size of nanoparticles is about 2.6 nm. The PL measurements display one main broad emission band at ~ 2.14 eV which is identified as basic interband transition in CdSe nanoparticle. The energy of basic transition in spherical CdSe quantum dot in effective mass approximation is calculated. Based on this model, the average radius of CdSe QD is found to be ~ 3 nm.