1 Introduction

Two-dimensional (2D) materials are materials that are periodic in two spatial directions but finite in the third, orthogonal direction. These materials gain particular attention after discovery of graphene, a one atom thick layer of carbon atoms arranged in a honeycomb lattice. In contrast to graphene, in which all atoms belong to a single plane, buckled silicene and germanene for example, occupy Wyckoff positions with unequal z-coordinates. Existence of massless electrons whose dynamics is described by Dirac (Weyl) equation is among notable properties of graphene and related, so called Dirac, materials.

Besides Dirac materials, there is another class of 2D materials in which electronic dispersion is Dirac-like (linear) along some direction in the 2D Brillouin zone (BZ), and quadratic along the orthogonal direction. Such semi-Dirac dispersion supports both massless and massive electrons at the same point of the BZ, thus giving rise to highly anisotropic material properties. Using density functional theory (DFT), semi-Dirac dispersion has been predicted in TiO\(_2\)/VO\(_2\) nanostructures (Pardo and Pickett 2009, 2010), in silicene oxide (Zhong et al. 2017) and in square selenene and tellurene (Xian et al. 2017). A tight-binding model show semi-Dirac dispersion in phosphorene under strain for certain critical values of hopping parameters (Duan et al. 2016). First experimental realization of material with semi-Dirac dispersion was reported in 2015. It was demonstrated that few-layer black phosphorus doped with potassium posses semi-Dirac dispersion at the BZ center for certain level of doping (Kim et al. 2015). The behavior of semi-Dirac fermions in external magnetic field and consequences that this dispersion imposes on Klein tunneling is examined in more detail in Banerjee et al. (2009) and Banerjee and Pickett (2012). Evolution of Hofstadter spectrum on a square lattice with the application of an on-site uniaxial staggered potential shows merging of two Dirac points into a semi-Dirac one (Deplace and Montambaux 2010). Analysis of semi-Dirac systems based on DFT show that in some cases, spin-orbit coupling (SOC) can open a small gap and can lead to topologically non-trivial bands, which contribute to non-zero total Chern number (Huang et al. 2015). Such systems are then suitable for demonstration of quantum Hall effect. Analogous conclusion is derived for semi-Dirac systems under laser light illumination (Saha 2016). On the other hand, Narayan (2015) concluded that for semi-Dirac semimetals circularly polarized light does not open a band gap. The influence of electronic correlations on semi-Dirac systems was also investigated. It was found by renormalization group theory, that interplay of Coulomb interaction between electrons and disorder can drive the semi-Dirac system to non-Fermi-liquid behavior (Zhao et al. 2016). Similarly, approximate solution of Schwinger–Dyson equation show that moderate Coulomb interaction can induce excitonic gap opening in semi-Dirac band structure (Wang et al. 2017). Anisotropic properties of semi-Dirac materials have potential applications in electronics (Mannhart and Schlom 2010). For example, a p–n junction made from such material would have negative differential conductance for certain bias voltage (Saha et al. 2017).

Group theory is a powerful tool in predicting various types of electronic dispersions. In some cases mere belonging of a crystal to some space groups, leads unavoidably to certain dispersion. For example, Mañes (2012) has found sufficient conditions for existence of bulk chiral fermions in 3D single crystals and has provided a list of space groups that host such dispersion in the vicinity of given points of the BZ. The non-symmorphic space group \(P2_12_12_1\) (No. 19 in notation of Hahn 2005) belongs to Mañes list. Geilhufe et al. (2017) have searched the Organic Materials Database and have found six compounds that belong to this space group and in addition have only Dirac points at the Fermi level. Another search was performed within reported DFT crystal structures collected in Materials Project database (Cheon et al. 2017). This search was for 3D crystal structures that consist of weakly interacting layers and hence, are suitable for obtaining 2D forms by e.g. exfoliation. Recently a list of four layer (diperiodic) groups that host semi-Dirac dispersion was given (Damljanović and Gajić 2017). The corresponding theory was formulated for non-magnetic, 2D materials with negligible SOC.

In this paper we have searched a list of layered 3D materials (Cheon et al. 2017), for structures that consist of layers belonging to layer group p11b (Dg5 in notation of Kopsky and Litvin 2002), with layers periodically repeated along the z-axis. The layer group p11b hosts semi-Dirac dispersion at A and B points of the BZ (Damljanović and Gajić 2017). In what follows, we have considered a tight-binding model from s-orbitals on a system isostructural to phosphorus sublattice in the single layer of material SnPSe\(_3\) that belongs to the list (Cheon et al. 2017).

2 Method and results

Space group P1c1 (No. 7) is obtained by periodic repetition of layer group Dg5 along the axis that is perpendicular to diperiodic plane. On the other hand, diperiodic plane is perpendicular to the y-axis in the space group P1c1. For these reasons we have searched 3D layered materials given in Cheon et al. (2017), belonging to the space group P1c1, such that layers are parallel to the unique glide plane. We have found following five materials whose structures satisfy these requirements: Al\(_2\)CdCl\(_8\) (Materials Project No. mp-28361 Bergerhoff et al. 1983; Staffel and Mayer 1987), Cr(PO\(_3)_5\) (mp-705019 Bergerhoff et al. 1983; Jain et al. 2011; Hautier et al. 2011; El-Horr and Bagieu Beucher 1986), LiTi(PO\(_3)_5\) (mp-684059 Bergerhoff et al. 1983; Jain et al. 2011; Hautier et al. 2011; El-Horr and Bagieu Beucher 1986), SnPSe\(_3\) (mp-570370 Bergerhoff et al. 1983; Israel et al. 1998) and SnPS\(_3\) (mp-13923 Bergerhoff et al. 1983; Dittmar and Schaefer 1974). If one would neglect SOC one would get semi-Dirac dispersion in these materials, irrespectively of the method used to calculate the band structure, as long as the approximation used is sufficiently fine (Damljanović and Gajić 2017). The inclusion of SOC would require analysis of double groups and it may be a topic of future research.

As an illustration, we will investigate electronic dispersion within a tight-binding model on a structure that belongs to layer group Dg5. In order to make the structure more realistic, we choose it to be isostructural with the sublattice of phosphorus ions in SnPSe\(_3\), a material whose stability was confirmed by DFT calculations (Bergerhoff et al. 1983; Israel et al. 1998). The crystal structure and corresponding BZ is shown on Fig. 1. The lattice parameters are 6.996 and 12.006 Å, while the oblique angle is \(124.6^{\circ }\). The Wyckoff position 2a is occupied twice, with nuclei having (fractional) coordinates (0.12600, 0.56620, 2.83 Å) and (0.87540, 0.43600, 1.17 Å). The positions of other nuclei are determined by symmetry (Kopsky and Litvin 2002). Although our system is isostructural with phosphorus sublattice of SnPSe\(_3\), we do not assume that it is made from phosphorus atoms. We consider a tight-binding (LCAO MO) model from s-orbitals, in order to make the model simple. The internuclear distances and hopping integrals are given in the Table 1. The tight-binding Hamiltonian is (\(*\) denotes complex conjugation):

$$\begin{aligned} {{\mathsf {H}}}({{\mathbf {k}}}) = \left( \begin{array}{llll} \gamma _{11}+2\gamma '_{11}\cos ({{\mathbf {k}}}\cdot {\mathbf {a}}) &{}\quad 0 &{}\quad \gamma _{13}e^{-i{{\mathbf {k}}}\cdot ({\mathbf {a}}+{\mathbf {b}})}+\gamma '_{13}e^{-i{{\mathbf {k}}}\cdot {\mathbf {b}}} &{}\quad \gamma _{14}+\gamma '_{14}e^{-i{{\mathbf {k}}}\cdot {\mathbf {a}}} \\ 0 &{}\quad \gamma _{11}+2\gamma '_{11}\cos ({{\mathbf {k}}}\cdot {\mathbf {a}}) &{}\quad \gamma _{14}+\gamma '_{14}e^{-i{{\mathbf {k}}}\cdot {\mathbf {a}}} &{}\quad \gamma '_{13}+\gamma _{13}e^{-i{{\mathbf {k}}}\cdot {\mathbf {a}}} \\ \gamma _{13}e^{i{{\mathbf {k}}}\cdot ({\mathbf {a}}+{\mathbf {b}})}+\gamma '_{13}e^{i{{\mathbf {k}}}\cdot {\mathbf {b}}} &{}\quad \gamma _{14}+\gamma '_{14}e^{i{{\mathbf {k}}}\cdot {\mathbf {a}}} &{}\quad \gamma _{33}+2\gamma '_{33}\cos ({{\mathbf {k}}}\cdot {\mathbf {a}}) &{}\quad h_{34} \\ \gamma _{14}+\gamma '_{14}e^{i{{\mathbf {k}}}\cdot {\mathbf {a}}} &{}\quad \gamma '_{13}+\gamma _{13}e^{i{{\mathbf {k}}}\cdot {\mathbf {a}}} &{}\quad h^*_{34} &{}\quad \gamma _{33}+2\gamma '_{33}\cos ({{\mathbf {k}}}\cdot {\mathbf {a}}) \\ \end{array} \right) , \end{aligned}$$
(1)
$$\begin{aligned} h_{34}=\gamma _{34}\left( 1+e^{i{{\mathbf {k}}}\cdot {\mathbf {b}}}\right) +\gamma '_{34}\left( e^{-i{{\mathbf {k}}}\cdot {\mathbf {a}}}+e^{i{{\mathbf {k}}}\cdot ({\mathbf {a}}+{\mathbf {b}})}\right) . \end{aligned}$$
(2)

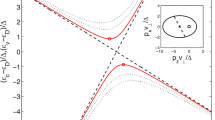
We are interested in the electronic band structure in the vicinity of points \({{\mathbf {k}}}_A=(-\mathbf {k_a}+\mathbf {k_b})/2\) and \({{\mathbf {k}}}_B=\mathbf {k_b}/2\). The band structure for certain ratios of hopping integrals is shown on Fig. 2. We can see in the vicinity of point (0, 0) the presence of dispersion which is Dirac-like along one direction in the BZ and quadratic along the perpendicular direction. In addition, we see that the band structure contains double spinless degenerate line (one line per each pair of bands) which is not caused by the TRS nor crystal symmetry.

Fig. 1
figure 1

a Crystal structure belonging to Dg5 for the tight-binding model. Black parallelogram denotes primitive unit cell. All nuclei are of the same type. Height of nuclei above the drawing plane is denoted by colors: blue + 2.83 Å, black + 1.17 Å, gray − 1.17 Å, turquoise − 2.83Å. b Corresponding Brillouin zone with basis vectors of the reciprocal lattice and positions of A and B points that host semi-Dirac dispersion. (Color figure online)

Full size image
Table 1 Internuclear distances and corresponding hopping parameters for the structure from Fig. 1
Full size table
Fig. 2
figure 2

The electronic band structure in the vicinity of A (a) and B (b) points of the BZ for \(\gamma _{13}/\gamma '_{11}=18\), \(\gamma _{14}/\gamma '_{11}=10.5\), \(\gamma _{34}/\gamma '_{11}=8\), \(\gamma '_{13}/\gamma '_{11}=6.5\), \(\gamma '_{34}/\gamma '_{11}=4.5\), \(\gamma '_{14}/\gamma '_{11}=2.5\), \(\gamma '_{33}/\gamma '_{11}=0.5\) and \((\gamma _{33}-\gamma _{11})/\gamma '_{11}=-0.5\). \({\mathbf {q}}\) is in units 1 / b in the direction parallel to \({\mathbf {b}}/b\), and in units \(1/(acos(34.6^{\circ }))\) in the direction perpendicular to \({\mathbf {b}}/b\). Coordinates of the A point in panel a, i.e. B point in panel b, are (0, 0)

Full size image

To determine more precisely the exact type of dispersion in the vicinity of given BZ points, we calculate analytically the band structure, first by the perturbation theory of degenerate energy level and later exactly, by solving quartic equation. In order to simplify calculations we assume \(\gamma '_{11}=\gamma '_{33}=\gamma '_{13}=\gamma '_{14}=\gamma '_{34}=0\) and, although not required by symmetry, \(\gamma _{11}=\gamma _{33}(=\gamma _1)\). The energies at both A and B points are \(E_0=\gamma _1-\sqrt{\gamma ^2_{13}+\gamma ^2_{14}}\) and \(E'_0=\gamma _1+\sqrt{\gamma ^2_{13}+\gamma ^2_{14}}\). Both \(E_0\) and \(E'_0\) are doubly degenerate. For the A-point we write \({\mathsf {H}}({{\mathbf {k}}}_A+{\mathbf {q}})={\mathsf {H}}({{\mathbf {k}}}_A)+{\mathsf {H}}'\) and apply first order perturbation theory of degenerate levels \(E_0\) and \(E'_0\), with \({\mathsf {H}}'={\mathsf {H}}({{\mathbf {k}}}_A+{\mathbf {q}})-{\mathsf {H}}({{\mathbf {k}}}_A)\) being perturbation. We do the same for the B-point. The final result for the B-point is:

$$\begin{aligned} E_{1,2}\approx E'_0-\frac{1}{2}C_2q'^2_2\pm \frac{1}{2}\sqrt{u_2q'^2_1+v_2q'^4_2}, \end{aligned}$$
(3)
$$\begin{aligned} E_{3,4}\approx E_0+\frac{1}{2}C_1q_2^2\pm \frac{1}{2}\sqrt{u_1q_1^2+v_1q_2^4}, \end{aligned}$$
(4)

while for the A-point we obtain:

$$\begin{aligned} E_{1,2}\approx E'_0-\frac{1}{2}C_1q_2^2\pm \frac{1}{2}\sqrt{u_1q_1^2+v_1q_2^4}, \end{aligned}$$
(5)
$$\begin{aligned} E_{3,4}\approx E_0+\frac{1}{2}C_2q'^2_2\pm \frac{1}{2}\sqrt{u_2q'^2_1+v_2q'^4_2}. \end{aligned}$$
(6)

Here \({\mathbf {q}}\) is a vector of small modulus, \(q_1\), \(q_2\), \(q'_1\) and \(q'_2\) are the projections of \({\mathbf {q}}\) along vectors \(\mathbf {e}_1\), \(\mathbf {e}_2\), \(\mathbf {e}_3\) and \(\mathbf {e}_4\), respectively. In addition:

$$\begin{aligned} u_{1,2}= \left[ 2\frac{\gamma _{13}\gamma _{14}}{\sqrt{\gamma ^2_{13}+\gamma ^2_{14}}}{\mathbf {a}}+\left( \frac{\gamma _{13}\gamma _{14}}{\sqrt{\gamma ^2_{13}+\gamma ^2_{14}}}\mp \gamma _{34}\right) {\mathbf {b}}\right] ^2, \end{aligned}$$
(7)
$$\begin{aligned} v_{1,2}= 4\frac{\left( {\mathbf {a}}\times {\mathbf {b}}\right) ^4\gamma ^6_{13}\gamma _{14}^2\gamma _{34}^2}{u_{1,2}^2(\gamma ^2_{13}+\gamma ^2_{14})^2}, \end{aligned}$$
(8)
$$\begin{aligned} C_{1,2}= \frac{\left( {\mathbf {a}}\times {\mathbf {b}}\right) ^2\gamma ^2_{13}}{u_{1,2}\sqrt{\gamma ^2_{13}+\gamma ^2_{14}}}\left( \frac{\gamma _{13}^2\gamma _{14}^2}{\gamma ^2_{13}+\gamma ^2_{14}}+\gamma _{34}^2\right) , \end{aligned}$$
(9)
$$\begin{aligned} \mathbf {e}_1= \frac{2}{\sqrt{u_1}}\frac{\gamma _{13}\gamma _{14}}{\sqrt{\gamma ^2_{13}+\gamma ^2_{14}}}{\mathbf {a}}+\frac{1}{\sqrt{u_1}}\left( \frac{\gamma _{13}\gamma _{14}}{\sqrt{\gamma ^2_{13}+\gamma ^2_{14}}}- \gamma _{34}\right) {\mathbf {b}}, \end{aligned}$$
(10)
$$\begin{aligned} \mathbf {e}_3= \frac{2}{\sqrt{u_2}}\frac{\gamma _{13}\gamma _{14}}{\sqrt{\gamma ^2_{13}+\gamma ^2_{14}}}{\mathbf {a}}+\frac{1}{\sqrt{u_2}}\left( \frac{\gamma _{13}\gamma _{14}}{\sqrt{\gamma ^2_{13}+\gamma ^2_{14}}}+ \gamma _{34}\right) {\mathbf {b}}, \end{aligned}$$
(11)
$$\begin{aligned} \mathbf {e}_{2,4}= \frac{\mathbf {e}_{1,3}\times ({\mathbf {a}}\times {\mathbf {b}})}{\left| {\mathbf {a}}\times {\mathbf {b}}\right| }. \end{aligned}$$
(12)

Since \(u_1\), \(u_2\), \(v_1\) and \(v_2\) are all greater than zero, the obtained dispersion is of semi-Dirac type as predicted by Damljanović and Gajić (2017), but the accidental double degeneracy is missed.

Exact solution, based on solving quartic characteristic equation, gives the following condition for double degeneracy:

$$\begin{aligned} \left( \gamma _{13}^2+\gamma _{14}^2\right) \gamma _{34}^2sin^2\left( {\mathbf {q}}\cdot {\mathbf {b}}/2\right) =\gamma _{13}^2\gamma _{14}^2sin^2\left( {\mathbf {a}}\cdot {\mathbf {q}}+{\mathbf {b}}\cdot {\mathbf {q}}/2\right) , \end{aligned}$$
(13)

which has solution for sufficiently small \(\left| {\mathbf {q}}\right|\), irrespectively of relations between \(\gamma _{13}\), \(\gamma _{14}\) and \(\gamma _{34}\). The Taylor expansion of the exact energy around \({\mathbf {q}}=0\) (B-point) gives \(E_{1,2}\approx E'_0\pm (1/2)\sqrt{u_2}\left| q'_1\right|\), in the direction \(\mathbf {e}_3\), and \(E_{1,2}\approx E'_0\pm (1/2)w_2\left| q'_2\right| ^3\), in the direction perpendicular to \(\mathbf {e}_3\). Similarly, \(E_{3,4}\approx E_0\pm (1/2)\sqrt{u_1}\left| q_1\right|\) in the direction \(\mathbf {e}_1\) and \(E_{3,4}\approx E_0\pm (1/2)w_1\left| q_2\right| ^3\), in the direction perpendicular to \(\mathbf {e}_1\). Here:

$$\begin{aligned} w_{1,2}=\frac{\left| {\mathbf {a}}\times {\mathbf {b}}\right| ^3}{3u_{1,2}^{3/2}}\frac{\gamma _{13}\gamma _{14}\gamma _{34}}{\sqrt{\gamma _{13}^2+\gamma _{14}^2}}\left( \frac{\gamma _{13}^2\gamma _{14}^2}{\gamma _{13}^2+\gamma _{14}^2}-\gamma _{34}^2\right) . \end{aligned}$$
(14)

For the A-point we make substitution \(\gamma _{13}\rightarrow -\gamma _{13}\) in the above formulas. It follows that the first order perturbation theory gives correct BZ-direction of Dirac-like dispersion and correct behavior of band structure in this direction. For the orthogonal direction as well as behavior of bands in complete vicinity of A, B-points the first order perturbation theory is not sufficient and higher order corrections are needed.

Regarding line of accidental spinless degeneracy found in exact solution of four-component Hamiltonian, one has to note that similar degeneracy occurs in the tight-binding example for layer group Dg48 of Damljanović and Gajić (2017). In this case the degeneracy is a consequence of the fact that model Hamiltonian is two-component and that third order polynomial has at least one real zero. By studding the compatibility relations of all four layer single groups found in Damljanović and Gajić (2017) in the vicinity of \({{\mathbf {k}}}_0\) we get that two-dimensional irrep decomposes into two nonequivalent, one-dimensional irreps: \(\varGamma _{2D}(G({{\mathbf {k}}}_0))=\varGamma _{1D}(G({{\mathbf {k}}}_0+{\mathbf {q}}))+\varGamma '_{1D}(G({{\mathbf {k}}}_0+{\mathbf {q}}))\), where \({\mathbf {q}}\) is small, jet non-zero wave vector. According to von Neumann–Wigner theorem, two bands touching at \({{\mathbf {k}}}_0\) do not repel each other at nearby points and may cross there too (Landau and Lifshitz 1981).

3 Conclusions

In summary, we have investigated electronic dispersion on a structure belonging to layer group Dg5, using tight-binding model from s-orbitals. We applied two methods for obtaining electronic dispersion: the first order perturbation theory of doubly degenerate level and exact diagonalization based on solving quartic equation. The first order perturbation method gives correct behavior in the Dirac-dispersion direction, while for other directions one needs higher order corrections. Accidental node line present in the exact method does not appear in the first order perturbation method. Further investigation should show if e.g. band topology cause these lines to always appear in four groups from Damljanović and Gajić (2017).

In addition, we have pointed out that in the literature there have already been reported numerically stable 3D structures, which consist of weakly interacting layers belonging to Dg5. Closer ab initio electronic band structure investigations of single layers of these structures, could give more insight into the particular types of semi-Dirac dispersion that are expected to appear.