Efficient coupling of the inhomogeneous current spreading model to the dynamic electro-optical solver for broad-area edge-emitting semiconductor devices

Abstract

We extend a 2 (space) + 1 (time)-dimensional traveling wave model for broad-area edge-emitting semiconductor lasers by a model for inhomogeneous current spreading from the contact to the active zone of the laser. To speedup the performance of the device simulations, we suggest and discuss several approximations of the inhomogeneous current density in the active zone.

1 Introduction

High-power edge-emitting broad-area semiconductor lasers (BALs) (Fig. 1a) are important light sources due to their numerous applications (Diehl 2000). Accurate modeling and simulation of BALs is critical for improving their performance or for the evaluation of novel design concepts (Wenzel 2013).

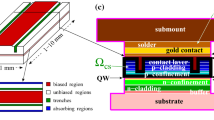
In this work we discuss an efficient implementation of a spatially resolved current spreading model defined in the vertical–lateral domain, see Fig. 1c, into a dynamic electro-optical solver BALaser (2017) acting in the longitudinal–lateral plane, see panel (b) of the same figure. Our most general approach relies on precalculation of the current spreading problem for all possible conditions in advance using a finite volume (FV) based numerical scheme. The current density distribution entering the electro-optical solver is mainly determined by the product of the precomputed matrix $\mathcal {M}_{AZ}$ and the dynamically changing discrete quasi-Fermi potential in the active zone (AZ). Once the considered current spreading problem satisfies some additional requirements, we can also exploit a semi-discrete separation of variables (SV) based method. It allows a precalculation of the smaller matrix $\mathcal {M}_{I}^{-1}$ used later for definition of the (dynamically changing) current flux in a finite distance from the AZ, whereas the current distribution in the AZ itself is estimated afterwards using discrete fast Fourier transform techniques.

Fig. 1

Schematic representation of an edge-emitting broad-area laser (a), its active zone described by the traveling wave model (b), and the transverse cross-section, where the current flow equations are solved (c). Vertical dashed lines and bullets in (c) represent the semidiscretization of the transversal domain in the separation of variables based method and corresponding mesh points at the upper-lower domain interface

Due to the large dimension of the above mentioned matrices, the multiple matrix-vector multiplications become the main reason of the slow-down of the simulations of the extended model. To speedup the calculations, we consider different approximations of the full numerical inhomogeneous current density in the AZ. The efficiency and the precision of these approximations are illustrated by several numerical examples.

Our paper is organized as follows. In Sect. 2 we briefly introduce the traveling wave model used in our electro-optical solver and the Laplace problem used to model the inhomogeneous current spreading in the p-doped part of the BAL. Sect. 3 gives an overview of two numerical methods used to solve the current spreading problem. The illustration of the differences between the old piecewise-constant and the new inhomogeneously broadened injected current models is given in Sect. 4. Section 5 discusses the efficiency of the coupling of both models. Here, different methods for speeding up the calculations are presented, and corresponding numerical performance results are shown.

2 Mathematical modeling

2.1 Electro-optical model

Nonlinear dynamics in BALs schematically represented in Fig. 1a is modeled by means of a 2(space)+1(time) dimensional traveling wave (TW) model (Radziunas and Čiegis 2014). According to this model we account only for the optical field and carrier dynamics within the thin active zone of the laser along the lateral and longitudinal coordinates x and z, whereas the influence of the vertical device structure (y-coordinate) is represented by a set of effective model parameters. In the computational domain shown in Fig. 1b we distinguish different areas according to the positions of the contacts, trenches, or unbiased regions. The spatio-temporal dynamics of the slowly varying complex amplitudes of the counter-propagating optical fields, $E^+(x,z,t)$ and $E^-(x,z,t)$, is governed by the TW equations

$$\begin{aligned} \begin{array}{l} \left[ \frac{n_g}{c_0}\partial _t \pm \partial _z +\frac{i}{2\bar{n}k_0}\partial _x^2\right] E^\pm \!=\! -i\beta E^\pm \! -\!i\kappa E^\mp \!+\!F^\pm _{sp}, \end{array} \end{aligned}$$

(1)

where the relative propagation factor $\beta (N,E,\omega )$ depends on the local carrier density N(x, z, t) and includes a frequency $\omega$ dependent model for material gain dispersion, can take into account nonlinear gain compression, two-photon absorption, and the impact of heating on the gain and the refractive index. At the laser facets, $z=0$ and $z=L$, the optical fields satisfy reflection conditions,

$$\begin{aligned} E^+(x,0,t)=r_0 E^-(x,0,t), \qquad E^-(x,L,t)=r_L E^+(x,L,t). \end{aligned}$$

At the lateral borders of the (broad enough) computational domain periodic conditions are imposed. The evolution of the carrier density N(x, z, t) in the active zone is governed by the diffusive carrier rate equation

$$\begin{aligned} \begin{array}{l} \partial _t N\! =\! \partial _x(D\partial _x N) \!+\! \frac{j(x,z,t)}{e d}\!-\!R_{sp}(N)-R_{st}(N,E,\omega ). \end{array} \end{aligned}$$

(2)

In our previous works, the effective lateral diffusion coefficient D was assumed to be constant, and the injection current density j(x, z, t) was set constant region-wise. For a more detailed description of the model equations and parameters, see Radziunas and Čiegis (2014), Spreemann et al. (2009). The TW model (1), (2) is efficiently integrated (Radziunas 2016) by the parallel distributed-memory based electro-optical solver BALaser (2017) developed at the Weierstrass Institute in Berlin.

2.2 Current spreading model

A proper description of injection and diffusion in the active zone of BALs, however, requires an adequate consideration of the current flow through the p-doped part of the device from the electrical contact towards the active zone. Since the length of the device is much larger than its width, we restrict our considerations to the study of the current flow within the transverse cross-section of the p-doped part of the device, see Fig. 1c. Within each of these 2-D domains $\Omega$ at appropriate positions $z_0$ and each time $t_0$, we have to solve the Laplace problem

$$\begin{aligned}&\nabla _{x,y} \cdot (\sigma (x,y) \nabla _{x,y}\varphi (x,y)) = 0,\quad (x,y)\in \Omega ,\nonumber \\&\varphi |_{\Gamma _c} = U,\quad \varphi |_{\Gamma _{az}} = \varphi _{AZ}(N(x,z_0,t_0)),\quad \partial _n \varphi |_{\Gamma \setminus (\Gamma _{az}\cup \Gamma _{c})} = 0,\nonumber \\&\varphi |_{(x,y)\in \Gamma _i^+} = \varphi |_{(x,y)\in \Gamma _i^-}, \quad \sigma \partial _n\varphi |_{(x,y)\in \Gamma _i^+} = -\sigma \partial _n\varphi |_{(x,y)\in \Gamma _i^-} \end{aligned}$$

(3)

for the quasi-Fermi potential $\varphi (x,y)$, where the piecewise constant function $\sigma (x,y)$ is the conductivity of materials within $\Omega$. $\Gamma$ is the full outer boundary of the domain $\Omega$, $\Gamma _c$ and $\Gamma _{az}$ are upper (contact-side) and lower (active zone-side) parts of this boundary determined by $y=H$ and $y=0$, respectively, whereas $\Gamma _i^+$ and $\Gamma _i^-$ are different sides of the internal boundaries $\Gamma _i$ between materials with different conductivity. U and $\varphi _{AZ}$ are the voltage at the contact and the Fermi voltage function defined according to the Joyce-Dixon approximation (Joyce and Dixon 1977) of the inverse Fermi integral, respectively. The injected current density entering the carrier rate Eq. (2) is defined by $j(x,z_0,t_0) = -\sigma (x,0)\partial _y\varphi (x,0)$. Finally, the carrier diffusion factor in the same equation can be replaced by the carrier dependent expression, $D = D(N,\partial _N\varphi _{AZ})$ (Joyce 1982).

3 Solution of the Laplace problem

To solve the Laplace problem defined above, we apply two different approaches.

The first semianalytic approach relies on the uniform discretization of the domain $\Omega$ along the x axis and substitution of the lateral derivatives $\partial _x$ in Eq. (3) by their finite difference analogs. Namely, the coordinate x is replaced by the discrete set $\{x_j: x_j=(j+0.5)h\}_{j=0}^{N_x}$ where $h=W/N_x$ is the discretization step, $x=0$ and $x=W$ are the left and right outer sides of the domain $\Omega$, see Fig. 1c. All x-dependent functions f(x) are substituted by the column vectors ${f}_h$ with the components $f_{h,j} = f(x_j)$. For a simple rectangular domain $\Omega$ and constant $\sigma$ we apply the method of separation of variables which implies

$$\begin{aligned}&\mathbf {\varphi }_{h}(y) = \sum _{k=0}^{N_x-1}\mu _k(y)\mathbf {\psi }_h^{(k)}, \qquad \text {where} \\&\frac{1}{h^2}\left( \psi ^{(k)}_{h,j+1}-2\psi ^{(k)}_{h,j}+\psi ^{(k)}_{h,j-1}\right) +\lambda _k\psi ^{(k)}_{h,j} = 0, \qquad \partial ^2_y\mu _k(y)=\lambda _k\mu _k(y). \end{aligned}$$

Due to homogeneous Neumann boundary conditions at the left and right sides of the domain, all vectors $\mathbf {\psi }_h^{(k)}$ and factors $\lambda _k$ can be defined as

$$\begin{aligned} \psi ^{(k)}_{h,j} = \cos \left( \frac{k\pi x_j}{N_x h}\right) ,\quad \lambda _k = \frac{4}{h^2}\sin ^2\left( \frac{k\pi }{2N_x}\right) ,\quad 0\le k,j<N_x. \end{aligned}$$

Moreover, all these vectors $\mathbf {\psi }^{(k)}_h$, $0\le k<N_x$, form an orthogonal basis of the corresponding grid function space, whereas $\mu _k(y)$ can be interpreted as the Fourier coefficients of the vector function $\mathbf {\varphi }_h(y)$. To locate the values of $\mu _k(y)$ or $\partial _y\mu _k(y)$ at the upper and lower parts of the domain, we use the discrete cosine transform (DCT) with respect to the upper and lower x-dependent boundary functions. After solving the ordinary differential equations for $\mu _k(y)$, we apply the DCT again for reconstruction of the quasi-Fermi potential $\varphi (x_j,y)$ and current flow $\sigma \partial _y\varphi (x_j,y)$.

The same method can be easily generalized for the rectangular domains with a conductivity $\sigma$ that is uniformly constant in x and piecewise constant in y [such that for all x we have $\sigma (x,y) = \sigma (y)$]. In this case, each interface of two materials $\Gamma _i$ is determined by the fixed vertical coordinate $y=y_i$, whereas the corresponding continuity conditions at $\Gamma _i$ in Eq. (3) can be replaced by $2N_x$ relations

$$\begin{aligned} \varphi _{h,j}(y_i^-) = \varphi _{h,j}(y_i^+), \quad \sigma (y_i^-)\partial _y\varphi _{h,j}(y_i^-) = \sigma (y^+)\partial _y\varphi _{h,j}(y_i^+),\quad 0\le j<N_x. \end{aligned}$$

For similar conductivities and more realistic domains consisting of the (single) lower and (one or several) upper subdomains joined at the interface height $y=y_I$, see Fig. 1c, the SV method can be applied separately within each of these subdomains. The boundary conditions of these subproblems at this interface are determined by the discrete flux vector $\mathbf {\kappa }_h =\sigma (y_I^-) \partial _y\mathbf {\varphi }_{h}(y_I^-)$, which is a representation of the flux function at the mesh points $(x_j,y_I)$ (bullets in Fig. 1c). $\mathbf {\kappa }_h$ has $N^u_x<N_x$ components corresponding to the unknown flux function values at the internal mesh points of the whole domain $\Omega$, see empty bullets in Fig. 1c. The remaining $N_x-N^u_x$ mesh points $(x_j,y_I)$ (full bullets in the same figure) belong to the boundary $\Gamma$ of the domain $\Omega$. Due to the Neumann boundary conditions, the corresponding components of $\mathbf {\kappa }_h$ are vanishing. The main challenge of the SV approach is finding $N^u_x$-dimensional vector $\mathbf {\kappa }_h^u$ determined by all unknown components of the larger flux vector $\mathbf {\kappa }_h$ so that $\mathbf {\kappa }_h^u$ and $\mathbf {\kappa }_h$ could be used for reconstruction of $\mathbf {\varphi }_h(y)$ in the whole domain. By exploiting continuation conditions (3) at the interface $y_I$, we can derive a linear system of $N_x^u$ equations

$$\begin{aligned} \mathcal {M}_{I}\mathbf {\kappa }^u_h = \mathbf {\nu }^u_h\quad \Rightarrow \quad \mathbf {\kappa }^u_h=\mathcal {M}_{I}^{-1}\mathbf {\nu }^u_h, \end{aligned}$$

(4)

where the $N_x^u$-dimensional vector $\mathbf {\nu }^u_h$ depends on U and $\mathbf {\varphi }_{h,AZ}$, whereas the $(N_x^u\times N_x^u)$-dimensional matrix $\mathcal {M}_I$ depends only on $\sigma (y)$ and, therefore, can be constructed and inverted in a preprocessing step.

Once the considered domain $\Omega$ or the conductivity function $\sigma (x,y)$ are more complex, for the solution of the Laplace problem (3) or, more precisely, for the location of the current distribution vector ${j}_h$ at the AZ as a function $\mathcal {J}$ of the actual boundary conditions U and $\mathbf {\varphi }_{AZ,h}$, ${j}_h=\mathcal {J}(U,\mathbf {\varphi }_{AZ,h})$, we use the method based on a full finite volume discretization of the whole domain. For the numerical solution of this problem, we apply the software toolkit pdelib 2017 developed at the Weierstrass Institute in Berlin. In order to avoid solving the whole Laplace problem at each $z_0$ and new time instant $t_0$, we precalculate the current distribution vectors ${j}_h$ for $N_x+1$ different pairs $(U,\mathbf {\varphi }_{AZ,h})$. Namely, we find

$$\begin{aligned} {j}^{0}_{h} = \mathcal {J}(1,{0_{h}}),\quad {j}^{s}_{h} = \mathcal {J}(0,\mathbf {\delta }^{s-1}_h),\quad 0< s \le N_x,\qquad \delta ^s_{h,l}= {\left\{ \begin{array}{ll}1& \hbox {for}\,\, l=s\\ 0 &{} \hbox {otherwise}. \end{array}\right. } \end{aligned}$$

Due to linearity of the problem (3), the required current distribution is given by

$$\begin{aligned} {j}_h = \mathcal {M}_{AZ}\mathbf {\varphi }_{AZ,h} +U {j}^0_h, \quad \text {where} \quad \dim (\mathcal {M}_{AZ})=(N_x\times N_x), \quad \mathcal {M}_{AZ,sl} ={j}^s_{h,l}. \end{aligned}$$

(5)

4 Examples

To test the numerical approaches, we apply them to single-stripe and multi-stripe BALs. The single-stripe BAL has a 90 $\mu$m broad electrical contact. The multi-stripe BAL consists of five 10 $\mu$m-broad contacts with 10 $\mu$m separation between them. Typical calculated quasi-Fermi potentials for these two lasers are shown in Fig. 2a and b, respectively. Panels (c) and (d) of the same figure show the distributions of the considered boundary function $\varphi _{AZ}(N(x,z_0,t_0))$ and corresponding carrier density $N(x,z_0,t_0)$. Black dashed-dotted and solid curves in panels (e) and (f) represent the spatially distributed carrier diffusion factor and the current density j(x) obtained by solving numerically the current spreading model (3). Red dashed lines in the same figure show our old piecewise constant injection approach. Note also, that in our previous modeling the total injection current $I\!=\!\int \!\!\!\int \! j(x,z)dxdz$ served as a control parameter. Now the voltage U takes this role.

Fig. 2

Current spreading in two laser devices. a and b: Fermi potential $\varphi (x,y)$ within the domain $\Omega$ calculated at $z_0\!=\!3$ mm for $U=1.564\,V$ and N(x), $\varphi _{AZ}(N)$ which are indicated in the panels c and d, respectively. e and f: corresponding lateral distribution of the effective carrier diffusion D (dash-dotted) and current density j(x) according to different modeling approaches

Fig. 3

Simulated longitudinal distributions of the normalized intensity and photon number (a) and of the cumulative in x current per length according to the solution of the full current spreading model and its Joyce approximation (b). Device geometry and parameters are the same as used in the left part of Fig. 2

Whereas the comparison of the old and new models for current density j(x) in Fig. 2e reveal only small differences, these differences become much more pronounced in the stripe array laser, see Fig. 2f. In contrast to the old piecewise constant model, the active zone regions just below the gaps between the adjacent contact stripes remain positively pumped. Thus, this advanced modeling of the inhomogeneous current spreading is more realistic when simulating broad area laser devices with structured electrical contacts (Radziunas et al. 2015).

Another example revealing possible importance of the inhomogeneous current spreading is presented in Fig. 3. Here we show longitudinal distributions of the (cumulative in x) field intensity, carrier number [panel (a)], and injected current [black curve in panel (b)] in typical 4 mm-long broad area laser already considered in Fig. 2a, c, and e. Due to the strongly asymmetric facet coatings (power reflectivities $|r_0|^2=0.95$ and $|r_L|^2=0.01$), the field, and, consequently, carrier distributions are nearly monotonous along the longitudinal coordinate z, see panel (a) of Fig. 3. Differences of N imply also differences of $\varphi _{AZ}(N)$ and, consequently, of the cumulative in x current density, which in our example shows up to 5% variation, see Fig. 3b.

5 Efficient implementation

An efficient implementation of the full (2D or even 3D) current spreading model into the electro-optical solver is related to several technical difficulties. The biggest challenge is overcoming a significant slowdown of computations, while the Laplace problem should, in general, be solved at each time instant $t_0$ and longitudinal position $z_0$. Since for the resolution of our TW model at each $(z_0,t_0)$ we use $\sim \, N_x\log (N_x)$ arithmetic operations, the estimation of j(x) at the $N_x$ points should require a similar or smaller number of operations.

A precomputation of $\mathcal {M}^{-1}_I$ in (4) with the following recovery of the $N_x^u$-dimensional vector $\mathbf {\kappa }_h^u$ and $N_x$-dimensional vector ${j}_h$ allows avoiding the solution of the full Laplace problem at each $(z_0,t_0)$. Whereas for the construction of $\mathbf {\nu }_h^u$ and ${j}_h$ one can exploit the FFT algorithm ($\sim \, N_x\log (N_x\!)$ operations), the matrix-vector product in Eq. (4) in general requires $\sim \, (N_x^u)^2$ operations which for $N_x^u\, \sim \, N_x$ computationally can be rather expensive. Similarly, one can exploit the linearity of the problem (3) and use the precomputed matrix $\mathcal {M}_{AZ}$ and formula (5). In this case, one avoids additional FFTs but performs even more ($\sim \,(N_x)^2$) expensive matrix-vector multiplication. Fortunately, the essential elements of the matrices $\mathcal {M}_{AZ}$ and, especially, $\mathcal {M}^{-1}_I$ are located around the center diagonal. Our tests have shown, that we can get a sufficient precision of $j(x_h)$ once using “cleaned” matrices $\mathcal {M}_\varepsilon$ obtained by deleting all matrix elements that by modulus are below some threshold $\theta _\varepsilon \!=\!\varepsilon \cdot \max (|\mathcal {M}_{ij}|)$. Typically, depending on $\varepsilon$, such cleaned matrices have only 10–40 non-vanishing diagonals, allowing to avoid the curse of an expensive matrix-vector multiplication.

Another computationally much cheaper approach requiring only $\sim \, N_x$ operations exploits the Joyce approximation of the solution of Eq. (3) (Joyce 1982). According to this method, j(x) is proportional to $U\!-\!\varphi _{AZ}(x)$ just below the electrical contact, and to $\partial _x^2\varphi _{AZ}(x)$ outside the contact, see thick green curves in Figs. 2c, d and 3b. Since the main weakness of this approach is at the edges of the contact, it can be useful when the contact is broad, but fails to provide reliable results when structuring of the electrical contacts on a few micrometer scale is applied.

The semianalytic SV method with the additional cleaning of the matrix $\mathcal {M}^{-1}_I$ and the Joyce approximation method as well as the laterally distributed carrier diffusion model were implemented into the electro-optical solver BALaser (2017). Test simulations of the extended TW model (1), (2) over one ns on a multi-core computer (HP BL460c Gen9 2xXeon Fourteen-Core 2600MHz with 256 GB RAM) at the Weierstrass Institute using ten processes have shown the following performance results. The simulations of the BAL using the old model with the piecewise constant j and constant D took 541 s. After inclusion of the distributed D, the simulation time was 556 s. After an additional inclusion of the Joyce approximation of j, this time was 568 s. The usage of a more precise j obtained by solving the Laplace problem with the matrix cleaning threshold of $10^{-3}$ and $10^{-7}$ was slowing down the simulations to 634 s and 639 s, respectively.

6 Conclusions

We have presented the inhomogeneous current spreading model, gave a short overview of the separation of variables based numerical method, and discussed several strategies of an efficient implementation of this model into the existing electro-optical solver. We have found, that this model can be especially important when studying lasers with structured electrical contacts. The efficiency of our model implementation was confirmed by numerical tests, which have shown only a moderate $\sim$ 17% reduction of the calculation speed.