Modeling and Simulations of Edge-Emitting Broad-Area Semiconductor Lasers and Amplifiers

Abstract

A (2+1)-dimensional partial differential equation model describing spatial-lateral dynamics of edge-emitting broad-area semiconductor devices is considered. A numerical scheme based on a split-step Fourier method is implemented on a parallel computing cluster. Numerical integration of the model equations is used for optimizing of existing devices with respect to the emitted beam quality, as well as for creating and testing of novel device design concepts.

M. Radziunas—This work was supported by EU FP7 ITN PROPHET, Grant No. 264687 and by the Einstein Center for Mathematics Berlin under project D-OT2.

1 Introduction

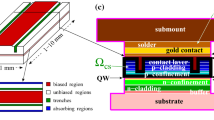
High power high brightness edge-emitting broad-area semiconductor (BAS) lasers and optical amplifiers are compact, efficient and reliable light sources playing a crucial role in different laser technologies, such as material processing, precision metrology, medical applications, nonlinear optics and sensor technology. BAS lasers and amplifiers have a relatively simple geometry [see Fig. 1(a)] allowing an efficient energy pumping through a broad electric contact on the top of the device and can operate at high power (tens of Watts) regimes.

However, BAS devices have one serious drawback: operated at high power, they suffer from a low beam quality due to simultaneous irregular contributions of different lateral and longitudinal optical modes. As a result, the emitted optical beam is irregular, has undesirable broad optical spectra, and large divergence. Thus, a quality improvement of the beam amplified in BAS amplifiers or generated by BAS lasers is a critical issue of the modern semiconductor laser technology.

Seeking to understand the dynamics of BAS devices, to suggest improvements of existing devices or to propose novel device design concepts we do a variety of related tasks. We perform modeling at different levels of complexity, do mathematical analysis of the hierarchy of models, create and implement efficient and robust numerical algorithms, and make numerical integration of the model equations. Typically, all these steps are done within research projects in cooperation with developers of the devices.

2 Mathematical Modeling and Numerical Algorithm

The dynamics of BAS devices can be described in different ways. The most comprehensive approach resolving the spatio-temporal evolution of full semiconductor equations self-consistently coupled to the optical fields is given by 3 (space) +1 (time)-dimensional nonlinear PDEs. Since the height of the active zone where the optical beam is generated and amplified (y dimension) is considerably smaller than the longitudinal (z) and lateral (x) dimensions of a typical BAS device [see Fig. 1(a)], a significant simplification can be achieved by averaging over the vertical direction and by describing certain effects phenomenologically. The resulting (2+1)-dimensional dynamical traveling wave (TW) model [1] can be resolved numerically orders of magnitudes faster allowing for parameter studies in an acceptable time.

Fig. 1.

(a): Schematic diagram of a BAS device. (b): Simplified representation of the BAS device, as considered by the (2+1)-dimensional TW model (Color figure online).

2.1 Basic (2+1)-Dimensional TW Model

The simplest version of the TW model is a degenerate system of second order PDEs for the slowly varying complex amplitudes of the counter-propagating optical fields, $E(z,x,t)=(E^+,E^-)^T$ [see white arrows in Fig. 1(b)], nonlinearly coupled to a rate equation for the real carrier density distribution N(z, x, t). It accounts for the diffraction of fields and diffusion of carriers in the lateral direction, whereas spatially non-homogeneous device parameters capture the geometrical design of the device. The normalized TW model reads as

$$ \begin{array}{l} \frac{\partial }{\partial t} E = \left[ \left( {}^{-1~0}_{~~0\,~1}\right) \frac{\partial }{\partial z} -\frac{i}{2} \frac{\partial ^2 }{\partial x^2}\right] E + \left[ B(N,\Vert E\Vert ^2) - \left( \alpha + i \delta \right) \mathcal{I}\right] E + F_{sp}, \end{array} $$

$$ \begin{array}{l} \frac{1}{\mu }\frac{\partial }{\partial t}N = D \frac{\partial ^2 }{\partial x^2}N + I(z,x) - R(N) - 2\mathfrak {R}e \left[ E^{*T} B(N,\Vert E^\pm \Vert ^2)E\right] , \end{array} $$

where $\mu$ is small, $\alpha$, $\delta$, $F_{sp}$, D, I, and $R(N)= AN+BN^2+CN^3$ represent the field losses, the built-in contrast of the refractive index, the spontaneous emission noise, the carrier diffusion, the injected current density, and the spontaneous recombination of carriers, respectively. The complex matrix B models the carrier and photon density dependent semiconductor material gain, $G(N,\Vert E^\pm \Vert ^2)$, the carrier-induced changes of the refractive index, $\tilde{n}(N)$, as well as the distributed coupling of the counter-propagating fields $\kappa ^\pm$:

$$ B_{11} = B_{22} = \frac{G(N,\Vert E\Vert ^2)}{2}+ i \tilde{n}(N),\qquad B_{12} = -i\kappa ^-,\quad B_{21} = -i\kappa ^+. $$

Here, for example,

$$ G(N,\Vert E \Vert ^2) =\frac{g^\prime \log \left( \max (N, N_{*})\right) }{1+ \varepsilon \Vert E\Vert ^2}, ~~~\tilde{n}(N) = \sigma \sqrt{N},~~~ \kappa ^+=\kappa ^-\in \mathbf {R}, $$

where $g^\prime$, $\sigma$, $\varepsilon$, and $N_{*}$ are the differential gain, the refractive index scaling, the nonlinear gain compression parameters, and the small positive carrier density used to determine an appropriate cut-off of the logarithmic gain function.

In general, this model should be considered in the (laterally) unbounded region $Q = Q_{z,x} \times (0, T]$, where $Q_{z,x} = \{ (z,x) : \; (z, x) \in (0, L) \times \mathbf {R} \}$ is the spatial domain, L represents the length of the device, x is the coordinate of the unbounded lateral axis of the device, and T defines the length of the time interval where we perform the integration. Far from the active zone, $|x|\gg 1$, the optical fields and carriers usually are well damped. Thus, in our numerical simulations we truncate the lateral domain at $x=-X$ and $x=X$ so that the truncated domain $Q^t_{z,x} = \{ (z,x) : \; (z, x) \in (0, L) \times [-X,X] \}$ [large rectangular in Fig. 1(b)] contains the considered BAS device [red area in the same figure]. Next, we assume either periodic boundary conditions [2, 3] or mixed Dirichlet (for the carrier densities)/approximate transparent (for the field functions) boundary conditions [4].

The boundary conditions for the optical fields at the longitudinal edges of the device, $z=0$ and $z=L$, account for reflections of the counter-propagating fields and optional injection of external optical beams, $a_{0,L}(x,t)$:

$$ \begin{array}{l} E^+(0, x, t) = r_0 E^- (0, x, t)+a_0(x, t), ~~ E^-(L, x, t) = r_L E^+ (L, x, t)+a_L(x, t), \end{array} $$

with $r_0$ and $r_L$ denoting the complex field reflectivity parameters at the laser facets.

2.2 Modifications of the TW Model

The basic TW model described above can be reduced to lower dimensional systems, allowing a more detailed analysis, understanding and control of specific dynamical effects. Different types of model reduction and analysis were discussed in Refs. [1, 5–8]. On the other hand, different extensions of the basic TW model allow to achieve a more precise description of various relevant properties of BAS devices.

First of all, an introduction of the couple of linear equations for induced polarization functions $P^+(z,x,t)$ and $P^-(z,x,t)$ enables modeling of nontrivial material gain dependence on the lasing frequency [9]:

$$ B_{\text {new}} = B - \mathcal{I} \mathcal{D},\qquad \mathcal{D} E^\pm := \overline{g} \left( E^\pm - P^\pm \right) , \quad \frac{\partial }{\partial t} P^\pm = i \overline{\omega } P^\pm + \overline{\gamma } \left( E^\pm - P^\pm \right) \!. $$

Here, the parameters $\overline{g}$, $\overline{\omega }$, and $\overline{\gamma }$ define the Lorentzian fit of the gain profile and denote the amplitude, the central frequency, and the half width at half maximum of this Lorentzian, respectively.

Another modification is related to the heating of the BAS device by the injected current. It is known, that the gain and refractive index change functions are depending on the local temperature of semiconductor material. A proper coupling of the TW model with the full heat transport equation and the numerical resolution of this extended model, however, is a challenging task due to different time scales. Whereas the typical time scale of the thermal diffusion in semiconductors is measured in microseconds, the carrier and the photon lifetimes are given in nanoseconds and picoseconds, respectively. Thus, in order to simulate the impact of the changing heating to the dynamics of BA lasers in a reasonable time, we propose to use the following parametric approach. Namely, in Refs. [1, 7] we have proposed to model injection current induced heating by the linear nonlocal dependence of the refractive index change and the gain peak frequency shift on the inhomogeneous injection I(x, z):

$$ \begin{array}{l} \delta _{\text {new}}(z,x) = \delta (z,x)+ \int \!\!\int c_T(z,x,\tilde{z},\tilde{x}) I(\tilde{z},\tilde{x}) d\tilde{z}d\tilde{x}, \end{array} $$

$$ \begin{array}{l} \overline{\omega }_{\text {new}}(z,x) = \overline{\omega }(z,x) + \int \!\!\int \nu _T(z,x,\tilde{z},\tilde{x}) I(\tilde{z},\tilde{x}) d\tilde{z}d\tilde{x}. \end{array} $$

Here, thermal factors $c_T$ and $\nu _T$ describe local and nonlocal crosstalk thermal effects in BAS devices with a single or several electrical contacts. This simple model with the properly defined [7] contact-wise constant coefficients $c_T$ and $\nu _T$ has allowed a proper theoretical reproduction of the state jumping behavior with tuning of the injected currents [1].

Another useful extension of the basic TW model can be performed when simulating an emitted field propagation through the external cavity (EC) and its re-injection to the BAS device [see thick green arrow in Fig. 1(b)]. In the presence of the optical feedback from the EC, the optical injection function $a_L(x,t)$ in the longitudinal boundary conditions should be replaced by the corresponding (delayed) feedback term. The form of this term depends on the different components within the EC as well as on the field propagation time along the EC.

For example, in the case of a simple EC composed of the collimating lens and the flat mirror located perpendicularly to the optical axis of the BAS device, the re-injection term can be given by a simple delayed term

$$ a_L(x,t) = t^2_L \sqrt{R_{ec}}\,e^{i\varphi _{ec}} E^+\left( L,x,t-2d_{ec}/c_0\right) \!. $$

Here, $t_L = \sqrt{1-|r_L|^2}$ is the field amplitude transmission through the right facet of the laser, $R_{ec}$ and $\varphi _{ec}$ are the field intensity reflection and phase change in the EC, whereas $d_{ec}$ is the distance from the center of the right facet of the BAS diode to the external reflector.

When the collimating lens is absent, and the reflector or the diffractive grating is located at the small angle $\alpha _{EC}$ to the optical axis, the feedback term turns to be more complicated [10]:

$$ \begin{array}{l} a_L(x,t) \approx t_L^2 \sqrt{\frac{-i}{2 d_{ec}\lambda _0}}\, \mathcal{F}\!\! \int \limits _{x' \in {\mathbf R}}\! E^+\left( L,x',t-2d_{ec}/c_0\right) e^{-ik_0\rho (x, x')} dx'. \end{array} $$

Here, $\rho (x,x')$ is the shortest distance between two lateral points $x'$ and x at the diode facet that the light takes to travel via the (infinitely broad) external reflector, whereas the operator $\mathcal{F}$ accounts for the spectral filtering by the external grating.

Another external cavity including the lens, the refractive grating located at the angle $\alpha _{ec}$ to the optical axis, and the small reflecting aperture was investigated experimentally in Ref. [11]. The corresponding feedback term in this case can be written as

$$ \begin{array}{l} a_L(x,t) \approx \frac{-r^2_{g} T^2_L}{2\pi } \int _\mathbf {R} \chi \left( \frac{\lambda _0 f\cot \alpha _{ec}}{2\pi c_0} \omega -x\right) \int _\mathbf {R} E^+(L,x,t') e^{-i\omega t'}\, dt' e^{i\omega (t- 8 f/c_0)} \,d\omega , \end{array} $$

where $\omega$ denotes the relative optical frequency of the field, f is the focal distance of the lense, $r_{g}$ and $\chi (x)$ are the field amplitude reflections at the grating and the aperture (the step-function $\chi (x)$ is non-vanishing if only x belongs to the aperture).

2.3 Performance of the Parallel Numerical Algorithm

Precise dynamic simulations of long and broad devices and tuning/optimization of the model parameters require huge process time and memory resources. A proper resolution of rapidly oscillating fields in typical BAS devices in a sufficiently large optical frequency range requires a fine space ($10^6-10^7$ mesh points) and time (up to $10^6$ points for typical 5 ns transients) discretization. Dynamic simulations of such devices can easily take several days or even weeks on a single processor. Some speedup of computations is achieved by using problem-dependent variable grid steps [4]. However, for extended parameter studies with the numerical integration times up to 1000 ns parallel computers and parallel solvers have to be employed.

For the numerical integration of the TW model, we use either a split-step fast Fourier transform based numerical method [2] or a full finite difference scheme [4]. The method of domain decomposition is used to parallelize the sequential algorithm. Namely, the numerical mesh of the full problem defined by $N_x$ lateral and $N_z$ longitudinal uniform discretization steps is splitted along the longitudinal z-direction into K (K: number of processors) non-overlapping rectangular subgrids of the similar size $N_x\times N_{z,j}$, $j=1,\ldots ,K$, $N_{z,j}\approx \text {ceil}(N_z/K)$ [2].

Exemplary simulations of three test problems on the parallel cluster of computers (see Fig. 2) show a good scaling of the algorithm [2]. For example, the simulations performed on 32 processors give a speedup factor of 25. That is, the simulations requiring two weeks of process time on a single processor computer can be efficiently performed over a single night. For a larger number of processes, the relative time needed for communications between them grows and implies a saturation of the speedup (see an increasing deviation of the test results from the ideal speedup in Fig. 2). More details on the performance and scalability of the parallel algorithm can be found in Ref. [2].

Fig. 2.

Speedup of computations in multi-process simulations of three test problems defined on spatial meshes with $N_x\times N_z = 1000\times 640$, $1000\times 320$, and $500\times 640$ points in lateral (x) and longitudinal (z) directions. Bullets of different color indicate tests with 1, 2, 4 or 8 processes used on each node (Color figure online).

3 Application: Suppression of Mode Jumps in MOPAs

The TW model and our numerical algorithms were successfully used for simulations of different BAS lasers and amplifiers, also showing good agreement with experimental observations [1]. In many cases, our simulations have helped to improve the design of the existing devices.

Fig. 3.

Schematic representation of Master Oscillator Power Amplifier (MOPA).

For example, the master oscillator (MO) tapered power-amplifier (PA) laser shown in Fig. 3 was analyzed theoretically and experimentally in [1, 12]. The narrow waveguide of the distributed feedback (DFB) MO generates a stable stationary optical field determined by a single transversal mode, which later is amplified in the tapered PA part of the device. An ideal MOPA laser should be able to maintain a good quality of the emitted beam. The operation of realistic MOPA devices, however, is spoiled by the amplification of the spontaneous emission in the PA, by the small separation of the MO and PA electrical contacts, and by the residual field reflectivity at the PA facet of the device.

Fig. 4.

Simulated optical spectra of DFB MOPA devices with different DFB field coupling coefficients $\kappa$ for increased injected current. More than three days of parallel 32-processor computations on $N_x\times N_z = 400\times 800$ spatial mesh with $\sim 2\cdot 10^7$ time steps were required for calculation of the data represented by each panel.

In Ref. [1] we have analyzed how this residual reflectivity and thermally induced changes of the refractive index imply experimentally observable unwanted switchings between operating states determined by adjacent longitudinal optical modes. We have found that these bifurcations are due to the changing phase relations of complex forward- and back-propagating fields at the interface of the MO and PA parts of the device. Simulations of a typical state-jumping behavior with increasing injected current is shown in the left panel of Fig. 4. In the theoretical paper [12] we have demonstrated that a proper choice of the field coupling parameter within the DFB MO part of the device makes it less sensitive to the optical feedback, leading to a stabilization of the laser emission (see second and fourth panels of Fig. 4).

4 Conclusions

In conclusion, we have presented several modifications of (2+1)-dimensional Traveling Wave model used to describe the nonlinear dynamics of broad-area edge-emitting semiconductor lasers and discussed implementation and performance of corresponding numerical algorithms on the parallel cluster of computers. We have found, that a speedup factor of typical problem simulations performed on 32 processors is around 25. For a larger number of processors, the saturation of this speedup factor is observed. Finally, we have presented an example of practical optimization simulations of Master Oscillator Power Amplifier semiconductor laser. Here, 32-processor parallel computations of a single numerical continuation diagram with the change of parameter took more than three days. Thus, without parallelization of the numerical algorithm, an efficient study of laser parameters in a reasonable time would not be possible.