1 Introduction

Researches on microwave bandpass filter have been reported in many papers (Wolff and Knoppik 1971; Wolff 1972; Matsuo et al. 2001; Gorur 2002; Gorur et al. 2003; Tan et al. 2005; Miguel et al. 2012; Feng et al. 2015; Gorur 2004; Lin et al. 2012; Athukorala and Budimir 2009; Jeng et al. 2006; Takan et al. 2015; Demirhan et al. 2016), and the related materials also published (Cameron 2003; Amari and Rosenberg 2001; Amari 2004; Hsieh and Chang 2002, 2003; Hong and Lancaster 1996; Chen et al. 2017; Chen and Jiang 2016; Chen and Yang 2016). The bandpass filters based on the dual-mode ring resonator have been extensively investigated since the first analysis of dual-mode characteristic of the ring resonator by Wolff and Knoppik (1971). The uniform ring resonator has a degenerate mode, which is orthogonal and produces identical resonant frequencies. When this uniform ring resonator is input with an asymmetric arrangement of feeding lines with the circuit profile perturbed and the degenerate mode becomes coupled, a narrow-band bandpass response occurs (Wolff 1972). Based on this mode perturbation mechanism, numerous dual-mode bandpass filters have been reported. The different perturbation schemes include (a) the distributed perturbation which uses step-impedance ring resonator (Matsuo et al. 2001; Lin et al. 2012); (b) the capacitive perturbation which leads to elliptic response, by the addition of single or multiple open stubs symmetrically on the ring (Gorur 2002; Gorur et al. 2003; Tan et al. 2005; Feng et al. 2015); (c) the inductive perturbation by cutting single or multiple notches on the ring (Wolff 1972; Tan et al. 2005; Gorur 2004; Lin et al. 2012; Athukorala and Budimir 2009).

In a previous study, Jeng et al. (2006) proposed a distributed perturbation scheme by coupling adjacent segments of the ring resonator. This scheme has the advantage of easy implementation, since extra stubs or notches are not needed. Furthermore, the self-coupled ring resonator can shift the resonant frequency toward the lower frequencies such that the circuit size can be reduced. In this study we propose an H-shaped dual-mode closed resonator with the distributed perturbation scheme. It has the same benefit of taking shorter ring length and can be easily folded but does not destroy the dual-mode characteristic. In Sect. 2, the mode perturbation owning to the self-coupled effect is analyzed. In Sect. 3, the generation and number of transmission zero are discussed. Since the periphery was not a simple round ring, to have transmission zeros symmetric to the passband, the optimum angle between input and output ports will not be 90 degrees anymore. The method of finding optimized taping positions of input and output ports is proposed. Bandpass filter applications with the proposed H-shaped self-coupled ring resonator and its folded schematic were described in Sect. 4, where the simulation and measurement results are discussed in detail and the transmission zeros by simulation and measurement is compared to the calculation one. Finally, a conclusion is given in Sect. 5.

2 Mode perturbation

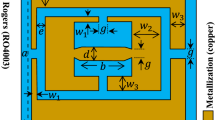
The schematic diagram of the proposed self-coupled ring resonator is composed of a coupled pair at the center section and two coupled pairs at the two ends shown in Fig. 1a. The central coupled section has a physical length of \(2\ell_{2}\), a coupling coefficient of \(c_{2}\), and a characteristic impedance of \(Z_{2}\). The two end coupled sections have the same parameters: physical lengths of \(\ell_{1}\), coupling coefficients of \(c_{1}\), characteristic impedances of \(Z_{1}\). The structure is symmetric to line \(\overline{BD}\) and line \(\overline{AC}\). In the following derivation, the effect of layout discontinuity is neglected.

Fig. 1
figure 1

Proposed self-coupled ring resonator, a schematic, b even-mode equivalent circuit, c odd-mode equivalent circuit

Full size image

2.1 Resonance conditions

Because the structure is symmetric with respect to line \(\overline{BD}\), the resonance condition can be derived using the even–odd mode theory with \(\overline{BD}\) as the reference plane. Following the processes of Jeng et al. (2006), the equivalent even- and odd-mode circuits obtained from the replacement of the reference plane \(\overline{BD}\) with the magnetic and electric walls are respectively given in Fig. 1b, c. Let the impedance ratio R = Z 1/Z 2 be the ratio of the characteristic impedances of the end coupled section to the central coupled section. Then the even-mode and odd-mode resonance conditions can be expressed as:

$$\tan \theta_{1e} \tan \theta_{2e} = R\sqrt {\frac{{1 - c_{2} }}{{1 + c_{2} }}} \cdot \frac{{1 + c_{1} \sec \theta_{1e} }}{{\sqrt {1 - c_{1}^{2} } }},$$
(1)
$$\tan \theta_{1o} \tan \theta_{2o} = \frac{1}{R}\sqrt {\frac{{1 - c_{2} }}{{1 + c_{2} }}} \cdot \frac{{1 + c_{1} \sec \theta_{1o} }}{{\sqrt {1 - c_{1}^{2} } }},$$
(2)

where \(\theta_{1e}\), \(\theta_{2e}\), \(\theta_{1o}\) and \(\theta_{2o}\) are the electrical lengths corresponding to the physical lengths \(\ell_{1}\) and \(\ell_{2}\) at the even-mode resonant frequency \(f_{re}\) and the odd-mode resonant frequency \(f_{ro}\), respectively. The even-mode and odd-mode impedances of parallel-coupled lines were used in the relationship of the coupling coefficient and characteristic impedance:

$$c_{1} = \frac{{Z_{1e} - Z_{1o} }}{{Z_{1e} + Z_{1o} }},\;Z_{1} = \sqrt {Z_{1e} Z_{1o} } ,\;{\text{and}}\;c_{1} = \frac{{Z_{1e} - Z_{1o} }}{{Z_{1e} + Z_{1o} }},\;Z_{2} = \sqrt {Z_{2e} Z_{2o} } .$$

From the derived resonance conditions (1) and (2), it is revealed that the even and odd modes are splitted because of the impedance change and the self-coupling of the ring. The impedance ratio \(R\) and the coupling coefficients, \(c_{1}\) and \(c_{2}\), determine the nature (capacitive or inductive) of the extent splitting mode.

2.2 Effect of impedance ratio R

By solving Eqs. (1) and (2), the even-mode and odd-mode resonant frequencies with the impedance ratio and coupling coefficients can be obtained. The dependence of mode resonant frequencies on impedance ratio is shown in Fig. 2 by an exemplary case of c 1 = 0.2 and c 2 = 0.4. For the situation of capacitive perturbation (R < 1), the odd-mode resonant frequency is higher than the even-mode. On the contrary, for the inductive perturbation situation (R > 1), the odd-mode frequency is lower than the even mode. The variation of even-mode and odd-mode resonant frequencies increases when impedance ratio R deviates further from 1. However, the geometric mean of resonant frequencies, \(f_{r,SCR} = \sqrt {f_{re} f_{ro} }\), is unaffected by the impedance ratio.

Fig. 2
figure 2

Normalized resonant frequencies with respect to the impedance ratio R

Full size image

2.3 Effect of coupling coefficient

To examine the effect of self coupling through the central section and end sections, the resonance conditions (1) and (2) are solved for six different situations and drawn in Fig. 3.

Fig. 3
figure 3

Calculated normalized resonant frequencies with respect to the electric length θ 1 a wider range, b small scope for cases of c 1 = 0.2, c 2 = 0.4, c small scope for cases of c 1 = 0, c 2 = 0.4

Full size image

In Fig. 3, the lines for \(R = 0.8\), \(R = 1.0\) and \(R = 1.2\) are almost coincide, indicating the geometric average resonant frequency, \(f_{r,SCR} = \sqrt {f_{re} f_{ro} }\), is insensitive to the impedance ratio R but susceptible to the coupling coefficient \(c_{1}\) and \(c_{2}\). Figure 3a shows that, the average resonant frequency \(f_{r,SCR} = \sqrt {f_{re} f_{ro} }\) decrease in both capacitive and inductive perturbations with the increasing of the central self-coupling coefficient \(c_{2}\) and the decreasing of the end self-coupling coefficient \(c_{1}\). Based on the ring resonator with a dominant central self-coupling, a bandpass filter has a smaller circuit size than the filters with uncoupled uniform ring resonator. Furthermore, for the case of \(c_{2} > c_{1}\), there exists a \(\theta_{1,\hbox{min} }\) with a minimum geometric average resonant frequency, \(f_{r,SCR} = \sqrt {f_{re} f_{ro} }\), and for the case of \(c_{2} \le c_{1}\), \(\theta_{1,\hbox{min} }\) approaches zero for either capacitive or inductive perturbations. In the case \(c_{1}\), shown in Fig. 3c, the minimum geometric average resonant frequency occurs at \(\theta_{1,\hbox{min} } = 45^{ \circ }\), which is similar to the structure proposed in the report of Jeng et al. (2006), but for the case of \(c_{2} = 0.2,c_{2} = 0.4\), shown in Fig. 3b, the minimum geometric average resonant frequency occurs at \(\theta_{1,\hbox{min} } = 35^{ \circ }\). Therefore, the value of \(\theta_{1,\hbox{min} }\) is a function of \(c_{1}\) and \(c_{2}\), but almost independence of impedance ratio R, and the ring resonator based on the dominant central self-coupling has the smallest resonate frequency.

3 Transmission zeros

We name the electric length between input and output ports as \(\theta_{IO}\). Unlike the conventional ring bandpass filter, the optimized angle \(\theta_{IO}\) of the H-type bandpass filter, with the transmission zeros symmetric to the passband, is not \(90^{ \circ }\) any more. We can turn locations of transmission-zeros by the parameter \(\theta_{IO}\), end coupling length, \(\theta_{1}\) and impedance ratio,R. To examine how \(\theta_{IO}\), \(\theta_{1}\) and R affect the existence and distribution of transmission-zeros, the coupling matrix method (Hong and Lancaster 2001; Cameron 2003; Amari and Rosenberg 2001) and the admittance matrix method (Matsuo et al. 2001; Gorur 2004) have been used. The following result is that the admittance matrix method is adopted.

First, consider the case of \(\theta_{IO} < \theta_{1}\): Referred to Fig. 4a, the trans-admittance of the self-coupled ring resonator can be obtained as below:

$$Y_{21} = Q_{L} + Q_{ac} \frac{{U(G_{L} + P_{R} ) - W(H_{L} + Q_{R} )}}{{(H_{L} + Q_{R} )^{2} - (G_{L} + P_{R} )^{2} }},$$
(3)

where

$$P_{R} = P_{2} - \frac{{2P_{1} P_{2}^{2} [2c_{2}^{2} (2P_{1} Q_{2} - Q_{1}^{2} ) + (1 + c_{2}^{2} )(2P_{1}^{2} - Q_{1}^{2} + 2P_{1} P_{2} )]}}{{\cos^{2} 2\theta_{2} [(2P_{1}^{2} - Q_{1}^{2} + 2P_{1} P_{2} )^{2} - (2P_{1} Q_{2} - Q_{1}^{2} )^{2} ]}},$$
$$Q_{R} = Q_{2} + \frac{{2P_{1} P_{2}^{2} [2c_{2}^{2} (2P_{1}^{2} - Q_{1}^{2} + 2P_{1} P_{2} ) + (1 + c_{2}^{2} )(2P_{1} Q_{2} - Q_{1}^{2} )]}}{{\cos^{2} 2\theta_{2} [(2P_{1}^{2} - Q_{1}^{2} + 2P_{1} P_{2} )^{2} - (2P_{1} Q_{2} - Q_{1}^{2} )^{2} ]}},$$
$$P_{1} = - \frac{{jY_{1} \cot \theta_{1} }}{{\sqrt {1 - c_{1}^{2} } }}(1 + c_{1} \sec \theta {}_{1}),\quad Q_{1} = \frac{{jY_{1} \cot \theta_{1} }}{{\sqrt {1 - c_{1}^{2} } }}(c_{1} + \sec \theta {}_{1}),$$
$$P_{2} = - \frac{{jY_{2} }}{{\sqrt {1 - c_{2}^{2} } }}\cot 2\theta_{2} ,\quad Q_{1} = \frac{{jY_{1} c_{2} }}{{\sqrt {1 - c_{2}^{2} } }}\cot 2\theta_{2} .$$
$$Q_{L} = Q_{ac} \frac{{(1 - c_{1}^{2} )\sin^{2} (2\theta_{a} + \theta_{c} )}}{{2M\sin \theta_{c} }},\quad G_{L} = - \frac{{Q_{ac} }}{{\sin \theta_{c} }}\frac{{J(2M - c_{1}^{2} J)}}{{2(1 - c_{1}^{2} )M}},\quad H_{L} = \frac{{Q_{ac} }}{{\sin \theta_{c} }}\frac{{c_{1}^{2} J}}{{2(1 - c_{1}^{2} )M}},$$
$$Q_{ac} = \frac{{jY_{1} \sqrt {(1 - c_{1}^{2} )} }}{{\left[ {c_{1} \sin \theta_{c} + \sin (2\theta_{a} + \theta_{c} )} \right]}},$$
$$\begin{aligned} U = & \frac{{c_{1} J\sin (2\theta_{a} + \theta_{c} )}}{{2(M\sin \theta_{c} )^{2} }}[2M\sin \theta_{c} + c_{1} J\sin (2\theta_{a} + \theta_{c} )] \\ W = & \left[ {\frac{{c_{1} J\sin (2\theta_{a} + \theta_{c} )}}{{2M\sin \theta {}_{c}}}} \right]^{2} + \left[ {2M\sin \theta_{c} + c_{1} J\sin (2\theta_{a} + \theta_{c} )} \right]^{2} \\ \end{aligned}$$
$$J = [c_{1} \sin \theta_{c} + \sin (2\theta_{a} + \theta_{c} )]\cos \theta_{c} - \sin 2\theta_{a} ,\quad M = [c_{1} \sin \theta_{c} + \sin (2\theta_{a} + \theta_{c} )]\cos \theta_{c} - c_{1}^{2} \sin 2\theta_{a} ,$$
Fig. 4
figure 4

Self-coupled ring resonator for a θ IO < θ 1, b θ 1 < θ IO < 2θ 1 and c 2θ 1 < θ IO < \(\frac{\pi }{2}\)

Full size image

Second, consider the case of \(\theta_{1} < \theta_{IO} < 2\theta_{1}\): Referred to Fig. 4b, the self-coupled ring resonator has the same trans-admittance equation as (3) but different parameters as below:

$$\begin{aligned} U = c_{1} \left[c_{1} + \frac{{2\sin (2\theta_{a} + \theta_{c} )}}{{\sin \theta_{c} }}\right], \hfill \\ W = \frac{{c_{1}^{2} }}{4} + \left[\frac{{\sin (2\theta_{a} + \theta_{c} )}}{{\sin \theta_{c} }} + \frac{{c_{1} }}{2}\right], \hfill \\ \end{aligned}$$
$$Q_{L} = Q_{ac} \frac{{\sin \theta_{c} }}{2J}\left( {1 - c_{1}^{2} } \right),\quad G_{L} = \frac{{Q_{ac} }}{{\sin \theta_{c} }}\left[ {\frac{{J(c_{1}^{2} - 2)}}{{2(1 - c_{1}^{2} )}} - \sin 2\theta_{a} } \right],\quad H_{L} = \frac{{Q_{ac} }}{{\sin \theta_{c} }}\frac{{c_{1}^{2} J}}{{2(1 - c_{1}^{2} )}},$$

Third, consider the case of \(2\theta_{1} < \theta_{IO} < \frac{\pi }{2}\): Referred to Fig. 4c and following the driving process in Jeng et al. (2006), the trans-admittance of the self-coupled ring resonator can be obtained as:

$$Y_{21} = Y_{21} + Y_{21R} ,$$
(4)

where

$$Y_{21R} = Q_{R} + 2P_{1} \frac{{(S_{R}^{2} + T_{R}^{2} )(2P_{1} Q_{R} - Q_{1}^{2} ) - 2S_{R} T_{R} (2P_{1}^{2} - Q_{1}^{2} + 2P_{1} P_{R} )}}{{(2P_{1}^{2} - Q_{1}^{2} + 2P_{1} P_{R} )^{2} - (2P_{1} Q_{R} - Q_{1}^{2} )^{2} }}$$
$$Y_{21L} = Q_{L} + 2P_{1} \frac{{(S_{L}^{2} + T_{L}^{2} )(2P_{1} Q_{L} - Q_{1}^{2} ) - 2S_{L} T_{L} (2P_{1}^{2} - Q_{1}^{2} + 2P_{1} P_{L} )}}{{(2P_{1}^{2} - Q_{1}^{2} + 2P_{1} P_{L} )^{2} - (2P_{1} Q_{L} - Q_{1}^{2} )^{2} }}$$
$$P_{R} = Y_{2} \frac{ - j}{{\sqrt {1 - c_{2}^{2} } }}\cot 2\theta_{R} \quad P_{L} = Y_{2} \frac{ - j}{{\sqrt {1 - c_{2}^{2} } }}\cot 2\theta_{L}$$
$$Q_{R} = Y_{2} \frac{{jc_{2} }}{{\sqrt {1 - c_{2}^{2} } }}\cot 2\theta_{R} \quad Q_{L} = Y_{2} \frac{{jc_{2} }}{{\sqrt {1 - c_{2}^{2} } }}\cot 2\theta_{L}$$
$$S_{R} = Y_{2} \frac{j}{{\sqrt {1 - c_{2}^{2} } }}\csc 2\theta_{R} \quad S_{L} = Y_{2} \frac{j}{{\sqrt {1 - c_{2}^{2} } }}\csc 2\theta_{L}$$
$$T_{R} = Y_{2} \frac{{ - jc_{2} }}{{\sqrt {1 - c_{2}^{2} } }}\csc 2\theta_{R} \quad T_{L} = Y_{2} \frac{{ - jc_{2} }}{{\sqrt {1 - c_{2}^{2} } }}\csc 2\theta_{L}$$

The transmission zero exists if \(Y_{21}\) of (3) or (4) vanishes. (3) and (4) are too complex to get familiar form solution, the spectral response of \(Y_{21}\) for the cases of various impedance ratio R or \(\theta_{IO}\) values with c 1 = 0.2 and c 2 = 0.4 is plotted from Figs. 5, 6, 7, 8, where the frequency axis is normalized with respect to the geometric average resonant frequency, \(f_{r,SCR} = \sqrt {f_{re} f_{ro} }\).

Fig. 5
figure 5

Spectral response of Y 21 of the self-coupled ring resonator versus the various value of θ IO in the case of c 1 = 0.2, c 2 = 0.4, R = 0.9 and a θ 1 = 60°, b θ 1 = 30°

Full size image
Fig. 6
figure 6

Spectral response of Y 21 of the self-coupled ring resonator versus the various value of θ IO in the case of c 1 = 0.2, c 2 = 0.4, and θ 1 = 30°

Full size image
Fig. 7
figure 7

Spectral response of Y 21 of the self-coupled ring resonator versus the various value of θ IO in the case of c 1 = 0.2, c 2 = 0.4, R = 1.05, and θ 1 = 60°

Full size image
Fig. 8
figure 8

Spectral response of Y 21 of the self-coupled ring resonator versus the various value of θ 1 in the case of c 1 = 0.2, c 2 = 0.4, and θ IO = 110°

Full size image

3.1 Effect of the angle between input and output ports \(\theta_{IO}\)

Figure 5 reveals that for a set of parameters, \(\theta_{1}\), R, c 1 and c 2, there exists a critical angle \(\theta_{IO,\hbox{max} }\) that when the angle \(\theta_{IO}\) is smaller than \(\theta_{IO,\hbox{max} }\), there are two transmission zeros near the fundamental passband located at either side of the passband. Furthermore, both transmission zeros shift to high frequency as the angle \(\theta_{IO}\) increased. When the angle \(\theta_{IO}\) becomes greater than \(\theta_{IO,\hbox{max} }\), the transmission zero at the upper stopband disappears but the transmission zero at the lower stopband remains. Figure 5a, b were drawn with the same parameters R, c 1 and c 2, except \(\theta_{1} = 60^{ \circ }\) in Fig. 5a and \(\theta_{1} = 30^{ \circ }\) in Fig. 5b, where they have the similar tendency but \(\theta_{IO,\hbox{max} }\) dropped off from 124° to 114° as \(\theta_{1}\) decreased from 60° to 30°.

In order to make the transmission zeros distribution symmetric to the fundamental passband, the optimum angle \(\theta_{IO,op}\) is 90° for traditional dual-mode ring resonator, but now its range is 100°–110° for H-type dual-mode ring resonator from Fig. 5.

3.2 Effect of impedance ratio R

Figure 6 is the spectral response of \(Y_{21}\) with c 1 = 0.2, c 2 = 0.4, \(\theta_{1} = 30^{ \circ }\), and \(\theta_{IO}\) varying form 90° to 110°, when \(\theta_{IO} = 110^{ \circ }\) and when R = 1 there exists only one transmission zero coinciding with the geometric average resonant frequency, \(f_{r,SCR}\), which destroys the resonating condition. When R decreases from one, it enters the capacitive perturbation situation, and two transmission zeros near the fundamental passband are created, each located at either side of the passband. If R increases from one, it becomes the inductive perturbation situation, and both two transmission zeros disappear. This observation is similar with the result found in Jeng et al. (2006), Amari and Rosenberg 2001). But when \(\theta_{IO}\) departs from \(\theta_{IO,op}\), for the case of R < 1, those two transmission zeros remain. When R = 1, there still exists two transmission zeros, with one of which coinciding with the geometric average resonant frequency, \(f_{r,SCR}\), resulting in destroyed inband performance. Even if R > 1, there is still the opportunity to get two transmission zeros in the same stopband, and it can be applied to suppress undesired wideband signal. Fig 7 presents the spectral response of \(Y_{21}\) of the self-coupled ring resonator vs. the varation of \(\theta_{IO}\) value for \(c_{1} = 0.2\), \(c_{2} = 0.4\), \(R = 1.05\), and \(\theta_{1} = 60^{ \circ }\). While for \(\theta_{IO} \le 85^{ \circ }\), there exists two transmission zeros in the lower stopband.

3.3 Effect of the electric length of end coupling \(\theta_{1}\)

Figure 8 shows the spectral response of \(Y_{21}\) with respect to the various value of R and \(\theta_{1}\) in the case of c 1 = 0.2, c 2 = 0.4, and \(\theta_{IO} = 110^{ \circ }\) and there is only one transmission zero for case of R = 1, that is, \(\theta_{IO,op}\) is insensitive to the length of end coupling \(\theta_{1}\). In practical application, the range \(R\) will be 0.9–1.1, and \(\theta_{IO,op}\) could adopt about 100°–110° in H-shape resonator design.

To examine the effect of the electric length of end sections upon the location of transmission zeros, the spectral response of \(Y_{21}\) was drawn in Fig. 9 with the various value of \(\theta_{1}\) in the case of c 1 = 0.2, c 2 = 0.4, \(R = 0.9\) and \(\theta_{IO} = 110^{ \circ }\). In Fig. 9a, the input and output ports are located in the central section, and from Fig. 3b, the angle \(\theta_{1,\hbox{min} }\) with a minimum geometric average resonant frequency, \(f_{r,SCR} = \sqrt {f_{re} f_{ro} }\), equals to 35°. When \(\theta_{1}\) increases and \(\theta_{1} < \theta_{1,\hbox{min} }\), the transmission zeros go away from \(f_{r,SCR}\), contrarily, as \(\theta_{1}\) increases and \(\theta_{1} > \theta_{1,\hbox{min} }\), the upper transmission zero changes direction to approach \(f_{r,SCR}\), but the location of the lower transmission zero almost remains. In Fig. 9b, the input and output ports are located in the end sections, when \(\theta_{1}\) increases, both the transmission zeros go to high frequencies, and the lower transmission zero shifts more quickly than the upper transmission zero. Furthermore, when \(\theta_{1}\) approaches 90°, the response, \(Y_{21}\), becomes more unsymmetrical.

Fig. 9
figure 9

Spectral response of Y 21 of the self-coupled ring resonator versus the various value of θ 1 in the case of c 1 = 0.2, c 2 = 0.4, R = 0.9, and θ IO = 110° for a the input and output ports are located in the central section, b the input and output ports are located in the end sections

Full size image

4 Bandpass filter application

A 2.45-GHz bandpass filter was designed with a proposed self-coupled ring resonator on a Rogers 25 N substrate. The substrate has a dielectric constant \(\varepsilon_{r}\) of 3.38, loss tangent of 0.0025, and a dielectric layer thickness of 762 μm, and then the circuit was implement. The design procedures are described from Sects. 4.1–4.3.

4.1 Initial dimension estimation

From the result in Sect. 3, to produce pseudo-elliptic filter performance, the capacitive perturbation was selected. An impedance ratio of \(R = 0.9\) was chosen. To minimize the ring size and consider constrains, in practice the ring structure with dominant central self-coupling, c 2 = 0.395 and c 1 = 0.197 was chosen. The even- and odd-mode normalized resonant frequencies are 0.97 and 1.03. Substituting these two values into Eqs. (1) and (2) and for the purpose of folding the end sections easily, we put \(\theta_{1} = 66^{ \circ }\) and \(\theta_{1} = 24^{ \circ }\) at normalized frequency, then the geometric average resonant frequency, \(f_{r,SCR}\) will be equal to 0.998. Therefore, we obtain the initial circuit dimensions by transforming \(f_{r,SCR}\) to 2.45 GHz and designing the H-type and folding EC-type bandpass filters with the same resonator structure. The input and output tapping positions are obtainted by solving \(Y_{21} = 0\) to get \(\theta_{IO} = 113^{ \circ }\), as discussed in Sect. 3. The calculated transmission zeros are 2.078, 2.782 and 5.505 GHz. The circuit layout and electromagnetic simulation are discussed in the following sections.

4.2 Layout

The layout scheme is illustrated in Fig. 10. The filter dimensions are 13.6×14.2 mm2 and 7×17.4 mm2 for H-shape and folded type, which are 35 and 20% of the dimension of the conventional dual-mode bandpass filter, respectively.

Fig. 10
figure 10

Photos of 2.45-GHz dual-mode bandpass filter a H-shape, b foldes EC-shape

Full size image

4.2.1 3D electromagnetic simulation

The electromagnetic simulator IE3D was designed to include dielectric loss, conductor loss, spurious coupling, and finite ground plane effects. The simulation results are shown by the dash lines in Figs. 11 and 12, where the simulation insertion loss is less than 0.8, 0.78 dB and the return loss is better than 17.5, 19 dB for H-type and folded type, respectively, in the range 2.4–2.5 GHz. The transmission zeroes locate at 2.085, 2.89, 4.105, 5.075 GHz and 2.12, 2.855, 4.945, 5.375 GHz, on both side of passband. The simulated results show that this filter belongs to a second-order filter. If higher-order response is needed, a cross-coupled arrangement as reported in Hsieh and Chang (2003), Hsieh and Chang (2002), Hong and Lancaster (1996) with such resonator can be used.

Fig. 11
figure 11

Measurement and simulation results of the H-shape bandpass filter using the self-coupled ring resonator with R = 0.9, θ 1 = 66°, θ 2 = 24°, c 1 = 0.197 and c 2 = 0.395

Full size image
Fig. 12
figure 12

Measurement and simulation results of the EC-shape bandpass filter using the self-coupled ring resonator with R = 0.9, θ 1 = 66°, θ 2 = 24°, c 1 = 0.197 and c 2 = 0.395

Full size image

4.3 Measurement

The SMA connector connected to the vector network analyzer to obtain the scattering parameters is used for the measurement. The measured results are illustrated by the solid line in Figs. 11 and 12, in which the measured insertion loss is less than 1.4, 1.15 dB and the return loss is better than 10.5, 13.5 dB, in the range of 2.4 GHz from to 2.5 GHz for H-type and folded one, respectively. The measured passband range is 2.4–2.5 GHz, which dovetails with the simulation result.

The transmission zeros are located at 2.059, 2.852, 4.092, 5.035 and 2.108, 2.828, 4.886, 5.332 GHz, on both side of passband for H-type and folded one, respectively. The measured transmission zeros, i.e. 2.059, 2.852, 5.035 and 2.108, 2.828, 5.332 GHz corresponding to 2.085, 2.89, 5.075 and 2.12, 2.855, 5.375 GHz of simulated results for H-type and folded type respectively closely match the resonator inherent transmission zeros 2.078, 2.782 and 5.505 GHz calculated by Eq. (3) with the same input and output ports positions. The stopband performance comparisons of the measurement and simulation to the calculated results of transmission zeros are listed in Tables 1, 2 for H-shape and folded EC-shape bandpass filters. The shift is defined as:\({\text{shifting}} = \frac{{(f_{zn,res} - f_{zn,cal} )}}{{f_{zn,cal} }} \times 100\%\),where \(f_{zn,res}\) is the nth transmission zero frequency of simulated or measured results and \(f_{zn,cal}\) is the nth transmission zero frequency calculated by Eq. (3). We can find that the shift of transmission zero frequencies near passband are all less than 4% and the shift of the 4th transmission zero frequencies are still within 9%. It can be concluded that the 1st, 2nd and 4th transmission zeros are from the resonator structure and Eqs. (3) and (4) are useful for a dual mode bandpass filters design.

Table 1 Transmission zeros compare of the measurement and simulation to calculated results for H-shape (GHz)
Full size table
Table 2 Transmission zeros compare of the measurement and simulation to calculated results for folded EC-shape (GHz)
Full size table

5 Conclusions

A new dual-mode ring resonator, which is composed of one central coupled section connected to two identical coupled sections at both ends, is proposed. The central coupled section has a coupling coefficient c 2, a characteristic impedance Z 2, and a length \(2\ell_{2}\). The coupled sections at both ends have the same coupling coefficient c 1, the characteristic impedance Z 1 and the length \(\ell_{1}\). The mode splitting mechanism is derived from the change of the ring characteristic impedance and the self-coupling through the central and end sections. The perturbation nature is fundamentally determined by the impedance ratio R. The capacitive perturbation is generated by \(R < 1\) and the inductive perturbation by \(R > 1\). The larger the impedance ratio, the greater the frequency difference between the even and odd modes. The average resonant frequency of the even- and odd-mode is insensitive to the impedance ratio. However, it decreases with the central coupling coefficient \(c_{2}\) and increases with the end coupling coefficient \(c_{1}\).

According to specifications requirement, the transmission zeros, on both or the same side of passband, are proved to exist only for proper combination of \(R\), \(c_{1}\), \(c_{2}\) and \(\theta_{1}\). This article proposed an analysis method to save the trial-and-error time.

Two bandpass filters were designed with the proposed self-coupled ring resonator of \(R = 0.9\), \(c_{1} = 0.197\) and \(c_{2} = 0.395\). The circuit sizes are only 35 and 25% of the uncoupled uniform ring case. The measured insertion loss is less than 1.4, 1.15 dB and the return loss is better than 10.5, 13.5 dB for H-type and folded EC shape one, respectively, in the range 2.4–2.5 GHz, which dovetails with the simulation result. The measurement transmission zeros 2.059, 2.852, 5.035 GHz for H-type and 2.108, 2.828, 5.332 GHz for folded type corresponded to 2.085, 2.89, 5.075 and 2.12, 2.855, 5.375 GHz of simulated results respectively, closely matching the resonator inherent transmission zeros 2.078, 2.782 and 5.505 GHz calculated by our proposed formulas with the same input and output ports positions. The shift of transmission zero frequencies near passband is less than 4% and the shift of the 4th transmission zero frequencies is still within 9%, and we can conclude the 1st, 2nd and 4th transmission zeros come from the resonator structure. The implement results show the analysis method can be used to design the bandpass filter and forecast its implement precisely.