1 Introduction

Microwave devices based on miniaturized electrical circuits represent the main objective of most designers. For the filtering field, multiband filters can meet the needs of miniaturization. See their electronic functions; multiband filters for bandpass behavior [1,2,3] can be exploited for several applications. The design of these filters, such as dual-band, tri-band, and quad-band, is influenced by two major factors, the interference problem [4] and loss constraint [5,6,7]. Therefore, an appropriate choice of design material for multiband filters is more recommended to solve the indicated problems also to avoid systematic constraints, especially in the microwave regime. After several studies, a new class of materials called « metamaterials» has shown its effectiveness and its usefulness during the design and the realization of multiband filters.

Since the first proposal to study and design them by the physicist V. Veselago [8] in 1967, metamaterials have enabled researchers and designers to develop devices and systems used in various technical fields. The first metamaterial structure (1-D) is made by J. Pendry [9]; this low-dimensional structure exhibits magnetic resonance for unusual physical properties. These physical properties where the electric permittivity and the magnetic permeability can have negative values [10, 11] define a new behavior of this kind of medium; it is left-handed medium [12, 13]. In microwaves, designing a device for small sizes with modest losses was an almost imaginary operation. Nowadays, the left-hand metamaterials dedicated to the resonators’ design involved in microwave devices offer the main advantage that can achieve this compromise of having a miniaturized device with low losses [14, 15].

In the fundamentals of multiband microwave filters (for the various frequency bands) designed by ordinary SRRs and complementary CSRRs split-ring resonators, the choice of the geometric shape, the optimization of the size, and the location of the resonator in the overall configuration can justify the difference in the electrical qualities of one filter from the other. A dual-band bandpass filter has been proposed in [16], in which two resonance frequencies are considered at 1.8 and 2.27 GHz, respectively. This filter is based on two split-ring co-directional resonators charged by interdigital capacitor. In [17], a modified CSRR structure at coplanar waveguide (CPW) ground plane is investigated for designing of dual-band bandpass filter with minimum insertion loss of 0.5 and 0.4 dB at 1.8 and 3.2 GHz, respectively. For the design of a tri-band filter, Jubaer et al. have proposed a novel nested circular-shaped metamaterial resonator, and this resonator has a labyrinth double-split open loop (ORLS). The designed filter shows a bandpass behavior for three center frequencies at 3.01, 7.39, and 12.88 GHz and covers S-, C-, and X-band [18]. In [19], a multilayer tri-band filter was realized based on a stub loaded U-shaped step impedance resonator (SLU-SIR). The realized filter shows three resonances at 2.45, 4, and 5.75 GHz. Bage et al. reported a quad-band filter based on the combination of a slot ring and complementary split-ring resonators. The obtained filter which is printed on the substrate of Roger RO 4350 resonates at frequencies 8.51/9.46/10.47/12.05 GHz for -3 dB bandwidth 0.256/0.2287/0.445/0.755 GHz, respectively [20]. In [21], a multiple-band terahertz metamaterial filter consisting of a U-type resonator surrounded by two same sizes of metallic split rings has been proposed. This filter has four resonance dips with near zero transmission rates, of which three dips have narrow line-widths, about one-quarter of the other dip. Sasi Princy et al. used two hexagonal-shaped metamaterial resonators for the design of a frequency-selective surface (FSS) filter operating in the terahertz range. The designed filter for band-stop behavior shows five resonances in TE modes at 0.078, 0.142, 0.3, 0.39, and 0.47 THz and four resonances in TM modes at 0.194, 0.308, 0.456, and 0.497 THz [22].

In this paper, we provide a triple-band bandpass filter for a new design. The proposed TBBPF consists of two metamaterial SRRs for the same E–Z tapered shape. The two EZ-SRRs are chosen from three studied resonators which have two different sizes and optimized to be able to cover the, C- and X-band. Our TBBPF is fed in parallel mode by two microstrip lines. These identical feed lines have lengths proportional to the proposed configuration of the global filter to have the necessary adaptation to 50 Ω. The two resonators forming the filter are interconnected by a conductive segment to create the third resonance. The novelty of this research is that the TBBPF is simple in design; it bases on a new shape of a minimal number of tapered metamaterial resonators EZ-SRRs. These resonators allowed the proposed filter to be compact and more miniature with dimensions of 1.10 \(\lambda_{0} \times\) 0.73 \(\lambda_{0}\); In addition, the proposed filter produces three fractional bandwidths of 5.21, 3.19, and 9.3% at frequencies of 4.22, 7.36, and 9.35 GHz, respectively. Among the novelties of this work, we note the use of the chain matrix of the proposed filter associated with the equivalent electrical circuit. The use of this approach has offered us a more detailed analysis of the electromagnetic qualities of the filter from its dispersion. The TBBPF provides a spectral response that covers both C- and X-bands that exhibited to fit for the application of wireless communication, sensors, and also radar systems.

The rest of this paper is described in the following sections. In Sect. 2, the design procedure is presented; the geometric parameters of the proposed EZ-SRR resonator and the configuration of the global filter are presented. Section 3 lists the simulation results with appropriate discussion. Finally, Sect. 4 concludes the paper with a summary describing the main lines of the proposed work.

2 Design procedure

2.1 Proposed EZ-SRR

As in the case of the ordinary split-ring metamaterial resonator SRR, the tapered metamaterial resonator can be represented by an equivalent inductance (\(L\)) and capacitance (\(C\)). The most important characteristic provided by the tapered resonator is that we can simultaneously increase its equivalent inductance and capacitance, which is not justified for the ordinary SRR. This increase can contribute to have a remarkable miniaturization for the circuits using tapered SRRs. For our design, we proposed a new geometric shape to obtain our EZ-SRR metamaterial tapered resonator. The designed EZ-SRR is formed by three copper patches; two of them are E-shaped and the third has a Z-shape. The two E-shaped patches are tapered to be able to add the other Z-shaped patch inside and also to have the maximum electromagnetic coupling. This configuration allows us to have a coupling in both horizontal and vertical planes between the outer rings of the resonator formed by the two E-shaped patches and the inner ring formed by the Z-shaped patch. The outer rings are coupled together by the \(g_{2}\) gap and for the inner ring are coupled by the \(g_{1}\) gap. The outer ring and inner segment that form the proposed EZ-SRR are shown in tapered mode by Fig. 1.

Fig. 1
figure 1

Proposed EZ-SRR, representation in ring with side view

Full size image

The resonance of each EZ-SRR is obtained according to its dimensions (the smallest one will have the largest resonance and vice versa, the medium-sized resonator will have a resonance located between the two lower and upper resonances). Our proposed EZ-SRR has the two different sides \( \left( {X,Y} \right)\); it should resonate in the C-band for the lower frequency. For this reason, the wavelength will be 75 mm for the lower frequency of the band which is 4 GHz. To select the desired frequency bands, we will study the EZ-SRR resonator for three different \( \left( {X,Y} \right)\) pairs (\(X_{1} =\) 18 mm, \(Y_{1} =\) 15 mm), (\(X_{2} =\) 22 mm, \(Y_{2} =\) 18 mm) and (\(X_{3} =\) 25 mm, \(Y_{3} =\) 22 mm). Therefore, the EZ-SRR that resonates in the C-band is the larger resonator EZ-SRR3. Since metamaterial structures can resonate at quarter-wave (\(\lambda /4\)) and the lower frequency in the c-band corresponds to 18.75 mm, so beyond this length (period), such a resonator (EZ-SRR3 in our case) can resonate at the desired C-band and all smallest resonators can resonate at other higher frequencies. For our choice, the EZ-SRR3 justifies this condition for both sides (\(X\) or \( Y \approx \lambda /4\), since for tapered shapes \( X \ne Y\)). For the three resonators, we fix the dimensions (\(w_{2} =\) 4 \(w_{1}\), \(g_{2} =\) 4 \(g_{1}\) with \( w_{1} = g_{1}\),\( w_{2} = g_{2}\), \(L =\) 1.2 mm and \(S =\) 0.6 mm). For these conditions, we obtain three EZ-SRR resonators of different sizes. The dimensions of the proposed EZ-SRR for the three sizes are summarized in Table 1.

Table 1 Dimensions of the EZ-SRR for different (\(X,Y\))
Full size table

2.2 Overall filter configuration

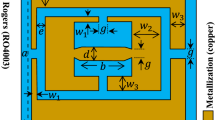
The overall filter is formed by two metamaterial resonators EZ-SRRs among the three resonators previously proposed for the study. We chose the resonators (EZ-SRR)2 and (EZ-SRR)3 which have a medium and the large area, respectively. These two metamaterial resonators are linked by a conductive segment of length (\(L_{s} = 2\theta + 2W + L_{2} + L_{3} + w_{1} + w_{1} =\) 9.7 mm: the first \(w_{1}\) for EZ-SRR2 and the second \(w_{1}\) for EZ-SRR3) and width (\(w_{s} =\) 0.8 mm). The electromagnetic coupling zone is located in the region of the filter where the constituent elements approach the feed lines (here, we discuss the coupling between the two EZ-SRRs connected by the segment with the feed lines). The coupling level reaches its maximum value when the spacing between the different elements will be in the micrometric scale; in this case, we will have a risk of increased losses in the filters. For our design, we have chosen dimensions in the millimeter scale to have the necessary miniaturization without increasing the losses.

The filter is fed in microstrip technology by two identical planar lines of lengths (\(L_{in} = L_{out} =\) 37.3 mm) and widths (\(W =\) 1.75 mm) at the input and output. The spacing between the segment and the fed lines is of the order of \(e =\) 1.5 mm, and this segment is connected in two Z-shaped by a distance \(\theta\) where (\(e - \theta =\) 0.6 mm). The global filter configuration is shown in Fig. 2.

Fig. 2
figure 2

Proposed TBBPF configuration with various geometrical parameters

Full size image

Our proposed TBBPF has an equivalent electrical circuit which has a chain matrix of parameters \( ABCD\). This circuit has impedances \(Z_{s}\) and \(Z_{p}\) in series and parallel branches, respectively. The equivalent electric circuit is represented by a quadrupole in \(\pi -\), and it is shown in Fig. 3.

Fig. 3
figure 3

Representation of the TBBPF by the equivalent circuit in π-

Full size image

The ABCD chain matrix of the filter (for a quadrupole representation) is given by

$$ \left[ {\begin{array}{*{20}c} {V_{1} } \\ {I_{1} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {A B} \\ {C D} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {V_{2} } \\ { - I_{2} } \\ \end{array} } \right]. $$
(1)

With

$$ \left[ {ABCD} \right] = \left[ {\begin{array}{*{20}c} {1 + \frac{{Z_{s} }}{{Z_{p} }} Z_{s} } \\ {\frac{2}{{Z_{p} }} + \frac{{Z_{s} }}{{Z_{p}^{2} }} 1 + \frac{{Z_{s} }}{{Z_{p} }}} \\ \end{array} } \right]. $$
(2)

3 Results and discussion

3.1 Analysis of the EZ-SRR characteristics

In planar technology, a good choice of dielectric substrate can improve the electrical qualities of our EZ-SRRs. The choice of such a substrate is generally made according to two criteria: losses and absorption coefficients. The Rogers (RO4003) represents the least absorber substrate, which meets the requirements of metamaterial filters [23, 24]. It is an available substrate which has a relative permittivity of 3.55 and dielectric loss tangent of 0.0027. The main advantage of the RO4003 is that it is a low-loss material and has two different types of glass cloth; as a result, it has superior electrical and mechanical properties. Among the significant features of the Rogers RO4003 are its ease of construction and its high-frequency characteristics, it is an essential component of every communication system. We will use this type of substrate for a thickness (\(h =\) 0.82 mm). The EZ-SRR of each proposed (\(X, Y\)) must be printed in copper for a thickness (t = 0.035 mm). The boundary conditions in simulation model for one of the three EZ-SRRs [(EZ-SRR)2 in Table 1] whose \(X =\) 22 mm and \(Y =\) 18 mm are shown in Fig. 4.

Fig. 4
figure 4

Boundary conditions for (EZ-SRR)2 simulation

Full size image

We have introduced the necessary boundary conditions which are fixed according to the electromagnetic field (\({\varvec{E}}\) and \({\varvec{H}}\)) propagating in our resonator (EZ-SRR)2. Therefore, the direction of propagation \({\varvec{k}}\) must be perpendicular to the dual E-shaped outer ring and the Z-segment forming the (EZ-SRR)2. Therefore, for the two faces perpendicular to \({\varvec{k}}\), we place the WAVEPORT1 and WAVEPORT2, respectively. The magnetic field \({\varvec{H}}\) must be perpendicular to the two gaps (\(g_{1}\) and \( g_{2}\)) of the resonator on the two surfaces of the ray box (PMC1 and PMC2). The electric field \({\varvec{E}}\) must be maintained in such a way that \({\varvec{E}}\)⊥\(\user2{ H}\) and \({\varvec{E}}\)⊥\(\user2{ k}\), as shown in Fig. 4.

The calculation of the reflection and transmission coefficients for the two ports of the resonator is obtained using the \(S\) parameters (according to the power flow through the ports)

$$ \left\{ {\begin{array}{*{20}c} {{\text{S}}_{11} = \frac{{\sqrt {{\text{Power reflected from port }}1} }}{{\sqrt {{\text{Power incident on port }}1} }}} \\ {{\text{S}}_{22} = \frac{{\sqrt {{\text{Power reflected from port }}2} }}{{\sqrt {{\text{Power incident on port }}2} }}} \\ \end{array} } \right. $$
(3)

and

$$ \left\{ {\begin{array}{*{20}c} {{\text{S}}_{12} = \frac{{\sqrt {{\text{Power delivered to port }}1} }}{{\sqrt {{\text{Power incident on port }}2} }}} \\ {{\text{S}}_{21} = \frac{{\sqrt {{\text{Power delivered to port }}2} }}{{\sqrt {{\text{Power incident on port }}1} }}} \\ \end{array} } \right., $$
(4)

where \({\text{S}}_{11}\) and \({\text{S}}_{22}\) are the reflection coefficients at the filter input and output, respectively.

After having applied all these criteria on each resonator, the reflexion and the transmission coefficients of the three EZ-SRRs are shown in Fig. 5.

Fig. 5
figure 5

Frequency response for the three EZ-SRRs: a reflection coefficient and b transmission coefficients

Full size image

Figure 5 shows in the [2 \(-\) 12] GHz range the reflection and the transmission coefficients of the three EZ-SRRs resonators for different sizes according to the different couples \( \left( {X,Y} \right)\). According to its frequency characteristics, we notice that each EZ-SRR has a band-stop behavior. The magnetic resonance of each resonator is obtained according to its dimensions. For the smallest EZ-SRR studied for \( \left( {X,Y} \right) =\) (18, 15), we have the most important resonance and vice versa. Therefore, for the (EZ-SRR)1, the resonance is 8.32 GHz with maximum attenuation of \(-\) 25.57 dB; for the (EZ-SRR)2, we have two resonances at 7.12 GHz and 7.78 GHz with maximum attenuations of \(-\) 23.54 dB and \(-\) 35.08 dB, respectively. For the (EZ-SRR)3, the resonance is 7.30 GHz with maximum attenuation of \(-\) 11.51 dB. According to these three frequency characteristics, it is noted that the two resonators, the larger and the middle resonate in the C-band [4 \(-\) 8] GHz, but the smaller one resonates outside this frequency band.

For the medium resonator (EZ-SRR)2, we will present the refractive index (\(n_{eff}\)) characteristics. Nicolson–Ross–Weir (NRW) method [25, 26] is more usual for extracting this kind of effective parameters. The information obtained from HFSS related to the reflection coefficient \(\left| {S_{11} } \right|\) and transmission coefficient \( \left| {S_{21} } \right|\) can be used in NRW approach to extract these parameter values. In this approach, two composite terms \( V_{1}\) and \( V_{2}\) are initiated by the subtraction and addition of \( \left[ S \right]\) parameter values [27, 28].

The refractive index of the (EZ-SRR)2 is defined by relation

$$ n_{eff}^{2} \left( f \right) = \mu_{eff} \left( f \right) \varepsilon_{eff} \left( f \right), $$
(5)

with

$$ \left\{ {\begin{array}{*{20}c} {\mu_{eff} \left( f \right) = \frac{2}{jkh}\frac{{1 - V_{1} }}{{1 + V_{1} }}} \\ {\varepsilon_{eff} \left( f \right) = \frac{2}{jkh}\frac{{1 - V_{2} }}{{1 + V_{2} }}} \\ \end{array} } \right.; $$
(6)

\(k\) is the wave number, it is equal to \(\omega /c_{0}\) (\(\omega\) is the frequency in rad/s), and \(c_{0}\) is the speed of light. \(h\) is the thickness of the used substrate.

and

$$ \left\{ {\begin{array}{*{20}c} {V_{1} = \left| {S_{21} } \right| - \left| {S_{11} } \right|} \\ {V_{2} = \left| {S_{11} } \right| + \left| {S_{21} } \right|} \\ \end{array} } \right.. $$
(7)

We find

$$ n_{eff} \left( f \right) = \frac{2}{jkh}\sqrt {\left( {\frac{{1 - \left| {S_{21} } \right| + \left| {S_{11} } \right|}}{{1 + \left| {S_{21} } \right| - \left| {S_{11} } \right|}}} \right)\left( {\frac{{1 - \left| {S_{21} } \right| - \left| {S_{11} } \right|}}{{1 + \left| {S_{21} } \right| + \left| {S_{11} } \right|}}} \right)} . $$
(8)

The real and imaginary parts of the refractive index of the (EZ-SRR)2 are shown in Fig. 6.

Fig. 6
figure 6

Refractive index of the (EZ-SRR); real and imaginary parts

Full size image

Our metamaterial resonator represents a complex refractive index when the two real and imaginary parts depend on the frequency. Figure 6 shows this variation in [2 \({-}\) 12] GHz range. We notice that around its magnetic resonance, the real part of the refractive index changes the sign (positive and becomes negative). Moreover, on the frequency range (where the real part is negative), the (EZ-SRR)2 represents an unconventional medium called "left-handed medium". In addition, this resonator can be represented by a resonant circuit (\(L_{l} , C_{l}\)) where \(C_{l}\) will be in the series branch and \(L_{l}\) will be in the parallel branch. At the 7.84 GHz resonance, the refractive index is written \(-\) 7.27 \(+\) \(i\) 6.68; this characteristic, which does not exist for other types of resonators, can improve the electrical qualities of our proposed filter especially for the minimization of losses.

The quality of the refractive index \(n\) of our (EZ-SRR)2 is defined by its Figure of Merit (FOM) which can estimate the losses in this structure. The FOM is given by the following expression [29]:

$$ FOM = - \frac{{Re\left( {n_{eff} } \right)}}{{Im\left( {n_{eff} } \right)}}. $$
(9)

The FOM is shown in Fig. 7.

Fig. 7
figure 7

The Figure of Merit (FOM) of the studied (EZ-SRR)

Full size image

Figure 7 shows the frequency characteristics of the Figure of Merit for the (EZ-SRR)2, and we note that the FOM of this resonator is resonated in the C-band, while a peak of maxima appears around the resonance, where we have exactly (FOM = 1.08) for the frequency 7.76 GHz. This maximum value of the FOM allows us to conclude that the (EZ-SRR)2 resonator can contribute to the design of our proposed filter or any other microwave device without correspondingly increasing the losses in these devices for the proposed dimensions.

3.2 Spectral responses of the proposed TBBPF

The two EZ-SRRs’ resonators constituting the filter and the feed lines are printed on the same substrate used for the study of EZ-SRRs and for the same thickness (\(h =\) 0.82 mm). Our global filter prepared for the simulation has a surface calculated according to each geometric parameter of the elements constituting this filter. We have (\(m = L_{in} + L_{out} + w_{s} + 2e\) and \( n = d_{1} + d_{2} + 2W + b_{2} + b_{3} + 2\theta\)). With \(d_{1} = d_{2} =\) 4.5 mm, \(b_{2} =\) 16.8 mm and \(b_{3} =\) 20.8 mm (\(b_{2} = b\) for the medium resonator and \(b_{3} = b\) for the large resonator), the global filter surface becomes \(\left( {m \times n} \right) =\)(78.4 \(\times\) 51.9) mm2 \(=\) 4068.96 mm2. The proposed TBBPF (for these dimensions) is shown in Fig. 8.

Fig. 8
figure 8

The proposed filter with feeding ports

Full size image

The spectral responses of the proposed TBBPF are shown in Fig. 9.

Fig. 9
figure 9

The proposed filter responses

Full size image

The frequency response of our filter is shown in Fig. 9. We notice that it is a tri-band bandpass filter for three different resonances. For the first two resonances 4.22 and 7.36 GHz located in the C-band, the filter has the insertion losses (IL) of 1.38 and 4.86 dB, respectively. The third band is centered on the 9.35 GHz resonance located in the X- band and the filter has the insertion losses (IL), 2.34 and 1.27 dB for this band. The electromagnetic qualities of the two metamaterial resonators constituting the filter make it possible to reduce the losses, which are justified by these modest values of (IL) at the frequencies of 4.22 and 9.35 GHz. In microstrip technology, the conductive segment connecting the two EZ-SRRs provides an inductive effect (L-value induction can associate with this segment). The location of this segment between the two microstrip feed lines causes a capacitive coupling justified by the electric field concentration located in this region (associated capacitance), which contributes to the creation of the third resonance of 7.36 GHz located between the two extreme resonances (lower in the C-band and higher in the X-band). We also observe two gaps between one bandwidth and the other. A significant gap is observed between the first and the second band which allows having an important rejection band of the order of 3.14 GHz. This band contains two zero transmission frequencies which are \(f_{z1} =\) 4.86 GHz and \(f_{z2} =\) 6 GHz, for the two rejections of \(-\) 86.68 and \(-\) 90.75 dB, respectively. The second rejection band is observed between the second and the third bandwidth, and it defines a rejection band of the order of 1.7 GHz for the third and the fourth zero transmission frequency of \(f_{z3} =\) 7.8 GHz and \(f_{z4} =\) 8.16 GHz, for the two rejections of \(-\) 64.19 and \(-\) 70.28 dB, respectively.

Applying the Bloch–Floquet theorem [30] on the obtained ABCD matrix of the filter (with the equivalent electrical circuit shown in Fig. 3), a dispersion diagram can be obtained as

$$ \beta \left( \omega \right) = \frac{1}{d}cos^{ - 1} \left[ {1 + Z_{s} \left( \omega \right)Y_{p} \left( \omega \right)} \right] = \frac{1}{d}cos^{ - 1} \left( {\frac{A + D}{2}} \right). $$
(10)

When

$$ \left\{ {\begin{array}{*{20}c} {A = \frac{{\left( {1 + S_{11} } \right)\left( {1 - S_{22} } \right) + S_{12} S_{21} }}{{2S_{21} }}} \\ {D = \frac{{\left( {1 - S_{11} } \right)\left( {1 + S_{22} } \right) + S_{12} S_{21} }}{{2S_{21} }}} \\ \end{array} } \right.. $$
(11)

We calculate the quantity \(\left( {A + D} \right)/2\), and the dispersion of the filter is obtained as a function of the reflection and transmission coefficients (at the input and the output) by the following expression:

$$ \beta d = cos^{ - 1} \left( {\frac{{1 - S_{11} S_{22} + S_{12} S_{21} }}{{2S_{21} }}} \right). $$
(12)

The dispersion diagram of the proposed filter is shown in Fig. 10.

Fig. 10
figure 10

Dispersion diagram for the proposed TBBPF

Full size image

Figure 10 represents the dispersion of the filter over the frequency range [2 \(-\) 12] GHz on which we observe the three Pass bands of the filter. For the first band (4.11 to 4.33 GHz), we notice that the dispersion characteristic has both a negative slope (\(\beta <\) 0) and another which is positive (\(\beta >\) 0), which makes it possible to define the first region composite right hand/left hand (CRLH1). For the second band (7.24 to 7.47 GHz), the same characteristic is observed which can define the second region CRLH2. From 8.91 GHz to 9.78 GHz, the CRLH3 can be observed. On the same figure, we notice that phase constant is null (\(\beta =\) 0) at the frequency of 7.95 GHz, which corresponds to the evanescent modes in the filter near the net zero transmission at this frequency (shown in Fig. 9).

For the three Pass band of the proposed filter, the Fractional Bandwidth is given by the following expression:

$$ FBW\left( \% \right) = \frac{\Delta f}{{f_{0} }}, \forall f \in \Delta f, $$
(13)

with \(\Delta f = f_{h} - f_{l}\) (\(f_{h}\) and \(f_{l}\) are the hightest and lowest cut-off frequencies, respectively) and \(f_{0} = \frac{\Delta f}{2} + f_{l}\) is the center frequency of each bandwidth.

We obtain

$$ FBW\left( \% \right) = 2\frac{{f_{h} - f_{l} }}{{f_{h} + f_{l} }}. $$
(14)

To understand the mechanism of the electromagnetic wave propagating in our filter, the electric field confinement for the three resonances is shown in Fig. 11.

Fig. 11
figure 11

Electric field distribution at resonance frequencies: a \(f_{{r_{1} }} =\) 4.22 GHz, b \(f_{{r_{2} }} =\) 7.36 GHz, and c \(f_{{r_{1} }} =\) 9.35 GHz

Full size image

Figure 11 represents the electric field distribution on the proposed filter at the three resonances. The transfer of electromagnetic energy (in the sense of density which is defined from the Poynting instantaneous vector expressed as a function of the electric and magnetic field) is obtained according to this distribution. For the first resonance, the electric field is condensed in both feed lines and also in the large resonator. At the second resonance, the electric field is concentrated in the coupling zone, especially in the arm connecting the two EZ-SRRs, which creates the band located between the two lower and upper bandwidths. At the third resonance, the electric field is transferred to the second and small EZ-SRR, which justifies the electromagnetic energy transfer for the two ports of the proposed filter. These results can be validated by comparing them with the experimental results of similar work reported in [31,32,33,34,35,36].

The obtained results can be generalized in the nanoscale, respecting the appearance of several parameters related to this scale. Generally, the transition to the nanoscale requires a parametric study of several physical phenomena that appear as a result. The most important among them is the phase transformation (PT). This transformation in our SRRs’ metamaterial demonstrates the formation of nanovoids. The existence of these nanovoids leads us to the study of several important parameters, except the evolution of the high-pressure phase (HPP) [37] and the formation of martensitic nanostructures [38]. Other parameters may be considered such as the ratio of solid–solid interface energies, mobility, and high-melting-point eXplosive (HMX) [39].

3.3 Comparison

To discuss the performance of our TBBPF, it was necessary to launch in this section a comparison of the different electrical qualities of the proposed filter with those of other works listed in the literature of multiband filters. Table 2 can describe this comparison.

Table 2 Comparison between the proposed TBBPF and some previously reported tri-band filters
Full size table

Table 2 represents a detailed performance comparison of our proposed TBBPF (Resonator structure, Frequency bands, Filter area, Fractional Bandwidth, Insertion and Return loss) with those of other tri-band bandpass filters listed in the literature [40,41,42,43,44]. It is seen from Table 1 that the filters studied in [40,41,42,43] are operated for the frequency bands P-, S-, L-, and C-. In [44], the two application bands are identical to those of the proposed filter (C- and X-band). Furthermore, for the IL losses of the filters studied in [40, 42], two bands have values less than 1 dB, while in [41, 44], only one band has losses (less than 1 dB). For our proposed filter and as in [43], the three bands have IL better than 1 dB, but we notice that they have values (\(<\) 3 dB) and also return loss better than 15 dB over the bandwidth. Besides, the filters designed in [40,41,42] have a Fractional Bandwidths better than 10%, and for the proposed TBBPF, the FBW of one band among the three obtained is better than 9%, whereas for the designs of [43, 44], the FBW are less than 8%.

4 Conclusions and future work

In summary, a new design approach for bandpass microwave filters has been provided in this paper. The TBBPF design procedure is based on the electromagnetic qualities of metamaterial tapered resonators proposed for an interconnected (E–Z) shape. The TBBPF consists of two EZ-SRRs chosen from three resonators studied and fed by two microstrip lines coupled in parallel. Our filter is optimized to have a surface area of (1.1 \(\lambda_{0} \times\) 0.73 \(\lambda_{0}\)) mm2 at the lower frequency of 4.22 GHz. The obtained results show a bandpass behavior for a frequency response covering the C- and X-band for three pass bands of widths 220, 230, and 870 MHz and Fractional Bandwidth of 5.21, 3.19, and 9.3%, respectively. The electromagnetic qualities of the TBBPF obtained by the proposed design show significant rejection bands (see 3.14 GHz and 1.7 GHz), which offers a main advantage to avoid interference with other microwave transmission systems. The novelty of this research is that the design of the proposed filter is based on a new shape of metamaterial resonators which allows it to have the desired electromagnetic qualities such as resonance on three different bandwidths for a compact size and also for minimal losses. The comparison of the performance of our proposed tri-band filter with other TBBPFs studied in the literature can justify the concordance of our design with microwave and wireless communications applications. It is anticipated that more novel fully balanced metamaterial filters will be seen in the near future. The transition to the micrometric scale which leads to THz frequencies provides designs and constructions that are enormously sensitive to physical phenomena. At the nanoscale, the behavior of the phase transformation in metamaterial resonators becomes mystifying. The phase field approach (PFA) becomes a necessity for the design of SRRs. Therefore, future research should examine more carefully the potential effects of the geometric shape and dimensions of metamaterial resonators on the electrical qualities of multiband filters. Obviously, the use of other methods and design techniques could be investigated, since they have an important influence on the results obtained at the end.