Efficient all-optical control of solitons

Abstract

We consider the phenomenon of an optical soliton controlled (e.g. amplified) by a much weaker second pulse which is efficiently scattered at the soliton. An important problem in this context is to quantify the small range of parameters at which the interaction takes place. This has been achieved by using adiabatic ODEs for the soliton characteristics, which is much faster than an empirical scan of the full propagation equations for all parameters in question.

1 Introduction

The idea of controlling light by light becomes increasingly popular as new optical and optoelectronic technologies become available (Miller 2010). A possible scheme is scattering of a low-intensity dispersive wave (DW) packet at an optical soliton mediated by cross-phase modulation (XPM) in a nonlinear fiber (De Sterke 1992). The XPM interaction induces frequency conversion of the DW (Yulin et al. 2004; Skryabin and Yulin 2005; Efimov et al. 2005; Lobanov and Sukhorukov 2010; Rosanov et al. 2011) if the group velocity of the DW is close enough to the group velocity of the soliton. The soliton in turn acquires a permanent shift in frequency and time delay. Moreover, it may experience an all-optical switching to a new state with considerable gain (loss) in peak power (Demircan et al. 2011, 2014). This phenomenon has been observed in experiments (Tartara 2012, 2015; Wimmer et al. 2013; Webb et al. 2014); it is a generic effect which appears in many nonlinear wave systems (Demircan et al. 2012).

The reflection of the DW depends on fiber dispersion, carrier frequencies of both pulses, their amplitudes, and initial delay. It only occurs in a very small range of parameters, and within this ranges it is most sensitive to the particular choice of initial delay and amplitude. Since parameter search by direct numerical simulations with the full generalized nonlinear Schrödinger equation (GNLSE) is time consuming, the prediction of adequate initial parameter ranges is particularly useful. We shall quantify the DW reflection and find the parameter ranges in which the changes in soliton characteristics are most pronounced.

The adequate parameter values were obtained by scale separation between the “fast” DW scattering and “slow” evolution of the soliton. We start with two simplified propagation equations, one for the soliton and one for the DW. These equations are coupled by the XPM terms. Using a multiscale approach we then introduce adiabatic equations for the soliton parameters. The solution resides in results from soliton perturbation theory combined with quantum mechanical scattering theory for the DW. The predicted optimal parameter values are tested against numerical solutions of the full GNLSE.

2 An exemplary numerical simulation

Figure 1a, b shows possible profiles (here for bulk silica) of the group delay $\beta '(\omega )$ and the group velocity dispersion $\beta ''(\omega )$ (GVD) that favor scattering of DWs at solitons. Here the dispersion relation is encoded by $k=\beta (\omega )$. The carrier frequencies of soliton and DW ($\omega _a$ and $\omega _b+\varOmega$ respectively) belong to opposite sides of the zero dispersion frequency at which $\beta ''(\omega )$ vanishes. The reference frequency $\omega _b$ is chosen such that $\beta '(\omega _{a})=\beta '(\omega _{b})$, note that $\beta ''(\omega _{a})<0$ and $\beta ''(\omega _{b})>0$. $\varOmega$ denotes the small initial DW frequency offset from $\omega _{b}$. The arrows in Fig. 1a indicate frequency shifts that lead to energy transport from the DW to the soliton and thus to increase of the soliton peak power.

Fig. 1

A typical (here: bulk silica) profile of a the group delay $\beta '(\omega )$ and b group velocity dispersion $\beta ''(\omega )$ that leads to the collision phenomenon shown in Fig. 2. Collision can only be realized for initial DW frequency offsets in a small interval (shaded grey) around the reference frequency of matching group velocity

Fig. 2

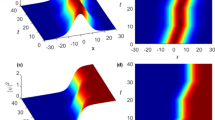
An exemplary reflection of a DW from a soliton. a Normalized power in space-time representation. The DW is less intense than the soliton. The chosen frame of reference co-propagates with the unperturbed soliton. b, c normalized power in frequency domain for soliton and DW respectively. See Fig. 1 for the carrier frequencies and text for explanation of the patterns A–D

Figure 2 shows how a DW scatters at a soliton in a typical simulation of the full GNLSE. The electromagnetic power density (Fig. 2a) is plotted in space-time domain in a frame that co-moves with the unperturbed soliton. The monochromatic DW (A) approaches the initially stationary soliton (B) and, being reflected, yields an interference picture (C). The soliton is compressed and deflected (B, D). The reflected part of the DW is frequency shifted, as clearly seen in the frequency domain (Fig. 2c). Like the DW, the soliton is frequency shifted during reflection (Fig. 2b), although this effect is less pronounced. The frequency shifts correspond to arrows in Fig. 1a and to the energy transfer from the DW to the soliton. Steepness of the fiber dispersion is of crucial importance for the soliton evolution. If a small increase in the soliton carrier frequency leads to a significant decrease of its GVD, the soliton peak power significantly increases. The peak-power increase for the profiles in Fig. 1a, b is clearly observable, though not very strong (see below).

3 Model

As can be seen in Fig. 2b, c, the spectra of soliton and DW are neatly separated and remain so even after scattering. This observation suggests to describe the total electric field by two envelopes: $\psi _a(z,\tau )$ for the soliton and $\psi _b(z,\tau )$ for the DW. Here $\tau =t-\beta '(\omega _a)z=t-\beta '(\omega _b)z$ is introduced as the common retarded time (Fig. 1a). The envelopes solve the following system of two GNLSEs

$$\begin{aligned} i\partial _z\psi _a + \sum _{j=2}^J \frac{\beta ^{(j)}_a}{j!} (i\partial _\tau )^j \psi _a + \frac{n_{2a}}{c} (\omega _a+i\partial _\tau ) \left( |\psi _a|^2+2|\psi _b|^2 \right) \psi _a =0, \end{aligned}$$

(1)

$$\begin{aligned} i\partial _z\psi _b + \sum _{j=2}^J \frac{\beta ^{(j)}_b}{j!} (i\partial _\tau )^j \psi _b + \frac{n_{2b}}{c} (\omega _b+i\partial _\tau ) \left( |\psi _b|^2+2|\psi _a|^2 \right) \psi _b=0, \end{aligned}$$

(2)

which are coupled by the XPM terms. The dispersion parameters $\beta _{a,b}^{(j)}$ are the derivatives $\beta ^{(j)}(\omega _{a,b})$, the total field is given by

$$\begin{aligned} E(z,t) = \mathop {\mathrm {Re}}\left[ \psi _{a}(z,\tau ) e^{i\left( \beta _{a}z-\omega _{a}t\right) } + \psi _{b}(z,\tau ) e^{i\left( \beta _{b}z-\omega _{b}t\right) }\right] , \end{aligned}$$

and $n_{2a,2b}$ quantify nonlinear refraction. We found $J=4$ to be sufficient. We reformulated the system (1–2) in the following three steps which were suggested by observations in numerical simulations.

Firstly, the soliton equation is split into two parts, where the LHS is a standard nonlinear Schrödinger equation providing a fundamental soliton solution. The RHS includes all remaining terms of Eq. (1), and is treated as a perturbation. It is responsible for evolution of the soliton parameters quantifying the higher-order dispersion effect, nonlinearities, and, most important, the influence of the DW. As a starting point we approximate $\psi _{a}$ by the fundamental soliton solution of the unperturbed equation:

$$\begin{aligned} |\psi _a|^2 \approx \frac{\vert \beta ''(\omega _{a}+\nu ) \vert c}{(\omega _{a}+\nu ) n_{2a}} \frac{1}{\sigma ^{2} \cosh ^{2} \frac{\tau -\mathcal {T}}{\sigma }}, \end{aligned}$$

(3)

with soliton frequency offset $\nu =\nu (z)$ from $\omega _{a}$, its time delay $\mathcal {T}=\mathcal {T}(z)$, and its duration $\sigma =\sigma (z)$. These parameters are yet unkown but to be identified in the third step.

Secondly, we need an analytic expression for the DW envelope $\psi _{b}$. We insert the approximate $\vert \psi _a\vert ^2$ from (3) into in the GNLSE (2). Equation (2) is then linearized with respect to $\psi _b$, as the DW has much lower intensity compared to the soliton (Fig. 2a). Both higher order dispersion and nonlinear terms are neglected. The resulting equation describes the scattering problem of a plane wave at a squared hyperbolic secant barrier. It can be solved analytically (Landau and Lifshitz 1965) for a static soliton barrier with vanishing $\mathcal {T}(z)$. To account for the soliton motion, a suitable Galilei transformation is applied to the standard scattering solution.

Thirdly, we insert the derived $|\psi _b|^2$ in the perturbation part of the already split Eq. (1) for the soliton. Then soliton perturbation theory (Hasegawa and Matsumoto 2003) results in a set of adiabatic ODEs for the soliton parameters, which provides a good prediction of the soliton evolution. We shall describe in Sect. 4 to which extent these equations have to be exploited for the present purposes. For a more thorough analysis see Ref. Pickartz et al. (2016).

4 Results

If we are merely interested in determining an appropriate set of initial parameters for the DW in order to produce earliest changes in a given soliton, it is sufficient to inspect the adiabatic ODEs at

Fig. 3

Initial effect of the DW on the soliton as predicted by perturbation theory (a), and soliton deflection at propagation distance of $1\,\text {m}$ from simulation with the full GNLSE (b)

$z=0$. We derive the following expression for the change of the soliton frequency offset at $z=0$ with $\nu (0)=0$ from Pickartz et al. (2016, Eqs. 36–37):

$$\begin{aligned} \left. \frac{d\nu }{dz} \right| _{z=0} = \frac{4 \mu \mathfrak {T}}{\sigma _{0} L_{d} } \int _0^1 \left| F \left( \mathfrak {a}, \mathfrak {b}, \mathfrak {c}, \zeta \right) \right| ^{2} \left( 2\zeta -1 \right) d\zeta , \end{aligned}$$

(4)

with initial soliton duration $\sigma _0=\sigma (0)$, dispersion length $L_d=\sigma _0^2/|\beta ''_a|$ and DW power $\mu$ normalized by that of the soliton. The arguments of the hypergeometric function F are

$${\mathfrak {a,b}} ={\frac{1}{2}}-i{\sigma _0}{\bar{\varOmega }}\pm is, \qquad {\mathfrak {c}}=1-i{\sigma _0}{\bar{\varOmega }},$$

(5)

with

$$\begin{aligned} \bar{\varOmega }=\varOmega +\frac{1}{\sigma _0^2\beta _b''} \left( \frac{\beta _a''}{\omega _a} - \frac{\beta _a'''}{6} \right) , \qquad s= \sqrt{ 4\frac{|\beta ''_a|}{\beta ''_b} \frac{\omega _{b}}{\omega _{a}} \frac{n_{2b}}{n_{2a}} -\frac{1}{4} }. \end{aligned}$$

(6)

The transmission coefficient reads

$$\begin{aligned} \mathfrak {T}= \frac{\sinh ^{2}(\pi \bar{\varOmega }\sigma _0)}{\cosh ^{2}(\pi s)+\sinh ^{2}(\pi \bar{\varOmega }\sigma _0)}. \end{aligned}$$

(7)

The easiest and least time consuming way to determine the realm of reflection is to evaluate the transmission coefficient (7) for any combination of two initial carrier frequencies $\omega _a$ and $\omega _b+\varOmega$ and possible values of $\sigma _0$. The soliton should be short enough such that $\mathcal T\approx 0$, the energy transfer is then most effective. According to our experience, a noticeable soliton transformation by a DW can be expected if at least $\mathcal T<0.1$.

To choose the optimal $\varOmega$ within the interval which allows reflection, we evaluate expression (4) for varying $\varOmega$, as depicted in the example of Fig. 3a for a soliton with $\omega _{a}=1.215\,\text {PHz}$ and initial duration $\sigma _0=55\,\text {fs}$. The curve shows the interval of interaction. The maximal $\varOmega$ at which the DW is still reflected is at $\varOmega \approx 0.07\,\text {PHz}$. At the peak we expect the strongest initial effect on the soliton. We confirmed this by a sequence of simulations with full GNLSE at different values of $\varOmega$, and read out the soliton delay $\mathcal T(z)$ at $z=1\,\text {m}$. Figure 3b shows that about the predicted optimal $\varOmega \approx 0.05\,\text {PHz}$ the absolute soliton deflection becomes maximal. For increasing values of z the optimal $\varOmega$ is slightly shifted to the left.

Moreover, the earliest increase of soliton peak power is to be expected at the optimal value of $\varOmega$ derived from Eq. (4) (Fig. 3a). This was again confirmed by direct simulations using the full GNLSE, as indicated in Fig. 4.

In conclusion, Eqs. (4–7) provide a simple and effective tool to estimate optimal parameters for investigations of a soliton controlled by a DW. The required calculations are very fast, as opposed to parameter search with the full GNLSE.

Fig. 4

Evolution of soliton amplitude for several values of $\varOmega$. Soliton amplification can be observed quickest for the determined optimal $\varOmega$