1 Introduction

The fractional Fourier transform (FrFT) is a kind of general optical Fourier transform. Its optical implementation system with single or double lens has been reported and analyzed by using Wigner distribution function (Lohmann 1993). The transform is also a useful tool of time–frequency representation in the field of digital/optical signal processing (Ozaktas et al. 2000). In recent years, the FrFT has been expanded by changing the variables or kernel function in its definitions of integral and series. The discrete fractional random transform has been proposed by randomizing the eigenvector matrix (Liu et al. 2005), which is generated from a random real symmetric matrix. By altering the eigenvalues of the FrFT into random values, the random Fourier transform and multiple-parameter FrFT have been presented with random fractional orders (Liu and Liu 2007a; Pei and Hsue 2006; Lang et al. 2010). The random fractional Fourier transform has been determined by a pair of conjugate phase filtering functions into the definition of the FrFT (Liu and Liu 2007b). A discrete version of random fractional Fourier transform has also been reported (Pei and Hsue 2009) for signal processing. The fractional angular transform has been investigated by taking a recursion calculation structure with an angle (Liu et al. 2008, 2012). The computational scheme of discrete FrFT, which is convenient for discrete signal processing, has been reported by using several algorithms, e.g. eigenvector decomposition (Pei and Yeh 1997; Chen et al. 2016a), sampling expansion (Chen et al. 2016b), and convolution (Yang et al. 2004). The FrFT has been applied for various signal processing issues, such as random signal (Zhang 2016), secret data (Lang et al. 2010) and filtering task (Lohmann 1993).

In this paper, we develop the FrFT into a generalized format expressed with convolution equation. Here the proposed transform is named as convolution-based fractional transform (CBFT). The expression of FrFT and gyrator transform (Rodrigo et al. 2007) is randomized to generalize the CBFT. Thereby the new transform has a changeable kernel function in its definition. The two phase filtering functions are arbitrary in this framework of expression. The phase filters can be designed for the different motivations of signal/image processing. The CBFT has several primary properties of fractional transform, such as index additivity, linearity and energy conservation. The proposed transform is also implemented with an optical 4f system or digitally. Several numerical results are provided for validating the transform and it potential applications.

The rest of this article is organized as follows. In Sect. 2, the convolution expressions of FrFT and gyrator transform are recalled and analyzed. The definition and properties of the proposed fractional transform are given in Sect. 3. Some numerical results are listed in Sect. 4. The conclusions are shown in the final section.

2 Preliminaries

The normalized FrFT of a 1D function f(x) can be written as follows

$${\mathbf{F}}^{\alpha } \left\{ {f\left( x \right)} \right\}\left( \xi \right) = \int {K^{\alpha } \left( {x,\xi } \right)f\left( x \right){\text{d}}x} ,$$
(1)

where α is the fractional order of this transform. The symbol \({\mathbf{F}}^{\alpha }\) represents the operator of FrFT. The function K α is the kernel and is calculated as

$$\begin{aligned} K^{\alpha } \left( {x,\xi } \right) & = A_{\alpha } \exp \left\{ {{\text{i}}\uppi\left[ {\frac{{\left( {x^{2} + \xi^{2} } \right)\cos \phi - 2x\xi }}{\sin \phi }} \right]} \right\}, \\ A_{\alpha } & = \sqrt {1 - {\text{i}} \cdot \cot \phi } ,\quad \, \phi = \alpha\uppi/2. \\ \end{aligned}$$
(2)

If the angle α is even, the kernel becomes

$$K^{\alpha } \left( {x,\xi } \right) = \left\{ {\begin{array}{*{20}l} {\delta \left( {x - \xi } \right),} \hfill & {{\text{if }}\alpha = 4n,} \hfill \\ {\delta \left( {x + \xi } \right),} \hfill & {{\text{if }}\alpha = 4n + 2,} \hfill \\ \end{array} } \right.$$
(3)

where n is an integer. The FrFT can be achieved in an optical system composed of one or two lenses (Lohmann 1993). The eigenvectors of FrFT, Hermite–Gaussian vector, can be calculated with the method (Liu et al. 2008). A convolution algorithm of discrete FrFT (Yang et al. 2004), however, has faster speed than the scheme (Pei and Yeh 1997). Yang et al. (2004) have proposed an expression of FrFT based on convolution as follows

$${\mathbf{F}}^{\alpha } \left\{ {f\left( x \right)} \right\}\left( \xi \right) = A_{\alpha } m^{\prime}_{\alpha } \left( \xi \right)\left[ {f^{\prime}\left( \xi \right) \otimes m_{\alpha } \left( \xi \right)} \right],$$
(4)

and

$$\begin{aligned} m^{\prime}_{\alpha } \left( \xi \right) & = \exp \left( {{\text{i}}\uppi\xi^{2} \tan \frac{{\alpha\uppi}}{4}} \right), \\ m_{\alpha } \left( \xi \right) & = \exp \left( {{\text{i}}\uppi\xi^{2} \csc \frac{{\alpha\uppi}}{2}} \right), \\ f^{\prime}\left( \xi \right) & = f\left( \xi \right)\exp \left( { - {\text{i}}\uppi\xi^{2} \tan \frac{{\alpha\uppi}}{4}} \right), \\ \end{aligned}$$
(5)

where m′ α and m α are two pure phases and serve as the modulation function and input function in Eq. 4, respectively. The function f′(x) includes input function and a phase term, which are also the conjugate of complex function m′ α . The 2D format of FrFT can be expanded according to Eqs. 1–5. The fast Fourier transform (FFT) becomes a basic unit in the calculation of convolution operation.

The gyrator transform is another format of fractional transform in optics and mathematics (Rodrigo et al. 2007). The transform can be used for the conversion between Hermite–Gaussian beam and Laguerre-Gaussian beam. Its integral expression is expressed as

$${\mathbf{G}}^{\alpha } \left[ {f\left( {x,y} \right)} \right]\left( {\xi ,\eta } \right) = \iint {f\left( {x,y} \right)H^{\alpha } \left( {x,y,\xi ,\eta } \right){\text{d}}x{\text{d}}y},$$
(6)

where the symbol \({\mathbf{G}}^{\alpha }\) is gyrator operator. The function f(x, y) is the input of gyrator transform. The parameter α is the transformation order. The kernel function H α is calculated as

$$\begin{aligned} H^{\alpha } \left( {x,y,\xi ,\eta } \right) & = C_{\varphi } \exp \left[ {2{\text{i}}\uppi\frac{{\left( {xy + \xi \eta } \right)\cos \varphi - \left( {x\eta + y\xi } \right)}}{\sin \varphi }} \right], \\ C_{\varphi } & = \frac{1}{|\sin \varphi |}, \, \quad \varphi = \frac{{\alpha\uppi}}{2}, \\ \end{aligned}$$
(7)

and α is the fractional order of the transform. Similarly, gyrator transform can be re-written into a convolution equation (Rodrigo et al. 2007; Liu et al. 2011a) as

$${\mathbf{G}}^{\alpha } \left[ {f\left( {x,y} \right)} \right]\left( {\xi ,\eta } \right) = C_{\varphi } n^{\prime}_{\alpha } \left( {\xi ,\eta } \right)\left\{ {\left[ {f\left( {\xi ,\eta } \right)n^{\prime}_{\alpha } \left( {\xi ,\eta } \right)} \right] \otimes n_{\alpha } \left( {\xi ,\eta } \right)} \right\},$$
(8)

where the functions n′ α and n α are evaluated as

$$\begin{aligned} n^{\prime}_{\alpha } \left( {\xi ,\eta } \right) & = \exp \left( { - 2 {\text{i}}\uppi\xi \eta \tan \frac{{\alpha\uppi}}{4}} \right), \\ n_{\alpha } \left( {\xi ,\eta } \right) & = \exp \left( { 2 {\text{i}}\uppi\xi \eta \csc \frac{{\alpha\uppi}}{2}} \right). \\ \end{aligned}$$
(9)

In gyrator transform, two phase-only functions in Eq. 9 are applied for modulating and joining convolution operation in Eq. 8. The characteristic of convolution in gyrator transform is similar to the FrFT. The cross-term and quadratic function of coordinates appear in the phase distribution functions for gyrator transform and the FrFT, respectively. The convolution operations will be analyzed and solved in next section.

3 Convolution-based fractional transform

3.1 Optical system of fractional transforms

From the convolution expression of FrFT and gyrator transform, we can conclude that the input function is modulated and imported into convolution calculation. In addition, the Fourier transform of the functions m α and n α can be obtained with an analysis solution as follows (Liu et al. 2011a)

$$\begin{aligned} M_{\alpha } \left( {\xi ,\eta } \right) & = {\mathbf{F}}\left[ {m_{\alpha } \left( {x,y} \right)} \right] \\ & = {\text{i}} \cdot \sin \frac{{\alpha\uppi}}{2}\exp \left[ { - {\text{i}}\uppi\left( {\xi^{2} + \eta^{2} } \right)\sin \frac{{\alpha\uppi}}{2}} \right] \\ \end{aligned}$$
(10)

and

$$\begin{aligned} N_{\alpha } \left( {\xi ,\eta } \right) & = {\mathbf{F}}\left[ {n_{\alpha } \left( {x,y} \right)} \right] \\ & = \sin \frac{{\alpha\uppi}}{2}\exp \left( { - 2{\text{i}}\uppi\xi \eta \sin \frac{{\alpha\uppi}}{2}} \right), \\ \end{aligned}$$
(11)

where the transformed results are a phase-only function and F denotes Fourier operator. According to the Fourier transform of convolution operation, the functions M(ξ, η) and N(ξ, η) are a modulation term in Eqs. 4 and 8, respectively. In Eqs. 10 and 11, the coefficients \({\text{i}} \cdot \sin (\alpha\uppi /2)\) and \(\sin (\alpha\uppi /2)\) can be considered as a constant for the coordinates ξ and η. Therefore phase filtering scheme can be introduced and employed to design the phase masks for performing the two optical fractional transforms.

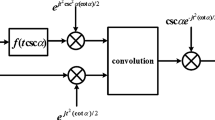
From Eqs. 4, 8, 10 and 11, the optical implementation of two kinds of fractional transform (the FrFT and gyrator transform) can be made by a 4f system in optics and shown in Fig. 1. The phase function m′ α (or n′ α ) is used for modulation of input and output planes, P1 and P3. At the plane P2 of Fourier frequency, the phase M α (or N α ) serves as a filter in Fourier spectrum. Here the concave lens has a negative focal length \(- {\text{f}}_{1}\) for generating a reverse Fourier transform in convolution. For FrFT, the phase filter masks in Eqs. 5 and 10 are consistent with convex lens according to the distribution of phase function. Adjusting phase is more convenient with spatial light modulator in experiment. Alternately, the joint transform correlation (Goodman 1968), in which the conjugate of m α (or n′ α ), can be also adopted for implementing the fractional transforms. The input and output of optical information processing experiment are digital, namely spatial light modulator and CCD are used for generating discrete data and recording intensity pattern, respectively. The continuous optical fractional transforms are adopted to deal with the two dimensional data. The fractional transforms have been applied for various issues in the field of information processing (Ozaktas et al. 2000). Especially, the changeable fractional orders in gyrator transform have been utilized to accelerate the convergence of a parallel iterative phase retrieval algorithm in the application measuring unknown object (Liu et al. 2015). A diffraction model between non-parallel planes, which can be considered as a kind of fractional transform, is used for multiple-image encoding (Liu et al. 2014).

Fig. 1
figure 1

An optical system for fractional transform

Full size image

3.2 Convolution-based fractional transform

In the modulation phase functions of FrFT (m α and m′ α ), the quadratic term x 2 + y 2, is from the lens and Fresnel diffraction. The cross-product term xy in the phase functions n α and n′ α in Eq. 9, is from the thin cylinder lens of the optical system achieving gyrator transform. The phase filters (m′ α and M α ) in Fig. 1, can be expanded in other expressions, such as

$$r^{\prime}_{\theta } \left( {x,y} \right) = \exp \left[ {{\text{i}}\uppi\theta \cdot r_{1} \left( {x,y} \right)} \right]$$
(12)

and

$$R_{\theta } \left( {\xi ,\eta } \right) = \exp \left[ {{\text{i}}\uppi\theta \cdot r_{2} \left( {\xi ,\eta } \right)} \right],$$
(13)

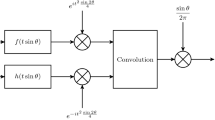
where r 1 and r 2 are the arbitrary or random functions producing two different data for multiple degrees of freedom of the CBFT. Another reason choosing different data is that the functions r 1 and r 2 are from the masks located in the planes P1 and P2, respectively. The phase distribution of two phase filter masks is controllable and changeable in this optical system in Fig. 1. In this paper, the symbol \({\mathbf{R}}^{\theta }\) is applied for expressing the CBFT. Here the order θ is reserved for representing fractional order and generating a simple inverse transform. The inverse of the transform \({\mathbf{R}}^{\theta }\) is \({\mathbf{R}}^{ - \theta }\), which can be proved by its definition. Figure 1 also implies that the fast algorithm of discrete CBFT can be performed by FFT method twice as follows

$$F\left( n \right) = A_{\theta } r^{\prime}_{\theta } \left( n \right){\text{IFFT}}\left\{ {{\text{FFT}}\left[ {f\left( n \right)r_{\theta }^{{{\prime }*}} \left( n \right)} \right]R_{\theta } \left( n \right)} \right\},$$
(14)

where the functions F and f are output and input of the CBFT, respectively. The symbol ‘*’ is to take a conjugate operation for input. In Eq. 14, a two-step FFT algorithm can improve the computational speed of the discrete CBFT by comparing with eigenvector decomposing method (Liu et al. 2005; Pei and Yeh 1997).

3.3 Properties

The CBFT is defined by phase-only modulation from the optical implementation system of FrFT in Fig. 1. Thereby the new transform has the properties of linearity and energy conservation. From the definition of two random phases in Eqs. 12 and 13, the transform has an order additivity equation as

$${\mathbf{R}}^{{\theta_{1} }} {\mathbf{R}}^{{\theta_{2} }} = {\mathbf{R}}^{{\theta_{2} }} {\mathbf{R}}^{{\theta_{1} }} = {\mathbf{R}}^{{\theta_{1} + \theta_{2} }} .$$
(15)

Here the functions, ‘tan’ and ‘csc’, in Eq. 5, are removed for generating a linear term for the parameter θ. The additivity property of FRFT in convolution (Yang et al. 2004), however, is not satisfied strictly in the discrete case.

A random property of CBFT is from the phase in Eqs. 12 and 13. The definition in Eq. 14 is a general framework for the fractional transform. The random phase can be selected for the various applications of signal processing. For example, the FrFT and gyrator transform can be fused into a hybrid format as follows

$$r^{\prime}_{\theta ,1} \left( {x,y} \right) = { \exp }\left[ { - 2i\uppi{\text{xy}}\tan \frac{{\theta\uppi}}{4}} \right]$$
(16)

and

$$R_{\theta ,1} \left( {\xi ,\eta } \right) = \exp \left[ { - {\text{i}}\uppi\left( {\xi^{2} + \eta^{2} } \right)\sin \frac{{\theta\uppi}}{2}} \right].$$
(17)

The periodicity of the CBFT depends on the phase functions in Eqs. 12 and 13. If the random functions (r 1 and r 2) are integer, the period of the transform equals to 1, namely \({\mathbf{R}}^{\theta + 1} = {\mathbf{R}}^{\theta }\). For a general case, CBFT has no a limited period, because the trigonometric functions (‘tan’ and ‘csc’) in the mother transforms (FrFT and gyrator transform) are removed from the definition in Eqs. 12 and 13.

4 Numerical result and discussion

4.1 Example of CBFT

Numerical simulation is used for testing the feature of CBFT. The phases in Eqs. 12 and 13 are selected as three different random sequences as follows

$$r_{1} = r_{2} = x_{n} ,$$
(18)
$$r_{1} = r_{2} = x_{n}^{2} ,$$
(19)
$$r_{1} = r_{2} = \cos \left( {4\uppi \cdot x_{n} } \right),$$
(20)

where the sampling point x n is uniformly-spaced located in the interval [0,1). The input signals are adopted as

$$y_{1} = {\text{rect}}\left( x \right) = \left\{ {\begin{array}{*{20}l} {1,} \hfill & {{\text{if |}}x |\le 1 ,} \hfill \\ {0,} \hfill & {{\text{if 1 < |}}x |\le 8 ,} \hfill \\ \end{array} } \right.$$
(21)

and

$$y_{2} = \varLambda \left( x \right) = \left\{ {\begin{array}{*{20}l} {1 - \left| x \right|,} \hfill & {{\text{if |}}x |\le 1 ,} \hfill \\ {0,} \hfill & {{\text{if 1 < |}}x |\le 8 ,} \hfill \\ \end{array} } \right.$$
(22)

where the total of sample point is fixed at 512. When the fractional order θ is taken at 0.5, the two functions in Eqs. 21 and 22 are regarded as input signal. The corresponding transformed results are shown in Fig. 2. For the normalized phases in Eqs. 18 and 19, the phases of transformed output have a continuous shape except about x = 0, in which the curve is interrupted due to the modulo 2π operation in the calculation of phase distribution. The interrupted phase curves can be restored by using phase unwrapping method. In Fig. 2c, f, the phase distributions have random trend, in which the amplitude data are closed to 0, and the amplitude distribution is more similar to input signal, which is different from other sub-graphs in Fig. 2. The energy of transform domain is concentrated mainly in the range of low frequency. From Fig. 2, the feature of output depends on the phase functions r 1 and r 2, which can be changed for different purposes of application. When the values of order θ are taken at the range [0, 4], the amplitude distributions of the two signals are computed and displayed in Fig. 3 in order to view a global status. The patterns are closed to two or one pulse functions. Here the CBFT has a period rule for amplitude from Fig. 3, in which the period is 1. The output phase, however, has no a period in this case.

Fig. 2
figure 2

The CBFT of 1D rectangular and triangle functions. (a, d), (b, e) and (c, f) are from the phase expression in Eqs. 18, 19 and 20, respectively. Here the fractional order θ is fixed at 0.8 for obtaining six sub-figures

Full size image
Fig. 3
figure 3

The amplitude distribution with various transform angles: (a) rectangle function, (b) triangle function. Here the normalized phases r 1 and r 2 are adopted as a linear distribution in Eq. 18

Full size image

When the phase functions r 1 and r 2 are random, the amplitude and phase distributions of the transform have changeable output. An example of CBFT of rectangle function, which is calculated with the same parameters with the figure in Fig. 2a, is given in Fig. 4a. Here r 1 and r 2 are two different random sequences. The order θ is equal to 0.5. The energy is not concentrated in low frequency region, which is different from the orthogonal transforms, such as Fourier transform and discrete cosine transform. The outline trend of output amplitude, however, is closed to input signal. The phase distribution is random in the range [\(-\uppi,\uppi\)].

Fig. 4
figure 4

The reconstructed signal with low frequency data: (a) amplitude and phase of CBFT, (b) the selected data, (c) the amplitude of retrieved signal

Full size image

An example of signal reconstruction is performed by use of the data in low frequency range. In Fig. 4b, the adopted data, amplitude and phase, is displayed. Here the data of amplitude and phase in high-frequency area is replaced with 0. By using correct fractional order and random phases, the inverse transform is utilized for recovering the signal. The retrieved signal is given in Fig. 4c, in which the main outline of the input signal is obtained.

The CBFT of two sets of two-dimensional signals is tested and displayed in Fig. 5. Here the normalized phases r 1 and r 2 are selected as follows

$$r_{1} = r_{2} = \left( {x_{n} - \frac{1}{4}} \right)\left( {y_{n} - \frac{1}{4}} \right),$$
(23)

where x n and y n are calculated with the method used in Eq. 20. The 2D rectangle function and the letter ‘E’ are converted by CBFT with the orders 0.25 and 0.5. The amplitude of CBFT is similar to effect of edge detecting operation. A part of energy of signal in the center of the patterns is diffused. The basic outline of input pattern is preserved. Figures 4 and 5 reflect that the CBFT has a time–frequency expression of the fractional transforms, in which the main outline and changed information exist in the output of the transform.

Fig. 5
figure 5

The CBFT of simple image: (a) input pattern, (b) θ = 0.25, (c) θ = 0.5, (d) input pattern, (e) θ = 0.25 and (f) θ = 0.5

Full size image

4.2 CBFT for transforming image

When input signal is an image, the transform result is achieved and illustrated in Fig. 6. In our calculation, the fractional order α is fixed at 0.4. The phase distribution shown in Fig. 6b is random and amplitude distribution is given in Fig. 6c, which loss more detail information. From Figs. 2 and Fig. 6c, the amplitude information of the transform has some information of input signal. At the same time, the stationary region of input becomes a uniform noise pattern in the CBFT. Figure 6d, e are calculated by use of phase distribution and amplitude distribution, respectively. Two retrieved images are similar to Fig. 6c, which is blurry and has the outline of input image. If all of the information is used for reconstruction, the recovered image in Fig. 6f is the same with original image.

Fig. 6
figure 6

The random fractional transform of 2D data: (a) original image, (b) phase, (c) amplitude, (d) reconstructed image obtained by using (b), (e) reconstructed image obtained by using (c), (f) reconstructed image obtained by amplitude and phase

Full size image

In Fig. 7, an example is computed for FrFT, gyrator transform and CBFT, in which the modulation phases in Eqs. 16 and 17 are adopted. The input data is from Fig. 6a. The orders α and θ are taken at 0.7. The patterns in Figs. 7a, c, e and 7b, d, f are the amplitude distribution and phase distribution of the three transforms, respectively. The amplitude patterns of FrFT and gyrator transform are contractible status of input image with noise. In the center area of phase distribution of FrFT and gyrator transform, geometric symmetric characteristic appears along x-axis and y-axis. In the amplitude pattern of CBFT, a quasi-diamond, the width of which depends on the order θ, is formatted along the diagonal. Moreover, the blurry outline of input image can be seen from Fig. 7e. In the phase pattern of CBFT, a series of squeezed homocentric circles, which is located at the two sides of the diagonal, is received. Thereby the combined CBFT is a time–frequency expression tool with a symmetric axis along the diagonal (Ozaktas et al. 2000; Liu et al. 2011b).

Fig. 7
figure 7

The result of three kinds of transforms: (a) amplitude of FrFT, (b) phase of FrFT, (c) amplitude of gyrator transform, (d) phase of gyrator transform, (e) amplitude of the CBFT, (f) phase of the CBFT

Full size image

4.3 Frequency doubling

When the modulation phase is designed and replaced with some special functions, the CBFT will have some interesting properties. Here an example of CBFT is listed for the phenomenon of frequency doubling. The two phase functions are fixed at \(r^{\prime}_{\theta } = R_{\theta } = \exp [2{\text{i}}\uppi\theta \cdot r(n)]\), where the function r(n) equals to

$$r\left( n \right) = \left\{ {\begin{array}{*{20}l} {0,} \hfill & {n{\text{ is odd,}}} \hfill \\ {1,} \hfill & {n{\text{ is even}}.} \hfill \\ \end{array} } \right.$$
(24)

In calculation, the order θ is taken at 0.25. The functions, rect(x) and sin(x), are regarded as input signal of CBFT. The corresponding result of CBFT is shown in Fig. 8. The frequency of the input functions is doubled by the amplitude of CBFT. The phase distribution of CBFT, however, has anomalous shape. The doubling result is from the modulation phases in Eq. 24, which is a periodic signal.

Fig. 8
figure 8

frequency doubling in CBFT: (a) rect(x), (b) cos(x)

Full size image

5 Conclusions

We propose a kind of fractional transform based on convolution operation. Two individual phases are applied for modulating the input and output of the first Fourier transform in the CBFT. The new transform is a general framework of fractional transforms. The FrFT and gyrator transform can be regarded as the special cases of CBFT. The proposed transform has some primary properties of fractional transform. Moreover the transform is a time–frequency representation tool. By using phase filtering in the optical 4f system, this transform can be implemented. The phase function is changeable for various application of signal processing. Numerical experiment with three cases of phase distribution is performed for testing the proposed transform.