Introduction

Filter design is a crucial step in signal processing and it is used to distinguishing the true underlying signal from the noise. Thus, different methods, exhibiting distinct filtering possibilities, are welcome to be introduced. Associated with this, several objects take a central role. Namely, the integral transform in use (and its eventual flexibility and associated properties), as well as the convolution (or multiplicative operation which allows a factorization identity for its associated integral transform). As about the possible integral transforms for the above purpose, the most classical one is the Fourier transform. Anyway, there are several generalizations. For instance, it is well-known that the Fractional Fourier Transform (FrFT), being a one parameter integral transform, includes, as a particular case, the Fourier Transform. The great generality of the FrFT has been widely illustrated in several applications (being the most popular ones performed in the fields of signal processing, optics and quantum mechanics); cf. [1, 6, 17, 19,20,21,22,23,24,25,26, 28, 33].

In this work, we start by proposing two new convolutions associated with the FrFT and, then, will exploit some of their consequences. In particular, significant new consequences in sampling theory and filter design will be exhibited. In a global sense, we would like to point out that new convolutions associated with integral transforms and equations continue to have a growing interest and exhibit a wide range of applications (cf., e.g., [2,3,4, 7,8,9,10,11,12,13,14,15,16, 18, 27, 31, 32] and the references therein).

In this section, we will recall the definition of the FrFT and some of its properties which we will use in the next sections. In view to have a better comparison, we start by presenting the definition of Fourier Transform (FT) and its inverse. We will use the FT and its inverse defined by

$$\begin{aligned}&F(u) := \varPsi _{FT}\big \{f(t)\big \}(u) := \int _{\mathbb {R}}f(t)e^{-iut}dt, \end{aligned}$$
(1)
$$\begin{aligned}&f(t)=\frac{1}{2\pi }\int _{\mathbb {R}}F(u)e^{iut}du, \end{aligned}$$
(2)

respectively. It is well-known that the convolution associated with the FT and the corresponding factorization property play a central role e.g. in signal processing. Namely, the conventional convolution theorem for the FT can be used with great efficiency when constructing multiplicative filters in the FT domain. We recall that if \(f, h \in L^1(\mathbb {R}),\) then for

$$\begin{aligned}&z(t):=(f*h)(t) := \int _{\mathbb {R}}f(\tau )h(t-\tau )d\tau , \end{aligned}$$
(3)

we have the factorization property \(Z(u)=F(u) \, H(u)\), which allows us to identify

$$\begin{aligned} (f*h)(t)=\varPsi ^{-1}_{FT}\big \{F(u) \, H(u)\big \}(t), \end{aligned}$$
(4)

where \(*\) stands for the classic Fourier convolution operation in the time domain and, according with the notation (1), the elements F(u), H(u) and Z(u) represent the FTs of the signals f(t),  h(t) and z(t), respectively.

The FrFT (see [22]) being a generalization of the Fourier transform, for any real angle \(\theta\), may be defined by the help of the kernel

$$\begin{aligned} \mathscr {K}_\theta (u,t) := K_\theta e^{i[\frac{\cot \theta }{2}u^{2}-ut\csc \theta +\frac{\cot \theta }{2}t^{2}]}, \qquad \sin \theta \ne 0, \end{aligned}$$

where

$$\begin{aligned} K_\theta =\sqrt{\frac{1-i\cot \theta }{2\pi }}. \end{aligned}$$

Indeed, the FrFT with angle \(\theta\) and its inverse are defined as

$$\begin{aligned} F_{\pm \theta }(u)=(\mathcal {F}_{\pm \theta } f)(u) := \int _{\mathbb {R} }{f(t)\mathscr {K}_{\pm \theta } (t,u)dt}, \end{aligned}$$
(5)

respectively.

In this paper, we will be always assuming that \(\sin \theta \ne 0\) (otherwise we would be simply dealing with a chirp multiplication operation).

Now we will recall some basic properties of \(\mathcal {F}_\theta\) which we will need later on. The majority of those properties follow basically from the definition of \(\mathcal {F}_\theta\).

In first place, it is clear that \(\mathcal {F}_\theta\) is a linear, continuous and a one-to-one map from the Schwartz space \(\mathcal {S}\) onto itself (and whose inverse is obviously also continuous).

Let \(C_0(\mathbb {R})\) be the Banach space of all continuous functions on \(\mathbb {R}\) that vanish at infinity and endowed with the supremum norm \(\Vert \cdot \Vert _\infty\), and let

$$\begin{aligned} \Vert f\Vert _p^p := \dfrac{1}{\sqrt{2\pi }}\int _{\mathbb {R}}|f(t)|^p dt\,,\qquad 1\le p < \infty , \end{aligned}$$

be the norm that we will use in \(L^p(\mathbb {R})\).

We have a Riemann–Lebesgue type lemma for the FrFT. Indeed, if \(f\in L^1(\mathbb {R})\), then \(\mathcal {F}_\theta f\in C_0(\mathbb R),\) and

$$\begin{aligned} {\Vert }\mathcal {F}_\theta f{\Vert }_{\infty }\le \frac{1}{\sqrt{|\sin \theta |}}\Vert f\Vert _1. \end{aligned}$$

We also have a Plancherel type theorem for the FrFT. Let f be a complex-valued function in the space \(L^2({\mathbb R})\) and let

$$\begin{aligned} \mathcal {F}_\theta f(u,k):=\int _{|t|<k}\mathscr {K}_{\theta }(u,t) f(t)\,dt. \end{aligned}$$

Then, as \(k\rightarrow \infty\), \(\mathcal {F}_\theta f(u,k)\) converges strongly (over \({\mathbb R}\)) to a function, say \(\mathcal {F}_\theta f \in L^2({\mathbb R})\); and, reciprocally,

$$\begin{aligned} f(u,k):=\int _{|t|<k} \mathscr {K}_{-\theta }(u,t) \mathcal {F}_{\theta } f(t)\,dt, \end{aligned}$$

converges strongly to f.

A Parseval type identity is also valid for the FrFT. For any \(f, h\in L^2(\mathbb {R})\), the following identity holds

$$\begin{aligned} \langle \mathcal {F}_\theta f, \mathcal {F}_\theta h\rangle =\langle f, g\rangle , \end{aligned}$$

where \(\langle \cdot ,\cdot \rangle\) is denoting the usual inner product in \(L^2(\mathbb {R})\). Obviously, in the special case of \(h=f\), it holds

$$\begin{aligned} \Vert \mathcal {F}_\theta f\Vert _2=\Vert f\Vert _2. \end{aligned}$$

Let us recall some known convolutions for the FrFT constructed in recent years. Zayed [34] derived a new expression for a convolution operator which can be given as

$$\begin{aligned} (f\underset{\theta }{*}h)(t)= \sqrt{\frac{1-i\cot \theta }{2\pi }}e^{-it^2\frac{\cot \theta }{2}}\left[ f(t)e^{it^2\frac{\cot \theta }{2}}*h(t)e^{it^2\frac{\cot \theta }{2}}\right] , \end{aligned}$$
(6)

and the convolution theorem associated with the FrFT can be written as

$$\begin{aligned} \mathcal {F}_\theta \left\{ (f\underset{\theta }{*}h)(t)\right\} (u)=e^{-iu^2\frac{\cot \theta }{2}}\cdot \mathcal {F}_\theta \{f(t)\}(u) \cdot \mathcal {F}_\theta \{h(t)\}(u). \end{aligned}$$
(7)

It easy to see that (6) requires three chirp multiplications to evaluate the defined integral convolution, and (7) does not exactly preserve the classical result for the FT since there exists an extra chirp multiplier in the right-hand side of it. Later, Wei and Ran [30] introduced a generalized convolution for the FrFT in the form

$$\begin{aligned} (f\underset{\theta }{*} h)(t)= \sqrt{\frac{1-i\cot \theta }{2\pi }}\int _{\mathbb R}f(\tau )h(t\Theta \tau )\mathrm {d}\tau , \end{aligned}$$
(8)

where

$$\begin{aligned} h(t\Theta \tau )= \sqrt{\frac{1-i\cot \theta }{2\pi }}\sqrt{\frac{1+i\cot \theta }{2\pi }}\mathrm {e}^{(t^2-\tau ^2)\frac{i\cot \theta }{2}}\int _{\mathbb {R}}\mathcal {F}_\theta \{h(t)\}(u)\mathrm {e}^{-\frac{i(t-\tau )u}{\sin \theta }}\mathrm {d}u. \end{aligned}$$

Therefore, the factorization identity is satisfied:

$$\begin{aligned} \mathcal {F}_\theta \left\{ (f\underset{\theta }{*} h)(t)\right\} (u)= \mathcal {F}_\theta \{f(t)\}(u) \cdot \mathcal {F}_\theta \{h(t)\}(u). \end{aligned}$$

However, the generalized operation (8) is not only dependent on the time variable but it also depends on the transform domain variable “u”. Moreover, it can not be expressed by a one dimensional integral. In 2017, Anh et al.[3] proposed a new convolution operator

$$\begin{aligned} (f\underset{\theta }{*}h)(t) = \sqrt{\frac{1-i\cot \theta }{2\pi }}e^{ - iat^2 } \left[ {f(t)e^{ iat^2 } *h\left( {t + \frac{1}{{2ab}}} \right) e^{ia(t^2 + t/ab)} } \right] . \end{aligned}$$
(9)

Therefore, in this case, the convolution theorem has the following form

$$\begin{aligned} \mathcal {F}_\theta \left\{ {f(\underset{\theta }{*} h)(t)} \right\} (u) = e^{ - iau^2 + iu}\mathcal {F}_\theta \{f(t)\}(u) \cdot \mathcal {F}_\theta \{h(t)\}(u), \end{aligned}$$
(10)

where \(a(\theta ) = \frac{{\cot \theta }}{2}\), \(b(\theta ) = \sec \theta .\) As can be seen, although (9) and (10) can be implemented in two different ways via the Fourier convolution, the corresponding convolution theorem (10) has an extra chirp multiplication. Furthermore, Wei [29] introduced a convolution operator for the FrFT, which can be defined as

$$\begin{aligned} (f\underset{\theta }{*}h)(t)=\sqrt{\frac{1-i\cot \theta }{\pi }} e^{-it^2\frac{\cot \theta }{2}}\left[ f(t)e^{it^2\frac{\cot \theta }{2}}*h\left( t\right) e^{it^2\frac{\cot \theta }{2}}\right] (\sqrt{2}t). \end{aligned}$$

Hence, the convolution theorem has the following form

$$\begin{aligned} \mathcal {F}_\theta \left\{ (f\underset{\theta }{*}h)(t)\right\} (u)= \mathcal {F}_\theta \{f(t)\}\left( \frac{u}{\sqrt{2}}\right) \cdot \mathcal {F}_\theta \{h(t)\}\left( \frac{u}{\sqrt{2}}\right) . \end{aligned}$$

Feng and Wang [15] derived a new expression for a convolution operator in the following way

$$\begin{aligned} (f\underset{\theta }{*}h)(t)= \csc \theta e^{-it^2\frac{\cot \theta }{2}}\left[ f(t\csc \theta )e^{\frac{it^2}{\sin 2\theta }}*h(t)e^{it^2\frac{\cot \theta }{2}}\right] . \end{aligned}$$

Thus, here the convolution theorem for the FrFT has the form

$$\begin{aligned} \mathcal {F}_\theta \left\{ (f\underset{\theta }{*}h)(t)\right\} (u)=\varPsi _{FT}\left\{ f(t)e^{it^2\frac{\cot \theta }{2}}\right\} (u) \cdot \mathcal {F}_\theta \{h(t)\}(u). \end{aligned}$$

This paper contains five sections organized as follows: Sections 2 and 3 introduce a new convolution and correlation for the FrFT, which present some simplifications and benefits in their properties. Moreover, the form of the new defined FrFT convolution and correlation operators are not only similar to the FT case but they also require less number of chirp multiplications (when compared with previous proposals). Section 4 derives two different ways to design filters as well as the multiplicative filters in the FrFT domain and the time domain, where some concrete cases are also exposed. Section 5 is the conclusion of the work.

New product and convolution theorem for FrFT

The main purpose of this section is to introduce new convolutions associated with the FrFT so that we will obtain a new factorization identity for the FrFT. Therefore, several consequences of such property can be achieved.

Definition 1

We define a new convolution for the FrFT of two signals f(t) and h(t) by

$$\begin{aligned} (f\underset{\theta }{\otimes }h)\left( t\right) := \frac{1}{2\pi }\int _{\mathbb R}f(\tau )h(t\sin \theta -\tau )e^{-\frac{it\cos \theta }{2}(t\sin \theta -2\tau )}\mathrm {d}\tau . \end{aligned}$$
(11)

Hence, according to the the classic Fourier convolution operation, the new convolution can be also expressed as

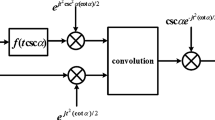
$$\begin{aligned} (f\underset{\theta }{\otimes }h)\left( t\right) := \frac{\sin \theta }{2\pi }\Big (e^{it^2\frac{\sin 2\theta }{4}}f(t\sin \theta )*e^{-it^2\frac{\sin 2\theta }{4}}h(t\sin \theta )\Big ). \end{aligned}$$
(12)

The implementation of the block diagram associated with the new convolution structure is shown in Fig. 1. Let \(\bar{f}(t)=f(t)e^{it^2\frac{\cot \theta }{2}},\) and \(\breve{h}(t)=h(t)e^{-it^2\frac{\cot \theta }{2}}\); then, the new convolution \(\underset{\theta }{\otimes }\) can be rewritten as

$$\begin{aligned} (f\underset{\theta }{\otimes }h)\left( t\right) = \frac{1}{2\pi }\Big (\bar{f}*\breve{h}\Big )(t\sin \theta ). \end{aligned}$$
(13)
Fig. 1
figure 1

Implementation process of the new convolution for FrFT

Full size image

Definition 2

Likewise, we define a dual operation of \(\underset{\theta }{\otimes }\) and simplify it as \(\underset{\theta }{\odot }\) by

$$\begin{aligned} (f\underset{\theta }{\odot }h)\left( t\right) :=\int _{\mathbb R}f(\tau )h(t\sin \theta -\tau )e^{\frac{it\cos \theta }{2}(t\sin \theta -2\tau )}\mathrm {d}\tau . \end{aligned}$$
(14)

The new dual convolution \(\underset{\theta }{\odot }\) can be expressed as

$$\begin{aligned} (f\underset{\theta }{\odot }h)\left( t\right) =\Big (\breve{f}*\bar{h}\Big )(t\sin \theta ). \end{aligned}$$
(15)

Theorem 1

Let \(F_{\theta }(u)\) and \(H_{\theta }(u)\) be the FrFT of the signals f(t), h(t) with parameter \(\theta\), respectively.

  1. (i)

    If \(f(t), h(t)\in L^1(\mathbb {R})\) then \((f\underset{\theta }{\otimes }h)(t)\in L^1(\mathbb {R})\). Moreover,

    $$\begin{aligned} \Vert f\underset{\theta }{\otimes }h\Vert _1 \le \frac{1}{|\sin \theta |} \Vert f\Vert _1\cdot \Vert h\Vert _1. \end{aligned}$$
    (16)
  2. (ii)

    We then have the factorization identity

    $$\begin{aligned} \varPsi _{FT}\Big \{\big (f\underset{\theta }{\otimes }h\big )(t)\Big \}(u)=F_{\theta }(u)H_{-\theta }(-u). \end{aligned}$$
    (17)

Proof

  1. (i)

    Using the Fubini’s theorem, we obtain

    $$\begin{aligned} \int _{\mathbb {R}}\left| (f\underset{\theta }{\otimes }h)(t)\right| \mathrm {d}t&=\frac{1}{2\pi } \int _{\mathbb {R}}\left| \int _{\mathbb {R}}f(\tau )h(t\sin \theta -\tau )e^{-\frac{is\cos \theta }{2}(t\sin \theta -2\tau )}\mathrm {d}\tau \right| \mathrm {d}t\\&\le \frac{1}{2\pi } \int _{\mathbb {R}}\int _{\mathbb {R}}\left| f(\tau )h(t\sin \theta -\tau )\right| \mathrm {d}t\mathrm {d}\tau \\&\le \frac{1}{ 2\pi |\sin \theta |} \int _{\mathbb {R}}\int _{\mathbb {R}}\left| f(\tau )\right| \left| h(t)\right| \mathrm {d}\tau \mathrm {d}t\\&=\frac{1}{|\sin \theta |}\Vert f\Vert _1 \cdot \Vert h\Vert _1. \end{aligned}$$
  2. (ii)

    We realize that

    $$\begin{aligned}F_{\theta }(u)H_{-\theta }(-u)&=\int _{\mathbb {R}}\int _{\mathbb {R}}f(\tau )h(v) \mathscr {K}_{\theta } (u,\tau )\mathscr {K}_{-\theta } (-u,v)\mathrm {d}\tau \text{d}v\\ &=K_{\theta }K_{-\theta }\int _{\mathbb {R}}\int _{\mathbb {R}}f(\tau )h(v)e^{i[u^2\frac{\cot \theta }{2}-u\tau \csc \theta +\tau ^{2}\frac{\cot \theta }{2}]} e^{-i[u^2\frac{\cot \theta }{2}+uv \csc \theta +v^{2}\frac{\cot \theta }{2}]}\mathrm {d}\tau \mathrm {d}v\\&=\frac{1}{2\pi \sin \theta }\int _{\mathbb {R}}\int _{\mathbb {R}}e^{i[-(\tau +v)u\csc \theta +\tau ^2\frac{\cot \theta }{2}-v^2\frac{\cot \theta }{2}]}f(\tau )h(v)\mathrm {d}\tau \mathrm {d}v. \end{aligned}$$

    Then, taking \(\tau =\tau\), \(s=(\tau +v)\csc \theta\), we have

    $$\begin{aligned}&F_{\theta }(u)H_{-\theta }(-u)\\&=\frac{1}{2\pi }\int _{\mathbb {R}}\int _{\mathbb {R}}e^{-ius}f(\tau ) e^{i\tau ^{2}\frac{\cot \theta }{2}}h(s\sin \theta -\tau )e^{-i(s\sin \theta -\tau )^{2}\frac{\cot \theta }{2}}\mathrm {d}\tau \mathrm {d}s \\&=\int _{\mathbb {R}}e^{-ius}\Big \{\frac{1}{2\pi }\int _{\mathbb {R}} f(\tau )e^{i\tau ^{2}\frac{\cot \theta }{2}}h(s\sin \theta -\tau )e^{-i(s\sin \theta -\tau )^{2}\frac{\cot \theta }{2}}\mathrm {d}\tau \Big \}ds\\&=\varPsi _{FT}\Big \{\big (f\underset{\theta }{\otimes }h\big )(s)\Big \}(u). \end{aligned}$$

This completes the proof of Theorem 1. \(\square\)

Theorem 2

Let \(F_{\theta }(u)\) and \(H_{\theta }(u)\) be the FrFT of the signals f(t), h(t) with parameter \(\theta\), respectively.

  1. (i)

    If \(f(t), h(t)\in L^1(\mathbb {R})\), then \((f\underset{\theta }{\odot }h)(t)\in L^1(\mathbb {R})\). Moreover,

    $$\begin{aligned} \Vert f\underset{\theta }{\odot }h\Vert _1 \le \frac{2\pi }{|\sin \theta |}\Vert f\Vert _1\cdot \Vert h\Vert _1. \end{aligned}$$
    (18)
  2. (ii)

    The factorization identity

    $$\begin{aligned} \varPsi _{FT}\Big \{f(v)h(v)\Big \}(t)=\big [F_{\theta }(u)\underset{\theta }{\odot }H_{-\theta }(-u)\big ](t) \end{aligned}$$

    holds true.

Proof

Having into account the knowledge of the last proof, here it is enough to prove item (ii). Using the definition of FrFT, we obtain

$$\begin{aligned}&\big [F_{\theta }(u)&\underset{\theta }{\odot }H_{-\theta }(-u)\big ](t)\\&=\int _{\mathbb R} F_{\theta }(\tau )e^{-i\tau ^2\frac{\cot \theta }{2}}H_{-\theta }(\tau -t\sin \theta )e^{i(\tau -t\sin \theta )^2\frac{\cot \theta }{2}}\mathrm {d}\tau \\&=K_\theta \int _{\mathbb R}\int _{\mathbb R} e^{i[\frac{\cot \theta }{2}\tau ^{2}-\tau v\csc \theta +\frac{\cot \theta }{2}v^{2}]}e^{-i\tau ^2\frac{\cot \theta }{2}}f(v) \\&\quad \times H_{-\theta }(\tau -t\sin \theta )e^{i(\tau -t\sin \theta )^2\frac{\cot \theta }{2}}\mathrm {d}\tau \mathrm {d}v. \end{aligned}$$

Then, taking the change of variables \(v=v\) and \(s=\tau -t\sin \theta\), we derive

$$\begin{aligned}\big [F_{\theta }(u)& \underset{\theta }{\odot }H_{-\theta }(-u)\big ](t)\\& =K_\theta \int _{\mathbb R}\int _{\mathbb R} e^{i[-v(s+t\sin \theta )\csc \theta +\frac{\cot \theta }{2}v^{2}]}f(v)H_{-\theta }(s)e^{is^2\frac{\cot \theta }{2}}\mathrm {d}s\mathrm {d}v\\& =\int _{\mathbb R}e^{-itv}f(v) \Bigg \{K_\theta \int _{\mathbb R}e^{i[\frac{\cot \theta }{2}s^{2}-vs\csc \theta +\frac{\cot \theta }{2}v^{2}]}H_{-\theta }(s)ds \Bigg \} \mathrm {d}v\\& \quad =\int _{\mathbb R}e^{-itv}f(v)h(v)\mathrm {d}v\\& =\varPsi _{FT}\Big \{f(v)h(v)\Big \}(t). \end{aligned}$$

The theorem is proved. \(\square\)

Moreover, when the parameter of the FrFT have the special form \(\theta ={\pi }/{2}\), the convolution here proposed for the FrFT reduces to a convolution in the FT domain.

New correlation structures for the FrFT

In the remaining part of this paper, the complex conjugation will be denoted by the superscript “*”.

Definition 3

A new correlation for the FrFT of two signals f(t) and h(t) is defined as follows:

$$\begin{aligned} (f\underset{\theta }{\circledast }h)\left( t\right) := \frac{1}{2\pi }\int _{\mathbb R}f(\tau )h^*(\tau -t\sin \theta )e^{-\frac{it\cos \theta }{2}(t\sin \theta -2\tau )}\mathrm {d}\tau . \end{aligned}$$
(19)

Let \(\hat{h}(t)=h^*(-t)e^{-it^2\frac{\cot \theta }{2}}\); then, the new correlation \(\underset{\theta }{\circledast }\) can be expressed as

$$\begin{aligned} (f\underset{\theta }{\circledast }h)\left( t\right) := \frac{1}{2\pi }\Big (\bar{f}*\hat{h}\Big )(t\sin \theta ). \end{aligned}$$
(20)

Definition 4

A dual operation of \(\underset{\theta }{\circledast }\), denoted by \(\underset{\theta }{\oplus }\), is defined by

$$\begin{aligned} (f\underset{\theta }{\oplus }h)\left( t\right) :=\int _{\mathbb R}f(\tau )h^*(\tau -t\sin \theta )e^{\frac{it\cos \theta }{2}(t\sin \theta -2\tau )}\mathrm {d}\tau . \end{aligned}$$
(21)

Let \(\tilde{h}(t)=h^*(-t)e^{it^2\frac{\cot \theta }{2}}\). Then, the new dual convolution \(\underset{\theta }{\oplus }\) can be rewritten in the form

$$\begin{aligned} (f\underset{\theta }{\oplus }h)\left( t\right) :=\Big (\breve{f}*\tilde{h}\Big )(t\sin \theta ). \end{aligned}$$
(22)

Theorem 3

Let \(F_{\theta }(u)\) and \(H^*_{\theta }(u)\) are the FrFT of the signals \(f(t), h^*(t)\) with parameter \(\theta\), respectively. We then have the factorization identity

$$\begin{aligned} \varPsi _{FT}\Big \{\big (f\underset{\theta }{\circledast }h\big )(t)\Big \}(u)=F_{\theta }(u)H^*_{\theta }(u). \end{aligned}$$

Proof

We find that

$$\begin{aligned}&F_{\theta }(u)H^*_{\theta }(u)=\int _{\mathbb {R}}\int _{\mathbb {R}}f(\tau )h(v) \mathscr {K}_{\theta } (u,\tau )\mathscr {K}^*_{\theta } (u,v)\mathrm {d}\tau \text{d}v \\&\quad=K_{\theta }K_{-\theta }\int _{\mathbb {R}}\int _{\mathbb {R}}f(\tau )h^*(v)e^{i[u^2\frac{\cot \theta }{2}-u\tau \csc \theta +\tau ^{2}\frac{\cot \theta }{2}]} e^{-i[u^2\frac{\cot \theta }{2}-uv \csc \theta +v^{2}\frac{\cot \theta }{2}]}\mathrm {d}\tau \mathrm {d}v\\&\quad =\frac{1}{2\pi \sin \theta }\int _{\mathbb {R}}\int _{\mathbb {R}}e^{i[-(\tau -v)u\csc \theta +\tau ^2\frac{\cot \theta }{2}-v^2\frac{\cot \theta }{2}]}f(\tau )h^*(v)\mathrm {d}\tau \mathrm {d}v. \end{aligned}$$

Then, taking \(\tau =\tau\), \(s=(\tau -v)\csc \theta\), we get

$$\begin{aligned}&F_{\theta }(u)H^*_{\theta }(u)\\&\quad =\frac{1}{2\pi }\int _{\mathbb {R}}\int _{\mathbb {R}}e^{-ius}f(\tau ) e^{i\tau ^{2}\frac{\cot \theta }{2}}h^*(\tau -s\sin \theta )e^{-i(\tau -s\sin \theta )^{2}\frac{\cot \theta }{2}}\mathrm {d}\tau \mathrm {d}s\\&\quad = \int _{\mathbb {R}}e^{-ius}\Big \{\frac{1}{2\pi }\int _{\mathbb {R}} f(\tau )e^{i\tau ^{2}\frac{\cot \theta }{2}}h^*(\tau -s\sin \theta )e^{-i(\tau -s\sin \theta )^{2}\frac{\cot \theta }{2}}\mathrm {d}\tau \Big \}ds\\&\quad =\varPsi _{FT}\Big \{\big (f\underset{\theta }{\otimes }h\big )(s)\Big \}(u). \end{aligned}$$

Thus, the proof of the theorem is achieved. \(\square\)

Here, we would like to remark that it is also possible to use the relationship between convolution and correlation definitions as a different technique to produce the above result (see [5] for a case involving the linear canonical transform).

Theorem 4

Let \(F_{\theta }(u)\) and \(H_{\theta }(u)\) be the FrFT of the signals f(t), h(t) with parameter \(\theta\), respectively. Then, the following factorization identity holds true:

$$\begin{aligned} \varPsi _{FT}\Big \{f(v)h^*(v)\Big \}(t)=\big [F_{\theta }(u) \underset{\theta }{\oplus }H^*_{\theta }(u)\big ](t). \end{aligned}$$

Proof

Having in mind the definition of FrFT, we have

$$\begin{aligned} \big [F_{\theta }(u)\underset{\theta }{\oplus }H^*_{\theta }(u)\big ](t)&= \int _{\mathbb R} F_{\theta }(\tau )e^{-i\tau ^2\frac{\cot \theta }{2}}H^*_{\theta }(\tau -t\sin \theta )e^{i(\tau -t\sin \theta )^2\frac{\cot \theta }{2}}\mathrm {d}\tau \\&=K_\theta \int _{\mathbb R}\int _{\mathbb R} e^{i[\frac{\cot \theta }{2}\tau ^{2}-\tau v\csc \theta +\frac{\cot \theta }{2}v^{2}]}e^{-i\tau ^2\frac{\cot \theta }{2}}f(v) \\&\qquad\times H^*_{\theta }(\tau -t\sin \theta )e^{i(\tau -t\sin \theta )^2\frac{\cot \theta }{2}}\mathrm {d}\tau \mathrm {d}v. \end{aligned}$$

Then, setting \(v=v\) and \(s=\tau -t\sin \theta\), we get

$$\begin{aligned}\big [F_{\theta }(u)&\underset{\theta }{\oplus }H^*_{\theta }(u)\big ](t)\\& =K_\theta \int _{\mathbb R}\int _{\mathbb R} e^{i[-v(s+t\sin \theta )\csc \theta +\frac{\cot \theta }{2}v^{2}]}f(v)H^*_{\theta }(s)e^{is^2\frac{\cot \theta }{2}}\mathrm {d}s\mathrm {d}v\\& =\int _{\mathbb R}e^{-itv}f(v) \Bigg \{K_\theta \int _{\mathbb R}e^{i[\frac{\cot \theta }{2}s^{2}-vs\csc \theta +\frac{\cot \theta }{2}v^{2}]}H^*_{\theta }(s)ds \Bigg \} \mathrm {d}v\\& =\int _{\mathbb R}e^{-itv}f(v)h^*(v)\mathrm {d}v\\& =\varPsi _{FT}\Big \{f(v)h^*(v)\Big \}(t). \end{aligned}$$

The theorem is proved. \(\square\)

Filter design implementation

Fig. 2
figure 2

The model of the multiplicative filter in the FrFT domain

Full size image

In this section, we will mainly discuss applications of the above new convolution theorems for the design of multiplicative filters in the FrFT domain.

First, the analysis of the hardware complexity is given. From (12), it is easy to find that there are two chirp multiplications in the time domain (TD) of the proposed convolution process. Moreover, the convolution structure (17) contains six chirp multiplications in the transform domain (TFD). Second, the computational complexity of the multiplicative filters will be derived. Using (12), (17) and Fig. 1, the computational complexity of multiplicative filters is as follows: N-point inverse, \(N^2+2N\) times of multiplication, and \(N(N-1)\) times of addition of complex number for length N input samples. Therefore, a tabular form shown in the Table 1 summarizes the comparative analysis of our proposed and known convolutions in [3, 35]. In this table, “Yes” is entered for the method where the relation is converted into the classical convolution theorem of FT at \(\theta =\frac{\pi }{2}\). From the Table 1, we derive that the positive fact that the computational complexity of our convolution is relatively small.

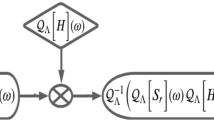
Table 1 Quantitative comparison of the computation times of multiplicative filters
Full size table

The symbols \(r_{in}(t)\) and \(r_{out}(t)\) are the input and output signals, respectively. Models of multiplicative filters in the FrFT domain have been discussed in [29, 35], which is shown in Fig. 2. Now, using the new convolution (17), we can express \(r_{out}(t)\) as

$$\begin{aligned} r_{out}(t)=\varPsi _{FT}^{-1}\Big \{F_{\theta }(u)H_{-\theta }(-u)\Big \}(t). \end{aligned}$$
(23)
Fig. 3
figure 3

New multiplicative filter in the FrFT domain

Full size image

From the above process, it is straightforward to realize that there are many ways to design a multiplicative filter based on different transform functions \(H_{-\theta }(-u).\) For instance, we can choose the filter impulse h(t) so that \(H_{-\theta }(-u)\) will be constant over \((u_1,u_2)\), and zero or rapidly decreasing outside that region, if we are interested only in the frequency spectrum of the FrFT in the region \((u_1,u_2)\) of the signal f(t).

Fig. 3 shows the new method of realizing the multiplicative filter in the FrFT domain. Comparing Fig. 3 and Fig. 2, it is easy to see that the computation of our new method is lower than the previous ones.

Now, the use of convolution in the time domain in multiplicative filter design will be discussed. We can use the new convolution (12) to implement the multiplicative filter. From (12), the output signal \(r_{out}(t)\) can be expressed as

$$\begin{aligned} r_{out}(t)=\frac{\sin \theta }{2\pi }\left( \bar{r}_{in}(t\sin \theta )*g(t)\right) , \end{aligned}$$
(24)

where g(t) is defined as

$$\begin{aligned} g(t)=\breve{h}(t\sin \theta ). \end{aligned}$$
(25)

This shows that the multiplicative filter can be achieved through the conventional convolution of \(r_{in}(t)\) and g(t) in the time domain. A realization of this method is given in Fig. 4. Thus, we can say that the performance of the method based on Fig. 4 is better than the one in Fig. 3 since the performance of the method in Fig. 3 needs to compute FT and FrFT, while for that in Fig. 4 we only need to compute through the Fast Fourier Transform.

Fig. 4
figure 4

Multiplicative filter in the FrFT domain using the convolution in the time domain

Full size image

According to the inverse FrFT formula, we get

$$\begin{aligned} h(t)&=\mathcal {F}_{\theta }\Big \{H_{-\theta }(u)\Big \}(t)\\&=K_{\theta } \int _{\mathbb R}H_{-\theta }(u)e^{i[u^2\frac{\cot \theta }{2}-tu\csc \theta +t^2\frac{\cot \theta }{2}]}\mathrm {d}u\\&=K_{\theta }e^{it^2\frac{\cot \theta }{2}}\int _{\mathbb R}H_{-\theta }(-u)e^{-iut\csc \theta }e^{iu^2\frac{\cot \theta }{2}}\mathrm {d}u\\&=2\pi e^{it^2\frac{\cot \theta }{2}}\varPsi _{FT}^{-1}\Big \{\hat{\hat{H}}(u)\Big \}(t\csc \theta ) \end{aligned}$$

where \(\hat{\hat{H}}(u)=K_{\theta }H_{-\theta }(u)e^{iu^2\frac{\cot \theta }{2}}.\) Thus, from (25), we realize that

$$\begin{aligned}&g(t)=\breve{h}(t\sin \theta )=h(t\sin \theta )e^{-i(t\sin \theta )^2\frac{\cot \theta }{2}}=2\pi \varPsi _{FT}^{-1}\Big \{\hat{\hat{H}}(u)\Big \}(t). \end{aligned}$$

According to (24), we have

$$\begin{aligned} r_{out}(t)&=\frac{\sin \theta }{2\pi }\left( \bar{r}_{in}(t\sin \theta )*g(t)\right) \\&=\frac{\sin \theta }{2\pi }\left( \bar{r}_{in}(t\sin \theta )*2\pi \varPsi _{FT}^{-1}\left\{ \hat{\hat{H}}(u)\right\} (t)\right) \\&=\sin \theta \cdot \left( \bar{r}_{in}(t\sin \theta )*\varPsi _{FT}^{-1}\left\{ \hat{\hat{H}}(u)\right\} (t)\right) . \end{aligned}$$

Using (4), we also obtain

$$\begin{aligned} r_{out}(t)=\sin \theta \cdot \varPsi _{FT}^{-1}\left[ \varPsi _{FT}\Big \{\bar{r}_{in}(t\sin \theta )\Big \}(u)\cdot \hat{\hat{H}}(u)\right] (t). \end{aligned}$$

Let \(\varphi (u)=\varPsi _{FT}\Big \{\bar{r}_{in}(t\sin \theta )\Big \}(u)\cdot \hat{\hat{H}}(u)\). Then, the output signal can be expressed as

$$\begin{aligned} r_{out}(t)=\sin \theta \cdot \varPsi _{FT}^{-1}\left\{ \varphi (u)\right\} (t). \end{aligned}$$
(26)

Therefore, from (26), we can use the Fast Fourier Transform to reduce the computational complexity of this multiplicative filter. Thus, we conclude that the computational complexity of the method in (24), based on the new convolution, for the length of N samples, is \(O(Nlog_{2}{N})\), which is the same as those introduced in [29, 32].

For the purpose of illustration, we use \(r_{in}(t)\) as the original input signal \(r_{in}(t)=e^{-t^2}+e^{i(t+10)^2},\) where \(X(t)=e^{-t^2}, N(t)=e^{i(t+10)^2}\) are the desired signal and the additive noise, respectively. The Wigner distribution (WD) of \(X(t), N(t), r_{in}(t)\) are plotted in Fig. 5.

Fig. 5
figure 5

The WD of the \(X(t), r_{in}(t)\)

Full size image

The value of the \(\theta\) angle for filtering in the FrFT domain can be found from [23].

Fig. 6 shows the output signal of the multiplicative filter achieved using the new convolution with the Mean Square Error (MSE) equal to 0, 0025.

Fig. 6
figure 6

The result of multiplicative filter achieved by using the new convolution

Full size image

Using MATLAB language (version R2015a) on a system having configuration Intel (R) Core(TM)i\(3-5005\)U CPU @2.00GHZ(4 CPUs), \(\sim 2.0\)GHz processor having 4096MB RAM, the Table 2 shows the MSE of the proposed domain filtering, fractional domain filtering, and frequency domain filtering in the real, imaginary and absolute components.

Table 2 Quantitative comparison of the computation MSE of proposed domain filtering, fractional domain filtering, and frequency domain filtering
Full size table

Conclusion

We have introduced new convolutions to the FrFT which allow the identification of several consequences associated with FrFT. A remarkable issue in the present convolutions is their simplicity in the sense that they can be seen as the classical convolution of two functions. Some special cases of our new convolution (e.g. with properties directly associated with the Fractional Fourier Transform and the Fourier Transform) were also introduced. As a main consequence and application, we have introduced different ways to design filters. Namely, a multiplicative filter in the FrFT domain have been analysed. We have concluded that the multiplicative filter through the convolution in the time domain can be realized by the classical FT and has the same capability, but less computational complexity, when compared with the method achieved in the FrFT domain. The results were illustrated in several concrete cases.