Scalable algorithms for designing CO₂ capture and storage infrastructure

Abstract

CO₂ capture and storage (CCS) is a climate change mitigation strategy that aims to reduce the amount of CO₂ vented into the atmosphere from industrial processes. Designing cost-effective CCS infrastructure is critical in meeting CO₂ emission reduction targets and is a computationally challenging problem. We formalize the computational problem of designing cost-effective CCS infrastructure and detail the fundamental intractability of designing CCS infrastructure as problem instances grow in size. We explore the problem’s relationship to the ecosystem of network design problems, and introduce three novel algorithms for its solution. We evaluate our proposed algorithms against existing exact approaches for CCS infrastructure design and find that they all run in dramatically less time than the exact approaches and generate solutions that are very close to optimal. Decreasing the time it takes to determine CCS infrastructure designs will support national-level scenario analysis, undertaking risk and sensitivity assessments, and understanding the impact of government policies (e.g., tax credits for CCS).

1 Introduction

CO₂ capture and storage (CCS) is the process of capturing CO₂ emissions from industrial sources, such as coal-fired and natural gas power plants, transporting the CO₂ via a dedicated pipeline network, and injecting it into geological reservoirs for the purpose of combating climate change and economic benefit (e.g., enhanced oil recovery, tax credits). CCS is a key technology in all climate change mitigation plans that limit global temperatures below 2 $^{\circ }$C of warming. To have a meaningful impact, this will involve optimizing infrastructure deployments for hundreds of sources and reservoirs, and thousands of kilometers of pipeline networks.

Deploying CCS infrastructure on a massive scale requires careful and comprehensive planning to ensure investments are made in a cost-effective manner (Smit 2014). At its core, designing CCS infrastructure is an optimization problem that aims to determine the most cost-effective locations and quantities of CO₂ to capture, route via pipeline, and inject for storage. Designing CCS infrastructure can naturally be formulated as a Mixed Integer Linear Program (MILP) that aims to minimize total cost, while capturing and injecting a target amount of CO₂. The MILP is parameterized with a candidate pipeline network constructed from a weighted cost surface, and economic and capacity data about the possible source and sink locations. We show in this research that designing CCS infrastructure is a generalization of the well-studied NP-Hard fixed charge network flow (FCNF) problem (Guisewite and Pardalos 1990). This means that optimal algorithms for designing CCS infrastructure do not efficiently scale as scenarios grow in size.

The intractability of designing CCS infrastructure impacts CCS infrastructure design studies in three ways. First, CCS infrastructure studies are moving from local scale projects with tens of sources and sinks to regional and national scale projects with thousands of sources and sinks. For instances of this size, MILP implementations have not been successful at executing in a reasonable time period (e.g., $40\%$ gap after 72 h). Second, many CCS infrastructure studies explore impacts of minute changes to input parameters that arise due to uncertainty (e.g., reservoir specific storage potential or injectivity). Studies of this type require ensemble runs, where thousands of differently parameterized instances are generated and solved, with results feeding the generation of more instances. Finally, studies are being proposed that consider continuous reservoir regions instead of discrete point locations. To solve these problems, the infrastructure design algorithm will need to be run many sequential times where, between runs, discrete reservoir locations are moved based on the previous iteration’s solution. It is not possible to rely on MILP formulations to solve these types of problems. New optimization techniques need to be developed to address the problem of designing CCS infrastructure for massive deployments.

In this research, we introduce the CCS Infrastructure Design (CID) problem and develop custom optimization algorithms for it. We prove that CID is a generalization of the well-studied FCNF problem and characterize its computational complexity. We then introduce three fast algorithms for the CID problem. Finally, we evaluate the performance of the algorithms on realistic datasets and find that they reduce running time compared to an optimal MILP, with a minimal increase in solution costs. Reducing the time it takes to determine CCS infrastructure designs will support national-level scenarios, undertaking risk and sensitivity assessments, and understanding the impact of government policies (e.g., tax credits for CCS).

The rest of this paper is organized as follows. We formalize the problem in Sect. 2 and characterize its computational complexity. Section 3 discusses related work. Our three algorithms are presented in Sect. 4. Experimental results are presented in Sect. 5 and we conclude in Sect. 6.

2 Problem formulation

Given a set of CO₂ emitters (sources), geological reservoirs, and a candidate pipeline network, the goal of the CCS Infrastructure Design (CID) problem is to determine, in a cost-minimal fashion, which sources to capture from, which reservoirs to inject into, and which (and what diameter) pipelines to build to capture a pre-determined system-wide quantity of CO₂.

The sources and reservoirs are parameterized with an economic model consisting of fixed costs to open locations (millions of dollars), and variable costs to utilize the locations (dollars per tonne of CO₂ captured/injected). These costs vary based on the ease of injection at that particular site. Candidate pipeline routes are constructed from a weighted cost surface (Hoover et al. 2020; Middleton et al. 2012; Yaw et al. 2019). Pipelines have construction and per-tonne utilization costs dependent on their geographic location and the quantity of CO₂ they transport. Pipelines can intuitively be represented as a number of discrete pipeline sizes (i.e. diameters) and their associated costs and capacities. Pipeline costs include construction and operation costs (e.g., pumping stations, maintenance). In a mixed integer linear program (MILP) formulation, this representation requires an integer variable for each possible pipeline edge/size pair, which results in a large number of variables and quickly leads to intractable formulations. To reduce the number of integer variables used in the MILP formulation, pipelines can be represented as a smaller set of linear functions (called trends) of pipeline capacity versus cost. The composition of these trends forms a pipeline capacity versus cost function that is increasing, piecewise linear, and subadditive. An example of two trends approximating the non-linear pipeline capacity versus cost function is presented in Fig. 1. The pipeline costs that the trends approximate were determined using the National Energy Technology Laboratory’s CO₂ Transport Cost Model (National Energy Technology Laboratory 2018). The increasing and subadditivity properties of the cost function enforces that a pipeline of a given capacity is cheaper than multiple pipelines of smaller capacities or a pipeline of a larger than necessary capacity. It is also assumed that the capacity of the largest pipeline trend is arbitrarily large. Using pipeline trends instead of explicit diameters allows for simpler formulations compared to the discrete formulation while still ensuring that the cost model is realistic (Middleton 2013). All fixed construction costs are annualized by way of a capital recovery factor that accounts for project financing. The CID problem based on linearized pipelines is formulated as an MILP below:

Fig. 1

Two linear trends approximating the cost of a pipeline given the transportation volume

Instance input parameters

$F_{i}^{src}$	Annualized fixed cost to open source i ($M/yr)
$F_{j}^{res}$	Annualized fixed cost to open reservoir j ($M/yr)
$V_{i}^{src}$	Variable cost to capture CO2 from source i ($/tCO2)
$V_{j}^{res}$	Variable cost to inject CO2 in reservoir j ($/tCO2)
S	Set of sources
R	Set of reservoirs
I	Set of vertices (sources, reservoirs, and pipeline junctions)
K	Set of candidate pipeline edges
C	Set of pipeline capacity trends
$Q_{i}^{src}$	Annual CO2 production rate at source i (tCO2/yr)
$Q_{j}^{res}$	Total capacity of reservoir j (tCO2)
$Q_{kc}^{max}$	Max annual capacity of pipeline k with trend c (tCO2/yr)
$Q_{kc}^{min}$	Min annual capacity of pipeline k with trend c (tCO2/yr)
$\alpha _{kc}$	Variable transport cost on pipeline k with trend c ($/tCO2)
$\beta _{kc}$	Annualized fixed cost for pipeline k with trend c ($M/yr)
L	Length of project (years)
T	Target CO2 capture amount for project (tCO2/yr)

MILP decision variables

$s_{i} \in \{0,1\}$	Indicates if source i is opened
$r_{j} \in \{0,1\}$	Indicates if reservoir j is opened
$y_{kc} \in \{0,1\}$	Indicates if pipeline k with trend c is opened
$a_{i} \in {\mathbb {R}}_{{\ge 0}}$	Annual CO2 captured at source i (tCO2/yr)
$b_{j}\in {\mathbb {R}}_{{\ge 0}}$	Annual CO2 injected in reservoir j (tCO2/yr)
$p_{kc} \in {\mathbb {R}}_{{\ge 0}}$	Annual CO2 in pipeline k with trend c (tCO2/yr)

The MILP is driven by the objective function:

$$\begin{aligned} \min \overbrace{\sum _{i \in S} (F_i^{src} s_i+V^{src}_i a_i)}^\text {capture cost} + \overbrace{\sum _{\begin{array}{c} k \in K\\ c \in C \end{array}}(\alpha _{kc} p_{kc} + \beta _{kc} y_{kc})}^\text {transport cost} + \overbrace{\sum _{j \in R} (F_j^{res} r_j + V_j^{res} b_j)}^\text {storage cost} \end{aligned}$$

Subject to the following constraints:

$$\begin{aligned}Q_{kc}^{min}y_{kc} \le p_{kc} \le Q_{kc}^{max}y_{kc},\quad \forall k \in K,\quad \forall c \in C \end{aligned}$$

(1)

$$\begin{aligned}&\sum _{\begin{array}{c} k\in K:\\ src(k)=n \end{array}} \sum _{c \in C} p_{kc} - \sum _{\begin{array}{c} k\in K:\\ dest(k)=n \end{array}} \sum _{c \in C} p_{kc} = {\left\{ \begin{array}{ll} a_{n} &{} \text {if}\,{ {n \in S}} \\ -b_{n} &{} \text {if}\,{ {n \in R}}\\ 0 &{} \text {otherwise} \end{array}\right. } , \quad \forall n \in I \end{aligned}$$

(2)

$$\begin{aligned}a_{i} \le Q_{i}^{src}s_{i},\quad \forall i \in S\end{aligned}$$

(3)

$$\begin{aligned}b_j L \le Q_{j}^{res}r_{j},\quad \forall j \in R\end{aligned}$$

(4)

$$\begin{aligned}\sum _{i \in S} a_{i} \ge T \end{aligned}$$

(5)

Where constraint 1 ensures that a pipeline is built before transporting CO₂ and that the pipeline’s capacity is appropriate for the amount of flow. Constraint 2 enforces conservation of flow at each internal vertex. Constraint 3 ensures a source is opened before capturing CO₂ and that the captured amount is limited by the source’s maximum production. Constraint 4 limits lifetime storage for each reservoir by its maximum capacity, and constraint 5 ensures the total system-wide capture amount meets the target.

2.1 Computational complexity

CID generalizes the Fixed Charge Network Flow (FCNF) problem: Consider a directed graph with edge capacities and fixed edge costs. Purchasing an edge incurs its fixed cost and allows it to host any amount of flow up to its capacity. A subset of the vertices are designated as sources and have an associated amount of flow they are able to supply. Likewise, a subset of the vertices are designated as sinks (analogous to reservoirs in the CID problem) and have an associated amount of flow they demand. The goal of the FCNF problem is to determine a least-cost set of edges that allows sufficient flow to be routed from the sources to the sinks to satisfy all of the sink demand (Kim and Pardalos 1999).

Theorem 1

There is no $\gamma \ln |V|$-approximation algorithm for the FCNF problem, where $0<\gamma <1$ is some constant, unless $P=NP$.

Proof

This complexity result is via an approximation-preserving reduction from the Dominating Set problem: Given a graph $G=(V,E)$, find a minimum sized $U \subseteq V$ such that for each vertex v in $V \setminus U$, there is some vertex u in U such that the edge (u, v) is in E.

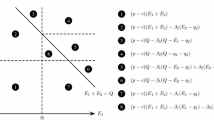
Let $G=(V,E)$ be an instance of Dominating Set where $|V|=n$. G reduces to an FCNF instance $G'=(V',E')$ as follows: For each vertex v in V, make a new vertex $v_{in}$. Make a directed edge with cost zero and capacity one from the new vertex to the original one (the dotted red edges in Fig. 2). For every edge $e=(u,v)$ in E, make the directed edges $(u,v_{in})$ and $(v,u_{in})$ with cost zero and capacity one (the solid black edges in Fig. 2). Create a new vertex s and for each vertex v in V, make the directed edge (s, v) with cost one and infinite capacity (the dashed green edges in Fig. 2). Let the original vertices V be the sinks and each have a demand of one. Let s be the single source and let its supply be |V|. Figure 2 shows the reduction from Dominating Set to FCNF.

Fig. 2

Dominating Set reduction to the FCNF problem where each edge is weighted as (cost, capacity)

Suppose that $U \subseteq V$ is a dominating set of G with $|U|=k$. For each vertex in $V\setminus U$, associate it with one neighbor that is in U. In this way, each vertex u in U is associated with a set of neighbors $N_u$ that are in $V \setminus U$. U can now be translated into a source-sink flow of cost k in $G'$. For each vertex u in U, push $|N_u| + 1$ units of flow from the source s to u. One unit of that flow will be consumed by u and the additional $|N_u|$ units of flow will be distributed to the neighbors in $N_u$. Consider a vertex v in $V \setminus U$. This vertex has been associated with a single neighbor vertex u that is in U. Since v and u are neighbors in G, the directed edges $(u,v_{in})$ and $(v_{in},v)$ are in $G'$ and form a path from u to v. The capacity of this path is one, so one unit of flow can be pushed to each vertex v in $V\setminus U$ from its associated neighbor vertex u in U. Therefore, this flow will satisfy all demand in $G'$ and its cost will be k since the only costs incurred are the fixed unit costs for sending flow to the nodes directly connected to source s (i.e. the vertices in U).

Suppose there is a flow solution to $G'$ of cost k. This means that every vertex in V receives one unit of flow from source s. Let U be the set of vertices receiving flow directly from source s. Since the only costs incurred in the flow network are on vertices receiving flow directly from source s, $|U|=k$. Consider a vertex v in $V \setminus U$. Suppose that v was able to forward flow to another vertex in $V'$. This would require v receiving more than one unit of flow, since v’s demand for one unit needs to be satisfied. There are only two directed edges into v: $(v_{in},v)$ and (s, v). Since v is not in U, the directed edge (s, v) is not carrying any flow. Since the capacity of $(v_{in},v)$ is one, all of the flow carried on this edge must be used to satisfy v’s demand. Therefore, there is no excess flow available for v to forward to another vertex in $V'$. This means that every vertex in $V \setminus U$ must be receiving flow from a neighbor that is in U, which means that U is a dominating set of V.

Since any dominating set in G of size k corresponds to a flow in $G'$ of cost k and conversely, inapproximability results the Dominating Set problem hold for the FCNF problem. It was shown by Raz and Safra (1997) that there exists a constant, $0<\gamma <1$, such that the Dominating Set problem cannot be approximated within a factor of $\gamma \ln |V|$ unless $P=NP$, thus this result holds for the FCNF problem as well. $\square$

Corollary 1

The CID problem has the same inapproximability result as the FCNF problem.

Proof

CID generalizes the classic FCNF problem by allowing parallel edges representing different pipeline sizes. Other apparent differences between CID and FCNF are not actually generalizations of the FCNF model: Source and reservoir costs and capacities can be pushed to a new edge between the original source/reservoir and a new node. Also, allowing only a subset of the demand to be captured can be enforced with a new source node that feeds the original sources and a new reservoir node connected to the original reservoirs with the required demand (i.e. the target CO₂ capture amount).

As such, CID cannot be easier to approximate than FCNF.

$\square$

Because of this complexity result, we pursue fast suboptimal algorithms for CID in Sect. 4.

3 Related work

Variations on the CID problem have been studied and numerous approaches have been developed to intelligently design CCS infrastructure. SimCCS is an economic-engineering optimization tool for designing CCS infrastructure and is the premier CCS infrastructure modelling tool (Middleton and Bielicki 2009; Middleton et al. 2020; Yaw and Middleton 2018). SimCCS concurrently optimizes selection of sources, reservoirs, and pipeline routes. One of the key features unique to SimCCS relative to other CCS infrastructure design models is the integration of routing based on geographical features (e.g., population density, topography, existing rights of way) (van den Broek et al. 2009; Gale et al. 2001; Morbee et al. 2011). Put another way, SimCCS uses a MILP solver to solve the CID problem stated in Sect. 2 whereas other CCS infrastructure design models can only solve simplified versions of the CID problem.

No work has been done trying to develop suboptimal solutions to the CID problem in faster running time than solving the MILP formulations. However, extensive work has been done in the context of the FNCF problem, which is a special case of the CID problem, as discussed in Sect. 2. FCNF is itself a variant of the minimum concave network flow (MCNF) problem, where the edge cost function is concave. Due to the economies of scale property inherent to concave cost functions, MCNF problems arise in a variety of applications ranging from offshore platform drilling (Glover 2005) to traffic networks (Poorzahedy and Rouhani 2007). Algorithms developed for MCNF problems can generally be categorized as: exact algorithms, genetic algorithms, simulated annealing algorithms, slope scaling heuristics, and/or greedy heuristics.

MCNF is an NP-Hard problem and cannot, in general, be solved optimally in polynomial time. However, useful instances of MCNF can still be solved optimally and, exact methods have been widely explored for these cases (Fontes and Gonalves 2012). Gallo et al. created a branch and bound procedure as one of the original algorithms for solving MCNF (Gallo et al. 1980). Since then, numerous studies have used a combination of relaxation, bounding, and cutting to find exact solutions (Fontes and Gonalves 2012; Hochbaum and Segev 1989; Kliewer and Timajev 2005; Khang and Fujiwara 1991; Crainic et al. 2005; Gallo et al. 1980; Kowalski et al. 2014; Dang et al. 2011).

Optimal techniques have also been developed for the FCNF problem relying on Benders decompositions (Costa 2005) and branch-and-cut techniques (Ortega and Wolsey 2003; Gendron and Larose 2014). Other approaches include cutting-plane and Lagrangian relaxation (Gendron 2011).

Genetic algorithms have been extensively studied to search for high quality solutions to MCNF problems. Fontes and Gonalves introduced one of the first genetic algorithms followed by a local search to improve results (Fontes and Gonalves 2007). Yan et al. developed a genetic algorithm that preforms better than several local search algorithms (Yan et al. 2005). Xie and Jia used a hybrid minimum cost flow and genetic algorithm (Xie and Jia 2012). Smith and Walters solved a variation of the problem where the base graph is a tree (Smith and Walters 2000).

Simulated annealing methods randomly explore the search space and gradually increase the probability of exploring edges that led to low cost solutions. Altiparmak and Karaoglan used a hybrid of simulated annealing and a tabu search strategy (Altiparmak and Karaoglan 2008). Yaghini et al. solved a multi-commodity flow network variant (Yaghini et al. 2012). Dang et al. used a variant of simulated annealing called deterministic annealing method to solve instances with high arc densities (Dang et al. 2011).

Slope scaling heuristics iteratively solve relaxed versions of the initial solution, updating costs after each iteration to find better approximations (Crainic et al. 2005; Gendron et al. 2018; Ekiolu et al. 1970; Kim and Pardalos 1999; Lamar et al. 1990). Crainic et al. developed a slope scaling heuristic which relaxes the solution by replacing the fixed and variable costs with a single variable cost. To avoid becoming stuck in local optima, they introduce a long-term memory procedure, which perturbs the solution based on previous flow values and significantly improves results (Crainic et al. 2005). Gendron et al. improved this algorithm by introducing an additional iterative linear program approach (Gendron et al. 2018). Due to the success of slope scaling heuristics in many application areas, we employ this technique in the design of the algorithm presented in Sect. 4.2.

Greedy heuristics are a popular technique for finding MCNF and FCNF solutions. Early heuristics relied on local searches with various adding, dropping, and swapping strategies (Billheimer and Gray 1973; Monteiro and Fontes 2005; Guisewite and Pardalos 1991). Later approaches often implemented memory via a tabu search to avoid getting stuck in local optima (Altiparmak and Karaoglan 2008; Bazlamacci and Hindi 1996; Kim et al. 2006; Poorzahedy and Rouhani 2007). Guisewite and Pardalos explored several local search heuristics based on finding a set of shortest paths between a single source and multiple sinks (Guisewite and Pardalos 1991). One such heuristic finds all shortest paths between the source and sinks and then selects the smallest number of cheapest paths that satisfy flow requirements. We follow a similar approach in the design of the algorithm presented in Sect. 4.1, with the main difference being that our algorithm recalculates the shortest paths after each path is selected, to take advantage of already used edge capacity. We chose this technique in an effort to explore provable performance and a potential approximation algorithm.

4 Algorithms

Existing approaches to solving CCS infrastructure design type problems rely on exact techniques, specifically solving MILPs like the one detailed in Sect. 2. The running time of MILP solvers does not scale linearly with linearly increasing input size. Large instances (e.g., thousands of vertices and pipeline components) cannot be solved by MILPs in a reasonable time, which motivates the search for sub-optimal techniques with better running time performance. In this section, we present three algorithms for CID.

4.1 Greedy add

The first algorithm we introduce iteratively builds a solution by greedily selecting cheap (source, reservoir) pairs, as well as the cheapest appropriately sized pipelines connecting them. This algorithm is presented in Algorithm 1 and detailed below with references to the applicable lines of Algorithm 1.

First, for each (source, reservoir) pair, the maximum amount of CO₂ that is able to be transferred between the pair is determined. This value is calculated as the minimum of the source’s uncaptured production, the reservoir’s unused capacity, and the amount of the target capture remaining (line 4).

Second, the (source, reservoir) pair’s capture and storage costs are calculated. Fixed costs are only included if the source or reservoir has not yet been opened (lines 6-11). Variable costs are included based on the amount of CO₂ that was determined to be transferred between the source and reservoir (line 5).

Third, the cheapest path between the source and reservoir for the amount of CO₂ that will be transferred is calculated. To calculate the cheapest path, the pipeline network first needs to be parameterized with costs that reflect the cost to transport that amount of CO₂ along each pipeline component. These costs need to take into account the following considerations:

• 1. Unused pipeline capacity that has already been purchased.

• 2. Upgrade costs associated with moving from one trend to a higher capacity trend.

• 3. Changes to the variable costs for CO₂ already being transported along that pipeline component associated with changing pipeline trends.

• 4. Cost savings associated with downsizing pipeline capacities due to redirecting CO₂ (i.e. pushing CO₂ in the opposite direction of CO₂ already being transported).

Parameterizing the pipeline network with costs is done in lines 13-27. Each pipeline component $e=(u,v)$ is sequentially considered as a directed edge. Depending on the pipeline trend already purchased and existing CO₂ flow on e or $e'=(v,u)$, there are three possibilities for the new pipeline’s required volume and the existing pipeline’s cost:

• 1. e is already hosting CO₂ (lines 14-16). In this case, the new volume of CO₂ on e will be the existing volume plus the new amount being transported. The old pipeline cost is the old cost of e.

• 2. $e'$ is already hosting CO₂ (lines 17-19). Pipelines cannot transport CO₂ in both directions. If $e'$ is already hosting CO₂, adding flow in the opposite direction on e represents redirecting CO₂ that was traveling from v to u. If $e'$ is hosting less CO₂ than the amount being transported, the new volume of CO₂ on e will be the new amount minus the amount $e'$ is currently hosting. If $e'$ is hosting more CO₂ than the amount being transported, the new volume of CO₂ on $e'$ would be the amount $e'$ is currently hosting minus the new amount. In either case, the magnitude of the difference is the new volume of CO₂, so line 18 captures both with the absolute value. In both cases, the old pipeline cost is the old cost of $e'$.

• 3. Neither e nor $e'$ is already hosting CO₂ (lines 20-22). In this case, the new volume of CO₂ on e will be the new amount being transported and there was no old pipeline cost.

The cost associated with using pipeline component e is then calculated by first determining the smallest trend that will fit the new volume of CO₂ (line 24). A pipeline of sufficient capacity is always available since the maximum capacity of the largest trend exceeds the target CO₂ capture amount. The new cost of the pipeline component is calculated as the fixed cost for the selected trend plus the utilization cost as a factor of the new volume of CO₂ (line 25). The cost of pipeline component e is set to be the new cost minus the old pipeline component cost (line 26). This is the cost to use pipeline component e, factoring in already purchased pipeline infrastructure. A consequence of this calculation is that the cost of e can be negative when $e'$ is hosting CO₂. If redirecting CO₂ results in the new cost of the pipeline component being lower than the old cost of $e'$, the cost to use e will be negative. Selecting e in this case represents redirecting some of the CO₂ that was traversing $e'$,thereby enabling a smaller pipeline trend for the remaining CO₂, less utilization, and a cost savings. The cheapest path can then be calculated between the source and reservoir (line 28). Since there can be negative edge weights in the network, and possibly negative cycles, we implemented this step by setting the capacity of each edge to 1 and finding the minimum-cost flow of value 1.

After the costs for each (source, reservoir) pair are calculated, the pair that captures, transports, and injects CO₂ for the lowest cost per tonne is added to the solution (lines 31-35). When the cheapest pair is selected, the infrastructure used to support the pair is updated for future iterations (lines 38-63). For the selected source and reservoir, they are added to the solution and their amounts captured and stored are updated (lines 39-40). The path between the source and reservoir is added one edge at a time (lines 42-63). In a similar fashion as was done to parameterize the costs for the pipeline network when finding cheapest paths, the new edge added to the solution depends on whether or not that edge (or its reverse) was already in the solution. If the edge was already in the solution, it will stay in the solution with a new volume of CO₂ being the old volume plus the new amount being transported (lines 43-45). If the edge in the reverse direction is already in the solution, the edge added to the solution and its volume of CO₂ depends on if the reverse edge was hosting more or less than the new amount of CO₂ being transported (lines 46-53). If neither the edge nor the reverse direction edge is already in the solution, the edge is added with a volume of CO₂ being the new amount being transported (lines 54-56).

This process then repeats until the target quantity of CO₂ is captured. The running time for Algorithm 1 is driven by lines 2-36. The running time for the algorithm is $O((|S||R|)^2(|K||C|+ShortestPath))$, where |S| is the number of sources, |R| is the number of reservoirs, |K| is the number of pipeline components, |C| is the number of trends, and ShortestPath is the running time for the shortest path algorithm used. Line 2 repeats until the capture target is met by maximizing the transfer between some (source, reservoir) pair at each iteration of the algorithm. Since the transfer between each pair is maximized, it cannot be revisited in future iterations. This means that line 2 cannot repeat more than |S||R| times. Line 3 repeats |S||R| times. Line 13-27 runs in |K||C| time and line 28 runs in whatever the running time is of the selected shortest path algorithm. When there are a reasonable number of trends, the shortest path algorithm at line 28 will dominate the running time. A preliminary version of this algorithm appeared in a poster at ACM’s e-Energy conference in 2019 (Whitman et al. 2019).

4.2 Iterative LP

The second algorithm we introduce iteratively solves linear programs that result from removing all integer variables from the mixed integer linear program formulated in Sect. 2. Removing integer variables allows the resulting linear programs to be solved optimally in polynomial running time. However, the integer variables in the original mixed integer linear program formulation provided the mechanism to charge the fixed cost based on the binary decision of whether infrastructure was used or not. Each type of infrastructure entity (i.e. source, pipeline, or reservoir) in the CID problem has a fixed utilization cost F and variable utilization cost V. This means that the total cost for an entity is $Fw+Vx$, where w indicates if the entity is in use and x is the continuous amount of CO₂ processed by the entity. To approximate fixed costs with only continuous variables, entity costs are reformulated by removing the fixed utilization component and changing the variable utilization coefficient from V to $\tfrac{F}{{\hat{x}}}+V$, where ${\hat{x}}$ is an estimate of what the value of x will be when the linear program is solved. Therefore, the closer x is to ${\hat{x}}$, the closer the reformulated cost is to the true cost. This results in the following linear program, where ${\hat{a}}$, ${\hat{p}}$, and ${\hat{b}}$ are the estimated capture, transportation, and injection amounts:

$$\begin{aligned} \min \overbrace{\sum _{i \in S} \left( \frac{F_i^{src}}{{\hat{a}}_i}+V^{src}_i\right) a_i}^\text {capture cost} + \overbrace{\sum _{\begin{array}{c} k \in K\\ c \in C \end{array}} \left( \alpha _{kc} + \frac{\beta _{kc}}{{\hat{p}}_{kc}}\right) p_{kc}}^\text {transport cost} + \overbrace{\sum _{j \in R} \left( \frac{F_j^{res}}{{\hat{b}}_j} + V_j^{res}\right) b_j}^\text {storage cost} \end{aligned}$$

(6)

Subject to constraints 2 and 5 from Sect. 2 and the following modified constraints:

$$\begin{aligned}0 \le p_{kc} \le Q_{kc}^{max},\quad \forall k \in K,\quad \forall c \in C \end{aligned}$$

(7)

$$\begin{aligned}a_{i} \le Q_{i}^{src},\quad \forall i \in S\end{aligned}$$

(8)

$$\begin{aligned}b_j L \le Q_{j}^{res},\quad \forall j \in R \end{aligned}$$

(9)

These constraints are similar to constraints 1, 3, and 4 from Sect. 2. Constraint 7 limits the maximum capacity of a pipeline. Constraint 8 limits the amount captured at each source by its maximum production, and constraint 9 limits lifetime storage for each reservoir by its maximum capacity.

An iterative scheme is used to generate estimated ${\hat{a}}$, ${\hat{p}}$, and ${\hat{b}}$ values: The estimated values are all initially set to one and the linear program is solved, resulting in solution values for a, p, and b. For each subsequent iteration, the estimated ${\hat{a}}$, ${\hat{p}}$, and ${\hat{b}}$ values are set to equal the previous iteration’s a, p, and b values. In this way, if an infrastructure entity’s utilization remains identical across iterations, its total cost will accurately reflect the correct fixed and variable costs, since $(F/{\hat{x}}+V)x=F+Vx$ when $x={\hat{x}}$. However, there is no guarantee that the utilization values will stabilize between iterations, so we cannot depend on this process by itself to return high-quality solutions.

Two procedures, motivated by Crainic et al. (2005), are used to explicitly search for improved solutions, instead of just aiming to accurately reflect costs. Both of these procedures incentivize use of specific infrastructure based on usage in previous iterations of the algorithm. The intensification procedure prioritizes heavily-used infrastructure to improve existing solutions. The diversification procedure prioritizes seldom used infrastructure to encourage exploration of new solutions. Both of these procedures modify the ${\hat{a}}$, ${\hat{p}}$, and ${\hat{b}}$ values based on utilization statistics from previous iterations. The relevant utilization statistics are the same for each family of variables in the linear program (i.e. a, p, and b), so they can all be represented with a generic variable x:

$$\begin{aligned} \begin{array}{l l} \text {avg}^{x_i}_n &{} \quad \hbox {Average value of } x_i \hbox { in first } n \hbox { iterations}\\ \text {max}^{x_i}_n &{} \quad \hbox {Maximum value of } x_i \hbox { in first } n \hbox { iterations}\\ \text {rat}^{x_i}_n &{} \quad \hbox {Equal to } \text {avg}^{x_i}_n/\text {max}^{x_i}_n\\ \text {num}^{x_i}_n &{} \quad \hbox {Number of times } x_i \hbox { was non-zero in first } n \hbox { iterations}\\ \mu ^x_n &{} \quad \hbox {Average number of non-zero } x'\hbox {s in first } n \hbox { iterations}\\ \sigma ^x_n &{} \quad \hbox {Standard deviation of number of non-zero } x'\hbox {s in } n \hbox { iterations} \end{array} \end{aligned}$$

This algorithm is presented in Algorithm 2 and detailed below. The algorithm alternates between intensification (lines 8-18) and diversification (lines 21-31) phases until the maximum number of iterations is exceeded (line 2). In the intensification phases, entities that are already extensively deployed are defined as entities $x_i$ where $\text {num}^{x_i}_n\ge \mu ^x_n + \frac{1}{2}\sigma ^x_n$ (line 10). For these entities, ${\hat{x}}_i$ is set to $1/(1-\text {rat}^{x_i}_n)$ (line 11) which makes the cost coefficient in the objective function for entity $x_i$ equal to $F(1-\text {rat}^{x_i}_n)+V$. On the other hand, uncommonly deployed entities are defined as entities $x_i$ where $\text {num}^{x_i}_n< \mu ^x_n$ (line 12). For these entities, ${\hat{x}}_i$ is set to $1/(2-\text {rat}^{x_i}_n)$ (line 13) which makes the cost coefficient in the objective function for entity $x_i$ equal to $F(2-\text {rat}^{x_i}_n)+V$. All other entities have ${\hat{x}}_i$ is set to 1 (line 15), which makes the cost coefficient in the objective function for entity $x_i$ equal to $F+V$. This results in incentivizing the use of extensively deployed entities (since $1-\text {rat}^{x_i}_n \le 1$), disincentivizing the use of uncommonly deployed entities (since $2-\text {rat}^{x_i}_n \ge 1$).

In the diversification phases, extensively and uncommonly deployed entities are defined in the same way as in the intensification phases. For extensively deployed entities, ${\hat{x}}_i$ is set to $1/(1+\text {rat}^{x_i}_n)$ (line 24) which makes the cost coefficient in the objective function for entity $x_i$ equal to $F(1+\text {rat}^{x_i}_n)+V$. For uncommonly deployed entities, ${\hat{x}}_i$ is set to $1/\text {rat}^{x_i}_n$ (line 26) which makes the cost coefficient in the objective function for entity $x_i$ equal to $F\cdot \text {rat}^{x_i}_n+V$. All other entities have ${\hat{x}}_i$ is set to 1 (line 28), which makes the cost coefficient in the objective function for entity $x_i$ equal to $F+V$. This results in incentivizing the use of uncommonly deployed entities (since $\text {rat}^{x_i}_n \le 1$), disincentivizing the use of extensively deployed entities (since $1+\text {rat}^{x_i}_n \ge 1$).

This algorithm alternates between intensification and diversification phases until the maximum number of iterations is exceeded (line 2). At each iteration, ${\hat{a}}$, ${\hat{p}}$, and ${\hat{b}}$ are determined and the linear program described above is formulated and solved (lines 33-34). The resulting solution is used to update the utilization statistics and the next iteration begins (line 42). Changing from intensification phases to diversification phases and back is done whenever solution costs fail to improve within some threshold number of iterations (lines 3-5 and 35-41). Once the target number of iterations is completed, the set of sources, reservoirs, and pipeline components from the last iteration is returned. Finally, the real cost of this infrastructure must be calculated, since the cost used in the algorithm is not the actual cost, but the scaled cost defined in the objective of the linear program in Sect. 4.2.

The running time for each iteration of Algorithm 2 is driven by the formulation and solving of the linear program in lines 33-34. The linear program has $O(|S|+|K||C|+|R|)$ variables and $O(|K||C|+|I|+|S|+|R|)$ constraints, where |S| is the number of sources, |R| is the number of reservoirs, |K| is the number of pipeline components, |C| is the number of trends, and |I| is the number of vertices in the pipeline network. The running time is then O(numIterations $\cdot$ |LP|), where numIterations is the number of iterations enforced in line 2 and |LP| is the running time associated with constructing and solving the linear program solver.

4.3 LP-greedy hybrid

The third algorithm we introduce is a hybrid of the first two algorithms. This algorithm is presented in Algorithm 3 and detailed below. First, an initial solution is generated by Algorithm 2 (line 1). The unit cost to transfer the maximum amount of CO₂ between each (source, reservoir) pair in the solution is then calculated (lines 4-29). Calculating this cost is done in a similar fashion to what was done in Sect. 4.1 when finding the cheapest path for a (source, reservoir) pair: First, the maximum amount of CO₂ transferable between the (source, reservoir) pair in the solution is calculated as the minimum of the CO₂ captured at the source and injected at the reservoir (line 5). Second, the capture and storage costs associated with that amount of CO₂ is calculated as the sum of the utilization costs (line 6) and applicable fixed costs (lines 7-12). Third, the shortest path in the solution between the (source, reservoir) pair is calculated by first parameterizing a network with the cost savings of removing this pair from the solution (lines 14-23). This is done by considering each directed edge in the solution that is hosting more CO₂ than the maximum transferable amount (lines 15-16). The cost of a new pipeline hosting the original amount of CO₂ minus the maximum transferable amount is calculated (lines 17-20). The cost of this edge in the cost network is set to be the difference between the cost of the pipeline in the solution and the new pipeline cost (line 21). The cheapest path for the (source, reservoir) pair is calculated by finding the shortest path in the cost network (line 24). These capture, transport, and storage costs and summed and the cost per ton of CO₂ calculated and recorded (line 27).

Once the pairwise costs of each (source, reservoir) pair is calculated, the cheapest (per ton of CO₂) reservoir for each source is identified (lines 31-35) and the most expensive pair is selected (line 36). The rationale for this step is that selecting the most expensive (source, reservoir) pair from the list of all pairs will likely select a pair with high transportation cost (i.e. physically distant from each other) that would not actually pair together to transfer CO₂ instead of a pair that would reasonably pair together. Instead, the list of cheapest pairs will reflect more likely pairings, of which we select the most expensive one for removal.

The most expensive of the cheapest, for each source, (source, reservoir) pairs is removed from the solution (lines 38-59). A pair is removed from the solution by removing the maximum transferable amount of CO₂ from the source and reservoir (lines 38-46). The cost and volume of CO₂ on each edge in the cheapest path between the (source, reservoir) pair is then calculated and updated (lines 48-59).

Finally, the cheapest replacement (source, reservoir) pairs are then added back to the solution using Algorithm 1 (line 62). Before Algorithm 1 is run, the solution variables in Algorithm 1 ($S'$, $R'$, $K'$) are set to be the $S'$, $R'$, and $K'$ values from this algorithm (line 61). This process is repeated for a fixed number of iterations and improves the solution by replacing expensive (source, reservoir) pairs with cheaper ones.

The driver of the running time for each iteration of Algorithm 3 is not as clear as the preceding algorithms. Algorithm 2 is run only once, in line 1. Lines 4-29 takes $O(|S||R|(|K||C| + ShortestPath))$, where |S| is the number of sources, |R| is the number of reservoirs, |K| is the number of pipeline components, |C| is the number of trends, and ShortestPath is the running time for the shortest path algorithm used. Line 62 calls Algorithm 1, which runs in $O((|S||R|)^2(|K||C|+ShortestPath))$ time, with possibly a different shortest path algorithm than Algorithm 3. In practice though, Algorithm 1 does not need to run many iterations, since the amount of captured CO₂ is still very close to the target. So, it is unlikely that Algorithm 1 will actually run for close to |S||R| iterations in its line 2, whereas lines 4-29 in Algorithm 1 will run in ${\Theta }(|S||R|(|K||C| + ShortestPath))$ time each iteration. Nonetheless, the running time is $O(numIterations + |S||R|(|K||C| + ShortestPath) + (|S||R|)^2(|K||C|+ShortestPath))$, where numIterations is the number of iterations enforced in line 2.

5 Results

For the algorithms presented in Sect. 4 to be useful in realistic applications, they must both (1) solve instances significantly faster than optimal MILP approaches and (2) find solutions whose costs are close to optimal. In this section, we present results from testing the GreedyAdd, IterativeLP, and Hybrid algorithms on real CCS datasets. These algorithms were implemented and integrated with the SimCCS CCS infrastructure optimization software. Optimal MILPs were formulated using SimCCS and the MILP presented in Sect. 2. The MILP implemented does not incorporate any enhancements (e.g., Benders decomposition) which could result in a lower execution time. Initial experiments suggested that parameterizing the IterativeLP algorithm to run for 200 iterations and to switch between intensification and diversification phases after 5 iterations of not improving the cost of the solution lead to the highest quality solutions in the quickest time. The Hybrid algorithm was parameterized with the same values for its execution of IterativeLP and was set to run through the component removal/addition process for 100 iterations. Results presented were produced running the algorithms implemented in SimCCS on a machine running Fedora 30 with an Intel Core i7-2450 processor running at 2.1 GHz using 32 GB of RAM. The optimal MILPs were solved on this machine using IBM’s CPLEX optimization tool, version 12.10.

Source and reservoir data were provided by the Great Plains Institute in support of the National Petroleum Council’s 2019 Carbon Capture, Use, and Storage study (National Petroleum Council 2019). This study involved a ground up economic analysis of hundreds of potential source locations and resulted in the most modern CO₂ capture database to date covering a vast geographic region and many industries. Reservoir data includes both storage without direct economic benefit (i.e. deep saline formation storage) as well as storage that incurs a direct economic benefit (i.e. enhanced oil recovery¹). This data spans most of the contiguous United States and has a total of 150 potential sources and 270 potential sinks. Candidate pipeline routes were generated in SimCCS using its novel network generation algorithms (Yaw et al. 2019). A sample infrastructure design is presented in Fig. 3.

Fig. 3

Sample CCS infrastructure design with 40 possible sources and 40 possible reservoirs. Selected sources and reservoirs are larger and in dark red (sources) and dark blue (reservoirs). The purple edges are the candidate network and the selected edges are green. (Color figure online)

The motivation for developing new CCS infrastructure design algorithms is the massive time requirement for solving optimal MILPs and input instances grow large. To evaluate the running time of the algorithms, four scenarios were considered that set the number of available sources and sinks as 20, 40, 80, or 160. For each scenario, 10 instances were generated that randomly selected the appropriate number of sources and sinks from the full available set. The average sizes of the resulting scenarios is presented in Table 1. The variation of instance sizes within each scenario is less than $10 \%$.

Table 1 Scenario sizes

Target capture amounts for each individual instance were set as the maximum amount of CO₂ able to be captured and stored, calculated as the minimum of the total capturable CO₂ and total annual reservoir storage capacity. The running time required for each algorithm on each scenario is recorded as the average of the running time over the 10 instances. Figure 4 presents the average running time required for each algorithm in each scenario. Note the logarithmic scale y-axis. Error bars representing the minimum and maximum values are presented to illustrate the variability in running time. For some algorithms and scenarios (e.g., GreedyAdd and IterativeLP), very little variation was found. All three algorithms substantially reduce running time compared to solving the MILP optimally. For the largest scenario, this improvement is near two orders of magnitude for the worst algorithm (GreedyAdd) and four orders of magnitude for the best (IterativeLP). It is also apparent that for larger scenarios, IterativeLP is significantly faster than both GreedyAdd and Hybrid. This performance difference is likely attributable to the rapid speed even very large linear programs can be solved.

Fig. 4

Average running time (logarithmic scale) versus input instance size

Though reducing the running time it takes to solve CCS infrastructure design problems is the primary objective of these algorithms, quick solutions are not beneficial if the quality of the solution is very poor. To evaluate the quality of the solution, the cost of the infrastructure designs from the running time experiment were compared. The true cost of the infrastructure that does not include any scaling factors used by the algorithms to manipulate costs was calculated and is reported here. Figure 5 presents average true solution costs of the infrastructure designs found by each algorithm in each scenario. Error bars representing the minimum and maximum values across all algorithms are presented to illustrate the variability in solution costs. Variability is very similar across the algorithms, and is much larger than the differences in the average values, so only the largest maximum and smallest minimum for each scenario is displayed. Solutions costs increase as the size of the input instances increase, since more infrastructure incurs a higher cost. Costs for all algorithms stay fairly close to the optimal costs.

Fig. 5

Average solution cost versus input instance size

Figure 6 presents the average percent each algorithm’s costs increased over the optimal cost. Error bars representing the minimum and maximum values across all algorithms are presented to illustrate the variability in solution costs. Variability is very similar across the algorithms, and is much larger than the differences in the average values, so only the largest maximum and smallest minimum for each scenario is displayed. The average, minimum, and maximum percent deviation over optimal for each algorithm in each scenario is provided in Table 2. All algorithms found solutions that were less than $13 \%$ more expensive than the cost of the optimal solution. Aside from some variability seen with small instances, GreedyAdd finds solutions with better costs than IterativeLP and Hybrid.

Fig. 6

Percent increase in average solution cost compared to optimal solution versus input instance size

Table 2 Percent deviation from optimal cost

This evaluation suggests that all three algorithms can greatly reduce running time while keeping solution costs close to optimal. One final interesting question is to consider the process for actually solving optimal MILPs. CPLEX tends to very quickly converge on good solutions and spends the majority of its time closing the final gap. Even if the algorithms presented here run in less time than it takes CPLEX to terminate, it is possible that CPLEX will find a solution that is better than the algorithm’s solution in less time than the algorithm took. Figure 7 presents the time it takes CPLEX to generate a solution whose value is better than the solution that GreedyAdd found. Note the logarithmic scale y-axis. Error bars representing the minimum and maximum values are presented to illustrate the variability in time. This was only presented for GreedyAdd since it was the algorithm that consistently found the lowest cost solutions. For the largest scenario, it takes CPLEX on average approximately 4.75 min before its solution has a lower cost than GreedyAdd’s solution.

Fig. 7

Average time it takes for CPLEX to find a lower cost solution than the algorithm (logarithmic scale) versus input instance size

Figure 8 presents the optimality gap that CPLEX had when it found a lower cost solution than the solution that GreedyAdd found. The optimality gap is the gap between the best integer solution found and the best relaxed solution in the remaining search space. As such, it does not correspond to the gap with the actual optimal solution, but instead it is the gap with current best lower bound on the optimal minimum cost. Error bars representing the minimum and maximum values are presented to illustrate the gap variability. For the largest scenario, the optimality gap was on average $20\%$ when CPLEX’s solution surpassed GreedyAdd’s solution, even though the eventual gap with the optimal solution was on average $5\%$ (Fig. 6).

Fig. 8

CPLEX optimality gap when CPLEX found a lower cost solution than the algorithm versus input instance size

Even though all algorithms greatly reduce running time compared to optimally solving MILPs, they do so to a varying degree and with a varying impact on solution costs. This presents a different use case for each algorithm. GreedyAdd is the most accurate, consistently staying within 7% of optimal. This suggests that GreedyAdd will work well for small to mid-ranged scenarios, consistently providing reliably good solutions. It also has the advantage of not requiring special software (e.g., CPLEX) to solve linear programs. Finally, GreedyAdd would be much more straightforward to parallelize than the other algorithms, which could open to door to constructing a high-performance computing workflow. IterativeLP is the fastest and also achieves high accuracy for some scenarios. Many CCS studies are proposing a high-level screening phase that will run thousands of instances reflecting the uncertainty involved in many of the economic and physical parameters. Having a tool like IterativeLP available, that can quickly give rough cost estimates, would enable this high-level screening. Hybrid is able to improve on the solutions chosen and could even be adapted to work as a refinement tool on other CCS infrastructure design algorithms.

6 Conclusion

In this research, we presented three algorithms for the CID problem demonstrated experimentally that they are fast with minimal loss in solution quality for realistic CCS data. These algorithms represent viable approaches for approximating CCS infrastructure designs for large scenarios. We explored the trade-offs between the algorithms and suggested specific use cases for each. This enables organizations to better explore scenarios that were previously hindered by the intractability of solving MILPs optimally.

Future practical work could focus on more testing and improving the high variability seen in the IterativeLP algorithm. Testing should take place on other data sets. Scenarios fed by other data sets may see differences in network structure, requiring modifications of each algorithm. In addition, further improvements should look at reducing the solution costs for all algorithms.

Future theoretical work could look at developing algorithms with theoretical performance guarantees (i.e. approximation algorithms). Such algorithms would be of interest to the larger community given the CID problem’s relationship with the FCNF problem, but would also provide insight into CCS infrastructure designs that cannot be compared to an optimal solution.