Abstract
Water supply of high-rise buildings requires pump systems to ensure pressure requirements. The design goals of these systems are energy and cost efficiency, both in terms of fixed cost as well as during operation. In this paper, cost optimal decentralized and tree-shaped water distribution networks are computed, where placements of pumps at different locations in the building are allowed. We propose a branch-and-bound algorithm for solving the corresponding mixed-integer nonlinear program, which exploits problem specific structure and outperforms state-of-the-art solvers. A further desirable feature is that the system is K-resilient, i.e., still able to operate under K pump failures during the use phase. Using a characterization of resilient solutions via a system of inequalities, the branch-and-bound scheme is extended by a separation algorithm to produce cost optimal resilient solutions. This implicitly solves a multilevel optimization problem which contains the computation of worst-case failures. Moreover, using a large set of test instances, the increased energy-efficiency of decentralized networks for the supply of building is shown and properties of resilient layouts are discussed.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Increasing population density and land prices in cities make high-rise buildings an attractive construction option. Such buildings have to be supplied with water, which requires so-called booster systems to increase the water pressure in order to reach all floors. The conventional network layout of high-rise buildings consists of a set of parallel pumps installed in the basement and of a single-stranded pipe system supplying the building’s single floors or several floors grouped into zones with the same pressure. This design has two advantages: (i) the piping cost is lowest for this layout, (ii) if one pump fails, water supply can be maintained by using parallel pumps.
However, besides the initial investment and the availability of the system, also its operation cost play a key role. Recent studies by Nault and Papa (2015) estimate that 70% of a pump system’s life cycle cost are caused by its electricity consumption. Thus, planning energy-efficient water distribution networks and especially optimizing their layout and operation simultaneously seems promising.
In this paper, we therefore investigate more complex, decentralized system layouts that may lead to a more efficient operation and thus to lower overall cost. As one main contribution, we present a branch-and-bound method to solve the corresponding design problem to global optimality, thereby exploiting the underlying tree-structure of the network. We demonstrate that this approach is faster than applying state-of-the-art mixed-integer nonlinear program (MINLP) solvers. In general, such problems are difficult to solve, due to the interaction of network design choices and nonlinear physics. Indeed, it seems that no global optimization approaches for this joint design and operation problem have appeared in the literature (see Sect. 2).
A second contribution concerns the anticipation of the system availability during the design phase. In this paper, we consider systems that are K-resilient, i.e., these systems allow to ensure a certain percentage of the demand even if up to K pumps in the system fail. Such problems are even harder to solve, since they involve a multi-level optimization structure: the goal is to find a cost efficient design such that for every possible failure scenario there exists an operation plan of the pumps such that the required demand is satisfied. Nevertheless, we show that the branch-and-bound method can be extended to this case and that it allows for the relative efficient computation of such K-resilient systems. Again, the underlying structure is exploited to this end.
These two contributions allow for the design of large realistic water supply systems of high-rise buildings. As a third contribution, we discuss the influence of decentralized layouts and its consequences for engineering such systems. Depending on the requirements on cost and resilience, there are clear advantages for certain layouts.
The paper is organized as follows. Section 2 contains an extensive literature review on optimal water distribution networks. In Sect. 3, we present the MINLP model which computes an optimal system layout as well as its operation. We also discuss the computational complexity of this model. In Sect. 4, we develop the branch-and-bound framework together with a relaxation to solve the MINLP more efficiently. In Sect. 5, we characterize resilient solutions and adapt the framework using a separation scheme to compute optimal solutions which can handle the failure of pumps. Section 6 contains the description of the creation of test instances and the performance of the proposed algorithms. The resulting realistic test instances allow us to draw conclusions on the design of efficient and also resilient water networks. We conclude the paper in Sect. 7 addressing future research directions.
2 Related work
The water supply of high-rise buildings can be regarded as a water distribution network. Mathematical programming has been successfully applied to optimize such networks for several decades. A detailed review is given, e.g., by D’Ambrosio et al. (2015). The complexity of the respective problems depends on (i) whether the network is fixed or designed, (ii) stationary or transient operation, (iii) the technical components considered (pipes, pumps, valves and/or tanks) and (iv) the underlying physical and technical models, which may comprise systems of partial differential equations (PDEs) and nonlinear component characteristics. In the following, we give a short overview of related work. We refer to Mala-Jetmarova et al. (2017) for an extensive overview. For an introduction to MINLP we refer to Belotti et al. (2013).
Optimization of water distribution network operation Optimizing the operation of water distribution networks with given design has been investigated in numerous works which all focus on special aspects of the problem.
The optimal stationary operation of a water distribution network is addressed by Gleixner et al. (2012). They include continuous operation decisions, such as volume flow and pressure, as well as discrete decisions to model the on/off-state of pumps. However, only pumps with fixed speed are considered. Handling non-convex nonlinearities in constraints and objective function using problem-specific reformulations and presolving, they are able to solve the resulting large real-world MINLP instances to global optimality.
To model dynamic aspects in water distribution networks, the so-called water hammer (mass and momentum) equations are used – a set of PDEs which model transient flow in pipes, cf. Ghidaoui et al. (2005). In optimization models these PDEs are usually discretized in time and/or space. Kolb and Lang (2012) use an implicit box scheme and solve the continuous control task using gradient-based optimization methods. This approach allows to find optimal rotational speeds of pumps, but does not cover their optimal switching.
To optimize pump switching and control, often referred to as “optimal pump scheduling”, several methods have been applied, such as linear (Jowitt and Germanopoulos 1992), nonlinear (Yu et al. 1994; Skworcow et al. 2014) and dynamic programming (Zessler and Shamir 1989). However, many of these approaches relax the problem by approximating the underlying physical laws or the technical characteristics.
In general, the physical models lead to non-convex constraints for the head-flow relations, and binary variables for pump switching. State-of-the-art methods for solving the respective MINLPs can be divided into non-convex optimization and approaches using piecewise linear approximations.
The latter has first been proposed in the joint works of Geißler et al. (2011) and Morsi et al. (2012). By a piecewise linearization of the nonlinear physical and technical constraints, the authors present a mixed-integer linear program (MIP) for optimizing the operation of water supply networks. Given these approximations, they are able to find an optimal operation strategy for a given network consisting of 20 pipes, three pumps, two tanks, one source and four sinks. Verleye and Aghezzaf (2013) have extended this approach to a network with multiple sources and reduced the amount of binary variables considerably, using a piecewise linear approximation by Vielma and Nemhauser (2011) that requires only a logarithmic number of binary variables.
Non-convex optimization in the context of pump scheduling has been introduced by Burgschweiger et al. (2009) for investigating the minimum cost operative planning of water supply networks for a time horizon of 24 h. However, the authors simplify the problem by subsuming single pumps within pump stations while approximating their aggregate efficiency, and by using smooth approximations of the hydraulic pressure loss. Since solving the resulting MINLP to global optimality is not practical for the network size they consider, they present a nonlinear programming (NLP) model and use special techniques to address the binary decisions. Using this approach, they compute near-optimum solutions for large networks in acceptable time.
Bonvin et al. (2017) treat the 1-day ahead optimal operation of a special class of branched water networks with one pumping station. They show that due to the presence of a flow control valve at each water tower, non-convex constraints modeling the hydraulic pressure loss and the pump characteristics can be relaxed. The resulting convex MINLP can then be solved with general-purpose solvers.
Another non-convex optimization approach in this context has been presented by Ghaddar et al. (2015), who use Lagrangian decomposition to find solutions with guaranteed upper and lower bounds. However, they assume in their model that all pumps have a constant rotational speed.
Optimization of layout and design Besides optimizing their operation, also the optimal layout and design of water distribution networks has been studied. Note that in this context the terms “layout” and “design” may be used to distinguish between different optimization problems, cf. De Corte and Sörensen (2013): While layout problems deal with finding an optimal network topology, i.e., with deciding where pipes, pumps and other components are placed and how they are connected, design problems deal with finding the optimal material and diameter of pipes, and the optimal pump types and sizes for a network with a given topology.
In the area of design problems, the majority of works focuses on the so-called gravity-fed design optimization problem, i.e., for a given layout solely the optimal selection of pipe types and diameters is treated. The optimal selection of active components like pumps is not considered. While some of the early works apply nonlinear programming approaches, in which the pipe diameter is a continuous variable, cf., e.g., Fujiwara and Khang (1990) or Varma et al. (1997), Bragalli et al. (2012) use a MINLP approach to select from a set of commercially available diameters and demonstrate its ability to find good solutions for practical instances. In Robinius et al. (2018) a tree-shaped potential flow-based (e.g., water-distribution) network is designed such that it is robust against uncertain demand.
Since the problem of selecting optimal pipe diameters for a water distribution network is NP-hard (Yates et al. 1984), also the development of (meta-)heuristic approaches has received considerable attention. Many of these approaches use external solvers such as EPANET, cf. Rossman (2000), to assess the feasibility of the hydraulic constraints. For a detailed review on the state-of-the-art in this context we refer to De Corte and Sörensen (2013).
While design problems typically only comprise pipe sizing, layout problems also comprise the piping layout as well as the selection, sizing and/or placement of other components such as pumps, valves or tanks. Lejano (2006) optimize the piping layout and design of a branched water distribution system. Assuming linear models for the investment cost of pipes and pumps and the pump operative costs, they solve the resulting MIP. Therefore, they aggregate pumps into pump stations and use linear models for their power consumption. To find the optimal placement of pressure reducing valves in an existing network and determine their optimal settings, Eck and Mevissen (2012) employed MINLP techniques, while using a quadratic approximation for the pipe head loss.
Joint optimization of layout and/or design and operation In addition to the initial investment, also the operation cost can make up a large proportion of the life cycle cost of a water distribution network. Thus, for cost-optimal planning, the simultaneous optimization of investment and operation cost should be addressed. While different approaches based on heuristic methods exist for this complex problem [cf., e.g., Dandy et al. (1994), Ostfeld and Tubaltzev (2008), Prasad (2009), Narayanan et al. (2012)], the global optimization of layout, design and operation of water distribution networks from scratch has to the best of the authors’ knowledge not yet been addressed.
Resilience and survivable networks Next to investment and operation cost, the concept of resilience has emerged as an important feature of water distribution networks, and numerous different resilience measures have been proposed in the literature. Shin et al. (2018) give an overview over different quantitative resilience measures used in the context of water distribution networks. The presented resilience measures are manifold and range from static to dynamic, and from deterministic to probabilistic approaches. One of the most prominent quantitative measures proposed is the so-called “resilience index” by Todini (2000). The idea of this index is that a surplus of pressure head in normal operating conditions will allow the network to overcome critical operating conditions, such as component failures.
Recently, also complex network theory and statistical graph metrics such as average path length, link density, central point dominance or k-shortest path length have gained increased interest to assess the resilience of different network topologies. Herrera et al. (2016) propose a graph-theoretic framework to assess the resilience of sectorized networks. They analyze the network’s connectivity by approximating it via averaging over the k-shortest paths from water sources to consumption nodes. Using a multiscale decomposition and since computations for the proposed index scale quasi-linearly with the number of nodes, they are able to assess the resilience of large sectorized networks against failures of multiple pipes. In another recent study, Meng et al. (2018) showed that for 85 benchmark water distribution networks, specific graph metrics strongly correlate with the network resilience against pipe closures.
While the work mentioned above is based on simulative approaches, the optimization of network topologies to guarantee performance in case of failures has been investigated in other fields. Especially in the field of telecommunication, designing survivable networks has become a major objective, cf., e.g., Grötschel et al. (1995). The goal is to design a network that is still connected if a specific number of vertices and/or edges is removed. This problem can be formulated as a MIP, cf. Goemans and Bertsimas (1993).
However, optimizing the layout of water distribution networks such that they may perform sufficiently in case of failures comprises more than just their connectivity. Not only the limited amount of paths after the failure, but also effects upon hydraulic head losses and subsequent pump adjustments have to be considered.
An alternative approach to resilience in the form of component failure gives rise to multi-level optimization problems, where an attacker chooses the worst-case failure scenario, with respect to an optimal response of a defender or a defender designs an optimal system which can withstand the worst-case actions of an attacker. Examples in this field include the work of Brown et al. (2006), Chen et al. (2014) and Bienstock and Verma (2010). Note that there are newly developed approaches for bilevel programming including integer variables, e.g., by Fischetti et al. (2017), Mitsos (2010) or Kleniati and Adjiman (2015).
Depiction of an exemplary design a with four pressure zones. Two pumps are installed in the ground floor and another pump is installed in the third pressure zone. This pipe layout is represented by the graph in b. c shows the graph \(\mathcal {G}\) of all possible connections for \(N=4\) pressure zones
3 Problem statement and model formulation
We consider the design of decentralized water distribution networks in high buildings. The decentralized arrangement of pumps leads to an efficient use of hydraulic power, since multiple floors can be supplied individually. To select the optimal layout consisting of different pump types and their number and placement in the system as well as to find the optimal pipe diameter design, we present a MINLP model, that is an extended model compared to Leise et al. (2018), Leise and Altherr (2018) and Altherr et al. (2018b). This model is based on a directed acyclic graph, which models the underlying pipe network. We partition the total number of floors of the high-rise building into several pressure zones. Next to the traditional approach, in which a booster station in the basement supplies all floors with one rising pipe, this is also a possible system layout according to the technical standard DIN 1988-500 (2011). In this case, each pressure zone consisting of multiple floors is supplied by a separate booster station and pipe. In our model, the number of pressure zones is given by N. We model rising pipes that supply different pressure zones as arcs and different pressure zones as nodes. It is possible to place pumps on each of these different arcs. This allows a decentralized placement and therefore potential energy and cost savings in the utilization phase, which results in lower overall costs. We consider pipe wall friction, but neglect friction losses of individual parts, like valves, pumps and fittings.
Hereafter we use the abbreviations \([n]:=\{1, \ldots , n\}\) and \([n]_0 :=\ \{0,\ldots , n\}\) and for a node v in a directed graph the set of incoming and outgoing arcs is given by \(\delta ^{-}(v)\) and \(\delta ^{+}(v)\), respectively. The used variables of the different presented models and further symbols used in this paper are collected in Tables 1 and 2, respectively.
Only steady state conditions are considered, i.e., a fixed amount of volume flow has to be transported from the water main, which is connected to the municipal water supply network, to each pressure zone. The objective consists of minimizing pipe and pump investment costs as well as pump operating costs. To transport water to each zone, it has to be connected to the water main. This is done either by connecting it to other lower zones or directly to the inlet. All possible pipe layouts are summarized in a directed graph \(\mathcal {G} =(\mathcal {V}, \mathcal {A})\) whose nodes represent the inlet 0 and the pressure zones 1 to N, so \(\mathcal {V} = \{0\} \cup [N]\). The arc set represents the possible connections of pressure zones, \(\mathcal {A} = \{(u, v) \in \mathcal {V}\times \mathcal {V}\, : \,u < v\}\), cf. Figure 1c. In the example building, Fig. 1a, all zones but the highest are connected to the water main, whereas the highest zone is connected to the zone directly below. In the graph, given in Fig. 1b, this is represented by four arcs which connect node 0 to nodes 1 to 3, and node 3 to node 4.
In this paper, we restrict the possible pipe layout by allowing only one connection from the water main to each zone, i.e., to connect a pressure zone v to the inlet, only one arc of \(\delta ^{-}(v)\) may be chosen. Therefore, only the directed spanning trees of \(\mathcal {G}\) rooted in node 0 form feasible connections.
For each used connection, a pipe diameter has to be selected from a finite set of possibilities. The chosen pipe diameters strongly influence energy losses due to friction. Furthermore, to overcome friction and geodetic height differences pumps of different types can be placed on used connections to increase the pressure. On each arc, a series connection of parallel pump groups of the same type can be placed. The pump’s optimal operating speed has to be determined in order to fulfill the water demand in each pressure zone, with the highest energy-efficiency possible. In the next section, we describe the physical behavior of pumps and pipes leading to the formulation of the presented MINLP.
3.1 Modeling of pumps
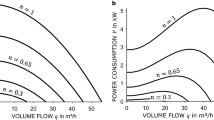
Variable speed pumps are used to increase pressure to supply all zones in the building. They have the advantage that their rotating speeds can be adapted to partial loads during operation, and it is possible to save energy in comparison to pumps with a fixed rotating speed, cf. Coelho and Andrade-Campos (2014). A pump with a variable rotating speed can be described by four variables. These are the volume flow in the pump q, the rotational speed \(\omega\), the induced pressure head \({\varDelta }h\) and the consumed power p. Fixing any two of theses values determines the other two. Typically, pump manufactures provide so-called characteristic diagrams which describe the head and power as a function of the volume flow. An example is shown in Fig. 2. Here, contour lines mark different speed levels \(\omega\). Note that the pressure head \({\varDelta }h\) is measured in meters. This is done by rescaling the pressure with \(1 / \rho g\), where \(\rho\) is the density of water and g the assumed to be constant gravitational acceleration.
To describe the feasible set of values given by a pair of characteristic diagrams, we use, based on Ulanicki et al. (2008), the quadratic and cubic approximation
to determine the pressure head and power for a given volume flow q and rotating speed \(\omega\). From the q-\({\varDelta }h\) diagram we furthermore derive a system of linear inequalities, which describe the possible domain of the pump. It includes a lower and upper bound on the normalized rotational speed \(\omega\), and also two inequalities for the left and right boundaries in Fig. 2. Altogether, we denote the feasible set of values for a pump by
In practice, a large selection of pumps are available to choose from. We denote this catalog of different pump types with \(\mathcal {C}\). Each pump type \(i\in \mathcal {C}\) leads to a different characteristic diagram and to a feasible set \({\varLambda }_i\). On each connection of the graph \(\mathcal {G}\) different types may be placed in series. Furthermore, up to \(M\in \mathbb {N}\) pumps of the same type may be placed in parallel on each connection. For running pumps of the same type, built in parallel, the optimal operating speeds are identical and the volume flow is shared equally among the parallel pumps, see Pedersen and Yang (2008) and Groß et al. (2017).
3.2 Scaling of pump characteristics
Since the available pump types in the catalog \(\mathcal {C}\) strongly influence the energy-efficiency of the future system, it is essential that \(\mathcal {C}\) consists of accurately modeled pumps. In order to include different pump sizes in an efficient way, we use a physically motivated method to scale pumps as shown in Gülich (2008). It is possible to describe the flow of multiple pumps with different sizes by a scaling law, if the flow conditions in the different pumps are comparable from a geometrical and dynamical point of view. Two pumps are geometrically similar, if all surfaces that conduct the flow are scaled by the same amount. Two pumps are dynamically similar, if they have the same Reynolds, Euler and Froude number. In this paper, we consider explicitly several series of similar pumps. Based on the characteristic diagrams of a model pump, as shown in Fig. 2, it is possible to derive the characteristic diagrams of multiple further pumps by varying the impeller size and the number of stages, which describes a series connection of multiple equivalent pump stages in one housing. Assuming that the volumetric and hydraulic efficiency, as well as the rotational speed and density of the fluid are equal for the reference pump and all derived pumps, it is possible to use the following scaling laws, as shown in Gülich (2008):
Here, d denotes the impeller diameter, \(\eta\) the hydraulic efficiency and \(z_{\text {st}}\) the number of stages. The index M represents the reference pump, whereas the values without an index represent the derived values for pumps with different impeller diameter d and stage number \(z_{\text {st}}\).
An example for the q-\({\varDelta }h\) relation of a model and a derived pump is shown in Fig. 3. The solid black curve represents the characteristic diagram of a reference pump. The dashed curve denotes the domain of a pump derived by using an impeller diameter ratio \(d / d_{\text {M}}\). The dotted lines represent corner points for multiple scaled pumps, which use a diameter ratio \(d / d_{\text {M}}\) between the model and upscaled pump.
The scaling of the q-p relationship, which is not shown in Fig. 3, is performed similarly. It requires the definition of the hydraulic efficiency \(\eta\) and depends on the Reynolds number and the relative roughness of the pump. In general, the efficiency of pumps increases with the diameter of the impeller. This increase is modeled with the help of a so-called majoration formula. In this example, we model the efficiency increase in the best point of different scaled pumps by using:
which is shown in Gülich (2008). If we include the Reynolds number \(Re = \frac{n\pi d^2}{\nu }\) for pumps, we can simplify Eq. (3) to obtain
This equation only depends on the diameter ratio \(d / d_{\text {M}}\) and on the hydraulic efficiency \(\eta _{\text {M}}\), which can be measured for each reference pump. Hereafter, \(\eta _{\text {M}}\) is represented by the efficiency in the best operating point and the scaled efficiency value is then used in (2) to adapt the hydraulic power for an increased impeller diameter.
3.3 Modeling of pipes
The fluid flow in pipes is a result of a pressure difference between both ends. On the one hand, the necessary pressure increase is usually created by pumps. On the other hand, pipe friction leads to a pressure loss. This decline depends on the length of the pipe L, the inner diameter d and the volume flow q. We use the Darcy-Weisbach equation
where \(\lambda\) is the friction coefficient and \(g\) is the standard gravity acceleration.
The computations in this paper consider volume flows between \(25\hbox { m}^{3}/\hbox {h}\) and \(35\hbox { m}^{3}/\hbox {h}\) as well as diameters between \(0.01\hbox { m}\) and \(0.1\hbox { m}\). These values lead to Reynolds numbers, cf. Spurk and Aksel (2008), that indicate a turbulent flow. Additionally, all computations are based on the assumption that we have steady flow conditions. We use the friction law of Nikuradse, Prandtl and von Kármán, cf. Brkić (2011), for a hydraulically rough pipe to estimate friction losses:
The pipe wall roughness parameter is set to \(K = 0.0015\hbox { mm}\), which represents stainless steel pipes, cf. DIN 1988-300 (2012). Equation (5) is valid for hydraulic rough flows and it only depends on the relative wall roughness. As a result it can be integrated in the optimization program more easily than other models, like for example the Colebrook-White model, which depends on the Reynolds number and the relative wall roughness. To simplify this inclusion into our model, we define for each pipe a and diameter d a function \({\varDelta }F_{a, d}:\mathbb {R}\rightarrow \mathbb {R}\) taking as argument a volume flow q to denote, based upon the above discussion, the friction in this pipe.
3.4 Optimization model
The MINLP model (6) to compute optimal solutions to the water distribution network problem is presented in Fig. 4. Variables are written in lower case letters, while parameters are written in capital letters. In the model indicator constraints are used, see Bonami et al. (2015) for a general discussion. The notation \(y=1 \;\Rightarrow \;g(x)\le 0\) for a binary variable y means that the constraint \(g(x) \le 0\) has to hold if \(y=1\). Several mathematical programming solvers, like CPLEX or SCIP are able to express and benefit from indicator constraints involving linear constraints. An alternative formulation of the model would involve so-called big-M constraints, which would make the model less compact. The implementation of indicator constraints, especially those involving nonlinear functions is specified in Sect. 6.2.
In Model (6) we use the sum of investment costs for pumps and pipes as well as energy costs in the utilization phase as the objective (6a).
The constraints of the MINLP enforce the following logical and physical properties of the problem. Constraints of type (6b) and (6c) are used to add the hydraulic characteristics of the pumps to the model, cf. Section 3.1. The constraints of type (6d) and (6e) provide lower bounds on the friction by using the friction law of Nikuradse, Prandtl and von Kármán and upper bounds on the volume flow depending on the chosen pipe diameter. The latter bound, \(Q^\text {dia}_d\), is necessary due to the maximal volume speed in pipes according to DIN 1988-300 (2012). The pressure height in each zone is determined by Constraints (6f): We consider the pressure increase of pumps, as well as pressure losses based on friction and height differences. Constraints (6g) and (6h) are used to define the inlet pressure at the water main and the desired pressure in each pressure zone of the building. The Constraints (6i) together with the Constraints (6j) determine the volume flow in the distribution network and enforce a volume flow balance for each pressure zone. To generate tree-shaped networks the Constraints (6k) restrict the number of connections to each pressure zone to one. Pumps may only be placed on used connections by (6l). Finally, for each used connection a pipe diameter must be set by Constraints (6m).
3.5 Computational complexity
Problem (6) contains difficult decisions on the choice of pipes and also nonlinearities. In the following, we examine its computational complexity to determine the structure that makes the problem challenging.
Proposition 1
Problem (6) is weakly NP-hard for\(N=1\), \(M=1\)and \(|{\mathcal {D}}|=1\), omitting friction and using fixed speed pumps.
Proof
We reduce the knapsack decision problem, see [MP0] in Garey and Johnson (1979), to the decision version of Problem (6). Given \({\tilde{n}}\) items it asks for a subset \({\tilde{S}}\subseteq [{\tilde{n}}]\) of the items, such that their weight does not exceed the knapsack capacity and the profits are at least a given value, i.e., \(\sum _{i \in {\tilde{S}}} \tilde{a}_i \le \tilde{b}\) and \(\sum _{i \in {\tilde{S}}} \tilde{c}_i \ge \tilde{d}\).
Given such a knapsack instance, we construct a corresponding water network instance, as follows. Each item is represented by a pump type, which has cost equal to the weight of the item and is able to increase the pressure by exactly the cost of the item. So, \({\varLambda }_i :=\{(q, \omega , {\varDelta }h, p) \in \mathbb {R}^4 \, : \,{\varDelta }h = \tilde{c}_i,\; p = 0\}\) and \(C^\text {pu}_i = \tilde{a}_i\) for \(i\in [{\tilde{n}}]\). Furthermore, the instance consists of \(N=1\) pressure zone of height \(\tilde{d}\).
Then a feasible solution to Problem (6) must fulfill the minimum pressure constraints (6f) to (6h), which correspond to the cost objective of the knapsack. Moreover, the capacity constraint of the knapsack instance corresponds to the question whether the objective of the water network solution is smaller or equal to \(\tilde{b}\). \(\square\)
Note that neither the network structure nor the nonlinear pump characteristic nor the friction nor the diameter selection problem is taken into account in the previous reduction.
One can further show that not only the catalog of pump types but also the network structure makes the problem intricate.
Proposition 2
Problem (6) is strongly NP-hard for\(|{\mathcal {C}}|=1\), \(M=1\)and\(|{\mathcal {D}}|=1\), omitting friction and using fixed speed pumps.
Proof
We reduce the bin packing problem, see [SR1] in Garey and Johnson (1979), to Problem (6). It is described by a collection of \({\tilde{N}}\) items with positive weights \(\tilde{a}_1, \ldots , \tilde{a}_{\tilde{N}}\) and seeks a partition of \([\tilde{N}]\) into \(\tilde{K}\) bins \(B_1, \ldots B_{\tilde{K}}\) such that the the items in each bin do not exceed the capacity \(\tilde{b}\), i.e., \(\sum _{v \in B_i} a_v\le \tilde{b}\) for \(i \in [\tilde{K}]\).
For such a bin packing instance, we construct the following water distribution network instance: We use for each item one pressure zone. Therefore \(N = \tilde{N}\). The demand \(D_v\) of each zone is given by the corresponding item weight \(\tilde{a}_v\). The lengths of the connections \(L_a\) are set to 0 and we assume \(H_\text {min} =1\) and \(H_\text {in} = 0\). The pump catalog \(\mathcal {C}\) contains one fixed speed pump which is able to transport a flow of up to \(\tilde{b}\) and build up a pressure of 1 without consuming power. Therefore, its feasible set can be written as
The instance also assumes non-existent friction and only one pipe diameter. Finally, investment cost are zero for built connections and 1 for the pump type, which can be built only one time in parallel.
It is easy to see that a solution for this instance consists of a topology which connects each zone to at least one pump which processes a volume flow of at most \(\tilde{b}\).
To deduce the reduction, we show that the network instance has a solution with objective value smaller \(\tilde{K}\) if and only if the bin packing instance has a solution. Let \(B_1, \ldots B_{\tilde{K}}\) be such a solution. A network solution topology is constructed as follows: For each bin i and pair of items \(u = \min {(B_i)}\) and \(v\in B_i\) with \(v\ne u\) we include a connection \(x_a=1\) on arc \(a=(u,v)\). Furthermore, the connection from 0 to \(\min {(B_i)}\) is used with one pump. Since there are \(\tilde{K}\) bins the objective value of this topology is also \(\tilde{K}\). Each pressure zone is connected to a pump by construction and the fact, that the bins form a partition of [N]. From the capacity restriction of the bins, one sees, that the volume flow on arcs with pumps does not exceed \(\tilde{b}\). Thus, all pumps work and are able to yield the needed pressure increase of one. This transformation is exemplified in Fig. 5.
The reverse direction is straightforward. Since one pump can increase the pressure to the height of each zone, an optimal solution does not supply any zone by two pumps. \(\square\)
Illustration of the reduction used in Proposition 2. Two water distribution network solutions are shown for two solutions of a bin packing instance with \({\tilde{N}} = 6\), item weights 3, 3, 2, 2, 2, 2 and bin capacity 7
4 Branch-and-bound framework
Despite the negative complexity results, Model (6) can be tackled using available MINLP solvers. The solving times nevertheless increase rapidly with the number of considered pumps and pressure zones. To solve the model more efficiently, we present a branch-and-bound framework which utilizes the underlying network structure.
As mentioned before, the connections used in a solution can be represented as an arborescence of \(\mathcal {G}\), i.e., a directed spanning tree rooted in node 0. This is imposed by Constraint (6k). The idea behind the branch-and-bound framework is to enumerate such trees and to compute for each a best placement of pumps, operating speed and pipe diameter selection.
This separation in two stages has the advantage that the volume flow is determined for a tree in the second stage. Thus, the complexity of the nonlinear polynomials \({\varDelta }H(\cdot , \cdot )\) and \(P(\cdot , \cdot )\) is reduced. Furthermore, the friction for a given diameter is fixed.
The disadvantage lies in the exponentially in N many directed trees, which need to be enumerated in the scheme. To reduce the number of inspections, we present a relaxation which lower bounds the objective costs of trees having a common structure. This is done by enumerating subtrees, which are trees rooted in 0 spanning the first n zones for some \(n\in [N]\). Using a given subtree, one can lower bound the objective value of each spanning tree containing the subtree.
To describe the algorithm, we denote by \(\mathcal {T}\) and \(\mathcal {S}\) the set of spanning trees and subtrees of \(\mathcal {G}\) rooted in 0, respectively. The arcs and vertices of a tree T are denoted \(\mathcal {A}_T\) and \(\mathcal {V}_T\), respectively. Algorithm 1 gives an overview of the scheme.

In the following, we will describe the model to compute the value for a given spanning tree. Building upon this model, a relaxation is derived and shown to be valid. Finally, some implementation details are explained.
4.1 Optimization model for a fixed spanning tree
In this section we use that fact that each tree T determines for each zone \(v\in \mathcal {V}_T\) a unique 0–v path denoted \(\mathcal {P}^T_v\subseteq \mathcal {A}_T\). To compute the optimal pump configurations on \(T \in \mathcal {T}\) we calculate the volume flow \(Q^T_a\) on each used connection \(a\in \mathcal {A}_T\). It is given by the sum of demands of those zones, which are supplied using a. So
Since the flow is fixed, we are able to compute for each pipe diameter \(d \in \mathcal {D}\) and connection \(a \in \mathcal {A}_T\) the resulting pressure losses along a due to friction by \({\varDelta }F^{T}_{a, d}:={\varDelta }F_{a, d}(Q^T_a)\). We also see that the constraints to determine the pressure in the zones, given by (6f), (6g) and (6h), can be simplified using
to denote the needed pressure head in zone v due to differences in height.
Model (8) in Figure 6 combines these considerations to compute the optimal pump placement and operation as well as diameter selection for the tree \(T\in \mathcal {T}\).
This model is bounded. If it is feasible, we denote its optimal solution value by \(\text {opt}(T)\). If it is infeasible \(\text {opt}(T)=\infty\). The correctness of the formulation is shown in the following lemma.
Lemma 1
Model (6) and
compute the same optimal solution values.
Proof
Every vector in
leads to a tree \(T\in \mathcal {T}\) with arcs \(\mathcal {A}_T = \{a \in \mathcal {A}\, : \,X_a = 1\}\) and vice versa. It remains to show that for such a pair X and T, the optimal solution value of Model (6) with variables x fixed to X agrees with \(\text {opt}(T)\), which is the optimal solution value of (8).
By comparing the constraints of both formulations, one can see that Problem (8) arises from (6) after setting \(x_a = 1\) for \(a \in \mathcal {A}_T\), projecting out variables as well as leaving out constraints belonging to arcs \(a \in \mathcal {A}{\setminus } \mathcal {A}_T\) and replacing the volume flow \(Q^T\) and the friction loss \({\varDelta }F^T\). Finally, the constraints which determine the pressure distribution between the pressure zones, (6f) to (6h) simplify to a telescoping sum, leading to Constraint (8d). \(\square\)
4.2 Relaxation built from subtrees
The idea behind the relaxation is to build the trees from the bottom up, zone by zone. For each such subtree one can solve an approximated optimal placement of pumps to supply the zones only in this subtree. For spanning trees containing this subtree we thus obtain a lower bound on the objective value. To achieve fast solving times of these relaxations, the nonlinearities of the pumps are disregarded using upper and lower bounds computed using the information of the subtree.
Given a subtree \(S\in \mathcal {S}\), the goal is to compute a lower bound for the objective costs for all spanning trees \(T\in \mathcal {T}\) which contain S, i.e., \(\mathcal {A}_S\subseteq \mathcal {A}_T\). As a first step, we determine tight bounds on the volume flow in the subtree which hold for all trees containing the subtree. These bounds are defined and shown to be correct in the following Lemma.
Lemma 2
Let \(S \in \mathcal {S}\)be a subtree and \(T \in \mathcal {T}\)be a spanning tree with\(\mathcal {A}_{S} \subseteq \mathcal {A}_T\). Then
and
for all connections in the subtree \(a \in \mathcal {A}_{S}\).
Proof
Since \(\mathcal {A}_{S} \subseteq \mathcal {A}_T\), we observe, that \(\mathcal {P}^{S}_v =\mathcal {P}^{T}_v\) holds for zones in the subtree \(v\in \mathcal {V}_{S}\). This implies
which together with the volume flow definition (7) implies the first inequality. For the second inequality we write
The first sum is equal to \(\underline{Q}^{S}_a\), by the first part of the proof. The second sum is not greater than the sum in the definition of \(\overline{Q}^{S}_a\).\(\square\)
An example for the Lemma and the evolution of tightened volume flow bounds is given in Fig. 7. Note that for spanning trees the lower bounds \(\underline{Q}^T\) and upper bounds \(\smash [t]{\overline{Q}^T}\) agree with \(Q^T\).
The computation of the relaxation should be fast since it is applied often. Thus, we ignore the nonlinearities of the hydraulics laws and derive simple bounds on the possible pressure increase and minimal power consumption as well as the friction loss in the pipes. To bound the former two, we drop their linkage through the operation speed to obtain the maximal pressure increase and minimal power consumption as follows:
The possible pressure head for a pump i built m times in parallel and volume flow bounds \(\underline{Q}\) and \(\overline{Q}\) can be overestimated by maximizing \(\omega\) and q over the feasible space of the characteristic diagram leading to
The total power intake of all m pumps is similarly underestimated
In case of infeasibility, we set \(\overline{{\varDelta }H}_{i, m}(\underline{Q}, \overline{Q})=0\) and \(\underline{P}_{i, m}(\underline{Q}, \overline{Q})=0\). For a fixed subtree S with the proven bounds on the pipe volume flow, we define \(\overline{{\varDelta }H}_{a, i, m}^{S}:=\overline{{\varDelta }H}_{i, m}(\underline{Q}^{S}_a, \overline{Q}^{S}_a)\) as well as \(\underline{P}_{a, i, m}^{S} :=\underline{P}_{i, m}(\underline{Q}^{S}_a, \overline{Q}^{S}_a)\).
The friction in a pipe grows for increasing volume flow. Thus, \(\underline{{\varDelta }F}^{S}_{a, d}:={\varDelta }F_{a, d}(\underline{Q}^{S}_a)\) yields a lower bound on the friction along a connection a and diameter d for each spanning tree containing S.
Combining these bounds we obtain Relaxation (9), see Fig. 8, which contains only linear constraints.
We conclude this section by showing the validity of this relaxation.
Lemma 3
For \(S \in \mathcal {S}\)and \(T\in \mathcal {T}\)with \(\mathcal {A}_{S} \subseteq \mathcal {A}_T\)Model (9) yields a lower bound on \(\text {opt}(T)\).
Proof
Let \((x^\text {dia}, y, w, {\varDelta }h, p)\) be an optimal solution of Problem (8) solved for tree T. Then by Lemma 2 and the construction of \(\underline{P}\) and \(\overline{{\varDelta }H}\)
holds. Lemma 2 and the definition of the friction term further imply
Thus, the pump placement y and diameter selection \(x^\text {dia}\) form also a feasible solution for Relaxation (9) (taking only the variable entries belonging to S). Comparing the terms in the objective, we further see that fewer terms and only the lower bound on the pressure consumption are used in the relaxation. Therefore, its objective values does not exceed \(\text {opt}(T)\). \(\square\)
4.3 Branch-and-bound details
In this section, we provide implementation details of Algorithm 1. In our implementation, the first inspected tree, which is thus the first node of the branch-and-bound tree, contains the lowest pressure zone and the pipe connecting the building to the water provider. If a branch-and-bound node, representing a subtree \(S\in \mathcal {S}\), can not be pruned using the relaxation, we add to S the next higher unconsidered zone and create a node for each possible connection of this node and S. This is depicted in Fig. 9. As in all branch-and-bound schemes, one has to specify the order of inspection of the branch-and-bound nodes. In our implementation we use a depth-first order, hopefully finding feasible solutions early in the scheme and allowing the early pruning of branch-and-bound nodes due to their dual bound.
5 Finding resilient topologies
In this section, we include the possibility of pump failures in our model. The goal is to design resilient networks, which are able to adapt to structural changes, in this case to the outage of pumps. To quantify different solutions according to their resilience we refer to their buffering capacity, which according to Altherr et al. (2018a) measures the amount of structural change for which a given performance of the system can still be guaranteed.
In the following, we measure the buffering capacity of a high-rise water distribution system by counting the maximum number of pumps which may fail such that the system’s worst case performance is still above a predefined minimum level. A high-rise water distribution network has a buffering capacity of K for some natural number K, if it is able to transport a predefined percentage \({\varGamma }\in (0,1]\) of the volume flow demand \(D_v\) to each pressure zone despite the failure of any combination of up to K pumps. In this case, we also call the water distribution network K-resilient.
One approach to generate networks with a high buffering capacity given the conventional basement layout is to install redundant pumps. The decentralized approach with more topological degrees of freedom regarding pipe layout and pump placement, may allow to reduce the number of redundant pumps, since in case of failure some pumps may be able to partially fulfill the function of others in different places in the network. Thus, compared to the state-of-the-art design of water distribution networks in buildings, in which additional parallel pumps are added to all used booster stations, c.f. DIN 1988-500 (2011), the decentralized approach may lead to less pumps while guaranteeing the same buffering capacity.
Note that a resilient network transports the volume flow demand \(D_v\) in regular operation and during the emergency the fraction \({\varGamma }\) to still enable a predefined minimum demand. In our approach, we do not consider the operation cost during an outage, but we ensure that there exists a feasible control of the pumps by operating them to yield the highest possible pressure increase. This includes the possibility of not operating intact pumps, which could be necessary, e.g., if a pump is not not designed to transport the reduced volume flow. Furthermore, we assume pipes and valves which allow to bypass failed pumps such that they do not block flow. Otherwise, a resilient solution would always need to place either zero or at least \(K+1\) pumps in parallel on each connection.
5.1 Mathematical characterization of resilience
The goal of this section is to construct a scheme which computes a cost optimal solution which is K-resilient.
We will modify our branch-and-bound algorithm by adding a class of linear constraints which allow only a K-resilient pump placement, operation and diameter selection for a spanning tree \(T \in \mathcal {T}\) to the subproblems. Using a polynomial time separation scheme, we avoid the disadvantage of the exponential cardinality of this class in K.
For the derivation of this characterization of resilience by linear inequalities let \(T\in \mathcal {T}\) be a spanning tree of \(\mathcal {G}\) rooted in zone 0. The tree T determines the volume flow \(Q^T\) according to the previous section. The volume flow in case of a pump failure is given by \({\varGamma }Q^T_a\) for each connection \(a \in \mathcal {A}_T\) in the tree.
We follow the notation of Relaxation (9) to define the maximal pressure increase of pump i built m times in parallel for the decreased volume flow
and the friction loss
Note that the maximum operation is needed since it may be favorable to disable some pumps in a group of parallel pumps. Also, by the definition of \(\underline{Q}^T\) and since \({\varDelta }F\) is strictly increasing, \(\underline{{\varDelta }F}^{T,\text {res}}_{a, d}\) gives the exact friction loss for spanning trees \(T\in \mathcal {T}\) and \(\underline{{\varDelta }F}^{S,\text {res}}_{a, d}\le \underline{{\varDelta }F}^{T,\text {res}}_{a, d}\) holds for \(S\in \mathcal {S}\) with \(\mathcal {A}_S\subseteq \mathcal {A}_T\).
To formulate the constraints which enforce K-resilience, we use the set of failure scenarios
where the value of \(z_{a, i}\) gives the number of failed pumps of type i on pipe a.
A K-resilient solution topology \((X, X^\text {dia}, Y)\), i.e., the solution values of the variables \((x,x^\text {dia}, y)\), must ensure for each failure scenario a sufficient pressure in each zone using the pumps of Y unaffected from the scenario. Therefore, we obtain a class of constraints, specified in the following lemma, which are necessary and sufficient to ensure a resilience of K.
Lemma 4
Let \((X, X^\text {dia}, Y)\)be a feasible system topology of (8) for a spanning tree \(T \in \mathcal {T}\). It isK-resilient if and only if
holds for each pressure zone \(v \in \mathcal {V}{\setminus }\{0\}\) and failure scenario \(z\in \mathcal {Z}\).
Proof
Without occurring failures, the system can transport the reduced volume flow \({\varGamma }D\) if and only if
holds for each pressure zone \(v \in \mathcal {V}{\setminus }\{0\}\). This can be seen by inspection of Problem (8), the definition of \(\underline{{\varDelta }F}^{T,\text {res}}\) and the definition of \(\overline{{\varDelta }H}^{T, \text {res}}\) which implies that there exists an operating speed \(\omega\) and power consumption p such that
for \(a \in \mathcal {A}_T\), \(i \in \mathcal {C}\) and \(m \in [M]\) with \(\overline{{\varDelta }H}_{a, i, m}^{T, \text {res}}>0\).
The latter definition also implies that for a failure scenario \(z\in \mathcal {Z}\) the maximal pressure increase of the pumps of type i built m times in parallel is \(\overline{{\varDelta }H}_{a, i, m-z_{a, i}}^{T, \text {res}}\) if \(m > z_{a, i}\) and zero otherwise.
Then, by combining this with (11), inequalities (10) follow as necessary and sufficient conditions that the system can transport the volume flow in case of failures. \(\square\)
The theorem and the definition of \(\overline{{\varDelta }H}^{T, \text {res}}\) and \(\underline{{\varDelta }F}^{S,\text {res}}\) implies that if \(S\in \mathcal {S}\) is not resilient then also \(T\in \mathcal {T}\) with \(\mathcal {A}_S\subseteq \mathcal {A}_T\) can not be resilient. This is used latter in an adaption of our branch-and-bound algorithm.
5.2 Separation of failure scenarios
To obtain a cost-optimal K-resilient system for a tree T one can solve a modified version of Problem (8), which also involves the inequalities of type (10). This, however, is not advisable since \(\mathcal {Z}\) grows exponentially in K.
We show in this section a way to dynamically generate violated constraints of type (10) in polynomial time. This makes it possible to compute trial solutions using Problem (8) and check whether such a solution is K-resilient. If this is not the case, a violated constraint is found and added to Problem (8). This is performed iteratively until the solution is K-resilient (which happens, since there are only finitely many cases).
In the following let a spanning tree \(T \in \mathcal {T}\), a diameter selection \(X^\text {dia}\in \{0, 1\}^{\mathcal {A}_T \times \mathcal {D}}\) and a pump placement \(Y\in \{0, 1\}^{\mathcal {A}_T \times \mathcal {C} \times M}\) be fixed. The goal is to check whether Inequality (10) is violated for some zone \(v \in \mathcal {V}{\setminus }\{0\}\) and failure scenario \(z \in \mathcal {Z}\). We consider each pressure zone separately. The only part of the inequality which is affected by pump failures is the left-hand sum. Thus, to check the constraint, we minimize this sum over \(\mathcal {Z}\), i.e., solve
and compare its optimal value to the remaining components of the inequality.
Program (12) can be solved using Dynamic Programming. Let
be the indices which denote the \(J\in \mathbb {N}\) pump groups placed on the way to v in T according to Y, i.e., \(J = \sum _{a \in \mathcal {P}^T_v}\sum _{i \in \mathcal {C}}\sum _{m \in [M]}Y_{a, i}^m\). Let \(H^{\max }_{j, \kappa }\) denote the maximal pressure provided by the first j pump groups if a worst-case failure of \(\kappa\) pumps occurs. Then the optimal value of Program (12) is given by \(H^{\max }_{J, K}\).
The idea is to compute the states \(H^{\max }_{j, \kappa }\) sequentially. For the first group of pumps we get for \(\kappa \in [K]_0\)
For the remaining groups we have the Bellman equation for \(j \in [J-1]\), \(\kappa \in [K]_0\):
Computing \(H^{\max }_{J, K}\) requires \(\mathcal {O}(JK^2) \subseteq \mathcal {O}(N|{\mathcal {C}}|MK^2)\) steps, if \(\overline{{\varDelta }H}^{T,\text {res}}\) is given. A factor of N is additionally needed if one computes \(H^{\max }_{J, K}\) for each pressure zone separately. However, this factor can be eliminated by observing that the states \(H^{\max }_{j, \kappa }\) are valid for different pressure zones, if the pumps supply both zones. Similar to other dynamic programming algorithms a worst-case failure scenario \({\tilde{z}}\in \mathcal {Z}\) (and thus a solution to Program 12) can be computed by storing the decisions leading to the value of \(H^{\max }_{J, K}\).
5.3 Adapted algorithm to compute resilient solutions
To obtain K-resilient solutions it is sufficient to change the branch-and-bound method (Algorithm 1), to include the separation of Inequality (10), when the optimal value of a tree is computed.
However, Relaxation (9) does not include the failure scenarios and thus supposedly leads to weak lower bounds for resilient solutions. To resolve this, we can again use the underestimation on the volume flow in the pipes \(\underline{Q}^T\). These lower and upper bounds are already regarded in the definition of the maximal pressure head \(\overline{{\varDelta }H}^{T,\text {res}}\). Therefore a tighter relaxation is obtained by adding Inequality (10) to the original Relaxation (9).
To avoid the separation of potentially unnecessary failure scenarios, we do not separate Inequalities (10) for partial trees, but keep track of the failure scenarios, which are separated for the full spanning trees. Only for these encountered scenarios we add the resiliency constraints to the relaxation. These constraints are also included when solving spanning trees, in the hope to reduce the number of separated redundant scenarios.
The modified scheme is outlined in Algorithm 2, where \(\mathcal {Z}'\) stores the separated scenarios.

6 Application examples
In this section, we first present the creation of a large set of realistic test instances. Afterwards we compare the performance of our proposed algorithm on this set to state-of-the-art MINLP software. The large number of instances, allows to assess the potential of the decentralized planning approach on the solution designs. We conclude with an evaluation of resilient solutions and derive characteristics of resilience.
6.1 Test instances
We first describe the design of multiple instances to evaluate the presented algorithm and to assess the impact of resilience. For all instances the input pressure \(H_\text {in}\) is equal to the minimal pressure in the zone \(H_\text {min}\), i.e., both are set to zero without loss of generality. This assumption implies the fulfillment of an arbitrary minimum net positive suction head to avoid cavitation. Therefore, we do not explicitly model the NPSH value. We also always allow three pumps built in parallel, i.e., \(M=3\).
To generate distinct instances, we vary the number of pressure zones N and assume their even distribution in the building. Furthermore, we consider different possibilities for the total volume flow demand of the house and the height of the house, which divided by N determines the volume flow demand of one zone \(D_v\) and the height of one zone, respectively. The energy cost parameter \(C^\text {en}\) is also varied assuming energy cost of 0.3 €/kWh and different operating periods. Effects on the power consumption based on the behavior of the electric drive in pumps are neglected in all test instances.
Our test set contains 144 instances obtained by combining \(N \in \{4, 5, 6, 7\}\) with three possible building heights 100 m, 150 m or 200 m, a total volume flow demand of the building of 25 \(\hbox {m}^3/\hbox {h}\), 30 \(\hbox {m}^{3} / \hbox {h}\) or 35 \(\hbox {m}^{3} / \hbox {h}\) as well as four different weights for the energy cost \(C^\text {en}\) given by an electricity price of 0.3 €/kWh and different operating times of 10, 15, 20 and 25,000 h.
Catalog of pumps Five different pump types are used, cf. Fig. 10. Their different characteristics are derived from a reference pump for high-rise water distribution networks by using the scaling technique described in Sect. 3.2. Based on this catalog, multiple pumps can be chosen and placed on a subset of the chosen pipes. The smallest pump type of our catalog, which is depicted in Fig. 10 by solid lines, is our reference pump. It was modeled by using the approach of Ulanicki et al. (2008), leading to the feasible set
Using the scaling laws and the majoration formula explained in Sect. 3.2, two bigger pump types are derived from the reference pump, which has a maximum hydraulic efficiency of \(\eta _{\text {M}} = 0.6639\). The two scaled pump types have an impeller diameter difference \(d/d_{\text {M}} = 1.575\) and \(d/d_{\text {M}} = 2.15\) and are shown in Fig. 10 with dotted lines. Furthermore, we use the reference pump, which already consists of 5 stages, and the first scaled pump type with a diameter difference of \(d/d_{\text {M}} = 1.575\) to derive two additional pump types by doubling the number of stages. These two additional pump types are shown as dashed lines in Fig. 10. Increasing the number of stages allows to increase the possible maximum pressure height, but to leave the maximum volume flow unchanged. The biggest pump type in the catalog is chosen to fulfill all possible demand settings with only one pump. The other pump types are chosen manually to cover volume flow and pressure ranges between the reference pump and the biggest pump type. Additionally, multiple parallel pumps in the optimization program can increase the total volume flow at fixed maximum pressure height. With these five different pump types and the possibility to use up to three parallel pumps of one type, a high variation of possible combinations is available to supply the considered example buildings.
Pump cost model To determine the cost of a pump we use for each derived pump type \(i\in \mathcal {C}\) its maximal possible volume flow \(\overline{Q}_i\) and maximal possible height \(\overline{{\varDelta }H}_i\). With these two features all derived pumps are distinguishable, since if more stages are used, the maximum height increases, but the maximum volume flow does not; by scaling both features increase. As the data basis of our cost model we used 33 available pumps designed for the water supply in buildings, that are members of the same product family, as the used reference pump. Our derived model for the estimation of cost is
We used a quadratic cost estimation, because of its high adjusted R-squared value of 0.988 which shows a high accuracy between the quadratic model function and the underlying data, cf. Chatterjee and Simonoff (2013).
Pipe cost model To compute the optimal selection of different pipe diameters in the MINLP in Fig. 4, it is essential to have a cost model which describes the different pipe costs based on their diameter and length. Savic and Walters (1997) and Bieupoude et al. (2012) describe the following nonlinear cost model:
Savic and Walters (1997) use the coefficients \(\gamma = 1.1\) and \(\delta = 1.5\) for pipes with diameters between 12 and 14 inches in water distribution networks. For the smaller pipes in buildings and for being able to measure the diameter in SI-units, we derive the parameters \(\gamma\) = 3593 €/m and \(\delta = 1.6975\). The possible pipe diameters are selected according to the standard DIN 1988-300 (2012), leading to the set \(\mathcal {D}= \{10, 13, 16, 19.6, 25.6, 32, 39, 51, 60, 72.1, 84.9, 104\}\) measured in mm. Note that these values and the pipe as well as the pump cost model are exemplary to derive realistic scenarios and can be easily changed to other cost models if desired.
6.2 Branch-and-bound performance
We implemented our branch-and-bound approach in C. To solve the MINLP (sub)systems we used SCIP 5.0.1, see Gleixner et al. (2018), compiled with IPOPT 3.12, see Wächter and Biegler (2006), and CPLEX 12.8. The computations were performed on a Linux cluster with Intel Xeon E5 CPUs with 3.50GHz, 10MB cache, and 32GB memory using a 2 h time limit.
Indicator constraints are implemented in SCIP and were used in our implemented model for linear inequalities which do not possess trivial big-M values. Easy big-M values are mostly obtained from the bounds on the volume flow, like \((N-v-1)D\) for the volume flow on arcs leading to node v. For the nonlinear constraints, we use the maximal feasible values for \({\varDelta }H(q, \omega )\), \(P(q, \omega )\) and \({\varDelta }F(q)\) as big-M values. The dimension of the model is further reduced by using pump variables in each node instead of each arc. This is possible because of Inequality (6k), which allows only one pipe leading into a zone.
To test Algorithm 1, we first compare its performance against SCIP solving Model (6), i.e., the model without resilience. In our experiments, the two main influences on the running time are the number of pressure zones as well as the magnitude of energy cost. Naturally, more pressure zones increase the number of feasible topologies, whereas an emphasis on operating costs also increases the importance of the difficult nonlinear pump constraints. Tables 3 and 4 show the shifted geometric mean, \(\left( \prod _{i=1}^{n} (t_i+s) \right) ^{1/n} - s\) with shift \(s = 10\) over the solving times \(t_i\) clustered by number of zones and operating times, respectively. Furthermore, the shifted geometric mean with a shift of 100 is shown for the number of encountered branch-and-bound nodes. The nodes of the branch-and-bound scheme comprise all nodes of the computations of Relaxation (9) and Problem (8). For the new approach also the number of visited spanning trees and the solving time of the relaxation in the subtrees is shown.
The branch-and-bound scheme solves all instances the MINLP approach can solve. Overall, 123 instances can be solved by branch-and-bound compared to 73 instances solvable with the MINLP solver. With the exception of four instances with small numbers of pressure zones, the branch-and-bound scheme is faster. From the tables we presume a solving time growth exponential in the number of pressure zones N and a growth nearly linear in the operating costs for both solving methods.
Since the maximum number of subtrees for a given N is given by \(\sum _{i=1}^N i!\) and we start the enumeration in our implementation directly in the first spanning tree, the total numbers of considerable trees of the algorithm are given by 30, 149, 868 and 5907 for N from 4 to 7. Comparing these numbers to the number of enumerated spanning trees, we see that the relaxation is actually too weak to cut off any node. Thus, the superior performance of the branch-and-bound algorithm over the MINLP solver seems to stem from the reduced complexity of the MINLP for fixed topologies and is not based on the relaxation. This is also supported by the at least one order of magnitude greater number of branch-and-bound nodes for the MINLP solver. In consideration of the negligible computing time of the current relaxations, we see the potential to further improve the performance of the branch-and-bound scheme using stronger but harder to solve relaxations. Further test runs on the instances with \(N=4\) showed that the MINLP solver BARON 18.5.8 (Tawarmalani and Sahinidis 2005) is slower than SCIP and we therefore do not present detailed results for BARON.
We also computed with our code the K-resilient solution of the instances presented above for \(K= 1, \ldots , 3\). Table 5 gives an overview of the solution process for these four different settings clustered according to the number of pressure zones. Again time and solved denote the shifted geometric mean of the solving time and the number of solved instances, respectively. Additionally, for instances which could be solved in 7200 s, the arithmetic mean over the number of scenarios for which Constraint (10) was added during the solving process, i.e., \(|{\mathcal {Z}'}|\), is shown. Furthermore, the arithmetic mean over the ratio of enumerated spanning trees and the total number of spanning trees in \(\mathcal {G}\) is given for those solved instances.
Taking failure scenarios into account influences the solving time, making the instances more difficult for increasing K. There exists only one combination of parameters for which the corresponding instance can be solved for K but not for \(K-1\). The size of \(\mathcal {Z}\) can be estimated by \(\left( {\begin{array}{c}|{\mathcal {A}}| |{\mathcal {C}}|M\\ K\end{array}}\right)\). Thus, our separation approach outperforms a naïve approach that solves for each \(z\in \mathcal {Z}\) the \(K=0\) case together with the appropriate resilience constraint by a wide margin.
As observed before, all spanning trees of \(\mathcal {G}\) need to be enumerated to compute a 0-resilient solution. However, to find resilient solutions fewer spanning trees are inspected and the stronger relaxation is able to cut off nodes. For larger N, it is possible that only instances for which the relaxation produces strong bounds are solvable, leading to this low percentage of enumerated spanning trees.
6.3 Potential of decentralized layouts
Considering new layouts for water distribution networks may open up a significant potential for energy savings, cf. Coelho and Andrade-Campos (2014). In this section we analyze the energy saving potential of Problem (6). This analytic consideration is based on the hydraulic power of a pump, which is defined by
where \(\rho\) is the density of the fluid, g the gravitational acceleration, q the volume flow, h the pressure increase, \(\eta _{\text {h}}\) the hydraulic efficiency and \(\eta _{\text {v}}\) the volumetric efficiency, cf. Gülich (2008).
The hydraulic power requirements of the complete building can be estimated by simplifying Eq. (13). We assume that the product of the volumetric efficiency \(\eta _{\text {v}}\) and hydraulic efficiency \(\eta _{\text {h}}\) is constant for all used pumps and abbreviate it with \(\eta _{\text {p}}\). The parameter \(\eta _{\text {p}}\) depends on the volume flow q and the height h, which we simplify within this assumption. Thus, \(\eta _{\text {p}}\) represents a scaling factor, which we can set to an arbitrary value. If we set this factor to the best possible efficiency, we underestimate the power consumption in partial load settings. We assume that each installed pump will be operated near its best point, since this reduces the power consumption the most for given investment costs.
Next to this major assumption, we neglect pipe friction, assume equivalent volume flow demands \(D_v\) in each pressure zone, set the pressure at the water main to the same value as the minimum pressure in each pressure zone, assume constant density \(\rho\) and gravitational acceleration g as well as equidistant distances \({\varDelta }H_v\) between the different pressure zones.
Considering these assumptions, it is possible to analytically estimate the increase in energy efficiency of decentralized systems compared to a conventional layout, where one booster station in the basement supplies all pressure zones. We consider four different layouts with different degrees of freedom regarding pipe layout and pump placement. As the baseline, we consider the basement layout with only one rising pipe that connects all pressure zones consecutively and one booster station in the basement, cf. Figure 11a. By still allowing only one rising pipe, but a decentralized placement of pumps, see Figure 11b, we derive what we call the one-branch layout. Another option is to keep all pumps in the basement, but to supply each pressure zone by individual pipes, which we call the multi-branch layout, cf. Figure 11c. As a fourth option, we consider a decentralized layout with an arbitrary tree-shaped pipe network structure and an arbitrary placement of pumps which is depicted in Fig. 11d.
For the basement layout, the required hydraulic power is
where \(\overline{D}=\sum _{v=1}^{N}D_v\) is the sum of all partial volume flow demands in each pressure zone and the sum of the heights \(\overline{{\varDelta }H} = \sum _{v=1}^{N}{\varDelta }H_v\). Based on the assumptions mentioned earlier, \(\overline{{\varDelta }H}\) is equal to the height of the highest pressure zone, which can be estimated by the building height. Figure 12a illustrates the hydraulic power of the basement layout for a building with four equidistant pressure zones and uses therefore a dimensionless axis scaling. The volume flow q is normalized with the volume flow demand of one pressure zone \(D_v\), the pressure height is normalized with the height of one pressure zone \({\varDelta }H_v\). The power consumption of the basement layout is given by the area of the rectangle.
For the one-branch layout, the lowest power consumption can be achieved using a booster station between every pair of adjacent pressure zones. For this layout, each booster station has to pump a share of the complete volume flow demand up to the next pressure zone. This share gets smaller with increasing height of the installed booster station, while the required pressure height stays constant for all booster stations. Overall, this yields the hydraulic power
The power consumption of the one-branch layout in a building with four equidistant pressure zones is illustrated in Fig. 12b. The areas of the single rectangles represent the power needed to supply the respective pressure zones. Power savings compared to the basement layout are given by the hatched area.
Equivalent power savings can also be derived for the multi-branch layout. In this layout each pressure zone is supplied by its own booster station. The hydraulic power needed by each pressure zone is then computed by multiplying the zone’s volume flow demand \(D_v\) by its respective height. The total hydraulic power is computed by summing over all pressure zones
This is illustrated in Fig. 12c, where the power savings compared to the conventional basement layout are again given by the hatched area.
From inspection of the formulas and Fig. 12 we conclude that increasing the number of pressure zones in a building enhances the potential energy savings. In the limit, if we use infinitely many pressure zones, the maximum possible savings in comparison to the basement layout are 50%.
To verify the cost saving potential implied by the shown discussion and the conceptualized savings in Fig. 12, we compare the optimal solutions which are constrained to have only pumps in the basement with the optimal solutions which are constrained to allow only one-branch, multi-branch or decentralized topologies. Furthermore, we omit the time limit on the computation for the decentralized system to obtain optimal solutions for all instances with up to six pressure zones. Table 6 summarizes the results, showing the arithmetic means of total and operational cost for the basement solution as well as the quotient of theses values of the one-branch, multi-branch and decentralized solutions compared to the basement solutions. The one-branch, multi-branch and decentralized solutions have almost equal energy savings and the power usage decreases with an increasing number of pressure zones N. The completely decentralized approach, in which any pipe layout implied by Fig. 1 can be chosen, yields the highest energy savings of up to 40% and total cost savings of nearly 35% when considering the underlying parameter sets. The one-branch and multi-branch approaches do not yield energy savings as high as the completely decentralized solution. Nevertheless, the differences between the approaches should vanish with more pumps in the construction catalog, as shown by the analytic consideration. The completely decentralized system, on the other hand, has the highest degree of freedom and therefore exploits the pump catalog the most. The computational results substantiate the aforementioned analytic assumptions and advocate the consideration of multi-branch, one-branch or decentralized layouts and designs to reduce the overall energy consumption.
6.4 Analysis of resilience properties
We introduced the principles and benefits of a resilient water distribution network layout and design in Sect. 5. In Fig. 13 the solutions for an exemplary chosen instance are shown for different levels of K-resilience. Based on the pump catalog in Fig. 10, multiple pumps were installed in the network for all different levels of K-resilience.
The resilience of a specific solution against arbitrary pump failures is determined by its pipe layout, the number of pumps, as well as by the operation range of the pumps installed, i.e., by their ability to cover failures of other installed pumps. Further, it is important to note that adequate valves and pipes must be installed to enable an immediate resilient pump rescheduling in the case of a component failure.
For the \(K=0\) solution the failure of only one arbitrary pump is critical. If for example the pump in the ground floor fails, the first pressure zone cannot be supplied anymore. The layout of the \(K=1\) solution can, however, withstand the failure of one arbitrary pump. All pressure zones except the highest one are connected to the source via pipes with at least two installed pumps. If the single pump installed in pressure zone 4 fails, pressure zone 5 can still be supplied by the pumps installed in pressure zone 3 using a bypass.
For \(K=2\), a pipe layout similar to the one-branch layout is chosen. Three pumps of the same type are installed in parallel in the basement. Additionally, two pumps of different type are installed to supply the 4th and 5th pressure zone. In case of failure of these two additional pumps, the operation range of the pumps of type c still allows to supply all pressure zones with an reduced amount of water, i.e., for the reduced volume flow the operation range of pump type c is sufficient to overcome the friction losses and the geodetic height difference from the basement to the 5th pressure zone. If on the other hand two pumps of type c fail, one working pump of type c is sufficient to guarantee the supply of pressure zones 1, 2, and 3, as well as of pressure zones 4 and 5, for which the pressure has to be further increased by the pumps of type a.
Compared to the layout for \(K=2\), one additional big pump of type d is installed in the basement to achieve \(K=3\). The failure of all three pumps of type c may be covered by one pump of type d. Note that the layout which installs a fourth pump of type c instead of type d is also 3-resilient, but is not included in our setting which only allows three parallel pumps.
In general, the proposed solutions allow for an energy-efficient operation during the normal utilization phase. At the same time they guarantee a reduced supply in case of arbitrary pump failures, entailing a possibly increased power consumption in this emergency situation. The proposed algorithm moreover leads to resilient and yet cost efficient designs: To achieve K-resiliency, the installed booster stations are not only supplemented by redundant pumps as suggested by DIN 1988-500 (2011), but the network topology as well as the operation range of other pumps installed in the system are taken into consideration. This may reduce the overall number of pumps needed to guarantee a specific resilience.
K-resilient solutions for five pressure zones, a building height of 100m, a total demand of 25 \(\hbox {m}^{3}/\hbox {h}\) and an operating time of 10.000 h. Pump type a corresponds to the reference pump, type b is a two-stage version of type a, type c corresponds to the reference pump scaled by \(d/d_M=1.575\) and type d is a two-stage version of type c
It is important to mention that system layouts as shown in Fig. 13 should only be considered by engineers in the early design stages of very high buildings, since they require additional components to be realized, which are not considered in the objective. For systems with pumps between different pressure zones, as shown in Fig. 13, additional check valves with relevant pressure losses and adjusted control strategies have to be considered. Additionally, it is important to ensure the net positive suction head for each used pump. This is only considered implicitly in the shown MINLP. Observe that we can interpret the different pumps in the pump catalog \(\mathcal {C}\) as building blocks for the finally used booster stations. Thus, groups of series-parallel pumps, as shown between node 0 and 1 in Fig. 13d, can also be replaced by a booster station with parallel pumps with adjusted characteristics to reduce the complexity generated by the MINLP and enable a faster realization in real buildings.
To further investigate the characteristics of resilience, we present in Table 7 the fraction of optimal solutions, which consist of the one-branch topology. Recall that in this topology all pressure zones are supplied by a single-stranded rising pipe layout. For an increasing resilience, the fraction of one-branch solutions increases, regardless of the operating time considered. The higher connectivity, cf. Meng et al. (2018), between pumps in lower areas of the building and pumps in higher pressure zones is the main factor to tend towards the one-branch solution. In case of failures in higher levels, the pumps in lower areas can still supply the respective pressure zones. Overall, a greater rate of redundancy can be achieved, since each booster station may supply not only one, but several zones. In contrast, the multi-branch layout may yield the same energy efficiency, but it is not ideal to achieve resiliency. In the multi-branch layout, each pressure zone is supplied by its own rising pipe and booster station. If a booster station fails, no other booster station of the system may cover for it.
If we increase the weight of the energy costs, e.g., by considering longer operating times, the fraction of one-branch solution decreases, cf. Table 7. In this case, a more decentralized layout than the one-branch solution leads to lower energy cost given the pump catalog \(\mathcal {C}\), and compensates the higher investment costs due to the higher number of pumps necessary to ensure resilience.
Table 8 provides an investigation of the costs of resilience. For \(N=4\), it shows the relative total costs of the resilient solution compared to the non-resilient one for \(K=0\). Resilient solutions are up to 50% more expensive for short operating times, but only up to around 25% for the longest operating time. Their increased total cost compared to non-resilient layouts is mainly due to increased investment costs, since resilient layouts consume only around 2% more power than their non-resilient counterparts. To achieve resilience the number of pumps installed and/or their size increases, leading to higher investment costs compared to the non-resilient layouts.
7 Conclusion
We presented a MINLP to derive resilient and energy-efficient systems with an optimized topology layout and pipe sizing for tree-shaped water distribution networks in high-rise buildings. Great attention has been paid to the trade-off between the accurate modeling of the underlying flow conditions and the solvability of the model. The structure of the model was then exploited in a branch-and-bound algorithm to reduce the complexity of the underlying MINLP and therefore decrease the solving time substantially compared to a state-of-the-art MINLP solver. Using a characterization of resilience for a fixed layout, we are able to expand the algorithm to find optimal resilient solutions.
Several computational results showed that additional energy savings as well as a resilient design of decentralized water distribution networks can be achieved by this method. They further indicate that a decentralized placement of pumps with variable rotating speeds can lead to major energy savings, especially in tall buildings.
It was shown that the most efficient layouts use a decentralized pump placement and pipe layout, however, the most resilient structures are given by a single-stranded layout. The decentralized placement of pumps between different pressure zones is still used in these solutions, which leads to an only slightly increased energy consumption compared to structures with multiple possibilities for pipe connections between the pressure zones. Based on the shown results, it could be estimated that a simpler pipe layout can still derive near global optimal solutions with respect to energy-efficiency and still prevent restrictions in the supply in the case of arbitrary failures.
The presented model can further be used by engineers and mathematicians in the early design stage of new buildings, as well as to support the energy-efficient retrofitting of existing buildings. The explicit consideration of pump failures leads to topologies with additional pumps. In comparison to state-of-the-art standard procedures to design booster stations, we are able to reduce the total number of redundant pumps and therefore minimize investment costs and still assure the operation in case of arbitrary pump failures.
The shown approach can be adapted in future work to new parameter settings as well as new water distribution networks besides the supply of high buildings with drinking water. For example, it is transferable to generate more resilient and yet cost and energy-efficient tree-shaped urban water distribution networks.
References
Altherr LC, Brötz N, Dietrich I, Gally T, Geßner F, Kloberdanz H, Leise P, Pelz PF, Schlemmer P, Schmitt A (2018a) Resilience in mechanical engineering—a concept for controlling uncertainty during design, production and usage phase of load-carrying structures. In: Pelz PF, Groche P (eds) Uncertainty in Mechanical Engineering III, Applied Mechanics and Materials, vol 885, pp 187–198
Altherr LC, Leise P, Pfetsch ME, Schmitt A (2018b) Algorithmic design and resilience assessment of energy efficient high-rise water supply systems. In: Pelz PF, Groche P (eds) Uncertainty in Mechanical Engineering III, Applied Mechanics and Materials, vol 885, pp 211–223
Belotti P, Kirches C, Leyffer S, Linderoth J, Luedtke J, Mahajan A (2013) Mixed-integer nonlinear optimization. Acta Numer 22:1–131
Bienstock D, Verma A (2010) The \(n-k\) problem in power grids: New models, formulations, and numerical experiments. SIAM J Optim 20(5):2352–2380
Bieupoude P, Azoumah Y, Neveu P (2012) Optimization of drinking water distribution networks: computer-based methods and constructal design. Comput Environ Urban Syst 36(5):434–444
Bonami P, Lodi A, Tramontani A, Wiese S (2015) On mathematical programming with indicator constraints. Math Program 151(1):191–223
Bonvin G, Demassey S, Le Pape C, Maïzi N, Mazauric V, Samperio A (2017) A convex mathematical program for pump scheduling in a class of branched water networks. Appl Energy 185:1702–1711
Bragalli C, D’Ambrosio C, Lee J, Lodi A, Toth P (2012) On the optimal design of water distribution networks: a practical MINLP approach. Optim Eng 13(2):219–246
Brkić D (2011) Review of explicit approximations to the Colebrook relation for flow friction. J Petrol Sci Eng 77(1):34–48
Brown G, Carlyle M, Salmerón J, Wood K (2006) Defending critical infrastructure. Interfaces 36(6):530–544
Burgschweiger J, Gnädig B, Steinbach MC (2009) Optimization models for operative planning in drinking water networks. Optim Eng 10(1):43–73
Chatterjee S, Simonoff JS (2013) Handbook of regression analysis. Wiley, Hoboken
Chen RLY, Cohn A, Fan N, Pinar A (2014) Contingency-risk informed power system design. IEEE Trans Power Syst 29(5):2087–2096
Coelho B, Andrade-Campos A (2014) Efficiency achievement in water supply systems—a review. Renew Sustain Energy Rev 30:59–84
D’Ambrosio C, Lodi A, Wiese S, Bragalli C (2015) Mathematical programming techniques in water network optimization. Eur J Oper Res 243(3):774–788
Dandy GC, Simpson AR, Murphy LJ (1994) Optimum design and operation of pumped water distribution systems. In: International Conference on hydraulics in civil engineering: “Hydraulics Working with the Environment”. Institution of Engineers, Australia, pp 149–155
De Corte A, Sörensen K (2013) Optimisation of gravity-fed water distribution network design: a critical review. Eur J Oper Res 228(1):1–10
DIN 1988-500 (2011) Codes of practice for drinking water installations–Part 500: pressure boosting stations with RPM-regulated pumps; DVGW code of practice
DIN 1988-300 (2012) Codes of practice for drinking water installations–Part 300: pipe sizing; DVGW code of practice
Eck BJ, Mevissen M (2012) Valve placement in water networks: Mixed-integer non-linear optimization with quadratic pipe friction. Report no RC25307 (IRE1209-014), IBM Research
Fischetti M, Ljubi I, Monaci M, Sinnl M (2017) A new general-purpose algorithm for mixed-integer bilevel linear programs. Oper Res 65(6):1615–1637
Fujiwara O, Khang DB (1990) A two-phase decomposition method for optimal design of looped water distribution networks. Water Resour Res 26(4):539–549
Garey MR, Johnson DS (1979) Computers and intractability: a guide to the theory of NP-completeness. Freeman, New York
Geißler B, Kolb O, Lang J, Leugering G, Martin A, Morsi A (2011) Mixed integer linear models for the optimization of dynamical transport networks. Math Methods Oper Res 73(3):339–362
Ghaddar B, Naoum-Sawaya J, Kishimoto A, Taheri N, Eck B (2015) A Lagrangian decomposition approach for the pump scheduling problem in water networks. Eur J Oper Res 241(2):490–501
Ghidaoui MS, Zhao M, McInnis DA, Axworthy DH (2005) A review of water hammer theory and practice. Appl Mech Rev 58(1):49–76
Gleixner AM, Held H, Huang W, Vigerske S (2012) Towards globally optimal operation of water supply networks. Numer Algebra Control Optim 2(2):695–711
Gleixner A, Eifler L, Gally T, Gamrath G, Gemander P, Gottwald RL, Hendel G, Hojny C, Koch T, Miltenberger M, Müller B, Pfetsch ME, Puchert C, Rehfeldt D, Schlösser F, Serrano F, Shinano Y, Viernickel JM, Vigerske S, Weninger D, Witt JT, Witzig J (2018) The SCIP optimization suite 5.0. Technical report, optimization online
Goemans MX, Bertsimas DJ (1993) Survivable networks, linear programming relaxations and the parsimonious property. Math Program 60(1–3):145–166
Groß T, Pöttgen P, Pelz PF (2017) Analytical approach for the optimal operation of pumps in booster systems. J Water Resour Plann Manag 143(8):04017029
Grötschel M, Monma CL, Stoer M (1995) Design of survivable networks. Handb Oper Res Manag Sci 7:617–672
Gülich JF (2008) Centrifugal pumps. Springer, Berlin
Herrera M, Abraham E, Stoianov I (2016) A graph-theoretic framework for assessing the resilience of sectorised water distribution networks. Water Resour Manag 30(5):1685–1699
Jowitt PW, Germanopoulos G (1992) Optimal pump scheduling in water-supply networks. J Water Resour Plann Manag 118(4):406–422
Kleniati PM, Adjiman CS (2015) A generalization of the branch-and-sandwich algorithm: from continuous to mixed-integer nonlinear bilevel problems. Comput Chem Eng 72:373–386
Kolb O, Lang J (2012) Simulation and continuous optimization. In: Mathematical optimization of water networks. Springer, pp 17–33
Leise P, Altherr LC (2018) Optimizing the design and control of decentralized water supply systems—a case-study of a hotel building. In: International conference on engineering optimization. Springer, pp 1241–1252
Leise P, Altherr LC, Pelz PF (2018) Energy-efficient design of a water supply system for skyscrapers by mixed-integer nonlinear programming. In: Operations research proceedings 2017. Springer, pp 475–481
Lejano RP (2006) Optimizing the layout and design of branched pipeline water distribution systems. Irrig Drain Syst 20(1):125–137
Mala-Jetmarova H, Sultanova N, Savic D (2017) Lost in optimisation of water distribution systems? A literature review of system operation. Environ Model Softw 93:209–254
Meng F, Fu G, Farmani R, Sweetapple C, Butler D (2018) Topological attributes of network resilience: a study in water distribution systems. Water Res 143:376–386
Mitsos A (2010) Global solution of nonlinear mixed-integer bilevel programs. J Global Optim 47(4):557–582
Morsi A, Geißler B, Martin A (2012) Mixed integer optimization of water supply networks. In: Mathematical optimization of water networks. Springer, pp 35–54
Narayanan I, Sarangan V, Vasan A, Srinivasan A, Sivasubramaniam A, Murt BS, Narasimhan S (2012) Efficient booster pump placement in water networks using graph theoretic principles. In: International green computing conference (IGCC), pp 1–6
Nault J, Papa F (2015) Lifecycle assessment of a water distribution system pump. J Water Resour Plann Manag 141(12):A4015004
Ostfeld A, Tubaltzev A (2008) Ant colony optimization for least-cost design and operation of pumping water distribution systems. J Water Resour Plann Manag 134(2):107–118
Pedersen GK, Yang Z (2008) Efficiency optimization of a multi-pump booster system. In: Proceedings of the 10th annual conference on Genetic and evolutionary computation. ACM, pp 1611–1618
Prasad TD (2009) Design of pumped water distribution networks with storage. J Water Resour Plann Manag 136(1):129–132
Robinius M, Schewe L, Schmidt M, Stolten D, Thürauf J, Welder L (2018) Robust optimal discrete arc sizing for tree-shaped potential networks. Preprint, optimization online, http://www.optimization-online.org/DB_HTML/2018/02/6447.html
Rossman LA (2000) EPANET 2 users manual. U.S Environmental Protection Agency, Cincinnati
Savic DA, Walters GA (1997) Genetic algorithms for least-cost design of water distribution networks. J Water Resour Plann Manag 123(2):67–77
Shin S, Lee S, Judi DR, Parvania M, Goharian E, McPherson T, Burian SJ (2018) A systematic review of quantitative resilience measures for water infrastructure systems. Water 10(2):164
Skworcow P, Paluszczyszyn D, Ulanicki B (2014) Pump schedules optimisation with pressure aspects in complex large-scale water distribution systems. Drink Water Eng Sci 7:53–62
Spurk J, Aksel N (2008) Fluid mechanics. Springer, Berlin
Tawarmalani M, Sahinidis NV (2005) A polyhedral branch-and-cut approach to global optimization. Math Program 103:225–249
Todini E (2000) Looped water distribution networks design using a resilience index based heuristic approach. Urban Water 2(2):115–122
Ulanicki B, Kahler J, Coulbeck B (2008) Modeling the efficiency and power characteristics of a pump group. J Water Resour Plann Manag 134(1):88–93
Varma KVK, Narasimhan S, Bhallamudi SM (1997) Optimal design of water distribution systems using an NLP method. J Environ Eng 123(4):381–388
Verleye D, Aghezzaf EH (2013) Optimising production and distribution operations in large water supply networks: a piecewise linear optimisation approach. Int J Prod Res 51(23–24):7170–7189
Vielma JP, Nemhauser GL (2011) Modeling disjunctive constraints with a logarithmic number of binary variables and constraints. Math Program 128(1–2):49–72
Wächter A, Biegler LT (2006) On the implementation of an interior-point filter line-search algorithm for large-scale nonlinear programming. Math Program 106(1):25–57
Yates D, Templeman A, Boffey T (1984) The computational complexity of the problem of determining least capital cost designs for water supply networks. Eng Optim 7(2):143–155
Yu G, Powell RS, Sterling MJH (1994) Optimized pump scheduling in water distribution systems. J Optim Theory Appl 83(3):463–488
Zessler U, Shamir U (1989) Optimal operation of water distribution systems. J Water Resour Plann Manag 115(6):735–752
Acknowledgements
Funded by Deutsche Forschungsgemeinschaft (DFG, German Research Foundation)—Project Number 57157498—SFB 805.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Altherr, L.C., Leise, P., Pfetsch, M.E. et al. Resilient layout, design and operation of energy-efficient water distribution networks for high-rise buildings using MINLP. Optim Eng 20, 605–645 (2019). https://doi.org/10.1007/s11081-019-09423-8
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11081-019-09423-8