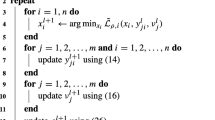1 Introduction

Aerospace engineered systems are a prime target for the application of numerical optimization due to the large impact that weight reduction has on system performance. This is evident in the fuel mass required to launch a satellite into orbit and in the operating cost of modern transport aircraft, where the primary cost driver is the fuel.

One of the first such applications by aerospace engineers was structural design optimization, first proposed by Schmit (1960). The field was made possible by the advent of the finite-element method for structural analysis (Argyris 1954; Turner et al. 1956), which enabled engineers to analyze much more complex geometries than was possible with analytic methods.

This work is motivated by aircraft wing design optimization using coupled, high-fidelity physics-based models of aerodynamics and structures (Kenway et al. 2014; Kenway and Martins 2014). In such problems, the objective, constraints, and derivative evaluations are expensive because of the expense of the aerodynamic and structural analyses.

The design optimization problem of interest can be stated in the general form

$$\displaystyle {\mathop {\mathrm{minimize}}\limits_{x \in {\mathbb {R}}^n}} \ f(x) \quad {\mathop {{\mathrm{subject\,to}}}}\ c(x) = 0, \ \ell \le x \le u, \quad {\mathrm{(NLP)}} $$

where \(f: {\mathbb {R}}^n \rightarrow {\mathbb {R}}\) and \(c: {\mathbb {R}}^n \rightarrow {\mathbb {R}}^m\) are twice continuously differentiable. For the time being, it is sufficient to note that any nonlinear program may be reformulated as (NLP).

Kennedy and Martins (2015) and (2014) solve aircraft design problems based on (NLP) using general-purpose sequential quadratic programming (SQP) software, such as SNOPT (Gill et al. 2002). This approach is particularly effective when used in conjunction with the adjoint method, which computes first derivatives efficiently (Kenway and Martins 2014; Lyu and Martins 2014; Lyu et al. 2015).

Structural design optimization problems often include both a large number of constraints (e.g., a failure criterion for each structural element), and a large number of variables (e.g., the thickness of each structural element). In addition, the constraint Jacobian is typically dense because the structures being optimized are statically indeterminate—the static equilibrium equations alone are not sufficient to compute the stress in each element of the structure. As a result, the stress in a given element depends not only on the properties of that element, but also on how the load is transmitted throughout the structure. In consequence, each failure constraint depends on many design variables.

To make a factorization-based SQP approach feasible, Poon and Martins (2007) aggregate constraints. The technique is effective for solving problems with hundreds of structural failure constraints (Kenway and Martins 2014, 2013) but causes the final structural mass to be overestimated because the objective is minimized on a subset of the feasible region (Poon and Martins 2007).

There is a need for an optimization approach that does not require aggregation, yet is still computationally efficient in the presence of dense Jacobians, and a matrix-free approach is the natural choice. However, providing a matrix-free implementation of an SQP or interior-point method is not straightforward, and the current state of optimization software is insufficient. A matrix-free approach exploiting inexact Hessian-vector products was recently proposed by Hicken (2014) and subsequently applied to an aerodynamic shape optimization problem (Dener et al. 2015), but this approach is currently restricted to problems with equality constraints. The handling of inequality constraints and bounds presents a particular challenge.

A matrix-free SQP method would compute steps as inexact minimizers of constrained quadratic programs. If bound constraints are kept explicit as in SNOPT, each SQP subproblem is a quadratic program with both equality and inequality constraints, and it is not immediately apparent how to solve such problems efficiently using a matrix-free method, even if they are convex.

Iterative methods for equality-constrained quadratic subproblems, however, have been developed in recent years. Arioli and Orban (2013) propose families of iterative methods that are suitable for matrix-free SQP or interior-point methods. Building upon those methods, Arreckx and Orban (2015) describe a matrix-free implementation of a fully-regularized SQP-type method for equality-constrained problems related to that of Armand et al. (2012), and highlight its relationship with the standard augmented Lagrangian method. Previously, Gill and Robinson (2013) highlighted relationships between a primal-dual augmented Lagrangian and regularized SQP methods.

If the bounds are enforced by way of a logarithmic barrier, as in, for example, IPOPT (Wächter and Biegler 2006) or KNITRO (Byrd et al. 2006), the subproblems are equality-constrained quadratic programs. IPOPT uses a line search filter scheme to guarantee global convergence while KNITRO uses a trust region with a merit function to ensure global convergence. A line-search variant of a matrix-free interior-point algorithm might employ an inexact Newton strategy on an appropriate formulation of the Newton equations. Numerous formulations are possible and can be regularized to mitigate ill-conditioning (Greif et al. 2014), but the linear systems must nevertheless be adequately preconditioned. Furthermore, the resulting steps must be checked to ensure continued progress toward optimality.

A matrix-free interior-point method of the trust-region type would suffer from the same ill-conditioning issue as the line-search variant. Furthermore, the step must be decomposed into components that lie in the null space and range space of the Jacobian. KNITRO uses a projected conjugate-gradient method (Gould et al. 2001) to compute the null-space component. Unfortunately, this approach requires accurate projections into the null space of the linear equality constraints and this is best achieved if the Jacobian is explicitly available.

The augmented-Lagrangian method may be simpler to implement as it requires the approximate solution of a sequence of reasonably-conditioned bound-constrained subproblems. The subproblem solutions are used to update estimates of the Lagrange multipliers for the constraints of (NLP). Direction-finding subproblems involve solving linear systems with a coefficient matrix of the form \( H = B + \rho J^T J \), where \(\rho > 0\) is a penalty parameter. Efficient iterative methods, typically variants of the conjugate-gradient method, are available for this type of system. Indeed if B is positive definite on the nullspace of J, J has full row rank, and \(\rho \) is sufficiently large, H is symmetric and positive definite. Note that operator-vector products with H require operator-vector products with the constraint Jacobian and its adjoint, an operation that is often available in practical large-scale applications. The main disadvantage is that augmented-Lagrangian methods typically do not exhibit the favorable local convergence properties of SQP methods. However, the ease with which bound constraints and inequality constraints can be treated in the algorithm provides us with a convenient starting point for experimenting with matrix-free optimization.

Augmented Lagrangian methods are a staple of the optimization library of numerical methods. It would be impossible to give a complete list of references here. We refer the reader to the general textbooks of Bertsekas (1982), Conn et al. (2000), and Nocedal and Wright (2006) for a thorough literature review and a complete convergence analysis.

The algorithm proposed in this paper is released as part of the open-source package NLPy (Orban 2014), a programming environment for designing numerical optimization methods written in the Python programming language.

Few other implementations of the augmented Lagrangian method exist. Amongst them MINOS (Murtagh and Saunders 1978, 2003), LANCELOT (Conn et al. 1992), and ALGENCAN (Andreani et al. 2008) are the most widely used. MINOS takes advantage of linear constraints in the problem and, like SNOPT, is a commercial product. Gawlik et al. (2012) develop a linearly-constrained augmented Lagrangian method for solving partial differential equation (PDE) constrained optimization problems as part of the Toolkit for Advanced Optimization (TAO) (Munson et al. 2012). Their matrix-free method is open-source, but only handles equality constraints. LANCELOT is designed to exploit the group-partially separable structure of the objective and constraints in order to gain efficiency when dealing with large sparse problems, which makes the code arduous to modify. Although the LANCELOT algorithm appears to require only matrix-vector products with the Jacobian, its current implementation requires the full Jacobian, and so technically does not qualify as matrix-free. ALGENCAN is similar to LANCELOT in that it uses a bound-constrained problem formulation, but ALGENCAN handles inequalities in a different way. While LANCELOT replaces inequalities with equalities by way of slack variables, ALGENCAN keeps inequalities intact, and uses the Powell-Hestenes-Rockafellar augmented Lagrangian function (Rockafellar 1973), which leads to discontinuous second derivatives in the objective of the subproblems. Our work follows the approach of LANCELOT.

We now introduce the notation used in the remainder of this paper. The i-th component of the vector x is \(x_i\), whereas \(x^k\) or \(x^{k,j}\) stands for the vector x at outer iteration k or inner iteration (k, j). Define the Lagrangian

$${\mathcal {L}}(x, \lambda ) := f(x) + \lambda ^T c(x),$$
(1)

where \(\lambda \in {\mathbb {R}}^m\) is the current approximation to the vector of Lagrange multipliers associated to the equality constraints of (NLP). The augmented Lagrangian function is

$$\Phi (x; \lambda , \rho ) := {\mathcal {L}}(x,\lambda ) + \tfrac{1}{2}\rho \Vert c(x)\Vert _2^2.$$
(2)

We separate \(\lambda \) and \(\rho \) from x by a semicolon in the arguments of \(\Phi \) to indicate that they are treated as parameters, and that \(\Phi \) is really a function of the primal variables x. For future reference, note that

$$\nabla _{xx} \Phi (x;\lambda ,\rho ) = \nabla _{xx} {\mathcal {L}}(x, \lambda + \rho c(x)) + \rho J(x)^T J(x).$$
(3)

Finally, \(P_{\Omega }(\bar{x})\) is the projection of the vector \(\bar{x} \in {\mathbb {R}}^n\) into the set of simple bounds

$$ \Omega := \left\{ x \in {\mathbb {R}}^n \mid \ell \le x \le u \right\} , $$

and is defined componentwise as \(P_{\Omega }(\bar{x})_i = {\text {median}}(\ell _i, \bar{x}_i, u_i)\) for \(i=1,\ldots ,n\).

The rest of this paper is organized as follows. Section 2 is devoted to a detailed description of our matrix-free algorithm and its implementation in the Python language. We provide numerical results on standard test problems in order to validate our implementation and to compare it to existing software. In Sect. 3 we explore in further detail the structural design optimization problem, and show the benefits of the matrix-free approach over SNOPT. Conclusions and future work are discussed in Sect. 4.

2 A matrix-free augmented Lagrangian implementation

2.1 Algorithmic details

In this section, we briefly cover the algorithmic details of our augmented Lagrangian framework. Although the framework itself is standard and well known, the description allows us to highlight certain algorithmic choices and relate them to implementation specifics described in Sect. 2.2.

The k-th outer iteration of the augmented-Lagrangian algorithm consists in approximately solving the subproblem

$$ \displaystyle {\mathop {\mathrm{minimize}}\limits_{x \in {\mathbb {R}}^n}} \ \Phi (x ; \lambda ^k, \rho ^k) \quad {\mathop {\mathrm{subject}}\,{\rm to}}\ \ell \le x \le u, $$
(4)

for fixed values of \(\lambda ^k\) and \(\rho ^k\). We enforce satisfaction of the bound constraints explicitly in the subproblem. Each subproblem solution is followed by updates to \(\lambda ^k\), \(\rho ^k\), and subproblem stopping tolerances. Those updates are typically based on the improvement in constraint violation achieved in the most recent subproblem. Algorithm 1 summarizes this process, and follows Nocedal and Wright (2006, Algorithm 17.4) and Conn et al. (1992). The parameter updates in Step 4 are classic and follow updates implemented in LANCELOT (Conn et al. 1992) and ALGENCAN (Andreani et al. 2008).

figure a

At every outer iteration, (4) must be solved efficiently. In our implementation, two options are available. The first option follows LANCELOT and uses the method of Moré and Toraldo (1989). The iterate at the j-th inner iteration corresponding to the k-th outer iteration will be denoted \(x^{k,j}\). We begin by building a quadratic model \(q^{k,j}\) of \(\Phi \) about \(x^{k,j}\):

$$ q^{k,j}(p) := \nabla _{\!x} \Phi (x^{k,j}; \lambda ^k, \rho ^k)^T p + \tfrac{1}{2}p^T B^{k,j} p,$$

where \(B^{k,j}\) is a symmetric approximation of \(\nabla _{\!xx} \Phi (x^{k,j}; \lambda ^k, \rho ^k)\) that need not be positive definite. Our implementation allows \(B^{k,j}\) to be defined as a limited-memory BFGS or SR1 approximation (Nocedal and Wright 2006). The step \(p^{k,j}\) is then obtained as an approximate solution of the bound-constrained quadratic program

$$\displaystyle {\mathop {\mathrm{minimize}}\limits_{p \in {\mathbb {R}}^n}} \ q^{k,j}(p) \quad {\mathop {\mathrm{subject\,to}}}\ p \in \Omega _{k,j}$$
(9)

where \(\Omega _{k,j} := \{p \in {\mathbb {R}}^n \mid x^{k,j}+p \in \Omega \; {\text{and}} \; \Vert p \Vert _{\infty } \le \Delta ^j \}\) and \(\Delta ^j > 0\) is the current trust-region radius. Note that \(\Omega _{k,j}\) is itself a box and there exist \(\ell ^{k,j}\) and \(u^{k,j}\) such that \(\Omega _{k,j} = \{x \in {\mathbb {R}}^n \mid \ell ^{k,j} \le x \le u^{k,j}\}\). The step \(p^{k,j}\) is accepted or rejected and the radius \(\Delta ^j\) is updated following standard trust-region criteria (Conn et al. 2000). Algorithm 2 summarizes the main steps involved in the inner iteration.

figure b

In Algorithm 2, the initial guess \(x^{k,0}\) may be simply set to the current outer iterate \(x^k\) or to a better approximation if one is available. In Step 3, \(p^{k,j}\) is computed using a simple extension of the method of Moré and Toraldo (1991) to nonconvex quadratic programs. In contrast with the trust-region subproblem solver used in LANCELOT, the method of Moré and Toraldo (1991) allows the addition of many constraints at a time to the active-set estimate \({\mathcal {A}}(x):=\{i \mid x_i= \ell ^{k,j}_i \quad {\text{or}} \quad x_i = u^{k,j}_i\}.\)

The face of \(\Omega _{k,j}\) containing x is defined as

$$ F_x := \left\{ y \in \Omega _{k,j} \mid y_i=x_i \quad {\text { if }} \quad x_i = \ell ^{k,j}_i \quad {\text { or }} \quad u^{k,j}_i \right\} .$$

The active-set method is divided into two stages. In the first stage, a projected gradient search is used to select a face of \(\Omega _{k,j}\) that will act as a prediction of the optimal active set of (9). In the second stage, a reduced quadratic model \(\hat{q}\) is formed involving only the free variables from the selected face, that is, the components of p that are not at their bounds. This model may be written

$$ {\hat{q}}(v) := q(p + Z_x v),$$

where \(Z_x\) is a prolongation operator consisting of columns of the identity that maps \(F_x\) to \({\mathbb {R}}^n\).

This reduced quadratic is then approximately minimized unconstrained using the conjugate gradient method to yield a search direction \(d=Z_x v\). If a direction of negative curvature is detected during the conjugate gradient iterations, we follow this direction to the boundary of \(\Omega _{k,j}\). A projected line search is then performed along d to ensure sufficient decrease, and satisfaction of the bound and trust-region constraints. Both the projected gradient search and the conjugate gradient algorithm are designed to terminate early and promote fast progress. We employ the same stopping conditions as Moré and Toraldo (1991).

The binding set at x is defined by

$$ {\mathcal {B}}(x) := \{i \mid (x_i = \ell ^{k,j}_i \quad {\text { and}} \quad \partial _i q(x) \ge 0), \quad {\text { or }} \quad (x_i = u^{k,j}_i \quad {\text{and}} \quad \partial _i q(x) \le 0)\}.$$

If the binding set at the iterate resulting from the projected search along the conjugate gradient direction coincides with the active set identified in the first stage, the conjugate gradient iterations are resumed to enforce further descent. Algorithm 3 summarizes the main steps involved in this active-set method. We refer the reader to Moré and Toraldo (1991) for more details on projected searches.

figure c

In practice, several improvements related to the management of the trust region can increase the efficiency of Algorithm 2. Two such improvements turned out to be effective in our implementation. The first is a non-monotone descent strategy (Toint 1997). As described, Algorithm 2 enforces a monotone descent in \(\Phi (\cdot ; \lambda ^k, \rho ^k)\). In a non-monotone trust-region algorithm, a trial point may be accepted even if it results in an increase in \(\Phi \). However, a sufficient decrease is required after a prescribed number of iterations, which is 10 in our implementation.

The second improvement is the simplified version of the backtracking strategy of Nocedal and Yuan (1998) described by Conn et al. (2000). If \(p^{k,j}\) is rejected at Step 4 of Algorithm 2, we perform an Armijo line search along \(p^{k,j}\) instead of recomputing a new trust-region step. We impose a maximum of five backtracking iterations. If the line search is unsuccessful, \(x^{k,j}\) remains the current iterate, the trust-region radius is reduced, and a new trust-region step is computed.

The second option to solve (4) is to use an existing method for bound-constrained problems, and our method of choice for this task is TRON (Lin and Moré 1998). TRON is an active-set method similar in spirit to the method of Moré and Toraldo (1991) that iteratively determines a current working set by way of a projected gradient method, and explores faces of the feasible set using a Newton trust-region method. In its default implementation, TRON has the significant disadvantage in that it requires the explicit Hessian in order to compute an incomplete Cholesky preconditioner to speed up the conjugate gradient iterations. We modified TRON so that only Hessian-vector products are required. This modification also allows us to use quasi-Newton approximations in place of the true Hessian. With this modification, the incomplete Cholesky factorization is made impossible, since we have no access to the Hessian. Matrix-free preconditioners, such as those of De Simone and di Serafino (2014) could be applied, but our current implementation uses no preconditioner in the conjugate gradient iterations.

2.2 Implementation

We implement the AUGLAG solver (Algorithms 1–3) in the Python language as part of the NLPy development environment for linear and nonlinear optimization (Orban 2014). Optimization problems are only accessed to evaluate the objective and its gradient, evaluate the constraints, and to compute operator-vector products with the Hessian of \({\mathcal {L}}(x,\lambda )\) and the constraint Jacobian. NLPy is open source and available at https://github.com/dpo/nlpy.

First derivatives must be provided. Second derivatives may be provided if they are available. However, in some applications, such as that described in Sect. 3, the Hessian of the augmented Lagrangian cannot be computed even in the form of Hessian-vector products, and we must be content with quasi-Newton approximations. Following the notation of Martínez (1988), the Broyden class of secant updates can be written as

$$S^{k,j+1} = S^{k,j} + \Delta _2(s,y,S^{k,j},v), $$
(10)

where \(S^{k,j}\) and \(S^{k,j+1}\) are the current and updated approximations, respectively,

$$ \Delta _2(s,y,S,v) = \frac{(y - S s) v^T + v (y - Ss)^T}{v^T s} - \frac{(y - S s)^T s}{(v^T s)^2} v v^T, $$
(11)

for some choice of \(v \in {\mathbb {R}}^n\), called the scale of the update, and \(s := x^{k,j+1} - x^{k,j}\). The vector y is chosen so that the update \(S^{k,j+1}\) satisfies a secant equation \(S^{k,j+1} s = y\). In the BFGS and SR1 updates, v is defined by \(v = y + (y^T s / s^T S s)^{\frac{1}{2}} S s\) and \(v = y - S s\), respectively.

For conciseness, in the following, we denote \(\nabla f_{k,j} := \nabla f(x^{k,j})\), \(J_{k,j} := J(x^{k,j})\), and \(c_{k,j} := c(x^{k,j})\). If \(\varphi : {\mathbb {R}}^n \rightarrow {\mathbb {R}}^n\) is a smooth function such that \(S^{k,j+1}\) should approximate \(\nabla \varphi (x^{k,j+1})\), then the choice \(y := \varphi (x^{k,j+1}) - \varphi (x^{k,j})\) is appropriate. The first possibility is to ask \(S^{k,j+1}\) to approximate \(\nabla _{xx} \Phi (x^{k,j+1} ; \lambda ^k, \rho ^k)\), and in that case, we should select

$$\begin{aligned} y&:= \nabla _x \Phi (x^{k,j+1} ; \lambda ^k, \rho ^k) - \nabla _x \Phi (x^{k,j} ; \lambda ^k, \rho ^k) \\&= \nabla f_{k,j+1} - \nabla f_{k,j} + J_{k,j+1}^T (\lambda ^k + \rho ^k c_{k,j+1}) - J_{k,j}^T (\lambda ^k + \rho ^k c_{k,j}). \end{aligned}$$

However, approximating (3) as a monolithic Hessian without exploiting its structure leads to poor numerical behavior. Because we assume that exact first derivatives are available, products with J(x) and \(J(x)^T\) may be evaluated, and it remains to approximate the Hessian of (1), as suggested by Dennis Jr. and Walker (1981) in the context of nonlinear least-squares problems using the DFP secant method. Martínez (1988) generalizes this DFP Hessian approximation to the Broyden class of secant methods, in particular to BFGS and SR1. In view of (3), the structured quasi-Newton update takes the form

$$\begin{aligned} B^{k,j+1} \approx \nabla _{xx} \Phi (x^{k,j+1} ; \lambda ^k, \rho ^k) = \nabla _{xx} {\mathcal {L}}(x^{k,j+1}, \lambda ^k + \rho ^k c_{k,j+1}) + \rho ^k J_{k,j+1}^T J_{k,j+1}. \end{aligned}$$

We therefore set \(B^{k,j+1} := S^{k,j+1} + \rho ^k J_{k,j+1}^T J_{k,j+1}\) and we seek an update \(S^{k,j+1} \approx \nabla _{xx} {\mathcal {L}}(x^{k,j+1}, \lambda ^{\sharp }_{k,j+1})\) that satisfies a secant equation, where \(\lambda ^{\sharp }_{k,j+1} := \lambda ^k + \rho ^k c_{k,j+1}\). The relevant function \(\varphi \) is now \(\varphi (x) := \nabla _x {\mathcal {L}}(x, \lambda ^{\sharp }_{k,j+1})\), and the appropriate secant equation is

$$\begin{aligned} S^{k,j+1} s&=\nabla _x {\mathcal {L}}(x^{k,j+1}, \lambda ^{\sharp }_{k,j+1}) - \nabla _x {\mathcal {L}}(x^{k,j}, \lambda ^{\sharp }_{k,j+1}) \nonumber \\&= \nabla f_{k,j+1} - \nabla f_{k,j} + \left( J_{k,j+1} - J_{k,j} \right) ^T (\lambda ^k + \rho ^k c_{k,j+1}). \end{aligned}$$
(12)

The updated \(S^{k,j+1}\) is then defined as in (10).

In practice, AUGLAG accepts problems with a mixture of general equality and inequality constraints and transforms the latter into non-negativity constraints, i.e., \(c_{\mathcal {E}}(x) = 0\) and \(c_{\mathcal {I}}(x) \ge 0\). We subsequently add slack variables to obtain constraints of the form

$$c_{\mathcal {E}}(x)=0, \quad c_{\mathcal {I}}(x) - t = 0, \quad t \ge 0, \quad \ell \le x \le u.$$

The augmented Lagrangian (2) becomes

$$ \Phi (x,t;\lambda ,\rho ): = f(x) + \lambda ^{T} \left[ {\begin{array}{*{20}l} {c_{{\mathcal{E}}} (x)} \\ {c_{{\mathcal{I}}} (x) - t} \\ \end{array} } \right] + \tfrac{1}{2}\rho \left\| {\left[ {\begin{array}{*{20}l} {c_{{\mathcal{E}}} (x)} \\ {c_{{\mathcal{I}}} (x) - t} \\ \end{array} } \right]} \right\|_{2}^{2}. $$

The latter augmented Lagrangian is iteratively minimized subject to the bounds \(t \ge 0\), \(\ell \le x \le u\).

In the presence of inequalities, \(\Phi (x, \cdot ; \lambda , \rho )\) is a convex quadratic function of t. Every time Algorithm 2 identifies a new inner iterate \((x^{k,j}, t^{k,j})\), we may further minimize \(\Phi \) in t subject to \(t \ge 0\). This yields the magical step (Conn et al. 1999, 2000)

$$t_i := \max \left( 0, \frac{\lambda _i}{\rho } + c_i(x^{k,j}) \right) , \quad i \in {\mathcal {I}}. $$

Finally, our solver may perform an automatic scaling of the problem. This procedure closely follows the one provided in IPOPT (Wächter and Biegler 2006), which is a scalar rescaling of the objective and constraint functions that ensures that the infinity norm of the gradient at the starting point after projection onto the bounds is less or equal to a given threshold value (100 in our implementation).

2.3 Benchmarks

The numerical results were obtained on a 2.4 GHz MacBook Pro with 4 GB of memory running Mac OS X 10.7. We report our results using the performance profiles of Dolan and Moré (2002).

We first present a comparison of our inner solver, SBMIN, versus the bound-constrained optimization code TRON (Lin and Moré 1998) on all the bound-constrained problems from the COPS 3.0 collection (Dolan et al. 2004) and from the CUTEr collection (Gould et al. 2003). This results in 255 problems, all of which were used in their default dimension. Each problem is given a limit of 3000 iterations and 1 hour of CPU time. The automatic problem scaling procedure available in NLPy is disabled for the AUGLAG and SBMIN results because none of the codes we compared to perform scaling of the problem.

By default TRON terminates the iterations as soon as

$$\Vert x^k - P_{\Omega }(x^k - \nabla f(x^k)) \Vert _2 \le 10^{-7} \, \Vert x^0 - P_{\Omega }(x^0 - \nabla f(x^0)) \Vert _2.$$

In order to make a fair comparison between the two solvers, we adjusted TRON ’s stopping criterion such that SBMIN and TRON stop as soon as the relative infinity norm of the projected gradient is below \(10^{-7}\). For both algorithms, the initial trust region radius is set to

$$ \Delta ^0 = \tfrac{1}{10} \Vert x^0 - P_{\Omega }(x^0 - \nabla f(x^0)) \Vert _{\infty }.$$

All other parameters for TRON are set to their default values. For SBMIN, we set \(\epsilon _1 = 10^{-4}\), \(\epsilon _2 = 0.9\), \(\gamma _1=0.25\) and \(\gamma _2=2.5\). In the bound-constrained quadratic program solver BQP, \(\zeta \) is set to \(10^{-3}\) and when tightened, to \(10^{-5}\), and \(\kappa =0.1\). These values are chosen because they result in good overall performance compared to other values we have explored.

When limited-memory quasi-Newton approximations of the Hessian are employed, all optimization codes are run with the same number of pairs in the history: 3 for LBFGS, and 5 for LSR1.

Fig. 1
figure 1

Comparison between SBMIN and TRON and their BFGS versions in terms of number of iterations and Hessian-vector products. Note that TRON-LBFGS and SBMIN-LBFGS don’t appear in the upper plot since they don’t use any Hessian vector-products

Full size image

Figure 1 shows performance profiles in terms of number of iterations and of Hessian-vector products. The results indicate that TRON is slightly more robust than SBMIN, and requires substantially fewer iterations and Hessian-vector products to converge. In this regard, it appears that enforcing the bound constraints at the level of the nonlinear problem as in TRON, instead of at the quadratic trust-region subproblem level, as in SBMIN, pays off in terms of efficiency.

We now compare the two variants of our matrix-free augmented-Lagrangian implementation AUGLAG, one using SBMIN as inner solver (AUGLAG-SBMIN) and the other one using TRON (AUGLAG-TRON), to LANCELOT A (Conn et al. 1992).

Because of the matrix-free nature of our algorithm and in order to do fair comparisons, we disable partial group separability in LANCELOT, use a box trust region, and disable the preconditioner in the conjugate gradient method. Furthermore, we set the Cauchy point calculation option to “approximate”. All other options are set to their default values. Finally, for both solvers, the relative stopping tolerances, on the infinity norm of the projected gradient and constraint violation, are set to \(10^{-7}\). The initial trust region radius is set to

$$\Delta ^0 = \tfrac{1}{10} \Vert (x,t)^0 - P_{\Omega }((x,t)^0 - \nabla \Phi ((x,t)^0; \lambda ^0, \rho ^0)) \Vert _{\infty },$$

where \(\lambda ^0\) is a least-square estimate of the Lagrange multipliers.

Finally, we compare the algorithms on all problems from the COPS 3.0 collection (Dolan et al. 2004) and from the CUTEr collection Gould et al. (2003) which possess at least one equality constraint or at least one bound constraint. This amounts to 675 problems. Again, a CPU time limit of 1 hour and an iteration count limit of 3000 is imposed. Figure 2 summarizes the performance of LANCELOT A and AUGLAG. The figure only reports the number of iterations because the LANCELOT A interface doesn’t provide the number of Hessian-vector products required. The results indicate that AUGLAG-TRON is more robust than the two other codes when using either exact Hessian or quasi-Newton approximations. Both versions of AUGLAG perform slightly better than LANCELOT A when using exact derivatives. With LSR1 update, LANCELOT A, AUGLAG-SBMIN, and AUGLAG-TRON perform well.

Fig. 2
figure 2

Comparison between AUGLAG-SBMIN, AUGLAG-TRON and LANCELOT A in terms of number of iterations with exact second derivatives (top) and with quasi-Newton approximations (bottom)

Full size image

3 Structural design optimization application

We now turn to a particular area of application for our matrix-free algorithm: aircraft structural design. Reducing the structural weight improves the fuel efficiency of the aircraft and therefore influences both the operating cost to the airline and the environmental impact of air transportation. Our goal is to minimize the mass of the structure subject to failure constraints. While many structural optimization problems are formulated with compliance (strain energy) constraints, the resulting solutions often show stress concentrations that would result in failure if the real structure were designed in that way. Therefore, optimization subject to failure constraints is more practical from an engineering design perspective. We start by describing the optimization problem formulation and how a matrix-free optimizer is helpful in this case before discussing the structural design optimization results.

3.1 Problem formulation and derivative evaluations

Structural analysis involves the solution of static equilibrium equations in the form of a discretized PDE so this problem may be interpreted as a special case of PDE-constrained optimization. However, the stress constraints place further restrictions on the optimal set of state variables, and eliminating the discretized PDEs does not eliminate all of the constraints involving state variables. The full-space (Biros and Ghattas 2005) or simultaneous analysis and design (SAND) problem (Haftka and Kamat 1989; Martins and Lambe 2013) is stated as

$$\begin{aligned} \displaystyle {\mathop {\mathrm{minimize}}\limits_{x,y}} \ F(x, y) \quad {\mathop {\mathrm{subject\,to}}}\ C(x, y) \le 0, \ R(x, y) = 0, \ \ell \le x \le u, \qquad {\mathrm{(SAND)}} \end{aligned}$$

where \(x \in {\mathbb {R}}^N\) are the design variables, \(y \in {\mathbb {R}}^M\) are the state variables, \(C: {\mathbb {R}}^N \times {\mathbb {R}}^M \rightarrow {\mathbb {R}}^m\) are design constraints, and \(R: {\mathbb {R}}^N \times {\mathbb {R}}^M \rightarrow {\mathbb {R}}^M\) are the discretized PDEs. Because we often use specialized software to solve the governing PDEs, and because N is usually much smaller than M, an alternative is to solve the reduced-space (Biros and Ghattas 2005) or nested analysis and design (NAND) problem (Haftka and Kamat 1989)

$$\displaystyle {\mathop {\mathrm{minimize}}\limits_{x}} \ f(x) \quad {\mathop {\mathrm{subject\,to}}}\ c(x) \le 0, \ \ell \le x \le u, \qquad {\mathrm{(NAND)}}$$

where y(x) is defined implicitly via \(R(x, y(x)) = 0\), \(f(x) := F(x, y(x))\), and \(c(x) := C(x, y(x))\). Despite its smaller size, even (NAND) can have thousands of variables and constraints. Furthermore, the governing equations \(R(x, y(x)) = 0\) must be re-solved for each new point computed by the optimizer, making function and gradient evaluation expensive. The chain rule and the implicit function theorem yield

$$\nabla c(x)= \nabla _x C(x, y(x)) + \nabla _x y(x) \nabla _y C(x, y(x)) $$
(13)
$$\quad = \nabla _x C(x, y(x)) - \nabla _x R(x, y(x)) \nabla _y R(x, y(x))^{-1} \nabla _y C(x, y(x))$$
(14)

where \(\nabla _x C(x, y(x))\) denotes the transpose Jacobian of C with respect to x, i.e., the matrix whose columns are the gradients with respect to x of the component functions of C. We use a similar notation for the derivatives of R, and use “\(-1\) ” for the matrix inverse. Each matrix-vector product with \(\nabla c(x)\) and \(\nabla c(x)^T\) involves solving a linear system with coefficient matrix \(\nabla _y R(x, y(x))\) and \(\nabla _y R(x, y(x))^T\), respectively. Because both operations involve the solution of a large system of linear equations, the computational cost of a single matrix-vector product is similar to the cost of evaluating all the objective and constraint functions. Therefore, the success of the matrix-free approach for solving problem (NAND) hinges on keeping the sum of function evaluations and matrix-vector products small.

3.2 Approximating Jacobian information

As mentioned in Sect. 2.2, exploiting the structure of the Hessian of the augmented Lagrangian leads to better performance on a wide range of problems. In particular, computing exact Jacobian-vector products within the trust-region solver and using a structured Hessian approximation to estimate the remaining terms is an effective strategy. However, this strategy can be too expensive when applied to structural design problems. Every time a Hessian-vector product is computed in the trust-region solver, two products with the Jacobian (one forward and one transpose) are required. We have observed many instances in which the number of Jacobian-vector products needed to solve a given trust-region subproblem exceeds the number of constraints of the problem. Under these circumstances, if sufficient memory were available, it would be more efficient to form and store the entire Jacobian for computing these products than to compute the products from scratch. Therefore, we need to further refine the basic algorithm to reduce the number of expensive matrix-vector products.

We propose two different approaches for reducing the number of Jacobian-vector products in our matrix-free algorithm. Both approaches rely on using the Jacobian-vector products to create more accurate trust-region subproblem models using additional quasi-Newton matrix approximations. By using approximate Jacobian information in the trust-region subproblem, we prevent the number of Jacobian-vector products in any given inner iteration from becoming too large and keep the cost of solving the subproblem low. Note that exact Jacobian-vector products are still used to compute gradients of the Lagrangian and augmented Lagrangian function. Approximate Jacobian information is only used in the trust-region subproblem.

The first approach estimates the Hessian of the quadratic penalty term of the augmented Lagrangian function separately from the Hessian of the Lagrangian. We refer to this approach as the “split” quasi-Newton method. Briefly setting aside the structured quasi-Newton method of Sect. 2.2, we define \(B_{\mathcal {L}} \approx \nabla ^2_{xx} {\mathcal {L}}\) and \(B_{\mathcal {I}} \approx \nabla ^2_{xx} \tfrac{1}{2}\rho c(x)^T c(x)\). The gradient of the infeasibility function is simply \(\rho J(x)^T c(x)\) so constructing the Hessian approximation is straightforward by splitting the gradient of the augmented Lagrangian function into the gradient of the Lagrangian and the gradient of the infeasibility function. We obtained the best results using the limited-memory SR1 approximation for \(B_{\mathcal {L}}\) and the limited-memory BFGS for \(B_{\mathcal {I}}\). The choice of a combination of quasi-Newton methods is informed by the fact that \(\nabla ^2_{xx} \tfrac{1}{2}\rho c(x)^T c(x) \approx J(x)^T J(x)\), a positive semidefinite matrix, near the optimal solution, while \(\nabla ^2_{xx} {\mathcal {L}}\) is not guaranteed to be definite near the optimal solution. To further improve the approximation provided by \(B_{\mathcal {I}}\), we use a starting diagonal that is an approximation of the true diagonal of \(J(x)^T J(x)\). The approximation is computed in the same way as the preconditioner proposed by De Simone and di Serafino (2014). Because both quasi-Newton approximations are limited-memory approximations, this approach is very memory-efficient for large optimization problems.

The second approach estimates the Jacobian matrix directly. In other words, we replace the true Jacobian-vector products for the algorithm outlined in Sect. 2.2 with the products of the same vectors with an approximate Jacobian matrix. In general, the Jacobian is not a square matrix, so alternative quasi-Newton approximations need to be used. Two such approximations are the two-sided rank-one (TR1) method, proposed by Griewank and Walther (2002), and the adjoint Broyden method, proposed by Schlenkrich et al. (2010). Because the TR1 method requires more frequent updates to the Lagrange multipliers than we have available in our algorithm, we have selected the adjoint Broyden method for implementation. Unfortunately, no convergence theory exists for limited-memory quasi-Newton Jacobian estimates and it is not obvious how to initiate a robust limited-memory approximation. Therefore, we have chosen to implement a full-memory version of this approximation.

The basic adjoint Broyden update is given by the formula

$$A^{k,j+1} = A^{k,j} + \frac{\sigma ^{k,j} \sigma ^{k,j,T}}{\sigma ^{k,j,T} \sigma ^{k,j}} \left( J(x^{k,j+1}) - A^{k,j}\right)$$
(15)

where A is the approximate Jacobian and \(\sigma \) is an “adjoint search direction.” Note that this update requires at least one (adjoint) Jacobian-vector product. Unlike traditional quasi-Newton methods, the choice of the search direction is not obvious. Schlenkrich et al. (2010) suggest several alternatives, from which we choose option (A), given by

$$\sigma ^{k,j} = (J(x^{k,j+1}) - A^{k,j})s^{k,j} $$
(16)

where \(s^{k,j} = x^{k,j+1} - x^{k,j}\), as the method to use with our algorithm. This particular choice of \(\sigma \) yields an update that is similar to the original TR1 update. Compared to the split quasi-Newton strategy, this strategy requires an additional Jacobian-vector product to compute \(\sigma ^{k,j}\). Despite the increase in required memory and higher cost of the update, this method has a distinct advantage over the split quasi-Newton approach in that the sparsity structure of any slack variables in the Hessian is preserved. That is, the block of \(\nabla ^2_{xx} \tfrac{1}{2}\rho c(x)^T c(x)\) associated with the slack variables is known exactly (an identity matrix) so it may be treated exactly in the Hessian-vector product. This approach leads to a much more accurate Hessian approximation than the split quasi-Newton method if the problem contains many slack variables.

We close this section with a few implementation details of the adjoint Broyden method. Similar to other quasi-Newton schemes, we reject the update if the denominator of the update term in (15) is sufficiently small, i.e., if \(\sigma ^T \sigma \le 10^{-20}\). Our initial approximation \(A^{0,0}\) is set to be the exact Jacobian \(J_{0,0}\). While this strategy has a very high up-front cost, we found that it paid off on our test problem in terms of many fewer inner iterations required by the optimization. We recognize that our strategy may not be sound for all problems, especially those in which the constraints are highly nonlinear. However, we expect the approach to be successful on many problems given the established robustness of quasi-Newton methods.

3.3 Optimization results

We use the following test problem to compare our matrix-free algorithm against an optimizer that requires the full Jacobian. The problem is to minimize the mass of a square, metallic plate that is clamped on all sides and subject to a uniform pressure load, as shown in Fig. 3. The structural analysis of the plate is performed using the finite-element program TACS (Kennedy and Martins 2014) with third-order shell elements. The optimization problem is constrained so that the maximum von Mises stress on any of the plate elements does not exceed the material yield stress. The design variables of the problem are the thicknesses of each plate element. Minimum and maximum thicknesses are imposed on each element. To simplify the problem, we analyze only one quarter of the plate and apply symmetry boundary conditions on the unclamped edges. Since each structural element is associated with one design variable (its thickness) and one constraint (the stress), the number of structural elements, design variables, and constraints is the same for a given problem. Except for the design variable bounds, all constraints are nonlinear.

Fig. 3
figure 3

Geometry and load condition of plate mass minimization problem

Full size image

While this test problem does not represent a complete aircraft structure, it shares two challenging features of such structures. First, the structure is a shell structure subject to a distributed load. This type of structure requires higher-order two- or three-dimensional finite elements to be used for accurate analysis of the structural behavior. The resulting analysis is therefore much more expensive than analyses using one-dimensional elements due to the larger number of degrees of freedom. Second, and more importantly, the structure is not statically determinate and has many degrees of indeterminacy. This means that the full finite-element analysis must be completed in order to compute stresses and strains; no shortcuts can be taken in evaluating the failure constraints. In practice, this finite-element analysis can be ill-conditioned so the NAND problem formulation (NAND) is used to hide the ill-conditioning from the optimizer.

Our benchmark optimizer for this test is the general-purpose optimizer SNOPT (Gill et al. 2002) which is accessed in Python through the pyOpt interface (Perez et al. 2012). SNOPT is an active-set SQP optimizer capable of solving nonlinear and nonconvex problems. While the full version of SNOPT has no limits on the number of variables or constraints in the problem, it is especially suited to problems with a large number of sparse constraints and few degrees of freedom. Like our optimizer, SNOPT does not require second derivatives because it approximates them using a limited-memory quasi-Newton method. Unlike our optimizer, SNOPT requires first derivative information from the objective and all constraint functions. Our optimizer just requires the gradient of the objective function and forward and transpose products with the constraint Jacobian.

Due to the design of the TACS software, we are able to accommodate both traditional optimizers like SNOPT and matrix-free optimizers. For our expression for the Jacobian of the reduced-space problem in (14), TACS provides modules for computing the action of \(\nabla _x R(x,y(x))\) and \(\nabla _x R(x,y(x))^T\) on vectors of appropriate length. The different partial derivatives of the constraints themselves are computed with respect to individual constraints, effectively providing column-wise evaluation of \(\nabla _x C(x,y(x))\) and \(\nabla _y C(x,y(x))\). The term \(\nabla _y R(x,y(x))^{-1}\) is computed implicitly by a specialized, sparse, parallel, direct factorization method. Every time we multiply this inverse or its transpose by a vector, we solve the appropriate upper- and lower-triangular systems by substitution. When computing the full Jacobian for SNOPT, TACS exploits parallel structure in the adjoint method to compute multiple adjoint vectors at the same time. This feature is not needed by the matrix-free optimizer since only individual matrix-vector products are ever called for. However, this added awareness of parallel computing does tend to skew the run-time results in favour of SNOPT.

We use the following settings in our matrix-free optimizer. The LSR1 Hessian approximation with five pairs of vectors is used to estimate the Hessian of the Lagrangian. The adjoint Broyden approximation is used to estimate the constraint Jacobian, where the initial Jacobian is computed exactly. In the split quasi-Newton strategy, the LBFGS approximation with five pairs of vectors is used to estimate the feasibility Hessian. Both magical steps and Nocedal–Yuan backtracking are turned on in the nonlinear, bound-constrained solver. In SBMIN, a limit of 50 iterations is imposed to solve the quadratic model problem. (On this specific problem, we found that SBMIN was superior to TRON.) Finally, parallel computations are used in the adjoint Broyden approximation to allow the approximate Jacobian to be stored in a distributed fashion.

For this optimization problem, we also introduced an update to the Lagrange multipliers, modified from the update specified by Algorithm 1, that we found to be effective at improving algorithm performance. The multiplier update now takes the form

$$\lambda ^{k+1} = \lambda ^k + \alpha ^k \rho ^k c(x^{k+1}) $$
(17)

where \(0 \le \alpha ^k \le 1\) is a chosen damping factor. Note that \(\alpha ^k = 1\) corresponds to the traditional update specified in Algorithm 1. In this damped update, \(\alpha ^k\) is computed as the solution to the convex minimization problem

$$\begin{aligned} \displaystyle {\mathop {\mathrm{minimize}}\limits_{\alpha ^k}} \ \frac{1}{2} ||\nabla f(x^{k+1}) + J(x^{k+1})^T \lambda ^{k+1} ||^2_2 \quad {\mathop {\mathrm{subject\,to}}}\ 0 \le \alpha ^k \le 1. \end{aligned}$$
(18)

The solution to Problem (18) is easily determined to be

$$\begin{aligned} \alpha ^k = {\text {median}} \left( 0, \frac{- \rho ^k c(x^{k+1})^T J(x^{k+1}) (\nabla f(x^{k+1}) + J(x^{k+1})^T \lambda ^{k})}{||\rho ^k J(x^{k+1})^T c(x^{k+1})||_2^2}, 1\right) . \end{aligned}$$
(19)

If \(J(x^{k+1})^T c(x^{k+1}) = 0\) then \(\alpha ^k\) is also set to zero. In practice, this modified update improves the multiplier estimates in the first few outer iterations. We also observe that \(\alpha ^k\) is chosen close to 1 after a few updates, suggesting that the traditional multiplier update is optimal when x and \(\lambda \) are near a solution.

Fig. 4
figure 4

Final thickness distributions for the 400-, 1600-, and 3600-element plate problems. These solutions were all obtained by the matrix-free optimizer. The solutions from SNOPT for the 400- and 1600-element problems are nearly identical

Full size image
Fig. 5
figure 5

Stress distributions as a fraction of the local yield stress for the 400-, 1600-, and 3600-element plate problems

Full size image

Example design solutions to the benchmark problem are shown in Fig. 4 for three different mesh sizes, and the corresponding stress distributions are shown in Fig. 5. In these figures, the x- and y-axes of the plots correspond to the clamped edges of the plate. The built-up regions of the plate along the clamped edges and in the center of the plate are clearly visible. For every case in which both solvers found an optimal solution, both SNOPT and AUGLAG converged to similar final designs. The feasibility and optimality tolerances of both solvers were set to \(10^{-5}\), and both solvers achieved these tolerances at the final designs.

Fig. 6
figure 6

Number of finite-element linear solve operations required to solve the plate optimization problem

Full size image
Fig. 7
figure 7

Run time to solve the plate optimization problem using 64 processors

Full size image

Figure 6 compares the number of finite-element linear systems—those involving \(\nabla _y R(x,y(x))\)—that are solved using each algorithm for a range of problem sizes. The finest mesh solved using either optimizer was \(70 \times 70\) elements. The corresponding optimization problem had 4900 thickness variables and 4900 failure constraints. We use the number of finite-element linear system solutions as the primary metric for comparing the optimizers because solving the linear system associated with the finite-element method is the most costly operation in the optimization process. This operation occurs once to evaluate the failure constraints and once for every Jacobian-vector product. To form the entire Jacobian for SNOPT, a linear system is solved to obtain one column of the matrix so the matrix size determines the total work. Figure 6 demonstrates that, by not forming the Jacobian at each iteration, both matrix-free algorithms successfully reduce the number of expensive linear solve operations as the problem size increases. In fact, for problems with more than 1000 variables and constraints, the reduction produced by the approximate Jacobian approach is nearly one order of magnitude over SNOPT.

Figure 6 also shows that the matrix-free optimizer was able to solve larger optimization problems than SNOPT. SNOPT was unable to solve any problems for meshes larger than \(50 \times 50\) elements due to a lack of memory. Each instance of the benchmark problem was solved in a distributed-memory computing environment. Because SNOPT was not designed to exploit this environment, it could only access the memory available to a single computing node, limiting the size of problem it could solve. We emphasize, however, that this is an artifact of the implementation of the SNOPT algorithm and not a fundamental limitation of the algorithm itself. There is no reason why an active-set SQP algorithm could not be developed to exploit the distributed-memory computing environment used to solve this problem.

Nevertheless, both matrix-free strategies lend themselves to more memory-efficient implementations. The reason for the high memory usage of SNOPT seems to be the symbolic factorization of the Jacobian as part of the active-set SQP algorithm. In the approximate Jacobian implementation of AUGLAG, we need to store the matrix, but we do not need to factorize it. While Message Passing Interface (MPI) standard commands are used, via the mpi4py library, to distribute the stored matrix across multiple nodes and compute matrix-vector products in parallel, a sequential implementation of the algorithm should be capable of solving the problem sizes shown here, though with a longer run time. In the split quasi-Newton implementation of AUGLAG, only limited-memory matrix approximations are used, and no special provisions are made for parallel computing. Therefore, if the optimizer were restricted to run on a single processor, we would expect the run time of that implementation to be identical.

Figure 7 shows a wall-time comparison for solving the optimization problems using 64 processors. Comparing Figs. 6 and 7, the large reduction in linear system solve operations does not translate into reduced run time. In fact, SNOPT is still the fastest optimizer for the problem sizes that it is able to solve. We attribute this behavior to two causes. First, as mentioned above, the TACS solver is able to parallelize the (implicit) multiplication of \(\nabla _y R(x,y(x))^{-1}\) by multiple right hand sides, reducing the time needed to form a large Jacobian. In other words, TACS is able to solve multiple adjoint systems simultaneously. This is a special feature of the TACS solver. Second, SNOPT requires many fewer iterations than our augmented Lagrangian solver to find the solution in each case. Fewer iterations means fewer points for which the partial derivative matrices must be recomputed. While this cost is small in comparison to the cost of a linear solve operation, the increase in the number of iterations outweighs the reduction in linear solves for this choice of algorithm.

One implementation decision that does not exert too much influence on the run time is the choice of implementation language of the optimizer. Figure 8 shows the fraction of the run time spent computing the next point in the optimizer for each case. When using SNOPT, only a small fraction of the run time is spent in the optimizer unless the problem is large. This increase in run time is probably due to the additional work needed to factorize the Jacobian in the active-set SQP algorithm. For the approximate Jacobian version of AUGLAG, the optimizer appears to take up the majority of the run time of the optimization process. However, nearly all of this time is spent forming matrix-vector products with the approximate Jacobian. Python makes use of both distributed-memory parallel processing and compiled-language libraries to complete this operation, so it is unlikely that moving to a compiled-language implementation would result in a large reduction in run time. For the split quasi-Newton version of AUGLAG, the fraction of the run time spent in the optimizer decreases with increasing problem size. Because so little time is spent within the optimizer itself using this approach, replacing the Python implementation of the algorithm with a compiled-language implementation would not result in large reductions in wall time.

Fig. 8
figure 8

Percentage of wall time spent in optimizer for each instance of the plate problem

Full size image

These results effectively show the intrinsic trade-off of matrix-free optimization in engineering design applications. As demonstrated in Fig. 6, if the engineering design problem has many constraints, using a matrix-free optimizer can lead to a massive reduction in the computational effort spent calculating gradient information. However, this reduction is offset by the overhead incurred by recomputing the design constraints and the relevant partial derivative matrices at more points in the design space. We suspect that changing the basic optimization algorithm from an augmented Lagrangian to an SQP or interior-point method would result in a matrix-free optimizer that is more competitive in terms of run time.

This example problem also raised the general issue of how to better exploit parallel computing within the optimization process. Because this particular problem is relatively small and dense, distributing the vectors used by the optimizer over multiple processors may not improve algorithm performance at all. The cost of communicating results between processors would outweigh the performance benefits of parallelized linear algebra. (The main exception to this statement is the matrix-vector products with the full-memory approximate Jacobian.) Instead, parallel processing is most beneficial in performing the structural analysis and computing functions and their gradients, including matrix-vector products. The only parallel capability in the TACS code that was not exploited by our matrix-free optimizer was the ability to form a group of gradients, i.e., a Jacobian matrix, using parallel matrix multiplication. The equivalent operation in a matrix-free optimizer would be to compute several matrix-vector products at the same time for a given design point. The optimizer and quasi-Newton approximations would need to be carefully chosen and structured to allow for this setup. Because the main bottleneck in parallel processing is often communication between processors, identifying operations that require a high computational effort but little communication between processors is critical to exploiting the parallel processing environment.

4 Conclusion and future work

This paper details the implementation of a matrix-free optimizer based on the augmented Lagrangian algorithm. Benchmarking results indicate that this optimizer is competitive with LANCELOT on standard test sets. We then extend the algorithm to store approximate Jacobian information to reduce the required number of matrix-vector products. The extended algorithm is then applied to a test problem motivated by aircraft structural design. Our results indicate that the matrix-free optimizer successfully reduces the computational work of the structural analysis, represented by the number of linear system solutions, when the structural design problem has a large number of design variables and a large number of constraints. The reduction can be as much as an order of magnitude when the number of variables and the number of constraints are both large.

Our study also highlighted key areas for improvement in terms of the capability of matrix-free optimizers. Namely, providing a solver for quadratic problems with both equality and inequality constraints, or equality and bound constraints, is the key to developing a matrix-free SQP method. In addition, because the problems for which matrix-free optimizers are most useful rely heavily on parallel computing, the matrix-free optimizer itself should exhibit strong, scalable performance in a parallel computing environment.

In the near future, we hope to extend our engineering application to the design of aircraft wings, including coupled aerodynamic and structural optimization (Kenway et al. 2014; Kenway and Martins 2014). The case of coupled aerodynamic and structural optimization is interesting because the features of the TACS solver that make it so fast on structural optimization problems (specialized parallel matrix factorization and parallel solution of multiple adjoint linear systems) would be nullified in the multidisciplinary optimization problem. In that case, we expect the matrix-free optimizer to become a particularly attractive option.