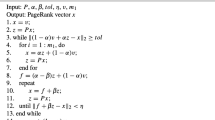1 Introduction

The PageRank model was originally introduced by S. Brin and L. Page in 1999 [1] to develop fast web search engines, and then studied and enhanced in a vast number of research papers (see, e.g., [2,3,4,5,6,7]). The model provides a powerful network centrality measure to identify the most important nodes within large graphs arising in several applications fields, such as in chemistry, bioinformatics, neuroscience, and bibliometrics [8]. In the original Web problem, the PageRank algorithm determines the ranking of each Web page by computing the stationary probability vector of a random walking process on the Web link graph, which is a directed graph representing the linking structure of the Web [7, 9]. The Web link graph is a binary matrix \(G\in \mathbb {N}^{n\times n}\), where n denotes the number of pages, such that G(i,j) = 1 when page j has a link pointing to page i, and G(i,j) = 0 otherwise. From a linear algebra viewpoint, the algorithm finds the vector x that satisfies

$$ A{\boldsymbol x} = {\boldsymbol x}, \quad \|{\boldsymbol x}\|_{1} = 1,~~{\boldsymbol x} > 0, $$
(1.1)

that is, it finds the principal unit positive eigenvector x [9] of the Google matrix

$$ A = \alpha (P + {\boldsymbol v}{\boldsymbol{d}}^{\top}) + (1 - \alpha){\boldsymbol v}{\boldsymbol e}^{\top}. $$
(1.2)

In (1.2), matrix \(P\in \mathbb {R}^{n\times n}\) is called the transition matrix with respect to the random walking process, and is defined as

$$ P(i,j)= \begin{cases} \frac{1}{\sum\limits_{k=1}^{n} G(k,j)}, & \text{if } G(i,j)=1, \\ 0, & \text{otherwise}. \end{cases} $$
(1.3)

The damping factor 0 < α < 1 defines the probability that random Web surfers choose a random link from the page they are visiting [25]. The teleporting vector \({\boldsymbol v}{~=[v_{1},\cdots ,v_{n}]^{\top }}\in \mathbb {R}^{n\times 1}\) (v ≥ 0 and ∥v∥1 = 1) defines the probability vi that the Web surfer jumps to an external page i. Finally, \({\boldsymbol d}\in \mathbb {N}^{n\times 1}\) is such that d(i) = 1 if page i has no hyperlink and 0 otherwise, and \({\boldsymbol e}=[1,1,\ldots ,1]^{\top }\in \mathbb {N}^{n\times 1}\).

The value of the damping factor α plays an important role in the PageRank model. Theoretically, it represents an upper bound 0 < |λ2|≤ α < 1 for the second largest eigenvalue, λ2, of A. Further properties of the Google matrix can be found in [2, 4,5,6,7, 10]. For low values of α (e.g., α = 0.85), λ2 is well separated from the largest eigenvalue of A, which is λ1 = 1, ensuring rapid convergence of the power algorithm applied to problem (1.1). On the other hand, convergence tends to slow down noticeably when α is very close to 1, requiring more robust algorithms than the simple power method. Some computational approaches proposed in the literature include Monte Carlo methods [11], adaptive algorithms [3, 12], extrapolation techniques [2, 7, 13], singular value decompositions [19,20,21] reordering [14, 15] and inner-outer solution strategies [16].

A significant amount of work has been devoted in the last years to the use of Krylov subspace methods based on the Arnoldi decomposition [17, 18] for large PageRank computations, mainly due to their memory efficiency and attractive inherent parallelism. Golub and Greif extended the refined Arnoldi procedure to PageRank by forcing a relevant shift to be 1, being able to circumvent the drawbacks due to complex arithmetic and showing overall very good algorithmic efficiency [22]. Many techniques have attempted to combine the conventional Arnoldi method and the power algorithm to produce faster solvers, e.g., the Power-Arnoldi [23,24,25], the Arnoldi-Extrapolation [26], and the Arnoldi-Inout [27] methods. In the technique proposed in [28], the weighted least squares problem is changed adaptively according to the component of the residual. Then, the generalized Arnoldi method is used to compute the approximate PageRank vector. However, when the dimension of the Krylov subspace is large, Arnoldi-based solvers tend to become very expensive in terms of memory and computational costs; on the other hand, if the dimension of the Krylov subspace is low, they sometimes fail to accelerate the basic power method, especially when the damping factor is high [22,23,24,25]. Similarly to the restarted GMRES algorithm [31], they may stagnate in many circumstances [32].

Motivated by costs considerations, other work developed PageRank solvers based on the Bi-Lanczos orthogonalization procedure [18, pp. 139-145] (see, e.g., [29, 30]) instead of Arnoldi. In this paper, we look in particular at the Hessenberg reduction process [33,34,35,36] that was introduced by K. Hessenberg in 1940 [33], and revived recently to establish a number of cost-effective Krylov subspace solvers for sparse matrix systems, due to its lower arithmetic and storage requirements. The method has been extended to compute the characteristic polynomial of matrices [33, 34, 37], to solve general nonsymmetric linear systems [17, 35, 36, 38, 39], including systems with multiple right-hand sides [40,41,42,43,44] and multi-shifted coefficient matrices [45,46,47], other types of matrix equations [42, 48, 49], the action of a matrix function f(A)v [47], and other related problems [51]. Theoretical and numerical studies have investigated the mathematical properties of the Hessenberg process, especially in relation with the more conventional Arnoldi procedure. The Arnoldi method was first introduced in 1951 as a means of reducing a dense matrix A into a Hessenberg form by unitary transformations, whereas the Hessenberg process applies similarity transformations [50] and is more suitable for parallel computing. In his paper, Arnoldi hinted that the eigenvalues of the Hessenberg matrix obtained after k ≪ n steps, where n is the size of A, could provide accurate approximations of some eigenvalue of A. It was later discovered that this strategy can lead to efficient techniques for approximating eigenvalues of large sparse matrices. In the current work, following a similar development, we modify the Hessenberg process to establish a new family of eigenvalue solvers. We combine the new solvers with the refined and explicitly restarted techniques introduced in [19, 22] to compute realistic PageRank problems. Finally, we analyze their convergence behavior and computational complexity.

The rest of this paper is organized as follows. In Section 2, the Hessenberg process is introduced and a novel family of eigenvalue solvers based on this procedure is described. Moreover, theoretical aspects of such eigenvalue solvers are highlighted in comparison with the classical Arnoldi-like methods. In Section 3, we derive the Hessenberg-type method with explicit restarting and refined techniques for computing PageRank. Both the convergence behavior and the computational cost of the proposed method are discussed. Numerical results in Section 4 show the effectiveness of the proposed algorithm, also against other popular PageRank algorithms. In Section 5, we present some conclusions arising from our study.

2 The Hessenberg process with applications to eigenvalue computations

In this section, we briefly review the Hessenberg procedure that is at the basis of our development. We recall some fundamental properties of the algorithm and then we describe a Hessenberg-based projection technique for computing eigenvalues of large nonsymmetric matrices. Our theoretical analysis demonstrates the feasibility of the method, showing some computational advantages over the more conventional Arnoldi procedure.

2.1 The Hessenberg process

The Hessenberg process is an an oblique projection technique that reduces a given nonsymmetric matrix \(A\in \mathbb {R}^{n\times n}\) to a Hessenberg form [34, pp. 377-381; 45]. Originally, the method was described as a way to compute the characteristic polynomial of a matrix [33]. The basic procedure is presented in Algorithm 1, where a pivoting strategy is included to ensure numerical stability.

figure a

Let \(L_{k}=\left [ {\boldsymbol l}_{1},\ldots ,{\boldsymbol l}_{m} \right ]\) denote a matrix, \(\bar {H}_{m}=\left [ h_{i,j} \right ]\) be an upper Hessenberg matrix and Hm the submatrix obtained from \(\bar {H}_{m}\) by deleting its last row. Finally, we denote by \(\mathcal {P}^{{\top }}_{k} = [{\boldsymbol e}_{p_{1}},{\boldsymbol e}_{p_{2}},\ldots ,{\boldsymbol e}_{p_{n}}]\) where the scalars pi’s (for i = 1,…,n) are defined in Algorithm 1. After k steps of Algorithm 1, the following matrix equation can be easily established,

$$ \begin{array}{ll} AL_{k} & = L_{k+1}\bar{H}_{k} \\ & = L_{k}H_{k} + h_{k+1,k}{\boldsymbol l}_{k+1} {\boldsymbol e}^{{\top}}_{k}, \end{array} $$
(2.1)

and \(\mathcal {P}_{k}L_{k}\) is lower trapezoidal [35, 39]. Unlike Arnoldi, the Hessenberg procedure with pivoting is not guaranteed to be backward stable in finite precision arithmetic [50]. However, the backward error is reported to be small for most practical problems [36, 39, 45]. This is also confirmed by our computational experiences. We did not observe noticeable numerical instabilities due to the non-orthogonality of the Krylov basis in our numerical experiments; see also [45] for a discussion of this topic.

2.2 Approximation of eigenpairs based on the Hessenberg process

Methods to approximate eigenpairs of a large nonsymmetric matrix A usually compute them from the Hessenberg decomposition of A given by (2.1). The upper Hessenberg matrix Hm can be seen as the projection of A onto the Krylov subspace

$$ \mathcal{K}_{m}(A,{\boldsymbol v}) = \text{span}\{{\boldsymbol v},A{\boldsymbol v},\ldots,A^{m-1}{\boldsymbol v}\}, $$
(2.2)

and the columns of the matrix Lm are a basis of \(\mathcal {K}_{m}(A,{\boldsymbol v})\). Under certain conditions, the eigenvalues of Hm converge to the eigenvalues of A [18, 34, 50]. Various eigenvalue solvers are built upon this idea, differing each other mainly on the type of projection technique that is used to derive the decomposition (2.1), for example, the Arnoldi process, the Bi-Lanczos procedure and the Induced Dimension Reduction (IDR) strategy [52, 53]. The approximate eigenpairs of A are retrieved in the form \((\theta _{i},~{\boldsymbol x}^{(i)} = L_{m}{\boldsymbol y}^{(i)})\), where \(\left (\theta _{i}, {\boldsymbol y}^{(i)}\right )\) are eigenpairs of the small dimensional matrix Hm, such that

$$ H_{m}{\boldsymbol y}^{(i)} = \theta_{i}{\boldsymbol y}^{(i)}\quad \text{with}~~\|{\boldsymbol y}^{(i)}\| = 1,~~{i=1,2,\cdots,m.} $$
(2.3)

A bound on the residual error can be established directly from (2.1), by writing

$$ \begin{array}{ll} A{\boldsymbol x}^{(i)} - \theta_{i}{\boldsymbol x}^{(i)} & = AL_{m}{\boldsymbol y}^{(i)} - \theta_{i} L_{m}{\boldsymbol y}^{(i)}\\ & = h_{m + 1,m}{\boldsymbol l}_{m+1}{\boldsymbol e}^{\top}_{m}{\boldsymbol y}^{(i)}. \end{array} $$

If we denote as [y(i)]m the m th component of the vector y(i), then we obtain

$$ \|A{\boldsymbol x}^{(i)} - \theta_{i}{\boldsymbol x}^{(i)}\| \leq |h_{m + 1,m}|\|{\boldsymbol l}_{m + 1,m}\| \left|[{\boldsymbol y}^{(i)}]_{m}\right| $$
(2.4)

or, if we normalize the vector lm,

$$ \|A{\boldsymbol x}^{(i)} - \theta_{i}{\boldsymbol x}^{(i)}\| \leq |h_{m + 1,m}| \left|[{\boldsymbol y}^{(i)}]_{m}\right|. $$
(2.5)

This analysis is in line with the results described in [19].

For the “west0479” problem, a real-valued 479-by-479 sparse matrix that has both real and complex eigenvalues, in Fig. 1, we plot the eigenvalues of A computed by the MATLAB command eig and those of the Hessenberg matrix produced by the IDR(s = 4) projection technique [52], the Sonneveld pencil [52, 53], the Arnoldi, and the Hessenberg procedures. We clearly see that the Hessenberg procedure can estimate the exterior Ritz values very well, in some cases even slightly more accurately than the Arnoldi procedure. The condition number of the Krylov basis matrix Lm is an effective metric to determine the accuracy of the method used. Figure 2 illustrates that for the Hessenberg process, this condition number does not grow significantly when the dimension of the Krylov subspace increases. The numerical error of the Hessenberg decomposition often remains small.Footnote 1 This observation is also exemplified by the stochastic analysis presented in [52, Section 3.3] that can produce (numerical) evidence that the Hessenberg process can be as efficient as the Arnoldi process for practical eigenvalue computations.

Fig. 1
figure 1

Plots of the Ritz values generated by the IDR(s = 4) factorization, the Sonneveld pencil, the Arnoldi and the Hessenberg procedures

Full size image
Fig. 2
figure 2

The quality of different basis matrices; Left: the error of different Hessenberg decompositions; Right: the condition number of basis matrices generated by different Hessenberg decompositions

Full size image

2.3 Relation between the Arnoldi and Hessenberg decompositions

In this subsection, we provide more theoretical background supporting the use of the Hessenberg process to approximate effectively eigenpairs of a given nonsymmetric matrix A. The starting point of our analysis is a comparison between the Hessenberg decompositions computed by the Arnoldi and by the Hessenberg procedures. After m steps of the Arnoldi method applied to A, starting with an initial vector v0 and assuming no breakdown, the following Hessenberg decomposition is derived:

$$ AV_{m} = V_{m}H_{m} + h_{m+1,m}{\boldsymbol v}_{m + 1}{\boldsymbol e}^{\top}_{m} = V_{m + 1}\bar{H}_{m}. $$
(2.6)

On the other hand, after m steps of the Hessenberg procedure applied to A with same initial vector l0, the resulting matrix factorization writes as

$$ AL_{m} = L_{m}H^{(h)}_{m} + h^{(h)}_{m+1,m}{\boldsymbol l}_{m+1}{\boldsymbol e}^{\top}_{m} = L_{m + 1}\hat{H}^{(h)}_{m}. $$
(2.7)

Differently from Arnoldi, however, the columns of Lm in (2.7) are not mutually orthogonal. By computing the reduced QR factorization of Lm+ 1,

$$ L_{m + 1} = Q_{m+1}R_{m + 1}, $$
(2.8)

we can establish the following relation between (2.7) and (2.8):

$$ AQ_{m} = Q_{m + 1}R_{m+1}\hat{H}^{(h)}_{m}R^{-1}_{m}. $$
(2.9)

Due to the uniqueness of the Arnoldi decomposition (see Section 3.3 in [52]), by comparing (2.6) and (2.9) we conclude that Qm+ 1 = Vm+ 1 and

$$ \bar{H}_{m} = R_{m+1}\hat{H}^{(h)}_{m} R^{-1}_{m}. $$
(2.10)

The above result is summarized in the following proposition:

Proposition 2.1

It follows that

$$ \begin{array}{@{}rcl@{}} H_{m} & = & R_{m}H^{(h)}_{m}R^{-1}_{m} + \frac{{h^{(h)}_{m+1,m}}}{r_{m,m}}\tilde{{\boldsymbol r}} {\boldsymbol e}^{\top}_{m}, \end{array} $$
(2.11)
$$ \begin{array}{@{}rcl@{}} \frac{h^{(h)}_{m+1,m}}{r_{m,m}} & = & \frac{h_{m+1,m}}{r_{m + 1,m + 1}}, \end{array} $$
(2.12)

where \(\tilde {{\boldsymbol r}} = [r_{i,m+1}]^{m}_{i=1}\) is the vector containing the first m components of the (m + 1)th column of Rm+ 1.

In fact, (2.11)–(2.12) can be also found in [38, 52]. According to (2.12), in exact arithmetic both procedures produce upper Hessenberg matrices with the same eigenvalues. If the Arnoldi process terminates successfully (i.e., a happy breakdown situation hm+ 1,m = 0 occurs), so does the Hessenberg procedure (\(h^{(h)}_{m + 1,m}= 0\)). On the other hand, a direct consequence of Proposition 2.1 is that the Ritz values produced by the Arnoldi and by the Hessenberg processes are not the same. The condition number of the Krylov basis matrix Lm, which is the same as the condition number of matrix Rm, gives a clear indication of the accuracy of the eigenvalues of \(H^{(h)}_{m}\) compared to those resulting from the Arnoldi process.

In conclusion, it can be expected that the Hessenberg process can produce feasible approximations of eigenpairs of large nonsymmetric matrices matrix.

3 A Hessenberg-type algorithm for computing PageRank

In this section, we will propose a Hessenberg-based algorithm to compute the PageRank vector, that is the positive unit eigenvector corresponding to the largest eigenvalue of the Google matrix. Golub and Greif suggested that the explicitly restarted Arnoldi process for computing eigenvalues and eigenvectors should be implemented in complex arithmetic, thus it is not suitable (it needs to be refined) to compute the PageRank vector [22]. Moreover, since the Hessenberg process is similar in nature to Arnoldi, except that it produces a non-orthogonal basis of the Krylov subspace, we follow a similar development to the refined Arnoldi method for PageRank problems. In other words, the solver described in this section may be called the refined Hessenberg method for PageRank. However, we do not approximate the eigenvectors of A from those of Hm (the so-called Ritz-like vectors). Instead, we compute the refined Ritz-like vectors, i.e., the singular vectors associated with the smallest singular values of A − 𝜃iI [19, 22], where \(\{\theta _{i}\}^{m}_{i=1}\) are named the Ritz-like values; cf. (2.3). The Hessenberg-based method enjoys similar numerical properties to the Arnoldi-based variant: an effective separation of the eigenvectors is ensured, complex arithmetic is avoided by using a shift equal to 1 (due to the fact that the largest eigenvalue of the Google matrix is known), the smallest singular value converges more smoothly to zero than the largest Ritz value to 1 [22, Section 3]. The Hessenberg-type method for computing the PageRank vector is presented in Algorithm 2. The following convergence result can be established after each cycle of m iterations of Algorithm 2.

figure b

Theorem 3.1

Let Qm = [q1,q2,⋯ ,qm] be the matrix obtained from running m-steps of either the Arnoldi or the Hessenberg procedures applied to A starting from an initial vector q0, then the Hessenberg matrix decomposition can be uniformly written as

$$ \begin{array}{ll} AQ_{m} & = Q_{m}H_{m} + h_{m+1,m}{\boldsymbol q}_{m+1}{\boldsymbol e}^{\top}_{m}\\ & = Q_{m+1}\bar{H}_{m}. \end{array} $$
(3.1)

Denote as σm the smallest singular value of Hm+ 1,m − [Im;0], then vm at Line 6 of Algorithm 2 is the corresponding right singular vector, and Qmvm is the approximate PageRank vector. The residual vector at each restarting cycle can be computed as r = σmQm+ 1um.

Proof

According to (3.1) and Algorithm 2, it follows that

$$ \begin{array}{ll} {\boldsymbol r} & = {A{\boldsymbol q}_{m} - {\boldsymbol q}_{m}} = AQ_{m}{\boldsymbol v}_{m} - Q_{m}{\boldsymbol v}_{m} \\ & = Q_{m+1}H_{m+1,m}{\boldsymbol v}_{m} - Q_{m}{\boldsymbol v}_{m}\\ & = Q_{m+1}\left[H_{m+1,m} - \begin{pmatrix} I_{m}\\ {\boldsymbol 0} \end{pmatrix}\right]{\boldsymbol v}_{m}\\ & = \sigma_{m}Q_{m+1}{\boldsymbol u}_{m}, \end{array} $$
(3.2)

where qm is an approximate PageRank vector. Thus, the assertion is verified. □

Below, we give the norms of the residual vectors computed by the Arnoldi and by the Hessenberg procedures, respectively:

$$ \|{\boldsymbol r}\|_{1} = \sigma_{m}\|Q_{m+1}{\boldsymbol u}_{m}\|_{1},~~ \text{where}~~ Q^{\top}_{m}Q_{m}: \begin{cases} = I_{m}\quad(\text{Arnoldi~process}),\\ \neq I_{m}\quad(\text{Hessenberg~process}), \end{cases} $$
(3.3)

and

$$ \|{\boldsymbol r}\|_{2} = \begin{cases} \sigma_{m}, & Q^{\top}_{m}Q_{m} = I_{m} \quad(\text{Arnoldi~process}),\\ \sigma_{m}\|Q_{m+1}{\boldsymbol u}_{m}\|_{2},& Q^{\top}_{m}Q_{m} \neq I_{m}\quad(\text{Hessenberg~process}). \end{cases} $$
(3.4)

Although the 2-norm of the Arnoldi residual vectors is much cheaper than the 2-norm of the Hessenberg residual vectors, it should be noted that for PageRank computations it is generally recommended to use the 1-norm; refer, e.g., to [2, 25, 26]. Therefore, the computational complexity of the stopping criterion (at line 8 of Algorithm 2) is almost the same for both methods [24, 28, 30].

Before we end this section, we provide estimates on the storage requirement and the computational complexity of the new algorithm, also compared against other popular methods.

Table 1 shows the memory required in addition to A for running k iterations of the power method (referred to as Power in the table), the power method with quadratic extrapolation (called as QE-power), the Arnoldi-type method (abbreviated as Arnoldi), the adaptively accelerated Arnoldi method (called as A-Arnoldi), and the Hessenberg-type method (abbreviated as Hessenberg). Here, w, x, u, and r are intermediate working vectors used at the k th step, and Qk denotes the k orthonormal vectors in the modified Gram-Schmidt process. Analogously, Lk denotes the n × k non-orthonormal matrix in the variant of the LU-like factorization process.

Table 1 Memory requirement for running k iterations of different PageRank algorithms
Full size table

Table 2 shows the computational workloads required to execute one cycle of each different iterative algorithm. Here, Nz represents the number of nonzero entries of matrix A. In fact, both Arnoldi and A-Arnoldi for computing PageRank enjoy the similar pseudo-code of Algorithm 2, the only difference is to choose the Hessenberg, Arnoldi, or generalized Arnoldi process at Line 4 of Algorithm 2. It implies that we need to compare the cost of the Hessenberg process with both the Arnoldi and generalized Arnoldi procedures. We can see that one cycle of the Hessenberg-type method is cheaper than for Arnoldi and for the generalized Arnoldi methods. Thus its use can be computationally attractive for large PageRank computation. The convergence performance of the Hessenberg method is also superior to Arnoldi algorithms (i.e., Arnoldi and A-Arnoldi), as proved numerically in the next section. Besides matrix-vector multiplications, also the computation of vector norms and SAXPYFootnote 2 (which stands for “Single-Precision A⋅X Plus Y” and is a combination of the scalar multiplication and vector addition) operations determines the total computational cost of these three algorithms. Overall, when m increases, the cost of each cycle increases too but the total number of iterations decreases. The optimal value of the restart parameter that minimizes the total solution time remains problem dependent, and this issue will be examined in our numerical experiments section.

Table 2 Computational cost of one cycle of different algorithms for computing PageRank
Full size table

4 Numerical experiments

In this section, numerical experiments are reported to illustrate the efficiency of the Hessenberg-based PageRank algorithm presented in this paper also against other popular PageRank algorithms that are the conventional power method including its variants with quadratic extrapolation [2] and with linear extrapolation [13], the Arnoldi-based PageRank method introduced in [22], and the adaptively accelerated Arnoldi method [28]Footnote 3. The performance of these methods were assessed in terms of number of matrix-vector products (or, equivalently, number of iteration steps for the first three algorithms) and elapsed CPU time (in seconds) required to achieve convergence to a prescribed accuracy. Unless otherwise stated, the stopping criterion used in our runs was

$$ \frac{\|A{\boldsymbol q} - {\boldsymbol q}\|_{1}}{\|{\boldsymbol q}\|_{1}} < tol ~= 10^{-8}, $$

and all the algorithms were started from the initial vector q0 = e/∥e∥1, where e = [1,…,1]T. According to Theorem 3.1, the cost of implementing the above stopping criterion can be alleviated for both Arnoldi- and Hessenberg-type methods, since Aq −q = σmQm+ 1um and the computation of σmQm+ 1um is actually cheaper than that of Aq −q, when m is not large. In our experiments with the method denoted as QE-power, the quadratic extrapolation technique was applied every five iterations, following the observations made in [2]. The experiments were run in MATLAB R2017b (64 bit) on a computer equipped with Intel Core i5-8250U processor (CPU 1.60\(\sim \)1.80 GHz), 8 GB of RAM using double precision floating point arithmetic with machine epsilon set equal to 10− 16.

The matrix problems used in our runs are obtained from the SuiteSparse Matrix Collection, which is available online at https://sparse.tamu.edu/. In Table 3, we describe the characteristics of our test matrices, including number of rows (n), number of nonzeros (Nz), number of zero columns (zcol), average nonzeros of every row (aNz), and density (den) which is defined as

$$ den = \frac{N_{z}}{n\times n}\times 100. $$

Here, the number of zero columns corresponds to the number of dangling nodes. The largest problem in our set has size 5,363,260 and 79,023,142 nonzeros.

Table 3 The characteristic of test matrices
Full size table
Table 4 Number of iterations required by the Arnoldi-, GArnoldi- and Hessenberg-based algorithms with different restart numbers. (problem soc-Slashdot0902 and tol = 10− 7)
Full size table
Table 5 Number of iterations required by the Arnoldi-, GArnoldi- and Hessenberg-type algorithms with different restart numbers (problem soc-Slashdot0902 and tol = 10− 8).
Full size table
Table 6 Matrix-vector products and CPU time in seconds versus damping factors
Full size table

4.1 Choice of the restart value m

First, we investigate the effect of the restart parameter m on the convergence of the Arnoldi (A-P), A-Arnoldi (GA-P) and Hessenberg (H-P) methods in terms of number of iterations and elapsed CPU time, since this parameter may noticeably affect the performance of Krylov subspace-based methods. The results are presented numerically in Tables 4, 5 and 6. In Figs. 3 and 4, for the test matrix ‘soc-Slashdot0902’ we plot the curves showing the total CPU time versus m for different damping factors and tol’s values.

Fig. 3
figure 3

Plot of the elapsed CPU time in seconds versus the restart number (i.e., m) for the test problem ‘soc-Slashdot0902’ using tol = 10− 7

Full size image
Fig. 4
figure 4

Plot of the elapsed CPU time in seconds versus the restart number m for the test problem ‘soc-Slashdot0902’ using tol = 10− 8

Full size image

According to the results reported in Tables 4–6, the number of iterations required to converge by these three algorithms tends to decrease for higher restart numbers m, especially for larger damping factors. This behaviour is expected because larger search spaces may provide better approximations. On the other hand, the total solution time of the three methods is not significantly reduced. As mentioned in Section 3, and explained in Tables 1–2, the storage requirement and the computational cost of one Arnoldi and Hessenberg cycles increase with m. However, it should be noted that Hessenberg is more cost effective than both Arnoldi and A-Arnoldi for larger m. In our numerical experiments, we choose the restart numbers equal to m = 8,10 due to memory constraintsFootnote 4, since the number of iterations and the total elapsed CPU time are still acceptable. It may be worth investigating techniques that can effectively reduce the dimension of the Krylov subspace for the Hessenberg method, e.g., by optimizing the choice of the starting vector [52] and by utilizing vector extrapolations [13], but this analysis is beyond the scope of this study.

4.2 Effect of damping factors on the CPU time and the number of iterations

For the five matrix problems listed in Table 3, we report on the number of matrix-vector products (Mvp in short) and the elapsed CPU time of the power method, the power methods with quadratic extrapolation and with linear extrapolation, the Arnoldi-type method, the adaptively accelerated Arnoldi method and the Hessenberg-type method for various values of the damping factor α ranging from 0.85 to 0.99.

We can see from the results of Table 6 that the power method accelerated by quadratic extrapolation outperforms the conventional power method and its linearly extrapolated variant, while in most cases our Hessenberg-based solver is the fastest method in terms of elapsed CPU time, with the only exception for matrix ‘IV’ using α = 0.99. It can be observed that Arnoldi is more cost-effective than A-Arnoldi at equal number of Mvp, especially for large problems. This behaviour is in agreement with the cost analysis presented in Table 2. Except these few cases, the A-Arnoldi method is still attractive to consider. On the other hand, one observes from Table 6 that the numerical behaviors of the Arnoldi, A-Arnoldi and Hessenberg algorithms relies on the choice of m and α. For example, when m is small, say m = 8, these three algorithms are only slightly better than the Power, Power-Tan and QE-Power methods. However, as m and α increase, their improvements become gradually more significant. Unlike the Arnoldi, A-Arnoldi, and Hessenberg, the Power, Power-Tan, and QE-Power methods are simple and their main computational cost is the evaluation of matrix-vector products. These characteristics often make them still feasible for computing PageRank when the damping factor α is not large.

In addition, it is interesting to mention that the Hessenberg-type method often needs more Mvp’s for convergence than both Arnoldi and A-Arnoldi, whereas the total CPU time of Hessenberg is still less. This is because the Hessenberg uses the cheap similarity transformations to reduce the large matrix into the Hessenberg form, whereas the latter two methods use expensive (weighted) unitary transformations.

5 Conclusions

In this paper, we proposed a novel approach for computing the PageRank problem. The proposed method has lower computational cost than both Arnoldi and A-Arnoldi to find the approximate PageRank vector; thus, it can afford to use higher dimensional Krylov subspaces. Extensive numerical experiments are reported to illustrate the efficiency of the proposed method also compared to other state-of-the-art matrix solvers for this problem class, especially when the damping factor is large. Hence, we conclude that the Hessenberg method as well as the Arnoldi and A-Arnoldi methods can be useful computational tools for practical large-scale PageRank computations.

Future research will focus on the theory of the Hessenberg process and the convergence of the Hessenberg-type algorithm is still required to be further analyzed. In addition, it is interesting to study how to optimize the restart number m and improve the convergence speed of our methods. Moreover, the proposed method can be extended to compute the more general Markov chains [8, 29], e.g., in ProteinRank and CiteRank.