Research on the time-varying mesh stiffness and dynamic characteristics of steel–POM gear pair with off-line meshing

Abstract

Plastic gears have been widely used in fields such as instruments, meters, and automotive electronics. In particular, metal–plastic gear pairs are commonly used in the low-speed stages of multi-stage gear transmissions to enhance load capacity and achieve lightweight design. However, due to the small elastic modulus and significant temperature sensitivity of plastic gears, off-line meshing phenomenon occurs in metal–plastic gear pairs during operation, which affects the overall system stiffness and dynamic behavior. Therefore, this study takes 45# steel-POM gear pair as the object of study, and considers the effect of temperature on the modulus of elasticity of the gear and the effect of out-of-line meshing on the time-varying stiffness of the gear pair , in which the 45# steel-POM gear pair refers to the combination of the steel and plastic gear pairs, with the pinion gear consisting of 45# steel gears, and the large gear made of POM gears. A lumped parameter method is used to establish a single-degree-of-freedom model of the gear transmission system, and the effect of load on the system’s dynamic behavior is investigated. Experimental validation shows that the stiffness varies linearly with the load, and the dynamic performance of the system deteriorates with increasing load. In the experimental study described in this article, as the load increased from 5 to 10 N m, the maximum dynamic transmission error increased by 62%. Under the same load, the system with consideration of off-line meshing exhibits better transmission accuracy compared to the one without consideration. Disregarding the dominant frequency of the system when there is no external meshing, the dominant frequency of the system increases by 1.4 times when considering external meshing. This study provides a theoretical basis for the design and transmission of plastic gears in the future.

1 Introduction

The steel–plastic gear pair, with the small gear made of 45# steel and the large gear made of POM, allows for the design of gears with equivalent lifetimes. However, the introduction of plastic gears reduces the stiffness of the gear system, thereby altering its dynamic performance. In the past, standards related to plastic gears, such as VDI2736, did not specifically mention ‘mesh stiffness.’ As the expanding range of applications for plastic gears, the mesh stiffness and dynamic performance of plastic gears have become increasingly important. Therefore, it is necessary to conduct in-depth research on the time-varying mesh stiffness (TVMS) and dynamic characteristics of steel–plastic gear pairs.

Existing research on plastic gears has covered various aspects, including temperature [1, 2], gear transmission [3,4,5,6], tooth surface wear [7,8,9], tooth surface damage [10, 11], load distribution [12,13,14], fatigue life [15, 16], etc. The time-varying mesh stiffness and nonlinear dynamics of gears have always been hot topics in the field of gear transmission. Currently, some researchers have studied the time-varying mesh stiffness and nonlinear dynamics. Jiang et al. [17] investigated the dynamic response of spur gears by considering the interaction of friction and vibration. The research results showed that the effects of vibration and sliding friction on gear dynamic response need to be considered. Meng et al. [18] calculated the time-varying mesh stiffness of gear pairs with different crack lengths and studied the influence of spalling at different widths, lengths, and positions on the time-varying mesh stiffness. Cao et al. [19] established a dynamic model for spur gear pairs with force-related mesh stiffness. Experimental results showed that this model has a wider range of applications compared to traditional models. Luo et al. [20] introduced the concept of thermal stiffness and investigated the modification of gear thermal tooth profiles. Ma et al. [21] considered the effects of delayed tooth contact, nonlinear contact stiffness, and gear profile modification and developed an improved analysis method applicable to gear pairs for determining time-varying mesh stiffness. Hasl et al. [22] employed the finite element method to consider the deformation of plastic gears and improved the calculation method of gear stiffness in the VDI 2736 standard when calculating the bending stress of plastic gears. Atanasiu et al. [23] obtained the time-varying mesh stiffness of a steel–plastic gear pair based on the principle of potential energy and established a dynamic model to analyze the dynamic characteristics of the steel–plastic helical gear pair. However, they did not consider the influence of load on gear stiffness. Muellner [24] used a quasi-static finite element method to determine the time-varying mesh stiffness of a plastic gear pair and analyzed the transmission error of the plastic gear pair.

In this study, we improve the stiffness calculation process of the steel–plastic gear pair by considering the meshing characteristics of plastic gears. Based on this, the dynamic characteristics of plastic gears are analyzed, providing a theoretical basis for the further design and application of plastic gears.

The following will be presented in four sections: the impact of temperature on the performance of plastic gears, the influence of external meshing on the time-varying meshing stiffness of steel–plastic gear pairs, the dynamic behavior of steel–plastic gear pairs, experimental validation, and conclusions.

2 Impact of temperature on plastic gear performance

The material properties of plastic gears are highly sensitive to temperature variations. Therefore, the Young's modulus of the POM material used in this study is selected based on the expected temperature, which depends on the concentrated load conditions [22]. The VDI 2736 guideline [25] provides a simple model for calculating the tooth root temperature and tooth flank temperature. According to Zorko et al. [26], the tooth root temperature is used as a substitute for gear temperature due to the very short flash temperature time. The tooth root temperature is defined by the following Eq. (1) [26]:

$$ \vartheta_{{{\text{Fu}}\beta }} = \vartheta_{0} + P \cdot \mu \cdot H_{V} \cdot \left( {\frac{{k_{{\vartheta ,{\text{Fu}}\beta }} }}{{b \cdot z \cdot \left( {v_{{\text{t}}} \cdot m_{{\text{n}}} } \right)^{0.75} }} + \frac{{R_{\lambda ,G} }}{{A_{G} }}} \right) \cdot E_{D}^{0.64} $$

(1)

where ϑ_Fuβ is root temperature, ϑ₀ is ambient temperature, P is nominal output power, μ is coefficient of friction, H_V is wear rate, k_ϑ,Fuβ is polymer gear heat transfer coefficient, b is tooth width, z is number of teeth, v_t is tangential velocity, m_n is normal module, R_λ,G is heat transfer resistance of the mechanism’s outer casing, A_G is heat dissipation area of the mechanism’s outer casing, and E_D is gear contact time relative to 10 min.

According to the VDI2736, some parameters have the following values: $\vartheta_{0} = 20\;^{ \circ } {\text{C}}$, $\mu = 0.2$ (for no lubrication conditions), $H_{V} = 0.1494$ (Calculated based on the geometric dimensions of the gear), $k_{{\vartheta ,{\text{Fu}}\beta }} = 900\frac{{{\text{K}} \cdot \left( {\frac{{\text{m}}}{{\text{s}}}} \right)^{0.75} \cdot {\text{mm}}^{1.75} }}{{\text{W}}}$, $b = 20\;{\text{mm}}$, z = 3, $m_{{\text{n}}} = 3\;{\text{mm}}$, $R_{\lambda ,G} = 0$, and $E_{D} = 1$. $v_{t}$ and $P$ are calculated depending on the load condition, and A_G is the heat-dissipating surface of the mechanism housing. The selected gear parameters are listed in Table 1.

Table 1 Parameters of steel–plastic gear pair

In the absence of experimental parameters, this article establishes the relationship between the Young’s modulus (E) of POM material and temperature using the empirical formula $E_{T}$ = $E_{0}$ − α($T_{a} - T_{0}$), as shown in Eq. (2). Here, α represents the temperature coefficient of the POM material, with a value of 0.0246. $T_{0}$ is the reference temperature set at 20 °C, and $E_{0}$ represents the Young's modulus of the material at room temperature [27]

$$ E_{{\text{T}}} = - 0.0246T_{a} + 3.494 $$

(2)

where $T_{a}$ represents the temperature of the material, and $E_{{\text{T}}}$ represents the Young's modulus of the material at this temperature. Based on Eqs. (1) and (2), the Young's modulus of POM under different load conditions can be obtained, as shown in Fig. 1.

Fig. 1

Young’s modulus of POM under different load conditions

3 Influence of off-line meshing on the time-varying meshing stiffness of steel–plastic gear pair

3.1 Contact ratio of steel–plastic gear pairs

Plastic gears exhibit unique phenomena of premature and delayed contact during the meshing process, which has been confirmed in previous studies [28]. Yelle et al. [29] proposed an iterative method to calculate the actual contact ratio of plastic gears. Jabbour et al. [30] used the Yelle method to calculate the actual contact ratio of steel–plastic helical gear pairs. Considering the relative complexity of the iterative method, Koffi et al. [31] proposed an empirical formula based on the iterative method to calculate the actual contact ratio of plastic gears. Subsequent studies [32,33,34,35] have largely relied on this empirical formula.

The simplified line of action for plastic gears is depicted in Fig. 2. The node is denoted as O, and AB represents the theoretical line of action. The theoretical initial contact point (TIP) and theoretical final contact point (TFP) of the steel–plastic gear pair are represented by points A and B, respectively. Assuming that the actual initial contact point (RIP) and actual final contact point (RFP) of the steel–plastic gear pair are A′ and B′, respectively. According to the method proposed by Koffi et al. [31], the actual meshing points are projected along the direction of the line AB, resulting in two points A* and B*. The actual contact ratio is defined as the ratio of the length of A*B* to the circular pitch.

Fig. 2

The actual line of action of a steel–plastic gear pair

Establish a Cartesian coordinate system with the origin at point O, the positive x-axis along AB, and the y-axis passing through point O and perpendicular to AB. In this coordinate system, we obtain the following equation:

$$ \left| {OA} \right| = \frac{{z_{2} }}{2\pi \cos \alpha }\left[ {\sqrt {\left( {1 + 2\frac{{h_{a}^{*} }}{{z_{2} }}} \right)^{2} - {\text{cos}}^{2} \alpha } - \left( {{\text{cos}}^{2} \alpha } \right)\tan \alpha_{0} } \right] $$

(3)

$$ \left| {OB} \right| = \frac{{z_{1} }}{2\pi \cos \alpha }\left[ {\sqrt {\left( {1 + 2\frac{{h_{a}^{*} }}{{z_{1} }}} \right)^{2} - {\text{cos}}^{2} \alpha } - \left( {{\text{cos}}^{2} \alpha } \right)\tan \alpha_{0} } \right]. $$

(4)

In Eqs. (3) and (4), |OA| and |OB| represent the distances between points A and O, and between points B and O, respectively. $z_{1}$ and $z_{2}$ represent the numbers of teeth on the small gear and the large gear, respectively. $h_{a}^{*}$ is the addendum coefficient, $\alpha$ and $\alpha_{0}$ represent the pressure angle and the working pressure angle, respectively. Based on the research conducted by Bravo et al. [36], the following results can be obtained:

$$ \Delta s = 0.131E_{2}^{ - 0.34} \left( {z_{2} \sqrt {wP\cos \alpha } } \right)^{0.7} \left( {\frac{{z_{2} }}{{z_{1} }}} \right)^{ - 0.55} $$

(5)

It is pointed out in Mijiyawa that for steel–plastic gear pair [34]

$$ \Delta s_{i} = \Delta s\left( {\frac{{E_{{{\text{T}}1}} }}{{E_{{{\text{T}}2}} }}} \right)^{\tau } P_{n} $$

(6)

where $\Delta s$ is an intermediate variable in Eqs. (5) and (6). $E_{{{\text{T}}1}}$ and $E_{{{\text{T}}2}}$ represent the Young’s modulus of the small gear and the large gear, respectively, at different temperature w is the unit load, P represents the pitch diameter (P = 25.4/module), $P_{n} { }$ is the circular pitch, i is a subscript, and τ is an exponent. Specifically, when i = 2, τ =  − 0.11, and when i = 1, τ =  − 0.05. If the Young's modulus of the small gear ${ }E_{{{\text{T}}1}}$ is larger than that of the large gear $E_{{{\text{T}}2}}$, i.e., $E_{{{\text{T}}1}}$ > $E_{{{\text{T}}2}}$, Eq. (6) remains unchanged. Otherwise, if $E_{{{\text{T}}1}}$ and $E_{{{\text{T}}2}}$ need to be modified in Eq. (6). The specific lengths of Δs1 and Δs2 can be determined according to Eq. (5) and by referring to Fig. 4, which can then be used to obtain the actual contact ratio.

3.2 Characteristics of off-line meshing

The key to calculating the time-varying mesh stiffness of steel–plastic gear pairs is to determine the mesh stiffness during the phases of premature contact and delayed contact Therefore, it is important to accurately determine the actual meshing positions of RIP and RFP, which depend on the real contact ratio. As shown in Fig. 3, it is reasonable to assume that during the phase of premature contact, the tooth tip of the large gear always contacts the tooth root of the small gear.

Fig. 3

Premature contact diagram of steel–plastic gear pair

In Fig. 3, $r_{b1}$ and $r_{b2}$ represent the radius of the base circle of the pinion and wheel, $T_{1}$ and $T_{2}$ represent the input and output torques acting on the pinion and wheel, $w_{1}$ and $w_{2}$ are the angular velocities of the pinion and wheel, and $r_{a1}$ and $r_{a2}$ represent the radius of the addendum circle of the pinion and wheel, respectively. In the PTC phase, the TIP is point $A$, assuming that the RIP is point A′. The wheel maintains contact with the pinion at the top of the tooth during the whole PTC phase. The rotation angle of the wheel is $\gamma$, the rotation angle of the pinion is $\theta$, and point $N$ is the reverse point of point $A$. Point $A^{*}$ is the projection point of point A′ along the direction of the line of action. The whole PTC phase can be approximately regarded as the tooth tip of the wheel sliding in the A′N section of the profile of the pinion. According to the geometric relationship shown in Fig. 3, Eq. (7) can be obtained as

$$ \left\{ {\begin{array}{*{20}l} {\beta = \arcsin \left[ {s_{2} \frac{{\sin \left( {\frac{\pi }{2} + \alpha_{0} } \right)}}{{r_{a2} }}} \right]} \hfill \\ {\gamma \cdot r_{a2} = \Delta s2/\cos \left( {\angle A^{*} AA^{\prime } } \right)} \hfill \\ {\angle A^{*} AA^{\prime } = \pi - \angle OAH - \angle A^{\prime } AH} \hfill \\ {\angle OAH = \pi - \beta - \left( {\alpha_{0} + \frac{\pi }{2}} \right)} \hfill \\ {\angle A^{\prime } AH = \frac{\pi - \gamma }{2}} \hfill \\ \end{array} } \right. $$

(7)

where $s_{2} = \left| {OA} \right|$, which can be obtained from Eq. (3),$\Delta s2$ can be obtained from Eq. (6), $r_{a2}$ is the radius of the addendum circle of the gear, and $\alpha_{0}$ is the working pressure angle, the other parameters are shown in Fig. 6. According to Eq. (7), the rotation angle of the wheel ${ }\gamma$ can be obtained. According to the relationship of the transmission ratio $i$, the rotation angle of the pinion ${ }\theta$ can be obtained from Eq. (8).

$$ \theta \approx \gamma \times i $$

(8)

The position of RIP on the smaller gear can be determined based on the value of θ and the location of point A.

In Fig. 4, we assume that during the period of delayed contact, the tooth tip of the smaller gear always contacts the tooth root of the larger gear. As shown in Fig. 6, during the delayed contact phase, TFP represents point B, and we assume RFP represents point B'. Throughout the delayed contact phase, the tooth tip of the smaller gear remains in contact with the tooth root of the larger gear. The rotation angle of the larger gear is denoted as $\gamma_{1}$, and the rotation angle of the smaller gear is denoted as $\theta_{1}$. Point K represents the reverse point of B. B* is the projection of B' along the action line. The entire delayed contact phase can be approximately seen as sliding of the tooth tip of the smaller gear on the profile B'K of the larger gear. Based on the geometric relationships shown in Fig. 4, Eq. (9) can be obtained.

$$ \left\{ {\begin{array}{*{20}l} {\beta_{1} = \arcsin \left[ {s_{1} \frac{{\sin \left( {\frac{\pi }{2} + \alpha_{0} } \right)}}{{r_{a1} }}} \right]} \hfill \\ {\theta_{1} \cdot r_{a1} = \Delta s1/\cos \left( {\angle B^{*} BB^{\prime } } \right)} \hfill \\ {\angle B^{*} BB^{\prime } = \pi - \angle OBP - \angle B^{\prime } BP} \hfill \\ {\angle OBP = \pi - \beta_{1} - \left( {\alpha_{0} + \frac{\pi }{2}} \right)} \hfill \\ {\angle B^{\prime } BP = \frac{{\pi - \theta_{1} }}{2}} \hfill \\ \end{array} } \right. $$

(9)

where $s_{1} = \left| {OB} \right|$,which can be obtained from Eq. (4), $\Delta s1$ can be obtained from Eq. (6), $r_{a1}$ is the radius of the addendum circle of the pinion, and $\alpha_{0}$ is the working pressure angle, the other parameters are shown in Fig. 4. According to Eq. (9), the rotation angle of the pinion ${ }\theta_{1}$ can be obtained. According to the relationship of the transmission ratio $i$, the rotation angle of the wheel ${ }\gamma_{1}$ can be obtained from Eq. (10).

$$ \gamma_{1} \approx \theta_{1} /i $$

(10)

Fig. 4

Extended contact diagram of steel–plastic gear pair

The position of RFP on the larger gear can be determined based on the value of $\gamma_{1}$ and the location of point B.

3.3 Calculating of the TVMS

In the realm of gear transmission, time-varying mesh stiffness refers to the phenomenon where the stiffness at the point of gear meshing undergoes changes over time. TVMS is an abbreviation for time-varying meshing stiffness. When the potential energy method is used to solve the TVMS, the gear tooth is regarded as a cantilever beam, as shown in Fig. 5. The potential energy $U$ in the meshing gear includes the bending potential energy $U_{{\text{b}}}$, shear potential energy $U_{{\text{s}}}$, compression potential energy $U_{a}$, Hertz potential energy $U_{{\text{h}}}$, and gear body potential energy $U_{f}$. The stiffness corresponding to the potential energy of each part is the Hertzian contact stiffness $K_{{\text{h}}}$, bending stiffness $K_{{\text{b}}}$, shear stiffness $K_{{\text{s}}}$, compression stiffness $K_{a}$, and gear body stiffness, respectively. $K_{f}$. According to the knowledge of material mechanics [37]:

$$ U = U_{{\text{b}}} + U_{{\text{s}}} + U_{a} + U_{{\text{h}}} + U_{f} = \frac{{F^{2} }}{2}\left( {\frac{1}{{K_{{\text{h}}} }} + \frac{1}{{K_{{{\text{b}}1}} }} + \frac{1}{{K_{{{\text{b}}2}} }} + \frac{1}{{K_{a1} }} + \frac{1}{{K_{a2} }} + \frac{1}{{K_{{{\text{s}}1}} }} + \frac{1}{{K_{{{\text{s}}2}} }} + \frac{1}{{K_{f1} }} + \frac{1}{{K_{f2} }}} \right) $$

(11)

where $F$ is the force at the meshing point. Subscripts 1 and 2 represent the pinion and wheel, respectively. The total meshing stiffness of a pair of gears is obtained as follows:

$$ K = \frac{1}{{\frac{1}{{K_{{\text{h}}} }} + \frac{1}{{K_{{{\text{b}}1}} }} + \frac{1}{{K_{{{\text{b}}2}} }} + \frac{1}{{K_{a1} }} + \frac{1}{{K_{a2} }} + \frac{1}{{K_{{{\text{s}}1}} }} + \frac{1}{{K_{{{\text{s}}2}} }} + \frac{1}{{K_{f1} }} + \frac{1}{{K_{f2} }}}}. $$

(12)

Fig. 5

Force on a single tooth of the gear

The single-tooth stiffness in Eq. (12) can be translated and superposed according to the contact ratio. For gears with a coincidence ratio not exceeding 2, the stiffness of the double-tooth meshing region can be determined by Eq. (13).The meshing stiffness of the double-tooth area can be obtained as follows:

$$ K_{{{\text{double}}}} = \mathop \sum \limits_{j = 1}^{2} \frac{1}{{\frac{1}{{K_{{{\text{h}},j}} }} + \frac{1}{{K_{{{\text{b}}1,j}} }} + \frac{1}{{K_{{{\text{s}}1,j}} }} + \frac{1}{{K_{a1,j} }} + \frac{1}{{K_{f1,j} }} + \frac{1}{{K_{{{\text{b}}2,j}} }} + \frac{1}{{K_{{{\text{s}}2,j}} }} + \frac{1}{{K_{a2,j} }} + \frac{1}{{K_{f2,j} }}}} $$

(13)

where ${ }j = 1$ denotes the first pair of gears that was meshed, and $j = 2$ denotes the second pair of gears that was meshed. According to Yang, the contact stiffness of two types of gears with different materials can be obtained as

$$ K_{{\text{h}}} = \frac{\pi B}{{2E^{\prime } }} $$

(14)

where

$$ E^{\prime } = \frac{{1 - v_{1}^{2} }}{{E_{1} }} + \frac{{1 - v_{2}^{2} }}{{E_{2} }} $$

(15)

In Eqs. (14) and (15), B is the tooth width, E′ is the comprehensive elastic modulus,${ }E_{1}$ and $E_{2}$ represent the elastic modulus of the pinion and wheel, and $v_{1}$ and $v_{2}$ represent the Poisson’s ratio of the pinion and wheel, respectively. The gear body stiffness $K_{f}$ can be obtained according to Sainsot [38]:

$$ K_{f} = \frac{1}{{\frac{{\cos^{2} \alpha_{B} }}{EL}\left\{ {L^{*} \left( {\frac{{u_{f} }}{{s_{f} }}} \right)^{2} + M^{*} \left( {\frac{{u_{f} }}{{s_{f} }}} \right)^{2} + P^{*} \left( {1 + Q^{*} /\tan^{2} \alpha_{B} } \right)} \right\}}} $$

(16)

where $\alpha_{B}$, $u_{f}$, and $s_{f}$ are the geometric parameters of the tooth, as shown in Fig. 5. $L^{*}$, $M^{*}$, $P^{*}$, and $Q^{*}$ are calculated by Eq. (13)

$$ X_{i}^{*} \left( {h_{fi} ,\theta_{f} } \right) = A_{i} /\theta_{f}^{2} + B_{i} /h_{fi}^{2} + C_{i} h_{fi} /\theta_{f} + D_{i} /\theta_{f} + E_{i} h_{fi} + F_{i} $$

(17)

where

$$ h_{fi} = r_{f} /r_{{{\text{int}}}} $$

(18)

In Eqs. (13) and (14), $r_{f}$ is the radius of the root circle, $r_{{{\text{int}}}}$ is the radius of the shaft, and $\theta_{f}$ is the angle between the x-axis and the connection between the gear center and points $D$. $A_{i}$, $B_{i}$, $C_{i}$, $D_{i}$, $E_{i}$, $F_{i}$, which can be obtained as listed in Table 2.

Table 2 Coefficient values in Eq. (16)

The compressive potential energy, shear potential energy and bending potential energy of the gear are obtained by formulas (19)–(21), respectively (Fig. 6).

$$ U_{a} = \mathop \int \limits_{{x_{D} }}^{{x_{B} }} \frac{{F_{x}^{2} }}{{2EA_{x} }}{\text{d}}x $$

(19)

$$ U_{s} = \mathop \int \limits_{{x_{D} }}^{{x_{B} }} \frac{{1.2F_{y}^{2} }}{{2GA_{x} }}{\text{d}}x $$

(20)

$$ U_{b} = \mathop \int \limits_{{x_{D} }}^{{x_{B} }} \frac{{M^{2} }}{{2EI_{x} }}{\text{d}}x $$

(21)

$$ \left\{ {\begin{array}{*{20}l} {F_{y} = F_{n} \cdot \cos \alpha_{B} } \hfill \\ {F_{x} = F_{n} \cdot \sin \alpha_{B} } \hfill \\ {I_{x} = \frac{2}{3}y^{3} b} \hfill \\ {A_{x} = 2yb} \hfill \\ {M = F_{y} \left( {x_{B} - x} \right) - F_{x} \cdot y_{B} } \hfill \\ \end{array} } \right. $$

(22)

Fig. 6

The schematic diagram of solving TVMS considering the ETC and PTC effects

In Eqs. (19)–(22), $F_{{\text{n}}}$ is the normal load between meshing teeth, $F_{y}$ is the component of the load $F_{n}$ in the y-direction, $F_{x}$ is the component of the load $F_{n}$ in the $x$-direction, $E$ is the elasticity modulus of the material, $G$ is the sheer modulus of the material, $A_{x}$ is the cross-sectional area, $I_{x}$ is the second moment of area, $M$ is the input torque, $\alpha_{B} { }$ is the pressure angle at the meshing point, $b$ is the tooth width, $y$ is the distance between the points on the tooth profile and x-axis, ${ }y_{B}$ is the distance between meshing point $B$ and x-axis, $x$ is the coordinate along the tooth center line from the gear rotation center, and $x_{D}$ and $x_{B}$ are the coordinates along the tooth centerline from the gear rotation center corresponding to the root circle point $D$ and meshing point $B$, respectively.

3.4 TVMS of steel–plastic gear pair considering the off-line meshing

The positions of the RIP and RFP were determined by the method mentioned above. According to the principle of the potential energy method, if the extension of the contact path effect caused by tooth deformation is not considered, then the meshing stiffness will change suddenly when single and double teeth alternate. In fact, considering the ETC and PTC effects, the meshing stiffness is no longer abrupt, but gradual during the period of alternating single and double teeth. Therefore, it is assumed that the meshing stiffness decreased and increased linearly during the period of PTC and ETC, respectively. Figure 8 shows that if the coordinates of $M$, $N$, $V$, and $U$ are determined, then the meshing stiffness curve during the period of PTC and ETC can be determined. Points $M$ and $V$ represent the highest and lowest points of double-tooth contact, respectively, which means that the values of $t1$, $t4$, $k1$, and $k4$ can be determined by the potential energy method. The values of $\theta$ and $\gamma_{1}$ were obtained in the previous section. Then, the values of $t2$ and $t3$ can be obtained from Eq. (23). t1 refers to the angle through which the gear rotates to reach the highest point during double-tooth delayed contact, t2 denotes the angle through which the gear rotates to reach the lowest point during double-tooth delayed contact, t3 indicates the angle through which the gear rotates to reach the highest point during double-tooth advance contact, and t4 represents the angle through which the gear rotates to reach the lowest point during double-tooth advance contact; λ1 signifies the rate of change of stiffness with respect to the angle during the gear's movement from the highest to the lowest point in advance contact, and λ2 represents the rate of change of stiffness with respect to the angle during the gear's movement from the highest to the lowest point in delayed contact. According to the principle of the potential energy method, the values of $k2$ and $k3$ can be determined by $t2$ and $t3$. Then, the slope of the stiffness curve during the period of PTC and ETC can be obtained by Eq. (24). According to the slope of $\lambda$ and the coordinates of point $M$, the analytical formula for the stiffness curve of the ETC can be determined. Similarly, the analytical formula for the stiffness curve of PTC can be obtained by $\lambda 1$ and point $V$.

$$ \left\{ { \begin{array}{*{20}l} { t2 = t1 + \gamma 1} \hfill \\ {t3 = t4 - \theta } \hfill \\ \end{array} } \right. $$

(23)

$$ \left\{ {\begin{array}{*{20}l} {\lambda = \frac{k2 - k1}{{t2 - t1}}} \hfill \\ {\lambda 1 = \frac{k4 - k3}{{t4 - t3}}} \hfill \\ \end{array} } \right. $$

(24)

3.5 Verification of TVMS by finite element method

The multitooth contact model was established using HyperMesh software [39].

The process of creating grid is as shown in Fig. 7.

Fig. 7

The process of creating grid

The mesh was refined in the contact area and fixed constraints were added to the ring gear of the wheel. A rigid coupling was established between the ring gear of the pinion and the rotating center, and torque was added. The finite element mesh model created through HyperMesh 14.0.is shown in Fig. 8.

Fig. 8

The finite element model of the steel–plastic gear pair

Figure 9 shows the simulation results of the proposed method and the finite element method. The meshing stiffness values with different methods under different loads were compared, and the results are shown in Table 3. It can be seen from Table 3 that compared with the finite element method, the error is larger at a rolling angle of 7.8° (the position of the highest point of double-tooth contact). In Fig. 9, the finite element method results show that the ETC period is longer, and starts before the theoretical double-tooth end-point, which is the main reason for the error. The average error of the simulation is 6%. Considering the influence of meshing accuracy and contact parameter settings on the finite element method results, it can be considered that the method proposed in this paper is credible.

Fig. 9

Comparison of TVMS obtained by different methods

Table 3 The relative error of different methods

3.6 Influence of load on TVMS of steel–plastic gear pair

The meshing stiffness values obtained with different methods under different loads were compared. It can be seen from Fig. 10 that the change in stiffness is basically linear with the load, i.e., as the load increased, the meshing stiffness decreased. This can be attributed to the reduction in the Young’s modulus, which also indirectly shows that temperature is the main factor affecting the meshing stiffness of the plastic gear. Compared with the potential energy method, the average stiffness considering PTC and ETC effects is larger. In addition, under a certain load, the mesh stiffness at the lowest point of single-tooth contact calculated with the proposed method is higher than that of the potential energy method. The mesh stiffness at the highest point of single-tooth contact calculated with the proposed method is lower than that of the potential energy method. The main reason for this is the increase in the double-tooth meshing area and the decrease in the single-tooth meshing area caused by the large deformation of the plastic gear under load.

Fig. 10

Comparison of meshing stiffness values with different methods under different loads

The influence of the load on the meshing stiffness is studied, and the TVMS under different loads is obtained, as shown in Fig. 11. Because the stiffness of the steel gear is two orders of magnitude different from that of the plastic gear, the TVMS of the steel–plastic gear pair is mainly affected by the stiffness of the plastic gear. It can be seen that with increased load, the single-tooth meshing area is shortened and the double-tooth meshing area is extended. In the PTC and ETC phases, the change in gear stiffness is relatively steep. The meshing stiffness of the whole gear pair decreased with the increase in load. The increase in transmission load leads to an increase in temperature, which reduces the elastic modulus of the plastic material. HPSTC refers to the calculated stiffness at the highest point of double-tooth contact, while LPSTC represents the calculated stiffness at the lowest point of double-tooth contact.

Fig. 11

TVMS of steel–plastic gear pair under different loads

4 Dynamic characteristics of steel–plastic gear pair

4.1 Dynamic characteristics of gear pair

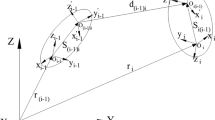
The stiffness of the gear shaft and bearing is much larger than that of the plastic gear body. Therefore, this study assumes that the shaft is rigid and the effect of friction is ignored. The change in gear backlash caused by the rise of tooth surface temperature was also considered in the dynamic model. The single-degree-of-freedom dynamic model of the steel–plastic gear pair was established by the lumped parameter method, as shown in Fig. 12.

Fig. 12

Single-degree-of-freedom dynamic model of steel–plastic gear pair

In the establishment of gear models, employing the lumped parameter method offers several potential advantages:

1. precision, 2. flexibility, 3. model interpretability, 4. data fitting and prediction, and 5. parameter optimization.

According to Newton's second law, Eq. (25) can be obtained as

$$ \left\{ {\begin{array}{*{20}l} {I_{1} \ddot{\theta }_{1} + r_{b1} c_{m} \left( {r_{b1} \dot{\theta }_{1} - r_{b2} \dot{\theta }_{2} - \mathop {e\left( \tau \right)}\limits^{ \cdot } } \right) + r_{b1} k\left( \tau \right)f\left( {r_{b1} \theta_{1} - r_{b2} \theta_{2} - e\left( \tau \right)} \right) = T_{1} } \hfill \\ {I_{2} \ddot{\theta }_{2} - r_{b2} c_{m} \left( {r_{b1} \dot{\theta }_{1} - r_{b2} \dot{\theta }_{2} - \mathop {e\left( \tau \right)}\limits^{ \cdot } } \right) - r_{b2} k\left( \tau \right)f\left( {r_{b1} \theta_{1} - r_{b2} \theta_{2} - e\left( \tau \right)} \right) = - T_{2} } \hfill \\ \end{array} } \right. $$

(25)

where $I_{1}$ and $I_{2}$ represent the moment of inertia of the pinion and wheel, $r_{b1}$ and $r_{b2}$ represent the radius of the base circle of the pinion and wheel, and $\theta_{1}$ and $\theta_{2}$ represent the rotation angles of the pinion and the wheel, respectively. $e\left( \tau \right)$ represents the static transmission error of the gear pair, $k\left( \tau \right)$ represents the TVMS of gear pair, $c_{m}$ is the meshing damping of the gear pair, and $T_{1}$ and $T_{2}$ represent the input and output torque acting on the pinion and the wheel, respectively. $f$ is the nonlinear function of the gear backlash. Considering the influence of temperature on the backlash, the actual meshing backlash $b_{{{\text{act}}}}$ of the gear pair is the sum of the designed backlash $b$ of the gear pair and the backlash increment $\delta b$ caused by the temperature rise.$\delta b$ can be calculated using Eq. (26) according to Chen et al. [39]

$$ \delta b = \frac{1}{2}\left( {\Delta T\lambda_{1} \left( {S_{b1} + r_{1} \sin \alpha_{b} } \right) + \Delta T\lambda_{2} \left( {S_{b2} + r_{2} \sin \alpha_{b} } \right)} \right) $$

(26)

where $\Delta T$ represents the temperature rise of the tooth surface, which can be obtained by Eq. (1). $r_{1}$ and $r_{2}$ represent the pitch radius of the pinion and wheel, $\lambda_{1}$ and $\lambda_{2}$ are the thermal expansion coefficients of steel and plastic, and $S_{b1}$ and $S_{b2}$ represent the thickness at the pitch circle of the pinion and wheel after thermal deformation, respectively. $\alpha_{b}$ is the working pressure angle of the gear pair after thermal deformation. The detailed calculation method of $\alpha_{b}$, $S_{b1}$, and $S_{b1}$ was provided by Chen et al. By introducing the dynamic transmission error $q\left( \tau \right) = r_{b1} \theta_{1} - r_{b2} \theta_{2} - e\left( \tau \right)$, Eq. (27) can be transformed into

$$ m_{e} \mathop {q\left( \tau \right)}\limits^{ \cdot \cdot } + c_{m} \mathop {q\left( \tau \right)}\limits^{ \cdot } + k\left( \tau \right)f\left( {q\left( \tau \right)} \right) = F_{m} + F_{e\left( \tau \right)} $$

(27)

where $m_{e} = \frac{{I_{1} I_{2} }}{{I_{2} r_{b1}^{2} + I_{1} r_{b2}^{2} }}$, $F_{e\left( \tau \right)} = - m_{e} \mathop {e\left( t \right)}\limits^{ \cdot \cdot }$, $c_{m} = 2\xi \sqrt {k_{m} c_{m} }$, $k_{m}$ is the average meshing stiffness of the steel–plastic gear pair under different loads shown in Fig. 12, $\xi$ is the damping ratio, and $\mathop {q\left( \tau \right)}\limits^{ \cdot }$ and $\mathop { q\left( \tau \right)}\limits^{ \cdot \cdot }$ are the first derivative and second derivative of $q$ to $\tau$, respectively. $\xi$ of the steel–plastic gear pair is taken as 0.3, and $F_{m}$ is the static meshing force of the gear $F_{m} = \frac{{T_{1} }}{{r_{b1} }} = \frac{{T_{2} }}{{r_{b2} }}$.

According to Yang et al., given the nominal dimension $b_{c}$, order $x = q/b_{c}$, $t = w_{n} \tau$, $\zeta = c_{m} /\left( {2m_{e} w_{n} } \right)$, $\Omega = w/w_{n}$, $w_{n} = \sqrt {k_{m} /m_{e} }$, $P_{e} = F_{m} /\left( {b_{c} m_{e} w_{n}^{2} } \right)$, $P_{h} = \left( {E\Omega^{2} \cos \left( {\Omega t} \right)} \right)/b_{c}$, and $P_{O} = P_{e} + P_{h}$, where $E$ is the error amplitude, according to Yang et al. The meshing stiffness is expanded by Fourier series to obtain Eq. (28).

$$ k\left( t \right) = \mathop \sum \limits_{j = 1}^{n} \left( {k_{2j - 1} \cos \left( {j\Omega t} \right) + k_{2j} \sin \left( {j\Omega t} \right)} \right) $$

(28)

Let $\varphi \left( t \right) = k\left( t \right)/\left( {b_{c} m_{e} w_{n}^{2} } \right)$, and the nonlinear function of the gear backlash $f$ can be transformed into Eq. (29).

$$ f\left( x \right) = \left\{ {\begin{array}{*{20}l} {x + \left( {1 + \frac{\delta b}{{b_{c} }}} \right)} \hfill & {x < - \left( {1 + \frac{\delta b}{{b_{c} }}} \right)} \hfill \\ 0 \hfill & { - \left( {1 + \frac{\delta b}{{b_{c} }}} \right) \le x \le 1 + \frac{\delta b}{{b_{c} }}} \hfill \\ {x - \left( {1 + \frac{\delta b}{{b_{c} }}} \right)} \hfill & {x > 1 + \frac{\delta b}{{b_{c} }}} \hfill \\ \end{array} } \right. $$

(29)

In this case, Eq. (27) can be simplified as

$$ \mathop x\limits^{ \cdot \cdot } + 2\zeta \dot{x} + \varphi \left( t \right)f\left( x \right) = P_{O} $$

(30)

where $t$ is the nondimensional time, $x$ is the nondimensional relative displacement, and $\dot{x}$ and $\mathop x\limits^{ \cdot \cdot }$ are the first derivative and second derivative of $x$ to $t$, respectively.

4.2 Influence of load on dynamic characteristics of steel–plastic gear pair

For metal gears, it is generally considered that the change in load will not affect the meshing stiffness of the gear pair; therefore, loads generally affect the dynamic characteristics of the system as external inputs. However, the stiffness of the plastic gear varies under different loads; hence, the internal excitation of the gear system also changes, which affects the dynamic performance of the system. According to the dynamic model established above, the steel–plastic gear pair was selected as shown in Table 1, and the fourth-order Runge–Kutta method was used to solve the system dynamic equations.

Utilizing the fourth-order Runge–Kutta Method for solving dynamic equations offers the following advantages:

1. higher accuracy, 2. versatility, 3. programmability, and 4. numerical stability.

The pinion speed used in the simulation is 800 r/min. Opting for a rotational speed of 800 revolutions per minute (rpm) ensures a smoother meshing interaction between the small and large gears, thereby enhancing the precision and stability of the results. The theoretical contact ratio of steel–plastic gear pair is 1.6535. According to the relationship between the load and contact ratio, if the load is too large, then the real contact ratio of the steel–plastic gear pair will be larger than 2, which will significantly affect the mesh stiffness and dynamic performance of the gear pair. Therefore, this study only considered the case in which the real contact ratio is less than 2. The case of a torque T of 20 N m was selected to compare the dynamic response when considering and ignoring the ETC and PTC. The numerical analysis results are shown in Fig. 13.

Fig. 13

Comparison of dynamic response at T = 20 N m

Figure 13i, ii show that under the same condition, both the relative displacement and acceleration using the potential energy method are larger than those of the proposed method. To further analyze the vibration response of the system after considering the PTC and ETC, we performed a Fourier transform on the time domain signal. Figure 13iii, iv shows the Fourier transform results of the displacement signal in (iii). It can be seen that regardless of the method used, the meshing frequency (f_m) is the dominant frequency. However, considering the effects of PTC and ETC, the amplitudes at 2 f_m, 2 f_m, and 6 f_m are larger than those of the potential energy method, while the amplitudes at other frequencies are relatively small.

The fast Fourier transform spectrum of acceleration is shown in Fig. 13iv. Considering the effects of PTC and ETC, the dominant frequency of acceleration changed from 8 f_m to 6 f_m, and the maximum amplitude is much smaller than that of the potential energy method, similar to the displacement. The acceleration amplitudes at 2 f_m, 2 f_m, and 6 f_m are larger than those of the potential energy method.

Considering the ETC and PTC, the influence of the load on the dynamic performance of the system was studied. As shown in Figs. 14 and 15, the dynamic performance of the system deteriorated with the increase in torque, and both displacement and acceleration increased with the increase in load. To further explore the effect of load on the vibration characteristics of the system, we calculated the root-mean-square (RMS) of different signals under different loads. Figure 16 shows that regardless of the load applied, when considering the influence of PTC and ETC, the RMS of both the displacement and acceleration are smaller than that of the potential energy method; this phenomenon became more evident with the increase in load. To observe the change of each index relative to the potential energy method, this study used the percentage form to observe the change of the statistical index with load, which is defined as Eq. (31).

$$ r_{{{\text{RMS}}}} = \left| {\frac{{{\text{RMS}}_{e} - {\text{RMS}}_{p} }}{{{\text{RMS}}_{p} }}} \right| \times 100{\text{\% }} $$

(31)

where ${\text{RMS}}_{e}$ represents the RMS of the signal considering the effects of ETC and PTC, ${\text{RMS}}_{p}$ represents the RMS of the signal obtained by the potential energy method, and $r_{{{\text{RMS}}}}$ is the relative change ratio of the RMS. The calculation results are shown in Fig. 17. It can be seen that with increased load, the relative change rate of the RMS of acceleration and displacement increased, with a more obvious increase in the relative change rate of the RMS of acceleration. This shows that with the increase in load, the fluctuations of acceleration and displacement are relatively small compared with the potential energy method. Compared with the potential energy method, the dynamic model considering PTC and ETC effects has more obvious advantages in terms of dynamic performance under higher loads.

Fig. 14

The nondimensional displacement under different torques

Fig. 15

The nondimensional acceleration under different torques

Fig. 16

The value of RMS under different torques with different methods

Fig. 17

The calculation results of relative change ratio about RMS

In general, it can be seen that compared with the potential energy method, the stiffness calculation method proposed in this study can improve the dynamic performance of the steel–plastic gear pair. Moreover, with the increase in the transmission load, the dynamic performance considering the effects of ETC and PTC is superior, and the advantages are more evident under higher loads.

5 Experimental verification

To further investigate the dynamic characteristics of steel–plastic gear pairs, this study conducted dynamic experiments on the gear pairs. Acceleration signals of the gear system were measured under different torque conditions. Additionally, the angular displacement of the master and slave gears was extracted for subsequent analysis of dynamic transmission errors.

5.1 Test bench equipment and composition

The geometric parameters of the gear used in the dynamic experiments were based on the aforementioned Table 1. The physical representation of the steel–plastic gear pair used in the experiments can be referred to in Fig. 18. Specifically, the small gear was made of steel with a blackened surface treatment, while the large gear was made of POM (Polyoxymethylene), a type of plastic material commonly used for gears.

Fig. 18

Steel–plastic gear pair for testing

The main equipment used in the experiment includes: the test steel–plastic gear pair, AC servo motor and servo drive, servo reducer, incremental encoder, torque-speed meter, acceleration sensor, magnetic powder brake and tension controller, integrated data acquisition system, and coupling, among others. The key parameters of the main equipment can be referenced in Table 4.

Table 4 Main equipment parameters

The composition of the gear dynamic test rig in this study is shown in Fig. 19. To achieve precise speed control and improve the accuracy of the experiment, a precision AC servo motor is employed. The motor is controlled by a servo drive through a PLC system. To increase the input torque, a servo reducer is added at the input end. The magnetic powder brake is controlled by a tension controller to provide load. Each input and output shaft is connected to a torque-speed meter for real-time measurement of the input and output torques of the gear pair. Two encoders are connected to the gear shafts to measure the angular displacement of the master and slave gears for calculating the dynamic transmission error. The gear pair is fixed on bearing supports using bearings. Acceleration sensors are arranged in predetermined directions to measure the system's acceleration signals. To ensure uniformity in the time domain for all measured physical quantities, all sensor data are collected by the same integrated data acquisition system.

Fig. 19

Gear testing experimental setup. 1. Magnetic powder brake, 2. coupling 3. torque tachometer, 4. angle encoder, 5. bearing bracket, 6. acceleration sensor, 7. servo reducer, and 8. servo motor

The adjustment of the input speed during the experiment can be controlled by a PLC (Programmable Logic Controller), while the load torque can be changed by varying the current of the magnetic powder brake through a tension controller. The sampling frequency of the integrated data acquisition system is set to 50,000 Hz.

5.2 Experimental results and data analysis

Consider the actual loading capacity of the test rig, the experimental conditions were set with an input shaft speed of 600 rpm and input shaft loads of 5 N m. and 10 N m. The angular displacement values of the master and slave gears were obtained through the encoders, while the dynamic transmission error was calculated using Eq. (32)

$$ {\text{DTE}} = \theta_{2} \cdot i - \theta_{1} . $$

(32)

In the above Eq. (32), $\theta_{2}$ represents the measured angular displacement of the slave gear, $\theta_{1}$ represents the measured angular displacement of the master gear,${ }i$ represents the gear ratio, and DTE represents the measured dynamic transmission error in terms of angular displacement. In this study, the measured dynamic transmission error in terms of angular displacement was converted to displacement along the line of action.

The encoders capture pulse signals, which can be processed and converted into gear rotation angle values using subsequent analysis software. Figure 20a, b displays the collected raw pulse signals from the encoders and the corresponding angle curves. Based on these curves and Eq. (32), the measured dynamic transmission errors along the line of action were calculated for load conditions of 5 N m and 10 N m as shown in Fig. 21a, b. Figure 21c, d displays the theoretical dynamic transmission errors along the line of action for load conditions of 5 N m and 10 N m, respectively.

Fig. 20

The raw signals collected from the encoders and rotation angle curves

Fig. 21

Simulation of dynamic transmission error and comparison of test results

Considering the errors introduced by the centralized parameter model employed in this study, as well as potential influences from instrument precision, test rig accuracy, and external disturbances, there may be some discrepancies between the measured experimental results and the simulated theoretical values of the dynamic transmission error in the time domain. Therefore, particular emphasis is placed on comparing and analyzing the maximum values of the dynamic transmission error for the two different load conditions. The maximum values of the dynamic transmission error obtained from theoretical simulations and experimental tests are presented in Table 5.

Table 5 The comparison of the maximum dynamic transmission error

By considering the maximum dynamic transmission error obtained from the experiments as the reference, it can be observed that the simulated results are relatively close to the experimental results, with an overall error within a range of about 20%. This level of overall error is within an acceptable range. Particularly for higher loads, the theoretical model in this study, considering the external meshing, demonstrates a reasonable agreement with the experimental results. In addition to the dynamic transmission error, the experiments also measured the acceleration signals of the system. As an example, Figs. 22 and 23 present the acceleration test curves in the line of action and the x-direction of the output shaft under different load conditions.

Fig. 22

The measured acceleration curves under a load of 5 N m

Fig. 23

The measured acceleration curves under a load of 10 N m

From the graph, it can be observed that regardless of the load condition, the acceleration test curves exhibit a significant amount of background noise. The input shaft speed of the master gear is 600 rpm, corresponding to a rotational frequency of $f_{{\text{r}}}$ = 10 Hz, while the output shaft frequency is $f_{{\text{r}}}^{\prime }$ = 5.68 Hz. The meshing frequency is $f_{{\text{m}}}$ = 210 Hz. In the time domain curves, periodic fluctuations can be roughly observed with a period of 1/$f_{{\text{r}}}$ or $1/f_{{\text{r}}}^{\prime }$.

Figure 24 depicts the theoretical simulation spectrum of the acceleration along the x-direction, with the horizontal axis given in terms of multiples of the meshing frequency.

Fig. 24

The simulated frequency spectrum of the acceleration along the x-direction

In the theoretical simulation curve shown in Fig. 24, no sideband components are observed. However, when considering the external meshing effect as shown in Fig. 24a, the dominant frequency in the system is found to be 5 times the meshing frequency, which is consistent with the experimental results. On the other hand, when not considering the external meshing effect, the simulated acceleration signal along the x-direction, as shown in Fig. 24b, exhibits a dominant frequency of 12 times the meshing frequency. The experimental results indicate the occurrence of external meshing phenomenon in the steel–plastic gear pair under the given load condition and provide some confirmation of the accuracy of the theoretical model proposed in this study.

It is worth noting that the experimental observations reveal the presence of some sideband noise in the signal. Additionally, apart from the dominant frequency, other frequency components are observed in the experimental results that were not present in the simulation. These additional frequency components can be a subject of further investigation in future studies. It is important to consider that the acquisition of the acceleration data in this study involved attaching the accelerometer to the gear support using adhesive at a specific angle. As a result, the signal pathway is relatively long, passing through the gear, shaft, bearings, and bearing seats, introducing various sources of error. Furthermore, manufacturing and assembly errors, as well as the instrument's resolution, also contribute to the overall measurement error. Overall, the test results of the acceleration signal and dynamic transmission error provide some validation of the accuracy of the proposed model in this study and exhibit a certain degree of reliability.

6 Conclusion

This study proposed an approximate method to calculate the time-varying mesh stiffness of steel–plastic gear pairs, considering the effects of backlash, flank contact ratio, and the material properties of plastic material at different temperatures. A dynamic model was established to analyze the dynamic characteristics of steel–plastic gear pairs under various loads. The influence of load on the time-varying mesh stiffness and dynamic behavior was also considered. Based on the analysis, the following conclusions were drawn:

• (1) An approximate method was proposed to determine the time-varying mesh stiffness, consider the external meshing effect and the material property variations of plastic gears at different temperatures. The reliability of the method was validated through finite element analysis, providing a new approach to obtain the time-varying mesh stiffness of plastic gears.

• (2) The influence of load on the time-varying mesh stiffness of steel–plastic gear pairs was investigated. The results showed that the stiffness variation exhibited a nearly linear relationship with the load. With increasing load, the temperature of the gear pair increased, leading to material softening and a decrease in stiffness.

• (3) The dynamic performance of steel–plastic gear pairs under different loads was compared. The results demonstrated that considering the effects of backlash and flank contact ratio resulted in superior dynamic response compared to neglecting these effects. This advantage became more pronounced with increasing load. Load variation significantly affected the vibration characteristics, and the dynamic performance of steel–plastic gear pairs decreased with increasing load.

In summary, this study provided insights into the time-varying mesh stiffness and dynamic behavior of steel–plastic gear pairs. The proposed method and findings contribute to the understanding and design of steel–plastic gear systems, considering the effects of load and temperature on their dynamic performance.

In future research, it is advisable to explore alternative materials and delve into the dynamic characteristics of the system when considering external meshing. Additionally, investigating the impact of temperature and load variations on the system's dynamics would be a valuable avenue of study.