1 Introduction

With the rapid development of space technology, the size of the satellite is becoming larger and larger. The satellite borne flexible structure has low natural frequencies because of its enormous size and flexibility. When the hoop antenna or solar wing is in orbit, it will inevitably generate a dynamic response accompanied by coupling vibration, nonlinear problems, etc.[1,2,3,4], owing to a periodic excitation, unbalanced inertial force, momentum wheel control torque, space debris, and other disturbances. The entire satellite’s performance is adversely affected by weak structural damping and slow vibration attenuation, such as orbit change failure, data transmission interruption, signal quality degradation, etc. [5]. If the disturbance frequency is close to or the same as the structure’s natural frequency, resonance will occur. Even severe oscillation will easily cause instability or abandonment of the satellite. Therefore, vibration control of satellite borne hoop antenna and solar wing is a key problem to be solved urgently.

In addition, when conducting tests on the ground, gravity significantly impacts the test results [6,7,8]. For example, the hoop antenna has serious static deformation because of flexibility. Dynamic testing becomes difficult, and the accuracy of experimental results is affected. what’s more, the hoop antenna has multiple modes, and its vibration has complex nonlinear phenomena such as geometric nonlinearity [2, 3, 9,10,11,12]. Complex vibration will affect the stability of the control system. Therefore, it is necessary to study the nonlinear problem in the ground suspension device of the flexible structure before designing the suspension device.

Among many low gravity simulation technologies, the rope suspension method has been adopted by many scholars. A lot of suspension systems have been designed. For example, Greschik et al. [13] proposed a “marionette” suspension device to support the weight of the mechanical arm, which was verified at Langley Research Center. Yuichi Sato and others developed an active constant force suspension space manipulator system with slings and a manipulator following [14]. Liu et al. [15] developed a gravity compensation system for the planet car, which realized constant force and gravity compensation based on active following. Fischer conducts low gravity experiments on solar wings using the passive following method [16]. Yang et al. [17] designed a suspension device for a solar panel, which has the function of motion following to complete the deployment of the panel. Luo [18, 19] An, etc. developed a single sling suspension device to lift a flexible hoop structure similar to the hoop antenna and measured the “shaking head” mode in the horizontal direction. Ma et al. [20] improves a suspension device, which can realize the flexible hoop structure’s vertical “nodding” mode. The rope used for the suspension device is long, thin and soft, and the mechanical model is simplified as a string. The nonlinear vibration of this string or belt is obvious [21, 22]. In order to realize gravity unloading and large swing angle movement, the suspension device inevitably produces nonlinear vibration problems. It can be seen that the vibration characteristics of spacecraft suspended by ropes are complex. Geometric nonlinearity occurs when the rope vibrates laterally in large amplitude, which will affect the vibration characteristics.

For the vibration control problem of satellites and other space structures, AVC is the main vibration control method. The AVC system combines sensors, measuring circuits, control algorithms, drivers, actuators, and controlled structures to form a closed-loop control system suitable for low-frequency vibration control of flexible structures. For the control algorithm, the robustness, complexity, and intelligence affect the control method’s effectiveness and reliability. Therefore, a core problem is designing and improving the control algorithm. Among many control algorithms, active control is useful to PD control, LQR(linear quadratic regulator) control, H ∞ control, LMS adaptive filtering control, fuzzy control, and other algorithms [23,24,25,26].

However, intelligent control algorithms include adaptive filtering control and fuzzy control algorithms. The intuitive reasoning and trial-and-error methods that humans possess are formalized or machine simulated and used in the analysis and design of control systems in order to realize the intellectualization of control systems to a certain extent [27]. For example, Wang et al. [28] proposed a notch filter based on the phase offset LMS adaptive filtering algorithm to achieve compensation control for multi-frequency excitation. Shi et al. [29] studied the ultra-low frequency vibration control of flexible structures using an adaptive filtering algorithm. Yang et al. [30] proposed an adaptive nonlinear control system for noise, which proved the effectiveness of the adaptive nonlinear vibration control system. Li et al. [31] proposed a hybrid PID-FxLMS algorithm and applied it to the vibration control of a piezoelectric cantilever. In order to improve the implementation effect of the FxLMS algorithm, Zhu et al. [32] proposed a filter x variable step minimum mean square error algorithm based on the inverse cotangent function. LMS adaptive filtering control is independent of initial conditions, VSS, low computational complexity, and unbiased convergence of mean value to the Wiener solution, which is suitable for AVC of complex structures. Fuzzy control usually establishes a two-dimensional Mamdani-type fuzzy logic rule base. It uses “if, then” statements to establish a rule base, also known as language control, which has good robustness and adaptability. However, Takagi Sugeno (T-S) fuzzy logic rules can directly output piecewise linear functions of control variables without a complicated clarification process. Based on state observation, Tang et al. [33] designed a T-S fuzzy controller for the suspension system. Wang et al. [34] used a T-S fuzzy control algorithm to suppress the vibration of flexible spacecraft. T-S fuzzy control algorithm recognizes, learns, and organizes its control mode according to the characteristics of the controlled dynamic process and controls the nonlinear system piecewise linearly, changing the controller structure and adjusting parameters. Zhang et al. [35] considered the input effects of dead zone nonlinearity and saturation nonlinearity when establishing the fuzzy control system. Among these control algorithms, the key advantage of the LMS adaptive filtering algorithm is that the control system is more stable than other algorithms [36]. The satellite borne flexible structures are vulnerable to unpredictable external disturbances in the space environment, so it is important to apply LMS adaptive filtering algorithm to achieve stability control.

This paper establishes the vibration equation of a nonlinear pendulum, and the influence of swing angle and lateral force on the vibration characteristics is discussed. The VSS-LMS adaptive filtering control of satellite borne flexible structure is studied. The step size parameters of control stability and convergence speed in the LMS adaptive filtering control are analyzed. The step size parameters are adjusted via PD modification or fuzzy inference of the Mamdani type, respectively. Furthermore, the low-frequency vibration parameters are attained through modal analysis, based on which, the AVC program was developed to examine the impact of the VSS-LMS adaptive filtering control method. These results provide theoretical and technical support for intelligent control scheme of satellite borne flexible structures on orbit.

2 Model analysis

2.1 Dynamic problems of multi-point suspension

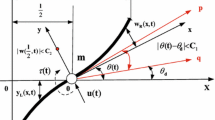
The advantages of hanging the spacecraft by ropes are simple, reliable, and small additional stiffness. If the rope length is long enough, low gravity or even zero gravity simulation of the spacecraft can be realized in both active and passive ways. However, the rope used in the suspension device is slender and soft, and the mechanical model is simplified as a string. In order to realize gravity unloading and follow-up movement, the suspension device inevitably produces vibration problems. Figure 1 shows the suspension model.

Fig. 1
figure 1

Hoop antenna suspension. a hoop antenna [18] b multi-point suspension model

Full size image

As the rope vibrates laterally, the nonlinear parameters significantly affect the dynamic characteristics of the rope (string). Therefore, the oscillation equation with the nonlinear term is established according to the law of motion of a nonlinear pendulum and considering the influence of the geometric nonlinearity of swing angle. Considering that there is a lateral force Ti between the poles of the hoop antenna, the vibration equation is,

$$ m_{i} l_{i} \ddot{\theta }_{i} \left( {t^{ * } } \right) + m_{i} g\sin \theta_{i} \left( {t^{ * } } \right) + T_{i} \cos \theta_{i} \left( {t^{ * } } \right) = 0 $$
(1)

where mi is the mass of suspension point, li is rope length, θi is swing angle. If the swing angle is medium, Taylor expansion is adopted,

$$ \sin \theta \left( {t^{ * } } \right) \approx \theta - \frac{{\theta^{3} }}{6} + O\left( {\theta^{3} } \right),\,\,\cos \theta \left( {t^{ * } } \right) \approx 1 - \frac{{\theta^{2} }}{2} + O\left( {\theta^{2} } \right) $$
(2)

The differential equation of motion is simplified as,

$$ \ddot{\theta }_{i} \left( {t^{ * } } \right) + \frac{g}{{l_{i} }}\theta_{i} \left( {t^{ * } } \right) - \frac{{T_{i} }}{{2m_{i} l_{i} }}\theta_{i}^{2} \left( {t^{ * } } \right) - \frac{g}{6l}\theta_{i}^{3} \left( {t^{ * } } \right) = - \frac{{T_{i} }}{{m_{i} l}}_{i} $$
(3)

Then, introduce dimensionless parameters and variable replacement,

$$ u = \theta_{i} ,t = \omega_{0} t^{ * } ,\omega_{0} = \sqrt {{g \mathord{\left/ {\vphantom {g l}} \right. \kern-0pt} l}_{i} } $$
(4)

The above equation is rewritten as,

$$ \ddot{u}\left( t \right) + u\left( t \right) + a_{2} u^{2} \left( t \right) + a_{3} u^{3} \left( t \right) = b $$
(5)

In the formula, the coefficients are,

$$ a_{2} = - \frac{{T_{i} }}{{2m_{i} g}},a_{3} = - \frac{1}{6},b = - \frac{{T_{i} }}{{m_{i} g}} $$
(6)

After introducing a small parameter τ = ωt, the free vibration equation is rewritten as,

$$ \omega^{2} \ddot{u}\left( \tau \right) + u\left( \tau \right) + a_{2} u^{2} \left( \tau \right) + a_{3} u^{3} \left( \tau \right) = 0 $$
(7)

By using of Lindstedt–Poincare method, u, ω are expanded as power series of parameters ε,

$$ u = \varepsilon u_{1} \left( \tau \right) + \varepsilon^{2} u_{2} \left( \tau \right) + \varepsilon^{3} u_{3} \left( \tau \right)...,\omega = 1 + \varepsilon \omega_{1} + \varepsilon^{2} \omega_{2} + ... $$
(8)

After substituting the above equation into the equation of motion, the coefficients of ε0 and ε are equal to 0. At this point, three equations must satisfy the following conditions,

$$ \left\{ \begin{gathered} u_{1}^{{\prime \prime }} + u_{1} = 0, \hfill \\ u_{2}^{{\prime \prime }} + u_{2} = - 2\omega _{1} {\mkern 1mu} u_{1}^{{\prime \prime }} - a_{2} {\mkern 1mu} u_{1}^{2} , \hfill \\ u_{3}^{{\prime \prime }} + u_{3} = - 2\omega _{1} {\mkern 1mu} u_{2}^{{\prime \prime }} - \left( {\omega _{1}^{2} + 2\omega _{2} } \right)u_{1}^{{\prime \prime }} - 2a_{2} {\mkern 1mu} u_{1} {\mkern 1mu} u_{2} - a_{3} {\mkern 1mu} u_{1}^{3} \hfill \\ \end{gathered} \right. $$
(9)

where the general solution of the first equation can be expressed as,

$$ u_{1} = A\cos \left( {\tau + \beta } \right) $$
(10)

Furthermore, the second equation becomes,

$$ u_{2}^{\prime \prime } + u_{2} = 2\omega_{1} A\cos \left( {\tau + \beta } \right) - a_{2} A^{2} \cos^{2} \left( {\tau + \beta } \right) $$
(11)

In order to eliminate long-term item of parameters u2 requirements ω1 = 0, the general solution of the first equation can be expressed as,

$$ u_{2} = - \frac{1}{2}a_{2} A^{2} + \frac{1}{6}a_{2} A^{2} \cos \left( {2\tau + 2\beta } \right) $$
(12)

After the above results are introduced into the third equation,

$$ u_{3}^{\prime \prime } + u_{3} = \left( {2\omega_{2} A - \frac{3}{4}a_{3} A^{3} + \frac{5}{6}a_{2}^{2} A^{3} } \right)\cos \left( {\tau + \beta } \right) - \left( {\frac{1}{4}a_{3} + \frac{1}{6}a_{2}^{2} } \right)A^{3} \cos \left( {3\tau + 3\beta } \right) $$
(13)

In order to eliminate long-term item of parameters u3 requirements,

$$ \omega_{2} = \frac{3}{8}a_{3} A^{2} - \frac{5}{12}a_{2}^{2} A^{2} $$
(14)

Therefore, we get the following formula,

$$ \tau = \omega t = \left( {1 + \left( {\frac{3}{8}a_{3} - \frac{5}{12}a_{2}^{2} } \right)\varepsilon^{2} A^{2} } \right)t + ...,\omega \approx 1 - \left( {\frac{1}{16} + \frac{5}{12}a_{2}^{2} } \right)\varepsilon^{2} A^{2} $$
(15)

Since the lateral force is generally less than the gravity at the node, the lateral force is expressed as Ti = k(mig). What is more, the natural frequency is written as,

$$ \omega \approx 1 - \left( {\frac{1}{16} + \frac{{5k^{2} }}{48}} \right)\varepsilon^{2} A^{2} $$
(16)

According to Eq. (16), the nonlinear vibration contains the fundamental frequency and nonlinear term. Figure 2 draws the relationship between natural frequency, lateral force and amplitude. It can be seen that the natural frequency decreases with the increase of lateral force and amplitude. In order to reduce the influence on the natural frequency, the lateral force and amplitude should be reduced.

Fig. 2
figure 2

Relationship between vibration frequency, lateral force and amplitude

Full size image

2.2 No lateral force situation

If this lateral force does not exist, it is simplified as another nonlinear system,

$$ \ddot{\theta }_{i} \left( t \right) + \frac{g}{{l_{i} }}\theta_{i} \left( t \right) - \frac{g}{{6l_{i} }}\theta_{i}^{3} \left( t \right) = 0 $$
(17)

This is a typical Duffing equation, which can also be solved by the Lindstedt–Poincare method. The nonlinear natural frequency is written as,

$$ \omega = \sqrt {\omega_{0}^{2} + \varepsilon \omega_{1} } \approx \omega_{0} \left( {1 + \varepsilon \frac{3}{8}\theta_{0}^{2} } \right) $$
(18)

Because the nonlinear factor exists, the frequency decreases with the increase of amplitude, so the swing angle must be controlled. When the lateral force is not considered, the vibration law is more obvious. Figure 3 shows the natural frequency varies with the angle and swing length. When the swing angle is about 0.4 rad(about π/8), the accuracy of the natural frequency reaches 99%. In addition, when the natural frequency is 1.1 Hz, as long as the rope length is greater than 0.2 m.

Fig. 3
figure 3

Relationship between vibration frequency, swing angle and rope length

Full size image

3 VSS-LMS adaptive filtering algorithm

For the satellite borne flexible structures, after discussing the vibration frequency of the suspended structure, AVC is applied to suppress vibration. When the measured response signal of the sensor is used as the feedback signal, the LMS adaptive filtering algorithm is used to calculate the feedback signal to generate the control signal. Based on the algorithm, the filter output signal is y(k),

$$ y\left( k \right) = \sum\limits_{i = 1}^{N - 1} {} W_{i} \left( k \right)x\left( {k - 1} \right) $$
(19)

After passing the transfer function h(k), the control signal is,

$$ C\left( k \right) = y\left( k \right)h\left( k \right) $$
(20)

where W(k) is the coefficient of finite impulse response filter (FIR), Wi(k) is the ith coefficient of FIR filter with sample k, N is the order of the FIR filter, and the coefficient of the next operation of the FIR filter is,

$$ W_{i} \left( k \right) = W_{i} \left( {k - 1} \right) + 2 \mu_{s} e\left( {k - 1} \right)x\left( {k - 1} \right) $$
(21)

where e(k) is an error signal. If there is an interference signal, it can be set equal to the feedback signal x(k), μs is a step parameter that controls stability and convergence rate. When the order of the filter is constant, the step size determines the convergence speed of the algorithm and the size of the steady-state offset. The convergence condition of the step size is,

$$ 0 < \mu_{s} < \frac{1}{{\lambda_{\max } }} $$
(22)

where λmax is the maximum eigenvalue of the correlation matrix R. In practical applications, it is usually difficult to obtain the maximum eigenvalue. Generally, the approximate range is estimated,

$$ \lambda = \sum\limits_{i = 0}^{L - 1} {{\text{E}}\left[ {|x(k - i)|^{2} } \right]} $$
(23)

Because LMS adaptive filtering algorithm is an improvement of the steepest descent method, the coefficient iteration relationship is,

$$ W_{i} \left( {k + 1} \right) = W_{i} \left( k \right) - \mu \nabla \left( k \right) $$
(24)

where \(\nabla \left( k \right)\) is the gradient of the performance function. μ The learning rate is a small positive number. The LMS algorithm directly takes the derivative of the square of the error signal as the estimate of the mean square error gradient. Therefore, the iterative process does not converge to the optimal solution as smoothly as the steepest descent method, which inevitably leads to errors, as shown in Fig. 4.

Fig. 4
figure 4

Comparison of trajectories of different algorithms

Full size image

It can be seen from the analysis of the below figures that the adaptive algorithm is convergent compared with the steepest descent method, but it still has some errors.

In addition, when the step factor is unreasonable, the adaptive algorithm may not converge. Therefore, in order to reduce the steady-state error, PD control or fuzzy control is used to adjust μs,

$$ \mu_{{{\text{vs}}}} = \left( { - k_{p} e - k_{d} \dot{e}} \right)\mu $$
(25)
$$ \mu_{{{\text{vs}}}} = {\text{fuzzy}}\left( { - k_{e} e, - k_{{{\text{ec}}}} \dot{e}} \right)k_{u} \mu $$
(26)

where kp and kd are PD control parameters, ke, kec and ku are fuzzy control parameters. After the step size adjustment, the LMS adaptive filtering algorithm is applied to the control system, and the state space equation becomes,

$$ \left\{ \begin{gathered} \dot{\user2{x}} = \user2{A x} + \user2{B u + y}\left( {e,t} \right) \hfill \\ {\varvec{x}}\left( 0 \right) = {\varvec{x}}_{0} ,{\varvec{y}}\left( 0 \right) = {\varvec{y}}_{0} \hfill \\ \end{gathered} \right. $$
(27)

where y is the input quantity y(k) generated according to the LMS adaptive filtering algorithm based on the generalized error signal e. Finally, reasonable adjustment parameters are selected to achieve the desired control effect.

4 Vibration control of flexible structure

4.1 Modal analysis of satellite borne flexible structure

According to the structural characteristics of the satellite, a three-dimensional reduced version model is established as shown in Fig. 5a. In addition, the model includes a satellite body, a hoop antenna structure and two solar wings, both of which are deployed. The geometric parameters are shown in Table 1.

Fig. 5
figure 5

Finite model and vibration mode. a SMAP satellite [37], b Satellite finite element model, c the 1st mode, d the 2nd mode, e the 6th bending mode, f the 14th bending mode

Full size image
Table 1 Model parameters
Full size table

The mode of the whole satellite obtained by finite element calculation includes nodding and shaking modes of the hoop antenna, and bending modes of the solar wing. Among them, the selected mode is the first order, second mode, sixth bending mode and fourteenth bending mode of the structure. The natural frequencies are 0.61 Hz, 0.68 Hz, 3.45 Hz, 24.54 Hz, respectively.

4.2 VSS-LMS adaptive filtering control system

The mode parameters above of the satellite borne flexible structure are extracted to establish a closed-loop control program shown in Fig. 6. To begin with, the structure is excited by a sinusoidal signal or random excitation, and the sinusoidal excitation frequency is just the natural frequencies. Assume that the swing angle of the flexible structure does not exceed π/8. The uncontrolled module contains the state space model. The remote node of the hoop antenna structure and the root node of the solar wing structure are selected as monitoring nodes, respectively. The displacement responses of the nodes measured by the sensor module are input into the LMS adaptive filtering controller module as feedback signals. In addition, VSS-LMS adaptive filtering algorithm is used to generate control signals which are converted into control force in the actuator module, and the actuating force acts on the extension arm and the root of the solar wing structure. If the PD or fuzzy control is used to adjust the step value, the PD or fuzzy module is directly embedded into the LMS control module.

Fig. 6
figure 6

VSS-LMS adaptive filtering control system

Full size image

4.3 Control curve after PD control adjusted step size

For the hoop antenna structure, the output force and displacement of piezoelectric actuator are placed at the root of the extension arm to control the structural response. Figure 7 shows the control curve before and after PD control adjusted step size in LMS adaptive filtering algorithm. When PD control adjusted step size is not adopted, it can be seen that the vibration response curve is unstable from the curves shown in Fig. 7a. After PD control adjusted step size is adopted, the variable step size factors are, respectively, kp = 1 and kd =  − 1. At this time, the vibration amplitude suppression rate reaches 97.77%, as shown in Fig. 7b.

Fig. 7
figure 7

LMS adaptive filtering control

Full size image

For the solar wing structure, the MFC flexible actuators output force and displacement to control structure vibration response, which are pasted at the root of the solar wing. When the VSS adjustment is not adopted, the vibration curve appears non-convergence as shown in Fig. 7c. After the step size is adjusted by PD control, the vibration amplitude suppression rate reaches 94.73%, as shown in Fig. 7d.

Figure 8 shows the control curve before and after PD control adjusted step size in LMS adaptive filtering algorithm. For the hoop antenna structure, the vibration response curve significantly decreases as shown in Fig. 8a and b. Furthermore, the power spectral density has also decreased by an order of magnitude shown in Fig. 8c–f. These results indicate that the PD adjustment is also effective in controlling random vibrations.

Fig. 8
figure 8

Control effect after random excitation

Full size image

4.4 Control curve after fuzzy control adjusted step size

Since the PD control adjusts the step size, the control effect is better. Similarly, when fuzzy control is used to adjust the step size, Mamdani-type fuzzy inference rules are embedded into the control module. In addition, the minimum–maximum method is used for fuzzy inference, and the rule base is established with “if, then” statements. Let the membership function degree of fuzzy variables e, ec and u be [− 6, 6], and the fuzzy sets are {NB, NM, NS, NO, PO, PS, PM, PB}. The input and output surface is drawn in Fig. 9 after the signal is processed by the fuzzification and anti-fuzzification. When there is only one displacement sensing signal, the fuzzy quantity e is retained. The fuzzy controller in Fig. 9 partially replaces the PD controller in Fig. 6. After the fuzzy control adjustment, the control signal is finally obtained to control the vibration of the structure.

Fig. 9
figure 9

fuzzy control adjusted step size and input and output surface

Full size image

Table 2 shows the control parameters and results. Similarly, after the step size is adjusted by fuzzy control, the vibration amplitude suppression rate reaches more than 90%. As shown in Fig. 10c, the VSS factors are ke = 20 and ku = 200, respectively. At this time, the amplitude suppression rate of the solar wing structure reaches 91.91%. It can be seen that the vibration response curve is also greatly reduced after fuzzy control adjustment, and the control effect is even better.

Table 2 Control parameters and results
Full size table
Fig. 10
figure 10

Fuzzy control adjustment VSS-LMS adaptive filtering control

Full size image

5 Conclusion

In this paper, the nonlinear vibration model of suspension rope is established, and the influence of swing angle and lateral force on the vibration characteristics is discussed. Then the VSS-LMS adaptive filtering algorithm is improved. PD or Mamdani-type fuzzy control algorithms is used to adjust the step size value. After the modal analysis is carried out, the AVC of satellite borne flexible structure is suppressed. The following conclusions can be drawn.

In order to reduce the influence on the natural frequency, the lateral force and swing angle should be reduced.

The vibration mode of satellite borne flexible structure is complex, and each part of the structure presents unique vibration mode, which is consistent with the vibration mode that has been studied separately.

After the step size is adjusted by PD control, the instability of the vibration curve caused by the unreasonable selection of the original step size is avoided. After the step size is adjusted by Mamdani-type fuzzy control, the non-convergence of the vibration curve is avoided. What is more, the suppression rate of the vibration amplitude reaches more than 90%, and the power spectral density also decreases significantly.

The above conclusions provide a theoretical basis for on orbit vibration suppression of satellite borne flexible structures as a whole. In addition, the adjustment parameters and step size values have a significant impact on the control effect, so the range of step size needs further research and confirmation.