Suspension Dynamics Analysis and LMS Adaptive Control of a Hoop Flexible Structure

Abstract

This paper proposes a scaled model to investigate the dynamic characteristics of suspension string and LMS adaptive control of hoop flexible structure. Firstly, the lateral vibration equation of micro segment string is established, along with the vibration frequency calculated. Also, the state space equation is theoretically obtained when the LMS adaptive algorithm is used to calculate the control force. Then, the scaled model is established by the finite element method before and after suspension, and there exist shaking mode and nodding mode. With this, a vibration control simulation is conducted for the hoop flexible structure to obtain the effect of LMS adaptive control. In the program, fixed step and variable step solvers are used to solve the state space equation, and Pulse, Square, Sawtooth and Random signals are applied as excitations. The simulation results show that the response curves are all obviously decreased after suspension. Moreover, the LMS adaptive control has a significant effect on steady-state response. It is concluded that the control results can be used as a reference for the large hoop truss antenna structure.

1 Introduction

With the rapid development of satellite technology, the size of satellite antenna is getting larger. For example, the new generation of satellite hoop truss antennas are developing towards large diameter. Even the diameter has reached hundreds of meters, which causes small damping and large flexibility. The result is that the natural frequency is low. In space weightlessness environment, when this kind of flexible structure is disturbed by external excitation due to the changes of orbits and attitudes, it is vulnerable to interference and easy to cause violent vibration and complex deformation, which seriously affects the accuracy, stability and reliability of the satellite. If the external excitation frequency is close to the fundamental frequency, resonance may lead to satellite malfunction even scrapping in severe cases. It can be inferred that the safety problems are very prominent. In the ground test before the satellites launch, gravity makes the hoop truss antenna serious static deformation, which increases the difficulty of dynamic test and affects the accuracy of data. Therefore, it is very necessary to solve the ground suspension problem and effective active vibration control (AVC) problem.

On the one hand, since the advent of low gravity simulation, suspension methods have attracted the attentions of many scholars and institutions. A lot of practical devices have been developed. For example, NASA specially developed a 6-DOF low gravity suspension device by using active sling to provide tension and displacement for astronaut [1]. Greschik proposed a string puppet suspension system to support weight, and NASA Langley research center verified this experiment [2]. Cambridge University designed a solar wing deployment mechanism by adopting passive following method to carry out low gravity experiment [3]. Yuichi Sato developed an active constant force suspension space manipulator in Fujitsu space laboratory, which simulates microgravity environment [4]. Luo developed a suspension device with single string to lift a hoop flexible structure, and obtained the horizontal “shaking mode” [5]. Ma improved the suspension device with three strings to lift a hoop flexible structure, which realizes the “noding mode” [6]. However, the vertical nodding mode is easily disturbed by the suspension device. Therefore it is required to analyze the suspension string within limited length range to realize the nodding mode.

On the other hand, the control algorithms is critical in the AVC. PD, fuzzy, robust, adaptive and other control algorithms are applied in the AVC simulation and test, and the results of vibration control are quite effective [5,6,7,8]. For example, Liu used direct adaptive control method to control the flexible spacecraft vibration [9]. Loghmani applied an adaptive feedforward controller for a cylindrical shell [10]. Generally, the cylindrical shell contains nonlinear vibration [11,12,13,14], and nonlinear characteristic should be considered in controller design. Furthermore, Poh used a kind of least mean square (LMS) algorithm to control small amplitude vortex-induced vibrations of flexible cylinders [15]. Wang designed the FxLMS algorithm combined with frequency estimation technique [16]. In these control algorithms, the main advantage of the LMS adaptive algorithm is that the control system is more stable than others. If the hoop flexible structure is susceptible to external disturbance after suspension, it is meaningful to apply LMS adaptive algorithm to achieve stable control.

In this paper, the vibration characteristics of suspension string are studied, and the LMS adaptive control of hoop flexible structure is carried out. In Sect. 2, the mechanical model of suspension string is established, and the relationship between vibration frequency and string length is obtained. In Sect. 3, the simulation of active vibration control based on LMS adaptive algorithm is established after obtaining the vibration characteristics of a scaled model. Finally, the main conclusions are obtained In Sect. 4.

2 Suspension and LMS Control Principle

2.1 Suspension Dynamics Analysis

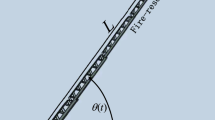
In the ground state, the hoop flexible structure is suspended by multiple strings at the nodes, and maintained horizontally. However, the length and load of each string may not be equal. Considering the typicalness of modeling, this paper firstly analyzes a string in the nodding mode vibration direction. The mechanical model is established as shown in Fig. 1. In the coordinate system Oxy, the upper part of the string is fixed, and a mass is hung on the the lower part. Generally, the string is made of high-strength materials, such as Kevlar fiber, steel wire rope, etc. As the string has mass m_i that may be ignored, ρ_i is the uniform density of the string. Then, l_i and G_i are the length of the string and bearing capacity. Take the micro segment dx of the string for mechanical analysis, T₁ and T₂ are the tension of the string, θ_i is the vibration deflection angle, and y (x, t) is the lateral vibration displacement,

Fig. 1.

Suspension diagram

According to Newton’s second law, the dynamic equation of dx lateral vibration of micro segment string is carried out,

$$ \rho_{i} \frac{{\partial^{2} y\left( {x,t} \right)}}{{\partial t^{2} }}dx = T_{1} \sin \left( {\theta + \frac{\partial \theta }{{\partial x}}dx} \right) - T_{2} \sin \theta ;T_{1} + \rho_{i} g{\kern 1pt} dx{\kern 1pt} \cos \theta_{i} = T_{2} $$

(1)

where the deflection angle θ is small, sinθ_i = θ_i, cosθ_i ≈ 1, θ_i = ${{\partial y} \mathord{\left/ {\vphantom {{\partial y} {\partial x}}} \right. \kern-\nulldelimiterspace} {\partial x}}$. By simplifying above equation, the following result is obtained,

$$ \rho_{i} \frac{{\partial^{2} y}}{{\partial t^{2} }}dx = T_{1} \left( {\frac{\partial y}{{\partial x}} + \frac{{\partial^{2} y}}{{\partial x^{2} }}dx} \right) - \left( {T_{1} + \rho_{i} g} \right)\frac{\partial y}{{\partial x}}dx $$

(2)

The relationship between tension and suspension weight is,

$$ T_{1} = \rho_{i} {\text{g}}\left( {l_{i} - x - dx} \right)\cos \left( {\theta + \frac{\partial \theta }{{\partial x}}dx} \right) = \rho_{i} g\left( {l_{i} - x - dx} \right),\rho_{i} = \frac{{m_{i} + G_{i} }}{{l_{i} }} $$

(3)

Substituting tension into Eq. (2), the simplification equation is obtained after the higher order term is removed,

$$ \frac{{\partial^{2} y}}{{\partial t^{2} }} = g\left( {\left( {l_{i} - x} \right)\frac{{\partial^{2} y}}{{\partial x^{2} }} - \frac{\partial y}{{\partial x}}} \right) $$

(4)

Then, let the solution of the above equation be in the form of separated variables y = Φ(x)cos(ωnt+φ). After substituting the solution into the above Eq. (10), we obtain,

$$ g\left( {l_{i} - x} \right)\varPhi^{\prime\prime} - g\varPhi^{\prime} + \omega_{n}^{2} \varPhi = 0 $$

(5)

There is a variable replacement, $\lambda_{i} = {{2\omega_{n} \sqrt {\left( {l_{i} - x} \right)g} } \mathord{\left/ {\vphantom {{2\omega_{n} \sqrt {\left( {l_{i} - x} \right)g} } g}} \right. \kern-\nulldelimiterspace} g}$. By substituting the replacement, a differential equation is obtained,

$$ \lambda^{2} \frac{{d^{2} \varPhi }}{{d\lambda^{2} }} + \lambda \frac{d\varPhi }{{d\lambda }} + \lambda^{2} \varPhi = 0 $$

(6)

This is a zero order Bessel equation. Let the meaningful solution of the equation be,

$$ \varPhi = CJ_{0} \left( \lambda \right) $$

(7)

$$ J_{0} \left( \lambda \right) = 1 - \frac{{\lambda^{2} }}{{2^{2} }} + \frac{{\lambda^{4} }}{{2^{4} \left( {2!} \right)^{2} }} - \frac{{\lambda^{6} }}{{2^{6} \left( {3!} \right)^{2} }} + ... + \left( { - 1} \right)^{k} \frac{{\lambda^{2k} }}{{2^{2k} \left( {k!} \right)^{2} }} $$

(8)

The solution of the equation is determined by homogeneous boundary conditions. In the first boundary condition such as the upper end of the suspension string, the mathematical formula is,

$$ J_{0} \left( {\lambda_{0} } \right)\left| {_{x = 0} } \right. = 0 $$

(9)

where the eigenvalue is $x_{n}^{0} = \lambda_{0}$.Therefore, the vibration frequency is,

$$ \omega_{n} = \frac{{x_{n}^{0} }}{2}\sqrt {\frac{g}{{l_{i} }}} = \frac{{x_{n}^{0} }}{{2l_{i} }}\sqrt {\frac{{m_{i} + G_{i} }}{{\rho_{i} }}} $$

(10)

$$ \omega_{0} = \sqrt {\frac{g}{{l_{i} }}} $$

(11)

where $x_{n}^{0}$ is the n^th root of the zero order Bessel equation. From the expression of natural frequency, it can be seen that the characteristic frequency of suspension string has nothing to do with the weight of the structure, but only with the length of the suspension string. As long as the suspension vibration frequency is consistent, the length is the same.

Fig. 2.

Solution of Bessel equation and natural frequency

The eigenvalue of the zero order Bessel function is 2.4 seen from the Fig. 2, and the relationship between string length and frequency can also be shown. For example, when the frequency is 1.45 Hz, the string length is 0.17 m or 0.12 m according to the Eqs. (10), (11). Besides, the trend of the curve is nonlinear.

2.2 LMS Adaptive Control

If negative feedback strategy is used in the active vibration control, the LMS adaptive filtering algorithm will be adopted to generate the control signal. The program of the LMS adaptive control is shown in Fig. 3.

Fig. 3.

LMS adaptive control

In the Fig. 3, W(k) is the coefficient of finite impulse response (FIR) filter, H(k) is transfer function, e(k) is error signal, d(k) is disturbing signal that is equal to feedback signal x(k), W_i(k) is the i^th coefficient of FIR filter with sample k, Y(k) is filter output,

$$ Y\left( k \right) = \sum\limits_{i = 1}^{N - 1} {} W_{i} \left( k \right)x\left( {k - 1} \right) $$

(12)

where N is the order of FIR filter, the next coefficient of FIR filter is,

$$ W_{i} \left( {k + 1} \right) = W_{i} \left( k \right) + 2\;\mu e\left( k \right)x\left( k \right) $$

(13)

where μ is a parameter for controlling stability and convergence speed,

$$ 0 < \mu < \lambda^{ - 1} $$

(14)

where $\lambda = x^{T} (k)x(k)$. If PD control is used to adjust μ, the variable-step is,

$$ \mu_{vs} = \left( { - k_{p} e - k_{d} \dot{e}} \right)\mu $$

(15)

Where k_p and k_d are parameters of PD controller.

Then, the control voltage V(k) is,

$$ V\left( k \right) = Y\left( k \right)H\left( k \right) $$

(16)

Furthermore, the vibration equation is established as,

$$ {\varvec{M}} \ddot{x}\user2{ + C}\dot{x}\user2{ + K}x = F_{e} + f_{a} V $$

(17)

At last, let substitute Eq. (16) into Eq. (17), and reduce the degree of freedom by means of mode truncation method, the vibration equation can be reduced to a state space equation Eq. (18) describing the transfer between the input and output parameters. Then the solution is just the vibration response.

$$ \dot{\user2{x}} = \user2{A x} + \user2{B f} $$

(18)

where x, A, B and f are state vector, system matrix, input matrix, force vector, respectively.

$$ {\varvec{x}} = \left\{ {\begin{array}{*{20}c} {\dot{x}} \\ x \\ \end{array} } \right\};\,{\varvec{A}} = {\mathbf{ - }}{\varvec{B}}\left[ {\begin{array}{*{20}c} {{\mathbf{ - }}{\varvec{M}}} & 0 \\ 0 & {\varvec{K}} \\ \end{array} } \right];\,{\varvec{B}} = \left[ {\begin{array}{*{20}c} 0 & {\varvec{M}} \\ {\varvec{M}} & {\varvec{C}} \\ \end{array} } \right]^{ - 1} ;\,{\varvec{f}} = \left[ {\begin{array}{*{20}c} 0 & { F_{e} + f_{a} V} \\ \end{array} } \right] $$

(19)

In addition, LMS algorithm is an improved algorithm of steepest descent method,

$$ W_{i} \left( {k + 1} \right) = W_{i} \left( k \right) - \mu \nabla \left( k \right) $$

(20)

where $\nabla \left( k \right)$ is gradient of performance function.

But it is difficult to get the function accurately. Therefore, LMS algorithm is an approximation of it. The iterative processes of steepest descent method and LMS algorithm are shown in the Fig. 4,

Fig. 4.

Comparison of steepest descent method and LMS algorithm

When μ is small, the objective function decreases rapidly. When μ is large, the transition process has oscillated. However, LMS algorithm is very sensitive to μ.

3 Case Analysis

3.1 Mode Analysis

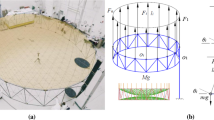
Because the size and mass of hoop truss antenna are too large, a scaled model is analyzed which is a hoop flexible structure shown in the Fig. 5. The mass of the scaled model is M₂ = 0.35 kg, and the mass of the extension arm is M₁ = 0.125 kg. Other geometric parameters are shown in the Table 1. The mass of counterweight is m_i = 0.070 kg, and the material of suspension string is Kevlar fiber rope. Compared with other structures, the mass of suspension string can be ignored.

Table 1. The parameters of hoop flexible structure

Then, the natural frequency and mode of the hoop flexible structure are analysed by the finite element method. MSC Patran is used to establish a three-dimensional model including 32 nodes and 38 bar elements, and the Lanczos method is applied to solve the vibration characteristics. when the string is 0.12 m, the first two natural frequencies are 1.44 Hz, 1.74 Hz, and 1.45 Hz, 5.05 Hz before and after suspension shown in the Fig. 6 respectively, and the first two modes are “nodding mode” and “shaking mode”, which belong to low frequency vibration. It means that the nodding mode is the up and down oscillation of the hoop flexible structure, and the shaking mode is lateral oscillation. This manuscript mainly studies the suspension device in nodding mode and shaking mode. In addition, there are other high-order modes, which are more complex.

Fig. 5.

Scaled model

Fig. 6.

Natural frequencies before and after suspension

3.2 Simulation Analysis

In the closed-loop control schematic, the structure is excited by sinusoidal excitation. Simultaneously, response signal is input to the controller as feedback signal. Then the control signal is generated by adopting LMS adaptive filtering algorithm. At last, the control voltage V(t) is input to the actuator to output control force.

Fig. 7.

Control simulation

Base on the working principle and control schematic, Matlab/Simulink is applied to establish the closed-loop control simulation for the noding mode after suspension. As shown in Fig. 7, the structure is excited by an excitation signal 0.03 sin(ω₁t). According to the finite element model, the excitation excites on the tip node 5 of the hoop flexible structure. The Uncontrol module containing the state space equation will directly output the response. The Control_truss module containing the state space equation as well, will output the response after controlling. The Measure module containing sensor will output the feedback signal, and then to be regarded as the source signal of the Algorithm. Here the control signal is produced by using LMS adaptive filtering algorithm. The Actuator module containing MFC actuator will convert the control signal into force Fa = 1V(t), Ma = 0.05V(t) for suppressing the vibration. The outputting force of actuator is linear. Besides, the mass M_n, stiffness K_n, and Rayleigh damping C_n are constructed by using the result of mode analysis. The Fig. 8 shows the other exitation signals such as Pulse, Square, Sawtooth and Random signals. The Figs. 9, 10 show the displacement response after LMS adaptive control. In addition the measure node 18 is located on the middle of the extended arm.

Fig. 8.

Exitation signals

Fig. 9.

Harmonic response after LMS adaptive control

Fig. 10.

Other responses after LMS adaptive control

It can be seen from the Fig. 9 and Fig. 10 that the responses are suppressed whether it is variable step solver (ODE45) or fixed step solver (step = 0.0002). What is more, the steady-state response tends to be stable, and it took about 300 s for the displacement to be suppressed. Therefore, it is clear that the response curves are all obviously decreased although the excitation signals and control parameters are different.

Fig. 11.

Variable-step (PD control) LMS adaptive control

The Table 2 shows the parameters of simulation and control results. The results show the amplitude suppression rates are nearly above 90%. For example, the displacement before control is 0.7 × 10⁻² m, but the displacement after control is 0.064 × 10⁻² m. The amplitude suppression rate is 90.86%. What is more, FIR filter length mainly affects the operation process. Most importantly, the control effect is the best when the PD control step is added shown in the Fig. 11. However, the effect of LMS adaptive control on random vibration is not obvious. That is meaning that LMS adaptive control has a significant effect on steady-state response except for random response in this simulation.

Table 2. Control results

4 Conclusions

In this paper, the dynamics characteristics of suspension string and LMS adaptive control of a hoop flexible structure are proposed to investigate the AVC after suspension.In particular, only when the frequency after suspension is satisfied can the LMS adaptive control be carried out.

The main conclusions are as follows: firstly, the relationship between vibration frequency and string length is obtained by the mechanical model of suspension string, and the dynamics characteristics of suspension string is analysed to guide the design of suspension device. Secondly, the first natural frequencies are 1.44 Hz and 1.45 Hz before and after suspension. That is meaning the frequency of nodding mode is close to each other, and the suspension string design is correct. Finally, based on the LMS adaptive control simulation, the responses are suppressed whether it is variable step solver or fixed step solver. The amplitude suppression rates are nearly above 90%. Consequently, these analyse and control methods provide effectively technical support for the ground vibration test of hoop flexible structure.