Robust adaptive flexible prescribed performance tracking and vibration control for rigid–flexible coupled robotic systems with input quantization

Abstract

With the increasing demands for more flexibility, lighter weight, and larger working space of industrial robotic systems in many fields, the rigid–flexible coupled robotic systems attract more attention. In this work, the desired angular tracking and vibration suppression issues are investigated for the rigid–flexible coupled robotic systems (RFCRSs) in the presence of input quantization. The vibrating displacement is coupled nonlinear due to the coupling between two joints’ angular positions and flexible displacements. Using the assumed mode principle, the nonlinear infinite-dimension dynamics of rigid–flexible coupled robotic systems are reduced by ordinary differential equations. With the backstepping-based Lyapunov method, robust adaptive flexible prescribed performance control (FPPC) law is developed to track the given angular positions and to reduce the vibration oscillations. Besides, the robust adaptive update law is incorporated into the quantized FPPC for estimating the unknown parameters of logarithmic quantizers in the face of input quantization. In terms of the above robust adaptive FPPC control, the tracking errors of the RFCRSs eventually converge to a compact set in face of input quantization. At last, three comparison cases are implemented to verify the efficacy of the proposed robust adaptive FPPC strategy in comparison with the PD feedback law.

1 Introduction

Rigid–flexible coupled robotic systems (RFCRSs) have attracted wide attention spurred by the rapid development of aerospace [1,2,3], marine engineering [4, 5], and modern medical technology [6, 7]. In general, the RFCRSs comprise a rigid link connected to a flexible link and are driven by the joint motor. Compared with the conventional rigid robotic system, the above RFCRSs are comparatively more agile and lighter[8]. However, the significant flaw of the RFCRSs mechanics is that the flexible beam is vulnerable to producing the flexible vibration that often leads to poor operational performance [9]. Hence, there are urgent requirements for vibration elimination of RFCRSs to prevent destruction and guarantee successful operation [10].

In reality, the elastic vibration of RFCRSs involves not only the time variable but also the spatial variable. Mathematically, RFCRSs can be described as distributed parameter systems governed by partial differential equations (PDEs). To be candid, modeling and analyzing precise dynamic equations for RFCRSs is a formidable challenge. This is primarily due to the extreme difficulty in solving exact solutions for the dynamics of infinite-dimensional systems, and the inherent complexity of PDEs presents significant obstacles and limitations in the development of vibration control strategies [11]. While there are control approaches designed to address the dynamic model of PDEs and tackle these challenges [12,13,14], many of these methods require the installation of an input force at the endpoint of the flexible structure to dampen vibrations. Unfortunately, implementing such a solution is often challenging, especially on the majority of industrial robots [15].

More recently, the reduced-model method which includes finite element methods, assumed mode method, and lumped parameter method, has been widely applied to transform PDEs into ordinary differential equations (ODEs) [16,17,18]. For instance, adopting the lumped spring-mass model, a flexible robotic mechanism with uncertain dynamics was controlled by an adaptive neural network (NN). [19]. By using the assumed mode method (AMM), a disturbance observer was added to the NN control for the reduced dynamics of a flexible beam to cope with unknown spatiotemporally variable disturbances in [20]. Based on the AMM, a planar two-link rigid–flexible manipulator was modeled by the reduced ODEs, and the uncalibrated visual servoing method was proposed subject to joint-space-velocity measurement [17]. A sliding mode control law-based adaptive tracking controller was put forward in [21] to enable an uncertain two-link rigid–flexible manipulator to achieve the necessary angles while being constrained by vibration amplitude. The existing studies on RFCRSs governed by PDEs principally handle the issues of input constraints though a barrier Lyapunov function, which is extensively applied to handle the output or state constraints, is investigated in [9, 13] to follow the given positions and suppress flexible displacements concurrently.

However, the prescribed performance functions selected in most references [23,24,25,26] can only be appended to exponential functions with symmetric features, which belong to the conventional prescribed performance scheme. Actually, the dynamic and steady-state process with the aforementioned scheme is still on the basis of intrinsic characterizes of the control input design (semi-global/global converge approach) [27, 28]. Therefore, the traditional performance functions have certain restrictions and lack flexibility. In this work, a more relatively flexible situation, where the steady-state performance of tracking errors relies on a flexible performance function [29], is concerned. The aforesaid literature on the RFCRSs did not consider the input quantization topic which is an inevitable issue in industrial control [30,31,32].

With the rapid development of network techniques, the integration of communication and control with the use of digital communication has triggered mounting research attention [33,34,35,36,37,38]. The input quantization is a core problem that usually combines with modern control methods to transform the control signal’s domain, which is continuous, into one that is discrete. The tradeoff between the controlled system stability and the admissible control precision has become more significant on account of quantization errors. Taking into account the input quantization of the RFCRSs which leads to the appearance of system instability makes the control issue of such rigid–flexible coupled systems relatively difficult [36, 37]. In the existing research on the RFCRSs, an adaptive boundary control with input signal quantization was proposed in three-dimensional space for an Euler–Bernoulli beam, and quantitative logarithmic laws were used to eliminate the elastic vibrations in [36]. With the help of the PDEs model, a feedback boundary quantized control law was designed to realize both joint angle tracking and vibration repression [37]. In comparison with the control issues in [36] and [37], the flexible prescribed performance of tracking errors case is considered in our work where the predefined flexible performance functions can be arbitrarily selected.

To construct the dynamic equation of RFCRSs and address the aforementioned difficulties, the reduced-model approach (AMM) is implemented and a novel flexible prescribed performance tracking approach with input quantization is proposed for such robotic systems. The main innovations of this work, as compared to previous research, include:

• 1. Unlike the traditional barrier Lyapunov functions, a novel parameter-type Lyapunov function is proposed in this paper. By virtue of constructing the parameter function $\varPi (t)$, the both dynamic and steady-state performance of tracking errors rely on the flexible prescribed performance functions.

• 2. A hybrid flexible prescribed performance controller (FPPC) with a robust adaptive parameter compensation scheme is developed. It is confirmed by backstepping-based Lyapunov’s stability and three numerical comparisons that input quantization-induced flexible vibrations and regulation of output errors will ultimately converge to zero over a compact neighborhood.

Fig. 1

Basic structure diagram of RFCRSs

The rest of the article is organized as follows. In Sect. 2, the reduced dynamic equations and problem statements for RFCRSs are presented. A novel FPPC scheme is proposed via the backstepping method in the face of quantized input signals in Sect. 3. Three numerical simulations are shown in Sect. 4 and conclusions are made in Sect. 5.

2 Dynamic modeling and control objectives of RFCRSs

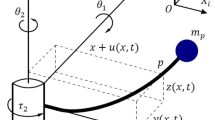
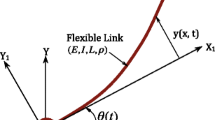
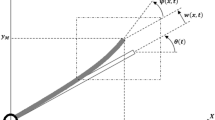
The fundamental structural components of RFCRSs consist of two links, as illustrated in Fig. 1. The first and second links of the RFCRS, located above the horizontal plane, are rigid and flexible, respectively. It is commonly assumed that the second link is modeled as an Euler–Bernoulli beam with a length of $l_2$. The coordinate axis of inertia is denoted as $\varXi OY$, while the local rotating reference frame mounted at hub O is represented as $\xi Oy$. The angular positions of the two joints, with $i=1,2$, are denoted by $\theta _{i}(t)$. The elastic displacement of the flexible link at a given position $\xi$ and time is denoted as $w(\xi ,t)$. The control inputs for this RFCRS, described by $\tau _i(t), i=1,2$, represent the joint torques. Additional characteristics of RFCRSs are presented in Table 1.

Table 1 Feature parameter configuration of RFCRSs

Remark 1

For ease of understanding, the following sections make use of these notations $(*)'=\partial (*)/\partial \xi$, $(*)^{''}=\partial ^2(*)/\partial \xi ^2$, $\dot{(*)}=\partial (*)/\partial t$, $\dddot{(*)}=\partial ^3(*)/\partial t^3$.

2.1 Dynamics formula of RFCRSs via energy analysis

The following dynamic equations are derivable from the energy analysis of RFCRSs using the expanded Hamilton’s principle [9, 22].

These are the angular positions $\theta (t)$ for which the dynamic model is given:

$$\begin{aligned}{} & {} M(\omega (\xi ,t),{\theta })\ddot{{\theta }}(t)\!+\!C(\dot{\omega }(\xi ,t),\theta (t))\dot{\theta }(t)\nonumber \\{} & {} \qquad \!+\!G(\theta (t),\dot{\theta },\dot{\omega }(\xi ,t),\ddot{\omega }(\xi ,t))\!=\!\mathcal {Q}(\tau (t)) \end{aligned}$$

(1)

Considered is the dynamic formula for the vibration displacement $w(\xi ,t)$:

$$\begin{aligned}{} & {} \rho \int _{0}^{l_2}\Big [\ddot{\omega }(\xi ,t)+ l_1(\dot{\theta }_{1}^2\sin \theta _{2}+\ddot{\theta }_{1}\cos \theta _{2})+ \xi (\ddot{\theta }_{1}\nonumber \\{} & {} \qquad +\ddot{\theta }_{2})+\omega (\xi ,t)(\dot{\theta }_{1}\nonumber \\{} & {} \qquad +\dot{\theta }_{2})^2 \Big ]d\xi +EI \int _{0}^{l_2}\omega ^{''''}(\xi ,t)d\xi +M_t\ddot{\omega }(l_2,t)\nonumber \\{} & {} \qquad +M_tl_1(\dot{\theta }_{1}^2\sin \theta _{2}+\ddot{\theta }_1\cos \theta _{2})\nonumber \\{} & {} \qquad +M_tl_2(\ddot{\theta }_{1}+\ddot{\theta }_{2})-M_t\omega (l_2,t)(\dot{\theta }_{1}+\dot{\theta }_{2})^2=0. \end{aligned}$$

(2)

The following boundary conditions apply to them:

$$\begin{aligned}{} & {} w^{''}(l_2,0)=w^{'''}(l_2,0)=0, \end{aligned}$$

(3)

$$\begin{aligned}{} & {} w(0,t)=w^{'}(0,t)=0, \end{aligned}$$

(4)

Remark 2

For the sake of simplicity and to facilitate the explanation of the subsequent reduced-order technique for infinite-dimensional systems, detailed information about the parameter matrices, such as $M(\omega (\xi ,t),{\theta })$, $C(\dot{\omega }(\xi ,t),\theta (t))$, $G(,\dot{\omega }(\xi ,t),\theta (t),\dot{{\theta }}(t))$, has been omitted in this section but can be found in our previous works [9, 22]. Additionally, $\mathcal {Q}(\tau (t))$ represents the quantized input signal of $\tau (t)$, which will be elaborated upon in the following section.

2.2 Reduced-order finite-dimensional dynamic model of RFCRSs

The aforementioned approach AMM is used to convert the infinite-dimension system model governed by PDEs into ODEs. The dynamic equations are usually truncated to some finite-dimensional models with the use of the assumed mode method (AMM). For the AMM, the elastic deflection is usually represented by an infinite number of separable harmonic modes theoretically, but practically only a finite number of modes with comparatively low frequencies are considered as they are generally dominant in the system dynamic behavior.

The method of arc approximation is used to represent the vibration displacement of the flexible link, which leads to the finite dimensional reduced-order dynamics. Following is a description of the vibration displacement of the flexible portion $w(\xi ,t)$.

$$\begin{aligned} w(\xi ,t)=\sum _{i=1}^{N}\phi _{i}(\xi )q_i(t) \end{aligned}$$

(5)

where the ith shape of the mode function is denoted by $\phi _i(\xi )$ and the ith generalized mode coordinate is represented by $q_i(t)$.

The ith mode shape function $\phi _{i}(\xi )$ is presented in [18] as

$$\begin{aligned} \begin{aligned} \phi _{i}(\xi )=&\frac{1}{\varXi _i}\left[ -\gamma _{i}\left( \sinh \left( \lambda _{i} \xi \right) -\sin \left( \lambda _{i} \xi \right) \right) \right. \\&\left. +\cosh \left( \lambda _{i} \xi \right) -\cos \left( \lambda _{i} \xi \right) \right] \\ \gamma _{i}=&\frac{\cosh \left( \lambda _{i} l_{2}\right) +\cos \left( \lambda _{i} l_{2}\right) }{\sin \left( \lambda _{i} l_{2}\right) +\sinh \left( \lambda _{i} l_{2}\right) }, \end{aligned} \end{aligned}$$

where if $M_t=0$, then $\varXi _i=\sqrt{l_{2}}$; otherwise,

$$\begin{aligned} \varXi _i=\left[ l_{2}+\frac{EI}{M_t\lambda _{i}^2}\left( \frac{1+\cosh (\lambda _{i}l_{2})\cos (\lambda _{i}l_{2})}{\sinh (\lambda _{i}l_{2})\sin (\lambda _{i}l_{2})}\right) ^2\right] ^{\frac{1}{2}} \end{aligned}$$

and $\lambda _{i}$ is the ith positive resolution such that

$$\begin{aligned}{} & {} \frac{M_t\lambda _{i}}{EIl_{2}}[-\sin (\lambda _{i})\cosh (\lambda _{i})+\cos (\lambda _{i})\sinh (\lambda _{i})]\\{} & {} \qquad +\cosh (\lambda _{i})\cos (\lambda _{i})=-1. \end{aligned}$$

Remark 3

It ought to be noticed that the first two modes are adequate to represent how the flexible beam vibrates, which can also refer to [8]-[10]. Only the first two modes are taken into consideration in this work to simplify the structure of the proposed tracking and vibration control technique, that is $w(\xi ,t)=q_1(t)\phi _{1}(\xi )+q_2(t)\phi _{2}(\xi )$.

The following vectors are utilized to recreate the finite-dimensional dynamic:

$$\begin{aligned} \tau (t)= & {} \begin{bmatrix} \tau _{1}(t)&\tau _{2}(t)&0&0 \end{bmatrix}^{\textrm{T}} \text {and}~\\{} & {} \varTheta (t)=\begin{bmatrix} \theta _{1}(t)&\theta _{2}(t)&q_1(t)&q_2(t) \end{bmatrix}^{\textrm{T}}. \end{aligned}$$

The dynamic equations of PDEs can be reduced into the form of ODEs by substituting (5) into (1) and (2), which could be described via the subsequent compact formula:

$$\begin{aligned} M\ddot{\varTheta }(t)+K\varTheta (t)+F(\varTheta (t),\dot{\varTheta }(t))=\mathcal {Q}(\tau (t)) \end{aligned}$$

(6)

where K represents a stiffness matrix and M specifies a positive-definite symmetric inertia matrix as follows:

$$\begin{aligned} K=\begin{bmatrix} 0 &{} 0 &{}0&{}0 \\ 0&{}0&{}0 &{} 0\\ 0&{}0&{}k_1&{}0\\ 0&{}0&{}0&{}k_2 \end{bmatrix}, k_i=EI\int _0^{l_{2}}[\phi _{i}^{''}(\xi )]^2 d\xi , i=1,2, \end{aligned}$$

and $F(\varTheta (t),\dot{\varTheta }(t))$ which denotes a hybrid Coriolis and centrifugal matrix satisfies the following property

$$\begin{aligned} F(\varTheta (t),\dot{\varTheta }(t))\!= & {} \!\frac{dM(\varTheta (t))}{dt}\dot{\varTheta }(t)\!-\!\frac{1}{2}\frac{\partial [\dot{\varTheta }^{T}M(\varTheta )\dot{\varTheta }]}{\partial \varTheta }\\= & {} C(\varTheta (t),\dot{\varTheta }(t))\dot{\varTheta }(t) \end{aligned}$$

Following are a few notations that have been included for clarity:

$$\begin{aligned} \left\{ \begin{aligned} \sigma _{i}=&\int _{0}^{l_{2}} \phi _{i}(\xi ) d \xi , \quad \psi _{i}=\int _{0}^{l_{2}} \xi \cdot \phi _{i}(\xi ) d \xi ,\\ \eta _{i}=&\int _{0}^{l_{2}} \phi _{i}^{2}(\xi ) d \xi , \quad \text {with} \quad i=1,2 \end{aligned}\right. \end{aligned}$$

Following are specifics on the inertia matrix M:

$$\begin{aligned} \begin{aligned} M_{11}&= J_{1}+I_{\textrm{h}}+M_{\textrm{h}} l_{1}^{2}+\rho _{2} l_{1}^{2} l_{2}+\frac{1}{3} \rho _{2} l_{2}^{3} \\&\quad +\rho _{2} l_{1} l_{2}^{2} \cos \theta _{2}-2 l_{1}\rho _{2}\sin \theta _{2} (q_{2}(t)\sigma _{2}+q_{1}(t)\sigma _{1})\\&\quad +M_t(l_{1}^{2}+ l_{2}^{2})+\rho _{2} l_{2}(q_1^2(t)\eta _{1}+q_2^2(t)\eta _{2})\\&\quad +M_t[q_{1}^2(t)\phi _{1}^2(l_{2})+l_{1}l_{2}\cos \theta _{2}+ q_{2}^2(t)\phi _{2}^2(l_{2}){]}\\&\quad -2l_1\sin \theta _{2}(q_2(t)\phi _{2}(l_{2})+q_1(t)\phi _{1}(l_{2}))\\&\quad +2q_{1}(t)q_{2}(t)\phi _{1}^2(l_{2})\phi _{2}^2(l_{2})\\ M_{12}&= I_{\textrm{h}}+\frac{1}{3} \rho _{2} l_{2}^{3}+\rho _{2} ( q_{1}^{2}(t)\eta _{1}+q_{2}^{2}(t)\eta _{2})\\&\quad +\frac{1}{2} \rho _{2} l_{1} l_{2}^{2} \cos \theta _{2}-\rho _{2} l_{1} \sin \theta _{2}(q_{1}(t)\sigma _{1}+q_{2}(t)\sigma _{2}) \\&\quad +M_t[l_{2}^{2}+l_{1} l_{2}\cos \theta _{2} -l_1\sin \theta _{2}(q_1(t)\phi _{1}(l_{2})\\&\quad +q_2(t)\phi _{2}(l_{2}))+q_{1}^2(t)\phi _{1}^2(l_{2})\\&\quad +\phi _{2}^2(l_{2})q_{2}^2(t)+2\phi _{1}(l_{2})q_{1}(t)q_{2}(t)\phi _{2}(l_{2})]\\ M_{13}&=\rho \psi _{1}+\rho l_1\sigma _{1}\cos \theta _{2}+M_tl_1\phi _{1}(l_2)\cos \theta _{2}\\&\quad +M_tl_2\phi _{1}(l_2)\\ M_{14}&=\rho \psi _{2}+\rho l_1\sigma _{2}\cos \theta _{2}+M_tl_1\phi _{2}(l_2)\cos \theta _{2}\\&\quad +M_tl_2\phi _{2}(l_2)\\ M_{22}&=I_{\textrm{h}}+\frac{1}{3} \rho _{2} l_{2}^{3}+\rho _{2} ( q_{1}^{2}(t)\eta _{1}+q_{2}^{2}(t)\eta _{2})\\&\quad +q_{2}^2(t)\phi _{2}^2(l_{2})\\&\quad +M_t[l_{2}^{2}+q_{1}^2(t)\phi _{1}^2(l_{2})+2\phi _{1}(l_{2})q_{2}(t)q_{1}(t)\phi _{2}(l_{2})]\\ M_{23}&=\rho \psi _{1}+M_tl_2\phi _{1}(l_2); M_{24}=\rho \psi _{2}+M_tl_2\phi _{2}(l_2)\\ M_{33}&=\rho \eta _{1}+M_t\phi _{1}^2(l_2); M_{34}=\phi _{2}(l_2)\phi _{1}(l_2)M_t;\\&\quad M_{44}=\rho \eta _{2}+M_t\phi _{2}^2(l_2) \end{aligned} \end{aligned}$$

and coriolis matrix’s equivalent components are:

$$\begin{aligned}{} & {} F_1(\varTheta ,\dot{\varTheta })\\{} & {} \quad =\left[ -\rho l_{1} \sin \theta _{2}l_{2}^{2} +2 \cos \theta _{2}l_{1}\rho \left( \sum \limits _{i=1}^{2} q_i(t)\sigma _{i}\right) \right. \\{} & {} \qquad \left. -2 \sin \theta _{2} l_{1}M_t l_{2} +2\cos \theta _{2} l_{1} M_t\sum \limits _{i=1}^{2} q_i(t)\phi _{i}(l_2) \right] \dot{\theta }_{1} \dot{\theta }_{2} \\{} & {} \quad \quad -\left[ \rho l_{1}\sin \theta _{2} \frac{l_{2}^{2}}{2} +\cos \theta _{2}l_{1}\rho \left( \sum \limits _{i=1}^{2} \sigma _{i}q_i(t)\right) \right. \\{} & {} \qquad \left. +M_t l_{1} l_{2} \sin \theta _{2}+ \cos \theta _{2}l_{1}M_t\sum \limits _{i=1}^{2} \phi _{i}(l_2) q_i(t)\right] \dot{\theta }_{2}^{2} \\{} & {} \quad \quad -\left[ 2 \rho \sin \theta _{2}l_{1}\sum \limits _{i=1}^{2} \dot{q}_i(t)\sigma _{i} -2 \rho \sum \limits _{i=1}^{2}{q}_i(t)\eta _{i}\dot{q}_i(t)\right. \\{} & {} \qquad +2 M_t l_{1} \sin \theta _{2}\sum \limits _{i=1}^{2} \dot{q}_i(t)\phi _{i}(l_2)\\{} & {} \quad \quad \left. -2M_t\sum \limits _{i=1}^{2}q_i(t)\phi _{i}(l_2)\sum \limits _{i=1}^{2}\dot{q}_i(t)\phi _{i}(l_2) \right] \left( \dot{\theta }_{1}+\dot{\theta }_{2}\right) \\{} & {} F_2(\varTheta ,\dot{\varTheta })\\{} & {} \quad = \left[ \rho l_{1}\sin \theta _{2} \frac{l_{2}^{2}}{2} +\cos \theta _{2}l_{1}\rho \left( \sum \limits _{i=1}^{2} \sigma _{i}q_i(t)\right) \right. \\{} & {} \qquad \left. +M t l_{1} l_{2} \sin \theta _{2}+\cos \theta _{2}l_{1}M t \sum \limits _{i=1}^{2} \phi _{i}(l_2)q_i(t) \right] \dot{\theta }_{1}^{2}\\{} & {} \quad \quad +2 \rho \sum \limits _{i=1}^{2}{q}_i(t)\eta _{i}\dot{q}_i(t)\cdot \left( \dot{\theta }_{1}+\dot{\theta }_{2}\right) \\{} & {} \qquad +\left[ 2 M_t \sum \limits _{i=1}^{2}\phi _{i}(l_2)q_i(t)+\sum \limits _{i=1}^{2}\phi _{i}(l_2)\dot{q}_i(t)\right] \cdot \left( \dot{\theta }_{1}+\dot{\theta }_{2}\right) \\{} & {} F_3(\varTheta ,\dot{\varTheta })\\{} & {} \quad =\rho q_1(t)\eta _1l_2(\dot{\theta }_{1}+\dot{\theta }_{2})^2-\dot{\theta }_{1}^2\rho l_1\sin \theta _{2}\sigma _{1}\\{} & {} \qquad +M_t(\dot{\theta }_{1}+\dot{\theta }_{2})^2(\phi _{1}(l_2)q_2(t)\phi _{2}(l_2)+q_1(t)\phi _{1}^2(l_2))\\{} & {} \qquad +l_1\dot{\theta }_{1}^2\sin \theta _{2}M_t\phi _1(l_2) \\{} & {} F_4(\varTheta ,\dot{\varTheta })\\{} & {} \quad =\rho q_2(t)\eta _2l_2(\dot{\theta }_{1}+\dot{\theta }_{2})^2-\dot{\theta }_{1}^2\rho l_1\sin \theta _{2}\sigma _{2}\\{} & {} \qquad +M_t(\dot{\theta }_{1}+\dot{\theta }_{2})^2(\phi _{2}^2(l_2)q_2(t)+\phi _{1}(l_2)q_1(t)\phi _{2}(l_2))\\{} & {} \qquad +l_1\dot{\theta }_{1}^2\sin \theta _{2}M_t\phi _2(l_2) \end{aligned}$$

2.3 Flexible prescribed performance control objectives

With the compact system described above, one can derive the equivalent formulation as follows:

$$\begin{aligned} \left\{ \begin{aligned}&\dot{x}_1(t)=x_2(t),\\&\dot{x}_2(t)=M(x_1)^{-1}\left[ \mathcal {Q}(\tau (t))-Kx_1(t)-C(x_1,{x}_2)x_2(t)\right] \end{aligned}\right. \end{aligned}$$

(7)

with $x_1(t)=\varTheta (t)$ and $x_2(t)=\dot{\varTheta }(t)$.

Concerning the RFCRSs (1) with prescribed performance, the flexible PPC law is developed via the backstepping-based Lyapunov strategy in the presence of quantization, so that the whole states of the closed-loop RFCRSs are semi-globally consistent and ultimately bounded under input quantization:

a) The tracking errors of two desired joint positions satisfy the prescribed performance, i.e., $e_i(t)$ meets $\mathcal {A}_{i}(t)<e_i(t)<\mathcal {B}_{i}(t)$ with $i=1,2$, and $e_i(t)$ is asymptotically close to $\frac{ \chi _{a{i}}+ \chi _{b{i}}}{2}$, where $\lim \limits _{t\rightarrow \infty }\mathcal {A}_{i}(t)= \chi _{a{i}}$ and $\lim \limits _{t\rightarrow \infty }\mathcal {B}_{i}(t)= \chi _{b{i}}$.

b) When achieving prescribed performance regulation, the mode vibration coordinates $q_i(t)$ of the flexible link under input quantization converge to a small confined area around the origin, indicating the successful suppression of vibrations.

3 Preliminaries

3.1 Logarithmic quantization

The logarithmic quantizer $\mathcal {Q}(\cdot ):\mathbb {R}\rightarrow \mathscr {X}$ is employed to quantize the system’s inputs $\tau (t)$. With a quantization density parameter $0<k<1$, the logarithmic set of quantization levels is represented as $\mathscr {X} = \{\pm x_j:x_j = k^j x_0,j = 0, \pm 1, \pm 2, \cdots \} \cup \{ 0\}$, where the initial value $x_0$ is a positive number.

The associated quantizer $\mathcal {Q}(\cdot )$ is defined as follows [35]:

$$\begin{aligned} \mathcal {Q}(\beta )=\left\{ \!\! \begin{array}{rcl} &{}x_i, &{}{\textrm{if}\quad \frac{1}{{1+\delta }}x_i< \beta \le \frac{1}{{1-\delta }}x_i, \beta >0};\\ &{}0, &{}{\textrm{if}\quad \beta =0};\\ &{}-\mathcal {Q}(-\beta ), &{}{\textrm{if}\quad \beta < 0}, \end{array}\right. \end{aligned}$$

(8)

with the sector bound $\delta =\frac{1-k}{1+k}\in (0,1)$.

3.2 Characteristic decomposition of logarithmic quantizer

In light of the approach proposed in [31], the logarithmic quantizer $\mathcal {Q}(\tau (t))$ can be constructed as below:

$$\begin{aligned} \mathcal {Q}(\tau (t))=g_1(t)\tau (t)+g_2(t), \end{aligned}$$

(9)

where two auxiliary parameters $g_j(t), j=1,2$ are defined as:

$$\begin{aligned} g_1(t)= & {} \left\{ \begin{array}{rcl} \frac{\mathcal {Q}(\tau (t))}{\tau (t)}, &{}{\textrm{if}\quad |\tau (t)|\geqslant b};\\ 1, &{}{\textrm{if}\quad |\tau (t)|< b}; \end{array}\right. \end{aligned}$$

(10)

$$\begin{aligned} g_2(t)= & {} \left\{ \begin{array}{rcl} 0, &{}{\textrm{if}\quad |\tau (t)|\geqslant b};\\ \mathcal {Q}(\tau (t))-\tau (t), &{}{\textrm{if}\quad |\tau (t)|< b}; \end{array}\right. \end{aligned}$$

(11)

Note that the $g_1(t)$ is greater than zero in (10) during the quantitative process. If $|\tau (t)|\le b$ with a positive input constraint $b>0$, then $\mathcal {Q}(\tau (t))$ has bound, and thus $g_2(t)$ has upper bound limitation, that is $|g_2(t)|\leqslant \bar{g}_2$, where $\bar{g}_2$ is a positive constant.

3.3 Novel flexible prescribed performance statement

Definition 1

(Novel flexible prescribed performance $\mathscr {K}$)

$$\begin{aligned} \mathscr {K}= & {} \left\{ (t,e(t))\in \mathbb {R}^+\!\times \mathbb {R}|\mathcal {A}(t)<e(t)<\mathcal {B}(t), \lim \limits _{t\rightarrow \infty }e(t)\right. \\= & {} \left. \frac{\chi _a+\chi _b}{2} \right\} \end{aligned}$$

where $\mathcal {A}(t)$ and $\mathcal {B}(t)$ are two smooth flexible prescribed performance functions that can be selected on the basis of actual circumstances, and the following requirements should be met in designing the flexible prescribed performance functions.

(i) Bounded property: $\mathcal {A}(t)$ and $\mathcal {B}(t)$ and their derivatives need to be bounded.

(ii) Limit condition: $\mathcal {A}(t)$ and $\mathcal {B}(t)$ exist limits such that $\lim \limits _{t\rightarrow \infty }\mathcal {A}(t)=\chi _a$ and $\lim \limits _{t\rightarrow \infty }\mathcal {B}(t)=\chi _b$.

(iii) Stability condition: $\mathcal {A}(t)$ and $\mathcal {B}(t)$ are chosen to meet that $\chi _a+\chi _b=0$ (nonessential flexible condition).

Furthermore, in order to analyze the system stability, Lemma 1 is given on the property of parameter-type functions as follows:

Lemma 1

The two parameter-type functions with respect to a function $\varPi (t)$ consist of the following:

$$\begin{aligned} \mathcal {L}_1(\varPi (t))=\ln \frac{\varpi }{\varpi -\varPi ^2(t)}, \mathcal {L}_2(\varPi (t))=\frac{\varPi ^2(t)}{\varpi -\varPi ^2(t)}, \end{aligned}$$

(12)

where $\varpi \leqslant 1$ is a positive parameter. Then, the subsequent inequality is satisfied during the interval $-\sqrt{\varpi }<\varPi (t)<\sqrt{\varpi }$,

$$\begin{aligned} \mathcal {L}_1(\varPi (t))\leqslant \mathcal {L}_2(\varPi (t)). \end{aligned}$$

(13)

Proof

By constructing $\mathcal {L}(\varPi (t))=\mathcal {L}_2(\varPi (t))-\mathcal {L}_1(\varPi (t))$, one has $\mathcal {L}(\varPi (t)=0)=0$, and differentiating $\mathcal {L}(\varPi (t))$ w.r.t. ${\varPi }(t)$ as follows:

$$\begin{aligned} \frac{d \mathcal {L}(\varPi (t))}{d \varPi (t)}\!= & {} \!\frac{d \mathcal {L}_2(\varPi (t))}{d \varPi (t)}-\frac{d \mathcal {L}_1(\varPi (t))}{d \varPi (t)}\nonumber \\= & {} \frac{2\varPi ^3(t)}{(\varpi -\varPi ^2(t))^2}, -\sqrt{\varpi }<\varPi (t)<\sqrt{\varpi }.\nonumber \\ \end{aligned}$$

(14)

In view of Eq. (14), one can derive $\frac{d \mathcal {L}(\varPi (t))}{d \varPi (t)}<0$ among the interval $-\sqrt{\varpi }<\varPi (t)<0$; it deduces that $\mathcal {L}(\varPi (t))$ can be monotonously reduced to zero, then $\mathcal {L}(\varPi (t))>0$ for $-\sqrt{\varpi }<\varPi (t)<0$. Accordingly, $\mathcal {L}(\varPi (t))>0$ among the interval $\sqrt{\varpi }>\varPi (t)>0$. Therefore, one can conclude that $\mathcal {L}(\varPi (t))=\mathcal {L}_2(\varPi (t))-\mathcal {L}_1(\varPi (t))\geqslant 0$ for $-\sqrt{\varpi }<\varPi (t)<\sqrt{\varpi }$, which also indicates $\mathcal {L}_2(\varPi (t))\geqslant \mathcal {L}_1(\varPi (t))$. $\square$

Remark 4

Different from the traditional prescribed performance design strategies [13, 23,24,25,26], the developed FPPC scheme of this work has the following three merits.

(i) To improve both the dynamic and steady-state performance of regulation errors in the controlled robotic system, we introduce the parameter-type function $\varPi (t)$ by selecting appropriate prescribed performance functions. Additionally, it’s worth noting that from Eq. (12), it is evident that both of these performance aspects can also be adjusted by the parameter $\varpi$.

(ii) As for the prescribed performance functions $\mathcal {A}(t)$ and $\mathcal {B}(t)$, we proposed can be more flexible than other performance functions in [13, 23,24,25,26], since they can be symmetrical or asymmetric.

(iii) Considering the global control strategy, the prescribed performance functions are generally chosen as the exponentially decaying function $\nu (t)=\nu _1e^{-l_1t}+\nu _{\infty }$ such that $\lim \limits _{t\rightarrow \infty }\nu (t)=\nu _{\infty }$, and $\nu _1,l_1$ and $\nu _{\infty }$ are normal constants. However, the $\nu _{\infty }$ in our work can be set as $\nu _{\infty }\geqslant 0$.

4 Robust flexible prescribed performance controller design

The FPPC controller design with flexible prescribed performance tracking without and under input quantization is developed in this section, respectively. Both control goals of the above two considered cases are to realize $\theta (t)$ follow the desired joint angular positions $\theta _{d}(t)$ in an expected compact error set with suppressing the vibration of the flexible link around zero eventually.

4.1 Novel flexible prescribed performance without input quantization

The prescribed performance tracking control aims to create a satisfactory tracking performance of $x_1(t)$ following $x_{1d}(t)$. For the simplicity of the whole paper, the tracking error variables e(t) as well as virtual error $z_2(t)$ are introduced as follows:

$$\begin{aligned} \left\{ \begin{aligned}&e(t)=x_1(t)-x_d(t)\\&z_2(t)=x_2(t)-\alpha (t) \end{aligned}\right. \end{aligned}$$

(15)

where $\alpha (t)$ is a virtual control variable to be determined.

Step 1. Concerning the novel prescribed performance $\mathcal {K}$, the following Lyapunov function candidate is defined as:

$$\begin{aligned} V_1(t)=\sum \limits _{j=1}^{4}\ln \frac{\varpi _j}{\varpi _j-\varPi _{j}^2(t)} \end{aligned}$$

with $\varPi _{j}(t)=\frac{e_{j}(t)-\mathcal {A}_{j}(t)}{\mathcal {B}_{j}(t)-\mathcal {A}_{j}(t)}+\frac{e_{j}(t)-\mathcal {B}_{j}(t)}{\mathcal {B}_{j}(t)-\mathcal {A}_{j}(t)}$. And its derivative w.r.t. time consists of the following:

$$\begin{aligned}{} & {} d{V_1}(t)/dt\nonumber \\{} & {} \quad =\sum \limits _{j=1}^{4}\frac{2\varPi _{j}(t)}{(\mathcal {B}_j(t)-\mathcal {A}_j(t))(\varpi _j-\varPi _{j}^2(t))}\nonumber \\{} & {} \qquad [2\dot{e}_j(t)-\dot{\mathcal {A}}_j(t) -\dot{\mathcal {B}}_j(t)-\varPi _{j}(t)(\dot{\mathcal {B}}_j(t)-\dot{\mathcal {A}}_j(t))]\nonumber \\{} & {} \quad =\sum \limits _{j=1}^{4}\frac{2\varPi _{j}(t)}{(\mathcal {B}_j(t)-\mathcal {A}_j(t))(\varpi _j-\varPi _{j}^2(t))}\nonumber \\{} & {} \qquad [2\dot{z}_{1j}(t)-\dot{\mathcal {A}}_j(t) -\dot{\mathcal {B}}_j(t)-\varPi _{j}(t)(\dot{\mathcal {B}}_j(t)-\dot{\mathcal {A}}_j(t))]\nonumber \\{} & {} \quad =\sum \limits _{j=1}^{4}\frac{2\varPi _{j}(t)}{(\mathcal {B}_j(t)-\mathcal {A}_j(t))(\varpi -\varPi _{j}^2(t))}\nonumber \\{} & {} \qquad [2(z_{2j}(t)+\alpha _j(t)-\dot{x}_{jd}(t))-\dot{\mathcal {A}}_j(t)-\dot{\mathcal {B}}_j(t)\nonumber \\{} & {} \qquad -\varPi _{j}(t)(\dot{\mathcal {B}}_j(t)-\dot{\mathcal {A}}_j(t))] \end{aligned}$$

(16)

Then, the virtual backstepping controller $\alpha _j(t)$ should be designed by:

$$\begin{aligned} \alpha _{j}(t)\!= & {} \!\dot{x}_{jd}(t)+\frac{1}{2}[\mathcal {\dot{A}}_{j}(t)+\mathcal {\dot{B}}_{j}(t)\nonumber \\{} & {} +\varPi _{j}(t)(\mathcal {\dot{A}}_{j}(t)-\mathcal {\dot{B}}_{j}(t))]\nonumber \\{} & {} -\frac{1}{2}k_1\varPi _{j}(t)(\mathcal {B}_{j}(t)-\mathcal {A}_{j}(t)), \end{aligned}$$

(17)

Substituting $\alpha _j(t)$ into $\dot{V}_1(t)$, one gets:

$$\begin{aligned} \dot{V_1}(t)= & {} \sum \limits _{j=1}^{4}\frac{2\varPi _{j}(t){z}_{2j}(t)}{(\mathcal {B}_j(t)-\mathcal {A}_j(t))(\varpi _i-\varPi _{j}^2(t))}\nonumber \\{} & {} -\sum \limits _{j=1}^{4}\frac{k_1\varPi _{j}^2(t)}{\varpi _j-\varPi _{j}^2(t)}, \end{aligned}$$

(18)

Step 2. To eliminate the term $z_{2j}(t)$ in Eq. (18), one can define:

$$\begin{aligned} V_2(t)=V_1(t)+\frac{1}{2}z_2^{\textrm{T}}(t)M(x_1(t))z_2(t). \end{aligned}$$

(19)

Accordingly, the time derivative of $V_2(t)$ gives:

$$\begin{aligned} \dot{V}_2(t)= & {} \dot{V}_1(t)+\frac{1}{2}z_2^{\textrm{T}}(t)\dot{M}(x_1(t))z_2(t)\nonumber \\{} & {} +z_2^{\textrm{T}}(t){M}(x_1(t))\dot{z}_2(t)\nonumber \\= & {} \dot{V}_1(t)+\frac{1}{2}z_2^{\textrm{T}}(t)\dot{M}(x_1(t))(x_2(t)-\alpha (t))\nonumber \\{} & {} +z_2^{\textrm{T}}(t){M}(x_1(t))(\dot{x}_2(t)-\dot{\alpha }(t))\nonumber \\= & {} \dot{V}_1(t)+z_2^\textrm{T}(t)\left[ {M}(x_1(t))(\dot{x}_2(t)-\dot{\alpha }(t))\right. \nonumber \\{} & {} \left. -\frac{1}{2}\dot{M}(x_1(t))\alpha (t)\right] \nonumber \\{} & {} +\frac{1}{2}z_2^{\textrm{T}}(t)\dot{M}(x_1(t))x_2(t) \end{aligned}$$

(20)

With the equivalent formal (7), one can obtain

$$\begin{aligned} \dot{V}_2(t)= & {} \sum \limits _{j=1}^{4}\frac{2\varPi (t){z}_{2j}(t)}{(\mathcal {B}_j(t)-\mathcal {A}_j(t))(\varpi _j-\varPi _{j}^2(t))}\nonumber \\{} & {} -\sum \limits _{j=1}^{4}\frac{\varPi _{j}^2(t)}{\varpi _j-\varPi _{j}^2(t)}+\frac{1}{2}z_2^\textrm{T}(t)\dot{M}(x_1(t))x_2(t)\nonumber \\{} & {} +z_2^{\textrm{T}}(t)\left[ {M}(x_1(t))(\dot{x}_2(t)-\dot{\alpha }(t))-\frac{1}{2}\dot{M}(x_1(t))\alpha (t)\right] \nonumber \\= & {} \sum \limits _{j=1}^{4}\frac{2\varPi (t){z}_{2j}(t)}{(\mathcal {B}_j(t)-\mathcal {A}_j(t))(\varpi _j-\varPi _{j}^2(t))}\nonumber \\{} & {} +z_2^{\textrm{T}}(t)[\tau (t)-Kx_1(t)-C(x_1,x_2)x_2(t)\nonumber \\{} & {} -{M}(x_1)\dot{\alpha }(t)-\frac{1}{2}\dot{M}(x_1(t))\alpha (t)]\nonumber \\{} & {} -\sum \limits _{j=1}^{4}\frac{k_1\varPi _{j}^2(t)}{\varpi _j-\varPi _{j}^2(t)}+\frac{1}{2}z_2^{\textrm{T}}(t)\dot{M}(x_1)x_2(t) \end{aligned}$$

(21)

Based on the property of inertia matrix [21], one gives that

$$\begin{aligned} C(x_1,x_2) x_2=\dot{M}(x_1)x_2-\frac{1}{2}\frac{\partial x_2^\textrm{T}(t)M(x_1)x_2(t)}{\partial x_1} \end{aligned}$$

Then, one has

$$\begin{aligned} \dot{V}_2(t)= & {} \sum \limits _{j=1}^{4}\frac{2\varPi _{j}(t){z}_{2j}(t)}{(\mathcal {B}_j(t)-\mathcal {A}_j(t))(\varpi _j-\varPi _{j}^2(t))}\nonumber \\{} & {} +z_2^{\textrm{T}}(t)[\tau (t)-Kx_1(t)-{M}(x_1(t))\dot{\alpha }(t)\nonumber \\{} & {} -\frac{1}{2}\dot{M}(x_1(t))\alpha (t)]-\sum \limits _{j=1}^{4}\frac{k_1\varPi _{j}^2(t)}{\varpi _j-\varPi _{j}^2(t)}\nonumber \\= & {} z_2^{\textrm{T}}(t)[\tau (t)-Kx_1(t)+2\tilde{H}(t) -{M}(x_1(t))\dot{\alpha }(t)\nonumber \\{} & {} -\frac{1}{2}\dot{M}(x_1(t))\alpha (t)]\nonumber \\{} & {} -\sum \limits _{j=1}^{4}\frac{k_1\varPi _{j}^2(t)}{\varpi _j-\varPi _{j}^2(t)} \end{aligned}$$

(22)

with $\tilde{H}(t)\in \mathbb {R}^{4}$, $\tilde{H}_{j1}(t)=\frac{\varPi _{j}(t)}{(\mathcal {B}_j(t)-\mathcal {A}_j(t))(\varpi _j-\varPi _{j}^2(t))}$.

Step 3. Then, the FPPC tracking law is proposed as follows:

$$\begin{aligned} \tau (t)\!\!= & {} \!-k_2(x_2(t)-\alpha (t))+Kx_1(t)+0.5\dot{M}(x_1)\alpha (t)\nonumber \\{} & {} -2\tilde{H}(t)+M(x_1)\dot{\alpha }(t) \end{aligned}$$

(23)

In view of the above analysis, the achieved results without input quantization effect $\mathcal {Q}(\cdot )$ is summarized in Theorem 1.

Theorem 1

For the closed-loop RFCRSs (1), the FPPC control scheme (23) is proposed by adaptive backstepping approach to realize the prescribed tracking performance and vibration suppression such that:

1) $\lim \limits _{t\rightarrow \infty }e_j(t)=\frac{(\chi _{aj}+\chi _{bj})}{2}=0, j=1,2$;

2) $\lim \limits _{t\rightarrow \infty }q_j(t)=\frac{(\chi _{aj}+\chi _{bj})}{2}=0, j=1,2$.

Proof

To better carry out the stable proof, an appropriate Lyapunov function is selected as follows:

$$\begin{aligned} {V}(t)=V_1(t)+\frac{1}{2}z_2^{\textrm{T}}(t)M(x_1(t))z_2(t). \end{aligned}$$

(24)

With the previous analysis (22), then substituting the above FPPC law (23) into Eq. (19), one has

$$\begin{aligned} \dot{V}(t)= & {} -k_1\sum \limits _{j=1}^{4}\frac{\varPi _{j}^2(t)}{\varpi _j-\varPi _{j}^2(t)} -k_2z^{\textrm{T}}_2(t)z_2(t)\nonumber \\= & {} -k_1\sum \limits _{j=1}^{4}\ln \frac{\varpi _j}{\varpi _j-\varPi _{j}^2(t)} -k_2z^{\textrm{T}}_2(t)z_2(t)\nonumber \\\le & {} -c_1V(t) \end{aligned}$$

(25)

with $c_1=\min \{k_1,\frac{2k_2}{\lambda _{max}(M(x_1))}\}$. $\square$

According to Ineq. (25), the two conclusions can be made in the following propositions:

Property 1

According to Ineq. (25) and Barbalat’s Lemma, one can derive

$$\begin{aligned} \lim \limits _{t\rightarrow \infty }\ln \frac{\varpi _j}{\varpi _j-\varPi _{j}^2(t)}=0. \end{aligned}$$

(26)

Since $\varPi _{j}(t)=\frac{e_{j}(t)-\mathcal {A}_{j}(t)}{\mathcal {B}_{j}(t)-\mathcal {A}_{j}(t)}+\frac{e_{j}(t)-\mathcal {B}_{j}(t)}{\mathcal {B}_{j}(t)-\mathcal {A}_{j}(t)}$, it follows that

$$\begin{aligned} \lim \limits _{t\rightarrow \infty }\varPi _{j}(t)=0&\Rightarrow \lim \limits _{t\rightarrow \infty }\left\{ \frac{e_{j}(t)-\mathcal {A}_{j}(t)}{\mathcal {B}_{j}(t)-\mathcal {A}_{j}(t)}+\frac{e_{j}(t)-\mathcal {B}_{j}(t)}{\mathcal {B}_{j}(t)-\mathcal {A}_{j}(t)}\right\} =0\nonumber \\&\Rightarrow \lim \limits _{t\rightarrow \infty }2e_j(t)=\lim \limits _{t\rightarrow \infty }(\mathcal {A}_j(t)+\mathcal {B}_j(t))\nonumber \\&\Rightarrow \lim \limits _{t\rightarrow \infty }e_j(t)=\lim \limits _{t\rightarrow \infty }\frac{1}{2}(\mathcal {A}_j(t)+\mathcal {B}_j(t)) \end{aligned}$$

Property 2

By virtue of Ineq. (25), one gives

$$\begin{aligned}{} & {} \Rightarrow \dot{V}(t)\leqslant -c_1V(t) \nonumber \\{} & {} \Rightarrow -\sqrt{\varpi _j-\varpi _j e^{-V(0)e^{-c_1t}}}\le \varPi _{j}(t)\nonumber \\{} & {} \quad \le \sqrt{\varpi _j-\varpi _j e^{-V(0)e^{-c_1t}}}\nonumber \\{} & {} \Rightarrow -1\le -\sqrt{\varpi _j}<\frac{2e_j(t)-\mathcal {A}_j(t)-\mathcal {B}_j(t)}{\mathcal {B}_j(t)-\mathcal {A}_j(t)}\nonumber \\{} & {} \quad<\sqrt{\varpi _j}\le 1\nonumber \\{} & {} \Rightarrow \mathcal {A}_j(t)<e_{j}(t)<\mathcal {B}_j(t), j=1,2. \end{aligned}$$

(27)

The above two properties deduce that this proposed method not only has the prescribed performance $\mathcal {A}_j(t)<e_{j}(t)<\mathcal {B}_j(t)$ but also can guarantee the limits of tracking errors meet that $\lim \limits _{t\rightarrow \infty }e_j(t)=\lim \limits _{t\rightarrow \infty }\frac{1}{2}(\mathcal {A}_j(t)+\mathcal {B}_j(t))$=$\frac{1}{2}(\chi _{aj}+\chi _{bj})=0$ with $j=1,2$. Accordingly, the mode vibration suppression can be realized such that $\lim \limits _{t\rightarrow \infty }q_j(t)=\frac{\chi _{aj}+\chi _{bj}}{2}=0$.

Theorem 1 has now been fully demonstrated.

Remark 5

In the context of measuring flexible vibration deformation, the utilization of two strain gauge sensors is employed (the quantity of sensors being determined by the truncation order). In the case of the first two vibration modes, namely $q_1(t)$ and $q_2(t)$, the specific approach involves affixing a strain gauge to the flexible arm. As the flexible arm undergoes movement within the system, it induces vibrations and deformations across a broad range of motion. Consequently, the strain gauge generates strain as a result. The ensuing analog voltage signal is acquired through the half-bridge method within a bridge box. Subsequently, the signal undergoes filtering and amplification via dynamic strain gauge equipment. The primary purpose of the strain gauge is to measure the bending deformation of the flexible arm.

Remark 6

In relation to the feasibility of implementing the proposed method in real-time, employing robust adaptive FPPC laws, it is evident that the controllers only require information about $\theta (t)$ and $\dot{\theta }(t)$, both of which can be measured using a photoelectric encoder and tachometer, respectively. However, it’s important to acknowledge that it’s practically impossible to entirely eliminate the influence of sensor noise, which can affect the implementation of control, especially when dealing with time-differentiating terms. The encoder and strain gauge sensor are capable of detecting the rotation angle $\theta (t)$ and deflection, providing real-time graphical data representation. To compute the signal derivatives for angular displacement $\dot{\theta }(t)$, a derivative filter is employed. For real-time experiments, the MATLAB Simulink module generates control input signals, and the associated control performance can be visualized on an oscillograph.

4.2 Quantized flexible prescribed performance control design

In light of the dynamic equations and the control objective, the appropriate logarithmic quantizer is utilized to quantize control signals. The quantized control law and parameter update law are developed to track the desired joint angular positions and to guarantee the controlled RFCRSs are stable. The control block of the above quantized FPPC scheme is depicted in Fig. 2.

Fig. 2

The quantized control block of the RFCRSs with flexible prescribed performance

Following are the two portions of the primary quantized control input:

$$\begin{aligned} \left\{ \begin{aligned}&\mathcal {Q}(\tau _i(t))\!=\!g_{i1}(t)\tau _i(t)+g_{i2}(t) \\&\tau _i(t)\!=\!-\!\frac{(x_{2i}(t)-\alpha _i(t))\hat{\mu }^2_i(t)\bar{\tau }_i^2(t)}{|(x_{2i}(t)-\alpha _i(t))\hat{\mu }_i(t)\bar{\tau }_i(t)|+\rho _i}, i=1,2 \end{aligned}\right. \end{aligned}$$

(28)

where $\rho _i$ is a normal constant and ${\mu }_i(t)=\frac{1}{\textrm{inf} g_{1i}(t)}$.

Two adaptive laws $\hat{\mu }(t)$ are expressed as:

$$\begin{aligned} \dot{\hat{\mu }}_j(t)=\gamma _jz_{2j}(t)\bar{\tau }_j(t)-\gamma _j\sigma _{j}{\hat{\mu }}_j(t), \quad j=1,2. \end{aligned}$$

(29)

with two positive control gains $\gamma _j,\sigma _{j}$.

The auxiliary control $\bar{\tau }(t)\in \mathbb {R}^4$ and virtual backstepping controller $\alpha _i(t)\in \mathbb {R}$ are proposed as below:

$$\begin{aligned} \bar{\tau }(t)\!\!= & {} \!\!-k_2(x_2(t)-\alpha (t))+Kx_1(t)+0.5\dot{M}(x_1)\alpha (t)\nonumber \\{} & {} \!\!+2{\tilde{H}(t)}+M(x_1(t))\dot{\alpha }(t). \end{aligned}$$

(30)

$$\begin{aligned} \alpha _j(t)\!= & {} \!\!\dot{x}_{jd}(t)+\frac{1}{2}[\dot{\mathcal {A}}_j(t)+\dot{\mathcal {B}}_j(t)\nonumber \\{} & {} +\varPi _{j}(t)(\dot{\mathcal {A}}_j(t) -\dot{\mathcal {B}}_j(t))]\nonumber \\{} & {} \!\!-\!\!\frac{1}{2}k_1\varPi _{j}(t)(\mathcal {B}_j(t)-\mathcal {A}_j(t)), j=1,2.\nonumber \\{} & {} {\tau }(t)=[I_2\quad 0]^T\bar{\tau }(t) \end{aligned}$$

(31)

with $\varPi _{j}(t)=\frac{e_j(t)-\mathcal {A}_j(t)}{\mathcal {B}_j(t)-\mathcal {A}_j(t)}+\frac{e_j(t)-\mathcal {B}_j(t)}{\mathcal {B}_j(t)-\mathcal {A}_j(t)}$.

5 Stability analysis of the controlled RFCRSs

In this section, the main results of the flexible prescribed performance control with input quantization are demonstrated in the subsequent Theorem 2.

Theorem 2

According to the reduced dynamics of the RFCRSs described by (7), with the quantized FPPC control law (28) and the adaptation law (29), the tracking errors of the controlled RFCRSs under the prescribed performance are guaranteed. Error signals, $z_2(t)$ and $\tilde{\mu }(t)$ will remain within the compact sets $\varOmega _{z_2}$, $\varOmega _{\tilde{\mu }}$, respectively, defined as follows:

$$\begin{aligned}{} & {} \varOmega _{z_2}:=\left\{ z_2(t)\in \mathbb {R}^4\Big |||z_2(t)||\leqslant \sqrt{\frac{D}{\lambda _{min}(M)}}\right\} \end{aligned}$$

(32)

$$\begin{aligned}{} & {} \varOmega _{\tilde{\mu }}:=\left\{ \tilde{\mu }(t)\in \mathbb {R}^2\big |||\tilde{\mu }(t)||\leqslant \sqrt{\gamma \mu D}\right\} \end{aligned}$$

(33)

where $D=2(V(0)+\lambda /c_2)$ with two positive constants $c_2$ and $\lambda$, and $\gamma =\max \{\gamma _1,\gamma _2\}$ as well as $\mu =\max \{\mu _1,\mu _2\}$.

Proof

In order to eliminate the input quantization influence, the control gains $g_{1i}(t)$ need to be estimated and the adaptive parameter law $\hat{\mu }_i(t)$ is introduced to observe the low bound value $\mu _i(t)=\frac{1}{\textrm{inf} \{g_{1i}(t)\}}$, the following Lyapunov function candidate is defined as follows:

$$\begin{aligned} {V}(t)= & {} \sum \limits _{i=1}^{2}\ln \frac{\varpi _i}{\varpi _i-\varPi _{i}^2(t)} +\sum _{i=1}^{2}\frac{1}{2\gamma _{i}\mu _{i}}\tilde{\mu }_{i}^2(t)\nonumber \\{} & {} +\frac{1}{2}z_2^{\textrm{T}}(t)M(x_1(t))z_2(t) \end{aligned}$$

(34)

where $\gamma _i>0,i=1,2$ is positive constants and $\tilde{\mu }(t)=\bar{\mu }(t)-\mu (t)$.

Because $g_1(t)>0$, we know $\mu (t)>0$. With the definition of $\bar{\mu }(t)$, the derivative of V(t) is:

$$\begin{aligned} \dot{V}(t)= & {} z_2^\textrm{T}(t)[\mathcal {Q}(\tau (t))-Kx_1(t)+2\tilde{H}(t) -{M}(x_1(t))\dot{\alpha }(t))\nonumber \\{} & {} -\frac{1}{2}\dot{M}(x_1(t))\alpha (t)]\nonumber \\{} & {} +\sum \limits _{i=1}^{2}\frac{1}{\gamma _i\mu _i(t)}\tilde{\mu }_i(t)\dot{\hat{\mu }}_i(t) -\sum \limits _{i=1}^{2}\frac{k_1\varPi _{i}^2(t)}{\varpi _i-\varPi _{i}^2(t)}\nonumber \\= & {} \sum \limits _{i=1}^{2}z_{2i}(t)[g_{1i}(t)\tau _i(t)+g_{2i}(t)]+z_2^\textrm{T}(t)[2\tilde{H}(t)\nonumber \\{} & {} -Kx_1(t)-{M}(x_1(t))\dot{\alpha }(t))\nonumber \\{} & {} -\frac{1}{2}\dot{M}(x_1(t))\alpha (t)]+\sum \limits _{i=1}^{2}\frac{1}{\gamma _i\mu _i(t)}\tilde{\mu }_i(t)\dot{\hat{\mu }}_i(t)\nonumber \\{} & {} -\sum \limits _{i=1}^{2}\frac{k_1\varPi _{i}^2(t)}{\varpi _i-\varPi _{i}^2(t)} \end{aligned}$$

(35)

With the analysis of logarithmic quantizer (9), one obtains

$$\begin{aligned} \dot{V}(t)= & {} \sum \limits _{i=1}^{2}z_{2i}(t)[g_{1i}(t)\tau _i(t)+g_{2i}(t)]+z_2^\textrm{T}(t)\nonumber \\{} & {} [-k_2z_2(t)+k_2z_2(t)-Kx_1(t)+2\tilde{H}(t)\nonumber \\{} & {} -{M}(x_1(t))\dot{\alpha }(t)) -\frac{1}{2}\dot{M}(x_1(t))\alpha (t)]\nonumber \\{} & {} +\sum \limits _{i=1}^{2}\frac{1}{\gamma _i\mu _i(t)}\tilde{\mu }_i(t)\dot{\hat{\mu }}_i(t) -\sum \limits _{i=1}^{2}\frac{k_1\varPi _{i}^2(t)}{\varpi _i-\varPi _{i}^2(t)}\nonumber \\= & {} \sum \limits _{i=1}^{2}z_{2i}(t)[g_{1i}(t)\tau _i(t)+g_{2i}(t)]-k_2z_2^{\textrm{T}}(t)z_2(t)\\{} & {} +z_2^{\textrm{T}}(t)\bar{\tau }(t)-\sum \limits _{i=1}^{2}\frac{k_1\varPi _{i}^2(t)}{\varpi _i-\varPi _{i}^2(t)}\nonumber \\{} & {} +\sum \limits _{i=1}^{2}\frac{1}{\gamma _i\mu _i(t)}\tilde{\mu }_i(t)\left[ \gamma _iz_{2i}(t)\bar{\tau }_i(t)-\gamma _i\sigma _{i}{\hat{\mu }}_i(t)\right] \nonumber \\\le & {} -k_2z_2^{\textrm{T}}(t)z_2(t)+\sum \limits _{i=1}^{2}z_{2i}(t)g_{1i}(t)\tau _i(t)\\{} & {} +\sum \limits _{i=1}^{2}\frac{1}{\mu _i(t)}\tilde{\mu }_i(t)\left[ z_{2i}(t)\bar{\tau }_i(t)-\sigma _{i}{\hat{\mu }}_i(t)\right] \nonumber \\{} & {} -\sum \limits _{i=1}^{2}\left[ \frac{k_1\varPi _{i}^2(t)}{\varpi _i-\varPi _{i}^2(t)}+z_{2i}(t)\bar{g}_{2i}(t)\right] \\{} & {} +\sum \limits _{i=1}^{4}z_{2i}(t)\bar{\tau }_{i}(t)\nonumber \end{aligned}$$

Substituting Eqs. (29)–(30) into the above inequality, one has

$$\begin{aligned} \dot{V}(t)\le & {} -k_2z_2^{\textrm{T}}(t)z_2(t) -\sum \limits _{i=1}^{2}\frac{k_1\varPi _{i}^2(t)}{\varpi _i-\varPi _{i}^2(t)}\nonumber \\{} & {} -\sum \limits _{i=1}^{2}z_{2i}(t)g_{1i}(t)\frac{(x_{2i}(t)-\alpha _i(t))\hat{\mu }^2_i(t)\bar{\tau }_i^2(t)}{|(x_{2i}(t)-\alpha (t))\hat{\mu }(t)\bar{\tau }(t)|+\rho _i}\nonumber \\{} & {} +\sum \limits _{i=1}^{2}\frac{1}{\mu _i(t)}\tilde{\mu }_i(t)\left[ z_{2i}(t)\bar{\tau }_i(t)-\sigma _{i}{\hat{\mu }}_i(t)\right] \nonumber \\{} & {} +\sum \limits _{i=1}^{2}z_{2i}(t)\bar{g}_{2i}(t)+\sum \limits _{i=1}^{4}z_{2i}(t)\bar{\tau }_{i}(t) \nonumber \\\le & {} -k_2z_2^{\textrm{T}}(t)z_2(t) -\sum \limits _{i=1}^{2}\frac{k_1\varPi _{i}^2(t)}{\varpi _i-\varPi _{i}^2(t)}\nonumber \\{} & {} +\sum \limits _{i=1}^{2}z_{2i}(t)\bar{g}_{2i}(t)+\sum \limits _{i=1}^{4}z_{2i}(t)\bar{\tau }_{i}(t)\nonumber \\{} & {} +\sum \limits _{i=1}^{2}\frac{1}{\mu _i(t)}\tilde{\mu }_i(t)\left[ z_{2i}(t)\bar{\tau }_i(t)-\sigma _{i}{\hat{\mu }}_i(t)\right] \nonumber \\{} & {} -\sum \limits _{i=1}^{2}g_{1i}(t)\frac{z_{2i}^2(t)\hat{\mu }^2_i(t)\bar{\tau }_i^2(t)}{|z_{2i}(t)\hat{\mu }_i(t)\bar{\tau }_i(t)|+\rho _i} \end{aligned}$$

(36)

Since

$$\begin{aligned} |\xi |-\frac{|\xi |^2}{\rho _i+|\xi |}=\frac{\rho _i|\xi |}{\rho _i+|\xi |}<\rho _i \end{aligned}$$

(37)

Then

$$\begin{aligned} -\frac{z_{2i}^2(t)\hat{\mu }^2_i(t)\bar{\tau }_i^2(t)}{|z_{2i}(t)\hat{\mu }_i(t)\bar{\tau }_i(t)|+\rho _i} <\rho _i-z_{2i}(t)\hat{\mu }_i(t)\bar{\tau }_i(t)\nonumber \\ \end{aligned}$$

(38)

Noticing that $g_{1i}(t)\geqslant g_{1imin}=\frac{1}{\mu _i(t)}>0$, one gets

$$\begin{aligned} -g_{1i}\frac{z_{2i}^2(t)\hat{\mu }^2_i(t)\bar{\tau }_i^2(t)}{|z_{2i}(t)\hat{\mu }_i(t)\bar{\tau }_i(t)|+\rho _i} <\frac{1}{\mu _i}(\rho _i-z_{2i}(t)\hat{\mu }_i(t)\bar{\tau }_i(t))\nonumber \\ \end{aligned}$$

(39)

With the above relationship (39), one has

$$\begin{aligned} \dot{V}(t)\le & {} -(k_2-1)z_2^{\textrm{T}}(t)z_2(t)+\sum \limits _{i=1}^{4}z_{2i}(t)\bar{\tau }_{i}(t) +\bar{g}_2^2(t)\nonumber \\{} & {} +\sum \limits _{i=1}^{2}\frac{1}{\mu _i}\rho _i \nonumber \\{} & {} +\sum \limits _{i=1}^{2}\frac{1}{\mu _i(t)}\left[ \tilde{\mu }_i(t)z_{2i}(t)\bar{\tau }_i(t)-z_{2i}(t)\hat{\mu }_i(t)\bar{\tau }_i(t)\right] \nonumber \\{} & {} -\sum \limits _{i=1}^{2}\left[ \frac{k_1\varPi _{i}^2(t)}{\varpi _i-\varPi _{i}^2(t)} +\frac{1}{\mu _i(t)}\tilde{\mu }_i(t)\sigma _{i}{\hat{\mu }}_i(t)\right] \nonumber \\\le & {} -(k_2-1)z_2^{\textrm{T}}(t)z_2(t)+\sum \limits _{i=3}^{4}z_{2i}(t)\bar{\tau }_{i}(t)\nonumber \\{} & {} -\sum \limits _{i=1}^{2}\frac{k_1\varPi _{i}^2(t)}{\varpi _i-\varPi _{i}^2(t)} \nonumber \\{} & {} -\sum \limits _{i=1}^{2}\frac{1}{\mu _i(t)}\tilde{\mu }_i(t)\sigma _{i}{\hat{\mu }}_i(t)+\bar{g}_2^2(t)+\sum \limits _{i=1}^{2}\frac{1}{\mu _i}\rho _i \end{aligned}$$

(40)

with $\bar{g}_2^2(t)=\max \{\bar{g}_{21}(t),\bar{g}_{22}(t)\}$. $\square$

Since the RFCRSs only has two real input $\tau _{j}(t)$ with $j=1,2$, and $\bar{\tau }_j(t)$ with $j=3,4$ in Eq. (30) is not required, there exists two extra virtual controller $\alpha _{j}(t)$ with $j=3,4$ such that

$$\begin{aligned} \sum \limits _{i=3}^{4}z_{2i}(t)\bar{\tau }_{i}(t)=0. \end{aligned}$$

(41)

With the above relation, one can obtain

$$\begin{aligned} \dot{V}(t) \!\le & {} \!-(k_2-1)z_2^\textrm{T}(t)z_2(t)-\sum \limits _{i=1}^{2}\frac{k_1\varPi _{i}^2(t)}{\varpi _i-\varPi _{i}^2(t)}+\bar{g}_2^2(t)\nonumber \\ \!\!\!{} & {} \!\!\!-\sum \limits _{i=1}^{2}\frac{1}{\mu _i(t)}\tilde{\mu }_i(t)\sigma _{i}{\hat{\mu }}_i(t)+\sum \limits _{i=1}^{2}\frac{1}{\mu _i}\rho _i \end{aligned}$$

(42)

Noticing that

$$\begin{aligned}{} & {} -\tilde{\mu }_i(t){\hat{\mu }}_i(t)\!=\!-\tilde{\mu }_i(t)(\tilde{\mu }_i(t)+\mu _i)=-\tilde{\mu }^2_i(t)-\tilde{\mu }_i(t)\mu _i\nonumber \\{} & {} \qquad \!\!\!\le \!-\tilde{\mu }_i^2(t)+\frac{1}{2}\tilde{\mu }_i^2(t)+\frac{1}{2}\mu _i^2(t) =-\frac{1}{2}\tilde{\mu }_i^2(t)+\frac{1}{2}\mu ^2_i(t)\nonumber \\ \end{aligned}$$

(43)

Then,

$$\begin{aligned} -\frac{1}{\mu _i}\tilde{\mu }_i(t)\sigma _{i}{\hat{\mu }}_i(t)\le -\frac{\sigma _{i}}{2}\tilde{\mu }_i^2(t)+\frac{\sigma _{i}}{2}\mu _i^2(t) \end{aligned}$$

(44)

Therefore, one has

$$\begin{aligned} \dot{V}(t) \!\le & {} \!-(k_2-1)z_2^\textrm{T}(t)z_2(t)-\sum \limits _{i=1}^{2}\frac{k_1\varPi _{i}^2(t)}{\varpi _i-\varPi _{i}^2(t)}+\bar{g}_2^2(t)\nonumber \\ \!\!\!{} & {} \!\!\!-\sum \limits _{i=1}^{2}\frac{\sigma _{1}}{2}\tilde{\mu }_i^2(t)+\sum \limits _{i=1}^{2}\frac{\sigma _{i}}{2}\mu _i^2(t)+\sum \limits _{i=1}^{2}\frac{1}{\mu _i}\rho _i \end{aligned}$$

(45)

By using Lemma 1, one can obtain

$$\begin{aligned} \dot{V}(t) \!\!\le & {} \!\!-(k_2-1)z_2^\textrm{T}(t)z_2(t)-k_1\sum \limits _{i=1}^{2}\ln \frac{\varpi _i}{\varpi _i-\varPi _{i}^2(t)}\nonumber \\ \!\!{} & {} \!\!-\sum \limits _{i=1}^{2}\frac{\sigma _{1}}{2}\tilde{\mu }_i^2(t)+\sum \limits _{i=1}^{2}\frac{\sigma _{i}}{2}\mu _i^2(t)\nonumber \\{} & {} +\sum \limits _{i=1}^{2}\frac{1}{\mu _i}\rho _i+\bar{g}_2^2(t)\nonumber \\ \!\!\le & {} \!\!-c_2V(t)+\lambda \end{aligned}$$

(46)

with $c_2=\min \{\gamma _1\sigma ,2k_1,\frac{2(k_2-1)}{\lambda _{max}(M(x_1))}\}$ and $\lambda =\bar{g}_2(t)+\sum \limits _{i=1}^{2}\frac{\sigma _{i}}{2}\mu _i^2(t)+\sum \limits _{i=1}^{2}\frac{1}{\mu _i}\rho _i$.

Then, one can derive that

$$\begin{aligned} {V}(t)\le \frac{\lambda }{c_2}+\left( V(0)-\frac{\lambda }{c_2}\right) e^{-c_2t} \le \frac{\lambda }{c_2}+V(0) \end{aligned}$$

(47)

Meanwhile, one has

$$\begin{aligned} \frac{1}{2}||z_2(t)||^2\le & {} \left( \frac{\lambda }{c_2}+V(0)\right) /\lambda _{min}(M), \end{aligned}$$

(48)

$$\begin{aligned} \frac{1}{2\gamma \mu }||\tilde{\mu }(t)||^2\le & {} \frac{\lambda }{c_2}+V(0) \end{aligned}$$

(49)

with $\gamma =\max \{\gamma _1,\gamma _2\}$ and $\mu =\max \{\mu _1,\mu _2\}$.

It can be seen from Ineq. (47) that $\sqrt{\ln \frac{\varpi _i}{\varpi _i-\varPi _{i}^2(t)}}$ is uniformly ultimately converge to a bounded compact set $\varXi$. Given any $\varsigma _*^2>\frac{2\lambda }{c_2}>0$, then it selects T meets that $\ln \frac{\varpi _i}{\varpi _i-\varPi _{i}^2(t)}\leqslant \varsigma _*^2,|z_i(t)|\leqslant \varsigma _*^2, \forall t>T$. Thus, the compact set $\varXi$ can be defined as $\{z_i\in \mathbb {R}^4: \ln \frac{\varpi _i}{\varpi _i-\varPi _{i}^2(t)}\leqslant \varsigma _*^2,|z_i(t)|\leqslant \varsigma _*^2\}$

In terms of the aforesaid observation, it follows that $\ln \frac{\varpi _i}{\varpi _i-\varPi _{i}^2(t)}\leqslant \varsigma _*^2$ and further derived as follows:

$$\begin{aligned} \ln \frac{\varpi _i}{\varpi _i-\varPi _{i}^2(t)}\leqslant \varsigma _*^2 \Rightarrow -\sqrt{\varpi _i e^{-\varsigma _*^2}}\leqslant \varPi _{i}(t) \leqslant \sqrt{\varpi _i e^{-\varsigma _*^2}}\nonumber \\ \Rightarrow e_i(t)\leqslant \frac{\mathcal {B}_{i}+\mathcal {A}_{i}+(\mathcal {B}_{i}-\mathcal {A}_{i})\sqrt{\varpi _i e^{-\varsigma _*^2}}}{2} \end{aligned}$$

(50)

Further, there selects $\mu ^*$ sufficiently small via adjusting the parameters, then tracking errors $e_i(t)$ approach $(\chi _{ai}+\chi _{bi})/2$ with $i=1,2$.

With the definition of $\varPi _{i}(t)$, one can derive

$$\begin{aligned}{} & {} \sqrt{\varpi _i e^{-\varsigma _*^2}}\leqslant \sqrt{\varpi _i}<1 \Rightarrow (\mathcal {B}_{i}-\mathcal {A}_{i})\sqrt{\varpi _i e^{-\varsigma _*^2}}< \mathcal {B}_{i}-\mathcal {A}_{i}\nonumber \\{} & {} \qquad \Rightarrow \frac{\mathcal {B}_{i}+\mathcal {A}_{i}+(\mathcal {B}_{i}-\mathcal {A}_{i})\sqrt{\varpi _i e^{-\varsigma _*^2}}}{2}<\mathcal {B}_{i} \end{aligned}$$

(51)

Similarly, one can also derive that

$$\begin{aligned} \frac{\mathcal {B}_{i}+\mathcal {A}_{i}-(\mathcal {B}_{i}-\mathcal {A}_{i})\sqrt{\varpi _i e^{-\varsigma _*^2}}}{2}>\mathcal {A}_{i} \end{aligned}$$

(52)

Combining Ineq. (50) with Ineqs. (51)–(52), one has

$$\begin{aligned} \mathcal {A}_{i}(t)<e_i(t)<\mathcal {B}_{i}(t)\quad \textrm{with}\quad i=1.2. \end{aligned}$$

(53)

It should be concluded from the above analysis that the tracking errors of angular position $e_i(t)$ are constricted between $\mathcal {A}_{i}$ and $\mathcal {B}_{i}$ by virtue of selecting appropriate functions $\mathcal {A}_{i}$ and $\mathcal {B}_{i}$, which also indicates that RFCRSs achieve prescribed performance $\mathcal {K}$ defined in Definition 1.

This is the end of Theorem 2.

6 Numerical simulation

To demonstrate the viability of the constructed control law with flexible prescribed regulation performance. These simulation results on the comparison with the PD law [39], different flexible functions, and logarithmic quantization will be divided into three cases to demonstrate.

Simulation of flexible prescribed performance control will be shown in the first part. A PD controller [39] will be introduced in the second part in comparison. Both the PD controller and the prescribed performance controller based on the logarithm quantizer will be revealed in the third part. The parameters of rigid–flexible robotic systems are specified in Table 1. The desired angular positions are chosen as $\theta _{1d}=0.5$, $\theta _{2d}=0.8$.

Case 1. Novel flexible prescribed performance control without quantization in comparison with PD control

Regarding this PD control law [39] is utilized to achieve the tracking control of angular position and the flexible link’s ability to reduce vibration in comparison with the proposed FPPC laws. The PD control is described by: $u_j(t)=-k_{jp}(\theta _{j}(t)-\theta _{jd})-k_{jd}\dot{\theta _{j}}(t)$, where $k_{jp}$ and $k_{jd}$ are positive gains with $j=1,2$.

The corresponding control values and performance functions are listed as follows: $k_{1p}=38$, $k_{1d}=22$, $k_{2p}=23$, $k_{2d}=5$;

$k_1=1.8$, $k_2=3.6$, $\mathcal {A}_1(t)=-0.65$ and $\mathcal {B}_1(t)=0.65+0.7e^{-8t}$, $\mathcal {A}_2(t)=-0.50-e^{-1t}$, $\mathcal {B}_2(t)=0.50+0.6e^{-0.72t}$.

The real profiles of two angular position regulation using PD and FPPC control are depicted in Figs. 3, 4, respectively. It is clear that the advocated FPPC method provides superior regulation performance than the comparative PD control [39], especially as can be seen from the small windows of Figs. 3 and 4. To show the deformation of flexible beam, the flexible displacements of general 1st and 2nd mode coordinates are shown in Figs. 5, 6. In view of the above vibrations in Figs. 5, 6, the vibration of the flexible beam is quickly eliminated approach zero, and the suppression effect of the developed FPPC law is faster than the compared PD control. It is noted that the first mode vibration is the dominant frequency and the second mode will also be suppressed as the first mode vibration reduces to zero in Figs. 5, 6. The corresponding vibration surface using the PD law and FPPC laws are revealed in Figs. 7, 8. Although the reduced rigid–flexible robotic system has high mode numbers, the regulation control performance is not influenced as shown in Figs. 9, 10. It can also be observed that the two-mode vibrations can be suppressed rapidly and smoothly with the proposed method in comparison with the PD control law [39].

In view of the above comparison simulations, although the traditional PD control [39] has a positive effect on trajectory regulation and vibration suppression, its control performance is not satisfactory in comparison with the developed robust adaptive FPPC method.

Fig. 3

Actual tracking of $\theta _{1d}$(rad) in Case 1

Fig. 4

Actual tracking of $\theta _{2d}$(rad) in Case 1

Fig. 5

1st mode vibration $q_1(t)$(m) in Case 1

Fig. 6

2nd mode vibration $q_2(t)$(m) in Case 1

Fig. 7

The total vibration surface $w(\xi ,t)$(m) under the PD law

Fig. 8

The total vibration surface $w(\xi ,t)$(m) under the FPPC law

Fig. 9

Regulation index $e_1(t)$(rad) under FPPC law in Case 1

Fig. 10

Regulation index $e_2(t)$(rad) under FPPC law in Case 1

The control gains for the quantized FPPC scheme are determined through the following procedures:

• 1. Setting the quantized parameters as $\rho _1=\rho _2=0.01$ and $k_1=k_2=0.01$. Then, increment the value of K from zero until the controlled system exhibits slight oscillations to some extent.

• 2. Determining the maximum error and error rate of the two angular positions under the tuned values of $k_1$ and $k_2$. Initially, choose half of the maximum error as the value for $k_1$ and half of the maximum error rate as $k_2$. Subsequently, increase the values of $\rho _j, j=1,2$ while simultaneously decreasing the value of K to further minimize the error, making necessary trade-offs between the two parameters.

• 3. Maintaining the tuning of $k_j, j=1,2$ and K achieved in the first two stages, and then increase the values of $\sigma _{ j}$ and $\gamma _{j}, j=1, 2$ to enhance dynamic regulation and vibration suppression performance. Next, finely adjust these two values and strike a balance between $\sigma _{j}$ and $\gamma _{j}$.

Case 2. Novel flexible prescribed performance with different functional sets $\mathcal {K}$

To better present the flexible prescribed performance under the limitations on a functional set $\mathcal {K}$. Some feature prescribed functions with different converge speeds are taken and the following three comparison conditions are considered:

Condition 1) $\mathcal {A}_{11}(t)=-0.58$, $\mathcal {B}_{11}(t)=0.58+0.3e^{-8t}$, and $\mathcal {A}_{12}(t)=-0.5-0.5e^{-0.75t}$, $\mathcal {B}_{12}(t)=0.5+0.6e^{-0.8t}$;

Fig. 11

Actual tracking of $\theta _{1d}$(rad) with different FPPCs in Case 2

Fig. 12

Actual tracking of $\theta _{2d}$(rad) with different FPPCs in Case 2

Fig. 13

Regulation index $e_1(t)$(rad)—Case 2

Fig. 14

Regulation index $e_2(t)$(rad)—Case 2

Condition 2) $\mathcal {A}_{21}(t)=-0.58$, $\mathcal {B}_{21}(t)=0.58+0.3e^{-1t}$ and $\mathcal {A}_{22}(t)=-0.5-0.45e^{-4t}$, $\mathcal {B}_{22}(t)=0.5+\frac{0.4}{1+t^2}$;

Condition 3) $\mathcal {A}_{31}(t)=-0.55$, $\mathcal {B}_{31}(t)=0.55+0.3e^{-0.5t}$ and $\mathcal {A}_{32}(t)=-0.5-0.45e^{-0.5t}$, $\mathcal {B}_{32}(t)=0.5+\frac{0.4}{1+2t^3}$.

In order to reflect the regulation ability of the different performance functions, the above selected functions are divided into two categories, i.e., $\varrho +\mu e^{-\kappa t}$, $\frac{\kappa }{\mu +t^\varsigma }$. As for the first exponential function, $\mathcal {B}_{i1}(t)=0.58+0.3 e^{-\kappa _i t}$ are chosen that varies with exponential index $\kappa _i$, which determines the convergent rate of regulation error.

From Fig. 11, the regulation convergent rate increases with the increase of exponential gain $\kappa _i$. It is clear from Fig. 12 that the convergence performance of the exponential function $\varrho +\mu e^{-\kappa t}$ is superior to fractional polynomial function $\frac{\kappa }{\mu +t^\varsigma }$. Accordingly, the regulation error of two angular positions with prescribed performance functions is displayed in Figs. 13 and 14. From Figs. 15 to 16, it indicates that the generalized

Fig. 15

1st vibration mode $q_1(t)$(m)—Case 2

Fig. 16

2nd vibration mode $q_2(t)$(m)—Case 2

Fig. 17

The total vibration surface $w(\xi ,t)$(m) for Condition 1

Fig. 18

The total vibration surface $w(\xi ,t)$(m) for Condition 2

Fig. 19

The total vibration surface $w(\xi ,t)$(m) for Condition 3

Fig. 20

Actual tracking of $\theta _{1d}$(rad) with input quantization in Case 3

mode vibration can be reduced to zero with different rates. As shown in Figs. 17, 18, 19, the vibration displacements under the above prescribed perform functions become smaller along the time axis in contrast with the fractional polynomial function.

Case 3. Novel flexible prescribed performance $\mathcal {K}$ with input quantization

To better illustrate the efficacy of the quantized FPPC law in this case, the following control gains and performance functions are listed. $k_1=1.8$, $k_2=3.6$, $\mathcal {A}_1(t)=-0.60$ and $\mathcal {B}_1(t)=0.60+0.45e^{-9t}$, $\mathcal {A}_2(t)=-0.31-0.55e^{-7t}$, $\mathcal {B}_2(t)=0.31+\frac{1}{2+2t^3}$, $\rho _1=0.025$, $\delta _1=0.25$, $\rho _{2}=0.01$, $\delta _2=0.25$, $\sigma _{1}=0.01$ and $\sigma _{2}=0.015$, $\gamma _1=1.6$ and $\gamma _2=1.8$.

Figures 20 and 21 show the regulation profiles of angular positions under the designed FPPC law with input quantization. Figure 22 represents the flexible displacement of the closed-loop RFCRSs with the quantized FPPC law. The corresponding control inputs of the RFCRSs with quantization are displayed in Figs. 23, 24. Note that the regulation errors cluster in a tiny area near zero in the presence of input quantization in Figs. 25, 26 in comparison with the regulation errors in Figs. 9, 10.

Fig. 21

Actual tracking of $\theta _{2d}$(rad) with input quantization in Case 3

Fig. 22

The total vibration surface $w(\xi ,t)$(m) in Case 3

Fig. 23

Quantized input $\mathcal {Q}(\tau _1(t))$(Nm) in Case 3

Fig. 24

Quantized input $\mathcal {Q}(\tau _2(t))$(Nm) in Case 3

Fig. 25

Regulation $e_1(t)$(rad) under quantization

Fig. 26

Regulation $e_2(t)$(rad) under quantization

In terms of the above results, it can be concluded that, with the developed FPPC law with quantization, the desired angular position can be reached with flexible prescribed performance and the vibration can also be eliminated.

7 Conclusions

In this work, the model of the RFCRSs has been obtained by using the reduced-order strategy—AMM. The derived model and the flexible prescribed performance control (FPPC) law have been proposed for both with and without quantization. According to the backstepping-based Lyapunov stability method, the tracking errors of RFCRSs with the proposed FPPC laws converge to a compact set within the prescribed performance in the presence of quantization. Meanwhile, the regulation errors of the rigid–flexible robotic systems without quantization eventually converge rapidly to zero. Finally, the cases of simulation demonstrate the feasibility of the proposed flexible prescribed performance control and the input quantization has very little effect on the controlled RFCRSs with robust adaptive FPPC law. In our forthcoming work, we will explore the experimental implementation of the proposed FPPC approaches on rigid–flexible robotic systems. This will involve utilizing dSPACE-MATLAB/Simulink real-time hardware-in-the-loop control technology to validate FPPC methods.