Coupling failure dynamics of tooth surface morphology and wear based on fractal theory

Abstract

This paper aims to reveal the coupling relationship between surface topography and wear and introduce a new coupling failure dynamic model of tooth surface topography and wear. Based on the fractal theory, the theoretical model of gear rough surface and the prediction model of wear are established and reveal the relationship between tooth surface roughness, wear depth, and meshing position. In particular, we analyze rough tooth surfaces’ time-varying meshing stiffness and system dynamic characteristics. The greater the contact surface roughness level, the more severe the wear behavior, and the greater the contact deformation of the gear; the vibration response and amplitude growth rate are highly related to the surface roughness. The results of coupled vibration characteristics show that the topography of the contact surface causes the system noise and shock to increase from the two aspects of stiffness excitation and error excitation. The multi-state coupled dynamic model of the contact surface can provide a theoretical basis for optimizing gear systems.

1 Introduction

In actual gear transmission systems, there are many concave and convex microstructures on the contact surface. The geometry, height, and density of asperities are randomly distributed. In engineering practice, the asperities on the contact surface of the gear have a great influence on wear, friction, transmission efficiency, and lubrication performance. Therefore, the calculation and simulation of the contact morphology are very important to promote the study of the gear contact characteristics [1,2,3,4,5]. In the gear transmission system, tooth surface morphology and wear are common surface features. They reduce the stability of the system, cause noise, and affect the overall performance of mechanical equipment. Researching the effect of tooth surface morphology and wear on the gear transmission system is significant for dynamic analysis and fault diagnosis [6]. In actual working conditions, rough tooth surfaces and some early faults often coexist in gears, and the effect of tooth surface roughness should not be ignored [7,8,9,10]. It is well-known that lubricating oil is forbidden in some more precise transmission and transportation systems or optical instruments, so the gear transmission system with dry friction exists in practice [11,12,13,14,15,16]. The research background of this paper is a dry friction gear transmission system. The gear surface comprises many asperities with different geometric shapes, heights, and densities. The size of asperities is directly related to the contact deformation. Different deformation regions are defined by using the bottom diameter of asperity and the critical condition of contact deformation. The failure mechanism of contact fatigue is analyzed according to the relationship between contact area and contact load.

The study of rough surfaces based on fractal theory has always been a difficult problem in the field of nonlinear tribology [17,18,19]. In engineering practice, the existence of surface roughness is an unavoidable problem, so many scholars are committed to the study of rough surface contact [20,21,22,23]. Rizmer et al. [24] studied the elastic–plastic deformation behavior of spheres and rigid planes. Based on fractal theory, Liu et al. [25, 26] analyzed the influence of friction force on the micro-morphology of contact surface, and established an analytical contact stiffness model considering friction factors. Zhai et al. [27] studied the effects of roughness and fractal parameters on fractal contact stiffness, and verified the rationality of the fractal contact stiffness model through experiments. Huang et al. [28, 29] established a dynamic model of fractal clearance gear, and explained the relationship between bifurcation, chaos, and microscopic characteristics of tooth surface in detail. This work is of great significance for promoting the development of fractal theory in the nonlinear field. With the development of fractal theory, more and more scholars are concerned about the application of fractal theory in practical engineering and solving some nonlinear problems in tribology [30,31,32,33]. Zhou et al. [34] established a rough surface model involving Gaussian height distribution and exponential autocorrelation function, and verified the accuracy of the model through experiments. Zhao et al. [35] studied the variation of normal contact stiffness during mechanical loading and unloading. Based on fractal theory and Hertz contact theory, Liao et al. [36] derived the relationship between contact stiffness and normal contact stiffness, which is of great significance for the development of fractal contact theory and the design and manufacture of mechanical parts.

The calculation of Time-varying meshing stiffness (TVMS) is a hot topic for many scholars, and the stiffness is affected by the meshing point, tooth profile parameters, and contact surface morphology. Based on existing research, the potential energy method is often used to calculate TVMS, which is the theoretical basis for calculating the meshing stiffness [37,38,39,40]. Ma et al. [41] considered the actual transition curve and modified the potential energy method. In addition, the meshing stiffness is divided into two models based on the size and position of the tooth root circle, and the rationality of the model is verified by finite element analysis. Xie et al. [42, 43] used the finite element method to calculate TVMS. It was found that the theoretical calculation results differed from the finite element method in the double-tooth meshing area. As a result, Xie proposed a corrected TVMS calculation model that considers the coupling effect between teeth in multi-tooth meshing, and the modified model was consistent with the finite element results. Chen et al. [44] proposed a contact stiffness calculation method that considered nonlinear contact load, which improved the Hertz contact stiffness calculation method. Shen et al. [45] studied the effect of wear on the TVMS of planetary gear trains and found that wear has a great influence on the stability of planetary gear trains. Contact stiffness is an essential part of TVMS, but only a few scholars have researched the contact stiffness of the tooth surface. Wang et al. [46] established a rough surface contact model which is close to the actual working condition than the traditional model and used a linear equation set to represent the contact load of the rough surface obtained through the experiment. This model can explain the wear of the tooth surface more effectively. Yun et al. [47] proposed a calculation model of the fractal rough surface contact stiffness that considers friction factors. They explained the relationship between the diameter of the bottom surface of the asperity and the contact area and studied the effect of surface morphology, contact load, friction coefficient, and material coefficient on fractal contact stiffness. Xiao et al. [48] explained the relationship between normal load and normal contact stiffness and set up the relationship between resonant frequency and contact load. Yang et al. [49,50,51,52,53,54,55,56,57,58,59,60,61] analyzed the fault mechanism of the gear transmission system, established the dynamic model of the multi-fault gear transmission system, and analyzed the dynamic characteristics of the system with different fault types, which has important guiding significance for the fault diagnosis and structural design of the transmission system.

Therefore, there have been many research results about the contact characteristics of rough tooth surfaces and the failure mechanisms of gears, a little attention has been paid to the coupling characteristics of rough tooth surfaces and early gear faults. To study the coupling vibration characteristics of rough surfaces and early gear faults, the tooth surface morphology of numerical simulation is introduced into the calculation model of wear. A wear prediction model is established by considering the relationship between the wear coefficient and the wear amount of different tooth surface morphologies. The dynamic response of the gear transmission system is calculated for different tooth surface wear and tooth surface topography. Moreover, the wear and topography have different effects on the gear transmission system. Therefore, studying the coupling vibration characteristics of tooth surface morphology and wear is highly significant for the quantitative analysis of contact characteristics of gear surfaces, transmission accuracy, meshing stability, and the safety of the gear transmission system.

2 Surface morphology and wear model

The microstructure of the surface of mechanical parts is one of the main reasons for the wear behavior of the tooth surface. To analyze the influence of the tooth surface’s microstructure on the tooth surface’s wear, we need to establish a theoretical model of the tooth surface morphology to analyze the influence of the microstructure on the wear coefficient and contact load of the contact surface. Thus, a coupling model of microstructure and tooth surface wear is established. The surface numerical simulation is widely used in tribology and lubrication performance and can also be introduced into the study of tooth surface contact characteristics.

The W-M function has been applied to the contact surfaces of gears in Ref. [16]. The modified W-M function is often used to simulate the actual tooth profile of the gear.

$$ z(x) = L_{r} \left( {\frac{G}{{L_{r} }}} \right)^{D - 1} ({\text{In}}\gamma )^{1/2} \sum\limits_{n = 0}^{\max } {\gamma^{(D - 2)n} } \left[ {\cos \Phi_{1,n} - \cos \left( {\frac{{2\pi \gamma^{n} x}}{{L_{r} }} - \Phi_{1,n} } \right)} \right] $$

(1)

z(x) is the height of rough tooth surface asperity; L_r is the length scale of the asperity; x is the coordinate of the rough tooth surface; G is the characteristic scale parameter of the rough tooth surface, which is related to the height amplitude of the asperity; D is the fractal dimension of the rough surface, which is related to the density of asperities on the rough tooth surface, γ is the parameter to control the surface undulation density; Ф is the random phase of the rough tooth surface.

The tooth surface generally has a transverse or longitudinal texture in the actual gear transmission system. To analyze the contact characteristics with different morphologies, it is necessary to establish a three-dimensional rough contact surface. We obtain a fractal simulation of the gear tooth surface by superimposing the W-M functions in the x and y directions.

$$\begin{aligned} z(x,y) = & L_{rx} \left( {\frac{{G_{x} }}{{L_{x} }}} \right)^{{D_{x} - 1}} ({\text{In}}\gamma )^{1/2} \sum\limits_{n = 0}^{\max } {\gamma^{{(D_{x} - 2)n}} } \left[ {\cos \Phi_{1,n} - \cos \left( {\frac{{2{\uppi }\gamma^{n} x}}{{L_{rx} }} - \Phi_{1,n} } \right)} \right] \\\quad { + } & \, L_{ry} \left( {\frac{{G_{y} }}{{L_{ry} }}} \right)^{{D_{y} - 1}} ({\text{In}}\gamma )^{1/2} \sum\limits_{n = 0}^{\max } {\gamma^{{(D_{y} - 2)n}} } \left[ {\cos \Phi_{1,n} - \cos \left( {\frac{{2{\uppi }\gamma^{n} y}}{{L_{ry} }} - \Phi_{1,n} } \right)} \right] \\ \end{aligned} $$

(2)

z(x,y) is the contour height of the rough surface; x and y are the coordinates of the rough tooth surface. To research the dynamic characteristics and mechanical behavior of rough tooth surfaces, a three-dimensional rough tooth surface model is established based on fractal geometry. The rough surface based on fractal geometry is shown in Fig. 1.

Fig. 1

Rough surface model based on fractal geometry

The modeling process of the rough tooth surface is shown in Fig. 2. First, a rough surface model is established and superimposed on the curved tooth surface. It is widely acknowledged that the relationship between surface morphology and wear is a hot and challenging topic in tribology. Surface morphology and wear can interact, but their exact interaction is unclear.

Fig. 2

The process of modeling rough tooth surfaces: a Smooth gear surface; b Rough surfaces with fractal characteristics; c Rough tooth surface; d Partial detail drawing of rough tooth surface; e Enlarged view of partial details

As shown in Fig. 3, the surface of the gear has a certain degree of roughness after manufacturing. Long-term working gear surface may be worn. We established a wear calculation model under different tooth surface morphologies based on the Archard model to analyse the relationship between surface morphology and surface wear.

Fig. 3

The development process of gear wear failure form

Under the action of a contact load, gears are more likely to exacerbate wear behavior, which affects the mechanical properties of the gears. The Archard model is shown in Eq. (3).

$$ \frac{V}{S} = k_{w} \frac{W}{H} $$

(3)

In the formula, V is the wear volume; S is the relative sliding distance; W is the contact load; H is the material hardness. Due to the change of wear depth being nonlinear, the wear condition is determined by the tooth surface data from the previous time step. Therefore, we used a progressive relationship to calculate the wear depth.

$$ h_{p,n} = h_{p,n - 1} + k_{w} P_{n - 1} S_{p} $$

(4)

$$ S_{p} = 2a_{H} \left| {1 - \frac{{V_{r1} }}{{V_{r2} }}} \right| $$

(5)

a_H is the contact half-width; V_r1 and V_r2 are the tangential velocities; P_n−1 is the contact force of the meshing point; S_p is the relative sliding distance of the meshing point; k_w is the wear coefficient of the gear tooth surface, which is regarded as a fixed value in most studies, but it should be a value that changes with the meshing angle and surface morphology.

The calculation of contact loads is very important for wear prediction, and the contact load is not evenly distributed on the tooth profile and changes with the mating position. As shown in Fig. 4, in the single tooth meshing zone, the tooth surface bears the maximum contact load, and the contact load curve is straight. The contact load on the double tooth meshing tooth surface is either increasing or decreasing. We introduced the morphology parameters into the regression formula of the wear coefficient and established a wear calculation model based on the fractal theory.

$$ k_{w} = \frac{{3.987 \times 10^{29} }}{{E_{e} }}P_{w}^{1.219} G_{w}^{ - 7.377} S_{w}^{1.589} $$

(6)

$$ \frac{{P_{w} }}{{P_{total} }} = \frac{{K_{i} }}{{K_{total} }}(i = 1,2) $$

(7)

Fig. 4

The distribution of contact load of the gear transmission system

G_w is the viscosity coefficient; P_w is the contact load changing with the meshing angle, which can be solved according to Eq. (6). S_w is the tooth surface contact parameters; K_i is the meshing stiffness of a single gear; K_total is the comprehensive time-varying meshing stiffness of gears. The derivation of Eq. (5) is in the Ref. [4]

$$ S_{w} = \frac{{R_{{{\text{rms}}}} }}{{R_{e} }} $$

(8)

R_e is the comprehensive radius of curvature; R_rms is the root mean square value of the roughness of the contact tooth surface. The local roughness of the gear can reflect the characteristics of the contact zone. So the fractal tooth surface topography model was used to numerically calculate the root mean square of the roughness under actual working conditions.

$$ R_{rms} = \frac{1}{{n^{1/2} }}\left\{ {\sum\limits_{i = 1}^{n} {L_{r} \left( {\frac{G}{{L_{r} }}} \right)^{D - 1} ({\text{In}}\gamma )^{1/2} \sum\limits_{n = 0}^{\max } {\gamma^{(D - 2)n} } \left[ {\cos \Phi_{1,n} - \cos \left( {\frac{{2\pi \gamma^{n} x_{i} }}{{L_{r} }} - \Phi_{1,n} } \right)} \right]} } \right\}^{1/2} $$

(9)

The fractal dimension D and scale parameter G can change the tooth surface contact parameters, and affect the wear coefficient. The fractal dimension and scale coefficient determine the density and size of the asperity. The fractal dimension represents the space occupied by the asperity, which means the density of the asperity. The larger the fractal dimension, which means that the shape of the gear surface is finer and smoother. Whereas, the scale coefficient represents the height amplitude of asperities. The asperity on the gear surface has a great influence on the tooth surface wear, so the theoretical model of tooth surface wear should also consider this factor.

The time-varying wear coefficient is a very important parameter in the wear prediction model, which is assumed to be constant in the previous literature. However, many contact parameters may change the wear coefficient. As shown in Fig. 5, as the fractal dimension increases and the scale coefficient decreases, the tooth surface becomes rough and the wear coefficient decreases. In addition, with the increase of gear rotation angle, the wear coefficient has been changing. This is because the contact load and curvature radius of each meshing point are not equal.

Fig. 5

Influence of different fractal parameters on time-varying wear coefficients: a Effect of fractal dimension; b Effect of scale coefficient

The wear coefficient is affected by the surface morphology and the working environment of the gear, which is a non-negligible factor for predicting the wear of the gear transmission system. To study the effect of surface morphology on tooth surface wear depth, this research introduced roughness to represent the surface morphology of gears. The roughness is determined by the fractal dimension and scale coefficient.

The basic parameters of the gear transmission system are shown in Table 1, There is a certain relationship between surface roughness and fractal parameters. In the research of Ref. [46, 47], an expression for the relationship between surface roughness was given, and it was found that surface roughness is directly proportional to fractal dimension and inversely proportional to surface roughness and scale coefficient. The surface roughness and fractal parameters data in Table 2 are validated in the cited literature.

Table 1 Gear transmission system parameter

Table 2 The surface roughness of the drivetrain corresponds to the fractal parameters

The technical flow chart of studying the coupling vibration characteristics of gear surface topography and wear is shown in Fig. 6. Firstly, the coupling model of tooth surface topography and wear is established. Secondly, the time-varying meshing stiffness between gear meshing pairs is solved based on the potential energy method. Finally, the dynamic response of the coupling complex fault of the gear transmission system is solved.

Fig. 6

Rough tooth surface and wear coupling technology flowchart

N is the meshing times of the gear pair. The wear depth of the tooth surface increases with the increase of the surface depth, and the wear depth increases in multiples. As shown in Fig. 7, the maximum wear depth curve corresponding to Ra3.2 is close to 0.04 mm, while the maximum wear curve corresponding to Ra1.6 is less than 0.02 mm. This means that the influence of surface morphology on tooth wear should not be ignored, and it is necessary to combine surface morphology features in the wear prediction model. As shown in Fig. 8, the wear depth of the tooth surface increases with the increase of the number of meshing times, and the surface characteristics of the gaer become worse.

Fig. 7

The wear depth of tooth surface with different surface roughness

Fig. 8

The wear depth of tooth surface with different meshing times

3 Model of time-varying meshing stiffness

To analyze the influence of microtopography and tooth surface wear on the bearing capacity and deformation resistance of the gear transmission system, the fractal contact stiffness of the gear is established based on fractal theory. Combined with the variable cross-section elasticity theory, the calculation model of time-varying meshing stiffness is improved, and the influence of microtopography and tooth surface wear on time-varying meshing stiffness is analyzed.

3.1 Fractal contact stiffness

The study of micro-contact mechanics is a difficult scientific problem, and the micro-mechanical model is difficult to verify in the actual macro-model. An idea of macro-analysis is provided in Ref. [4], in which the distribution function of the micro-convex body and the contact coefficient of the curved surface are used to characterize the macro-contact model. These asperities undergo deformation under the contact load, and these deformed regions can be categorized into complete elastic deformation, elastic–plastic deformation, and complete plastic deformation. The distribution function of the asperity is expressed as follows.

$$ n(a) = \frac{D}{2}\psi^{{\frac{D - 2}{2}}} a_{L}^{\frac{D}{2}} a^{{\frac{ - D - 2}{2}}} $$

(10)

a_L is the contact area of the largest asperity; ψ is the scale expansion coefficient; The value of ψ is related to the fractal dimension and can be solved according to Eq. (11).

$$ D\left[ {\psi^{(2 - D)/D} - \left( {1 + \psi^{ - D/2} } \right)} \right]/(2 - D) = 1 $$

(11)

The real contact area is the sum of the contact areas of all asperities. The real contact area can be obtained by integrating the distribution function of the contact area.

$$ A_{r} = \int_{0}^{{a_{L} }} {a^{2} } n(a)da = \frac{D}{4 - D}\psi^{{\frac{D - 2}{2}}} a_{L}^{2} $$

(12)

A_r is the contact area, the critical deformation under different conditions can be used to judge the deformation of the asperity on the gear surface. According to the Hertz theory, the elastic critical deformation of asperity is known.

$$ \delta_{re} = \left( {\frac{{\pi K_{v} H}}{2E}} \right)^{2} R_{n} $$

(13)

$$ R_{n} = \frac{1}{{\left| {d^{2} z\left( x \right)/dx^{2} \left| {_{x = 0} } \right.} \right.}} $$

(14)

$$ A_{re} = {\uppi }R_{n} \delta_{re} = \left( {\frac{{K_{v} H}}{2E}} \right)^{2} {\uppi }^{3} R_{n}^{2} $$

(15)

H is the hardness of the material; K_v is the hardness coefficient, which is related to the Poisson’s ratio of the material; E is the equivalent elastic modulus; R_n is the curvature radius of the asperity peak; δ_re is the elastic critical deformation of asperity; A_re is the elastic critical contact area of the asperity, and asperities undergo complete elastic deformation when the contact area is less than the elastic critical contact area.

$$ \left\{ \begin{aligned} A_{rep} = & 7.1197A_{re} \\ \;A_{rp} = & 205.3827A_{re} \\ \end{aligned} \right. $$

(16)

A_rep is the first critical area of elastoplastic deformation; A_rp is the second critical area of elastoplastic deformation, There is a relationship between the critical contact area of the first elastic–plastic deformation and the second elastic–plastic deformation with the elastic critical contact area. In addition, Eq. (16) is derived from Ref. [5].

To establish the contact model of two rough surfaces, the coupling effect between the contact area and the base diameter is analyzed. The size of the bottom diameter affects the height and deformation of the asperity. Moreover, the deformation state of the asperity changes when the bottom diameter exceeds a certain constant. The deformation state of the asperity is limited by the size of the bottom diameter. The deformation of the micro-convex body satisfies the relation shown in Eq. (18). We can get the relation of the bottom diameter by taking the relation under the limit condition.

$$ \delta_{h} = G^{D - 1} (In\gamma )^{1/2} \left( {\frac{L}{{\gamma^{n} }}} \right)^{(2 - D)} $$

(17)

$$ \delta_{re} > \delta_{h} $$

(18)

By substituting Eqs. (13) and (17) into Eq. (18), the elastic critical length l_re at the bottom of the asperity is derived. The first elastic–plastic deformation critical length l_rep1 and the second elastic–plastic deformation critical length l_rep2 are derived.

$$ l_{re} = \left[ {\left( {\frac{{{\uppi }k_{v} H}}{2E}} \right)^{2} \left\{ {\frac{{\gamma^{n(2 - D)} }}{{{\uppi }^{2} G^{(2D - 2)} (In\gamma )^{1/2} }}} \right\}} \right]^{{\frac{1}{2 - 2D}}} $$

(19)

The elastic critical deformation in Eq. (13) is replaced by the first elastic–plastic deformation, and the first elastic–plastic critical length at the bottom of the asperity is derived from l_rep.

$$ l_{rep} = \left[ {6\left( {\frac{{{\uppi }k_{v} H}}{2E}} \right)^{2} \left\{ {\frac{{\gamma^{n(2 - D)} }}{{{\uppi }^{2} G^{(2D - 2)} (In\gamma )^{1/2} }}} \right\}} \right]^{{\frac{1}{2 - 2D}}} $$

(20)

By replacing the elastic critical deformation in Eq. (13) with the second elastic–plastic deformation, the second elastic plastic critical length at the bottom of asperity is deduced l_p.

$$ l_{p} = \left[ {110\left( {\frac{{{\uppi }k_{v} H}}{2E}} \right)^{2} \left\{ {\frac{{\gamma^{n(2 - D)} }}{{{\uppi }^{2} G^{(2D - 2)} (In\gamma )^{1/2} }}} \right\}} \right]^{{\frac{1}{2 - 2D}}} $$

(21)

The fractal dimension D is greater than 1, so l_re > l_rep > l_p; when the bottom diameter of asperity satisfies the relation l > l_re, only plastic deformation occurs. When the bottom diameter of the asperity satisfies l_re > l > l_rep, which may occur elastic deformation or the first elastoplastic deformation. When the bottom diameter of the asperity satisfies l_rep > l > l_p, may occur elastic deformation, first elastic–plastic deformation, or second elastic–plastic deformation. Moreover, when the bottom diameter l < l_p, may occur elastic deformation, first elastoplastic deformation, second elastoplastic deformation, and complete plastic deformation. The bottom diameter length and the contact area determine the deformation state of the asperity. The transformation relationship between the contact area and the deformation is shown in Eq. (16). To explain the deformation state of the asperity more intuitively, we use the deformation and the bottom diameter to describe the deformation state of the asperity, as shown in Fig. 9. δ_rp is the second elastic–plastic critical deformation δ_rp = 110δ_re; δ_rep is the first elastic–plastic critical deformationδ_rep = 6δ_re. These two relations are given in Ref. [40].

Fig. 9

Relationship between the bottom diameter of asperity and deformation interval

The contact stiffness of the gear is equal to the sum of the contact stiffness of all asperities on the entire contact tooth surface, that is, the sum of the contact stiffness of all asperities under different deformation states. The calculation formula is as the Ref. [10].

$$ K_{h} = K_{re} + K_{rep1} + K_{rep2} + K_{rp} $$

(22)

K_re is the sum of the contact stiffness of asperity in the elastic deformation state; K_rep1 is the sum of the contact stiffness of the asperity in the first elastoplastic state; K_rep2 is the sum of the contact stiffness of the asperity in the second elastoplastic state; K_rp is the sum of the contact stiffness of the asperity under the condition of complete plastic deformation. In previous studies, K_rp is generally considered to be zero when the contact surface undergoes complete plastic deformation, which is explained in detail in Yun’s research [16]. Due to the tooth being curved, the density of the asperity on the tooth surface is affected by the curved surface, so the tooth surface contact coefficient of the gear is introduced.

$$ \lambda = \left\{ {\frac{{\left[ {3PR_{p} R_{g} /4E\left( {R_{p} + R_{g} } \right)} \right]^{2/3} }}{{4\left( {R_{p}^{2} + R_{g}^{2} } \right)}}} \right\}^{{\frac{2}{{R_{p} }} + \frac{2}{{R_{g} }}}} $$

(23)

λ is the unit load coefficient along the contact line; The fractal contact stiffness of the rough surface is calculated. The calculation method is shown in Eq. (24).

$$ K_{h} = \int_{{l_{0} }}^{{l_{rep} }} {\int_{0}^{{A_{re} }} {\lambda k_{re} } } n(a){\text{d}}a{\text{d}}l + \int_{{l_{0} }}^{{l_{re} }} {\int_{{A_{re} }}^{{A_{rep} }} {\lambda k_{rep1} } } n(a){\text{d}}a{\text{d}}l + \int_{{A_{rep} }}^{{A_{rp} }} {\lambda k_{rep2} n(a){\text{d}}a} {\text{d}}l $$

(24)

k_rep1, k_rep2 is the stiffness of the first elastic–plastic deformation and the second elastic–plastic deformation of a single asperity; k_re is the elastic deformation of the contact stiffness. The formulas for these three parameters are given in Ref. [15]. n(a) is the distribution function of asperity on a rough tooth surface.

Contact load and contact stiffness are the key parameters to describe the mechanical contact and compression behavior, and the contact surface undergoes deformation under the action of contact load. Surface roughness can increase the deformation of the contact surface under load, which is the ratio of contact load to contact stiffness. As shown in Fig. 10, the contact stiffness of the tooth surface decreases greatly with the increase of the roughness of the surface; that is, the finer the tooth surface, the better the contact performance of the gear, the rougher the tooth surface, the worse the bearing capacity of the gear, and the more prone to contact fatigue.

Fig. 10

Contact stiffness corresponding to different surface roughness

3.2 Calculation model of time-varying meshing stiffness

The gear teeth deform under the action of external load in the meshing process, which affects the normal operation of mechanical equipment. Therefore, it is necessary to analyze the deformation of the gear transmission system in detail,

The calculation of comprehensive TVMS is very important for the design of gear transmission systems and the research of fault diagnosis. According to the theory of variable cross-section elastic cantilever beam in Ref. [41, 42], the gear is regarded as a cantilever beam structure. Through the accurate modeling of the gear tooth profile and the analysis of the force and deformation, the comprehensive TVMS of the gear is calculated by the potential energy method. As shown in Fig. 11R_b is the base circle radius; R_f is the radius of the tooth root circle; F is the external load on the gear meshing point; d is the effective tooth length of integral; β is the angle between the meshing force and the direction perpendicular to the tooth center line; α₁ is the half tooth angle corresponding to the base circle; α₂ is the half tooth angle corresponding to the tooth root circle; α₁ and α₂ can be calculated by the tooth thickness formula at the base circle.

$$ \frac{1}{{k_{b} }} = \int_{ - \beta }^{{\alpha_{1} }} {\frac{{3{\rm M}^{2} (\alpha_{1} - \alpha )\cos (\alpha ) \times {\rm M}^{2} }}{{2EL\left[ {\sin (\alpha ) + (\alpha_{1} - \alpha )\cos (\alpha )} \right]^{3} }}} d\alpha + \int_{0}^{{R_{b} - R_{f} }} {\frac{{[(d - x)\cos \beta - h\sin \beta ]^{2} }}{{EI_{x1} }}} dx $$

(25)

$$ \frac{1}{{k_{s} }} = \int_{ - \beta }^{{\alpha_{1} }} {\frac{{1.2(1 + v)(\alpha_{1} - \alpha )\cos \alpha \cos^{2} \beta }}{{EL\left[ {\sin (\alpha ) + (\alpha_{1} - \alpha )\cos (\alpha )} \right]}}} d\alpha + \int_{0}^{{R_{b} - R_{f} }} {\frac{{1.2\cos^{2} \beta }}{{GA_{x1} }}dx} $$

(26)

$$ \frac{1}{{k_{a} }} = \int_{ - \beta }^{{\alpha_{1} }} {\frac{{(\alpha_{1} - \alpha )\cos \alpha \sin^{2} \beta }}{{EL\left[ {\sin (\alpha ) + (\alpha_{1} - \alpha )\cos (\alpha )} \right]}}} d\alpha + \int_{0}^{{R_{b} - R_{f} }} {\frac{{\sin^{2} \beta }}{{EA_{x1} }}dx} $$

(27)

G is the material shear deformation-related parameters; E is the elastic modulus; k_b is the bending stiffness of the gear; k_a is the axial compression stiffness of the gear; k_s is the shear stiffness of the gear; v is the Poisson’s ratio; β is the pressure angle at the gear meshing; L is the length of contact line; M is parameters related to tooth profile, and the calculation formula is as follows.

$$ {\text{M}} = 1 + \cos (\beta )\left[ {(\alpha_{1} - \alpha )\sin (\alpha ) - \cos (\alpha )} \right] $$

(28)

Fig. 11

Geometric parameters of gear tooth profile: a Geometric parameters of matrix stiffness; b Tooth profile geometric parameters

According to the latest research of Xie [41, 42], there is a coupling phenomenon between teeth in the meshing process of gears, that is the load on a single tooth is halved when two teeth are engaged. There are two or more teeth loaded at the same time during gear meshing, so the coupling between teeth can not be ignored. The coupling stiffness between the teeth is as follows:

$$ \begin{aligned} \frac{1}{{k_{f21} }} = & \frac{1}{EL}\cos \left( {\beta_{1} } \right)\cos \left( {\beta_{2} } \right)\left[ {L_{1} \left( {\frac{{u_{1} u_{2} }}{{S_{f}^{2} }}} \right)^{2} + \left( {\tan \beta_{2} M_{1} + P_{1} } \right)\frac{{u_{1} }}{{S_{f} }}} \right. \\ + & \left. {\left( {\tan \beta_{1} Q_{1} + R_{1} } \right)\frac{{u_{2} }}{{S_{f}^{2} }} + \left( {\tan \beta_{1} S_{1} + T_{1} } \right)\tan \beta_{2} + U_{1} \tan \beta_{1} + V_{1} } \right] \\ \end{aligned} $$

(29)

$$ \begin{aligned} \frac{1}{{k_{f12} }} = & \frac{1}{EL}\cos \left( {\beta_{1} } \right)\cos \left( {\beta_{2} } \right)\left[ {L_{2} \left( {\frac{{u_{1} u_{2} }}{{S_{f}^{2} }}} \right)^{2} + \left( {\tan \beta_{1} M_{2} + P_{2} } \right)\frac{{u_{2} }}{{S_{f} }}} \right. \\ \, & + \left. {\left( {\tan \beta_{2} Q_{2} + R_{2} } \right)\frac{{u_{1} }}{{S_{f}^{2} }} + \left( {\tan \beta_{2} S_{2} + T_{2} } \right)\tan \beta_{1} + U_{2} \tan \beta_{2} + V_{2} } \right] \\ \end{aligned} $$

(30)

The values of L_i, M_i, P_i, Q_i, S_i, T_i, U_i, and V_i(i = 1,2) is the parameter related to matrix deformation, and there is a detailed calculation process in Ref. [41, 42]. u_{i (i = 1,2)} = R_b/cos(β)−R_f, S_f is the tooth root arc length S_f = 2θ_fR_f, θ_f is half of the tooth root arc corresponding to the center angle, h_f = r_f /r_int, r_int is the hub radius, r_f is the tooth root radius.

$$ K_{i} = \frac{1}{{k_{h,i} }} + \frac{1}{{k_{fp,i} }} + \frac{1}{{k_{ap,i} }} + \frac{1}{{k_{sp,i} }} + \frac{1}{{k_{{bp_{1} ,i}} }} + \frac{1}{{k_{fg,i} }} + \frac{1}{{k_{ag,i} }} + \frac{1}{{k_{sg,i} }} + \frac{1}{{k_{bg,i} }}(i = 1,2) $$

(31)

$$ K_{mesh} = \frac{{K_{1} + K_{2} - K_{1} K_{2} \left( {1/k_{f12} + 1/k_{f21} } \right)}}{{1 - K_{1} K_{2} /k_{f12} k_{f21} }} $$

(32)

k_h is the gear contact stiffness; K_mesh is the comprehensive TVMS. According to Eq. (31), K₁ and K₂ are calculated and substituted into Eq. (32) to solve the comprehensive TVMS. It should be noted that the value of K₂ is regarded as zero when only a pair of gear teeth are engaged. To study the effect of gear tooth surface microstructure, the gear fractal contact stiffness is adopted. Substituting the calculated fractal contact stiffness into Eq. (31), the gear’s comprehensive TVMS considering the tooth surface’s micro-morphology can be solved. The TVMS model based on tooth surface morphology was established by substituting the fractal contact stiffness into the traditional model. In Fig. 12, the meshing stiffness of the gear decreases with the increase in surface roughness.

Fig. 12

Time-varying mesh stiffness of gears with different Surface roughness

The surface roughness causes local elastic deformation of the contact point, which changes the stress distribution around the meshing point. This change introduces additional vibration and energy loss during the contact process, thus affecting the meshing stiffness. When the surface roughness grade is higher than Ra1.6, the meshing stiffness of the gears decreases obviously. In addition, surface roughness also affects wear behavior during gear meshing. When discussing the influence of surface roughness on meshing stiffness, the influence of tooth surface wear on time-varying meshing stiffness should also be discussed.

The effect of wear on the meshing stiffness is shown in Fig. 13, and the number of engagements represents the level of wear behavior. Due to the rough contact surface, TVMS shows obvious fluctuations. It can be seen that the influence of tooth wear on time-varying meshing stiffness is relatively small, so the influence of wear on stiffness excitation can be ignored in the dynamic modeling of the gear transmission system.

Fig. 13

Effect of tooth wear on time-varying mesh stiffness for surface roughness Ra3.2

4 Tooth surface morphology and gear wear coupling fault dynamic model

Tooth surface topography and tooth surface wear often coexist in engineering practice. To investigate the effect of tooth surface topography and tooth surface wear on the working performance of gears, we establish a coupled dynamic model of tooth surface topography and wear. The wear of the tooth surface changes the tooth profile, reduces the tooth thickness, and increases the working side clearance. So, the wear is considered a tooth profile error. The surface morphology cause a significant change in the stiffness excitation, which is taken into account in the dynamic model. A coupled fault dynamic model considering TVMS, comprehensive error, and time-varying meshing damping is established [50,51,52,53,54,55,56].

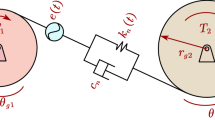
The dynamic model of the gear transmission system is shown in Fig. 14. m_p is the quality of the driving gear; m_g is the quality of the driven gear; J is the moment of inertia; T is the torque applied to the gear; K_p1, K_p2 is the radial support stiffness; C_p1, C_p2 is the radial support damping; K_m is TVMS of the gear; C_m is the meshing damping between teeth.

$$ \left\{ \begin{gathered} m_{p} \mathop {x_{1} }\limits^{..} + c_{p1} \mathop {x_{1} }\limits^{.} + k_{p1} x_{1} - \left( {k_{m} \left( {\left( {y_{1} - y_{2} } \right) - \left( {r_{1} \theta_{1} - r_{2} \theta_{2} } \right) - e_{i} } \right) + c_{m} \left( {\left( {\mathop y\limits^{.}_{1} - \mathop y\limits^{.}_{2} } \right) - \left( {r_{1} \mathop \theta \limits^{.}_{1} - r_{2} \mathop \theta \limits^{.}_{2} } \right) - \mathop e\limits^{.}_{i} } \right)} \right)_{f} = 0 \hfill \\ m_{p} \mathop {y_{1} }\limits^{..} + c_{p1} \mathop {y_{1} }\limits^{.} + k_{p1} y_{1} + \left( {k_{m} \left( {\left( {y_{1} - y_{2} } \right) - \left( {r_{1} \theta_{1} - r_{2} \theta_{2} } \right) - e_{i} } \right) + c_{m} \left( {\mathop y\limits^{.}_{1} - \mathop y\limits^{.}_{2} } \right) - \left( {r_{1} \mathop \theta \limits^{.}_{1} - r_{2} \mathop \theta \limits^{.}_{2} ) - \mathop e\limits^{.}_{i} } \right)} \right) = 0 \hfill \\ J_{1} \mathop \theta \limits^{..}_{1} - Rb_{1} \left( {k_{m} \left[ {\left( {y_{1} - y_{2} } \right) - \left( {r_{1} \theta_{1} - r_{2} \theta_{2} } \right) - e_{i} } \right] + c_{m} \left[ {\left( {\mathop y\limits^{.}_{1} - \mathop y\limits^{.}_{2} } \right) - \left( {r_{1} \mathop \theta \limits^{.}_{1} - r_{2} \mathop \theta \limits^{.}_{2} } \right) - \mathop e\limits^{.}_{i} } \right]} \right) = T_{1} \hfill \\ m_{g} \mathop {x_{2} }\limits^{..} + c_{p2} \mathop {x_{2} }\limits^{.} + k_{p2} x_{2} - \left( {k_{m} \left( {\left( {y_{1} - y_{2} } \right) - \left( {r_{1} \theta_{1} - r_{2} \theta_{2} } \right) - e_{i} } \right) + c_{m} \left( {\left( {\mathop y\limits^{.}_{1} - \mathop y\limits^{.}_{2} } \right) - \left( {r_{1} \mathop \theta \limits^{.}_{1} - r_{2} \mathop \theta \limits^{.}_{2} } \right) - \mathop e\limits^{.}_{i} } \right)} \right) = 0 \hfill \\ m_{g} \mathop {y_{2} }\limits^{..} + c_{p2} \mathop {y_{2} }\limits^{.} + k_{p2} y_{2} + \left( {k_{m} \left[ {\left( {y_{1} - y_{2} } \right) - \left( {r_{1} \theta_{1} - r_{2} \theta_{2} } \right) - e_{i} } \right] + c_{m} \left[ {\left( {\mathop y\limits^{.}_{1} - \mathop y\limits^{.}_{2} } \right) - \left( {r_{1} \mathop \theta \limits^{.}_{1} - r_{2} \mathop \theta \limits^{.}_{2} } \right) - \mathop e\limits^{.}_{i} } \right]} \right) = 0 \hfill \\ J_{2} \mathop \theta \limits^{..}_{2} - Rb_{2} \left( {k_{m} \left[ {\left( {y_{1} - y_{2} } \right) - \left( {r_{1} \theta_{1} - r_{2} \theta_{2} } \right) - e_{i} } \right] + c_{m} \left[ {\left( {\mathop y\limits^{.}_{1} - \mathop y\limits^{.}_{2} } \right) - \left( {r_{1} \mathop \theta \limits^{.}_{1} - r_{2} \mathop \theta \limits^{.}_{2} } \right) - \mathop e\limits^{.}_{i} } \right]} \right) = T_{2} \hfill \\ \end{gathered} \right. $$

(33)

Fig. 14

Tooth surface morphology and wear coupling dynamic wear

In Eq. (34), r₁ is the radius of the driving gear dividing circle; r₂ is the radius of the dividing circle of the driving gear, and e_i is the comprehensive error. When we do not consider the effect of tooth profile error caused by tooth surface wear, the calculation formula of comprehensive error is as shown in Eq. (34).

$$ e_{i} = e_{l} + e_{s} $$

(34)

e_l is the long-period error; e_s is the short-period error. According to the gear transmission system parameters of the table, the vibration response of different tooth surface topography is simulated and calculated.

When considering the effect of tooth surface wear on early fault gear, the comprehensive error of the gear accounts for the tooth profile error resulting from tooth surface wear. The calculation formula is shown in Eq. (35).

$$ e_{i} = e_{l} + e_{s} + e_{w} $$

(35)

e_w is the tooth profile error. The effect of tooth surface wear on the tooth side clearance is regarded as a tooth profile error on the tooth surface. The wear depth of the driving gear and the driven gear is equivalent to the amplitude of the tooth profile error.

$$ e_{w} = \min \left( {\left[ {E_{pi} + E_{gi} } \right]_{i = 1,2...N} } \right) $$

(36)

E_ji(j = p, g) is the gear tooth deviation value, which is related to the tooth surface wear depth; i is the number of teeth involved in meshing. The tooth profile errors shown in Fig. 15, which is associated with the number of meshing cycles and increase as the number of meshing cycles increases. The tooth profile error exhibits periodic characteristics that are by the gear transmission system. Equation (36) is substituted into the dynamic model to solve the vibration response of the gear transmission system.

Fig. 15

Tooth profile error considering tooth surface wear depth

N is meshing times (N₁ = 0.5 × 10⁸, N₂ = 1.0 × 10⁸, N₃ = 1.5 × 10⁸). The vibration responses of different tooth surfaces are shown in Figs. 16 and 17. Wear exacerbates gear transmission system vibration, and tooth surface morphology also influences vibration levels. It is very important to solve the coupling vibration response of tooth surface topography and wear for early fault diagnosis of gears. However, it is a hot and challenging point to identify the signal of wear or rough surface from the coupled vibration response. First, we compare the correlation between the maximum and root mean square values of the coupled vibration response and assess the effect of surface roughness and wear on the gear transmission system.

Fig. 16

Coupling vibration response of tooth surface topography (Ra0.4 and Ra0.8)

Fig. 17

Coupling vibration response of tooth surface topography (Ra1.6 and Ra3.2)

As shown in Fig. 18, as gear surface roughness increases, the vibration response becomes more prominent. Consequently, tooth surface morphology augments the overall noise level during gear meshing, and as the number of meshing cycles increases, the effect of rough surface gradually grows on the gear transmission system.

The existence of surface roughness makes the actual contact area of the transmission system smaller than the theoretical contact area, and the bearing capacity and anti-deformation ability of the gear surface decrease, which causes the impact characteristics of the transmission system. Moreover, the surface roughness also increases the friction coefficient and wear coefficient of the contact tooth surface in the transmission system, which aggravates the noise level and wear behavior of the transmission system. To further reveal the effect of surface roughness on the gear transmission system, we analyze the frequency domain characteristics of the vibration response, as shown in Fig. 19. We found several exciting sideband frequencies, which are 441 Hz, 1083 Hz, and 1484 Hz. These frequency shifts indicate that the contact state of the tooth surface has changed, but the contact state of the tooth surface can not be judged. We employ variational mode decomposition (VMD) to break the vibration response into IMF components and corresponding spectra, each component signifying different variable parameters in the vibration response curve. The VMD-constrained variational model is as follows.

$$ \begin{gathered} \mathop {\min }\limits_{{\{ u_{k} ,w_{k} \} }} \left\{ {\sum\limits_{k} {\left\| {\partial_{t} \left[ {\delta (t) + \frac{j}{\pi t}*u_{k} (t)} \right]e^{{ - jw_{k} t}} } \right\|_{2}^{2} } } \right\} \hfill \\ \, s.t. \, \sum\limits_{k} {u_{k} } = f \hfill \\ \end{gathered} $$

(37)

$$ u_{k} (t) = A_{k} (t)\cos (\phi_{k} (t)) $$

(38)

Fig. 18

Statistical index of coupled vibration response: a Maximum; b RMS

Fig. 19

Frequency domain characteristics of vibration response: a Ra0.4; b Ra0.8; c Ra1.6; d Ra3.2

u_k is each mode function; w_k is each mode center. By comparing the changes of IMF components under different conditions, the coupling vibration characteristics of surface roughness and tooth surface wear are studied. The contact state of the gear surface is identified from the response curve. The vibration response curves are decomposed by VMD., the coupling vibration response curves are divided into four components: IMF1, IMF2, IMF3, and IMF4.

As shown in Fig. 20, the frequency-domain characteristics of IMF2, IMF3, and IMF4 are similar to several sideband frequencies of the vibration response. In the frequency domain of the original signal, only the amplitude of 120.6 Hz and 200.7 Hz is obvious, and it is difficult to identify the fault components of the original signal. At this point, we can analyze the vibration response by the frequency domain characteristic of IMF2, IMF3, and IMF4 in VMD decomposition which is similar to the sideband frequency.

Fig. 20

VMD decomposition of coupled vibration response (Ra0.4, N₁ = 0.5 × 10⁸)

In addition, the time-domain characteristics of the IMF1 component were similar to the original signal curve with a decrease in amplitude and a decrease in frequency-domain characteristics at 200.7 Hz. As shown in Fig. 21, the blue curve represents the different wear conditions, the red curve represents the roughness grade of failure, and the roughness-induced change in IMF1 is greater.

Fig. 21

The maximum statistical index level of IMF 1 component

5 Conclusion

The nonlinear coupling relationship between surface morphology and tooth wear has always been a challenge in tribology. This paper introduces a calculation model of tooth surface morphology and contact stiffness based on fractal theory, and the wear prediction model is improved by using the tooth surface morphology obtained by simulation. To analyze the influence of roughness and wear on the system’s dynamic characteristics, a fault dynamics model of roughness and wear coupling is established. The conclusions are summarized as follows.

• (1) By studying the relationship between contact surface roughness and wear, it was found that surface morphology with fractal characteristics alters the wear behavior of tooth surfaces by affecting the time-varying wear coefficient. With the increase of fractal dimension and the decrease of scale coefficient, the time-varying wear coefficient can be increased, and the wear behavior of the tooth surface can be aggravated. The wear depth of tooth surfaces varies greatly under different surface roughness, and there is almost a multiple increase between them.

• (2) As the surface roughness increased, the contact stiffness of the gear continued to increase, but the time-varying meshing stiffness curve of the gear did not always increase with the increase in surface roughness. When the surface roughness level is less than Ra1.6, the time-varying meshing stiffness curve infinitely approaches a value and does not change. By analyzing the system’s dynamic characteristics, it was found that there were significant differences in the dynamic response before and after Ra1.6, and the difference between dynamic responses with roughness levels lower than Ra1.6 was very small. This indicates that when the tooth surface accuracy reaches a certain standard, the contact deformation is much smaller than the tooth deformation and matrix deformation.

• (3) Both surface morphology and tooth wear can cause severe vibrations in the system. However, the results indicate that surface morphology has a greater impact on the vibration response of the system, as it not only affects stiffness excitation but also exacerbates wear behavior, thereby affecting the system response. There is a positive proportional relationship between surface morphology, tooth wear, and vibration response. Therefore, improving tooth surface accuracy during gear manufacturing is of great significance for improving the lifespan and efficiency of transmission systems.

• (4) To extract the signal of surface topography and wear from the coupled vibration response, the response curve is decomposed into four components: IMF1, IMF2, IMF3, and IMF4. Through comparing the frequency-domain characteristics, we find that the frequency-domain characteristics of the modal components in VMD decomposition are similar to the frequencies of several sidebands of the vibration response. So, IMF1, IMF2, IMF3, and IMF4 can be used to evaluate and predict the contact state of the tooth surface. Which has essential theoretical guiding significance for the evaluation of gear surface morphology.