Nonlinear low-velocity impact response of GRC beam with geometric imperfection under thermo-electro-mechanical loads

Abstract

This paper presents an investigation on thermo-electro-mechanical nonlinear low-velocity impact behaviors of the geometrically imperfect functionally graded (FG) graphene-reinforced composite (GRC) beam with surface-bonded piezoelectric layers. Both uniformly distributed and FG patterns of graphene nanoplatelets (GPLs) are considered along the thickness of the GRC host beam. The effective Young’s modulus is calculated by the Halpin–Tsai model. The Poisson ratio and mass density are calculated by the rule of mixture. The modified nonlinear Hertz contact law is employed to predict the impact force between the spherical impactor and the geometrically imperfect GRC piezoelectric beam during impacting. By considering the first-order shear deformation theory and von Kármán nonlinear displacement–strain relationship, the nonlinear governing equations are obtained by Hamilton principle and dispersed by differential quadrature (DQ) method. The Newmark-β method associated with Newton–Raphson iterative process is adopted to parametrically identify the impact force and the dynamic response of the system. The effects of geometric imperfection, weight fraction and distribution pattern of GPLs, temperature variation, thickness of piezoelectric layer and impactor’s initial velocity on nonlinear low-velocity impact behaviors of geometrically imperfect GRC beams are discussed in detail. Our results illustrate that the coupling effect of geometric imperfection and thermo-electro-mechanical load has a significant effect on the nonlinear low-velocity impact behavior of GRC beam, and GPLs distributing into the piezoelectric layers is better for reducing the impact response of geometrically imperfect GRC piezoelectric beam.

1 Introduction

Geometric imperfections are inevitable in engineering structures due to the influence of manufacturing and environmental factors, and these imperfections have significant effects on the mechanical behaviors of structures [1,2,3], especially for the vibration, buckling and nonlinear dynamic behaviors [4,5,6]. Sheinman et al. [6] studied the imperfection sensitivity of an isotropic beam under a nonlinear elastic foundation. Farokhi et al. [7] investigated the effect of geometric imperfection on the nonlinear resonance of the Timoshenko microbeam. Wadee [8] proposed the one-dimensional imperfection model to simulate various global and localized imperfections existing in engineering structure, and then conducted a detailed research on buckling and post-buckling behaviors of the geometrically imperfect sandwich panel. Their results shown that the mechanical behaviors of structures are very sensitive to the geometric imperfections. Obviously, the research on the dynamic behaviors of structures with geometric imperfections is of great significance in engineering design.

Except the isotropic homogeneous structures mentioned above, more and more lightweight and high strength materials and high-performance composite structures are emerging in the field of aerospace and engineering applications, such as the functionally graded materials (FGM), fiber-reinforced composite structures and carbon-based composite structures [9,10,11,12]. In the framework of isogeometric analysis [13], Nguyen and his co-workers calculated the static and dynamic behaviors of the high-performance composite structures, such as the vibration of FGM piezoelectric porous microplates [14] and postbuckling of functionally graded carbon nanotube-reinforced composite (CNTRC) shells [15]. When the high-performance composite structures operate under thermo-electro-mechanical loads, their mechanical behaviors can significantly be affected by their working conditions. Yang and his co-authors [16, 17] analyzed the large amplitude vibration and thermal bifurcation buckling of carbon nanotube-reinforced composite (CNTRC) beams bonded with piezoelectric layers. Liew’s group [18, 19] researched active vibration control of FG composite plates bonded with the piezoelectric actuator and sensor. Wu et al. [20, 21] analyzed the post-buckling and free vibration of FG-CNTRC beam with geometric imperfections under thermal–mechanical-electrical loads.

Recently, graphene nanoplatelets (GPLs) have shown tremendous potentials in the development of high-performance composites due to its unique mechanical properties since its first report by Novoselov et al. [22]. Extensive theoretical and experimental investigations have shown that the dispersion of GPLs in the polymer matrix can significantly improve its mechanical properties [23,24,25]. Yang’s group firstly proposed the functionally graded (FG) GPLs-reinforced composite (GRC) structures and carried out a detailed study on their bending, buckling and vibration behaviors [26,27,28,29]. Mao et al. [30,31,32,33] conducted a detailed analysis of the static and dynamic behaviors of FG-GRC structures. Rahimi et al. [34, 35] employed a semi-analytical solution to obtain the three-dimensional bending and free vibration behaviors of FG-GRC cylindrical shells. Furthermore, many scholars have studied the vibrations and stability of FG-GRC structures under various loads, including transverse excitation [36, 37], axial compression [38], thermal loads [39] and impact loads [40]. Results illustrated that the GPL reinforcements can significantly enhance the stiffness of the GRC structures, and the enhancement effect largely depends on the distribution pattern of GPLs in matrix.

According to the researches about nonlinear behaviors of FG-GRC structures with geometric imperfections, shapes and amplitudes of geometric imperfections have significant effects on the buckling [41, 42], nonlinear vibration [4, 43] and resonance [44] of FG-GRC structures. It is worth noting that impact is one of common loads for engineering structures, which may result in internal damage and even lead to severe failure of structures. Introducing the modified Hertz model, Fan et al. [45, 46] discussed the low-velocity impact response of FG-GRC structures resting on visco-elastic foundations. Based on the energy-balance and spring-mass model, Dong et al. [47] predicted the low-velocity impact response of FG-GR cylindrical shells under axial load and thermal loads. Selim et al. [48] examined the impact behaviors of FG-GRC plates resting on Winkler-Pasternak elastic foundations by using a meshless approach.

The existing literature have researched the low-velocity impact behaviors of intact GRC structures and the nonlinear dynamic behaviors of geometrically imperfect GRC structures in detail separately. To our best knowledge, there is no relevant reports on the impact behavior of GRC beam with geometric imperfections. But it is the utmost important for the safety and longevity of engineering structures, especially for the high-performance composite structures working under complex loading, such as the situation among thermal, electrical and mechanical loads.

In order to investigate the couple effect of the low-velocity impact and geometric imperfections on the nonlinear dynamic behaviors of the GRC beam subjected to thermal–mechanical-electrical loads, the present work introduces a theoretical model and numerical analysis method. For the geometric imperfect GRC beam with surface-bonded piezoelectric layers subjected to low-velocity impact and thermo-electro-mechanical loads, the governing equations of motion are derived based on the first-order shear deformation theory, von Kármán nonlinear displacement–strain relationship and Hamilton’s principle, and dispersed by differential quadrature (DQ) method. The Newmark-β method associated with Newton–Raphson iterative method is employed to study the effects of the weight fraction and distribution pattern of GPLs, the types and amplitude of geometric imperfections, temperature variation, impact velocity, as well as thickness of the piezoelectric layer on impact force and impact response of the geometrically imperfect GRC piezoelectric beam.

2 Theoretical models

2.1 Geometry model

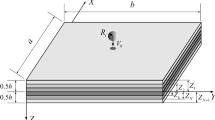
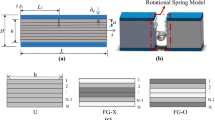
Figure 1a illustrates a GRC beam with geometric imperfection. The length, width and thickness of the GRC beam are L, b and h, respectively. Two piezoelectric layers with a thickness of h_p are perfectly bonded on the upper and lower surfaces of the geometrically imperfect GRC beam and respectively applied with voltage U₀. The hinged supported boundary conditions are considered. The GRC beam is subjected a uniform temperature variation $\Delta T = T - T_{0}$ and it is stress-free at initial temperature T₀. It is assumed that the material properties of GRC beam are independent of the varying temperatures to focus on the coupled effect of the temperature variation and geometric imperfection on the nonlinear low-velocity impact response of the GRC piezoelectric beam. The geometrically imperfect GRC piezoelectric beam is impacted by a spherical impactor with initial velocity V₀. m_i and R_i respectively denote the mass and radius of the impactor.

Fig. 1

Structural schematic: a A model of an N-layered geometrically imperfect GRC piezoelectric beam subjected to low-velocity impact, b GPLs distribution patterns: UD, FG-X, FG-O

The geometric imperfection $w^{*} \left( x \right)$ is simulated in the form of the product of the trigonometric and hyperbolic functions [8]

$$ w^{ * } \left( x \right) = A_{0} h{\text{sech}} \left[ {a\left( {x/L - c} \right)} \right]\cos \left[ {b\pi \left( {x/L - c} \right)} \right]. $$

(1)

where a is a constant, representing the localization degree of the imperfection, and A₀ is the dimensionless amplitude of the geometric imperfection. The spherical impactor impacts to the concave surface of the GRC beam for A₀ > 0, as shown in Fig. 1, and the convex surface is impacted for A₀ < 0. Note that $w^{*} (x)$ is symmetric about $x/L = c$, and b is the half-wave numbers of the imperfection in x-axis. Sine, global (G) and localized (L) imperfections are considered. As presented in Fig. 2, the varying values of constants a, b and c represent various geometric imperfections, Sine, G_s and L_s (s = 1, 2, 3, 4).

Fig. 2

Geometric imperfection modes

2.2 Nonlinear Hertz model

Based on Newton’s second law, the governing equation of motion for the impactor can be expressed as

$$ m_{i} \ddot{y}_{i} \left( t \right) + F_{C} \left( t \right) = 0, $$

(2)

where $y_{i} \left( t \right)$ is the displacement of the impactor, and $F_{C} \left( t \right)$ is the impact force between the impactor and the impacted geometrically imperfect GRC piezoelectric beam.

When the contact area between the impactor and the impacted beam is much smaller than the geometries of the beam, Hertz contact theory can be utilized to calculate the impact force. The nonlinear low-velocity impact process can be divided into two phases, namely, loading phase and unloading phase [46, 49]. The loading phase starts from the moment that the impactor impacts to the target beam, and ends when the local contact indentation reaches to the maximum. The unloading phase begins at the local contact indentation reaching to the maximum, until the impactor totally departing from the geometrically imperfect GRC piezoelectric beam. According to the modified nonlinear Hertz contact proposed by Yang and Sun [50], the varying impact force $F_{C} \left( t \right)$ during these two different phases can be predicted through two different equations.

During the loading phase [49],

$$ F_{C} \left( t \right) = K_{C} \alpha^{3/2} \left( t \right), $$

(3)

with the contact stiffness $K_{C}$ and the local contact indentation $\alpha \left( t \right)$

$$ K_{C} = \frac{4}{3}\sqrt {R_{i} } \left( {\frac{{1 - \nu_{i}^{2} }}{{Y_{i} }} + \frac{{1 - \nu_{{\tilde{t}}}^{2} }}{{Y_{{\tilde{t}}} }}} \right)^{ - 1} ,\alpha \left( t \right) = y_{i} (t) - w_{C} (t) $$

(4)

where Y and $\nu$ are the Young's modulus and Poisson ratio, respectively, and the subscript “i” and “$\tilde{t}$” respectively represent the impactor and the top surface of the geometrically imperfect GRC piezoelectric beam. Besides, $w_{C}$ denotes the deflection of the geometrically imperfect GRC piezoelectric beam at the impacted point.

During the unloading phase [49],

$$ F_{C} \left( t \right) = F_{\max } \left( {\frac{{\alpha \left( t \right) - \alpha_{0} }}{{\alpha_{\max } - \alpha_{0} }}} \right)^{5/2} , $$

(5)

where $\alpha_{\max }$ and $F_{\max }$ are respectively the maximum local contact indentation and the corresponding impact force, and $\alpha_{0}$ is the permanent indentation of the target beam. If the plastic deformation is not considered, $\alpha_{0} = 0$.

2.3 Physical parameter model

It is assumed that the GRC beam is composed by a mixture of an isotropic matrix and GPLs with length $l_{G}$, width $w_{G}$ and thickness $h_{G}$. GPLs disperse into the GRC beam along its thickness direction. Both uniformly distributed (UD) and functionally graded (FG) patterns are taken into consideration, as shown in Fig. 1(b), namely UD, FG-X and FG-O. GPL volume fraction respectively decreases and increases in FG-X and FG-O from the top and bottom layers to the middle layers. In other words, the GPL volume fractions of the middle layers are the lowest in FG-X, but the GPL volume fractions of the middle layers are the highest in FG-O. GPL volume fraction $V_{G}^{\left( k \right)}$ in the kth layer of the GRC beam can be expressed as

$$ {\text{U}}:V_{G}^{\left( k \right)} = V_{G}^{ * } , $$

(6)

$$ {\text{FG}} - {\text{X}}:V_{G}^{\left( k \right)} = {{2V_{G}^{ * } \left( {2k - N - 1} \right)} \mathord{\left/ {\vphantom {{2V_{G}^{ * } \left( {2k - N - 1} \right)} N}} \right. \kern-\nulldelimiterspace} N}, $$

(7)

$$ {\text{FG}} - {\text{O}}:V_{G}^{\left( k \right)} = {{2V_{G}^{ * } \left( {1 - \left| {2k - N - 1} \right|} \right)} \mathord{\left/ {\vphantom {{2V_{G}^{ * } \left( {1 - \left| {2k - N - 1} \right|} \right)} N}} \right. \kern-\nulldelimiterspace} N}, $$

(8)

where

$$ V_{G}^{ * } = \frac{{f_{G} }}{{f_{G} + \left( {{{\rho_{G} } \mathord{\left/ {\vphantom {{\rho_{G} } {\rho_{M} }}} \right. \kern-\nulldelimiterspace} {\rho_{M} }}} \right)\left( {1 - f_{G} } \right)}}. $$

(9)

$f_{G}$ denotes the total GPL weight fraction. $\rho {}_{G}$ and $\rho {}_{M}$ are respectively the mass density of the GPLs and matrix, and $k = 1,\,2,\, \cdots ,\,N$.

According to the Halpin–Tsai model [24] and the rule of mixture, the effective material properties, including Young’s modulus $Y_{C}^{\left( k \right)}$, Poisson ratio $\nu_{C}^{\left( k \right)}$, mass density $\rho_{C}^{\left( k \right)}$ and thermal expansion coefficient $\alpha_{C}^{\left( k \right)}$ of the kth GRC layer, can be predicted by

$$ Y_{C}^{\left( k \right)} = \frac{{3\left( {1 + 2\xi_{{{\text{LW}}}} \xi_{{{\text{WH}}}} \eta_{L} V_{G}^{\left( k \right)} } \right)}}{{8\left( {1 - \eta_{L} V_{G}^{\left( k \right)} } \right)}} \times Y_{M} + \frac{{5\left( {1 + 2\xi_{{{\text{WH}}}} \eta_{W} V_{G}^{\left( k \right)} } \right)}}{{8\left( {1 + \eta_{W} V_{G}^{\left( k \right)} } \right)}} \times Y_{M} , $$

(10)

$$ \rho_{C}^{\left( k \right)} = \rho_{G} V_{G}^{\left( k \right)} + \rho_{M} \left( {1 - V_{G}^{\left( k \right)} } \right), $$

(11)

$$ \nu_{C}^{\left( k \right)} = \nu_{G} V_{G}^{\left( k \right)} + \nu_{M} \left( {1 - V_{G}^{\left( k \right)} } \right), $$

(12)

$$ \alpha_{C}^{\left( k \right)} = \alpha_{G} V_{G}^{\left( k \right)} + \alpha_{M} \left( {1 - V_{G}^{\left( k \right)} } \right), $$

(13)

with

$$ \eta_{L} = \frac{{{{Y_{G} } \mathord{\left/ {\vphantom {{Y_{G} } {Y_{M} - 1}}} \right. \kern-\nulldelimiterspace} {Y_{M} - 1}}}}{{{{Y_{G} } \mathord{\left/ {\vphantom {{Y_{G} } {Y_{M} + 2\xi_{{{\text{LW}}}} \xi_{{{\text{WH}}}} }}} \right. \kern-\nulldelimiterspace} {Y_{M} + 2\xi_{{{\text{LW}}}} \xi_{{{\text{WH}}}} }}}},\eta_{W} = \frac{{{{Y_{G} } \mathord{\left/ {\vphantom {{Y_{G} } {Y_{M} - 1}}} \right. \kern-\nulldelimiterspace} {Y_{M} - 1}}}}{{{{Y_{G} } \mathord{\left/ {\vphantom {{Y_{G} } {Y_{M} + 2\xi_{{{\text{WH}}}} }}} \right. \kern-\nulldelimiterspace} {Y_{M} + 2\xi_{{{\text{WH}}}} }}}}, $$

(14)

where the subscripts “M” and “G” represent matrix and GPLs, respectively. $\xi_{{{\text{LW}}}}$ and $\xi_{{{\text{WH}}}}$ are respectively the length-to-width ratio and width-to-thickness ratio of the GPLs, expressed by

$$ \xi_{{{\text{LW}}}} = \frac{{l_{G} }}{{w_{G} }},\xi_{{{\text{WH}}}} = \frac{{w_{G} }}{{h_{G} }}. $$

(15)

3 Nonlinear dynamic equations

In this study, the first-order shear deformation theory is used to estimate the deformation of the geometrically imperfect GRC piezoelectric beam. The axial and transverse displacements $\tilde{u}\left( {x,z,t} \right)$ and $\tilde{w}\,\left( {x,z,t} \right)$ of the novel beam can be presented by its mid-plane axial, transverse and rotary displacements $u\left( {x,t} \right)$, $w\,\left( {x,t} \right)$ and $\varphi \left( {x,t} \right)$, combined with the initial transverse geometric imperfection $w^{*} \left( x \right)$

$$ \begin{aligned}&\tilde{u}\left( {x,z,t} \right) = u\left( {x,t} \right) + z\varphi \left( {x,t} \right),\\&\tilde{w}\left( {x,z,t} \right) = w\left( {x,t} \right) + w^{ * } \left( x \right).\end{aligned} $$

(16)

Referring to von Kármán nonlinear displacement–strain relationship, the normal strain $\varepsilon_{xx}$ and shear strain $\gamma_{xz}$ of the geometrically imperfect GRC piezoelectric beam are gained as

$$ \varepsilon_{{{\textit{xx}}}} = \frac{\partial u}{{\partial x}} + \frac{1}{2}\left( {\frac{\partial w}{{\partial x}}} \right)^{2} + z\frac{\partial \varphi }{{\partial x}} + \frac{\partial w}{{\partial x}}\frac{{{\text{d}}w^{ * } }}{{{\text{d}}x}},\gamma_{xz} = \frac{\partial w}{{\partial x}} + \varphi . $$

(17)

The linear constitutive relations for the kth GRC layer and piezoelectric layers can be expressed as

$$ \sigma_{{{\textit{xx}}}}^{\left( k \right)} = Q_{11}^{\left( k \right)} \left( {\varepsilon_{{{\textit{xx}}}} - \alpha_{C}^{\left( k \right)} \Delta T} \right),\tau_{{{\textit{xz}}}}^{\left( k \right)} = Q_{55}^{\left( k \right)} \gamma_{{{\textit{xz}}}} , $$

(18)

$$ \begin{gathered} \sigma_{{{\textit{xx}}}}^{P} = Q_{11}^{P} \left( {\varepsilon_{{{\textit{xx}}}} - \alpha_{P} \Delta T} \right) - e_{31} E_{z} ,\tau_{{{\textit{xz}}}}^{P} = Q_{55}^{P} \left( {\frac{\partial w}{{\partial x}} + \varphi } \right), \hfill \\ D_{Z} = e_{31} \varepsilon_{{{\textit{xx}}}} + k_{33} E_{Z} , \hfill \\ \end{gathered} $$

(19)

where

$$ Q_{11}^{\left( k \right)} = \frac{{Y_{C}^{\left( k \right)} }}{{1 - \nu_{C}^{\left( k \right)2} }},Q_{55}^{\left( k \right)} = \frac{{Y_{C}^{\left( k \right)} }}{{2\left( {1 + \nu_{C}^{\left( k \right)} } \right)}}, $$

(20)

$$ Q_{11}^{P} = \frac{{Y_{P} }}{{1 - \nu_{P}^{2} }},Q_{55}^{P} = \frac{{Y_{P} }}{{2\left( {1 + \nu_{P} } \right)}} $$

(21)

$Y_{P}$ and $\nu_{P}$ are Young’s modulus and Poisson ratio of the piezoelectric layer, respectively, $e_{31}$, $k_{33}$ and $D_{Z}$ are respectively the piezoelectric stress constant, permittivity constant and electric displacement of the piezoelectric layer. The electric potential variation is considered to be linear throughout the thickness of piezoelectric layer as Ref. [51], so the electric field $E_{Z}$ can be expressed as

$$ E_{Z} = \frac{{U_{0} }}{{h_{P} }}. $$

(22)

Based on Hamilton principle, the partial differential governing equations of motion for geometrically imperfect GRC piezoelectric beam under low-velocity impact are obtained as

$$ \frac{{\partial N_{x} }}{\partial x} = I_{1} \frac{{\partial^{2} u}}{{\partial t^{2} }} + I_{2} \frac{{\partial^{2} \varphi }}{{\partial t^{2} }}, $$

(23)

$$ \frac{\partial }{\partial x}\left( {N_{x} \frac{\partial w}{{\partial x}} + N_{x} \frac{{\partial w^{ * } }}{\partial x}} \right) + \frac{\partial Q}{{\partial x}} + F_{C} \left( t \right)\delta \left( {x - x_{C} } \right) = I_{1} \frac{{\partial^{2} w}}{{\partial t^{2} }}, $$

(24)

$$ \frac{{\partial M_{x} }}{\partial x} - k_{s} Q_{x} = I_{2} \frac{{\partial^{2} w}}{{\partial t^{2} }} + I_{3} \frac{{\partial^{2} \varphi }}{{\partial t^{2} }}, $$

(25)

where the shear correction factor $k_{s} = 5/6$ and $x_{C}$ is the location of the impacted point. $I_{j}$ (j = 1, 2 and 3) are the inertia related terms

$$ \left( \begin{gathered} I_{1} \hfill \\ I_{2} \hfill \\ I_{3} \hfill \\ \end{gathered} \right) = \sum\limits_{k = 1}^{N} {\int_{h/2 - k\Delta h}^{{h/2 - \left( {k - 1} \right)\Delta h}} {\rho_{C}^{\left( k \right)} } } \left( \begin{gathered} 1 \hfill \\ z \hfill \\ z^{2} \hfill \\ \end{gathered} \right){\text{d}}z + \int_{ - H/2}^{ - h/2} {\rho^{P} \left( \begin{gathered} 1 \hfill \\ z \hfill \\ z^{2} \hfill \\ \end{gathered} \right)} \;{\text{d}}z + \int_{h/2}^{H/2} {\rho^{P} \left( \begin{gathered} 1 \hfill \\ z \hfill \\ z^{2} \hfill \\ \end{gathered} \right)\;} {\text{d}}z. $$

(26)

The in-plane force $N_{x}$, bending moment $M_{x}$ and shear forces $Q_{x}$ are respectively expressed by

$$ N_{x} = A_{11} \left[ {\frac{\partial u}{{\partial x}} + \frac{1}{2}\left( {\frac{\partial w}{{\partial x}}} \right)^{2} + \frac{\partial w}{{\partial x}}\frac{{\partial w^{ * } }}{\partial x}} \right] + B_{11} \frac{\partial \varphi }{{\partial x}} - N_{x}^{P} - N_{x}^{T} , $$

(27)

$$ M_{x} = B_{11} \left[ {\frac{\partial u}{{\partial x}} + \frac{1}{2}\left( {\frac{\partial w}{{\partial x}}} \right)^{2} + \frac{\partial w}{{\partial x}}\frac{{\partial w^{ * } }}{\partial x}} \right] + D_{11} \frac{\partial \varphi }{{\partial x}} - M_{x}^{P} - M_{x}^{T} , $$

(28)

$$ Q_{x} = A_{55} \left( {\frac{\partial u}{{\partial x}} + \varphi } \right). $$

(29)

where the stiffness components $A_{11}$, $B_{11}$, $D_{{{11}}}$ and $A_{55}$ are respectively given by

$$ \left( \begin{gathered} A_{11} \hfill \\ B_{11} \hfill \\ D_{11} \hfill \\ \end{gathered} \right) = \sum\limits_{k = 1}^{N} {\int_{h/2 - k\Delta h}^{{h/2 - \left( {k - 1} \right)\Delta h}} {Q_{11}^{\left( k \right)} } } \left( \begin{gathered} 1 \hfill \\ z \hfill \\ z^{2} \hfill \\ \end{gathered} \right){\text{d}}z + \int_{ - H/2}^{ - h/2} {Q_{11}^{P} \left( \begin{gathered} 1 \hfill \\ z \hfill \\ z^{2} \hfill \\ \end{gathered} \right)} \,{\text{d}}z + \int_{h/2}^{H/2} {Q_{11}^{P} \left( \begin{gathered} 1 \hfill \\ z \hfill \\ z^{2} \hfill \\ \end{gathered} \right)} \,{\text{d}}z, $$

(30)

$$ A_{55} = \sum\limits_{k = 1}^{N} {\int_{h/2 - k\Delta h}^{{h/2 - \left( {k - 1} \right)\Delta h}} {Q_{55}^{\left( k \right)} k_{s} {\text{d}}z} } + \int_{ - H/2}^{ - h/2} {Q_{55}^{P} k_{s} {\text{d}}z} + \int_{h/2}^{H/2} {Q_{55}^{P} k_{s} {\text{d}}z} . $$

(31)

The thermal and electric related loads are written as

$$ \left( \begin{gathered} N_{x}^{T} \hfill \\ M_{x}^{T} \hfill \\ \end{gathered} \right) = \sum\limits_{k = 1}^{N} {\int_{h/2 - k\Delta h}^{{h/2 - \left( {k - 1} \right)\Delta h}} {Q_{11}^{\left( k \right)} \alpha_{c}^{\left( k \right)} } } \left( \begin{gathered} 1 \hfill \\ z \hfill \\ \end{gathered} \right)\,{\text{d}}z + \int_{ - H/2}^{ - h/2} {Q_{11}^{P} \alpha_{P} \left( \begin{gathered} 1 \hfill \\ z \hfill \\ \end{gathered} \right)} \,{\text{d}}z + \int_{h/2}^{H/2} {Q_{11}^{P} \alpha_{P} \left( \begin{gathered} 1 \hfill \\ z \hfill \\ \end{gathered} \right)} \,{\text{d}}z, $$

(32)

$$ \left( \begin{gathered} N_{x}^{P} \hfill \\ M_{x}^{P} \hfill \\ \end{gathered} \right) = \int_{ - H/2}^{ - h/2} {e_{31} E_{Z} \left( \begin{gathered} 1 \hfill \\ z \hfill \\ \end{gathered} \right)} \,{\text{d}}z + \int_{h/2}^{H/2} {e_{31} E_{Z} \left( \begin{gathered} 1 \hfill \\ z \hfill \\ \end{gathered} \right)} \,{\text{d}}z, $$

(33)

Obviously, $M_{x}^{P} = {0}$. In this study, the geometrically imperfect GRC piezoelectric beam has hinged supported boundary conditions at both ends (x = 0, L). The corresponding boundary conditions are given as follows

$$ u = 0,w = 0,M_{x} = 0 $$

(34)

Introducing the following dimensionless quantities

$$ \begin{gathered} X = \frac{x}{L},\left( {U,W,W^{ * } } \right) = \frac{{\left( {u,w,w^{ * } } \right)}}{h},\psi = \varphi ,\eta = \frac{L}{h},\tau = \frac{t}{L}\sqrt {\frac{{A_{110} }}{{I_{10} }}} , \hfill \\ \left( {a_{11} ,a_{55} ,b_{11} ,d_{11} } \right) = \left( {\frac{{A_{11} }}{{A_{110} }},\frac{{A_{55} }}{{A_{110} }},\frac{{B_{11} }}{{A_{110} h}},\frac{{D_{11} }}{{A_{110} h^{2} }}} \right),\left( {\tilde{I}_{1} ,\tilde{I}_{2} ,\tilde{I}_{3} } \right) = \left( {\frac{{I_{1} }}{{I_{10} }},\frac{{I_{2} }}{{I_{10} h}},\frac{{I_{3} }}{{I_{10} h^{2} }}} \right), \hfill \\ \left( {\tilde{N}^{P} ,\tilde{N}^{T} } \right) = \frac{{\left( {N^{P} ,N^{T} } \right)}}{{A_{110} }},F_{C}^{ * } = \frac{{F_{C} L}}{{A_{110} h}},A_{110} = \frac{{Y_{M} }}{{1 - \nu_{M}^{2} }}h,I_{10} = \rho_{M} h, \hfill \\ \end{gathered} $$

(35)

The partial differential governing Eqs. (23)–(25) can be rewritten in the dimensionless forms

$$ \begin{gathered} a_{11} \left[ {\frac{{\partial^{2} U}}{{\partial X^{2} }} + \frac{1}{\eta }\frac{{\partial^{2} W}}{{\partial X^{2} }}\left( {\frac{\partial W}{{\partial X}} + \frac{{dW^{ * } }}{dX}} \right) + \frac{1}{\eta }\frac{\partial W}{{\partial X}}\frac{{d^{2} W^{ * } }}{{dX^{2} }}} \right] + b_{11} \frac{{\partial^{2} \psi }}{{\partial X^{2} }} \hfill \\ = \tilde{I}_{1} \frac{{\partial^{2} U}}{{\partial \tau^{2} }} + \tilde{I}_{2} \frac{{\partial^{2} \psi }}{{\partial \tau^{2} }} \hfill \\ \end{gathered} $$

(36)

$$ \begin{gathered} \left[ {a_{11} \left( {\frac{1}{\eta }\frac{{\partial^{2} U}}{{\partial X^{2} }} + \frac{1}{{\eta^{2} }}\frac{{\partial^{2} W}}{{\partial X^{2} }}\frac{\partial W}{{\partial X}} + \frac{1}{{\eta^{2} }}\frac{{\partial^{2} W}}{{\partial X^{2} }}\frac{{{\text{d}}W^{ * } }}{{{\text{d}}X}} + \frac{1}{{\eta^{2} }}\frac{\partial W}{{\partial X}}\frac{{{\text{d}}^{2} W^{ * } }}{{{\text{d}}X^{2} }}} \right) + \frac{{b_{11} }}{\eta }\frac{{\partial^{2} \psi }}{{\partial X^{2} }}} \right]\left( {\frac{\partial W}{{\partial X}} + \frac{{{\text{d}}W^{ * } }}{{{\text{d}}X}}} \right) \hfill \\ + \left\{ {a_{11} \left[ {\frac{1}{\eta }\frac{\partial U}{{\partial X}} + \frac{1}{{2\eta^{2} }}\left( {\frac{\partial W}{{\partial X}}} \right)^{2} + \frac{1}{{\eta^{2} }}\frac{\partial W}{{\partial X}}\frac{{{\text{d}}W^{ * } }}{{{\text{d}}X}}} \right] + \frac{{b_{11} }}{\eta }\frac{\partial \psi }{{\partial X}} - \tilde{N}_{x}^{T} - \tilde{N}_{x}^{P} } \right\}\left( {\frac{{\partial^{2} W}}{{\partial X^{2} }} + \frac{{{\text{d}}^{2} W^{ * } }}{{{\text{d}}X^{2} }}} \right) \hfill \\ + a_{55} \left( {\frac{{\partial^{2} W}}{{\partial X^{2} }} + \eta \frac{\partial \psi }{{\partial X}}} \right) + F_{C}^{ * } \left( t \right)\delta \left( {X - X_{C} } \right) = \tilde{I}_{1} \frac{{\partial^{2} W}}{{\partial \tau^{2} }} \hfill \\ \end{gathered} $$

(37)

$$ \begin{gathered} b_{11} \left[ {\frac{{\partial^{2} U}}{{\partial X^{2} }} + \frac{1}{\eta }\frac{\partial W}{{\partial X}}\frac{{\partial^{2} W}}{{\partial X^{2} }} + \frac{1}{\eta }\frac{{\partial^{2} W}}{{\partial X^{2} }}\frac{{{\text{d}}W^{ * } }}{{{\text{d}}X}} + \frac{1}{\eta }\frac{\partial W}{{\partial X}}\frac{{{\text{d}}^{2} W^{ * } }}{{{\text{d}}X^{2} }}} \right] + d_{11} \frac{{\partial^{2} \psi }}{{\partial X^{2} }} - a_{55} \left( {\eta \frac{\partial W}{{\partial X}} + \eta^{2} \psi } \right) \hfill \\ = \tilde{I}_{2} \frac{{\partial^{2} U}}{{\partial \tau^{2} }} + \tilde{I}_{3} \frac{{\partial^{2} \psi }}{{\partial \tau^{2} }}. \hfill \\ \end{gathered} $$

(38)

4 Solution procedure

In this paper, the differential quadrature (DQ) method [32, 52] and Newmark-β method [53] combined with Newton–Raphson iterative process [13, 54] are introduced to numerically analyze the nonlinear low-velocity impact response of the geometrically imperfect GRC piezoelectric beam subjected to thermo-electro-mechanical loads. According to DQ method, the dimensionless displacement components U, W, $\psi$ of the geometrically imperfect GRC piezoelectric beam and their rth derivatives with respect to $X_{i}$ are approximated in following forms

$$ \left\{ {U, \, W, \, \psi } \right\} = \sum\limits_{m = 1}^{n} {l_{m} \left( X \right)\left\{ {U_{m} , \, W_{m} , \, \psi_{m} } \right\}} , $$

(39)

$$ \left. {\frac{{\partial^{r} }}{{\partial X^{r} }}\left\{ {U, \, W, \, \psi } \right\}} \right|_{{X = X_{i} }} = \sum\limits_{m = 1}^{n} {C_{im}^{\left( r \right)} \left\{ {U_{m} , \, W_{m} , \, \psi_{m} } \right\}} , $$

(40)

where $\left\{ {U_{m} , \, W_{m} , \, \psi_{m} } \right\} = \left. {\left\{ {U, \, W, \, \psi } \right\}} \right|_{{X = X_{m} }}$, $l_{m} \left( X \right)$ is the Lagrange interpolation polynomial, $C_{{{\text{im}}}}^{\left( r \right)}$ is the weighting coefficients of the rth derivative at $X = X_{i}$, n is the total number of nodes distributed along the whole length of the GRC beam. In the present work, the distribution of nodes is given by the following equation

$$ X_{i} = \frac{1}{2}\left[ {1 - \cos \frac{{\pi \left( {i - 1} \right)}}{n - 1}} \right] \, \left( {i = 1, \, 2, \ldots ,n} \right). $$

(41)

Substituting Eqs. (39) and (40) into Eqs. (36)–(38), the dimensionless partial differential governing equations for nonlinear low-velocity impact response of geometrically imperfect GRC piezoelectric beam can be written as following ordinary differential equations

$$ \begin{gathered} a_{11} \sum\limits_{m = 1}^{n} {C_{{{\text{im}}}}^{\left( 2 \right)} U_{m} + } \frac{{a_{11} }}{\eta }\left[ {\sum\limits_{m = 1}^{n} {C_{{{\text{im}}}}^{\left( 1 \right)} W_{m} } \sum\limits_{m = 1}^{n} {C_{{{\text{im}}}}^{\left( 2 \right)} W_{m} } + \left. {\frac{{{\text{d}}W^{ * } }}{{{\text{d}}X}}} \right|_{{X = X_{i} }} \sum\limits_{m = 1}^{n} {C_{{{\text{im}}}}^{\left( 2 \right)} W_{m} } } \right. \hfill \\ \left. { + \left. {\frac{{{\text{d}}^{2} W^{ * } }}{{{\text{d}}X^{2} }}} \right|_{{X = X_{i} }} \sum\limits_{m = 1}^{n} {C_{{{\text{im}}}}^{\left( 1 \right)} W_{m} } } \right] + b_{11} \sum\limits_{m = 1}^{n} {C_{{{\text{im}}}}^{\left( 2 \right)} \psi_{m} } = \tilde{I}_{1} \ddot{U}_{i} + \tilde{I}_{2} \ddot{\psi }_{i} \hfill \\ \end{gathered} $$

(42)

$$ \begin{gathered} \left[ {\frac{{a_{11} }}{\eta }\sum\limits_{m = 1}^{n} {C_{im}^{\left( 2 \right)} U_{m} } + \frac{{a_{11} }}{{\eta^{2} }}\left( {\sum\limits_{m = 1}^{n} {C_{{{\text{im}}}}^{\left( 1 \right)} W_{m} } \sum\limits_{m = 1}^{n} {C_{{{\text{im}}}}^{\left( 2 \right)} W_{m} } + \left. {\frac{{{\text{d}}W^{ * } }}{{{\text{d}}X}}} \right|_{{X = X_{i} }} \sum\limits_{m = 1}^{n} {C_{{{\text{im}}}}^{\left( 2 \right)} W_{m} } + \left. {\frac{{{\text{d}}^{2} W^{ * } }}{{{\text{d}}X^{2} }}} \right|_{{X = X_{i} }} \sum\limits_{m = 1}^{n} {C_{{{\text{im}}}}^{\left( 1 \right)} W_{m} } } \right)} \right. \hfill \\ + \left. {\frac{{b_{11} }}{\eta }\sum\limits_{m = 1}^{n} {C_{{{\text{im}}}}^{\left( 2 \right)} \psi_{m} } } \right]\left( {\sum\limits_{m = 1}^{n} {C_{{{\text{im}}}}^{\left( 1 \right)} W_{m} } + \left. {\frac{{{\text{d}}W^{ * } }}{{{\text{d}}X}}} \right|_{{X = X_{i} }} } \right) + \left( {\frac{{a_{11} }}{\eta }\sum\limits_{m = 1}^{n} {C_{{{\text{im}}}}^{\left( 1 \right)} U_{m} } } \right. + \frac{{a_{11} }}{{\eta^{2} }}\left. {\frac{{{\text{d}}W^{ * } }}{{{\text{d}}X}}} \right|_{{X = X_{i} }} \sum\limits_{m = 1}^{n} {C_{{{\text{im}}}}^{\left( 1 \right)} W_{m} } \hfill \\ + \frac{{a_{11} }}{{2\eta^{2} }}\sum\limits_{m = 1}^{n} {C_{{{\text{im}}}}^{\left( 1 \right)} W_{m} } \sum\limits_{m = 1}^{n} {C_{{{\text{im}}}}^{\left( 1 \right)} W_{m} } + \left. {\frac{{b_{11} }}{{\eta^{2} }}\sum\limits_{m = 1}^{n} {C_{{{\text{im}}}}^{\left( 1 \right)} \psi_{m} } - \left. {\tilde{N}_{x}^{T} } \right|_{{X = X_{i} }} - \left. {\tilde{N}_{x}^{P} } \right|_{{X = X_{i} }} } \right)\left( {\sum\limits_{m = 1}^{n} {C_{{{\text{im}}}}^{\left( 2 \right)} W_{m} + \left. {\frac{{{\text{d}}^{2} W^{ * } }}{{{\text{d}}X^{2} }}} \right|_{{X = X_{i} }} } } \right) \hfill \\ + a_{55} \left( {\sum\limits_{m = 1}^{n} {C_{{{\text{im}}}}^{\left( 2 \right)} W_{m} } + \eta \sum\limits_{m = 1}^{n} {C_{{{\text{im}}}}^{\left( 1 \right)} \psi_{m} } } \right) = \tilde{I}_{1} \ddot{W}_{i} - F_{C}^{ * } \left( \tau \right)\delta \left( {X - X_{C} } \right)\left| {_{{X = X_{i} }} } \right., \hfill \\ \end{gathered} $$

(43)

$$ \begin{gathered} b_{11} \sum\limits_{m = 1}^{n} {C_{{{\text{im}}}}^{\left( 2 \right)} U_{m} + } \frac{{b_{11} }}{\eta }\left( {\sum\limits_{m = 1}^{n} {C_{{{\text{im}}}}^{\left( 1 \right)} W_{m} } \sum\limits_{m = 1}^{n} {C_{{{\text{im}}}}^{\left( 2 \right)} W_{m} } + \left. {\frac{{{\text{d}}W^{ * } }}{{{\text{d}}X}}} \right|_{{X = X_{i} }} \sum\limits_{m = 1}^{n} {C_{{{\text{im}}}}^{\left( 2 \right)} W_{m} } + \left. {\frac{{{\text{d}}^{2} W^{ * } }}{{{\text{d}}X^{2} }}} \right|_{{X = X_{i} }} \sum\limits_{m = 1}^{n} {C_{im}^{\left( 1 \right)} W_{m} } } \right) \hfill \\ + d_{11} \sum\limits_{m = 1}^{n} {C_{{{\text{im}}}}^{\left( 2 \right)} \psi_{m} } - a_{55} \left( {\eta \sum\limits_{m = 1}^{n} {C_{{{\text{im}}}}^{\left( 1 \right)} W_{m} } + \eta^{2} \psi_{i} } \right) = \tilde{I}_{2} \ddot{U}_{i} + \tilde{I}_{3} \ddot{\psi }_{i} . \hfill \\ \end{gathered} $$

(44)

With the DQ method, the boundary conditions in Eq. (34) can be rewritten as

$$ \begin{gathered} b_{11} \left[ {\sum\limits_{m = 1}^{n} {C_{1m}^{\left( 1 \right)} U_{m} } + \frac{1}{2\eta }\left( {\sum\limits_{m = 1}^{n} {C_{1m}^{\left( 1 \right)} W_{m} } } \right)^{2} + \frac{1}{\eta }\left. {\frac{{{\text{d}}W^{ * } }}{{{\text{d}}X}}} \right|_{{X = X_{1} }} \sum\limits_{m = 1}^{n} {C_{1m}^{\left( 1 \right)} W_{m} } } \right] + d_{11} \sum\limits_{m = 1}^{n} {C_{1m}^{\left( 1 \right)} \Psi_{m} } \hfill \\ - \left. {M_{x}^{T} } \right|_{{X = X_{1} }} = 0,U_{1} = 0,W_{1} = 0, \hfill \\ \end{gathered} $$

(45)

$$ \begin{gathered} b_{11} \left[ {\sum\limits_{m = 1}^{n} {C_{{{\text{nm}}}}^{\left( 1 \right)} U_{m} } + \frac{1}{2\eta }\left( {\sum\limits_{m = 1}^{n} {C_{{{\text{nm}}}}^{\left( 1 \right)} W_{m} } } \right)^{2} + \frac{1}{\eta }\left. {\frac{{{\text{d}}W^{ * } }}{{{\text{d}}x}}} \right|_{{X = X_{n} }} \sum\limits_{m = 1}^{n} {C_{{{\text{nm}}}}^{\left( 1 \right)} W_{m} } } \right] + d_{11} \sum\limits_{m = 1}^{n} {C_{{{\text{nm}}}}^{\left( 1 \right)} \Psi_{m} } \hfill \\ - \left. {M_{x}^{T} } \right|_{{X = X_{n} }} = 0,U_{n} = 0,W_{n} = 0 \hfill \\ \end{gathered} $$

(46)

Hence, the above ordinary differential equations can be written as the following matrix equation

$$ {\mathbf{M}}{\ddot{\mathbf{d}}} + \left( {{\mathbf{K}}_{{\mathbf{L}}} + {\mathbf{K}}_{{{\mathbf{NL}}}} } \right){\mathbf{d}} = {\mathbf{F}} + {\mathbf{R}}, $$

(47)

where ${\mathbf{d}} = \left\{ {\left\{ {U_{i} } \right\}^{T} ,\left\{ {W_{i} } \right\}^{T} ,\left\{ {\psi_{i} } \right\}^{T} } \right\}^{T}$ is the unknown displacement vector, $i = 1 \cdots n$. ${\mathbf{M}}$ denotes the mass matrix, ${\mathbf{K}}_{{\mathbf{L}}}$ and ${\mathbf{K}}_{{{\mathbf{NL}}}}$ denote the structural linear and nonlinear stiffness matrix. Additionally, F and R are respectively time-dependent and time-independent load vectors, which respectively generated by impact and the geometrically imperfect combined with the thermo-electro-mechanical load

$$ \begin{aligned}&{\mathbf{F}} = \left( \begin{gathered} \left\{ 0 \right\}_{n \times 1}^{{}} \hfill \\ \left\{ {F_{C}^{ * } \left( \tau \right)\delta \left( {X - X_{C} } \right)\left| {_{{X = X_{i} }} } \right.} \right\}_{n \times 1}^{{}} \hfill \\ \left\{ 0 \right\}_{n \times 1}^{{}} \hfill \\ \end{gathered} \right),\\&{\mathbf{R}} = \left( \begin{gathered} \left\{ 0 \right\}_{n \times 1}^{{}} \hfill \\ \left\{ {\left( {\tilde{N}_{x}^{T} + \tilde{N}_{x}^{P} } \right)\left. {\frac{{{\text{d}}^{2} W^{ * } }}{{{\text{d}}x^{2} }}} \right|_{{X = X_{i} }} } \right\}_{n \times 1}^{{}} \hfill \\ \left\{ 0 \right\}_{n \times 1}^{{}} \hfill \\ \end{gathered} \right).\end{aligned} $$

(48)

Stiffness-proportional damping matrix ${\mathbf{C}} = \left( {{{2\zeta } \mathord{\left/ {\vphantom {{2\zeta } {\omega_{l} }}} \right. \kern-\nulldelimiterspace} {\omega_{l} }}} \right)\,{\mathbf{K}}_{{\mathbf{L}}}$ [55,56,57] is considered to model energy dissipation of the impacted geometrically imperfect GRC piezoelectric beam, Eq. (44) can be written as

$$ {\mathbf{M}}{\ddot{\mathbf{{d}}}} + {\mathbf{C}}{\dot{\mathbf{{d}}}} + \left( {{\mathbf{K}}_{{\mathbf{L}}} + {\mathbf{K}}_{{{\mathbf{NL}}}} ({\mathbf{d}})} \right){\mathbf{d}} = {\mathbf{F}} + {\mathbf{R}} $$

(49)

where $\zeta$ is modal damping factor, and $\omega_{l}$ is the corresponding natural frequency. In this paper, $\omega_{l}$ is taken as the first natural frequency.

Assuming the initial conditions of the impactor as

$$ y_{i} \left( 0 \right) = 0,\dot{y}_{i} \left( 0 \right) = V_{0}, $$

(50)

the governing equations of motion for the impactor, Eq. (2), and the ordinary differential equation of motion for the geometrically imperfect GRC piezoelectric beam, Eq. (49), can be solved parametrically by combining the Newmark-β method [53] with the Newton–Raphson iterative method [13, 54] to analyze the time-dependent impact force $F_{C} \left( t \right)$ and nonlinear dynamic behaviors of the low-velocity impact system. Figure 3 is the flowchart for the solution procedure, which is processing as below.

• i. For the first time-step, assuming an initial impact force F_C0, the displacements $y_{i1}$ and ${\mathbf{d}}_{1}$ of the impactor and geometrically imperfect GRC piezoelectric beam can be respectively solved by Eq. (2) and Eq. (49) according to initial conditions ${\mathbf{d}}_{0}$, ${\dot{\mathbf{d}}}_{0}$, ${\ddot{\mathbf{d}}}_{0}$, $y_{i0}$ and ${\dot{y}_{i0}}$.

• ii. Applying the displacements obtained from step i into Eq. (3), a new impact force F_C1 and local contact indentation can be predicted (Note that when the local contact indentation reaches the maximum, the new impact force needs to be calculated by Eq. (5)). If F_C1 is close to F_C0, turn to step iii. If not, take the new impact force F_C1 as the initial impact force, and repeat step i.

• iii. Treating the displacements and impact force obtained from steps i and ii as the initial conditions for the next time-step, repeat steps i and ii.

• iv. When the central displacement of the geometrically imperfect GRC piezoelectric beam remains unchanged, the iterative process ends.

Fig. 3

Flowchart for solving the nonlinear dynamic equations of geometrically imperfect GRC piezoelectric beams under low-velocity impact

5 Results and discussions

In this section, the nonlinear low-velocity impact behaviors are analyzed numerically for the GRC beam with geometric imperfections under thermo-electro- mechanical loads. The effects of weight fraction f_G and distribution pattern of GPLs, mode and amplitude A₀ of imperfections, initial impact velocity V₀, temperature variation $\Delta T$ and thickness ratio $h_{P} /h$ on the impact force and dynamic response of the system are discussed in detailed.

Epoxy is selected as the matrix material of GRC beam, and the piezoelectric material is made by Polyvinylidene fluoride (PVDF). Material parameters [32, 33, 58] of epoxy, GPLs and PVDF are respectively

$$ {\text{Epoxy:}}\;E_{M} = 3.0\;{\text{GPa}}, \, \rho_{M} = 1200{\text{ kg}}/m^{3} ,\nu_{M} = 0.34,\alpha_{M} = 60 \times 10^{ - 6} /K $$

$$ {\text{GPLs}}:E_{G} = 1010\;{\text{GPa}},\;\rho_{G} = 1060{\text{ kg}}/m^{3} ,\nu_{M} = 0.186,\alpha_{G} = 5 \times 10^{ - 6} /K $$

$$ \begin{gathered} {\text{PVDF}}:E_{P} = 1.44{\text{ GPa,}}\; \, \rho_{P} = 1929{\text{ kg/m}}^{{3}} ,\;\nu_{P} = 0.29,\;\alpha_{P} = 14{5} \times 10^{ - 6} {\text{/K}},\;e_{31} = 0.05043{\text{ C/m}}^{{2}} , \hfill \\ k_{33} = 0.5957 \times 10^{ - 9} {\text{ V/cm}} \hfill \\ \end{gathered} $$

If there is no special instruction, length of the considered GRC beam $L = 50\;{\text{mm}}$, thicknesses of GRC host beam and piezoelectric layers are respectively $h = {10}\;{\text{mm}}$ and $h_{p} = 0.5\;{\text{mm}}$, dimensionless amplitude of the geometric imperfection $A_{0} = 0.02$, the applied piezoelectric actuator voltage $U_{0} = 400\;{\text{V}}$, temperature variation $\Delta T = 50\;{\text{K}}$ and damping factor $\zeta = 0.1$. The total number of the layers in the GRC host beam is $N = 12$. The geometric parameters of GPLs are $l_{G} \times w_{G} \times h_{G} = 2.5\;\mu {\text{m}} \times 1.5\;\mu {\text{m}} \times 1.5\;{\text{nm}}$ and total weight fraction of GPLs is $f_{G} = 0.3\%$. The impactor is made of steel, and its material parameters are $Y_{i} = {207}\;{\text{GPa}}$, $\rho_{i} = {7960}\;{\text{kg/m}}^{{3}}$ and $\nu_{i} = {0}.3$. It is assumed that the impactor's radius is $R_{i} = {5}\;{\text{mm}}$, and the impactor with initial velocity $V_{0} = {5}\;{\text{m/s}}$ impacts on the center ($X_{C} = {0}.5$) of the top surface for the geometrically imperfect GRC piezoelectric beam.

Convergence and comparison studies are firstly performed to ensure the effectiveness and accuracy of the present method. Figure 4 calculates and compares the effect of geometric imperfection modes on (a) the highest impact force and the (b) maximum central deflections of the geometrically imperfect GRC piezoelectric beams with varying nodes number n during the impact process. Obviously, L-mode imperfections converge slowly. It is because L-mode imperfections have sudden changes in geometric characteristics (Fig. 2). Even G₁-mode has the lowest impact force, it leads to the biggest center deflection. Hence, G₁-mode imperfection is the most harmful geometric imperfection for the stability of the GRC piezoelectric beam under impact. In the following analyses, we pay attention to the G₁-mode imperfect GRC piezoelectric beam with nodes number $n = 13$.

Fig. 4

Convergence results: the a highest impact force and b maximum central deflection of X-GRC piezoelectric beam with different geometric imperfections

The comparison results are given in Table 1 and Fig. 5. In Table 1, the nonlinear frequency ratios are compared with Wu et al.’s results [59] for the intact and L₁-mode imperfect FG-X CNTRC beams with nodes number $n = 39$. Figure 5 compares the impact force history with Kiani et al.’s results [60] for the intact FG-X CNTRC beam subjected to a low-velocity impact with $V_{0} = {3}\;{\text{m/s}}$. The comparison results show that our results are in good agreement with the existing literature results.

Table 1 Comparison results: Nonlinear frequency ratios of FG-X CNTRC beams with/without L₁-mode imperfection

Fig. 5

Comparison of impact force history of the FG-X CNTRC beam under low-velocity impact load

Figure 6 shows the influence of GPL distribution patterns (FG-X, UD, FG-O) on the impact force and impact response of the geometrically imperfect GRC piezoelectric beam. The case of pure epoxy piezoelectric beam’s results is also given for comparing. GPLs distributing into the GRC core beam and the piezoelectric layers are respectively considered in Fig. 6a, b. It is known that GPL reinforcements can largely improve the stiffness of the matrix. Keeping in mind that the dynamic displacement and impact force $F_{{\text{C}}}$ are respectively closely related to the bending stiffness of the structure and contact stiffness of the impacted area. Therefore, when GPLs distribute into the GRC core beam, the varying GPL distribution pattern can significantly affect the dynamic behaviors, but has little effect on the impact force $F_{{\text{C}}}$. To the contrary, the impact force is distinctly affected by the different GPL distribution pattern when GPLs distribute into the piezoelectric layers. In addition, the FG-X pattern has the lowest central deflection $W_{{{\text{mid}}}}$. For brief, only geometrically imperfect GRC piezoelectric beams with FG-X distributed GPLs are analyzed below.

Fig. 6

Effect of GPL distribution patterns on the impact force and impact response of the geometrically imperfect GRC piezoelectric beam: a GPLs distributing into the GRC core beam and b GPLs distributing into the piezoelectric layers

Figure 7 illustrates the influence of GPL weight fractions ($f_{G} = 0.0\%$, 0.1%, 0.3% and 0.5%) on the (a) impact force history and (b) impact response of the geometrically imperfect FG-X GRC piezoelectric beams. $f_{G} = 0.0\%$ stands for the case of pure epoxy piezoelectric beam. As seen, both impact force $F_{{\text{C}}}$ and central deflection $W_{{{\text{mid}}}}$ decrease with the increase in GPL weight fractions, and the central deflection $W_{{{\text{mid}}}}$ is more sensitive to the varying weight fraction of GPLs. It indicates that even a small amount of GPLs can contribute to a great increase in bending stiffness of the geometrically imperfect FG-X GRC piezoelectric beam.

Fig. 7

Effect of GPL weight fractions on the a impact force and b impact response for X-GRC piezoelectric beams

Figure 8 displays the effect of the imperfection amplitude A₀ (A₀ = − 0.02, − 0.01, 0, 0.01, 0.02) on the (a) impact force and (b) impact response of the geometrically imperfect GRC piezoelectric beam. A₀ = 0 means the intact GRC piezoelectric beam. As seen, the impact force for the convex surface (A₀ < 0) of the GRC beam impacted is obviously greater than that for the concave surface (A₀ > 0) impacted. What’s more, the impact force decreases with the increasing imperfection amplitude A₀ of the imperfection. Obviously, the final equilibrium position of the geometrically imperfect GRC piezoelectric beam is also related to the sign of the imperfection amplitude A₀. Bigger the absolute value of the imperfection amplitude is, further the final equilibrium position is apart from the z-axis. It is leaded by the direction and value of the component along z-axis of the force vector R in Eq. (49).

Fig. 8

Effect of imperfection amplitude on the a impact force and b impact response of the geometrically imperfect X-GRC piezoelectric beam

Note that the force vector R generated by the geometrically imperfect and the thermo-electro-mechanical load. R = 0 when the GRC piezoelectric beam is intact.

To illustrate the coupled effect of the geometric imperfection and thermo-electro-mechanical load on the nonlinear low-velocity impact behavior, Fig. 9 shows the effect of temperature variation ($\Delta T = 0\;{\text{K}}$, 25 K, 50 K) on the nonlinear low-velocity impact response of (a) geometrically imperfect ($A_{0} = - 0.02$ and 0.02) and (b) intact ($A_{{0}} = {0}$) GRC piezoelectric beams. It can be observed that the impact force and impact response of the imperfect cases are much more sensitive to the varying temperature than those of the intact one. In other words, the influence of thermal load on the nonlinear low-velocity impact response is barely for the intact GRC piezoelectric beam, but can be largely amplified once the geometric imperfection appearing.

Fig. 9

Effect of temperature variation on the impact force and impact response of the a geometrically imperfect and b intact X-GRC piezoelectric beam

Figure 10 demonstrates the (a) impact force history and (b) impact response of geometrically imperfect GRC piezoelectric beam impacted by different initial impactor velocities ($V_{0} = {3}\;{\text{m/s}}$, 5 m/s and 7 m/s). As seen that the increase in the initial impactor velocity $V_{0}$ leads to the remarkably increase in the maximum impact force, but obviously decreases the impacted time. Besides, the maximum center displacement increases a little for the increasing initial impactor velocity, which accompany with an increasing initial energy.

Fig. 10

Effect of initial indenter velocity on the a impact force and b impact response of the geometrically imperfect X-GRC piezoelectric beam

Figure 11 demonstrates the effect of the thickness ratio ($h_{P} /h = 0$, 1/10, 1/5) of piezoelectric layer to GRC host beam on the (a) impact force $F_{{\text{C}}}$ and (b) central deflection $W_{{{\text{mid}}}}$ for the geometrically imperfect GRC piezoelectric beam. Here, we keep the thickness of GRC host beam unchanged. $h_{P} /h = 0$ represents GRC beam without any piezoelectric layers. Because the increase in piezoelectric layer thickness can improve the stiffness of the GRC piezoelectric beam, the impact force $F_{{\text{C}}}$ increases, and the absolute value of the central deflection $W_{{{\text{mid}}}}$ decreases.

Fig. 11

Effect of thickness ratio on the a impact force and b impact response of geometrically imperfect X-GRC piezoelectric beam

6 Conclusions

The nonlinear low-velocity impact responses of GRC beam with geometric imperfection under thermo-electro-mechanical loads are investigated. The impact force is calculated by the modified nonlinear Hertz contact law. Based on the first-order shear deformation beam theory, von Kármán nonlinear displacement–strain relationship and Hamilton principle, the nonlinear dynamic equations are deduced, and solved by the DQ method and Newmark-β method combined with Newton–Raphson iterative method. Comprehensive numerical results are presented to investigate the effects of the distribution pattern and weight fraction of GPLs, the mode and amplitude of imperfection, initial velocity of the spherical impactor, temperature variation, thickness of piezoelectric layer, as well as the coupled effect of geometric imperfection and thermo-electro-mechanical load on the low-velocity impact characteristics of the geometrically imperfect GRC piezoelectric beam. The major conclusions are given as follows.

• (1) When calculating the impact behaviors of geometrically imperfect GRC piezoelectric beam via DQ method, the geometric imperfection with sudden changes require more nodes number. G₁-mode is the most harmful imperfection for the stability of the GRC piezoelectric beam under impact.

• (2) When GPL reinforcements are distributed into GRC core beam, only FG-X pattern reduces the low-velocity impact response of geometrically imperfect GRC piezoelectric beam. For GPL reinforcements distributing into the piezoelectric layers, all the patterns are effective for reducing the central deflection of the geometrically imperfect GRC piezoelectric beam under impact.

• (3) The thermal load has barely effect on the impact behaviors of intact GRC piezoelectric beam. Once the geometric imperfection appearing, the thermal effect is largely amplified.