Slow–fast analysis of a modified Leslie–Gower model with Holling type I functional response

Abstract

In this paper, we consider a modified Leslie-type prey–generalist predator system with piecewise–smooth Holling type I functional response. Considering the reproduction rate of the prey population higher than that of the predator, the model becomes a slow–fast system that mathematically leads to a singular perturbation problem. To analyse the stability of the boundary equilibrium on the switching boundary, we use a generalized Jacobian that enables us to investigate how the eigenvalues jump at the boundary point. We investigate the slow–fast system by employing geometric singular perturbation theory and blow-up technique that reveal a wide range of interesting complicated dynamical phenomena. We have studied existence of saddle-node bifurcation, Bogdanov–Takens bifurcation, bistability, singular Hopf bifurcation, canard orbits, multiple relaxation oscillations, saddle-node bifurcation of limit cycle and boundary equilibrium bifurcations. Numerical simulations are carried out to substantiate the analytical results.

1 Introduction

Natural systems like biology, physics, and chemistry [16, 17, 23, 45, 48, 49] often have components that vary on two or more distinct timescales and that may be important for researchers to take more attention to time scales. This type of difference in time scales can often be characterized by a singularly perturbed mathematical model in the form of ordinary differential equations which are called fast–slow systems [24]. Qualitatively, the essential notion for the investigation of a slow–fast system is to separate the subprocesses acting at the distinct time scales, comprehend each subsystem separately, and finally try to portray the complete dynamics based on the dynamics of the subsystems. A slow–fast system encapsulates remarkable predictions of complex oscillations [23, 24].

Relaxation oscillations are one of the most typical phenomena that appear in such slow–fast systems. Consider a simple model having two time scales, given by

$$\begin{aligned} {\dot{x}}&= f\left( x, y, \mu , \epsilon \right) , \end{aligned}$$

(1a)

$$\begin{aligned} {\dot{y}}&= \epsilon g\left( x, y,\mu , \epsilon \right) , \end{aligned}$$

(1b)

where $x, y \in {\mathbb {R}}$ are the fast and the slow variables, respectively, $\mu \in {\mathbb {R}}^k$ ($k\ge 1$) are system parameters, $0 < \epsilon \ll 1$ is the ratio between the two time scales, and the over dot $(~ \dot{}~ )$ denotes differentiation with respect to the fast time $t \in {\mathbb {R}}$. In general, f and g are the sufficiently smooth functions and system (1) may be termed as continuous slow–fast smooth system. Geometric singular perturbation theory (GSPT) which was developed based on Fenichel’s work [15] is an efficient technique to study the dynamical behaviour of the system (1) for small $\epsilon \rightarrow 0$. GSPT is a geometric approach to singular perturbation problems where the normally hyperbolic condition plays a key role [20]. For the preliminary definitions and related terminologies on slow–fast systems and GSPT, readers are referred to [14, 20, 24, 46]. When a submanifold is normally hyperbolic, Fenichel’s theorem (see [12,13,14,15]) can be used and the method of blow-up [8, 10, 21, 23] can be employed when submanifold losses the normal hyperbolicity. Geometric singular perturbation theory can also be extended to piecewise–smooth slow–fast systems [32, 35]. Existence of canard orbit was studied for piecewise linear vector fields (see [2]), continuous piecewise–smooth vector fields [30, 33, 34] and discontinuous piecewise–smooth vector fields [5].

A key component of any slow–fast system exhibiting periodic phenomenon is the existence of relaxation oscillations. It is a periodic orbit $\varGamma _\epsilon$ in the phase plane of the slow–fast system converging to a piecewise–smooth curve called ‘singular orbit’ $\varGamma _0$ consisting of attracting slow and fast segments of the slow–fast flow forming a closed loop as $\epsilon \rightarrow 0$ in the Hausdorff distance [24]. The Van der Pol’s equation [24, 31] is a classic example where relaxation oscillations are observed. For some other examples, readers are referred to [1, 3, 4, 24, 27, 36, 42, 48]. Relaxation oscillations are also observed in non-smooth slow–fast systems [26, 33, 47]. To show the existence of relaxation oscillation, one can employ the entry–exit function [1, 19]. The phenomenon of multiple relaxation oscillations is rarely studied in the literature [1, 7, 18, 26] ourselves. In the case of predator–prey systems, when the prey population has a higher reproduction rate than the predator, the system becomes a slow–fast system that mathematically leads to a singular perturbation problem. In the plankton food chain model, the rate of reproduction of algae is much faster than most of the zooplankton species, which in turn are faster than fish [37]. The herbivores like hares, squirrels, and small rodents reproduce faster than their predators like lynx, coyote, and red fox [41]. Although there are examples where prey reproduces slower than predator (see [28]), we confine ourselves in the study of the co-evolution of prey–predator system where the prey population has a higher reproduction rate in comparison to the predator. Such a system can be regarded as a slow–fast system of ordinary differential equation with the fast-growing prey and relatively slow growth of their predator. Because of this fact, in the current article, we have considered a continuous non-smooth slow–fast prey–predator system where the functional response representing the consumption rate of prey per unit of predator density is piecewise smooth. In contrast to a system with a Holling type II functional response [39] established that system with a non-smooth Holling type I functional response can give rise to a global cyclic-fold bifurcation and exhibits discontinuous Hopf bifurcations. In [38], authors included a predator–interference term into the Holling type I functional response, and they have shown the system exhibits much richer dynamics than Beddington–DeAngelis functional response. They have analysed the cyclic-fold, saddle-fold, homoclinic saddle connection, and multiple crossing bifurcations. Slow–fast analysis and existence of relaxation oscillations are not studied in detail in the existing literature. Recently, in [26], authors have investigated the relaxation oscillations in a Gauss-type slow–fast prey–predator model involving piecewise–smooth Holling type I response function with a predator interference term. They have employed GSPT and proved the existence of exactly two nested relaxation oscillations surrounding a stable equilibrium point. In this paper, we have considered a slow–fast dynamical system by modifying the prey–predator system proposed in [39] where we have taken the predator to act as a generalist predator. Such consideration enables the predator to avoid extinction by utilizing an alternative food source.

The present manuscript aims to study the consequences of considering such continuous, piecewise Holling type I functional response in the modified Leslie–Gower system consisting of prey and generalized predator. We shall study the detailed dynamics of such a piecewise–smooth slow–fast system by employing Geometric Singular Perturbation Theory. This study mainly concerns the existence of bistability, singular Hopf bifurcation, canard orbits, multiple relaxation oscillations, boundary equilibrium bifurcations, and several other bifurcations. We shall investigate two significant coexistences, namely (1) stable and unstable relaxation oscillations and (2) stable relaxation oscillation and canard orbit. We are also interested to investigate how eigenvalues jump at the corner of the prey nullcline by analysing the generalized Jacobian matrix.

The paper is organized as follows. In Sect. 2, we have proposed the model and the basic results including invariance, boundedness, the existence of equilibria, linearized stability analysis, and saddle-node bifurcation of equilibria. Then, in Sect. 3 the slow–fast analysis is carried out. The existence of relaxation oscillations is studied in Sect. 4 with the help of the entry–exit function. Singular Hopf bifurcation and canard orbits are reported in Sect. 5. The boundary equilibrium bifurcation analysis is carried out in Sect. 6. A final discussion in Sect. 7 concludes the paper.

2 The model and basic stability results

We consider the modified Leslie–Gower predator–prey model with logistic growth for both the prey and predator given by:

$$\begin{aligned} \frac{du}{dT}&=ru\left( 1- \frac{u}{\kappa }\right) -\varPhi (u)v, \end{aligned}$$

(2a)

$$\begin{aligned} \frac{dv}{dT}&=sv\left( 1-\frac{v}{h_1+h_2u}\right) , \end{aligned}$$

(2b)

subjected to nonnegative initial conditions $u(0)\ge 0$, $v(0)\ge 0$, where $\varPhi (u)$ is the Holling type I functional response given by

$$\begin{aligned} \varPhi (u)={\left\{ \begin{array}{ll} \frac{\beta }{\alpha }u, &{} u\le \alpha , \\ \beta , &{} u\ge \alpha . \end{array}\right. } \end{aligned}$$

(3)

Here, u and v represent population sizes of the prey and predator, respectively, where the predator is generalist in nature, i.e. the predator does not exist on its prey but also has some source of alternative food to avoid its extinction. The parameters r, $\kappa$, s, $\alpha$, $\beta$, $h_1$, and $h_2$ are positive constants. In model system (2), r stands for intrinsic growth rate for prey, $\kappa$ is the carrying capacity of the environment, s is the intrinsic growth rate for the predator, $\alpha$ is the half-saturation constant, that is, the number of prey at which the per capita consumption rate is half of its maximum $\beta$, $\beta$ is a maximum per capita consumption rate, $h_1$ is the amount of alternative food available for the predator, and $h_2$ is the measure of the food quality (prey) for the predator.

For $h_1=0$, the equation for a predator becomes a growth function of logistic type where the environmental carrying capacity for a predator is prey-dependent given by $h_2u$. The associated prey–predator model is termed as a Leslie–Gower. When the prey population is absent, the predator will go to extinction.

On the other hand, the parameter $h_1>0$ defined that to generalist predator since the predator hunts for an alternate food source when its preferred prey is absent (i.e. when $x = 0$). In this case, the environmental carrying capacity for the predator is expressed as $h_1+h_2u$. If $v > h_1+h_2u$, $\frac{dv}{dt}<0$ which indicate that predator population is going to extinction under such situation. The associated prey–predator model is termed as modified Leslie–Gower model. When the favourite food source is limited, the generalist predator can survive on other food sources and avoid extinction. When the prey population is available in abundance, the predator will switch to hunt the favourite prey population as it becomes beneficial for them [43]. For an ecological example, in the boreal forest area of Fennoscandia, the species weasels (Mustela nivalis) will turn to an alternate food source when their most preferable food supply, namely vole (Microtus Agrestis), is not abundantly available [29, 43, 44].

Non-dimensionalizing the system (2) using the rescaling transformations:

$$\begin{aligned} t = rT,~~ x = \frac{u}{\alpha }, ~~y = \frac{\beta v}{r\alpha }, \end{aligned}$$

(4a)

we have

$$\begin{aligned} \frac{dx}{dt}&=x\left( 1-\frac{x}{k}\right) -\phi (x)y=f(x,y), \end{aligned}$$

(5a)

$$\begin{aligned} \frac{dy}{dt}&=\epsilon y\left( 1-\frac{y}{ax+b}\right) =\epsilon g(x,y), \end{aligned}$$

(5b)

such that

$$\begin{aligned} \phi (x)={\left\{ \begin{array}{ll} x, &{} x\le 1, \\ 1, &{} x\ge 1, \end{array}\right. } \end{aligned}$$

(6)

where x, y are the new dimensionless variables and new dimensionless parameters are $k=\frac{\kappa }{\alpha }$, $\epsilon =\frac{s}{r}$, $a=\frac{\beta h_2}{r}$, $b=\frac{\beta h_1}{r\alpha }$. The parameters are positive with $0<\epsilon \ll 1$.

The system (5) is a continuous piecewise smooth system, and from an ecological standpoint, we shall restrict our attention to study the dynamics in the first quadrant in the (x, y) plane, denoted by

$$\begin{aligned} {\mathbb {R}}^2_+=\left\{ (x,y)\in {\mathbb {R}}^2 \,\big |\, x\ge 0, y\ge 0)\right\} , \end{aligned}$$

(7)

with the assumption on initial condition $x(0)\ge 0$ and $y(0)\ge 0$.

The system (5) is continuous along the line $x=1$ which is known as the switching boundary, and we denote it by $\varSigma$. Thus, the switching boundary $\varSigma =\left\{ (x,y)\in {\mathbb {R}}^2_+ \,\big |\, x=1\right\}$ partitions the interior of the phase space ${\mathbb {R}}^2_+$ into two regions, namely $\varSigma ^-=\left\{ (x,y)\in {\mathbb {R}}^2_+ \,\big | 0<x<1\right\}$ and $\varSigma ^+=\left\{ (x,y)\in {\mathbb {R}}^2_+ \,\big |x>1\right\}$ in which the system (5) is smooth and governed by the following equations.

(8)

and

(9)

The systems (8) and (9) are referred as the left-half and right-half systems and by continuity $f^-=f^+$ on the switching boundary $\varSigma$. Trajectories of the model system (5) cut $\varSigma$ transversally. The fundamental existence and uniqueness theory for the system (5) is applicable here as the vector field is locally Lipschitz [40]. We assume throughout the paper that $k>4$ so as to guarantee that the prey nullcline lying in $\varSigma ^+$ has a maximum at the point $(\frac{k}{2}, \frac{k}{4})$ with ordinate greater than 1. The reason behind this assumption will be discussed in Sect. 3.

Some basic properties of the system are presented below.

Lemma 1

The first quadrant ${\mathbb {R}}^2_+$ is invariant under the flow generated by the vector field $F=f\frac{\partial }{\partial x}+\epsilon g\frac{\partial }{\partial y}$.

Proof

The first quadrant ${\mathbb {R}}^2_+$ is invariant because the x and y axes are invariant under the flow.

Lemma 2

The system (5) is a bounded system.

Proof

We have already shown that ${\mathbb {R}}^2_+$ is invariant under the flow. We now consider the line

$$\begin{aligned} L_1=\left\{ (x,y)\in {\mathbb {R}}^2_+\,\big |\, x=k, y\ge 0\right\} . \end{aligned}$$

(10)

We then have

$$\begin{aligned} \frac{d}{dt}(x-k)&=-ky<0, x< 1,\\&=-y, x\ge 1. \end{aligned}$$

Thus, any trajectory in ${\mathbb {R}}^2_+$ cuts the line $L_1$ inward. Next, we consider the following line

$$\begin{aligned} L_2=\left\{ (x,y)\in {\mathbb {R}}^2_+\,\big |\, y=ak+b, 0\le x\le k\right\} . \end{aligned}$$

(11)

Then,

$$\begin{aligned} \frac{d}{dt}(y-ak-b)=\epsilon (ak+b)\frac{a(x-k)}{ax+b}<0. \end{aligned}$$

Thus, any trajectory in ${\mathbb {R}}^2_+$ cuts the line $L_2$ inward. Hence, any trajectory in ${\mathbb {R}}_+^2$ is confined in the rectangular region $R=\left\{ 0\le x\le k, y=0; x=k,\right.$ $\left. 0\le y\le \right.$$\left. ak+b; y=ak+b, 0\le x \le k; x=0, 0\le y\le ak\right.$$\left. +b\right\}$ in forward time. Now, one can analytically extend the systems (8) and (9) to the Poincaré sphere and it can be shown that the singularities at infinity correspond to the points along x and y directions. We know that the x- and y-axes are invariant, along the x-axis we have $\frac{dx}{dt}<0$ for $x>k$, and along the y-axis, $\frac{dy}{dt}<0$ for $y>b$. Thus, the singularities at infinity which lie along the x and y directions are not attractors. Hence, all the solutions in ${\mathbb {R}}^2_+$ for the system (5) are bounded and enters the rectangular region R in forward time. $\square$

Figure 1 illustrates the rectangular region R bounded by the axes along with two lines $L_1$ and $L_2$ as defined in Lemma 2. Figure demonstrates that any trajectory starting from an interior point of ${\mathbb {R}}^2_+$ is confined in the rectangular region R.

Fig. 1

The rectangular region R is positively invariant. The vertical line $L_1$ is given by the equation $x=k$ for $y\ge 0$, and the horizontal line $L_2$ is given by the equation $y=ak+b$ for $0\le x\le k$. The vector field points inward on the boundary of R. The parameter values are $a=0.527, b=0.05, k=5, \epsilon =0.1$

Lemma 3

The system (5) has no periodic orbit lying entirely in the region $\varSigma ^-$.

Proof

Since the region $\varSigma ^-$ is simply connected and in $\varSigma ^-$, the system (5) is governed by the smooth flow generated by the vector field $F_-= f_-\frac{\partial }{\partial x}+\epsilon g\frac{\partial }{\partial y}$, we will be using the Dulac’s criteria to show that the system (5) has no periodic orbit lying entirely in the region $\varSigma ^-$. We consider the Dulac function $D:\varSigma ^-\rightarrow {\mathbb {R}}$, given by $D(x,y)=\frac{1}{xy}$. We have

$$\begin{aligned} \mathrm{div} (DF_-)&= \frac{\partial }{\partial x} (Df_-) + \epsilon \frac{\partial }{\partial y} (Dg)\\&= -\left( \frac{1}{ky} +\frac{\epsilon }{x(ax+b)}\right) <0. \end{aligned}$$

Hence, by Dulac’s criteria, the system (5) has no periodic orbit lying entirely in the region $\varSigma ^-$. $\square$

Thus, we see that if there exists a periodic orbit for the system (5), then it will lie either entirely in the region $\varSigma ^+$ or part of it will be in $\varSigma ^+$ and part of it will be in $\varSigma ^-$ crossing transversally the switching boundary $\varSigma$.

2.1 Existence of equilibria and their stability

The equilibria for (5) are the intersection points of prey and predator nullclines, i.e. the equilibria can be obtained by the solutions of the equations

$$\begin{aligned} f_{-}(x,y)=0=g(x,y) ~~\text {or} ~~ f_{+}(x,y)=0=g(x,y). \end{aligned}$$

(12)

Now, if $f_{-}(x,y)=0=g(x,y)$, then the equilibrium is said to be an admissible equilibrium if $x<1$ and virtual equilibrium if $x>1$ and vice versa if $f_{+}(x,y)=0=g(x,y)$. An equilibrium is said to be a boundary equilibrium if $f_(x,y)=f_{+}(x,y)=g(x,y)=0$ and also lies on the switching boundary $\varSigma$.

The model system (5) has trivial admissible equilibria $E_0\left( 0,0\right)$, $E_k(k,0)$, and $E_b(0,b)$. The equilibrium $E_0$ is an unstable node, and the boundary equilibrium $E_k$ is a saddle point having the x-axis as the stable manifold. The equilibrium $E_b$ is a saddle point for $b<1$ having the y-axis as the stable manifold and a stable node for $b>1$. For $b=1$, the equilibrium $E_b$ is an attracting saddle-node [25].

We now consider the parametric region

$$\begin{aligned} D=\left\{ \sigma =(a,k,b)\in {\mathbb {R}}^3_+: a>0, b>0, k>4\right\} \end{aligned}$$

(13)

and the following subregions of D

$$\begin{aligned} D_1&=\left\{ \sigma =(a,k,b)\in D\big |\,a\ge 1, b\ge 1,\,\, \mathrm{or}\,\, \right. \nonumber \\&\quad \left. a<1, b\ge 1, k^2(1-a)^2<4kb\right\} , \end{aligned}$$

(14a)

$$\begin{aligned} D_2&=\left\{ \sigma =(a,k,b)\in D\,\big |\, b<1, a\ge 1 \,\,\mathrm{or}\,\, b<1, a<1,\right. \nonumber \\&\quad \left. k^2(1-a)^2<\,\mathrm{min}\,\,\{4kb, (1+kb)^2\}\right\} , \end{aligned}$$

(14b)

$$\begin{aligned} D_3&=\left\{ \sigma =(a,k,b)\in D\,\big |\,a< 1, b \right. \nonumber \\&\quad \left. \ge 1, k^2(1-a)^2>4kb\right\} , \end{aligned}$$

(14c)

$$\begin{aligned} D_4&=\left\{ \sigma =(a,k,b)\in D\,\big |\,a< 1, \right. \nonumber \\&\quad \left. b<1, 4kb<k^2(1-a)^2<(1+kb)^2\right\} , \end{aligned}$$

(14d)

$$\begin{aligned} D_5&=\left\{ \sigma =(a,k,b)\in D\,\big |\,a< 1,\right. \nonumber \\&\quad \left. b<1, k(1-a)=1+kb>2\right\} , \end{aligned}$$

(14e)

$$\begin{aligned} D_6&=\left\{ \sigma =(a,k,b)\in D\,\big |\,a< 1, \right. \nonumber \\&\quad \left. b<1, k(1-a)>1+kb\right\} , \end{aligned}$$

(14f)

$$\begin{aligned} D_7&=\left\{ \sigma =(a,k,b)\in D\,\big |\,a<1, \right. \nonumber \\&\quad \left. b<1, k(1-a)=1+kb\le 2\right\} , \end{aligned}$$

(14g)

$$\begin{aligned} D_8&=\left\{ \sigma =(a,k,b)\in D\big |\,a<1,\right. \nonumber \\&\quad \left. b\ge 1, k^2(1-a)^2=4kb\right\} , \end{aligned}$$

(14h)

$$\begin{aligned} D_9&=\left\{ \sigma =(a,k,b)\in D\big |\,a<1, \right. \nonumber \\&\quad \left. b< 1, k^2(1-a)^2=4kb>4\right\} , \end{aligned}$$

(14i)

$$\begin{aligned} D_{10}&=\left\{ \sigma =(a,k,b)\in D\big |\, 1-\frac{2}{k}<a<1, b< 1\right\} . \end{aligned}$$

(14j)

Now, we have the following trivial results on the existence of admissible interior equilibria:

Lemma 4

• (i) If $\sigma \in D_1$, then there does not exist any admissible interior equilibrium point.

• (ii) If $\sigma \in D_2$, then there exists only one interior equilibrium point, say $E_1(x_1,y_1)$ where $x_1=\frac{k(1-b)}{1+ka}$, $y_1=\frac{ka+b}{1+ka}$. The equilibrium lies in $\varSigma ^-$ where the prey and predator nullclines intersect.

• (iii) If $\sigma \in {D}_3$, then there exist two admissible interior equilibrium points $E_2(x_2,y_2)$ and $E_3(x_3,y_3)$ in $\varSigma ^+$ and $x_2=\frac{k(1-a)-\sqrt{k^2(1-a)^2-4kb}}{2}$, $y_2=x_2\left( 1-\frac{x_2}{k}\right)$, $x_3=\frac{k(1-a)+\sqrt{k^2(1-a)^2-4kb}}{2}$, $y_3=x_3\left( 1-\frac{x_3}{k}\right)$.

• (iv) If $\sigma \in {D}_4$, then there exist three admissible interior equilibrium points $E_1(x_1,y_1)$,$E_2(x_2,y_2)$ and $E_3(x_3,y_3)$ where $E_1$ lie in $\varSigma ^-$ and $E_2$, $E_3$ lie in $\varSigma ^+$.

• (v) If $\sigma \in {D}_5$, then there exist two equilibrium points of which the equilibrium $E_c(x_c, y_c)$ is a boundary equilibrium lying on $\varSigma$ where $x_c=1, y_c=1-\frac{1}{k}$. The other admissible equilibrium $E_3(x_3, y_3)$ lies in $\varSigma ^+$, where $x_3=kb$, $y_3=ax_3+b$.

• (vi) If $\sigma \in {D}_6$, then there exists only one admissible equilibrium point $E_3(x_3, y_3)$ in $\varSigma ^+$.

• (vii) If $\sigma \in {D}_7$, then there exists only the boundary equilibrium point $E_c(x_c, y_c)$ at the corner on $\varSigma$.

• (viii) If $\sigma \in {D}_8$, then there exists only one admissible equilibrium $E_*(x_*, y_*)$ lying in $\varSigma ^+$ where $x_*=\frac{k(1-a)}{2}$, $y_*=ax_*+b$. The existence of $E_*$ occurs when the two admissible equilibria $E_2$ and $E_3$ in $\varSigma ^+$ get merged.

• (ix) If $\sigma \in {D}_9$, then there exist two admissible equilibria $E_1$ lying in $\varSigma ^-$ and $E_*$ lying in $\varSigma ^+$.

• (x) If $\sigma \in {D}_{10}$, then varying $c=\frac{k(1-b)}{1+ka}$, there exists one admissible interior equilibrium point, say, $E({\bar{x}}, {\bar{y}})$ such that $E=E_1$ when $c<1$; $E=E_c$ when $c=1$; $E=E_3$ when $c>1$. Thus, it follows that $D_{10}\subset D_2\cup D_6\cup D_7$ and as the parameter c is varied the admissible equilibrium becomes virtual when collides with the boundary equilibrium $E_c$. We then have boundary equilibrium bifurcation which we have investigated in Sect. 6.

The number of interior equilibrium points can be studied from the intersections of the non-trivial predator nullcline $y=ax+b$ and non-trivial prey nullcline $y={\left\{ \begin{array}{ll} 1-x/k, &{} x\le 1, \\ x\left( 1-x/k\right) , &{} x\ge 1 \end{array}\right. }$ in the interior of ${\mathbb {R}}_+^2$. The non-trivial predator nullcline is the straight line passing through the (0, b) with the slope a. In the first quadrant, the non-trivial prey nullcline is a continuous curve passing through the points (k, 0) and (0, 1), and it is differentiable for all $x\ge 0$ except at $\left( 1,1-\frac{1}{k}\right)$. On the interval $0 \le x\le 1$, the non-trivial prey nullcline is a linearly decreasing straight line, and on the interval $1 \le x\le k$, it is a parabolic curve with a maximum at $Q(\frac{k}{2}, \frac{k}{4})$. Mutual position of the prey and predator nullclines of the system (5) is illustrated in Fig. 14, and it describes that there can be 0, 1, 2 or 3 interior equilibria corresponding to coexistence of prey and predator populations of the system. We have observed four different mutual positions of the prey and predator nullclines of the system for four different ranges of b.

2.2 Linear stability analysis

Let $J_-$ and $J_+$ be the left and right Jacobian matrices evaluated at the interior admissible equilibrium $E_j (x_j, y_j)$ which lie on $\varSigma ^-$ and $\varSigma ^+$, respectively. Then,

$$\begin{aligned} J_{\pm }=\left[ \begin{array}{cc} f_{\pm x}(x_j, y_j) &{} f_{\pm y}(x_j, y_j)\\ a\epsilon &{}-\epsilon \end{array} \right] . \end{aligned}$$

(15)

We note that the Jacobian matrix for the boundary equilibrium point $E_c$ is not defined. We now have the following results on the stability of various equilibrium points.

• (i) The equilibrium point $E_1$ is a stable node or a stable focus depending on weather $\varDelta _1=\left( \frac{x_1}{k}-\epsilon \right) ^2-4a x_1\epsilon \ge ~~ \text {or}~~ <0$.

• (ii) The equilibrium point $E_2$ is saddle point.

• (iii) The equilibrium point $E_3$ is a stable equilibrium point if the point coincides with the maximum point, i.e. $x_3=\frac{k}{2}$ of the prey nullcline in $\varSigma ^+$ or lies to the right of this maximum point, i.e. $x_3>\frac{k}{2}$. In this case, $E_3$ is either a stable node or a stable focus if

  $$\begin{aligned} \varDelta _2&=\left( \left( Tr~J^3_+\right) ^2-4 \det J^3_+\right] \nonumber \\&=\left\{ \left( 1-\frac{2x_3}{k}\right) -\epsilon \right\} ^2-4\epsilon \left\{ \left( \frac{2x_3}{k}-1\right) +a\right\} \ge \nonumber \\ {}&~~\text {or} ~~< 0. \end{aligned}$$

  (16)

Now, if $E_3$ lies to the left of the maximum point in $\varSigma ^+$, i.e. if $x_3<\frac{k}{2}$, then $E_3$ can be a stable or unstable equilibrium point if $Tr~ J^3_+= \left( 1-\frac{2x_3}{k}\right) -\epsilon <0 ~~ \text {or}~~ >0$ and then it will be either node or focus depending on the sign of $\varDelta _2$.

In this case, we note that with the variation of parameters, $Tr~ J^3_+$ can be made equal to 0 and consequently, a smooth Hopf bifurcation around $E_3$ may take place which will be studied in detail in the frame of slow–fast dynamics in the next section.

We know that the Jacobian matrix for the boundary equilibrium $E_c(1, 1-\frac{1}{k})$ on $\varSigma$ is not defined and correspondingly following [6] we consider the generalized Jacobian

$$\begin{aligned} J_c=\left( 1-\theta \right) J_-+\theta J_+, ~~ 0\le \theta \le 1 \end{aligned}$$

(17)

which is a convex combination of the left and right Jacobian matrices in (15). Here, we assume that either $\sigma \in D_5$ or $\sigma \in D_7$ so that we can have always the existence of the boundary equilibrium $E_c$ on $\varSigma$.

The generalized Jacobian evaluated at $E_c$ is given by

$$\begin{aligned} J_c&=\left[ \begin{array}{cc} \theta \left( 1-\frac{1}{k}\right) -\frac{1}{k}&{}-1\\ a\epsilon &{}-\epsilon \end{array}\right] . \end{aligned}$$

(18)

$$\begin{aligned} Tr~J_c&=\theta \left( 1-\frac{1}{k}\right) -\left( \frac{1}{k}+\epsilon \right) , \end{aligned}$$

(19)

$$\begin{aligned} \det {J_c}&=-\epsilon \left\{ \theta \left( 1-\frac{1}{k}\right) -\frac{1}{k}\right\} +a\epsilon >0. \end{aligned}$$

(20)

Now, varying $\theta$ in the interval [0, 1], we see that the eigenvalues of the Jacobian $J_c$ trace a path in the complex plane. When a pair of complex conjugate eigenvalues cross the imaginary axis as $\theta$ varies from 0 to 1 during the jump, a bifurcation occurs and is known as discontinuous bifurcation or boundary equilibrium bifurcation.

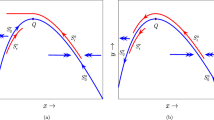
The path of the eigenvalues of the generalized Jacobian (17) is depicted in Fig. 2.

Fig. 2

Paths of the eigenvalues of the generalized Jacobian (17). The arrows indicate the direction of eigenvalues that start from an open circle corresponding to $q=0$ and end at an open square where $q=1$. The blue and red solid circles are the two eigenvalues of the generalized Jacobian (17). (a) The eigenvalues do not cross the imaginary axis (black vertical line) as q varies from 0 to 1 for $\epsilon =0.9$ (b) The eigenvalues cross the imaginary axis as q varies from 0 to 1 for $\epsilon =0.1$. The other parameter values are $a=0.75, b=0.05, k=5$

2.3 Saddle-node bifurcation

We assume the parametric conditions $a<1$ and $b\ge 1$. Then for $k^2(1-a)^2>4kb$, there exist two admissible interior equilibrium points in $\varSigma ^+$, namely $E_2$ and $E_3$ where $E_2$ is a saddle point; for $k^2(1-a)^2=4kb$, the two equilibrium points coalesce at the degenerated equilibrium point (saddle-node) $E_*(x_*,y_*)$ in $\varSigma ^+$ and for $k^2(1-a)^2<4kb$ there exists no equilibrium in $\varSigma ^+$. Thus, we have S-N (saddle-node) bifurcation of equilibria and the S-N curve is given by $k^2(1-a)^2=4kb$, i.e. $b=b_{s}=\frac{k^2(1-a)^2}{4k}$. Now, it can be shown that varying the parameter b there may take place subcritical smooth Hopf bifurcation around $E_3$ and one may ask about the existence of relaxation oscillation in such a case. We have seen that for $b=b_{s}=\frac{k^2(1-a)^2}{4k}$, the equilibrium points $E_2$ and $E_3$ coalesce at $E_*$ which is a saddle-node singularity. Further, we see that for $a=a_{s}=\epsilon$, the singularity $E_*$ is a Bogdanov–Taken (BT) singularity. One thus has to consider the BT–bifurcation phenomena arising in slow–fast system varying the parameter (a, b) in a neighbourhood of $(a_s, b_s)$. We may have various phenomena which occur in case of co-dimension 2 BT–bifurcation. We will not consider the detailed study of BT bifurcation in this article and leave it for future work.

The possible types of phase portraits and bifurcation diagrams are drawn corresponding to two different cases namely the number of feasible interior equilibrium points is either one or three. Varying slopes of the predator nullcline determined by the parameter value a and $b=0.05, k=5, \epsilon =0.1$, the phase portraits and bifurcation diagram in the case when there exists only one interior equilibrium point lying in $\varSigma ^-$ ($\sigma \in D_2$) or corner point on $\varSigma$ ($\sigma \in D_7$) or in $\varSigma ^+$ ($\sigma \in D_6$) of the system (5) are illustrated in Fig. 3. Possible phase portraits and bifurcation diagram by varying the parameter b in the case of existence of three interior equilibria ($\sigma \in D_4$) of the system (5) are illustrated in Fig. 4. The equilibrium point E(0, 0) is unstable node, $E_k(k,0)$ is a saddle, and $E_b(0,b)$ is a saddle (here $b<1$). The nature of stability of the interior equilibrium point(s) is mentioned in the caption of Figs. 3 and 4. Bifurcation diagram with a as the bifurcation parameter for the case when the number of feasible interior equilibria is one is drawn in Fig 3. Here, a is along horizontal axis and the x component of the unique interior equilibrium point is along the vertical axis. The blue curve is the stable branch, and red curve is the unstable branch of the x component of the equilibrium point. The figures in Fig. 3b to Fig. 3d are associated with the boundary equilibrium bifurcation which we have studied in detail in Sect. 6. When the number of feasible interior equilibria is three, we take b as the bifurcation parameter, and the bifurcation diagram of the system is shown in Fig. 4e where b is along the horizontal axis and the x components of the equilibrium point $E_3$ are along the vertical axis. Stability changes from unstable focus to stable focus through a Hopf bifurcation when b crosses a critical value $b_H=0.5625$. A unstable limit cycle emerges for $b<0.5625$. This limit cycle expands and continues to exist until b crosses a critical value $b_{HL}=0.5449542$, and the unstable limit cycle disappears through Homoclinic bifurcation. For $b<b_{HL}$, the Homoclinic orbit disappears and system exhibits bistability of the coexistence equilibrium points $E_1$ and $E_3$. The stable manifold of the saddle equilibrium point $E_2$ is the separatrix curve (black) which separates the phase plane into two basins of attraction of the two stable equilibria $E_1$ and $E_3$. Trajectories which initiated from one side (or opposite side) of separatrix curve are attracted to $E_1$ (or $E_3$), respectively (see Fig. 4b). This suggests that solutions close to the separatrix curve are quite sensitive to the initial sizes of prey and predator populations.

Fig. 3

Phase portraits and bifurcation diagram by varying the parameter a in the case of existence of only one interior equilibrium point lying in $\varSigma ^-$ or on $\varSigma$ or in $\varSigma ^+$ of the system (5). (a) $E_1$ lying in $\varSigma ^-$ is stable for $a=0.99$. (b) Two limit cycles exist enclosing the stable equilibrium point $E_1$ lying in $\varSigma ^-$ for $a=0.95$. The outer limit cycle (green) is stable, and the inner (black) one is unstable. (c) One stable limit cycle (green) for $a=0.75$ around the equilibrium point $E_c(1, 0.8)$ at the corner on $\varSigma$. (d) One limit cycle at the right branch for the parameter values $a=0.6$ around the unstable equilibrium point $E_*(1.8660, 1.1696)$ lying in $\varSigma ^+$. (e) Two limit cycles at the right branch for the parameter values $a=0.5275$ around the spirally stable equilibrium point $E_*(2.25140, 1.2376)$ lying in $\varSigma ^+$. (f) One interior equilibrium point (stable focus) lying in $\varSigma ^+$ for $a=0.51$. (g) One parameter bifurcation diagram with a as the bifurcation parameter. The x-component of the unique interior equilibrium point is depicted by blue (corresponding to stable branch of the interior equilibrium point) and red (corresponding to unstable branch of the interior equilibrium point) colour curves. All other parameter values are $b=0.05, k=5, \epsilon =0.1$

Fig. 4

Phase portrait and bifurcation diagram by varying the parameter b in the case of existence of three interior equilibria of the system (5) where $E_1$ and $E_2$ are always stable and saddle, respectively. (a) $E_3$ is unstable focus for $b=0.57$, (b) Hopf bifurcation arises for $b=b_H=0.5625$, and a unstable limit cycle (black) exists for $b=0.55<b_H$ surrounding the stable equilibrium point $E_3$. (c) As b decreases, the unstable limit cycle expands and for $b=b_{HL}=0.5449542$, the unstable limit cycle disappears through Homoclinic bifurcation. (Homoclinic orbit is shown by the black curve.) (d) By further decreasing b, say $b=0.54$, the homoclinic orbit disappears and bistability appears. The stable manifold of the saddle equilibrium point $E_2(x_2, y_2)\in \varSigma ^+$ is the separatrix curve (black) dividing the phase plane into two basins of attraction of the two stable equilibria $E_1(x_1, y_1)\in \varSigma ^-$ and $E_3(x_3, y_3)\in \varSigma ^+$. (e) One-parameter bifurcation diagram with respect to the parameter b. The x-components of the three interior equilibria $E_1$, $E_2$, and $E_3$ are depicted by blue (corresponding to stable branch of the interior equilibria) and red (corresponding to unstable branch of the interior equilibria) colour curves. The heavy red curves lying between two black parallel lines $x=b_{HL}$ and $x=b_H$ represent the maximum and minimum of the amplitude of the periodic orbit. The other parameter values are $a=0.3$, $k=5, \epsilon =0.1$

3 Dynamics of the slow–fast system

By a time rescaling $\tau = \epsilon t$, the system (5) changed to the following system in terms of $\tau$:

$$\begin{aligned} \epsilon \frac{dx}{d\tau }&=x\left( 1-\frac{x}{k}\right) -\phi (x)y, \end{aligned}$$

(21a)

$$\begin{aligned} \frac{dy}{d\tau }&=y\left( 1-\frac{y}{ax+b}\right) , \end{aligned}$$

(21b)

subjected to nonnegative initial condition where $\phi (x)$ is defined in (6). Under the condition that the parameter $\epsilon$ is sufficiently small, system (5) or (21) is a standard form of slow–fast system with t as the fast time scale and $\tau$ as slow time scale, respectively. We refer x and y, respectively, as fast and slow variables. Evidently, systems (5) and (21) are equivalent for $\epsilon \ne 0$. To understand the dynamics of system (5) or (21) for $0<\epsilon \ll 1$, we now examine the limiting systems obtained from (5) and (21) by setting $\epsilon =0$. For $\epsilon =0$, the system (5) becomes a fast subsystem given by

(22)

and

(23)

which is often called a ‘layer system’ describing the dynamics on the fast timescale.

For $\epsilon =0$, the system (21) becomes the slow subsystem given by

(24)

and

(25)

which is often called a ‘reduced subsystem’ describing the dynamics on the slow timescale. We have $f_+=f_-$ for $(x,y)\in \varSigma$. The slow flow is constrained on the critical set M given by $f_+=0=f_-$ and comprises of two kinds of critical manifolds given by

$$\begin{aligned} M_{10}&=\left\{ (x,y)\,\big |\,x=0\right\} , \end{aligned}$$

(26a)

$$\begin{aligned} M_{20}&=\left\{ (x,y)\,\big |\,y=\psi _-(x)=1-\frac{x}{k},\, x\right. \nonumber \\&\quad \left. \le 1~ \text {and}~ y=\psi _+(x)=x\left( 1-\frac{x}{k}\right) ,\, x\ge 1\right\} . \end{aligned}$$

(26b)

Further, we decompose the critical manifold $M_{20}$ into the following branches

$$\begin{aligned} M_{20}^-&=C_0^{a-}=\left\{ (x,y) \,\big |\, y=\psi _-(x), 0<x<1\right\} ,\\ M_{20}^+&={\left\{ \begin{array}{ll} C_0^r =\left\{ (x,y) \,\big |\, y=\psi _+(x), 1<x<\frac{k}{2}\right\} ,\\ C_0^{a+}=\left\{ (x,y) \,\big |\, y=\psi _+(x), \frac{k}{2}<x<k \right\} . \end{array}\right. } \end{aligned}$$

Now, we state the following result:

Lemma 5

Consider $0<\epsilon \ll 1$. Then,

• (i) $M_{20}$ looses its normal hyperbolicity at $P\left( 0, 1\right)$ and $Q\left( \frac{k}{2}, \frac{k}{4}\right)$.

• (ii) The branches $C_0^{a-}$ and $C_0^{a+}$ are normally hyperbolic attracting, and $C_0^r$ is normally hyperbolic repelling.

Proof

• (i) We have $\left. \frac{\partial f_-}{\partial x}\right| _{(x,\psi _-(x))}=-\frac{x}{k}$ and $\left. \frac{\partial f_+}{\partial x}\right| _{(x,\psi _+(x))}=1-\frac{2x}{k}$. Evidently, $\left. \frac{\partial f_-}{\partial x}\right| _{P(0,1)}=0$ and $\left. \frac{\partial f_+}{\partial x}\right| _{Q\left( \frac{k}{2},\frac{k}{4}\right) }=0$. Therefore, $\frac{\partial f_-}{\partial x}$ has zero eigenvalue at P and $\frac{\partial f_+}{\partial x}$ has zero eigenvalue at Q, respectively, and consequently, $M_{20}$ looses its normal hyperbolicity at P and Q.

• (ii) Clearly, $\left. \frac{\partial f_-}{\partial x}\right| _{(x,\psi _-(x))}< 0$, for $0<x<1$; $\left. \frac{\partial f_+}{\partial x}\right| _{(x,\psi _+(x))}> 0$, for $1<x<\frac{k}{2}$ and $\left. \frac{\partial f_+}{\partial x}\right| _{(x,\psi _+(x))}<0$ for $\frac{k}{2}<x<k$. Thus, the branches $C_0^{a-}$ and $C_0^{a+}$ are normally hyperbolic attracting whereas $C_0^r$ is normally hyperbolic repelling.

$\square$

The slow flow that evolves on a continuous and piecewise–smooth manifold $M_{20}=M_{20}^-\cup M_{20}^+$ is given by,

$$\begin{aligned} \frac{dx}{d\tau }= {\left\{ \begin{array}{ll} -\frac{\left( 1+ak\right) \left( 1-\frac{x}{k}\right) \left( x-x_1\right) }{ax+b}, \text {for}~ x< 1,\\ \frac{x\left( 1-\frac{x}{k}\right) \left( x-x_2\right) \left( x-x_3\right) }{k\left( ax+b\right) \left( 1-\frac{2x}{k}\right) }, \text {for}~ x> 1. \end{array}\right. } \end{aligned}$$

(27)

The slow flow is not defined at the point Q, and Fig. 5 indicates the direction of the flow on the critical manifold $M_{20}$. Now for $0<\epsilon \ll 1$, Fenichel’s theorem tells us that $C_0^{a\pm }$ and $C_0^r$ can be perturbed to $C_{\epsilon }^{a\pm }$ and $C_{\epsilon }^r$ which are within ${\mathcal {O}}(\epsilon )$ distance from $C_0^{a\pm }$ and $C_0^r$, respectively.

Fig. 5

The dynamics of the fast subsystem (22)-(23) and of the slow subsystem (24)-(25). All the three possible interior equilibrium points $E_1, E_2$, and $E_3$ are shown by solid red circles. P and Q (solid blue circle) are the two non-hyperbolic points. The branches $C_0^{a-}$ (from P to the corner point on $\varSigma$) and $C_0^{r+}$ (from the corner point on $\varSigma$ to Q) of the critical manifold $M_{20}$ (red curve) are normally hyperbolic repelling, and $C_0^a$ (from Q to S) of the critical manifold $M_{20}$ is normally hyperbolic attracting. Manifold $M_{10}$ is along the positive y-axis. Double arrows on the horizontal lines indicate fast flow, and single arrows on the critical manifolds indicate slow flow

We now consider the asymptotic expansions of the perturbed manifolds $C_{\epsilon }^{a-}$ and $C_{\epsilon }^{r}$, given by

$$\begin{aligned} y_+(x)&=a_0(x)+\epsilon a_1(x)+ {\mathcal {O}}(\epsilon ^2), \end{aligned}$$

(28a)

$$\begin{aligned} y_-(x)&=b_0(x)+\epsilon b_1(x)+ {\mathcal {O}}(\epsilon ^2), \end{aligned}$$

(28b)

where $a_0(x)=x\left( 1-\frac{x}{k}\right)$ for $1\le x<\frac{k}{2}$ and $b_0(x)=1-\frac{x}{k}$ for $0<x\le 1$.

Now,

$$\begin{aligned} y'_+(x)=a'_0(x)+\epsilon a'_1(x)+ {\mathcal {O}}(\epsilon ^2) \end{aligned}$$

(29)

which leads to

$$\begin{aligned}&\left( a'_0(x)+\epsilon a'_1(x)+ {\mathcal {O}}(\epsilon ^2)\right) \nonumber \\&\quad \left( x\left( 1-\frac{x}{k}\right) -a_0(x)-\epsilon a_1(x)-{\mathcal {O}}(\epsilon ^2)\right) \nonumber \\&\quad =\epsilon \left( a_0(x)+\epsilon a_1(x)+\right. \nonumber \\ {}&\quad \left. {\mathcal {O}}(\epsilon ^2)\right) \left( 1-\frac{1}{ax+b}\left( a_0(x)+\epsilon a_1(x)+ {\mathcal {O}}(\epsilon ^2)\right) \right) . \end{aligned}$$

(30)

Comparing the powers of $\epsilon$ of (30), we get

$$\begin{aligned}&a_0(x)=x\left( 1-\frac{x}{k}\right) ,~~\nonumber \\&a_1(x)=-\frac{x\left( 1-\frac{x}{k}\right) \left( x-x_2\right) \left( x-x_3\right) }{\left( ax+b\right) \left( 1-\frac{2x}{k}\right) }. \end{aligned}$$

(31a)

Similarly,

$$\begin{aligned} b_0(x)=1-\frac{x}{k}, ~~ b_1(x)=-\frac{\left( 1+ka\right) \left( 1-\frac{x}{k}\right) \left( x-x_1\right) }{ax+b}. \end{aligned}$$

(32a)

Clearly, $a_0(1)=b_0(1)$ but $a_1(1)\ne b_1(1)$ and hence $y_+(1)\ne y_-(1)$.

Thus, we have that the perturbed manifolds $C_{\epsilon }^{a-}$ and $C_{\epsilon }^{r}$ do not create a continuous manifold across $\varSigma$ and the size of discontinuity is ${\mathcal {O}}(\epsilon )$.

Similarly, if we consider the asymptotic expansion of $C_{\epsilon }^{a+}$ and $C_{\epsilon }^{r}$, it can be shown that the expansion is not valid in a neighbourhood of the fold point Q. This has been shown in [21] using blow-up techniques introduced by [9, 11] that such perturbed manifolds $C_{\epsilon }^r$ and $C_{\epsilon }^{a\pm }$ can be continued beyond the non-hyperbolic fold point Q and for some parameter values may get connected forming a maximal canard. In the next section, we will carry out a detailed analysis of singular Hopf bifurcation occurring for the slow–fast system (5) in a neighbourhood of the fold point Q and the formation of canard cycles.

4 Relaxation oscillation

In this section, our aim is to show the existence of relaxation oscillation for the slow–fast system (5) assuming $0<\epsilon \ll 1$. A relaxation oscillation for the system (5) is by definition a closed orbit $\varGamma _\epsilon$ which converges to a piecewise–smooth singular periodic orbit $\varGamma _0$ consisting of slow and fast segments as $\epsilon \rightarrow 0$ in the Hausdorff distance. We assume that the system parameters $\{a,b,k\}$ belong to one of the parametric regions $D_2$ or $D_6$ or $D_7$, i.e. $\sigma \in D_2\cup D_6\cup D_7$. In such cases, we have the existence of only one admissible interior equilibrium $E_1$ or $E_c$ or $E_3$. We further assume that the admissible interior equilibrium $E_3$ should lie to the left of the maximum point $Q(\frac{k}{2}, \frac{k}{4})$ of the branch of the prey nullcline in $\varSigma ^+$, i.e. $0<x_3<\frac{k}{2}$ whenever it exists. Under the above parametric restrictions, we now intend to show the following results regarding the existence of relaxation oscillation for the system (5) for $\epsilon$ very small.

• 1. The existence of the admissible interior equilibrium $E_3$ or the boundary equilibrium $E_c$ implies the existence of a relaxation oscillation $\varGamma _{\epsilon }$ which is stable.

• 2. The existence of the admissible equilibrium $E_1$ implies the existence of exactly two relaxation oscillations $\varGamma _{\epsilon }$ and $\gamma _\epsilon$ of which $\varGamma _\epsilon$ is stable but $\gamma _\epsilon$ is unstable.

We will use the entry–exit function technique which plays a key role in showing the existence of periodic orbits which exhibit relaxation oscillations for slow–fast systems.

4.1 Entry–exit function

We know that the critical manifold $M_{10}$, i.e. the y-axis, is normally hyperbolic attracting for $y>1$ and normally hyperbolic repelling for $y<1$. We consider the system (8) and observe that for $\epsilon =0$, the y-axis consists of equilibria, attracting for $y>1$ and repelling for $y<1$. For $\epsilon >0$, very small a trajectory starting at $(x_0,y_0)$, $x_0>0$ very small, $y_0>1$ gets attracted towards the y-axis and then drifts downward and when cross the line $y=1$ gets repelled from the y-axis. Thus, for $\epsilon >0$ very small, the trajectory re-intersects the line $x=x_0$ at $(x_0, p_\epsilon (y_0))$ such that $\displaystyle \lim _{\epsilon \rightarrow 0}p_\epsilon (y_0)=p_0(y_0)$, where $p_0(y_0)$ is determined by

$$\begin{aligned} \int _{y_0}^{p_{0(y_0)}}\frac{1-y}{y(1-\frac{y}{b})}dy=0. \end{aligned}$$

(33)

The function $y_0\rightarrow p_0(y_0)$ defined above implicitly is known as the entry–exit function in the literature.

Lemma 6

There exists a unique $y'$, where $b<y'<1$ such that

$$\begin{aligned} J(y)=\int _{\frac{k}{4}}^y \frac{1-y}{y(1-\frac{y}{b})}dy=0 \,\,\mathrm{at}\,\,y=y'. \end{aligned}$$

(34)

Proof

We have,

$$\begin{aligned} J(y)&=\int _{\frac{k}{4}}^y \frac{1-y}{y(1-\frac{y}{b})}dy = (b-1)\int _{\frac{k}{4}}^y\frac{1}{y-b}dy\\&\quad +\int _{\frac{k}{4}}^y\frac{1}{y} dy \rightarrow +\infty \,\,\,\mathrm{as}\,\,y\rightarrow b^{+}. \end{aligned}$$

Further,

$$\begin{aligned} J'(y)=\frac{b(1-y)}{y(b-y)}<0\,\,\, \mathrm{for}\,\, b<y<1. \end{aligned}$$

Hence, J(y) decreases strictly for $b<y<1$. We also have,

$$\begin{aligned} J(1)=\int _{\frac{k}{4}}^1\frac{b(1-y)}{y(b-y)} dy=-\int _1^{\frac{k}{4}}\frac{b(1-y)}{y(b-y)} dy<0. \end{aligned}$$

Thus, it follows that there exists a unique $y'$ where $b<y'<1$ such that $J(y')=0$. $\square$

The critical manifolds $M_{10}$ and $M_{20}$ cease to have normal hyperbolicity at P(0, 1) and $Q(\frac{k}{2}, \frac{k}{4})$. The point P is termed as transcritical point as it corresponds to transcritical bifurcation for the subsystem (22), and the point Q is termed as fold point as it correspond to fold bifurcation for the subsystem (23). We also have

$$\begin{aligned} \left. \frac{\partial f_+}{\partial y}\right| _Q=-1< 0. \end{aligned}$$

and as we have assumed $1-\frac{2}{k}<a<1$, it follows that

$$\begin{aligned} \left. g\right| _Q=\frac{k}{4}\left( \frac{k(2a-1)+4b}{ka+2b}\right) >0. \end{aligned}$$

We also see that

$$\begin{aligned} \left. \frac{\partial ^2 f_+}{\partial x^2}\right| _{Q}=-\frac{2}{k}< 0 \end{aligned}$$

Hence, Q is a generic fold point for the system (9) and is also a jump point as at this point the fast flow (23) is moved away from the critical manifold $M_{20}$. The fast flow then intersects the switching manifold $\varSigma$ transversally following which the fast flow is governed by the fast subsystem (22) and gets attracted towards the attracting branch of the critical manifold $M_{10}$.

Similarly, for the transcritical point P, we have

$$\begin{aligned}&\left. \frac{\partial f_-}{\partial x}\right| _{P}= 0 =\left. \frac{\partial f_-}{\partial y}\right| _{P}, ~~\left. \frac{\partial ^2 f_-}{\partial x^2}\right| _{P}=-\frac{2}{k}<0, \\&\left. g\right| _P=1-\frac{1}{b}<0, \end{aligned}$$

and

$$\begin{aligned} \left[ \begin{array}{cc} \frac{\partial ^2 f_-}{\partial x^2} &{}\frac{\partial ^2 f_-}{\partial x\partial y} \\ \frac{\partial ^2 f_-}{\partial x \partial y} &{}\frac{\partial ^2 f_-}{\partial y^2}\end{array} \right] _{P} =-1<0, \end{aligned}$$

and consequently, P is a generic transcritical point for the system (8). The point P is also a jump point as at this point fast flow (22) is moved away from the critical manifold $M_{10}$. The fast flow then intersects the switching manifold $\varSigma$ transversally following which it is governed by the fast subsystem (23) and gets attracted towards the attracting branch of the critical manifold $M_{20}$.

We now consider a singular slow–fast cycle $\varGamma _0$ as follows: From $S(0, \frac{k}{4})$, follow the slow flow (24) down the y-axis to $T(0,y')$, follow the fast flow (22) to the right to intersect the switching manifold $\varSigma$ and then follow a layer of the flow (23) to intersect the attracting branch $C_0^{a_+}$ at $T'(x_a', y')$, follow the slow flow along $C_0^{a_+}$ to $Q(\frac{k}{2}, \frac{k}{4})$; follow the fast flow (23) to the left to intersect $\varSigma$ and then finally follow the fast flow (22) to the left to $S(0, \frac{k}{4})$. Thus, we have a singular orbit $\varGamma _0$ consisting of slow and fast segments for which T, Q are jump points and $T', S$ are drop points as at these points, the fast flow is moved towards the critical manifolds (see Fig. 6).

Theorem 1

Let $\sigma \in D_6\cup D_7$, $x_3<\frac{k}{2}$ and N be a tubular neighbourhood of $\varGamma _0$. Then, for each fixed $0 < \epsilon \ll 1$ there exists a unique limit cycle $\varGamma _\epsilon \subset N$ which is strictly attracting with characteristic multiplier bounded by $-K/\epsilon$ for some constant $K > 0$. Moreover, the cycle $\varGamma _\epsilon$ converges to $\varGamma _0$ in the Hausdorff distance as $\epsilon \rightarrow 0$.

Fig. 6

Existence of a stable relaxation oscillation $\varGamma _\epsilon$ (thick red curve) surrounding the unstable coexistence equilibrium point $E_3$. The singular slow–fast cycle $\varGamma _0$ is represented by thick blue curve such that $\varGamma _\epsilon \rightarrow \varGamma _0$ as $\epsilon \rightarrow 0$ in the Hausdorff distance. Coordinates of various points are explained within the text. Double arrows stand for the direction of fast flow, and single arrows represent the direction of slow flow

Proof

The conditions mentioned in the theorem ensure the existence of only one admissible equilibrium point, either $E_3(x_3, y_3)$ in $\varSigma ^+$ which lies to the left of the point Q or the boundary equilibrium $E_c$. For $\epsilon >0$ very small, following Fenichel’s theorem $C_0^{a+}$ and $C_0^+$ ($C_0^+$ is the attracting branch of the critical manifold $M_{10}$, i.e. $C_0^+=M_{10}\cap \left\{ (x,y)\in {\mathbb {R}}_+^2: y>1\right\}$ perturb to nearby slow manifolds $C_\epsilon ^{a+}$ and $C_\epsilon ^+$ and by theorem (2.1) of [21], the slow manifold $C_\epsilon ^{a+}$ can be continued beyond the generic point Q and by theorem (2.1) of [22], the slow manifold $C_\epsilon ^+$ can be continued beyond the generic transcritical singularity P. The slow manifold $C_\epsilon ^{a+}$ (resp. $C_\epsilon ^+$) lies close to $C_0^{a+}$ (resp. $C_0^+$) until it arrives at the vicinity of the generic fold point Q (resp. generic transcritical point P) and then follow roughly a layer of the flow (23) (resp. a layer of the flow (22) intersecting $\varSigma$ above $E_c$ (resp. below $E_c$) and then follow a layer of the flow (22) (resp. a layer of the flow (23)) until it reaches the attracting slow manifold $C_\epsilon ^+$ (resp. $C_\epsilon ^{a+}$).

We consider a small vertical section $\varDelta =\{(x_0, y)|y\in [\frac{k}{4}-\epsilon _0, \frac{k}{4}+\epsilon _0]\}$ where $0<x_0<1$, $0<\epsilon _0\ll 1$. We know that for every point $(0,y_0)$, $y_0\in [\frac{k}{4}-\epsilon _0, \frac{k}{4}+\epsilon _0]$ we can define $p_0(y_0)$ such that $b<p_0(y_0)<1$ by the result derived in lemma 6.

We now follow tracking two trajectories $\varGamma _\epsilon ^{1,2}$ starting on $\varDelta$ at the points $(x_0, y^{1,2})$. For $0 < \epsilon \ll 1$, it follows by Fenichel’s theorem that $\varGamma _\epsilon ^{1,2}$ get attracted towards the slow manifold $C_\epsilon ^+$ exponentially with a rate ${\mathcal {O}}(e^{-1/\epsilon })$ and move downward slowly. Then by theorem (2.1) of [22] $\varGamma _\epsilon ^{1,2}$ pass by the generic transcritical singularity P contracting exponentially towards each other and then leave the repelling branch $C_0^-$ $\left( C_0^-=M_{10}\cap \left\{ (x,y)\in {\mathbb {R}}_+^2: y<1\right\} \right)$ of the critical manifold $M_{10}$ at the points $(0, p_0(y^{1,2}))$ and then jump horizontally to $(x_0, p_\epsilon (y^{1,2}))$ where $\displaystyle \lim _{\epsilon \rightarrow 0}p_\epsilon (y^{1,2})= p_0(y^{1,2})$. The trajectories then intersect $\varSigma$ following a layer of the flow (22) and then follow a layer of the flow (23)) until they arrive at a neighbourhood of $C_\epsilon ^{a+}$. Now by Fenichel’s theorem, $\varGamma _\epsilon ^{1,2}$ are attracted towards the slow manifold $C_\epsilon ^{a+}$ and pass the generic fold point Q contracting exponentially until they arrive at a neighbourhood of $C_\epsilon ^+$ and thus finally return to $\varDelta$.

Tracking the forward trajectories, we thus have a return map $\varPi : \varDelta \rightarrow \varDelta$ inducted by the flow of (5) for $0 < \epsilon \ll 1$. The returned map $\varPi$ is a contraction map as the trajectories contract towards each other with the rate ${\mathcal {O}}(e^{-1/\epsilon })$ and by the contraction mapping theorem $\varPi$ has a unique fixed point which is stable. This fixed point is the desired limit cycle $\varGamma _\epsilon$ which exists in a tubular neighbourhood of the singular slow–fast cycle $\varGamma _0$, and as the contraction is exponential, the characteristic multiplier of $\varGamma _\epsilon$ is bounded above by $-K/\epsilon$ for some $K>0$. Again applying Fenichel’s theorem, theorem (2.1) of [22] and theorem (2.1) of [21], we conclude that the periodic orbit $\varGamma _\epsilon$ converges to the singular orbit $\varGamma _0$ as $\epsilon \rightarrow 0$ in the Hausdorff distance. $\square$

For a geometrical description of the proof of theorem 1, see Fig. 6.

Theorem 2

Let $\sigma \in D_2$. Then for each fixed $0 < \epsilon \ll 1$ there exists exactly two limit cycle $\varGamma _\epsilon$ and $\gamma _\epsilon$ of which $\varGamma _\epsilon$ is stable but $\gamma _\epsilon$ is unstable. Moreover, the cycle $\varGamma _\epsilon$ (resp. $\gamma _\epsilon$) converges to $\varGamma _0$ (resp. $\gamma _0$) in the Hausdorff distance as $\epsilon \rightarrow 0$.

Proof

The conditions mentioned in the theorem ensure the existence of only one admissible interior equilibrium $E_1$ in $\varSigma ^-$ and following the stability analysis as presented in Sect. 2 the equilibrium is stable. For $0<\epsilon \ll 1$, proceeding in the same fashion as in theorem  1 we can show the existence of stable relaxation oscillation $\varGamma _\epsilon$ in a neighbourhood of $\varGamma _0$ such that $\varGamma _\epsilon$ converges to $\varGamma _0$ as $\epsilon \rightarrow 0$ in Hausdorff distance. Thus, we have the existence of a stable equilibrium point surrounded by a stable cycle $\varGamma _\epsilon$ and correspondingly, the region bounded by the basins of attraction of the stable cycle $\varGamma _\epsilon$ and the stable equilibrium is negatively invariant. Hence, by the Poincaré–Bendixson theorem there exists at least one limit cycle in the region. We intend to show here that there exists exactly one unstable cycle in the region which is the desired relaxation oscillation $\gamma _\epsilon$ for $0<\epsilon \ll 1$.

We consider the dynamics of the slow–fast time-reversal system obtained from (5) replacing ‘t’  by ‘$-t$’. We observe that for the system the stable branches of the critical manifolds $M_{10}$ and $M_{20}$ become unstable and vice versa. Let $y''$ be such that $1<y''<\frac{k}{4}$ and

$$\begin{aligned} J(y'')=\int _{1-\frac{1}{k}}^{y''} \frac{1-y}{y(1-\frac{y}{b})}dy=0. \end{aligned}$$

The existence of $y''$ is unique and is guaranteed following lemma 6. We now consider the singular orbit $\gamma _0$ for the time-reversal system as follows:

From $S_1(0, 1-\frac{1}{k})$, follow the slow flow (24) above the y-axis to $S_2(0,y'')$, follow the fast flow (22) to the right intersecting the switching manifold $\varSigma$ and then follow a layer of the flow (23) to $S_3( x_a'', y'')$ ; follow the slow flow along the branch $C_0^r$ to $S_4(1, 1-\frac{1}{k})$ and the finally follow a layer of the flow (22) to $S_1$. We observe that the directions of the singular orbit $\gamma _0$ will be reverse if we consider it for the system (5) (see Fig. 7).

Now, by applying theorem 1 it follows that there exists a unique stable cycle $\gamma _\epsilon$ in a tubular neighbourhood of $\gamma _0$ for the time-reversal system such that $\gamma _\epsilon \rightarrow \gamma _0$ as $\epsilon \rightarrow 0$ in the Hausdorff distance. Thus, replacing $`t'$ by $-`t'$ again in the time-reversal system we conclude that for $0<\epsilon \ll 1$, $\gamma _\epsilon$ is the desired unstable relaxation oscillation for the system (5) such that $\gamma _\epsilon \rightarrow \gamma _0$ as $\epsilon \rightarrow 0$ in the Hausdorff distance. $\square$

For a geometrical description of the proof of theorem 2, see Fig 7. The non-smooth functional response is responsible for the existence of two relaxation oscillations simultaneously: one of them is stable, and the other one is unstable.

Fig. 7

The unique coexistence stable equilibrium point $E_1$ is surrounded by an unstable relaxation oscillation $\gamma _\epsilon$ (thick black curve), nested within a stable relaxation oscillation $\varGamma _\epsilon$ (thick red curve) for small $\epsilon >0$. The singular slow–fast cycles $\gamma _0$ (inner) and $\varGamma _0$ (outer) are represented by cyan and blue curves, respectively, such that $\varGamma _\epsilon \rightarrow \varGamma _0$ and $\gamma _\epsilon \rightarrow \gamma _0$ as $\epsilon \rightarrow 0$ in the Hausdorff distance. Double arrows stand for the direction of fast flow, and single arrows represent the direction of slow flow

Fig. 8

Relaxation oscillations for the system (5) with $0<\epsilon \ll 1$. (a) Two nested relaxation oscillations surrounding a stable equilibrium point $E_1$ lying in $\varSigma ^-$ for the parameter values $a=0.99$. The unstable relaxation oscillation (black curve) is nested within a stable relaxation oscillation (green curve). (b) Unique relaxation oscillation (green curve) surrounding the corner point $E_c$ lying on $\varSigma$ for the parameter value $a=0.75$ (c) Unique relaxation oscillation (green curve) surrounding the unique interior equilibrium point $E_*$ lying in $\varSigma ^+$ for the parameter values $a=0.6$. The other parameter values are $b=0.05, k=5$ and $\epsilon =0.001$

We have shown earlier the existence of relaxation oscillations for $0 < \epsilon \ll 1$ whenever we have the existence of only one admissible equilibrium point $E_1$ or $E_c$ or $E_3$, i.e. $\sigma \in D_2\cup D_6\cup D_7$ such that $x_3<\frac{k}{2}$. In the next, we will show that there will be no relaxation oscillation whenever $\sigma \in D_1\cup D_3\cup D_4\cup D_5\cup D_8\cup D_9$ for $0 < \epsilon \ll 1$. In such cases, there will be no interior equilibrium or the existence of more than one admissible interior equilibrium or the existence of only the degenerate equilibrium $E_*$.

Proposition

Let $\sigma \in D_1\cup D_3\cup D_4\cup D_5\cup D_8\cup D_9$. Then, there do not exist any relaxation oscillation for the slow–fast system (5) for $0 < \epsilon \ll 1$.

Proof

By the Hopf’s theorem, a periodic orbit for a planar flow must enclose at least one equilibrium point. Now, if $\sigma \in D_1$, then there does not exist any interior equilibrium point and correspondingly, the slow–fast system (5) has no periodic orbit in the interior of ${\mathbb {R}}^2_+$ and hence no relaxation oscillation.

Let $\sigma \in D_3$. Then, there exist two admissible interior equilibrium points $E_2$ and $E_3$ lying on the right branch $\varSigma ^+$ of the prey nullcline. The equilibrium $E_2$ is always a saddle point, whereas $E_3$ can be either a stable or an unstable equilibrium point. The Poincaré indices of $E_2$ and $E_3$ are -1 and +1, respectively. Therefore, by the Hopf’s theorem there cannot be a periodic orbit enclosing only the equilibrium $E_2$ and also enclosing both the equilibrium points $E_2$ and $E_3$. So, we now have the possibility of having a periodic orbit enclosing $E_3$. The emergence of a periodic orbit due to Hopf bifurcation around $E_3$ has been shown in the next section. However, in this case, such a periodic orbit will not be a relaxation oscillation. To be a relaxation oscillation, the periodic orbit should converge to a singular piecewise–smooth closed orbit of type $\varGamma _0$ constructed to prove the theorem 1 as $\epsilon \rightarrow 0$ in the Hausdorff distance. Now, if we construct such a singular piecewise–smooth closed orbit enclosing $E_3$ and consisting of attracting slow–fast segments, then it also encloses the singularity $E_2$ and hence the relaxation oscillation if exists should also enclose both the equilibrium points $E_2$ and $E_3$ which contradicts the Hopf’s theorem.

Let $\sigma \in D_4$. Then, there exist three admissible interior equilibrium points $E_1$, $E_2$, and $E_3$ . The equilibrium point $E_1$ is always a stable equilibrium point, $E_2$ is a saddle point, and $E_3$ can be either a stable or unstable equilibrium point. We have already shown with the help of Dulac’s criteria that the system (5) has no periodic orbit enclosing $E_1$ and lying entirely in $\varSigma ^-$. By the Hopf bifurcation theorem, there cannot exist a periodic orbit enclosing $E_2$; enclosing $E_1$ and $E_2$; enclosing $E_1$ and $E_3$; and also enclosing $E_2$ and $E_3$. By the same argument as above, we cannot have a relaxation oscillation enclosing $E_3$ only. Therefore, we have the possibility of having a periodic orbit enclosing either $E_1$ or a periodic orbit enclosing all the equilibrium points $E_1, E_2$, and $E_3$.

Assume that there exists a periodic orbit enclosing $E_1$. Then, the periodic orbit will be an unstable periodic orbit and as the region R is invariant, by the Poincaré–Bendixson theorem there will also be a stable periodic orbit enclosing the unstable periodic orbit and $E_1$. We have shown earlier the existence of stable and unstable relaxation oscillations assuming the existence of only the admissible equilibrium $E_1$ but, in this case, we have the existence of the equilibrium points $E_2$ and $E_3$ as well. Now, as $E_2$ is a saddle point, a part of the stable or unstable separatrix of $E_2$ will be along the repelling branch $C_0^r$ of the slow manifold $M_{20}$ for $0 < \epsilon \ll 1$. Consequently, the stable or unstable separatrix of the saddle point $E_2$ will intersect the periodic orbit and this violates the fundamental existence and uniqueness result for the slow–fast system (5). Thus, there does not exist a periodic orbit and hence a relaxation oscillation enclosing $E_1$. Similarly, if we assume that there exists a periodic orbit enclosing the equilibria $E_1, E_2$, and $E_3$, then following the same argument as above in this case also there will be a violation of the fundamental existence and uniqueness result for the system (5) and consequently there will be no relaxation oscillation enclosing the equilibria $E_1, E_2$ and $E_3$.

Let $\sigma \in D_5$. Then, in this case we have the existence of the two equilibrium $E_c$ and $E_3$ of which $E_c$ is the boundary equilibrium and $E_3$ is the stable equilibrium lying to the right of the point Q on the branch $\varSigma ^+$ of the prey nullcline. Following the results of the boundary equilibrium bifurcations as carried out in Sect. 6 it follows that the boundary equilibrium $E_c$ is an unstable equilibrium point and consequently there does not exist a periodic orbit enclosing both the equilibria $E_c$ and $E_3$. Thus, there may exist a periodic orbit enclosing either $E_c$ or enclosing $E_3$. Assume that there exists a stable periodic orbit enclosing $E_c$. Now, depending on the nature of the slow–fast flow, the only possibility that this stable periodic orbit will be a stable relaxation oscillation provided it converges to a singular slow–fast cycle of type $\varGamma _0$ as $\epsilon \rightarrow 0$ in the Hausdorff distance. Now, as $E_3$ is a stable singularity, any trajectory approaching the attracting branch $C_0^a$ of the slow manifold $M_{20}$ must tend to $E_3$ as $t\rightarrow \infty$. Consequently, there will be no stable relaxation oscillation.

Assume that there exists an unstable periodic orbit enclosing $E_3$. Then in this case also by the Poincaré–Bendixson theorem, there will be at least two periodic orbits, stable and unstable periodic orbits. But, as mentioned above that to be a stable relaxation oscillation this stable periodic should converge to $\varGamma _0$ as $\epsilon \rightarrow 0$. Thus, for $0 < \epsilon \ll 1$, the stable relaxation oscillation will enclose both the singularity $E_c$ and $E_3$. But, we have already claimed that there cannot be a periodic orbit enclosing both $E_c$ and $E_3$. Hence, there also does not exist any relaxation oscillation enclosing $E_3$.

Let $\sigma \in D_8$. Then, there exists only one admissible interior equilibrium point $E_*$ which is by nature a degenerate equilibrium, in fact, a saddle-node equilibrium having Poincaré index 0. Consequently, there does not exist a periodic orbit enclosing $E_*$ and hence, no relaxation oscillation.

Let $\sigma \in D_9$. Then, there exist two admissible interior equilibrium points $E_1$ and $E_*$ of which $E_1$ is stable equilibrium point and $E_*$ is a degenerate equilibrium point. Now, if we assume that there exists a periodic orbit enclosing $E_1$, then for $0 < \epsilon \ll 1$ the separatrix along the repelling branch $C_0^r$ of the slow manifold $M_{20}$ of the degenerate equilibrium $E_3$ will intersect the periodic orbit and consequently, the fundamental existence and uniqueness result for the slow–fast system (5) will be violated. Hence, there will be no relaxation oscillation enclosing $E_1$. We have already claimed that there cannot be a periodic orbit enclosing the saddle-node equilibrium $E_*$.

Assume that there exists a periodic orbit enclosing both the equilibrium points $E_1$ and $E_*$. Then, the separatrices corresponding to the degenerate equilibrium $E_*$ will intersect the periodic orbit violating again the fundamental existence and uniqueness result for the slow–fast system (5). Therefore, there does not exist a relaxation oscillation enclosing both the equilibrium points $E_1$ and $E_*$. $\square$

5 Singular Hopf bifurcation and canard orbits

We assume the parametric restrictions $a<1, b<1$ and $\frac{k(1-b)}{1+ka}>1$ so that we have the existence of only one admissible equilibrium point $E_3$ lying in $\varSigma ^+$. For $k(1-2a)=4b$, i.e. for $b=b^*=\frac{k(1-2a)}{4}$, the singularity $E_3$ passes through the fold point Q. We also see the following conditions hold:

$$\begin{aligned}&\left. f_+ \right| _{Q=E_3} =0,~ \left. g\,\right| _{Q=E_3}=0, ~ \left. \frac{\partial f_+}{\partial x}\right| _{Q=E_3} \\&\quad =0, ~ \frac{\partial f_+}{\partial y}=-1<0,~ \frac{\partial ^2 f_+}{\partial x^2}=-\frac{2}{k}<0. \end{aligned}$$

Under the above conditions, the singularity Q is a generic folded singularity. We now restrict our analysis in a neighbourhood of the folded singularity Q. To use the theory as developed in [23], we use the following transformation $X=x-x_3$, $Y=y-y_3$, $\mu =b-b^*$ to write the system (9) into the following standard slow–fast normal form near the folded singularity Q.

$$\begin{aligned} \frac{dX}{dt}&=-Yh_1(X,Y,\mu )+X^2h_2(X,Y,\mu , \epsilon )\nonumber \\&\qquad + \epsilon h_3(X,Y,\mu , \epsilon ) \end{aligned}$$

(35a)

$$\begin{aligned} \frac{dY}{dt}&=\epsilon \left( Xh_4(X,Y,\mu )-\mu h_5(X,Y,\mu )\right. \nonumber \\&\qquad \left. + Y h_6(X,Y,\mu )\right) \end{aligned}$$

(35b)

where $h_1=1, h_2=-\frac{1}{k}, h_3=0, h_4=a-4\frac{a^2}{k}X+{\mathcal {O}}(X, Y, \mu )$, $h_5=-1+ {\mathcal {O}}(X, Y, \mu )$, $h_6=-1+\frac{8a}{k}X-\frac{4}{k}Y+ {\mathcal {O}}(X, Y, \mu )$. Now, by the formulae of (3.12) and (3.13) of [23] we have

$$\begin{aligned} a_1&=\frac{\partial h_3}{\partial X}(0,0,0)=0, \end{aligned}$$

(36a)

$$\begin{aligned} a_2&=\frac{\partial h_1}{\partial X}(0,0,0)=0,\end{aligned}$$

(36b)

$$\begin{aligned} a_3&=\frac{\partial h_2}{\partial X}(0,0,0)=0,\end{aligned}$$

(36c)

$$\begin{aligned} a_4&=\frac{\partial h_4}{\partial X}(0,0,0)=-\frac{4a^2}{k},\end{aligned}$$

(36d)

$$\begin{aligned} a_5&=h_6(0,0,0)=-1,\end{aligned}$$

(36e)

$$\begin{aligned} A&=-a_2+3a_3-2a_4-2a_5=\frac{8a^2}{k}+2>0. \end{aligned}$$

(36f)

Thus, following the formulae (3.15) and (3.16) of [23] we have the singular Hopf bifurcation curve $\mu =\mu _H\left( \sqrt{\epsilon }\right) =\frac{\epsilon }{2}+{\mathcal {O}}(\epsilon ^{3/2})$ and maximal canard curve $\mu =\mu _c\left( \sqrt{\epsilon }\right) =\frac{1}{4k}\left( k-4a^2\right) \epsilon + {\mathcal {O}}(\epsilon ^{3/2})$ for the system (35). The singular Hopf bifurcation curve $\mu _H\left( \sqrt{\epsilon }\right)$ and the maximal canard curve $\mu _c\left( \sqrt{\epsilon }\right)$ can also be written as

$$\begin{aligned}&b_H\left( \sqrt{\epsilon }\right) =b^*+\frac{\epsilon }{2}+{\mathcal {O}}(\epsilon ^{3/2}), \end{aligned}$$

(37a)

$$\begin{aligned}&b_C\left( \sqrt{\epsilon }\right) =b^*+\frac{1}{4k}\left( k-4a^2\right) \epsilon +{\mathcal {O}}(\epsilon ^{3/2}) \end{aligned}$$

(37b)

Now, following the formulae in [23], the first Lyapunov coefficient is given by

$$\begin{aligned} \bar{l_1}=\frac{A}{8}\sqrt{\epsilon }+{\mathcal {O}}(\epsilon ) \end{aligned}$$

(38)

We always have $A>0$, and consequently, the Hopf bifurcation is subcritical. Thus, the canard cycles that emerge through this Hopf bifurcation are unstable. The canard orbit exists for $b<b_H\left( \sqrt{\epsilon }\right)$ in an ${\mathcal {O}}(\epsilon )$ range.

Thus, we have shown that for $b=b_H\left( \sqrt{\epsilon }\right)$, a subcritical Hopf bifurcation takes place resulting in the existence of unstable canard orbits for $b=b_c\left( \sqrt{\epsilon }\right) <b_H\left( \sqrt{\epsilon }\right)$ in an ${\mathcal {O}}(\epsilon )$ range. The equilibrium point $E_3$ is a stable focus surrounded by unstable canard orbits for $b=b_C\left( \sqrt{\epsilon }\right) <b_H\left( \sqrt{\epsilon }\right)$ in an ${\mathcal {O}}(\epsilon )$ range, and for $b\ge b_H\left( \sqrt{\epsilon }\right)$, the equilibrium point $E_3$ is an unstable focus. Hence, we see that unstable canard orbits exist prior to the bifurcation which get destroyed after the bifurcation.

We have shown earlier in Sect. 2 that the following rectangular region $R=\left\{ 0\le x\le k, y=0; x=k, \right.$$\left. 0\le y\le ak+b; y=ak+b, 0\le x \le k; x=0, \right.$

$\left. 0\le y\le ak+b\right\}$ is forward invariant, and one can made the region R as large as possible to investigate all possible dynamics of the system (5). Let $\gamma$ be the periodic orbit (unstable canard orbit) which emerges prior to the bifurcation for $b=b_c\left( \sqrt{\epsilon }\right) <b_H\left( \sqrt{\epsilon }\right)$ in ${\mathcal {O}}(\epsilon )$ range. Let V be the region enclosed by $\gamma$. Trajectories starting in V will remain in V and approach the equilibrium in forward time. Trajectories outside V will remain outside V. Thus, $R\backslash V$ is positively invariant. Now, under the given parametric restrictions, the trivial equilibrium $E_0$ is an unstable node and the axial equilibria $E_b$ and $E_k$ are saddle points having the y- and x-axes as the stable separatrices. Consequently, a trajectory $\varGamma '$ will approach to the axial equilibria $E_b$ and $E_k$ in forward time provided the trajectory $\varGamma '$ gets started from y- or x-axis. Now, by the Poincaré–Bendixson theorem, if we start a trajectory $\varGamma '$ from an interior point in $R\backslash V$, then the $\omega$-limit set of $\varGamma '$, i.e. $\omega (\varGamma ')$, will be either an equilibrium point or a periodic orbit or a graphic. But, the equilibria $E_0$, $E_b$, and $E_k$ cannot be its $\omega$-limit and similarly, no graphic joining the equilibria can be its $\omega$ limit set. Thus, by the Poincaré–Bendixson theorem, the only possibility of being the $\omega$ limit set of the trajectory $\varGamma '$ is a periodic orbit $\varGamma$ (see Fig. 9). Hence, there exists an attracting periodic orbit in $R\backslash V$ which will be the $\omega$-limit set of the trajectory $\varGamma '$ and as this periodic orbit is bounded away from the repelling branch of the critical manifold $M_{20}$, it is a relaxation oscillation for $0<\epsilon \ll 1$.

Fig. 9

There exist two periodic orbits $\gamma$ and $\varGamma$. The unstable canard orbit $\gamma$ emerges prior to the Hopf bifurcation, and V is the region enclosed by $\gamma$. The stable periodic orbit $\varGamma$ exists due to global property of the system. The parameter values are $a=0.527, b=0.05, k=5, \epsilon =0.1$

Similarly, for $b\ge b_H$ in ${\mathcal {O}}(\epsilon )$ range, the equilibrium $E_3$ is an unstable focus and following the same argument as above, we have an attracting periodic orbit in R and also following the same argument as in theorem 2, the attracting periodic orbit is a relaxation oscillation for $0<\epsilon \ll 1$. Thus, we have seen that for $b<b_H$ in ${\mathcal {O}}(\epsilon )$ range, we have the existence of a stable equilibrium point, unstable canard orbit, and stable relaxation oscillation and for $b\ge b_H$ in ${\mathcal {O}}(\epsilon )$ range, we have an unstable equilibrium point surrounded by an attractive periodic orbit which is a stable relaxation oscillation.

By numerical simulation, we exhibit the relaxation oscillations and canard cycle for the system (5) in Fig. 10 when $0<\epsilon \ll 1$.

Fig. 10

Relaxation oscillations and canard cycle for the system (5) for $0<\epsilon \ll 1$. Unique stable relaxation oscillation (green curve) surrounding the folded singularity $E_*$ for the parameter values $a=0.48, b=0.05115063$. The inner black curve is the unstable canard cycle which emerges due to singular Hopf bifurcation around $E_*$. The other parameter values are $k=5, \epsilon =0.001$

6 Boundary equilibrium bifurcations

A boundary equilibrium bifurcation (BEB) is said to occur for a piecewise–smooth system when an admissible equilibrium collides with a switching boundary upon varying a parameter and following a BEB there shall be the creation of some invariant sets (equilibria and limit cycles for two dimensional systems). In this section, we will show the phenomena of BEBs for the system (5). We assume $1-\frac{2}{k}<a<1$ and $b<1$ so that there exist only one admissible interior equilibrium point $E({\bar{x}}, {\bar{y}})$ such that $E=E_1$ when $c<1$; $E=E_c$ when $c=1$ and $E=E_3$ in when $c>1$, where $c=\frac{k(1-b)}{1+ka}$. The equilibria $E_1$, $E_c$ and $E_3$ lie in $\varSigma ^-$, $\varSigma$ and $\varSigma ^+$, respectively. Thus, the boundary equilibrium $E_c(1, 1-\frac{1}{k})$ for $c=1$ is an admissible equilibrium for both the left and right-half systems. Generically, there can be two scenarios regarding co-dimension—one BEB: both the equilibria coexist in one of the half systems, collide at the boundary equilibrium, and annihilate known as a non-smooth fold or one equilibrium is admissible on each side of the bifurcation known as persistence. Consequently, for the system (5) we have the phenomenon of persistence as for $c<1(c>1)$ we have the existence of admissible equilibrium $E_1 (E_3)$ for the left-half (right-half) system. In the following, we will be discussing the following two cases: (i) persistence with different stability and emergence of limit cycles which is the non-smooth analogue of Andronov–Hopf bifurcation, (ii) persistence with different stability and emergence of a limit cycle known as supercritical super-explosion bifurcation.

For $c\ne 1$, the Jacobian matrices for the right and left half systems at the equilibrium $E({\bar{x}}, {\bar{y}})$ are given by

$$\begin{aligned} J=J_{\pm }=\left[ \begin{array}{cc} \frac{\partial f_{\pm }({\bar{x}},{\bar{y}})}{\partial x}&{} \frac{\partial f_{\pm }({\bar{y}},{\bar{y}})}{\partial y}\\ \epsilon \frac{\partial g({\bar{x}},{\bar{y}})}{\partial x}&{}\epsilon \frac{\partial g({\bar{x}},{\bar{y}})}{\partial y}\end{array}\right] . \end{aligned}$$

(39)

On simplification,

$$\begin{aligned} J_+=\left[ \begin{array}{cc} 1-\frac{2{\bar{x}}}{k}&{}-1\\ a\epsilon &{}-\epsilon \end{array}\right] ~~ \text {and}~~ J_-=\left[ \begin{array}{cc} -\frac{{\bar{x}}}{k}&{}-{\bar{x}}\\ a\epsilon &{}-\epsilon \end{array}\right] . \end{aligned}$$

(40)

Now, as $c\rightarrow 1^{\pm }$, the eigenvalues of $J_\pm$ tend to

$$\begin{aligned} \gamma _+ \pm \sqrt{\delta _+} ~~ \text {and}~~ \gamma _- \pm \sqrt{\delta _-} \end{aligned}$$

(41)

where, $\displaystyle \gamma _+=\frac{1-\frac{2}{k}-\epsilon }{2}$, $\delta _+=\frac{1}{2}\left\{ \left( 1-\frac{2}{k}+\epsilon \right) ^2\right.$$\left. -4a\epsilon \right\}$; and $\gamma _-=-\frac{1}{2}\left( \epsilon +\frac{1}{k}\right)$, $\delta _-=\frac{1}{2}\left\{ \left( \epsilon -\frac{1}{k}\right) ^2\right.$$\left. -4a\epsilon \right\}$.

We always have $\gamma _+>\gamma _-$, $\delta _+>\delta _-$, $\det {J_-}>0$ and because of the parametric condition $a>1-\frac{2}{k}$ we also have $\det {J_+}>0$. This shows that the boundary equilibrium $E_c$ is an isolated hyperbolic equilibrium for both the left-half and right-half systems. The equilibrium $E_1$ whenever admissible is always a stable equilibrium point; we also have shown in Sect. 5 the smooth Hopf bifurcation results in the vicinity of the admissible equilibrium $E_3$ around $b=b_H(\sqrt{\epsilon })$ and consequently, in the following we assume that $\gamma _+>0$ so that $E_3$ is an unstable equilibrium point. We then have the following theorem regarding the non-smooth analogue of Hopf bifurcation.

Theorem 3

For the system (5), with the following parametric restrictions $1-\frac{2}{k}<a<1, b<1$, $0<\epsilon \ll 1$, $\gamma _+>0$, there emerges a periodic orbit in the vicinity of the boundary equilibrium $E_c$ through a bifurcation as c passes through $c=1$ ($b=b_*=1-a-\frac{1}{k}$). The bifurcation is described by the following

• (i) If $\delta _+<0$ and $\delta _- < 0$, then there is a non-smooth Hopf bifurcation. The bifurcation is supercritical if $\varLambda >0$ and subcritical if $\varLambda <0$ where $\varLambda =\frac{\gamma _+}{\sqrt{-\delta _+}}+\frac{\gamma _-}{\sqrt{-\delta _-}}$.

• (ii) if $\delta _+\ge 0$ and $\delta <0$, then the bifurcation is a supercritical Hopf like bifurcation; the stability of the limit cycle is same as that of the equilibrium node.

Proof

• (i) If $\delta _+<0$ and $\delta _-<0$, then there exists a unique admissible equilibrium in a neighbourhood of $(1, 1-\frac{1}{k}, b_*)$: a stable focus for the left-half system and an unstable focus for the right-half system. Thus, as c increases through 1 (b decreases through $b_*$), small enough, we have the transition from stable focus to unstable focus. Hence, following [40] there is a non-smooth Hopf bifurcation and the criticality is measured by $\varLambda$. (See Fig. 11.)

• (ii) If $\delta _+\ge 0$ and $\delta <0$ then as c increases through 1 (b decreases through $b_*$), small enough, the unique admissible equilibrium in a neighbourhood of $(1, 1-\frac{1}{k}, b_*)$ has a transition from stable focus for the left-half system to unstable node for the right-half system. Following [40], there emerges a limit cycle for $c<1$ ($b>b_*$), i.e. the Hopf like bifurcation is a supercritical bifurcation (see Fig. 12). Let $\gamma$ be the unstable periodic orbit which emerges due to the bifurcation as c decreases through 1 (b increases through $b_*$), small enough and let V be the region enclosed by $\gamma$. Trajectories starting in V will remain in V and approach to the equilibrium stable focus for the left-half system in forward time. Trajectories outside V will remain outside V and consequently, $R\backslash V$ is positively invariant and by the same argument as in Sect. 5, there exists an attractive periodic orbit $\varGamma$ in the interior of $R\backslash V$. Thus, we see that as c decreases through 1, (b increases through $b_*$), small enough, there exists an attracting equilibrium, a repelling periodic orbit $\gamma$, and an attracting periodic orbit $\varGamma$; the two such periodic orbits give rise to unstable and stable relaxation oscillations for $0<\epsilon \ll 1$ whose existence we already have shown in Sect. (4). Now, if we increase b further, then the unstable limit cycle $\gamma$ collides with the coexisting stable limit cycle $\varGamma$ and then annihilates following a saddle-node bifurcation of limit cycles.

We also see that $\delta _+>0$ whenever $\delta _-\ge 0$ and correspondingly, the unique admissible equilibrium in a neighbourhood of $(1, 1-\frac{1}{k}, b_*)$ cannot have a transition from a stable node for the left-half system to an unstable focus for the right-half system (See Fig.13). $\square$

Fig. 11

Phase portraits for boundary equilibrium bifurcations (BEBs): the unique admissible equilibrium point has a transition from stable focus to unstable focus as b decreases through $b_*$. The piecewise–smooth slow–fast systems (5) experience a supercritical ($\varLambda =1.18>0$) non-smooth Hopf bifurcation for $b=b^*=0.1$. (a) For $b=0.08<b^*$, the equilibrium unstable focus at the right branch of the prey nullcline is enclosed with a coexisting stable limit cycle. (b) As b increases through $b=b_*=0.1$, the admissible equilibrium has a transition from an unstable focus to stable focus and for $b=0.106>b^*$ there emerges an unstable limit cycle. The inner black limit cycle is unstable, and the outer green one is the coexisting stable limit cycle. (c) As the value of b is increased further, the inner limit cycle collides with the outer stable limit cycle for $b=0.107719$ and then disappears following a saddle–node bifurcation of limit cycle (SNLC) for $b=0.11>0.107719$. The other parameter values are $a=0.7$, $k=5$, $\epsilon =0.3$

Fig. 12

Phase portraits for boundary equilibrium bifurcations (BEBs): the unique admissible equilibrium point has a transition from stable focus to unstable node as b decreases through $b_*$. The piecewise–smooth slow–fast systems (5) experience a supercritical non-smooth Hopf bifurcation for $b=b^*=0.1$. (a) For $b=0.08<b^*$, the equilibrium unstable node at the right branch of the prey nullcline is enclosed with a coexisting stable limit cycle. (b) As b increases through $b=b_*=0.1$, the admissible equilibrium has a transition from an unstable node to stable focus and for $b=0.144>b^*$, there emerges an unstable limit cycle. The inner black limit cycle is unstable, and the outer green one is stable limit cycle. (c) As b is increased further, the inner limit cycle collides with the unstable limit cycle for a critical value of $b = 0.146549$ and then disappears following a saddle–node bifurcation of limit cycle (SNLC) which occurs for $b=0.15>0.146549$. The other parameter values are $a=0.7$, $k=5$, $\epsilon =0.2$

Thus, we have discussed the Hopf-like bifurcation scenarios for the piecewise–smooth continuous system (5) except considering the case in which we have the transition of the equilibrium point from stable node to unstable node. We assume that $\delta _{\pm }\ge 0$, i.e. $4a\epsilon \le \min \left\{ \left( 1-\frac{2}{k}+\epsilon \right) ^2, \left( \epsilon -\frac{1}{k}\right) ^2\right\}$ including the other parametric conditions as mentioned in theorem 3. It then follows that there exists a unique equilibrium in a neighbourhood of $(1, 1-\frac{1}{k}, b_*)$: a stable node for the left-half system and an unstable node for the right-half system. Thus, as c increases through 1 (b decreases through $b_*$), small enough the equilibrium point has a transition from stable node to unstable node. This case does not resemble a non-smooth analogue of Hopf bifurcation because of the absence of a focus equilibrium, but there may emerge large amplitude limit cycles due to super-explosion bifurcation of the system. Super-explosion bifurcation is a characteristic of a non-smooth system in which at the bifurcation value there exists a nested family of homoclinic orbits and as the bifurcation parameter increases through the critical value, there appears a limit cycle [33, 34]. Here, we follow the same argument as in [33, 34] to investigate the super-explosion bifurcation of the system (5).

Fig. 13

Phase portraits for boundary equilibrium bifurcations (BEBs) of the piecewise–smooth slow–fast systems (5): the unique admissible equilibrium point has a transition from stable node to unstable node as b decreases through $b_*$. The piecewise–smooth slow–fast systems (5) experiences a supercritical super-explosion bifurcation for $b=b^*=0.1$. (a) For $b=0.08<b^*$, the equilibrium unstable node at the right branch of the prey nullcline is enclosed with a coexisting stable limit cycle. (b) Existence of a family of homoclinic orbits around the boundary equilibrium point for $b=b_*=0.1$. The black vertical line $\varSigma$ is the switching boundary. The two samples of the family of Homoclinic orbits are presented by magenta and black curves. The black homoclinic orbit is the largest separatrix cycle. For $b>b^*$, there emerge two limit cycles and for $b<b^*$, only one limit cycle emerges. (c) For $b=0.14>b^*$, there emerges an unstable limit cycle. The inner black limit cycle is unstable, and the outer green one is stable limit cycle. It is to mention that the two limit cycles do not collide within the admissible range (transition from stable node to unstable node) of $b\in (0,0.2828235]$. The other parameter values are $a=0.7$, $k=5$, $\epsilon =0.01$

Let $v_1=(p_1,q_1)$, $v_2=(p_2,q_2)$ be the eigenvectors of $J_+$ for the eigenvalues $0<\lambda _{1} <\lambda _2$ and $v_1'(p_1', q_1')$, $v_2'(p_2', q_2')$ be the eigenvectors of $J_-$ for the eigenvalues $\lambda _1'<\lambda _2'<0$. Then, we have

$$\begin{aligned} \frac{p_j}{q_j}=\frac{a\epsilon }{\lambda _j+\epsilon } \,\,\mathrm{and}\,\,\frac{p_j'}{q_j'}=\frac{a\epsilon }{\lambda _j'+\epsilon }, \,\,j=1,2. \end{aligned}$$

(42)

Thus, the slope of the eigenvectors can be made very small for $\epsilon$ small enough. As c increases through 1 (b decreases through $b_*$), $0<\epsilon \ll 1$, the unstable trajectory leaves the critical manifold $M_{20}$ to the right of the fold point $Q\left( \frac{k}{2}, \frac{k}{4}\right)$ and then follows the attracting branch $C_0^{a+}$ of the critical manifold $M_{20}$, passes the point Q, and enters in the region $\varSigma ^-$ intersecting the switching boundary $\varSigma$ transversally and then gets attracted towards the attracting branch of the critical manifold $M_{10}$ and then following it moves to the right until it crosses the switching boundary $\varSigma$ again below the corner point $E_c\left( 1,1-\frac{1}{k}\right)$ and then intersects the predator (slow) nullcline. Let V be the region enclosed by the trajectory and the slow nullcline. Then, trajectories outside of V will remain outside of V and consequently, $R\backslash V$ is positively invariant, the region V is negatively invariant and by the same argument as in Sect. 5, there must exist a stable periodic orbit in the interior of $R\backslash V$ which gives rise to a stable relaxation oscillation.

At the bifurcation point $c=1$ ($b=b_*$), when we view the boundary equilibrium $E_c$ from the right-half system, it is an unstable node and when we view it from the left-half system it corresponds to a stable node and correspondingly, at the bifurcation point, the strong unstable trajectory enters the region $\varSigma ^-$ and then returns to the boundary equilibrium following $C_0^{a-}$. Hence, at the bifurcation point $c=1$ ($b=b_*$), there is a formation of a homoclinic orbit. The region inside this separatrix cycle consists of a nested collection of homoclinic orbits whereas trajectories outside this region tend to the coexisting stable limit cycle in forward time as $t\rightarrow \infty$. Now, as c decreases through 1 (b increases through $b_*$), there emerges an unstable periodic orbit $\gamma$ enclosing the equilibrium stable node, i.e. the system undergoes a bifurcation known as a supercritical super-explosion bifurcation in the literature and does not occur for smooth systems.

Let $V'$ be the region enclosed by the unstable periodic orbit $\gamma$ which emerges through the bifurcation as b increases through $b_*$. Then, the trajectories starting in $V'$ will remain in $V'$ and approach the equilibrium stable node for the left-half system in forward time. Trajectories outside $V'$ will remain outside $V'$ and consequently, $R\backslash V'$ is positively invariant and by the same argument as in Sect. 5, there exists an attractive periodic orbit $\varGamma$ in the interior of $R\backslash V'$. Thus, we see that as c decreases through 1, (b increases through $b_*$), small enough, there exists an attracting equilibrium, a repelling periodic orbit $\gamma$ and an attracting periodic orbit $\varGamma$; the two such periodic orbits give rise to unstable and stable relaxation oscillations for $0<\epsilon \ll 1$ whose existence we already have shown in Sect. 4. $\square$

7 Discussion

The study of piecewise–smooth predator–prey models is an emerging area of research in recent years to capture nonlinear phenomena observed in a real-life context. In this paper, we consider a modified Leslie-type prey–generalist predator system with a piecewise–smooth Holling type I functional response term that yields a piecewise–smooth slow–fast system. The basic model represents the interaction between prey and its generalist predator which has an alternative food source. The model admits stable steady state as well as oscillatory coexistence scenarios depending upon the magnitudes of parameters.

We have divided the parameter space into nine different regions $D_i, i = 1,2,\dots ,9$ and shown the various results on the existence of admissible interior equilibria as the parameters are shifted from one region to another. We have investigated the stability of each equilibrium including the boundary equilibrium point. We have studied how eigenvalues jump at the corner of the prey nullcline by analysing the generalized Jacobian matrix. In the case when $\epsilon$ is not comparatively small, the various bifurcations are observed such as the saddle-node bifurcation, Hopf bifurcation, and Bogdanov–Takens bifurcation. The existence of various types of local bifurcations indicates the complex dynamics exhibited by a simple model involving Holling type I functional response having only one non-smooth point. This type of functional response represents the saturation of consumption of prey by the predator within the setup of the Holling type I function.

The main contribution of the present work is a detailed study of the system dynamics in the presence of a slow–fast time scale of a modified Leslie–Gower system consisting of prey and generalized predator species having a non-smooth functional response. We have studied the detailed dynamics of such a non-smooth slow–fast system by employing geometric singular perturbation theory and the blow-up technique. This study mainly concerns the existence of singular Hopf bifurcation, canard orbits, multiple relaxation oscillations, and boundary equilibrium bifurcations. We have shown the emergence of an unstable canard cycle around the folded singularity prior to the bifurcation surrounded by a stable limit cycle which gives rise to a stable relaxation oscillation for $0 < \epsilon \ll 1$. It has also been shown that there exist two relaxation oscillations, stable and unstable for $0 < \epsilon \ll 1$ whenever the parameters belong to the region $D_2$, i.e. the unique admissible equilibrium lies on the left branch of the prey nullcline. We have also identified parametric regions for which there is no relaxation oscillation for $0 < \epsilon \ll 1$.

We have also studied all the possible scenarios that may occur due to a boundary equilibrium bifurcation (BEB) for the slow–fast planar piecewise–smooth system under consideration. We have shown that upon varying the parameter b, an unstable focus or unstable node after colliding the switching boundary $\varSigma$ becomes a stable focus and the instability is transferred to an unstable limit cycle. This phenomenon is also known as non-smooth Hopf bifurcation in literature. Geometrically, it can be interpreted as the magnificent bifurcation scenario that arises when the non-trivial predator nullcline crosses the point of non-differentiability on the non-trivial prey nullcline. The unstable limit cycle arising through the BEB is surrounded by a stable limit cycle due to a global bifurcation of the system, and the two limit cycles give rise to relaxation oscillations, respectively, for very small $\epsilon$. We have also investigated the case when there is a transition from a stable node to an unstable node upon passing through the switching boundary $\varSigma$. This is not a non-smooth analogue of Hopf bifurcation as either of the equilibrium is not a focus equilibrium. In such a case, it has been shown that there emerges an unstable limit cycle due to super-explosion bifurcation of the system. In all the cases of BEBs, we have observed that upon varying the parameter b, the stable and unstable limit cycles collide with each other and disappear through a saddle-node bifurcation of the limit cycle.

Fig. 14

The mutual position of the prey and predator nullclines of the system (5). The red curve is the prey nullcline, and predator nullclines are plotted for various values of a. Depending on the slope and position of the predator nullcline, there can be 0, 1, 2, or 3 interior equilibria. (a) It illustrates that there exists unique interior equilibrium point in $\varSigma ^+$, corner point on $\varSigma$ and in $\varSigma ^+$ for parameter values $b = 0.05, k = 5$, $\epsilon = 0.1$ with three different positions of predator nullcline for $a = 0.65$ (blue line), 0.75 (green line), and 0.98 (black line). The parameters belong to the region $D_{10}$. Geometrically, as we increase the slope of the predator nullcline keeping b small, the parameter $c=\frac{k(1-b)}{1+ka}$ decreases, and as it decreases through 1, the position of the interior equilibrium changes from $\varSigma ^+$ to $\varSigma ^-$. (b) With five different positions of predator nullcline, the figure illustrates that the system can have 1 (one in $\varSigma ^+$), 2 (one at the corner point on $\varSigma$, i.e. the boundary equilibrium, and one in $\varSigma ^+$), 3 (one in $\varSigma ^-$ and two in $\varSigma ^+$), 2 (one in each $\varSigma ^\pm$), or 1 (in $\varSigma ^-$) equilibrium points for the parameter values $b = 0.7, k = 5$, $\epsilon = 0.1$ with different values of a given by 0.05 (magenta), 0.1 (blue line), 0.17 (green line), 0.2516685226 (cyan line), and 0.6 (black line). For different positions of the predator nullcline, the parameters belong to the regions $D_6$, $D_5$, $D_4$, $D_9$, $D_2$ and consequently, the existence result of the interior equilibria is consistent as proposed in lemma 4. (c) It illustrates that there exist 3 (one in $\varSigma ^-$ and two in $\varSigma ^+$), 2 (one in each $\varSigma ^\pm$), or 1 (in $\varSigma ^-$) equilibrium points for the parameter values $b = 0.82, k = 5$, $\epsilon = 0.1$ with different values of a given by 0.05 (blue line), 0.1900617308 (green line), and 0.5 (black line). The parameter values for the different cases belong to $D_4$, $D_9$ and $D_2$. (d) System can have, respectively, 2 (both in $\varSigma ^+$), 1 (in $\varSigma ^+$), or no admissible interior equilibrium points for the parameter values $b = 1.1, k = 5$, $\epsilon = 0.1$ with different values of a given by 0.02 (blue line), 0.06192 (green line), and 0.2 (black line). As we increase the slope of the predator nullcline, the parameters shift from the region $D_3$ to $D_8$, and region $D_8$ to $D_1$. The interior and boundary equilibrium points are marked with solid red circles, and the maximum point Q of the right branch of the prey nullcline is shown as a solid blue circle

It also follows trivially that when the parameters belong to the region $D_3$, we have the basins of attraction for the admissible interior equilibrium $E_3$ and the axial equilibrium $E_b$ separated by the stable manifolds of the saddle point $E_2$. Geometrically, this implies that if initially, the prey species lie to the left of the stable separatrix of $E_2$, then in the long run the prey species will die out otherwise both the species will coexist. The prey species will die out in the long run if the parameters belong to the region $D_1$.

The transfer of the stable and unstable manifolds of various equilibrium points leads to some global bifurcations, and such bifurcations are generic in nature with respect to the difference of time scale. (They exist for $\epsilon = 1$ as well as for $\epsilon \ll 1$.)

Hopf-bifurcating periodic solutions exhibit relaxation oscillation when the magnitude of the slow–fast time scale parameter is reduced. This time scale parameter sometimes alters the Hopf bifurcation threshold [3, 36]. Most of the investigations for canard cycle, relaxation oscillation, and singular Hopf bifurcation are performed with the models which exhibit super-critical Hopf bifurcation and result in a stable limit cycle. However, no canard explosion occurs for the slow–fast system (5). The main contribution of this work is to study the change in dynamic behaviour due to the presence of slow–fast time scale, and the model is capable to generate a stable and unstable limit cycle simultaneously. We have shown that the particular choice of parameter values and for the appropriate magnitude of the slow–fast time scale parameter can capture the existence of two relaxation oscillations: one is stable, and the other is unstable. It is important to note that the existence of two limit cycles is not due to the saddle-node bifurcation of limit cycles rather one of them is generated through boundary point bifurcation. The presence of boundary point bifurcation is due to the consideration of a non-smooth functional response. Change in system dynamics due to the boundary point bifurcation with the variation of the slow–fast time scale parameter is another significant contribution of this work. Our future goal will be to check the structural sensitivity of the obtained results for other models of interacting populations which exhibit sliding mode bifurcations, which is prototypical dynamics produced by Filippov-type models.

Appendix