On occurrence of sudden increase of spiking amplitude via fold limit cycle bifurcation in a modified Van der Pol–Duffing system with slow-varying periodic excitation

Abstract

The main purpose of the paper is to reveal the mechanism of certain special phenomena in bursting oscillations such as the sudden increase of the spiking amplitude. When multiple equilibrium points coexist in a dynamical system, several types of stable attractors via different bifurcations from these points may be observed with the variation of parameters, which may interact with each other to form other types of bifurcations. Here we take the modified van der Pol–Duffing system as an example, in which periodic parametric excitation is introduced. When the exciting frequency is far less than the natural frequency, bursting oscillations may appear. By regarding the exciting term as a slow-varying parameter, the number of the equilibrium branches in the fast generalized autonomous subsystem varies from one to five with the variation of the slow-varying parameter. The equilibrium branches may undergo different types of bifurcations, such as Hopf and pitchfork bifurcations. The limit cycles, including the cycles via Hopf bifurcations and the cycles near the homo-clinic orbit, may interact with each other to form the fold limit cycle bifurcations. With the increase of the exciting amplitude, different stable attractors and bifurcations of the generalized autonomous fast subsystem involve the full system, leading to different types of bursting oscillations. Fold limit cycle bifurcations may cause the sudden change of the spiking amplitude, since at the bifurcation points, the trajectory may oscillate according to different stable limit cycles with obviously different amplitudes. At the pitchfork bifurcation point, two possible jumping ways may result in two coexisted asymmetric bursting attractors, which may expand in the phase space to interact with each other to form an enlarged symmetric bursting attractor with doubled period. The inertia of the movement along the stable equilibrium may cause the trajectory to pass across the related bifurcations, leading to the delay effect of the bifurcations. Not only the large exciting amplitude, but also the large value of the exciting frequency may increase inertia of the movement, since in both the two cases, the change rate of the slow-varying parameter may increase. Therefore, a relative small exciting frequency may be taken in order to show the possible influence of all the equilibrium branches and their bifurcations on the dynamics of the full system.

1 Introduction

The coupling of different scales can be observed widely in science and engineering problems, which may result in special dynamical behaviors in the combinations of small and large amplitude oscillations, such as the mixed-mode oscillations in the catalytic reactions [1] and the relaxation oscillations in tether satellites [2]. To investigate the mechanism of the oscillations, a geometrical singular perturbation theory was proposed [3], in which the geometric view was introduced to account for the transitions between the slow and fast subsystems [4]. Based on the method, a so-called slow-fast analysis method was developed to cope with the bifurcations at the connection between the quiescent states and spiking states [5, 6]. For a typical slow-fast system with one-dimensional slow subsystem in the form

$$\begin{aligned} \begin{aligned} {\dot{x}}&= f(x,y),\ \ \ \ \mathrm {(fast \ subsystem)}, \\ {\dot{y}}&= \varepsilon g(x,y),\ \ \ \mathrm { (slow \ subsystem)}, \end{aligned} \end{aligned}$$

(1)

where $x\in R^M$, $y\in R$, and $0<\varepsilon \ll 1$ measures the ratio between the two scales, regarding the slow-varying state variable y as the slow-varying parameter, one may obtain the equilibrium branches and the bifurcation sets of the fast subsystem expressed in the forms $E(X_0,y)=0$ and $B(X_0, Y_B)=0$, respectively [7, 8]. Overlapping the phase portrait $\varGamma (x,y)$ of the full system and $E(X_0,y)=0$ as well as $B(X_0, Y_B)=0$ on the (x, y) plane, one may obtain the influence of the equilibrium branches and their bifurcations on the structures of the bursting attractors of the full system, which reveals the mechanism of the bursting oscillations [9, 10].

The slow-fast analysis method is valid to investigate the bifurcation mechanism of the bursting oscillations in the autonomous system, in which there exist obvious slow and fast subsystems [11, 12]. However, the traditional approach cannot be used for mechanism analysis of the bursting oscillations in the non-autonomous system. Note that for a typical periodically excited system in the form

$$\begin{aligned} {\dot{x}}=f[x, A\sin (\varOmega t )], \end{aligned}$$

(2)

when the exciting frequency is far less than the natural frequency, implying the coupling of two scales in frequency domain exists, bursting oscillations can often be observed. In order to investigate the mechanism, referring to the traditional method, we extended a modified slow-fast analysis method [13], in which the whole exciting term $w=A\sin (\varOmega t )$ is regarded as a slow-varying parameter, just like slow state variable y in (1). Here we call w a generalized state variable, which forms the slow subsystem. Therefore, we can define the fast subsystem

$$\begin{aligned} {\dot{x}}=f(x, w), \end{aligned}$$

(3)

as a generalized autonomous system. Similarly, the equilibrium branches and the bifurcation sets can be derived in the forms $E_G(X_0,w)=0$ and $B_G(X_0, W_B)=0$, respectively. By introducing the transformed phase portrait $\varGamma _G (x,w)\equiv \varGamma _G [x,A\sin (\varOmega t)]$, one may obtain the effect of the equilibrium branches and the bifurcations on the full system by overlapping $\varGamma _G(x,w)$, $E_G(X_0,w)=0$ and $B_G(X_0, W_B)=0$ [14].

Most of the research for the bursting oscillations in the dynamical systems with periodic excitation focused on the case with no more than three equilibrium branches [15, 16]. Furthermore, only two relatively simple types of bifurcations, i.e., the fold and Hopf bifurcations, are considered for the transitions between the quiescent states and spiking states [17]. When more equilibrium branches coexist, the limit cycles, including the cycles with relatively large amplitude near the homo-clinic orbits and the cycles bifurcated via Hopf bifurcations may interact with each other to form fold limit cycle bifurcations [18, 19], which may lead more complicated bursting behaviors.

Here we consider a three-dimensional dynamical system with fifth-order nonlinear terms, in which the number of the equilibrium points may vary between one to five. The fold limit cycle bifurcations can be observed not only for the interactions between the stable and unstable limit cycles via Hopf bifurcations, but also for the interactions between the limit cycles near the homo-clinic orbit and the cycles via Hopf bifurcations. When a slow-varying periodic parametric excitation is introduced, with the variation of the exciting amplitude, several forms of bursting oscillations with qualitatively different topological structures are obtained. A few interesting phenomena, such as the sudden change of the amplitude of the spiking oscillations, the disappearance of the influence of some stable attractors and the bifurcations of the fast subsystems on the full system, are presented, the mechanism of which is investigated by employing the bifurcation analysis on the transitions between the quiescent states and spiking states.

2 Mathematical model

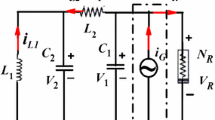
For the modified van der Pol–Duffing circuit system, in which a quintic nonlinear resistor in parallel with the inductor of the original circuit is introduced [20, 21], when the characteristics of the nonlinear resistor is of $i_N=F(v_1)=av_1+bv^3_1+dv^5_1 (a<0,b<0,d>0)$, by applying Kirchhoff’s laws to the circuit, the non-dimensional mathematical model can be expressed as

$$\begin{aligned} \begin{aligned} {\dot{x}}&=-{\mu }(-w{x}+{\alpha }x^3+{\kappa }x^5-y),\\ {\dot{y}}&=x-{\gamma }y-z, \\ {\dot{z}}&={\beta }y, \end{aligned} \end{aligned}$$

(4)

where the parameters satisfy the conditions ${\alpha }<0,{\beta }>0,{\gamma }>0,{\kappa }>0$ and ${\mu }>0$. Here we choose the parameter w as the controlling parameter in the form $w=A\sin (\varOmega t)$ for the parametric exciting case, where A and $\varOmega$ correspond to the exciting amplitude and the frequency, respectively. To investigate the influence of the coupling of two scales on the dynamics, we assume the exciting frequency $\varOmega$ is far less than the natural frequency of the system, denoted by $\omega$, i.e., $\varOmega \ll \omega$.

Many results have been obtained for the case when the parameter w is a constant [22]. Cascading of period-doubling bifurcations as well as homo-clinic bifurcations may be observed [23, 24], which may result in chaos for certain parameter values [25]. Furthermore, since there may exist different types of equilibrium points, the locations as well as the properties may change with the variation of parameter. The interaction between the attractors via the bifurcations of the equilibrium points may lead to more complicated behaviors, such as 2-D torus [26]. However, when w is replaced by a slow-varying exciting term, some special movements, such as bursting oscillations, which behave in the combinations between large-amplitude oscillations and small-amplitude oscillations, may appear. With the variation of the exciting amplitude and the frequency, the forms of the bursting oscillations may change. In the following, we focus on the evolution of the bursting oscillations to explore the mechanism of the behaviors.

3 Bifurcation analysis of the generalized autonomous system

For the periodically excited system, one may generally eliminate the exciting term to compute the natural frequency via the corresponding autonomous system. The computation of natural frequency of a nonlinear system is a bit complicated, since the natural frequency is closely related to the behaviors of the system. For example, when the trajectory tends to a stable focus point, the natural frequency can be approximated by the imaginary parts of the pair of conjugate complex eigenvalues, while when the system behaves in periodic oscillations, the natural frequency can be determined by the oscillating frequency.

When the exciting frequency $\varOmega$ is far less than the natural frequency, one may regard the whole exciting term $w=A\sin (\varOmega t)$ as the slow-varying parameter, called the slow subsystem, which leads to the fast subsystem in generalized autonomous form, expressed in (4).

To explore the properties of the fast subsystem in generalized autonomous form, here we take w as a bifurcation parameter to investigate the dynamical evolution of the fast subsystem with the variation of w.

Fig. 1

Distribution of equilibrium points on the (w,$\alpha$) plane

Fig. 2

Equilibrium branches as well as their bifurcations with the variation of w in (a), with locally part in (b)

The equilibrium points of system (4) can be expressed in the form $EQ(x,y,z)=(X_0,0, X_0)$, where $X_0$ satisfies

$$\begin{aligned} -wX_0+{\alpha }X_0^3+{\kappa }X_0^5=0, \end{aligned}$$

(5)

from which one may find the number as well as the locations of the equilibrium points depend on the slow-varying parameter w [27]. Since $\kappa >0$, $-\alpha ^2/(4\kappa )<0$. For $w\in (-\infty ,-\alpha ^2/(4\kappa ))$, only one equilibrium point with $X_0=0$ exists, for $w\in (-\alpha ^2/(4\kappa ),0)$, five equilibria coexist with $X_0=0$, and $X_0= \pm \frac{\sqrt{-2\kappa (\alpha \pm \sqrt{\alpha ^2+4{\kappa }w})}}{2\kappa }$, respectively, while for $w\in (0, +\infty )$, three equilibria coexist with $X_0$=0, and $X_0=\pm \frac{(\sqrt{2}\sqrt{\kappa (-\alpha +\sqrt{\alpha ^2+4{\kappa }w})}}{2\kappa }$,respectively.

The stability of equilibrium points can be determined by the associated characteristic equation, written as

$$\begin{aligned} {\lambda }^3+m_1{\lambda }^2+m_2{\lambda }+m_3=0, \end{aligned}$$

(6)

where

$$\begin{aligned} \begin{aligned} m_1&={\gamma }-{\mu }w+3{\alpha }{\mu }X_0^2+5\kappa {\mu }X_0^4,\\ m_2&={\beta }-{\mu }-{\gamma }{\mu }w+3{\alpha }{\gamma }{\mu }X_0^2+5{\gamma }\kappa {\mu }X_0^4,\\ m_3&=-{\beta }{\mu }w+3{\alpha }{\beta }{\mu }X_0^2+5{\beta }\kappa {\mu }X_0^4. \end{aligned} \end{aligned}$$

(7)

The equilibrium point is stable if the conditions

$$\begin{aligned} \left\{ \begin{aligned}&m_1>0,\\&m_3>0,\\&m_1m_2-m_3>0, \end{aligned} \right. \end{aligned}$$

(8)

are satisfied. When the parameters satisfy

$$\begin{aligned} \mathbf{FB }: \ \ \left\{ \begin{aligned}&m_3=0,\\&-wX_0+{\alpha }X_0^3+{\kappa }X_0^5=0, \end{aligned} \right. \end{aligned}$$

(9)

a zero eigenvalue can be obtained, which means fold bifurcation may occur, leading to the jumping between different stable equilibrium points. Similarly, on the set

$$\begin{aligned} \mathbf{HB }: \ \ \left\{ \begin{aligned}&m_1m_2-m_3=0,\\&-wX_0+{\alpha }X_0^3+{\kappa }X_0^5=0, \end{aligned} \right. \end{aligned}$$

(10)

a pair of pure imaginary eigenvalues can be observed, which implies Hopf bifurcation may be possible, resulting in periodic oscillations with the frequency approximately at $\varOmega _H=\sqrt{m_2}$ [28].

Table 1 Evolution of the dynamics with the variation of w

Because of the complicated expressions of the equilibrium points as well as the associated characteristic equations, the theoretical analysis related to the stabilities of the solutions is a bit difficult. Here we turn to the numerical simulations. A typical distribution of equilibria on the (w,$\alpha$) plane for the parameters fixed at $\beta =3.0,\gamma =0.6,\mu =2.0,\kappa =1.5$ is shown in Fig. 1, from which one may find the parameter plane is divided into three regions, corresponding to different number of the equilibrium points, respectively.

Different types of bifurcations of the equilibrium points can be observed with the variation of parameters. For example, when $\alpha =-1.5$, the evolution of the dynamics of the generalized autonomous system is presented in Fig. 2. It can be found that with the variation of w, the equilibrium points form equilibrium branches, denoted by $E_0$, $E_{\pm 1}$ and $E_{\pm 2}$, on which different types of bifurcations can be observed.

The bifurcation points divide the w-axis into serval intervals corresponding to different behaviors in the generalized autonomous fast subsystem, the details of which are presented in Table 1.

For $w\in (- \infty , -1.4799)$, only a stable focus at the origin with $X_0=0$ exists. At $P_1$ for $w=-1.4799$, fold limit cycle bifurcation occurs, at which the stable limit cycle with relatively large amplitude $LC_2$ meets the unstable limit cycle $LC_1$ bifurcated from the point $P_2$ with $w=-1.1572$ via sub-Hopf bifurcation. For $w\in (-1.4799,-1.1572)$, the stable focus $E_0$ coexists with the two limit cycles $LC_{1,2}$. Sub-Hopf bifurcation at $P_2$ results in the disappearance of the unstable limit cycle $LC_1$, which causes the stable focus to change to an unstable saddle. Therefore, only stable limit cycle $LC_2$ for $w\in (-1.1572, -0.5611)$ occurs.

The stable limit cycle $LC_3$ bifurcated from the point $P_9$ with $w=-0.2172$ via super-critical Hopf bifurcation meets the unstable limit cycle $LC_4$ at $P_3$ with $w=-0.5611$ to form another fold limit cycle bifurcation. With the increase of w, the amplitude of the unstable $LC_4$ increases and finally interacts with the large-amplitude limit cycle $LC_2$ at $P_4$ with $w=-0.3891$, yielding fold limit cycle bifurcation. Therefore, for $w\in (-0.5611, -0.3891)$, two stable limit cycles $LC_{2,3}$ coexist. While for $w\in (-0.3891,-0.2172)$, because of possible appearance of the other four equilibrium points, the attractors may behave in a bit complexity.

We now turn to the locally enlarged part, shown in Fig. 2b. It can be found that for $w\in (-0.3891,-0.3750)$, only stable $LC_3$ exists. For $w=-0.3750$ at the point $P_5$, the unstable equilibrium branches $E_{\pm 1}$ meet the stable equilibrium branches $E_{\pm 2}$, respectively, yielding two saddle-focus bifurcations at the points $D_{\pm 1}$. When $w\in (-0.3750, -0.3683)$, the stable limit cycle $LC_3$ coexists with the two stable foci, located on $E_{\pm 2}$, respectively.

Two super-critical Hopf bifurcations occur at the point $D_{\pm 2}$ on the stable equilibrium branches $E_{\pm 2}$, respectively, resulting in two stable limit cycles $LC_{\pm 5}$. For $w\in (-0.3683,-0.2802)$, three stable limit cycles coexist, denoted by $LC_3$ and $LC_{\pm 5}$. Two unstable limit cycles $LC_{\pm 6}$ via sub-critical Hopf bifurcations at $D_{\pm 3}$ meet the two stable cycle $LC_{\pm 5}$ at $P_8$ with $w=-0.2582$, respectively, to form fold limit cycle bifurcations, resulting in the disappearance of these limit cycles. For $w\in (-0.2802,-0.2582)$, the three stable limit cycles $LC_3$ and $LC_{\pm 5}$ coexist with the two stable foci located on $E_{\pm 2}$, respectively.

When $w\in (-0.2582, -0.2172)$, because of the fold limit cycle bifurcations at $P_8$ as well as the Hopf bifurcation at $P_9$, only stable $LC_3$ and two stable foci on $E_{\pm 2}$ can be observed. Further increase of w causes the disappearance of $LC_3$, implying for $w\in (-0.2172, 0.0)$, one stable focus on $E_0$ and two stable foci on $E_{\pm 2}$ coexist. When $w\in (0.0, +\infty )$, the two stable foci on $E_{\pm 2}$ coexist, since the pitch-fork bifurcation at $P_{10}$ with $w=0.0$ results in the transition of the stability of the equilibrium point on $E_0$.

From the analysis of the equilibrium branches, it can be found that with the variation of the slow-varying parameter w, different types of bifurcations may appear, leading to different types of stable attractors. Since the slow varying parameter w changes between $-A$ and $+A$ periodically, therefore, for different exciting amplitude A, different types of bifurcations and the attractors may involve the behaviors of the system with the coupling of two scales, yielding different forms of bursting oscillations as well as the related mechanism.

In the following, we will investigate the dynamical evolution with the increase of the exciting amplitude to show how the related bifurcations and the stable attractors affect the structures of the bursting oscillations.

4 Dynamical evolution of the system with the variation of exciting amplitude

Since some of the stable attractors exist for very short intervals of w, and a few bifurcation points are very close to each other, in order to show the influence of these stable attractors and the bifurcations on the dynamics of the full system more thoroughly, we need to choose the exciting frequency as small as possible to ensure enough slowness of the exciting term. Here we set $\varOmega =0.0001$ to explore the behaviors with the variation of the exciting amplitude A.

It can be checked that symmetric dynamics exists, since the system keeps the same under the transformations $(x,y,z,t)\rightarrow [-x,-y,-z,(\pi /\varOmega -t)]$.

Furthermore, all the equilibrium branches and their bifurcations of the fast subsystem are derived with the variation of w in above section. To show their influence on the structure of the attractors of the full system, we first introduce the conception of transformed phase portrait to reveal the mechanism of the dynamical behaviors.

4.1 Transformed phase portrait

For the generalized autonomous system, the equilibrium branches can be derived in the form $E_G(X_0,w)=0$, while locations of the bifurcations can be expressed as $B_G(X_0,W_B)=0$, which implies that not only the equilibrium branches but also the bifurcation points are determined by the special relationship between the state variable x and the slow-varying parameter w. The traditional phase portrait of the attractor, expressed by $\varGamma :\equiv \{[x(t),y(t),z(t)]| t\in R\}$, can only be used to describe the relationship between different state variables with the evolution of time. In order to explore the influence of the behaviors of the generalized autonomous system on the full system, one need to know the relationship between the state variables and the slow-varying parameter w. For the purpose, we define $\varGamma _G:\equiv \{[x(t),y(t),z(t),w(t)]| t\in R\}=\{[x(t),y(t),z(t),A\sin (\varOmega t)]| t\in R\}$, or the projections on the sub-plane such as the (x, w) plane, as the transformed phase portraits of the attractors, in which the slow-varying parameter w is regarded as a generalized state variable.

Overlapping the equilibrium branches $E_G(X_0,w)=0$ and bifurcation sets $B_G(X_0,W_B)=0$ of the fast subsystem in generalized autonomous form with the transformed phase portrait $\varGamma _G(x,w)$ on the (w, x) plane, the influence of the equilibrium branches and their bifurcations on the structures of the attractors of the full system can be obtained, which can be used to account for the mechanism of the oscillations.

4.2 Point-cycle bursting oscillations

For $A<0.2582$, implying $w\in (-0.2582, +0.2582)$, from the bifurcation analysis described above, there always exist stable $E_{\pm 2}$ in the generalized autonomous fast subsystem. Numerical simulations reveal that two coexisted stable limit cycles oscillating around the stable $E_{\pm 2}$, respectively, with the same frequency as that of the parametric excitation, can be observed.

Fold limit cycle bifurcations at $w=-0.2582$ cause the two limit cycles evolve to two coexisted point-cycle bursting attractors, respectively, oscillating between the $LC_{\pm 5}$ and $E_{\pm 2}$, respectively, for $A\in (0.2582,0.3750)$.

Fig. 3

Bursting oscillations for $A=0.37$ with the initial condition $(x_0,y_0,z_0,t_0)=(0.1, 0.1, 0.1, 0)$. a Phase portrait on the (x, y, z) space by skipping the transient process; b Phase portrait on the (x, z) plane; c Phase portrait on the (x, y) plane; d Time history of x; e Overlap of the transformed phase portrait and the equilibrium branches on the (w, x) plane with locally enlarged part of in (f). The trajectory in pink corresponds to the transient process, which finally settles down to the stable attractor in black. To show the delay effect of the bifurcation, the trajectory in cyan in (f) represents the return route from $E_{+2}$ to $D_{+2}$

To illustrate the bursting oscillations, Fig. 3 presents one of the two coexisted attractors with the initial condition $(x_0, y_0, z_0, t_0)=(0.1, 0.1, 0.1, 0)$ for $A=0.37$, where the transient process is skipped, while the other attractor can be obtained by setting the initial condition at $(x_0, y_0, z_0, t_0)=(-0.1, -0.1, -0.1, \pi /\varOmega )$, which keeps $O_2$ symmetry with the attractor in Fig. 3, omitted here for simplicity.

It can be found that the trajectory of the stable attractor oscillates according to $LC_{+5}$ and $E_{+2}$ in turn, which can be observed clearly from the overlap of the equilibrium branches and the transformed phase portrait in Fig. 3e, f.

An interesting phenomenon occurs that for $A<0.3750$ corresponding to $w\in (-0.3750, +0.3750)$, the trajectory does not oscillate around the stable limit cycle $LC_3$ and the stable segment of $E_0$ between the two points $P_9$ and $P_{10}$ in Fig. 2. The reason can be explained as follows.

For $A<0.2582$, implying $w\in (-0.2582, +0.2582)$, besides the existence of the stable equilibrium branches $E_{\pm 2}$, there exists stable limit cycle $LC_3$ for $w\in (-0.2582, -0.2172)$ and stable equilibrium branch $E_0$ for $w\in (-0.2172, 0)$. When the slow-varying parameter $w\in (-0.2582, -0.2172)$, the trajectory tends to oscillate according to the stable limit cycle $LC_3$. With the increase of w, the amplitude of the oscillation decreases gradually, until w increases to $w=-0.2172$ at $P_9$, at which the trajectory settles down to stable $E_0$. The trajectory moves almost strictly along $E_0$ to $P_{10}$ with $w=0.0$, at which pitch-fork bifurcation occurs. The trajectory jumps to one of the two stable equilibrium branches $E_{\pm 2}$, and moves along $E_{\pm 2}$ until w reaches its maximum value $w=+A$. The trajectory then turns to the left since w decreases with the increase of time. No bifurcation occurs on the stable equilibrium branches $E_{\pm 2}$, implying the trajectory may move strictly along $E_{\pm 2}$ back and forth with the variation of w.

Skipping the transient process, the trajectory may always remain on one of the two $E_{\pm 2}$, which results in the coexistence of two limit cycles around $E_{\pm 2}$ with the same period of the excitation.

Now we focus on the bursting structure in Fig. 3. For $0.2582<A<0.3750$, two stable limit cycles $LC_{\pm 5}$ bifurcated from $D_{\pm 2}$ on $E_{\pm 2}$ at $w=-0.3683$, respectively, can be observed, which means $LC_{\pm 5}$ exist for $w\in (-0.3683, -0.2582)$.

Assuming the trajectory starts in the neighborhood of the point $P_9$, it moves along the stable equilibrium branch $E_0$, passing across the pitch-fork bifurcation point $P_{10}$ because of the delay effect of the bifurcation. When the effect of pitch-fork bifurcation appears, the trajectory may jump to one of two stable equilibrium branches $E_{\pm 2}$. Therefore, two possible routes exist, depending on the conditions of the trajectory at the jumping point.

For the attractor presented in Fig. 3e, the trajectory jumps to $E_{+2}$ and turns to move along $E_{+2}$. When w reaches its maximum value, the trajectory then turns to the left. Fold limit cycle bifurcation may cause the trajectory to begin spiking oscillations, the amplitude of which may change almost strictly according to $LC_{+5}$. Obvious delay effect of fold limit cycle bifurcation can be observed, shown in Fig. 3f, from which one may find the trajectory moves along unstable segment of $E_{+2}$ and passes across the sub-Hopf bifurcation point $D_{+3}$.

When the trajectory settles down to the stable segment of $E_{+2}$ via Hopf bifurcation at $D_{+2}$, it moves along $E_{+2}$ until w reaches its minimum value. With the evolution of time, the trajectory oscillates according to $E_{+2}$ and $LC_{+5}$ in turn, seeing the time history plotted in Fig. 3d, behaving in a periodic Hopf/Hopf bursting attractor.

On the contrary, when proper initial condition is taken, the trajectory from the neighborhood of the point $P_9$ may jump to $E_{-2}$, which may finally evolve to another periodic Hopf/Hopf bursting attractor oscillating according to $E_{-2}$ and $LC_{-5}$ in turn.

Therefore, two periodic point-cycle bursting attractors coexist, corresponding to different attracting basins. Here we would like to point out that, not only the two coexisted attractors, but also the attracting basins, keep the $O_2$ symmetry, defined by the full system.

Furthermore, for $A<0.3750$, though the stable limit cycle $LC_3$ and the stable segment of $E_0$ may affect the transient process of the trajectory, the influence of them on the dynamics of the full system finally disappears, seeing Fig. 3c.

Note: The numerical results of the differential equations in the manuscript are obtained via fixed-step fourth-order Runge–Kutta method with different fixed-steps varying from $H=0.001$ to $H=0.0001$, which have also been demonstrated by the variable step-length fourth-order Runge–Kutta method to ensure the correctness. Furthermore, all the stable attractors are plotted by skipping the transient process.

Fig. 4

Bursting oscillations for $A=0.55$ with the initial condition $(x_0,y_0,z_0,t_0)=(0.1, 0.1, 0.1, 0)$. a Phase portrait on the (x, y) plane; Time history of x in (b) with locally enlarged parts in (c) and (d)

4.3 Symmetric Hopf/fold-cycle/Hopf/pitchfork bursting

When $w=-0.3750$, saddle-focus bifurcation causes the trajectory to jump to the stable limit cycle $LC_3$, which, therefore, leads to the interaction between the two coexisted point-cycle bursting attractors. An enlarged symmetric bursting attractor appears because of the influence of $LC_3$ and $E_0$ on the dynamics. Further decrease of w may cause the trajectory to oscillate around $LC_3$, $LC_{\pm 5}$, $E_0$ and $E_{\pm 2}$ in turn, until w decreases to $w=-0.5611$, at which fold limit cycle bifurcation at $P_3$ corresponding to $FC_2$ occurs.

Fig. 5

Bursting oscillations for $A=0.55$. Overlap of the transformed phase portrait and the equilibrium branches on the (w, x) plane in (a) with locally enlarged parts in (b) and (c)

Therefore, for $0.3750<A<0.5611$, a symmetric bursting oscillations can be observed, seeing the attractor in Fig. 4 for $A=0.55$, in which the phase portrait on the (x,y) plane is presented in Fig. 4a, while the related time history of x is plotted in Fig. 4b with locally enlarged parts in Fig. 4c,d. The attractor is the sole movement of the system since no change of the attractor can be observed with the variation of the initial conditions except the transient process.

From the time history of x in Fig. 4, one may find that the trajectory can be divided into twelve segments, described by $QS_i (i=1,2,\ldots ,6)$ for six quiescent states and $SP_i (i =1,2,\ldots ,6)$ for six spiking states, respectively.

To investigate the mechanism of the bursting oscillations, we turn to the overlap of the transformed phase portrait and the equilibrium branches of the generalized autonomous system, shown in Fig. 5a with locally enlarged parts in Fig. 5b, c. Here we focus on one period of the periodic bursting oscillations.

For the trajectory starting from the point $S_0$ in Fig. 5 with maximum $w=+A=+0.55$, it turns to the left since slow-varying parameter w decreases with the increase of time. The trajectory moves almost strictly along the stable $E_{-2}$, passing across the sub-Hopf bifurcation point $D_{-3}$, appearing in quiescent state $QS_1$. Further decrease of w causes the trajectory to jump to the stable limit cycle $LC_{-5}$ to begin the repetitive spiking oscillation $SP_1$. The amplitude of the oscillations decreases gradually and finally the trajectory settles down to the stable segment on $E_{-2}$, behaving in quiescent state $QS_2$.

When w decreases to $w=-0.3750$, fold bifurcation causes the trajectory to jump to the stable limit $LC_3$, leading to spiking oscillations $SP_2$. The amplitude of the oscillations increases gradually almost strictly according to the limit cycle $LC_3$ until w reaches its minimum value $w=-A=-0.55$.

The trajectory then turns to the right because of the increase of w. Similarly, the amplitude of the spiking oscillations decreases almost strictly according to $LC_3$ until Hopf bifurcation occurs at $P_9$, which causes the trajectory to move almost strictly along the stable segment on $E_0$, passing across the pitchfork bifurcation point $P_{10}$ and then moves along the unstable $E_0$, appearing in quiescent state $QS_3$.

The influence of the pitchfork bifurcation at $P_{10}$ causes the trajectory to jump to stable $E_{+2}$. The transient process with oscillations forms the spiking state $SP_3$, which may disappear very quickly. When the trajectory settles down to $E_{+2}$, it moves almost strictly along $E_{+2}$ in quiescent state $QS_4$ until the slow-varying parameter w reaches its maximum value $w=+A=+0.55$.

When the trajectory arrives at the point $S_1$, half period of the bursting oscillations is finished, while the other half period of the movement is omitted here for simplicity because of the symmetry.

From the bifurcations connecting the QSs and SPs, the type of oscillations can be called periodic Symmetric Hopf/fold-cycle/Hopf/pitchfork bursting.

Remark: The period of the bursting oscillations is two times of exciting period for the same reason described above. When the trajectory moves almost along the stable segment of $E_0$, it may just pass across the bifurcation point $P_{10}$, and turn to move almost strictly along the unstable segment of $E_0$, since the inertia of the movement along the stable equilibrium branch, which leads to delay influence of the related pitchfork bifurcation. Though the trajectory oscillating according to $LC_{\pm 5}$ may settle down to the stable segments of the equilibrium branches $E_{\pm 2}$ via Hopf bifurcations, respectively, while fold bifurcations at $D_{\pm 1}$ occur with further decrease of w, the trajectory may jump to the limit cycle $LC_3$ immediately, because of the short intervals between the points related to the two types of bifurcations.

Fig. 6

Bursting oscillations for $A=0.65$ with the initial condition $(x_0,y_0,z_0, t_0)=(0.1,0.1,0.1,0)$. a Phase portrait on the (x,y) plane; b Time history of x; Overlap of the transformed phase portrait and the equilibrium branches on the (w,x) plane in (c) with locally enlarged part in (d)

Here we would like to point out that, the repetitive spiking oscillations $SP_{1,4}$ and $SP_{2,5}$ are caused by the bifurcations to the limit cycles $LC_{\pm 5}$ and $LC_3$, respectively, which implies that the frequencies of the spiking oscillations can be approximated by the frequencies of the associated limit cycles. For example, for $SP_{1}$, the frequency can be computed approximately at $\varOmega _1=2\pi /T_1=1.6804$ via the time history of x in Fig. 4c, which agrees well with the frequency, $\varOmega _H=1.6961$, related to the super-critical Hopf bifurcation at $D_{+2}$.

The spiking oscillations $SP_{3,6}$ correspond to the transient processes from the point on $E_0$ to the stable equilibrium branches $E_{\pm 2}$. Therefore the frequencies can be approximated by the imaginary parts of the pair of conjugate eigenvalues of the corresponding points on $E_{\pm 2}$, computed at $\varOmega _s=1.1707$, which agrees well with the numerical result at $\varOmega _2=2\pi /T_2=1.1832$, via time history in Fig. 4d.

4.4 Asymmetric and symmetric Hopf/fold/fold cycle/Hopf/pitchfork bursting

Further increase of the exciting amplitude may cause the influence of the stable limit cycle $LC_2$ on the bursting attractor for $A>0.5611$, implying w may arrive at the bifurcation point $P_3$ for $w=-0.5611$, at which fold limit cycle bifurcation corresponding to $FC_2$ appears. Stable limit cycle $LC_2$ with large-amplitude appears until w decreases to point $P_1$ with $w=-1.4799$, at which another fold limit cycle bifurcation takes place. Therefore, for $0.5611<A<1.4799$, qualitatively different bursting oscillations can be observed. Numerical simulations reveal that the dynamics may alternate between two coexisted asymmetric attractors and one symmetric attractor in turn. Figure 6 gives one of the two coexisted asymmetric bursting attractors for $A=0.65$, while the other one is presented in Fig. 7.

Fig. 7

Bursting oscillations for $A=0.65$ with the initial condition $(x_0,y_0,z_0,t_0)=($-$0.1,-0.1,-0.1,0)$. a Phase portrait on the (x,y) plane; b Time history of x; c Overlap of the transformed phase portrait and the equilibrium branches on the (w,x) plane

Fig. 8

Bursting oscillations for $A=0.68$ with the initial condition $(x_0,y_0,z_0,t_0)=($-0.1, -0.1, -0.1, 0). a Phase portrait on the (x,y) plane; b Time history of x; c Overlap of the transformed phase portrait and the equilibrium branches on the (w,x) plane; (d)Phase portrait on the (x,y,z) space

From the time history of x in Fig. 6b, the trajectory of asymmetric attractor can be divided into six segments, corresponding to three quiescent states $QS_i (i=1,2,3)$ and three spiking states $SP_i (i=1,2,3)$.

We still turn to the overlap of the transformed phase portrait and the equilibrium branches of the generalized autonomous system to investigate the mechanism of the oscillations, shown in Fig. 6c with locally enlarged part in Fig. 6d.

The trajectory starting at the point $S_0$ with $w=+A=+0.65$ moves along $E_{+2}$ in quiescent state $QS_1$ until the influence of limit cycle $LC_{+5}$ via Hopf bifurcation at $D_{+2}$ takes place. Repetitive spiking oscillations $SP_1$ occur, the amplitude of which changes almost strictly according to $LC_{+5}$. The trajectory finally settles down to the stable segment of the equilibrium branch $E_{+2}$ because of the disappearance of $LC_{+5}$, resulting in the quiescent state $QS_2$.

When the trajectory moving along the stable segment on $E_{+2}$ arrives at the point $D_{+1}$, fold bifurcation occurs, at which the trajectory tries to jump to the stable limit cycle $LC_3$ via Hopf bifurcation at $P_9$ to begin spiking oscillations $SP_2$. The amplitude of the spiking oscillations increases gradually according to $LC_3$ until fold limit cycle bifurcation $FC_2$ at $P_3$ occurs, seeing Fig. 2.

The trajectory turns to oscillate according to the limit cycle $LC_2$, which causes the sudden increase of the oscillating amplitude. When the slow-varying parameter w decreases to $w=-A=-0.65$, the trajectory oscillating according to $LC_2$ turns to the right, still oscillating according to $LC_2$. Fold limit cycle bifurcation $FC_3$ at $P_4$ causes the trajectory to turn to move according to $LC_3$, at which the sudden change of oscillating amplitude appears again.

The amplitude of the oscillations decreases gradually and finally settles down to $E_0$ when Hopf bifurcation at $P_9$ takes place. Quiescent state $QS_3$ can be observed in which the trajectory moves almost strictly along $E_0$. Pitchfork bifurcation at $P_{10}$ may finally cause the trajectory to jump to stable $E_{+2}$, leading to $SP_3$. The trajectory finally settles down to $E_{+2}$.

When the trajectory moving along $E_{+2}$ reaches the point $S_0$, one period of the bursting oscillations is finished, the period of which is the same as that of excitation. According to the bifurcation mechanism, the type of attractor can be called periodic asymmetric Hopf/fold/fold cycle/Hopf/Pitchfork bursting oscillations.

With the variation of the exciting amplitude, the two coexisted bursting attractors may expand in the phase space and finally interact with each other to form an enlarged symmetric periodic bursting attractor, seeing the example in Fig. 8 for $A=0.68$.

It is worthy to point out here that, for the two coexisted asymmetric bursting attractor, the period of the bursting oscillations is the same as that of the excitation, while for the symmetric bursting attractor, the period is doubled, which implies that the trajectory of the symmetric attractor spends the same time to visit the two coexisted asymmetric attractors in turn.

Detailed numerical simulations reveal that the occurrence of the symmetric attractor and the two coexisted asymmetric attractors may appear alternatively. For the trajectory moving along the stable segment of $E_0$, if the influence of the pitch-fork bifurcation causes the trajectory to jump to the two stable equilibrium branches $E_{\pm 2}$ in turn, symmetric bursting attractor can be observed, while if the trajectory always jumps to one of $E_{\pm 2}$, two coexisted asymmetric attractors occur. Therefore, the occurrence of the two types of solutions depend on the relationship between the trajectory and the two attracting basins of $E_{\pm 2}$.

4.5 Asymmetric and symmetric periodic fold/fold cycle/fold cycle/pitchfork bursting attractor

For $A>1.4799$, the fold limit cycle bifurcation at $P_1$ with $w=-1.4799$ may occur, yielding the stable segment of $E_0$, which may affect the structure of the bursting oscillations. Similarly, since the influence of the pitch-fork bifurcation at $P_{10}$ may cause two forms of jumping phenomenon, the bursting behaviors change between two coexisted asymmetric attractors and one symmetric attractor. Figure 9 gives one of two coexisted asymmetric bursting attractors for $A=1.80$ by skipping the transient process, while the other is omitted here for simplicity.

Fig. 9

Bursting oscillations for $A=1.8$ with the initial condition $(x_0,y_0,z_0,t_0)=(0.1,0.1,0.1,0)$. a Phase portrait on the (x, y) plane. b Time history of x; c Overlap of the transformed phase portrait and the equilibrium branches on the (w,x) plane with locally enlarged part of in (d)

The trajectory can be divided into four stages corresponding to two quiescent states and two spiking states, respectively. From the overlap of the transformed phase portrait and the equilibrium branches of the generalized autonomous system in Fig. 9c,d, one may find that the trajectory from $S_0$ with $w=+A=+1.80$ moves almost strictly along the stable and unstable segments of $E_{+2}$, passing across the two Hopf bifurcation points $D_{+3}$ and $D_{+2}$, until the fold bifurcation at $D_{+1}$ occurs, at which the trajectory tries to jump to the stable limit cycle $LC_3$ via Hopf bifurcation at $P_9$ to begin spiking oscillations. The amplitude of the spiking oscillations increases gradually according to $LC_3$ until fold limit cycle bifurcation $FC_2$ at $P_3$ occurs, seeing Fig. 9c.

The trajectory turns to oscillate according to the limit cycle $LC_2$, which causes the sudden increase of the oscillating amplitude. Fold limit cycle bifurcation $FC_1$ at $P_1$ causes the trajectory to jump to the stable segment of $E_0$ to begin the quiescent state until w decrease to $w=-A=-1.80$.

The trajectory turns to the right along $E_0$ with further increase of time, passing across the bifurcation points on $E_0$. When the trajectory along $E_0$ passes across $P_{10}$ to an extent, the influence of pitchfork bifurcation occurs, causing the trajectory to jump to the stable segment of $E_{+2}$.

When the trajectory along $E_{+2}$ reaches the starting point $S_0$, one period of the bursting oscillations is finished. Similarly, the type of bursting oscillations can be called asymmetric periodic fold/fold cycle/fold cycle/pitchfork bursting attractor.

The two coexisted asymmetric attractors may interact with each other to form an enlarged symmetric bursting attractor in which the trajectory visits the two asymmetric attractors in turn, the details of which are omitted here for simplicity.

From the structure of the bursting oscillations in Fig. 9, one may find that the influence of $LC_{\pm 5}$ on the dynamics disappears. Now we focus on the reason for the phenomenon. The inertia of the movement along the stable segment of $E_{\pm 2}$ causes the trajectory to pass across the sub-Hopf bifurcation point $D_{+3}$, and the trajectory turns to move along the unstable segment of $E_{\pm 2}$ until the influence of $LC_{\pm 5}$ appears. Since the inertia of the movement increases with the increase of the exciting amplitude, the trajectory moves longer along the unstable segment for larger A, which leads to shorter stage of spiking oscillations caused by the limit cycles $LC_{\pm 5}$, called the delay effect of the related bifurcation.

The phenomenon can be demonstrated by the time history of the spiking oscillations, shown in Fig. 10 for different exciting amplitudes. For $A=0.55$, the time length of the spiking stage can be approximated at $L_1=1002.3$, while $L_2=642.5$ for $A=0.65$ and $L_3=560.8$ for $A=0.68$.

When the exciting amplitude increases to an extent, the inertia of the movement along $E_{\pm 2}$ begins large enough to pass across the whole interval of w corresponding to the occurrence of $L_{\pm 5}$, the influence of the two stable limit cycles $LC_{\pm 5}$ disappears, yielding the topological change of the bursting structure, seeing bursting attractor in Fig. 9, in which the spiking stage related to the stable $L_{\pm 5}$ disappears.

Fig. 10

Time histories of x for the related spiking oscillations with different exciting amplitudes

5 The influence of exciting frequency on the dynamic behaviors

Though the equilibrium branches and their bifurcations may be the same for different slow exciting frequency if the whole exciting term is regarded as a slow parameter, the ratio between slow and fast scales still influences the dynamical behaviors. For relatively small ratio, the inertia of the movement may lead to the disappearance of effect of some of the stable attractors and the bifurcations of the generalized autonomous system on the full system, especially for stable attractors bifurcated from the equilibrium branches. As an example, Fig. 11 gives the behaviors of the full system in the neighborhood of $LC_{+5}$ for $A=0.55$ with different ratios.

Fig. 11

Bursting properties in the neighborhood of $LC_{+5}$ with different exciting frequencies for $A=0.55$. a Equilibrium branches and their bifurcations in the neighborhood of $LC_{+5}$; Overlap of the transformed phase portrait and the equilibrium branches with $\varOmega =0.005$ in (b), $\varOmega =0.0001$ in (c) and $\varOmega =0.00001$ in (d)

For $\varOmega =0.005$, with the decrease of w, the trajectory moves almost strictly along the stable and unstable segment of $E_{+2}$, passing across the two Hopf bifurcation points $D_{+2,3}$ directly, until fold bifurcation at $D_{+1}$ occurs, followed by the jumping phenomenon, which implies that the effect of the limit cycle $LC_{+5}$ on the dynamics disappears, shown in Fig. 11b.

When $\varOmega$ decreases to an extent, the influence of $LC_{+5}$ occurs, seeing Fig. 11c,d for $\varOmega =0.0001$ and $\varOmega =0.00001$, respectively. Furthermore, the ratio also affects the length of the movement along the unstable segment of $E_{+2}$, resulting in different delay effect of the bifurcation on the structure. From the figure, one may find that the repetitive spiking oscillations according to $LC_{+5}$ occur when $w\in (-0.3714,-0.3323)$ for $\varOmega =0.0001$, while for $\varOmega =0.00001$, the spiking oscillations exist when $w\in (-0.3694,-0.2966)$.

From the example, we may conclude here that, when the exciting frequency is far less enough, corresponding relative large ratio, the effect of the stable attractors on the dynamics may be observed. With the decrease of the ratio, the delay effect of the bifurcation on the dynamical structure becomes more obvious, which may finally cause the disappearance of influence of the stable attractors and the related bifurcation of the generalized autonomous system.

6 Conclusion

For the nonlinear oscillators, there often coexist different equilibrium points and limit cycles, while the fold of these equilibria and the limit cycles may cause different types of bifurcations. When the coupling of different scales involves the vector field, these attractors may influence the dynamical behaviors. For the typical case with the introduction of parametric excitation, when the exciting frequency is far less than the natural frequency, implying the coupling of two scales in frequency domain exists, by regarded the whole exciting term as a slow-varying parameter, the equilibrium branches and their bifurcations can be derived. With the variation of the slow-varying parameter, the equilibrium points form different equilibrium branches, on which different types of bifurcations for certain special values of the slow-varying parameter may take place. For different exciting amplitudes, not only the equilibrium branches but also the bifurcations involved in the full system are different, which may yield different types of bursting attractors.

It is found that the ratio between the two scales may influence the structures of the bursting oscillations. When smaller the exciting frequency is taken, the effect of all the stable equilibrium branches as well as the bifurcations of the generalized autonomous system on the dynamics of the full system may appear, possibly resulting in more spiking states and quiescent states. The fold limit cycle bifurcation may lead to the sudden increase of the amplitude of the spiking oscillations, since the trajectory may jump to oscillate according to different stable limit cycles. The pitchfork bifurcation may cause the trajectory to jump to two symmetric stable equilibrium branches with different attracting basins, respectively, which may lead to two coexisted asymmetric bursting attractors. When the two coexisted asymmetric bursting attractors expand in the phase space with the variation of parameters, they may interact with each other to form an enlarged symmetric bursting attractor. Here we should point out that the period of the two coexisted asymmetric bursting attractors is the same as that of the excitation, while the period is doubled for the enlarged symmetric attractor.

An interesting phenomenon can be observed that, the inertia of the movement along the stable equilibrium branches may cause the trajectory to pass across the bifurcation point, resulting in the movement of the trajectory along an unstable equilibrium branches before the effect of the bifurcation on the behavior of the full system appears. The phenomenon can often be called the delay effect of the bifurcation. When the exciting amplitude or the exciting frequency increases to an extent, the delay induced by the inertia of the movement becomes large, which may cause the trajectory to pass across the parameter regions of the stable attractors via the bifurcation. The influence of the bifurcation as well as the stable attractor induced by the bifurcation on the dynamics may disappear, which may lead to relatively simple bursting structures.