1 Introduction

Optical communication has developed rapidly, which is one of the supporting systems of the modern internet age [1,2,3,4,5,6,7,8,9]. The solitons have been investigated extensively after they were proposed in 1980, because they can keep their shapes to transmit in a long distance for the balance between the dispersion and nonlinear effects [10,11,12,13,14,15,16,17,18]. Besides, some methods have been used to solve the soliton solutions [19,20,21,22,23,24]. Furthermore, soliton interactions have been used to design optical switches [25,26,27,28]. Therefore, the research of solitons is hot in nonlinear science, and solitons have turned into an important topic in the area of communication systems [29,30,31,32].

In this paper, we will study soliton interactions in an inhomogeneous optical fiber by the following fifth-order nonlinear Schödinger (NLS) equations [33]:

$$\begin{aligned}&iu_{x}+d_{1}(x)u_{tt}+d_{2}(x)\left| u\right| ^{2}u-i[a_{1}(x)u_{ttttt}\nonumber \\&\quad +a_{2}(x)\left| u\right| ^{2}u_{ttt}+a_{3}(x)(u\left| u_{t}\right| ^{2})_{t}+ a_{4}(x)u^{*}u_{t}u_{tt}\nonumber \\&\quad +a_{5}(x)\left| u\right| ^{4}u_{t}]=0, \end{aligned}$$
(1)

where \(u(x,t)\) is a function, which represents the varying envelope wave. x is the normalized distance, and t is the normalized time. \(d_{1}(x)\) is the group velocity dispersion (GVD), \(a_{1}(x)\) is the fifth-order dispersion, and \(d_{2}(x)\) is the Kerr nonlinearity. \(a_{j}(x)(j=2,3,4,5)\) are the fifth-order nonlinearity coefficients.

As we all know, two-soliton interactions are important. By studying the soliton interactions, we can effectively enhance the communication capacity and improve the stability of the system [34,35,36]. Besides, to improve the quality of the communication in some long-distance optical systems, some factors such as higher-order dispersion and nonlinear effects should be considered [37,38,39,40]. Further, when the soliton duration is femto-second, high-order dispersion and high-order nonlinear effects will appear while solitons are transmitted in optical fibers. Meanwhile, the variable coefficient NLS equation can describe physical phenomenon more generally than the constant-coefficient equations [41,42,43,44]. Thus, it is necessary to use Eq. (1) to study the soliton interactions and analyze the nonlinear dynamic characteristics of these higher-order effects [11]. For Eq. (1), the dark soliton solutions and the integrability have been given [33]. However, the bright two-soliton solutions of Eq. (1) and their interactions have not been investigated under certain constraints in the existing reports.

We will use the Hirota method to get the bright soliton solutions, and their interactions will be given in this paper. It is organized as: the bright soliton solutions will be given in part 2; the interactions between bright solitons will be carried out in part 3; the conclusion will be derived in part 4.

2 Analytic bright soliton solutions

We introduce a dependent variable \(u=g/f\) with g(x, t) as the complex one and f(x, t) as the real one [45]. Using this transformation, we can get the bilinear forms as [32]

$$\begin{aligned} \begin{aligned}&\left[ iD_{x}+\frac{1}{2}\phi _{1}(x)D_{t}^{2}-i\phi _{2}(x)D_{t}^{5}\right] g\cdot f\\&\quad -5i\phi _{2}(x)hg^{*}_{t}-5i\phi _{2}(x)g^{*}s=0,\\&D_{t}^{2}(g\cdot g)-hf=0,\\&2D_{t}(g\cdot g_{tt})-sf+hf_{t}=0,\\&D_{t}^{2}(f\cdot f)-2gg^{*}=0. \end{aligned} \end{aligned}$$
(2)

Here, \(D_{t}\) and \(D_{x}\) are the bilinear operators [13]. We introduce the constrains as follows [33],

$$\begin{aligned} \begin{aligned} d_{1}(x)&=\frac{\phi _{1}(x)}{2},\quad d_{2}(x)=2d_{1}(x),\quad a_{1}(x)=\phi _{2}(x),\\ a_{2}(x)&=a_{3}(x)=10\phi _{2}(x),\\ a_{4}(x)&=2a_{2}(x),\quad a_{5}(x)=3a_{2}(x). \end{aligned} \end{aligned}$$
(3)

To get the bright one-soliton solutions, the functions of \(g\), \(f\), \(h\) and \(s\) can be expanded as follows:

$$\begin{aligned} f=1+\varepsilon ^2 f_{2},\quad g=\varepsilon g_{1},\quad s=0,\quad h=0. \end{aligned}$$
(4)
Fig. 1
figure 1

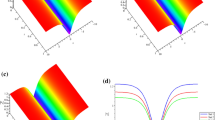
Propagation characteristics of parabolic solitons for Eq. (1). Parameters are \(\phi _{1}=\sin x-x\), \(\phi _{2}=0.2x\) with a \(\omega =0.48+1.1i\), \(\delta =1+2i\); b \(\omega =0.68+1.1i\), \(\delta =1+2i\); c \(\omega =0.48+1.1i\), \(\delta =-2+2i\)

Full size image
Fig. 2
figure 2

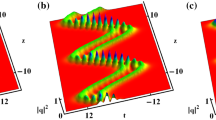
In-phase interaction characteristics of parabolic solitons for Eq. (1). Parameters are \(\phi _{1}=\sin x-x\), \(\phi _{2}=0.2x\), \(\omega _{1}=0.4-1.3i\), \(\omega _{2}=0.73+1.1i\), \(\delta _{1}=1+2i\) with a \(\delta _{2}=4+2i\); b \(\delta _{2}=2+2i\); c \(\delta _{2}=1+2i\)

Full size image

And then we assume that

$$\begin{aligned} g_{1}=e^{\theta },\quad f_{2}=Be^{\theta +\theta ^{*}},\quad \theta =k(x)+\omega t+\delta , \end{aligned}$$
(5)

where \(\omega \) and \(\delta \) are the complex constants, \(k(x)\), \(\phi _{1}(x)\) and \(\phi _{2}(x)\) are real functions. Setting \(\varepsilon = 1\), we can get

$$\begin{aligned} \begin{aligned} k(x)&=\int \frac{1}{2}\Big (i\omega ^{2}\phi _{1}(x)+2\omega ^{5}\phi _{2}(x)\Big )\mathrm{d}x,\\ B&=\frac{1}{(\omega +\omega ^{*})^{2}}. \end{aligned} \end{aligned}$$
(6)

We write the undetermined functions as follows to get the bright two-soliton solutions,

$$\begin{aligned} \begin{aligned} f&=1+\varepsilon ^2 f_{2}+\varepsilon ^4 f_{4},\quad g=\varepsilon g_{1}+\varepsilon ^{3} g_{3}, \\ s&=s_{0}+\varepsilon ^{2}s_{2},\quad h=h_{0}+\varepsilon ^{2}h_{2}. \end{aligned} \end{aligned}$$
(7)

We assume that

$$\begin{aligned} \begin{aligned} g_{1}&=e^{\theta _{1}+\theta _{2}},\\ f_{2}&=B_{1}e^{\theta _{1}+\theta _{1}^{*}}+B_{2}e^{\theta _{1}+\theta _{2}^{*}}+B_{3}e^{\theta _{2}+\theta _{1}^{*}}+B_{4}e^{\theta _{2}+\theta _{2}^{*}},\\ g_{3}&=m_{1}e^{\theta _{1}+\theta _{2}++\theta _{1}^{*}}+m_{2}e^{\theta _{1}+\theta _{2}++\theta _{2}^{*}},\\ f_{4}&=Me^{\theta _{1}+\theta _{1}^{*}+\theta _{2}+\theta _{2}^{*}},\\ s_{0}&=h_{0}=0,\quad s_{2}=Ae^{\theta _{1}+\theta _{2}},\quad h_{2}=Qe^{\theta _{1}+\theta _{2}},\\ \theta _{1}&=k_{1}(x)+\omega _{1} t+\delta _{1},\quad \theta _{2}=k_{2}(x)+\omega _{2} t+\delta _{2},\\ \end{aligned} \end{aligned}$$
(8)

where \(\omega \) and \(\delta \) are the complex constants, \(k(x)\), \(\phi _{1}(x)\) and \(\phi _{2}(x)\) are real functions. We set \(\varepsilon = 1\), and will get

$$\begin{aligned} \begin{aligned} k_{1}(x)&=\int \frac{1}{2}\Big (i\omega _{1}^{2}\phi _{1}(x)+2\omega _{1}^{5}\phi _{2}(x)\Big )\mathrm{d}x,\\ k_{2}(x)&=\int \frac{1}{2}\Big (i\omega _{2}^{2}\phi _{1}(x)+2\omega _{2}^{5}\phi _{2}(x)\Big )\mathrm{d}x,\\ Q&=2(\omega _{1}-\omega _{2})^{2},\quad A=-Q(\omega _{1}+\omega _{2})^{2},\\ M&=B_{1}B_{2}B_{3}B_{4}QQ^{*}/4, \\ B_{1}&=\frac{1}{(\omega _{1}+\omega _{1}^{*})^{2}},\quad B_{2}=\frac{1}{(\omega _{1}+\omega _{2}^{*})^{2}},\\ B_{3}&=\frac{1}{(\omega _{2}+\omega _{1}^{*})^{2}},\quad B_{4}=\frac{1}{(\omega _{2}+\omega _{2}^{*})^{2}},\\ m_{1}&=\frac{Q B_{1}}{2(\omega _{2}-\omega _{1}^{*})^{2}},\quad m_{2}=\frac{Q B_{2}}{2(\omega _{2}-\omega _{2}^{*})^{2}}. \end{aligned} \end{aligned}$$
(9)
Fig. 3
figure 3

Inverse interaction characteristics of parabolic solitons for Eq. (1). Parameters are \(\phi _{1}=\sin x-x\), \(\phi _{2}=0.2x\), \(\omega _{1}=0.8-1.3i\), \(\omega _{2}=-0.43+1.1i\), \(\delta _{2}=2+2i\) with a \(\delta _{1}=4+2i\); b \(\delta _{1}=1+2i\); c \(\delta _{1}=-2+2i\)

Full size image

3 Discussion

We obtain the one-soliton and two-soliton solutions in Sect. 2, and the characteristics and interactions of solitons can be explored in this part. Taking different functions for \(\phi _{1}(x)\) and \(\phi _{2}(x)\) can result in different distributions of dispersion. In Fig. 1, there is a common soliton. When we set \(\omega =0.68+1.1i\), the soliton intensity in Fig. 1b gets lager compared with Fig. 1a. And then, we set \(\delta =-2+2i\), the soliton in Fig. 1c moves away while the other characteristics are not changed.

Some interactions between solitons are presented in Fig. 2, and the interactions between two solitons are discussed by changing \(\delta _{2}\) as different numbers. When we set \(\phi _{1}(x)=\sin (x)-x\) and \(\phi _{2}(x)=0.2x\), the two solitons are attracting and repelling each other periodically.

After we change \(\delta _{2}=2+2i\) and \(1+2i\), the distance between two solitons becomes smaller. The value of \(\delta _{2}\) gets smaller, two solitons get closer, and the intensity of interactions gets stronger. Therefore, we can control the distance between two solitons to reduce the relative effect by adjusting \(\delta _{2}\). This method can increase the soliton energy and amplitude effectively.

In Fig. 3, we can see two solitons spread in different directions. When we alter the real part of \(\delta _{1}\), one soliton moves along the t axis. Therefore, the interaction strength between solitons is changed because of the changing of the distance. When we let \(\delta _{1}\) to be \(1+2i\) and \(-2+2i\), respectively, the interaction strength between two solitons changes gradually. So we can control the interaction strength between solitons through controlling the value of \(\delta _{1}\).

4 Conclusion

We have studied the variable coefficients fifth-order NLS Eq. (1). The bright one-soliton and two-soliton solutions (4) and (7) have been obtained by the Hirota method. The interaction strength between solitons has been discussed theoretically. The intensity of solitons has been changed with the different numbers of \(\omega \). When we have increased the real part of \(\omega \), the soliton has gotten higher. Meanwhile, we have analyzed the influence of \(\delta _{1}\) and \(\delta _{2}\) on the soliton transmission. With the changes of the real parts of \(\delta _{1}\) and \(\delta _{2}\), the distance between solitons has gotten smaller or larger, so soliton interactions have become larger or smaller. As a result, we have realized how to control the interaction strength between solitons. The results in this work may have scientific value about the solitons transmission control.