1 Introduction

As the core component of CNC machine tools, spindle bearing system will generate a lot of heat when running at a high speed, which will have a great impact on the cutting stability and machining accuracy of CNC machine tools [1]. Therefore, it is very important to analyze and evaluate the dynamic characteristics of system for improving its machining accuracy and providing guidances to optimize its design. At present, the machining accuracy of CNC machine tools is required to be higher and higher [2]. The research on the thermal effect of bearings is a very complicated work [3], which involves the change of thermal resistance, bearing parameters, lubricant viscosity and the calculation of heat source, etc., because the dynamic characteristics of system are directly affected by bearing performance, especially the thermal effect of bearings [4, 5]. Therefore, the study of dynamic characteristics of CNC lathe spindle-bearing system should not only consider the mechanical characteristics of spindle, but also the thermal–mechanical coupling effect caused by the high-speed operation of bearings [6,7,8].

Angular contact ball bearings are most frequently used in machine tools due to their favorable stiffness properties, low friction loss and ability to bear axial and radial loads. With the increase of friction heat generated by bearings, the temperature distribution inside bearings will have a significant impact on their stiffness, working accuracy and even service life [9]. Over the years, many researchers have devoted themselves to the study of bearing heat transfer. Palmgren [10] was one of the early researchers who studied the mechanism of bearing temperature and put forward an empirical formula to calculate the friction torque. Subsequently, Harris and Kotzalas [11] proposed one of the most widely used comprehensive formula of bearing friction loss power on the basis of Palmgren's research. Later, Brecher et al. [12] proposed a new, simple calculation model to estimate the cage-induced frictional losses in spindle bearings under high rotational speed by experiments. Than et al. [13] present an inverse method to estimate time-varying heat sources in a high-speed spindle based on experimental temperatures of housing surface, because the thermal estimation accuracy of the empirical formula is relatively low. The frictional thermal mechanism of bearings was further studied by many scholars for more accurate assessments. Tong et al. [14] explored the running torque when the angular misalignment of angular contact ball bearings was factored. A skidding analysis of angular contact ball bearings subjected to various boundary conditions was implemented by Oktaviana et al. [15]. Zhang et al. [16] proposed a friction torque model of ball bearings with geometrical imperfections.

Combining the friction heat source and the nodes of spindle-bearing system, the heat balance equations can be established to solve the node temperatures by the thermal network method [17]. The thermal deformations of the balls and the inner and outer raceways can be obtained by the temperature distribution of bearing parts [18]. Lin and Tu [19] introduced the thermal deformations of rolling bodies into the study on thermal–mechanical coupling of bearings. Alfares et al. [20] investigated thermal variation impact on the dynamics of a spindle-bearing system by considering thermal deformation. However, the change of contact angle was not taken into account, so that the calculation of friction heat is inaccurate. Zheng et al. [21, 22] established a ball load balance model considering centrifugal force, gyroscopic torque and thermal deformation, where the change of contact angle was considered to improve the accuracy of calculation results. Subsequently, the effect of structure and assembly constraints on temperature of high-speed angular contact ball bearings with thermal network method was investigated by Zheng et al. [23]. Liu et al. [24] proposed the closed-loop iterative modeling method of thermal characteristics and analyzed the thermal–structure interaction mechanism to improve the modeling accuracy.

As the most complex and accurate theoretical model to describe the dynamic characteristics of spindle, Timoshenko beam model takes into account the moment of inertia and shear deformation [19, 25]. In recent years, many scholars have proposed a coupling model based on finite element spindle model and bearing model [26,27,28]. Li et al. [29] presented the dynamic model of high-speed motorized spindle in free state and working state. Xi et al. [30] proposed a new dynamic modeling method for a spindle-bearing system supported by angular contact ball bearings and floating displacement bearings to study the influence of key parameters on the system dynamics. The above model provides a theoretical basis for the study of rotor dynamics, but ignores the thermal effect of bearings. Li and Shin [31, 32] proposed a bearing load model including thermal deformation based on discrete spindle dynamic model, and then analyzed the bearing stiffness, thermal deformation and natural frequency of spindle system. Truong et al. [33] proposed a new workflow for analyzing the thermal–mechanical properties of a spindle-bearing system by adding the stiffness coefficient affected by temperature into the finite element model. Zheng et al. [34] studied the thermal estimation of angular contact ball bearings with vibration effects. Based on the error mechanism of spindle system, Liu et al. [35] carried out thermal error modeling and compensation.

According to the above research, few studies take thermal effect into consideration in spindle-bearing system and carry out thorough research on its nonlinear characteristics, which is not conducive to the analysis of dynamic behaviors of system. The purpose of this work is to propose a comprehensive spindle-bearing system model of CNC lathe considering thermal effect to analyze the nonlinear characteristics of system. Firstly, a spindle model based on the Timoshenko’s beam theory is established, and a five DOF quasi-static model of bearings considering thermal effect is proposed. The validity of spindle-bearing thermal model is verified by experiments at different speeds. Then, the comparison between numerical results and experimental results of system response shows that the proposed model is feasible. And then, the variation of contact angle, contact load and bearing stiffness with rotational speed and preload between balls and raceways are compared and analyzed under the condition of considering thermal effect or not. In order to investigate the effects of rotational speed, pulley eccentricity and bearing preload on the nonlinear characteristics of system, time history curve, frequency-spectrum curves, phase diagram, Poincare section and bifurcation diagram are employed. Finally, some conclusions are drawn to predict the motion accuracy and stability of system.

2 Dynamic model of spindle-bearing system

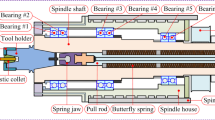
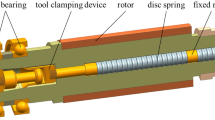
A lathe spindle refers to the shaft on the lathe that drives the workpiece to rotate. As shown in Fig. 1, a spindle component is usually composed of a shaft, a bearing, and a transmission element (pulley). It is mainly used to support transmission parts in machine tools to transmit motion and torque. The spindle contains two sets of angular contact ball bearings. The front two bearings are in tandem and three bearings are tandem at the rear. Preload is used for positioning and preload the inner raceway of bearings, which is conducive to obtaining higher bearing stiffness.

Fig. 1
figure 1

A CNC spindle-bearing system

Full size image

2.1 Dynamic equation of the spindle

According to the structure of spindle, it is discretized into a finite number of beam elements in Fig. 2. The specific spindle unit parameters can be found in Table 1. Timoshenko beam is used to model the beam elements, where each node has three translational degrees of freedom and two rotational degrees of freedom. Similar to the kinetic energy of pulley, the total kinetic energy of beam element includes horizontal motion energy and rotational kinetic energy. The total potential energy of beam element includes the elastic bending potential energy, shear potential energy and axial compression potential energy of beam.

Fig. 2
figure 2

Finite element node diagram of the machine tool spindle

Full size image
Table 1 Dimensions of CNC lathe spindle unit
Full size table

According to the generalized Hamilton’s Principle, the dynamic equation of the spindle obtained is rewritten into the matrix form by finite element method as follows:

$$ \left( {M^{s} + M^{p} } \right)\ddot{q} - \Omega \left( {G^{s} {\text{ + }}G^{p} } \right)\dot{q} + \left( {K^{s} - \Omega ^{2} M_{C}^{s} } \right)q = F^{p} $$
(1)

where \(M^{s}\) is the mass matrix of spindle, \(M^{p}\) represents the mass matrix of pulley, \(M_{C}^{s}\) is the mass matrix used for computing the centrifugal forces, \(G^{s}\) is the gyroscopic matrix of spindle, \(G^{p}\) represents the gyroscopic matrix of pulley, \(K^{s}\) is the stiffness matrix, and \(F^{p}\) represents unbalanced force. \(q = \left( {x,y,z,\varphi _{y} ,\varphi _{z} } \right)^{T}\) represents displacement vector. The details of matrices can be obtained by the finite element matrices [36].

2.2 Thermal model of spindle-bearing system

2.2.1 Ball loads analysis of angular contact ball bearing

In fact, the thermal effect of bearing parts will change the center position of rolling bodies. Thus, the contact deformation of ball-raceway changes accordingly. In this paper, the thermal effect of bearing parts is integrated into the normal contact forces Qij and Qoj between the jth ball with the inner and outer raceways. The centrifugal force \(F_{{cj}}\) and gyroscopic moment \(M_{{gj}}\) of balls at any position \(\psi _{j}\) are considered. The load equilibrium equations of the jth ball can be as follows [11]:

$$ \left\{ \begin{aligned} & Q_{{ij}} \sin \alpha _{{ij}} - Q_{{oj}} \sin \alpha _{{oj}} - {\raise0.7ex\hbox{${M_{{gj}} }$} \!\mathord{\left/ {\vphantom {{M_{{gj}} } {D_{b} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${D_{b} }$}}\left( {\lambda _{{ij}} \cos \alpha _{{ij}} - \lambda _{{oj}} \cos \alpha _{{oj}} } \right) = 0 \hfill \\ & Q_{{ij}} \cos \alpha _{{ij}} - Q_{{oj}} \cos \alpha _{{oj}} + {\raise0.7ex\hbox{${M_{{gj}} }$} \!\mathord{\left/ {\vphantom {{M_{{gj}} } {D_{b} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${D_{b} }$}}\left( {\lambda _{{ij}} \sin \alpha _{{ij}} - \lambda _{{oj}} \sin \alpha _{{oj}} } \right) + F_{{cj}} = 0 \hfill \\ \end{aligned} \right. $$
(2)

where \(\lambda _{{ij}}\) = 0 and \(\lambda _{{oj}}\) = 2 represent the friction coefficients between the jth ball and the inner and outer raceways, respectively, which can be determined according to the outer raceway control theory [37]. \(\alpha _{{ij}}\) and \(\alpha _{{oj}}\) are the normal contact forces and contact angles between the jth ball with the inner and outer raceways, respectively.

The geometric constraint equations considering the thermal expansion of bearing parts shown in Fig. 3 can be expressed as [11]:

$$ \left\{ \begin{aligned} & \left( {A_{{1j}} - Z_{{1j}} } \right)^{2} + \left( {A_{{2j}} - Z_{{2j}} } \right)^{2} - \left( {(f_{i} - 0.5)D_{b} + \delta _{{ij}} - \varepsilon _{b} } \right)^{2} = 0 \hfill \\ & Z_{{1j}}^{2} + Z_{{2j}}^{2} - \left( {(f_{o} - 0.5)D_{b} + \delta _{{oj}} - \varepsilon _{b} } \right)^{2} = 0 \hfill \\ \end{aligned} \right. $$
(3)

where \(D_{b}\) is the ball diameter, \(\varepsilon _{b}\) represents the thermal expansion of ball.\(f_{i}\) and \(f_{o}\) denote the groove curvature coefficients of inner and outer raceways, respectively;\(Z_{{1j}}\), \(Z_{{2j}}\), \(A_{{1j}}\) and \(A_{{2j}}\) are the auxiliary variables to describe the position relationship between bearing parts. A1j and A2j can be expressed as:

$$ \left\{ \begin{aligned} & A_{{1j}} = BD_{b} \sin \alpha + u_{x} = BD_{b} \sin \alpha + \delta _{x} + R_{i} \varphi _{z} \cos \psi _{j} - R_{i} \varphi _{y} \sin \psi _{j} \hfill \\ & A_{{2j}} = BD_{b} \cos \alpha + u_{r} = BD_{b} \cos \alpha + \delta _{z} \sin \psi _{j} + \delta _{y} \cos \psi _{j} + \varepsilon _{{ir}} + u_{\text{cent}} - \varepsilon _{{or}} \hfill \\ \end{aligned} \right. $$
(4)

where \(\delta _{x}\), \(\delta _{y}\), \(\delta _{z}\), \(\varphi _{y}\), \(\varphi _{z}\) denote the displacements of inner raceway;\(\varepsilon _{{ir}}\) and \(\varepsilon _{{or}}\) denote the thermal expansion of inner and outer raceways, respectively;\(R_{i}\) denotes the orbit radius of inner raceway groove curvature center [10]. The centrifugal expansion \(u_{{cent}}\) of inner raceway can be estimated as [22]:

$$ u_{\text{cent}} = \frac{{\rho \omega _{c}^{2} }}{{32E}}d_{m} \left[ {D_{i}^{2} (3 + \mu ) + d_{m}^{2} (1 - \mu )} \right] $$
(5)

where \(D_{i}\) is the inner diameter of spindle; \(\omega _{c}\) is the rotational speed of spindle;\(\rho\), E and \(\mu\) are the density, elastic moduli and Poisson ratio of material of spindle, respectively.

Fig. 3
figure 3

Deformation relationship between ball and inner and outer raceways

Full size image

Taking inner raceway as analytic targets, the force equilibrium equations can be obtained as:

$$ \left\{ \begin{aligned} & F_{x} - \sum\limits_{{j = 1}}^{{j = Z}} {\left( {Q_{{ij}} \cos \alpha _{{ij}} + \frac{{\lambda _{{ij}} M_{{gj}} }}{{D_{b} }}\sin \alpha _{{ij}} } \right)\cos \psi _{j} = 0} \hfill \\ & F_{y} - \sum\limits_{{j = 1}}^{{j = Z}} {\left( {Q_{{ij}} \cos \alpha _{{ij}} + \frac{{\lambda _{{ij}} M_{{gj}} }}{{D_{b} }}\sin \alpha _{{ij}} } \right)\sin \psi _{j} = 0} \hfill \\ & F_{z} - \sum\limits_{{j = 1}}^{{j = Z}} {\left( {Q_{{ij}} \sin \alpha _{{ij}} - \frac{{\lambda _{{ij}} M_{{gj}} }}{{D_{b} }}\cos \alpha _{{ij}} } \right) = 0} \hfill \\ & M_{x} - \sum\limits_{{j = 1}}^{{j = Z}} {\left[ {\left( {Q_{{ij}} \sin \alpha _{{ij}} - \frac{{\lambda _{{ij}} M_{{ij}} }}{{D_{b} }}\cos \alpha _{{ij}} } \right)R_{i} + \frac{{\lambda _{{ij}} M_{{gj}} }}{{D_{b} }}f_{i} } \right]\sin \psi _{j} = 0} \hfill \\ & M_{y} - \sum\limits_{{j = 1}}^{{j = Z}} {\left[ {\left( {Q_{{ij}} \sin \alpha _{{ij}} - \frac{{\lambda _{{ij}} M_{{ij}} }}{{D_{b} }}\cos \alpha _{{ij}} } \right)R_{i} + \frac{{\lambda _{{ij}} M_{{gj}} }}{{D_{b} }}f_{i} } \right]\cos \psi _{j} = 0} \hfill \\ \end{aligned} \right. $$
(6)

where \(F_{x}\), \(F_{y}\), \(F_{z}\), \(M_{x}\) and \(M_{y}\) represent the external forces and moments acted on the inner raceway of bearing.\(Z\) indicates the number of balls.

The initial values of main variables \(\delta _{x}\), \(\delta _{y}\), \(\delta {}_{z}\), \(\varphi _{x}\), \(\varphi _{y}\) are set, and the Newton–Rapshon method is used to solve the Eqs. (2) and (3) to obtain the auxiliary variables \(X_{{1j}}\), \(X_{{2j}}\), \(\delta _{{ij}}\) and \(\delta _{{oj}}\). The obtained auxiliary variables are brought into Eq. (6) to verify whether the main variables meet the accuracy requirement. If the requirement is not met, the main variables are updated and returned to the previous step. The iteration will be terminated until the main variables meet the accuracy requirement. Finally, the contact forces Qij, Qoj and contact angles \(\alpha _{{ij}}\), \(\alpha _{{oj}}\) can be obtained.

2.2.2 Heat generation model

The friction torque [10] of rolling bearing is composed of two parts as shown in Eq. (7)

$$ M = M_{v} + M_{1} $$
(7)

where \(M_{v}\) is frictional torque generated by the viscous friction of lubricant and \(M_{1}\) is frictional torque caused by applied load, which can be obtained according to reference [11].

The friction torque is distributed to the contact surfaces of balls with the inner and outer raceways [10]. The resulting power loss between the balls and the inner and outer raceways can be expressed as:

$$ \left\{ \begin{aligned} P_{{ij}} = \omega _{{mj}} {{D_{b} } \mathord{\left/ {\vphantom {{D_{b} } {\left( {Zd_{i} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {Zd_{i} } \right)}}M \hfill \\ P_{{oj}} = \omega _{{mj}} {{D_{b} } \mathord{\left/ {\vphantom {{D_{b} } {\left( {ZD_{o} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {ZD_{o} } \right)}}M \hfill \\ \end{aligned} \right. $$
(8)

where \(\omega _{{mj}}\) is revolution speed of balls.

The spin-induced friction torques Msj between the balls and the inner raceway can be rewritten as:

$$ \left\{ \begin{aligned} &M_{{sj}} = \frac{{3\mu _{{si}} Q_{{ij}} \sum _{j} }}{8} \hfill \\ & P_{{sj}} = \omega _{{sj}} M_{{sj}} \hfill \\ \end{aligned} \right. $$
(9)

where \(\mu _{{si}}\) is the friction coefficient between the balls and inner raceway,\(\omega _{{sj}}\) is the spin speed of balls and \(\Sigma _{j}\) is the second kind of complete contact elliptic integral between the balls and the raceways.

Combined with the above factors, the power loss of bearing, namely the total friction heat generated by the heat source, can be expressed as:

$$ P_{\text{total}} = P_{i} + P_{o} = \sum\limits_{{j = 1}}^{Z} {\left( {P_{{ij}} + P_{{sj}} } \right)} + \sum\limits_{{j = 1}}^{Z} {P_{{oj}} } $$
(10)

2.2.3 Transient thermal network model

Based on the principle of heat flux conservation, the general form of transient heat balance equation can be established as:

$$ \frac{{T_{0}^{{k + 1}} - T_{1}^{{k + 1}} }}{{R_{{0 - 1}} }} + \frac{{T_{0}^{{k + 1}} - T_{2}^{{k + 1}} }}{{R_{{0 - 2}} }} + \frac{{T_{0}^{{k + 1}} - T_{3}^{{k + 1}} }}{{R_{{0 - 3}} }} + \frac{{T_{0}^{{k + 1}} - T_{4}^{{k + 1}} }}{{R_{{0 - 4}} }} = Q_{0} - C_{0} \rho _{0} V_{0} \frac{{T_{0}^{{k + 1}} - T_{0}^{k} }}{{\Delta t_{k} }} $$
(11)

where \(T_{0}^{{k + 1}}\) is the heat source temperature at \(t_{{k + 1}}\); \(T_{0}^{k}\) is the heat source temperature at \(t_{k}\); \(T_{i}^{{k + 1}}\) is the outside node temperature at \(t_{{k + 1}}\); R0-i is the thermal resistance between the heat source and the outside node (i = 1,2,3,4);\(Q_{0}\) is the total frictional heat generated by the heat source;\(\Delta t_{k} = t_{{k + 1}} - t_{k}\) is the step size of time series.

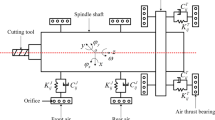
Figure 4 shows the cross section of thermal network diagram of spindle-bearing element, which is divided into 9 nodes in this study. Therefore, we can obtain 9 equations similar to Eq. (11) to solve the temperature field of spindle-bearing system.

Fig. 4
figure 4

Spindle unit thermal network node diagram

Full size image

All nodes in Fig. 4 include three types of thermal resistance: conduction thermal resistance, contact thermal resistance and convection thermal resistance. The specific expressions of each thermal resistance are shown in Tables 2, 3 and 4.

Table 2 Formula of thermal conduction resistance
Full size table
Table 3 Contact thermal resistance formula
Full size table
Table 4 Convection thermal resistance formula
Full size table

Based on the above analysis, the process of solving the transient temperature field of spindle- bearing system by thermal network method can be obtained as shown in Fig. 5. The front and rear bearing sets adopt 7016C and 7014C, respectively. More detailed spindle-bearing system parameters are shown in Table 5. Firstly, given the spindle speed and system loading conditions, the ball loads equilibrium equations of bearings are established according to Sect. 2.2.1 to obtain the contact angle and contact load of balls. Then, the friction heat generated by bearings is calculated according to Sect. 2.2.2. At the same time, combining bearing parameters and taking room temperature as the initial temperature, the heat transfer coefficient of system components can be obtained according to the formulas in Tables 2, 3 and 4. Subsequently, the transient heat balance equations of system are established and solved based on Sect. 2.2.3. In the process of iterative solution, we only need to solve the corresponding linear equations. If the temperature value obtained at this time does not converge, then the bearing parameters, lubricant viscosity and heat transfer coefficient are updated according to this temperature value and taken as the inputs for the next iteration calculation. The calculation does not stop until the results of temperature field meet the given convergence condition. Finally, the temperature values of key nodes of system are output to calculate the deformations of the rolling bodies.

Fig. 5
figure 5

Solution flow of transient temperature field of spindle-bearing system

Full size image
Table 5 Specifications of spindle-bearing system
Full size table

Subsequently, \(\varepsilon _{b}\) and \(\varepsilon _{\text{in}}\) are the thermal expansion of balls and inner raceway can be calculated from Stein and Tu [46].\(\varepsilon _{\text{out}}\) is the thermal expansion of housing, which can be obtained as [47].

Hence, the total deformation \(\delta _{{ijt}}\) of bearings caused by thermal effect can be expressed as:

$$ \delta _{{ijt}} = \varepsilon _{b} + \frac{{\left( {\varepsilon _{\text{in}} - \varepsilon _{\text{out}} } \right)}}{2} $$
(12)

2.2.4 Calculation of stiffness matrix of angular contact ball bearing

Under the condition of high-speed rotation of angular contact ball bearing, the balls are under the combined action of centrifugal force, gyroscopic moment and the thermally-induced preload. According to the relationship between bearing parts deformation and acting force, it can be expressed as [31]:

$$ K^{b} = - \frac{{\partial F}}{{\partial \delta ^{T} }} = - \sum\limits_{{j = 1}}^{Z} {\left[ R \right]} ^{T} \frac{{\partial Q_{j}^{T} }}{{\partial u_{j} }}\left[ R \right] $$
(13)

where

$$ \frac{{\partial Q_{j}^{T} }}{{\partial u_{j} }} = \left[ {\begin{array}{*{20}c} {J_{o} J_{b}^{{ - 1}} J_{i} } & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} } \right] $$
(14)
$$ R = \left[ {\begin{array}{*{20}c} {\cos (\psi _{j} )} & {\sin (\psi _{j} )} & 0 & { - R_{p} \sin (\psi _{j} )} & {R_{p} \cos (\psi _{j} )} \\ 0 & 0 & 1 & {R_{i} \sin (\psi _{j} )} & { - R_{i} \cos (\psi _{j} )} \\ 0 & 0 & 0 & { - \sin (\psi _{j} )} & {\cos (\psi _{j} )} \\ \end{array} } \right] $$
(15)

where \(R_{p}\) is the axial distance between the center of ball and the center of bearing inner raceway, \(J_{b}\) can be obtained by deriving the load balance Eq. (2) of balls in horizontal and vertical directions. \(J_{b} = J_{i} + J_{o}\) is the obtained stiffness matrix.

2.2.5 Nonlinear restoring forces and moments associated with the bearings

The influence of thermal expansion of bearing parts on bearing performance is vital. Therefore, it is very necessary to consider the thermal effect of bearings to analyze the nonlinear dynamic characteristics of CNC lathe spindle-bearing system. The schematic diagram of system is shown in Fig. 6. Since the two sets of bearings are mounted back to back, the left bearing coordinate is consistent with the system coordinate, while the right bearing is opposite. Hence, the nonlinear restoring forces and moments of two sets of bearings should be derived respectively.

Fig. 6
figure 6

Geometric relationship of spindle-bearing system

Full size image

Ignoring the eccentricity of spindle, the dynamic displacements of spindle will only lead to the changes of deformation between balls and inner raceway. The dynamic deformation of the jth ball in the left bearing could be approximately expressed as [48]:

$$ \delta _{{ijdL}} = \left[ \begin{gathered} - z\sin (\psi _{j} )\cos (\alpha _{{ij}} ) + y\cos (\psi _{j} )\cos (\alpha _{{ij}} ) + \hfill \\ \left( {x + \varphi _{z} R_{i} \cos (\psi _{j} ) - \varphi _{y} R_{i} \sin (\psi _{j} )} \right)\sin (\alpha _{{ij}} ) \hfill \\ \end{gathered} \right] $$
(16)

where \(x,y,z,\varphi _{y} ,\varphi _{z}\) denote the dynamic displacements of bearing inner raceway.\(\delta _{{ijtL}}\) is the thermal deformation, which can be derived from Eq. (12). Then, the total deformation of the jth ball of left bearing could be expressed as:

$$ \delta _{{TL}} = \delta _{{ijdL}} + \delta _{{ijsL}} + \delta _{{ijtL}} = \delta _{{ijdL}} + \delta _{{ijsL}} + \varepsilon _{b}^{L} + \frac{{\left( {\varepsilon _{{in}}^{L} - \varepsilon _{{out}}^{L} } \right)}}{2} $$
(17)

where \(\delta _{{ijsL}}\) means the dynamic deformation and static deformation between the jth ball and inner raceway.

The nonlinear restoring forces and moments of the jth ball of left bearing in the global coordinate system could be determined as:

$$ \left\{ \begin{aligned} & F_{{Lx}} {\text{ = }} - K\delta _{{TL}} ^{{1.5}} \sin (\alpha _{{ij}} ) \hfill \\ & F_{{Ly}} {\text{ = }} - K\delta _{{TL}} ^{{1.5}} \cos (\alpha _{{ij}} )\cos (\psi _{j} ) \hfill \\ & F_{{Lz}} {\text{ = }}K\delta _{{TL}} ^{{1.5}} \cos (\alpha _{{ij}} )\sin (\psi _{j} ) \hfill \\ & M_{{Ly}} {\text{ = }}K\delta _{{TL}} ^{{1.5}} \sin (\alpha _{{ij}} )R_{i} \sin (\psi _{j} ) \hfill \\ & M_{{Lz}} {\text{ = }} - K\delta _{{TL}} ^{{1.5}} \sin (\alpha _{{ij}} )R_{i} \cos (\psi _{j} ) \hfill \\ \end{aligned} \right. $$
(18)

where \(K\) is the load–deflection parameter between the jth ball and the inner and outer raceways [11].

Similarly, the nonlinear restoring forces and moments of the jth ball of right bearing in the global coordinate system could be expressed as:

$$ \left\{ \begin{aligned} & F_{{Rx}} {\text{ = }}K\delta _{{TR}} ^{{1.5}} \sin (\alpha _{{ij}} ) \hfill \\ & F_{{Ry}} {\text{ = }} - K\delta _{{TR}} ^{{1.5}} \cos (\alpha _{{ij}} )\cos (\psi _{j} ) \hfill \\& F_{{Rz}} {\text{ = }} - K\delta _{{TR}} ^{{1.5}} \cos (\alpha _{{ij}} )\sin (\psi _{j} ) \hfill \\ & M_{{Ry}} {\text{ = }}K\delta _{{TR}} ^{{1.5}} \sin (\alpha _{{ij}} )R_{i} \sin (\psi _{j} ) \hfill \\ & M_{{Rz}} = K\delta _{{TR}} ^{{1.5}} \sin (\alpha _{{ij}} )R_{i} \cos (\psi _{j} ) \hfill \\ \end{aligned} \right. $$
(19)

By assembling equations of spindle and bearings, the nonlinear dynamic equations for CNC lathe spindle-bearing system can be obtained:

$$ M\ddot{q} + C\dot{q} + Kq = F\left( t \right) $$
(20)

where \(M = M^{s} + M^{p}\),\(C = G^{s} + G^{p} + C^{s}\),\(F\left( t \right) = F^{b} \left( q \right) + F^{p}\),\(K = K^{s} - \Omega ^{2} M_{C}^{s}\),\(F^{b} \left( q \right)\) is the vector of nonlinear restoring force and moments associated with bearings from Eqs. (18) and (19). Among them,\(C^{s} {\text{ = }}\alpha M + \beta K\) is the structural damping which can be expressed as [49]:

$$ \left\{ \begin{aligned} & \alpha = 2{{\left( {\frac{{\xi _{2} }}{{\omega _{2} }} - \frac{{\xi _{1} }}{{\omega _{1} }}} \right)} \mathord{\left/ {\vphantom {{\left( {\frac{{\xi _{2} }}{{\omega _{2} }} - \frac{{\xi _{1} }}{{\omega _{1} }}} \right)} {\left( {\frac{1}{{\omega _{2}^{2} }} - \frac{1}{{\omega _{1}^{2} }}} \right)}}} \right. \kern-\nulldelimiterspace} {\left( {\frac{1}{{\omega _{2}^{2} }} - \frac{1}{{\omega _{1}^{2} }}} \right)}} \hfill \\ & \beta = {{2\left( {\xi _{2} \omega _{2} - \xi _{1} \omega _{1} } \right)} \mathord{\left/ {\vphantom {{2\left( {\xi _{2} \omega _{2} - \xi _{1} \omega _{1} } \right)} {\left( {\omega _{2}^{2} - \omega _{1}^{2} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {\omega _{2}^{2} - \omega _{1}^{2} } \right)}} \hfill \\ \end{aligned} \right. $$
(21)

where \(\omega _{1}\) and \(\omega _{2}\) are the first two natural frequencies of CNC lathe spindle-bearing system, respectively.\(\xi _{1}\) and \(\xi _{2}\) are the corresponding damping ratios, respectively.

By using the restoring force method, the total nonlinear restoring forces and moments of bearings are added into the force vector of system. The specific parameters of CNC lathe spindle-bearing system can be obtained from the Tables 1 and 5 in this paper. Thus, the mathematical expression of system differential equation can be obtained. For this purpose, the ODE45 function (an explicit Rung-Kutta method) is used to solve Eq. (20) through MATLAB software.

3 Experimental validation

The experiment rig of CNC lathe spindle-bearing system shown in Fig. 7 is used to verify the feasibility of proposed model. The specific parameters of CNC lathe spindle-bearing system are listed in Tables 1 and 5. The schematic diagram of system experimental device is shown in Fig. 8. The rear bearing (NSK 7013C) of system is taken as the experimental object in this study. The infrared thermal imager (model: FLUKE Ti32) is used to monitor the temperature of housing at the tail of spindle. All tests are carried out in a laboratory with a controlled ambient temperature of 24–26 °C and a relative humidity of 20–25%.

Fig. 7
figure 7

Radial response experiment rig for CNC lathe spindle-bearing system

Full size image
Fig. 8
figure 8

Schematic diagram of CNC lathe spindle-bearing system experiment rig

Full size image

The spindle-bearing system is frequency swept by using an experimental device as shown in Fig. 7. The rotational speed of spindle starts from 0 r/min, and the rotational speed increment is 100 r/min and increases to 3000 r/min. The radial displacement data of spindle end are measured by using laser displacement sensor (model: optoNCDT2300-20) and LabView software in the computer. Fast Fourier Transform is carried out on the radial responses at each rotating speed to obtain their corresponding amplitudes, and all amplitudes are fitted to obtain the frequency response curve as shown in Fig. 9. Where \(\omega _{{a1}}\) = 250 r/min, \(\omega _{{b1}}\) = 318 r/min, \(\omega _{{n1}}\) = 280 r/min and \(\omega _{{a2}}\) = 530 r/min, \(\omega _{{b2}}\) = 600 r/min, \(\omega _{{n2}}\) = 560 r/min. The damping ratio is estimated by using the half power bandwidth method, which can be expressed as [50]:

$$ \xi _{i} = {{\left( {\omega _{{bi}} - \omega _{{ai}} } \right)} \mathord{\left/ {\vphantom {{\left( {\omega _{{bi}} - \omega _{{ai}} } \right)} {\omega _{{ni}} }}} \right. \kern-\nulldelimiterspace} {\omega _{{ni}} }} $$
(22)
Fig. 9
figure 9

Frequency response experimental curve of CNC lathe spindle

Full size image

The first two damping ratios of CNC lathe spindle-bearing system are \(\xi _{1}\) = 0. 1214 and \(\xi _{2}\) = 0. 0625, respectively.

As shown in Fig. 10, the trend of the theoretical values is the same as the experimental results. The deviation between theoretical values and experiment results is small and the coincidence degree is high, which proves that the thermal model adopted is reasonable for the thermal calculation of CNC lathe spindle-bearing system. With the spindle operating, the laser displacement sensor (model: optoNCDT2300-20) collects the radial response of spindle to be tested in real time.

Fig. 10
figure 10

Comparison of theoretical and experimental results of housing temperature

Full size image

Figure 11 depicts the comparison of simulation values and experimental results for the variation of spindle radial response with operation time at three different rotational speeds of 1500 r/min, 2000 r/min and 2500 r/min. With the increase of rotational speed, the radial response of spindle gradually increases and tends to be stable. Compared with the simulation values without thermal effect, the experimental results are closer to the simulation values with thermal effect, which proves the correctness of proposed model in this study.

Fig. 11
figure 11

Comparison of simulation and experiment results of radial response of CNC lathe spindle-bearing system: a 1500 r/min; b 2000 r/min; c 2500 r/min

Full size image

4 Results and discussion

4.1 The influence of rotational speed and preload on contact angle and contact load

Figure 12 shows the variation of contact angle and contact load with rotational speed when the bearing preload is 500 N with or without thermal deformation. The contact angle and contact load considering thermal deformation are smaller than those without thermal deformation. Because the thermal deformation of bearing parts makes the radial distance between the curvature centers of inner and outer raceways of bearing large, this causes a decrease in the contact angle. Meanwhile, due to the temperature rise of bearing parts is uneven and the size of outer raceway is larger than that of inner raceway, which lead to a negative total thermal deformation, resulting in a reduction in the contact load between balls and raceways.

Fig. 12
figure 12

Relationship between spindle speed and contact angle and contact load of bearing

Full size image

In Fig. 13, it can be seen the variation of contact angle and contact load with preload when the rotating speed is 4000 r/min with and without thermal deformation. The contact angle between balls and inner and outer raceways with thermal deformation is smaller than without thermal deformation. The contact angle of inner raceway decreases with the increase of preload, while the contact angle of outer raceway is opposite. This is mainly because the effect of centrifugal force is weakened by preload. The contact load between balls and inner and outer raceways with thermal deformation is smaller than that without thermal deformation, because the total thermal deformation between balls and inner and outer raceways is negative, which will make balls and inner and outer raceways relaxed and lead to a decrease in contact load.

Fig. 13
figure 13

Relationship between preload and contact angle and contact load of bearing

Full size image

4.2 The influence of rotational speed and preload on bearing stiffness

The bearing stiffness will also be changed by the variation of contact angle and contact load between balls and inner and outer raceways. Figure 14 shows the variation trend of bearing stiffness with spindle speed when the preload is set to 500 N. With the increase of spindle speed, the bearing stiffness decreases gradually. This reflects the softening effect of rotational speed on stiffness. The bearing stiffness considering thermal deformation is smaller than that without thermal deformation. As can be seen from Fig. 12c and d, the contact load between balls and inner and outer raceways decreases by considering the thermal deformation of bearing parts, which leads to the decrease of bearing stiffness.

Fig. 14
figure 14

Relationship between spindle speed and bearing stiffness

Full size image

According to the variation trend of bearing stiffness with preload when the rotating speed is set to 4000 r/min. It can be seen from Fig. 15, the greater the bearing preload, the greater the bearing stiffness. However, the bearing stiffness considering thermal deformation is smaller than that without considering thermal deformation. The same reason is that the bearing parts generate thermal deformation. However, the total thermal deformation of balls and inner and outer raceways is negative, which results in lowing the bearing stiffness.

Fig. 15
figure 15

Relationship between preload and bearing stiffness

Full size image

4.3 The stability analysis of system

As shown in Fig. 16, Lyapunov exponent is used to further study the influence of thermal effect on the stability of response of spindle-bearing system of CNC lathe. The Lyapunov exponents were similar to each other. When the thermal effect is not taken into account, the chaotic motion of the system appears between 1400 r /min and 1600 r /min. When thermal effects are taken into account, the chaotic motion of the system shifts to between 1200 r /min and 1800 r /min. This indicates that after considering the thermal effect, with the increase of the rotational speed, the chaotic motion appears at an earlier rotational speed and the interval of the chaotic region increases.

Fig. 16
figure 16

The largest Lyapunov exponent of the CNC lathe spindle-bearing system

Full size image

4.4 The influence of rotational speed on dynamic characteristics of system without thermal effect

The pulley eccentricity is set to 5 um, and the rotational speed of spindle is limited to 1790 r /min to 2090 r /min without considering the thermal effect of spindle-bearing system of CNC lathe. The bifurcation diagrams and 3-D spectrum plots of shaft end of CNC lathe spindle-bearing system with five DOF are shown in Figs. 17, 18, 19, 20 and 21. The comparison of five directional bifurcation diagrams and three-dimensional spectrum plots show that the variation trend of motion state and frequency composition at the shaft end are basically the same, but the response amplitudes are different in different degrees of freedom.

Fig. 17
figure 17

Bifurcation diagram and 3-D spectrum of horizontal radial of shaft end in the spindle-bearing system. a Bifurcation diagram, b 3-D spectrum plot

Full size image
Fig. 18
figure 18

Bifurcation diagram and 3-D spectrum of vertical radial of shaft end in the spindle-bearing system. a Bifurcation diagram, b 3-D spectrum plot

Full size image
Fig. 19
figure 19

Bifurcation diagram and 3-D spectrum of axial of shaft end in the spindle-bearing system. a Bifurcation diagram, b 3-D spectrum plot

Full size image
Fig. 20
figure 20

Bifurcation diagram and 3-D spectrum of horizontal radial torsion of shaft end in the spindle-bearing system. a Bifurcation diagram, b 3-D spectrum plot

Full size image
Fig. 21
figure 21

Bifurcation diagram and 3-D spectrum of vertical radial torsion of shaft end in the spindle-bearing system. a Bifurcation diagram, b 3-D spectrum plot

Full size image

In order to study the vibration characteristics of shaft end of CNC lathe spindle-bearing system, the horizontal radial degree of freedom of shaft end will be regarded as an example in the following. The nonlinear dynamic behaviors of system responses are investigated through the time history, frequency spectrum, phase plane diagram and Poincare section. With the increase of rotational speed, the system experiences chaotic motion, single-periodic, 7T-periodic, 4T-periodic, quasi-periodic, 2T-periodic motions shown in Figs. 22, 23, 24, 25, 26, and 27. In Fig. 22, chaotic motion can be seen based on the time domain response is no longer periodically changing, the frequency domain presents continuous spectrum, and the phase diagram and Poincare section are full of a large number of discrete points. The system presents single-periodic, 7T-periodic, 4T-periodic, and 2T-periodic motions, which can be determined by the frequency demultiplication component and discrete Poincare points in Figs. 23, 24, 25 and 27. The quasi-periodic motion appears at rotational speed reaches 2800 r/min; it can be seen from the continuous frequency components in the spectrum plot and a number of Poincare points form a closed loop in Fig. 26.

Fig. 22
figure 22

Nonlinear responses at \(\omega\) = 1400 r/min: a time history, b frequency spectrum, c phase plane diagram and Poincare section

Full size image
Fig. 23
figure 23

Nonlinear responses at \(\omega\) = 1800 r/min: a time history, b frequency spectrum, c phase plane diagram and Poincare section

Full size image
Fig. 24
figure 24

Nonlinear responses at \(\omega\) = 2720 r/min: a time history, b frequency spectrum, c phase plane diagram and Poincare section

Full size image
Fig. 25
figure 25

Nonlinear responses at \(\omega\) = 2754 r/min: a time history, b frequency spectrum, c phase plane diagram and Poincare section

Full size image
Fig. 26
figure 26

Nonlinear responses at \(\omega\) = 2800 r/min: a time history, b frequency spectrum, c phase plane diagram and Poincare section

Full size image
Fig. 27
figure 27

Nonlinear responses at \(\omega\) = 3900 r/min: a time history, b frequency spectrum, c phase plane diagram and Poincare section

Full size image

4.5 The dynamic characteristics of system with thermal effect

4.5.1 The influence of rotational speed on dynamic characteristics of system

In order to investigate the influence of thermal effect on CNC lathe spindle-bearing system, the bifurcation diagrams and 3-D spectrum plots of five DOF of shaft end are employed shown in Figs. 28, 29, 30, 31 and 32. Similarly, the pulley eccentricity is set to 5 um and the rotational speed of spindle is limited to 1790 r/min to 2090 r/min. The variation trend of motion state and frequency composition at the shaft end are similar, but the response amplitudes are different in different degrees of freedom. Comparing with the above situation without thermal effect shown in Figs. 17, 18, 19, 20 and 21, the response amplitude of system considering thermal effect is significantly larger than the system without thermal effect. This is due to thermal effect causes bearing stiffness to decrease, which increases the response of system.

Fig. 28
figure 28

Bifurcation diagram and 3-D spectrum of horizontal radial of shaft end in the spindle-bearing system. a Bifurcation diagram, b 3-D spectrum plot

Full size image
Fig. 29
figure 29

Bifurcation diagram and 3-D spectrum of vertical radial of shaft end in the spindle-bearing system. a Bifurcation diagram, b 3-D spectrum plot

Full size image
Fig. 30
figure 30

Bifurcation diagram and 3-D spectrum of axial of shaft end in the spindle-bearing system. a Bifurcation diagram, b 3-D spectrum plot

Full size image
Fig. 31
figure 31

Bifurcation diagram and 3-D spectrum of horizontal radial torsion of shaft end in the spindle-bearing system. a Bifurcation diagram, b 3-D spectrum plot

Full size image
Fig. 32
figure 32

Bifurcation diagram and 3-D spectrum of vertical radial torsion of shaft end in the spindle-bearing system. a Bifurcation diagram, b 3-D spectrum plot

Full size image

In order to investigate the influence of thermal effect on the vibration characteristics of shaft end of CNC lathe spindle-bearing system, the horizontal radial degree of freedom of shaft end taken as an example for analysis. Figures 33, 34, 35, 36, 37, 38 and 39 demonstrate the time history curve, frequency spectrum plot, phase plane diagrams and Poincare sections under different rotational speeds. With the increase of rotational speed, the system exhibits single-periodic, 3T-periodic, 5T-periodic, chaotic motion, 25T-periodic, quasi-periodic and 2T-periodic motions. The 5T-periodic motion occurs as shown in Fig. 35 when rotational speed is increased to 1058 r/min, which can be determined by \({f \mathord{\left/ {\vphantom {f 5}} \right. \kern-\nulldelimiterspace} 5}\) frequency demultiplication component and 5 discrete Poincare points. The chaotic motion in Fig. 36 is determined based on the time-domain response without periodic changes, the continuous spectral components and the phase diagram and Poincare section are full of a large number of discrete points. In the same way, we can identify the motions in Figs. 33, 34, 37 and 39 as single periodic, 3T-periodic, 25T-periodic and 2T-periodic respectively. As shown in the frequency spectrum and Poincare section in Fig. 38, when the rotation speed is 3110 rad/min, an obvious quasi-periodic motion appears, which can be seen from the continuous frequency components and a number of Poincare points form a closed loop.

Fig. 33
figure 33

Nonlinear responses at \(\omega\) = 1000 r/min: a time history, b frequency spectrum, c phase plane diagram and Poincare section

Full size image
Fig. 34
figure 34

Nonlinear responses at \(\omega\) = 1056 r/min: a time history, b frequency spectrum, c phase plane diagram and Poincare section

Full size image
Fig. 35
figure 35

Nonlinear responses at \(\omega\) = 1058 r/min: a time history, b frequency spectrum, c phase plane diagram and Poincare section

Full size image
Fig. 36
figure 36

Nonlinear responses at \(\omega\) = 1800 r/min: a time history, b frequency spectrum, c phase plane diagram and Poincare section

Full size image
Fig. 37
figure 37

Nonlinear responses at \(\omega\) = 2996 r/min: a time history, b frequency spectrum, c phase plane diagram and Poincare section

Full size image
Fig. 38
figure 38

Nonlinear responses at \(\omega\) = 3110 r/min: a time history, b frequency spectrum, c phase plane diagram and Poincare section

Full size image
Fig. 39
figure 39

Nonlinear responses at \(\omega\) = 3732 r/min: a time history, b frequency spectrum, c phase plane diagram and Poincare section

Full size image

4.5.2 The influence of pulley eccentricity on dynamic characteristics of system

From the model of CNC lathe spindle-bearing system considering thermal effect, it can be found that the eccentric load of pulley is used as excitation, then the eccentricity will affect the dynamic behaviors of system. Therefore, the range of eccentricity is set at 2 to 200 um to investigate the nonlinear characteristics of system. Figures 40, 41, 42 and 43 depict the horizontal radial bifurcation diagrams and 3-D spectrum diagrams of shaft end at rotational speeds of 1000 r/min, 2000 r/min, 3000 r/min, 4000 r/min, respectively. With the increase of spindle speed, the vibration system presents single-periodic, double-periodic, multiple-periodic and quasi-periodic motions.

Fig. 40
figure 40

Bifurcation diagram and 3-D spectrum of horizontal radial torsion of shaft end in the spindle-bearing system at \(\omega\) = 1000 r/min. a Bifurcation diagram, b 3-D spectrum plot

Full size image
Fig. 41
figure 41

Bifurcation diagram and 3-D spectrum of horizontal radial torsion of shaft end in the spindle-bearing system at \(\omega\) = 2000 r/min. a Bifurcation diagram, b 3-D spectrum plot

Full size image
Fig. 42
figure 42

Bifurcation diagram and 3-D spectrum of horizontal radial torsion of shaft end in the spindle-bearing system at \(\omega\) = 3000 r/min. a Bifurcation diagram, b 3-D spectrum plot

Full size image
Fig. 43
figure 43

Bifurcation diagram and 3-D spectrum of horizontal radial torsion of shaft end in the spindle-bearing system at \(\omega\) = 4000 r/min. a Bifurcation diagram, b 3-D spectrum plot

Full size image

Figures 44, 45, 46, 47 and 48 depict the change of motion state of shaft end of CNC lathe spindle-bearing system shown in Fig. 43 at different eccentricity amounts when the spindle speed is 4000 r/min. The system will undergo single-periodic, 2T-periodic, 3T-periodic, 14-periodic and quasi-periodic motions accordingly under the eccentricity is 2 um, 76 um, 112 um, 114 um and 190 um, respectively.

Fig. 44
figure 44

Nonlinear responses at(Ec = 2 um): a time history, b frequency spectrum, c phase plane diagram and Poincare section

Full size image
Fig. 45
figure 45

Nonlinear responses at(Ec = 76 um): a time history, b frequency spectrum, c phase plane diagram and Poincare section

Full size image
Fig. 46
figure 46

Nonlinear responses at(Ec = 112 um): a time history, b frequency spectrum, c phase plane diagram and Poincare section

Full size image
Fig. 47
figure 47

Nonlinear responses at(Ec = 114 um): a time history, b frequency spectrum, c phase plane diagram and Poincare section

Full size image
Fig. 48
figure 48

Nonlinear responses at(Ec = 190 um): a time history, b frequency spectrum, c phase plane diagram and Poincare section

Full size image

4.5.3 The influence of bearing preload on dynamic characteristics of system

Bearing preload will affect the contact deformation and load distribution of bearing parts, thus affecting the contact angle between balls and inner and outer raceways, bearing heat generation, bearing stiffness and even the dynamic behaviors of the whole system. Therefore, the preload will play an important role in CNC lathe spindle-bearing system. In order to investigate the dynamic nonlinear characteristics of system, the range of preload is set from 0 to 600 N. Figures 49, 50, 51 and 52 depict the horizontal radial bifurcation diagrams and 3-D spectrum diagrams of shaft end at rotational speeds of 1000 r/min, 2000 r/min, 3000 r/min, 4000 r/min, respectively. With the increasing of spindle speed, the vibration system presents rich nonlinear behaviors.

Fig. 49
figure 49

Bifurcation diagram and 3-D spectrum of horizontal radial torsion of shaft end in the spindle-bearing system at \(\omega\) = 1000 r/min. a Bifurcation diagram, b 3-D spectrum plot

Full size image
Fig. 50
figure 50

Bifurcation diagram and 3-D spectrum of horizontal radial torsion of shaft end in the spindle-bearing system at \(\omega\) = 2000 r/min. a Bifurcation diagram, b 3-D spectrum plot

Full size image
Fig. 51
figure 51

Bifurcation diagram and 3-D spectrum of horizontal radial torsion of shaft end in the spindle-bearing system at \(\omega\) = 3000 r/min. a Bifurcation diagram, b 3-D spectrum plot

Full size image

Figures 53, 54, 55, 56 and 57 depict the change of the motion state of shaft end shown in Fig. 52 at different preloads when the spindle speed is 4000 r/min. The system will undergo single-periodic, 2T-periodic, 4T-periodic, 5T-periodic and quasi-periodic motions accordingly, when the preload is 60 N, 117 N, 136 N, 140 N and 300 N, respectively.

Fig. 52
figure 52

Bifurcation diagram and 3-D spectrum of horizontal radial torsion of shaft end in the spindle-bearing system at \(\omega\) = 4000 r/min. a Bifurcation diagram, b 3-D spectrum plot

Full size image
Fig. 53
figure 53

Nonlinear responses at (Preload = 60 N): a time history, b frequency spectrum, c phase plane diagram and Poincare section

Full size image
Fig. 54
figure 54

Nonlinear responses at (Preload = 117 N): a time history, b frequency spectrum, c phase plane diagram and Poincare section

Full size image
Fig. 55
figure 55

Nonlinear responses at (Preload = 201 N): a time history, b frequency spectrum, c phase plane diagram and Poincare section

Full size image
Fig. 56
figure 56

Nonlinear responses at (Preload = 207 N): a time history, b frequency spectrum, c phase plane diagram and Poincare section

Full size image
Fig. 57
figure 57

Nonlinear responses at (Preload = 450 N): a time history, b frequency spectrum, c phase plane diagram and Poincare section

Full size image

5 Conclusions

The dynamic performance of spindle-bearing system is very important to the machining accuracy and working stability of CNC lathe. Therefore, a comprehensive dynamic model of CNC lathe spindle-bearing system considering thermal effect is proposed to analysis the dynamic characteristics of system. The experimental results are in good agreement with the numerical simulation results, which verifies the correctness of the proposed model. The effects of spindle speed, pulley eccentricity and bearing preload on the dynamic behaviors of system are analyzed. In addition, the effects of rotational speed and preload on the contact angle, contact load and stiffness of bearings are also fully studied. Some conclusions are exhibited as follows:

The contact angle and contact load between balls and inner and outer raceways considering thermal effect are smaller than those without thermal effect. The bearing stiffness considering thermal effect is smaller than that without thermal effect. These are all attributed to the thermal deformation of bearing parts which makes the radial distance between the curvature centers of inner and outer raceways of bearing large and the temperature rise of bearing parts is uneven.

The response of system considering thermal effect is larger than the system without thermal effect, which is due to the decrease of bearing stiffness considering thermal effect.

In the whole range of rotational speed, the nonlinear characteristics of system considering thermal effect are richer than the system without considering thermal effect. Moreover, after the thermal effect is taken into account, the rotation speed of chaotic motion is advanced, and the interval of chaotic region is increased.

The rotational speed, pulley eccentricity and preload have great influence on the nonlinear characteristics of system which can be studied by means of time history curve, 3-D frequency spectrum curve, phase diagram, Poincare section and bifurcation diagram, among which pulley eccentricity and preload are the most sensitive to the influence of system.