1 Introduction

Permanent magnet synchronous motor (PMSM) has been widely used in electric vehicle and other fields because of its high power density, high power factor and good reliability [1]. In addition, permanent magnet synchronous motor has the highest power density, the efficiency can reach 97%, and it can output the maximum power and acceleration for the electric vehicle. In the high-performance applications, field-oriented control with double-loop cascade structure is often adopted, in which the outer speed loop and the inner current loop typically adopt conventional proportional integral(PI) controllers [2, 3]. However, PMSM is a multivariable and strongly coupled nonlinear system, and the motor drive system often faces the problems of load disturbance and uncertain parameters in actual operation. The conventional method may not meet the actual requirements. Recently, predictive control [4], active disturbance rejection control [5], backstepping control [6], sliding mode control [7], intelligent control [8] and disturbance attenuation technique [9] have been presented for PMSM drive system, and they can improve motor control performance in different ways.

Sliding mode control (SMC) has been proved to be a potentially useful approach in complex nonlinear system, and it shows outstanding advantages in strong robustness, quick response and simple implementation [10,11,12]. However, due to the existence of the sliding mode switching function, the large switching gain, which is needed to ensure the robustness, will produce the chattering problem in SMC. To reduce the chatting, the boundary layer integral sliding mode control technique is proposed in [13], but this method will affect the robustness of the drive system. To improve dynamic response performance and robustness, the sliding mode control method based on the new exponential reaching law is proposed for the speed control of PMSM in [14]. A new sliding mode controller with extended sliding mode disturbance observer is designed to optimize the speed-control performance of PMSM in [15], and the designed reaching law can dynamically adapt to the variations of the controlled system. Considering the large chattering phenomenon caused by high switching gain, sliding-mode control methods based on extended state observer is proposed to the speed control of PMSM in [16]. The sliding mode controller is used to realize the feedback tracking control, and the extended state observer is used to estimate the disturbance. In [17], an integral fixed-time sliding mode controller with disturbance compensation technology is proposed for the speed regulation of PMSM. The sliding mode control and deadbeat controller are employed to the speed and current control of PMSM in [18], respectively, and to suppress the disturbance in the drive system, the high-order sliding mode observer is designed. To realize finite-time convergence, the terminal sliding mode controllers based on a non-singular terminal sliding mode manifold are designed for the speed loop in [19-21], in which the motor speed can reach the reference value in finite time, and a faster convergence speed can be achieved. Meanwhile, to further improve the anti-disturbance performance, the disturbance observer or extended state observer is introduced to the sliding mode controller. In [22, 23], the position or current control methods based on sliding mode control have been presented for PMSM drive. In addition, the sliding mode control can also be used for the sensorless control of PMSM [24, 25].

The sliding mode control methods above are usually used in the speed loop or current loop through replacing the conventional proportional integral controller for PMSM drives. In this structure, the controller parameters should be tuned separately from the inner to the outer loop. And to avoid ringing and large overshoots, bandwidth of cascade controllers is often limited. Thus, a fairly modest speed control dynamic is achieved [26, 27]. With the rapid development of micro-computer technology, the control periods between the speed loop and current loop of PMSM gradually decreased, even have been disappeared, therefore, the cascade control with the speed loop and current loop is no longer necessary for PMSM drive system [28].

An alternative approach is the speed and current single-loop controller with non-cascade structure. In this method, the speed loop controller and q-axes current controller are designed by one controller. Compared with the sliding mode control with cascade structure for PMSM, there are few researches about non-cascade sliding mode control strategy. A non-cascade speed controller is designed in [13], and a input-output linearization method is adopted in the paper. In [29], a terminal sliding mode single-loop control method is proposed, but the feedback linearization technology is also needed in the design process of the controller, the controller is complex and only simulation results are provided. In [30], a non-cascade backstepping sliding mode controller is proposed for PMSM, and a three-order extended state observer is designed to estimate the disturbance. The linear sliding mode surface is designed, and the finite-time convergence cannot be guaranteed. In [31], by considering the lumped disturbance in the system, a discrete-time sliding mode controller with disturbance observer is proposed for the non-cascade control of PMSM.

Meanwhile, from the literatures above, to further improve the robustness and reduce the chatting of sliding mode control, a kind of simple and effective method is to use disturbance estimation technology. Through estimating the lumped disturbance in the system, the estimated disturbance is used for the feed-forward compensation control. The disturbance estimation and attenuation techniques for PMSM drives have been summarized in [9], such as, extended sliding mode disturbance observer [15, 18], extended state observer [16, 21] and disturbance observer [19, 20, 32, 33].

In this paper, a novel speed and current control method is proposed for PMSM drives with matched and mismatched disturbance. The major contribution of this work is: (1) a continuous integral-type terminal SMC method (ITSMC) is proposed for the speed control of PMSM. Different from the conventional controller, the controller adopts the single-loop control, where the speed loop and q-axes current loop controller are designed together. (2) The lumped disturbance (matched and mismatched disturbance) is introduced to the design of sliding mode surface, and a new sliding mode controller is constructed. A nonlinear disturbance observer is designed to estimate the lumped disturbance, and the anti-disturbance performance is effectively improved. (3) The experiment based on the proposed method is completed, and the comparison of the results indicates that the proposed control methods have excellent robustness and dynamic behavior.

This paper is organized as follows. In Sect. 2, the mathematical model of PMSM considering the lumped disturbance is introduced. In Sect. 3, the novel SMC speed controller is proposed. In Sect. 4, the composite controller with disturbance observer is constructed. The corresponding experimental results are demonstrated in Sect. 5. The conclusion is given in Sect. 6.

2 The mathematical model of PMSM

The dynamic model of PMSM in d-q synchronous reference frame can be written as [13, 30]

$$\begin{aligned} \left\{ \begin{array}{l} \frac{{\mathrm{{d}}{i_d}}}{{\mathrm{{d}}t}} = \frac{{ - {R_s}{i_d}}}{{{L_d}}} + {n_p}\omega \frac{{{L_q}}}{{{L_d}}}{i_q} + \frac{1}{{{L_d}}}{u_d} - {f_d}\\ \frac{{\mathrm{{d}}{i_q}}}{{\mathrm{{d}}t}} = \frac{{ - {R_s}{i_q}}}{{{L_q}}} - \frac{{{n_p}\omega {L_d}{i_d}}}{{{L_q}}} - \frac{{{n_p}\omega \varPhi }}{{{L_q}}} + \frac{1}{{{L_q}}}{u_q} - {f_q}\\ \frac{{d\omega }}{{dt}} = \frac{{{T_e}}}{J} - \frac{{{T_L}}}{J} - {f_w} \end{array} \right. \end{aligned}$$
(1)

The electromagnetic torque in d-q synchronous reference frame is

$$\begin{aligned} {T_e} = {n_p}\left[ {({L_d} - {L_q}){i_d}{i_q} + \varPhi {i_q}} \right] \end{aligned}$$
(2)

where \({L_d}\) and \({L_q}\) represent d-axes and q-axes stator inductances, respectively. \({i_d}\) and \({i_q}\) are the stator current. \({u_d}\) and \({u_q}\) are the stator input voltage in dq-axes reference frame. \({R_s}\) is the per-phase stator resistance. \({n_p}\) is the number of pole pairs. \(\omega \) is the mechanical angular speed of the rotor. \(\varPhi \) is the rotor flux. J is the moment of inertia. \({T_e}\) is the electromagnetic torque. \({T_L}\) is the load torque. \({f_d}\) , \({f_q}\) and \({f_w}\) represent the uncertainties, which are caused by parameter variations and model uncertainties, and they are assumed to be bounded and changed slowly in the system.

For the surface mounted PMSM, the d-axes inductance is considered equal to q-axes inductance(\({L_d} = {L_q}\)), thus the electromagnetic torque can be expressed as \({T_e} = {n_p}\varPhi {i_q}\). From the third equation of (1), the motion equation can be simplified as

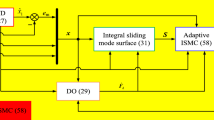
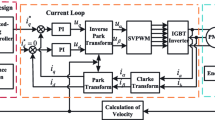
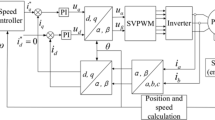
$$\begin{aligned} \frac{{d\omega }}{{dt}} = \frac{{{n_p}\varPhi {i_q}}}{J} - \frac{{{T_L}}}{J} - {f_w} \end{aligned}$$
(3)

The control structure of PMSM speed drive system based on conventional PI controller and the proposed method are shown in Fig. 1 and Fig. 2, respectively. Different from the classical double-loop control method with the inner q-axes current loop and the outer speed loop in Fig. 1, the novel controller adopts the speed and current single-loop control with continuous integral-type SMC and disturbance observer. In addition, the control system includes a surface mounted PMSM, an inverter, space vector pulse width modulation(SVPWM) and coordinate transformation modules, d-axes current controller with PI method. The d-axes reference current \(i_d^*\) is usually set to zero to ensure a constant flux operating condition [34]. \({\omega ^*}\) is the reference speed.

Fig. 1
figure 1

The control structure of PMSM speed drive system with PI control

Full size image
Fig. 2
figure 2

The control structure of PMSM speed drive system with the proposed method

Full size image

3 Design of the novel SMC controller

Given the model of PMSM, the objective of this paper is to devise a novel motor control strategy with continuous adaptive integral-type terminal sliding mode control to realize the speed tracking control of PMSM drive, and the controller adopts the non-cascade structure.

Firstly, an equivalent model of (1) and (3) is constructed. Define \({{x'}_1} = {\omega ^*} - \omega \) and \({{x'}_2} = {i_q}\), the following can be derived as

$$\begin{aligned} \left\{ \begin{array}{l} {{\dot{x}'}_1} = {{{\dot{\omega }} }^*} - {\dot{\omega }} = {{{\dot{\omega }} }^*} - \frac{{{n_p}\varPhi {i_q}}}{J} + \frac{{{T_L}}}{J} + {f_w}\\ {{\dot{x}'}_2} = \frac{{ - {R_s}{i_q}}}{{{L_q}}} - \frac{{{n_p}\omega {L_d}{i_d}}}{{{L_q}}} - \frac{{{n_p}\omega \varPhi }}{{{L_q}}} + \frac{1}{{{L_q}}}{u_q} - {f_q} \end{array} \right. \end{aligned}$$
(4)

The model (4) can be further expressed as

$$\begin{aligned} \left\{ \begin{array}{l} {{\dot{x}'}_1} = {k_{11}}{{x'}_2} + {d_1}\\ {{\dot{x}'}_2} = {k_{21}}{{x'}_1} + {k_{22}}{{x'}_2} + {k_{23}}{u_q} + a(x) + {{d'}_2} \end{array} \right. \end{aligned}$$
(5)

where \({k_{11}} = - \frac{{{n_p}\varPhi }}{J}\), \({k_{21}} = \frac{{{n_p}{L_d}{i_d}}}{{{L_q}}} + \frac{{{n_p}\varPhi }}{{{L_q}}}\), \({k_{22}} = - \frac{{{R_s}}}{{{L_q}}}\), \({k_{23}} = \frac{1}{{{L_q}}}\), \(a(x) = - \frac{{{n_p}{L_d}{i_d} + {n_p}\varPhi }}{{{L_q}}}{\omega ^*}\), \({d_1} = {{\dot{\omega }} ^*} + \frac{{{T_L}}}{J} + {f_w}\) and \({d'_2} = - {f_q}\).

Then, define the state variables as \({x_1} = {x'_{\mathrm{{1}}}}\), \({x_2} = {k_{11}}{x'_2}\). From (5), a second-order system with matched and mismatched disturbance is derived

$$\begin{aligned} \left\{ \begin{array}{l} {{\dot{x}}_1} = {x_2} + {d_1}\\ {{\dot{x}}_2} = f(x) + bu + {d_2} \end{array} \right. \end{aligned}$$
(6)

where \(f(x) = {k_{11}}{k_{21}}{x_1} + {k_{22}}{x_2} + {k_{11}}a(x)\), \(b = {k_{11}}{k_{23}}\) is input coefficient. \(u = {u_q}\) is the sliding mode control input to be designed. \({d_1}\) and \({d_2} = {k_{11}}{d'_2}\) are the disturbance. \({d_1}\) represents the mismatched disturbance, and \({d_2}\) represents the matched disturbance.

Since the disturbance is mainly caused by parameter uncertainty and external disturbance in PMSM drive, and the change of these disturbance is relatively slow [19, 35], it is assumed that \(\left| {{d_1}} \right| \le {D_1}\), \(\left| {{d_2}} \right| \le {D_2}\) and \(\left| {{{\dot{d}}_1}} \right| \le {D_{11}}\), \(\left| {{{\dot{d}}_2}} \right| \le {D_{22}}\), where \({D_1}\), \({D_2}\) and \({D_{11}}\), \({D_{12}}\) are positive.

Next, according to (6), the sliding mode speed controller will be designed. Firstly, a sliding mode function is designed as \({s_0} = {\dot{x}_1} + {c_0}{x_1}\), then

$$\begin{aligned} {s_0} = {x_2} + {d_1} + {c_0}{x_1} \end{aligned}$$
(7)

Taking a Lyapunov candidate function as \({V_0} = \frac{1}{2}s_0^2\), and the differential of \({V_0}\) with respect to time is

$$\begin{aligned} {\dot{V}_0} = {s_0}{\dot{s}_0} = {s_0}({\dot{x}_2} + {\dot{d}_1} + {c_0}{\dot{x}_1}) \end{aligned}$$
(8)

A virtual control input needs to be designed for the reference of \({x_2}\), According to (8), a virtual control input is chosen as \(x_2^* = - {c_0}{x_1} - \int _0^t {{k_0}{\mathrm{sgn}} {s_0}d\tau } \), and substitute it into \({\dot{V}_0}\)

$$\begin{aligned} {\dot{V}_0} = - {k_0}{s_0}{\mathrm{sgn}} {s_0} + {s_0}{\dot{d}_1} \le - {k_0}\left| {{s_0}} \right| + {D_{11}}\left| {{s_0}} \right| \end{aligned}$$
(9)

If \({k_0} > {D_{11}}\) is chosen in the controller, then \({\dot{V}_0} \le 0\) can be derived. Consequently, \({x_1}\) will be asymptotically converged to zero [36].

Then, a sliding mode control input u should be designed to force \({x_2}\) to track \(x_2^*\). The tracking error of \({x_2}\) is defined as \({e_2} = {x_2} - x_2^*\), and the differential of \({e_2}\) with respect to time is

$$\begin{aligned} {{\dot{e}}_2}= & {} {{\dot{x}}_2} - \dot{x}_2^*\nonumber \\= & {} f(x) + bu + {d_2} - \dot{x}_2^*\nonumber \\= & {} f(x) + bu + {d_2} + {c_0}{{\dot{x}}_1} + {k_0}{\mathrm{sgn}} {s_0}\nonumber \\= & {} f(x) + bu + {d_2} + {c_0}{x_2} + {c_0}{d_1} + {k_0}{\mathrm{sgn}} {s_0} \end{aligned}$$
(10)

From (10), in order to obtain the sliding mode control law, a non-singular terminal sliding mode manifold is chosen as

$$\begin{aligned} {s_1} = {\dot{e}_2} + {c_1}{e_2}^{{{{p_1}} / {{q_1}}}} \end{aligned}$$
(11)

where \({c_1} > 0\), \({p_1}\) and \({p_2}\) are positive odd integers, and \(1< {{{p_1}} / {{q_1}}} < 2\).

Substituting (10) into (11)

$$\begin{aligned} {s_1}= & {} {{\dot{e}}_2} + {c_1}{e_2}^{{{{p_1}} /{{q_1}}}}\nonumber \\= & {} f(x) + bu + {d_2} + {c_0}{x_2} + {c_0}{d_1} \nonumber \\&+ {k_0}{\mathrm{sgn}} {s_0} + {c_1}{e_2}^{{{{p_1}} / {{q_1}}}} \end{aligned}$$
(12)

Finally, the continuous integral sliding mode control law can be derived as

$$\begin{aligned} {u_q} = u = - \frac{1}{b}\left[ \begin{array}{l} f(x) + {c_0}{x_2} + {k_0}{\mathrm{sgn}} {s_0}\\ + {c_1}{e_2}^{{{{p_1}} / {{q_1}}}} + \int _0^t {{k_1}{\mathrm{sgn}} ({s_1})d\tau } \end{array} \right] \end{aligned}$$
(13)

Considering the follow Lyapunov function \({V_1} = \frac{1}{2}{s_1}^2\), \({\dot{V}_1}\) can be written as

$$\begin{aligned} {{\dot{V}}_1}= & {} - {k_1}{s_1}{\mathrm{sgn}} {s_1} + {s_1}({{\dot{d}}_2} + {c_0}{{\dot{d}}_1})\nonumber \\&\le - {k_1}\left| {{s_1}} \right| + \left| {{s_1}} \right| ({D_{22}} + {c_0}{D_{11}}) \le 0 \end{aligned}$$
(14)

Similarly, if \({k_1} \ge {D_{22}} + {c_0}{D_{11}}\) is chosen, \({\dot{V}_1} \le 0\) can be ensured. Therefore, the control system with the proposed continuous integral-type sliding mode controller is asymptotically stable. To ensure the stability and strength the robustness of the system, the larger sliding mode switching gains \({k_0}\), \({k_1}\) should be designed. Inevitably, the chattering of the control system will be increased. Therefore, the switching gains should be given in a reasonable range.

4 Design of composite controller with disturbance observer

The external disturbance and parameter uncertainties are real existence in the drive system. To further improve the anti-disturbance performance, a nonlinear disturbance observer, which is used to estimate the matched and mismatched disturbance in the system, is introduced to the ITSMC in this part. In order to complete the controller, the design of sliding mode controller needs to be improved, and the detailed design process can be divided into the following two steps.

(1) According to the design steps of the upper sliding mode controller, a virtual control input is afresh chosen as \(x_2^* = - {c_0}{x_1} - {d_1} - \int _0^t {{k_0}{\mathrm{sgn}} {s_0}d\tau } \). Obviously, the mismatched disturbance is included in the virtual input. And substitute it into \(\dot{V_0}\) in (8), then \({\dot{V}_0} = - {k_0}{s_0}{\mathrm{sgn}} {s_0} \le 0\) can be obtained.

Then, the differential of tracking error \({e_2}\) with respect to time can be expressed as

$$\begin{aligned} {{\dot{e}}_2}= & {} {{\dot{x}}_2} - \dot{x}_2^*\nonumber \\= & {} f(x) + bu + {d_2} + {c_0}{x_2} + {c_0}{d_1} + {{\dot{d}}_1} + {k_0}{\mathrm{sgn}} {s_0}\nonumber \\ \end{aligned}$$
(15)

According to the selected sliding mode manifold \({s_1}\) in (11), it can be rewritten as

$$\begin{aligned} {s_1}= & {} {{\dot{e}}_2} + {c_1}{e_2}^{{{{p_1}} / {{q_1}}}}\nonumber \\= & {} f(x) + bu + {d_2} + {c_0}{x_2} + {c_0}{d_1}\nonumber \\&+ {{\dot{d}}_1} + {k_0}{\mathrm{sgn}} {s_0} + {c_1}{e_2}^{{{{p_1}} / {{q_1}}}} \end{aligned}$$
(16)

Then, the sliding mode control law can be redesigned as

$$\begin{aligned}&{u_q} = u \nonumber \\&\quad =- \frac{1}{b}\left[ \begin{array}{l} f(x) + {d_2} + {c_0}{x_2} + {c_0}{d_1}\\ + {{\dot{d}}_1} + {k_0}{\mathrm{sgn}} {s_0}\\ + {c_1}{e_2}^{{{{p_1}} / {{q_1}}}} + \int _0^t {{k_1}{\mathrm{sgn}} ({s_1})d\tau } \end{array} \right] \end{aligned}$$
(17)

From the virtual control input and the control law (17), the disturbance information exists in the designed controller. Although sliding mode control has a certain robustness for the disturbance by designing a large sliding mode switching gain, it may not satisfy the actual requirements in some applications. An alternative solution for the disturbance is to make the control law adaptive to the disturbance, which is estimated online by an observer [37, 38].

In addition, although the disturbance observer method has been used for PMSM in [15, 18,19,20], the designed observers above are only applicable for the matched uncertainties, which mean that the uncertainties exist in the same channel as that of the control input [27]. In fact, the mismatched disturbance exists in the model (6) and the sliding mode controller (17). Therefore, these methods cannot estimate the lumped disturbance in the system.

(2) To effectively estimate the lumped disturbance, the nonlinear disturbance observer method is introduced [39], and it is used for the disturbance compensation for PMSM.

Consider the system with uncertainty and external disturbance, define \(x = {\left[ {\begin{array}{*{20}{c}} {{x_1}}&{{x_2}} \end{array}} \right] ^\mathrm{T}}\) and \(d = {\left[ {\begin{array}{*{20}{c}} {{d_1}}&{{d_2}} \end{array}} \right] ^\mathrm{T}}\). From the second-order system (6), the following can be derived as

$$\begin{aligned} \left\{ \begin{array}{l} \dot{x} = {f_1}(x) + {g_1}(x)u + {g_2}(x)d\\ y = h(x) \end{array} \right. \end{aligned}$$
(18)

where \({f_1}(x) = {\left[ {\begin{array}{*{20}{c}} {{x_2}}&{f(x)} \end{array}} \right] ^\mathrm{T}}\), \({g_1}(x) = \left[ {\begin{array}{*{20}{c}} 0&{}0\\ 0&{}b \end{array}} \right] \) and

\({g_2}(x) = \left[ {\begin{array}{*{20}{c}} 1&{}0\\ 0&{}1 \end{array}} \right] \).

The nonlinear disturbance observer can be designed as

$$\begin{aligned} \left\{ \begin{array}{l} \dot{p} = - l{g_2}(x)p - l({g_2}(x)lx + {f_1}(x) + {g_1}(x)u)\\ {\hat{d}} = p + lx \end{array} \right. \end{aligned}$$
(19)

where p is the observer’s internal state variables.

\(l = \left[ {\begin{array}{*{20}{c}} {{l_1}}&{}0\\ 0&{}{{l_2}} \end{array}} \right] \) is observer gain matrix. \({\hat{d}} = {\left[ {\begin{array}{*{20}{c}} {{{{\hat{d}}}_1}}&{{{{\hat{d}}}_2}} \end{array}} \right] ^\mathrm{T}}\) is the estimated disturbance by the disturbance observer.

The error of the matched and mismatched disturbance estimation is defined as \({e_d} = d - {\hat{d}}\), then

$$\begin{aligned} \dot{e}_d = \dot{d} - \dot{{\hat{d}}} \end{aligned}$$
(20)

Substitute (18) (19) into (20), the following can be derived as

$$\begin{aligned} {{\dot{e}}_d}= & {} \dot{d} - \dot{{\hat{d}} }\nonumber \\= & {} \dot{d} - (\dot{p} + l\dot{x})\nonumber \\= & {} \dot{d} - \left[ { - l{g_2}(x)p - l({g_2}(x)lx + {f_1}(x) + {g_1}(x)u)} \right] \nonumber \\&- l\left[ {{f_1}(x) + {g_1}(x)u + {g_2}(x)d} \right] \nonumber \\= & {} \dot{d} + l{g_2}(x)({\hat{d}} - lx) + l{g_2}(x)lx - l{g_2}(x)d\nonumber \\= & {} \dot{d} - l{e_d} \end{aligned}$$
(21)

Choosing a Lyapunov function as \({V_d} = \frac{1}{2}{e_d}^2\), the differential of \({V_d}\) can be expressed as \({\dot{V}_d} = {e_d}{\dot{e}_d}\). According to the assumption that \(\dot{d}\) is bounded, there is a suitable observer gain l satisfying \({\dot{V}_d} \le 0\), thus the estimation error will asymptotically converge to zero.

Through the observer in (19), the lumped disturbance d can be effectively estimated. In addition, due to the disturbance changes slowly in the actual system, thus, the derivative of disturbance is considered to be zero in the controller. To sum up, by combining the designed continuous terminal sliding mode control laws (17) and the disturbance observer (19), the control voltage reference signal can be derived as

$$\begin{aligned} {u_q} \!=\! u \!=\! - \frac{1}{b}\left[ \begin{array}{l} f(x) \!+\! {{{\hat{d}}}_2} + {c_0}{x_2} + {c_0}{{{\hat{d}}}_1} \!+\! {k_0}{\mathrm{sgn}} {s_0}\\ + {c_1}{e_2}^{{{{p_1}} / {{q_1}}}} + \int _0^t {{k_1}{\mathrm{sgn}} ({s_1})d\tau } \end{array} \right] \nonumber \\ \end{aligned}$$
(22)

Substitute (22) into (16), \({s_1}\) can be rewritten as

$$\begin{aligned} {s_1} = - {{\hat{d}}_2} - {c_0}{{\hat{d}}_1} - \int _0^t {{k_1}{\mathrm{sgn}} ({s_1})d\tau } + {d_2} + {c_0}{d_1} \end{aligned}$$
(23)

Then

$$\begin{aligned} {\dot{s_1}} = - {\dot{\hat{d_2}}} - {c_0}{\dot{\hat{d_1}}} - {k_1}{\mathrm{sgn}} ({s_1}) + {\dot{d_2}} + {c_0}{\dot{d_1}} \end{aligned}$$
(24)

Define \({\tilde{d_1}} = {d_1} - {{\hat{d}}_1}\), and \({{\tilde{d}}_2} = {d_2} - {{\hat{d}}_2}\). It is assumed that \(\left| {{{{\tilde{d}}}_1}} \right| \le {C_1}\) and \(\left| {{{{\tilde{d}}}_2}} \right| \le {C_2}\) where \({C_1}\), \({C_2}\) are positive.

Substitute the disturbance observer (19) into (24), the following can be derived as

$$\begin{aligned} {{\dot{s}}_1}= & {} - {l_2}({{{\hat{d}}}_2} - {d_2}) - {c_0}{l_1}({{{\hat{d}}}_1} - {d_1})\nonumber \\&+ {c_0}{{\dot{d}}_1} + {{\dot{d}}_2} - {k_1}{\mathrm{sgn}} ({s_1})\nonumber \\\le & {} {l_2}{C_2} + {c_0}{l_1}{C_1} - {k_1}{\mathrm{sgn}} ({s_1}) \end{aligned}$$
(25)

According to the chosen Lyapunov function \({V_1} = \frac{1}{2}{s_1}^2\), if \({k_1} \ge {l_2}{C_2} + {c_0}{l_1}{C_1}\) is satisfied, \({\dot{V}_1} \le 0\) is derived. Thus, the asymptotical stability of the closed-loop speed control is proved.

5 Experimental results and analysis

In this section, the experiment is developed on a PMSM platform to verify the feasibility of the proposed integral-type terminal sliding mode control method under the disturbance. The configuration of experimental system is introduced in Fig. 3. The experimental platform is shown in Fig. 4. The platform consists of a 130MB150A non-salient pole PMSM coupled to the load motor, a power converter based on IGBT, and the LINKS-RT rapid prototyping system as the controller. The main circuit adopts the technology of ac-dc-ac variable frequency. The switching frequency is set as 10kHz. The parameters of PMSM are listed in Table 1.

Fig. 3
figure 3

The configuration of experimental system

Full size image
Fig. 4
figure 4

The experimental platform

Full size image
Table 1 Parameters of PMSM
Full size table
Fig. 5
figure 5

The speed response waveforms of 600 r/min under three groups of parameters

Full size image
Fig. 6
figure 6

The speed change waveforms of 600 r/min with load disturbance under three groups of parameters

Full size image
Fig. 7
figure 7

The steady-state speed waveforms of 600 r/min under three groups of parameters

Full size image
Fig. 8
figure 8

The speed response waveforms of 600 r/min with PI and ITSMC

Full size image
Fig. 9
figure 9

The response waveforms of 600 r/min with ITSMC: a dq-axes current, b electromagnetic torque and c dq-axes voltage

Full size image
Fig. 10
figure 10

The speed change waveforms of 600 r/min under load disturbance with PI and ITSMC

Full size image
Fig. 11
figure 11

The changed waveforms of 600 r/min under load disturbance with ITSMC: a dq-axes current, b electromagnetic torque and c dq-axes voltage

Full size image
Fig. 12
figure 12

The speed waveforms with 1000   r/min based on PI and ITSMC: a the transient response waveforms, b the change waveforms under load disturbance

Full size image
Fig. 13
figure 13

The speed waveforms with 200 r/min based on PI and ITSMC: a the transient response waveforms, b the change waveforms under load disturbance

Full size image
Fig. 14
figure 14

The speed response waveforms with ITSMC, TSMC+DOB and ITSMC+DOB: a 600 r/min, b 1000 r/min, c 200 r/min

Full size image
Fig. 15
figure 15

The response waveforms of 600 r/min with ITSMC+DOB: a dq-axes current, b electromagnetic torque and c dq-axes voltage

Full size image
Fig. 16
figure 16

The speed change waveforms under load disturbance with ITSMC TSMC+DOB and ITSMC+DOB: a 600 r/min, b 1000 r/min, c 200 r/min

Full size image
Fig. 17
figure 17

The changed waveforms of 600 r/min under load disturbance with ITSMC+DOB: a dq-axes current, b electromagnetic torque and c dq-axes voltage

Full size image

First of all, the experiment is completed with ITSMC. The speed reference trajectory is realized by a second-order linear filter with fast dynamics. Moreover, to reveal the superiority of the proposed integral sliding mode control, it is compared with the conventional cascade control with PI controller in terms of dynamic response and robustness. According to the frequency-domain model of speed control system, the PI parameters are adjusted by trial and error to achieve a good control performance. The PI parameters for speed loop controller are selected as \({k_p} = 0.04\) and \({k_i} = 0.5\), respectively. The parameters for current loop controller are \({k_p} = 9\) and \({k_i} = 100\), respectively. The parameters of ITSMC are chosen as \({c_0} = {c_1} = 250\) and \({{{p_1}} / {{q_1}}} = 1.4\). Then, different sliding mode control gain \({k_0}\) and \({k_1}\) are set to test the speed tracking performance, and they are chosen as \({k_0} = {k_1} = 3000\), \({k_0} = {k_1} = 5000\) and \({k_0} = {k_1} = 7000\), respectively. To test the dynamic performance of ITSMC, the reference speed of the motor is given as 600 r/min, and the initial load torque is 0.5 N m. The speed response waveforms are shown in Fig. 5. To test the robustness for the disturbance, when the motor steadily operates at 600 r/min, the load disturbance about 3.5 N m is added on the drive system at \(t=5\)s, and it is removed at \(t = 10\)s, the speed change waveforms are shown in Fig. 6. The steady-state speed waveforms under three groups of parameters are shown in Fig. 7.

From Fig. 5, we can see that the speed overshoot increases along with the increase in sliding mode control gain, and the overshoot is 7 r, 9 r and 21 r, respectively. The settling time is about 0.2 s under three groups of parameters. The steady-state tracking error can quickly converge to zero. The controller has good speed tracking performance. When the load disturbance is added, as seen in Fig. 6, the speed has the fluctuation, and the speed fluctuation is about 69 r, 66 r and 68 r, respectively. The recovery time is 0.5 s, 0.35 s and 0.25 s, respectively. The speed fluctuations in steady state are 4 r, 7 r and 10 r, respectively, as seen in Fig. 7.

In summary, the results above show that the overshoot turns larger with the increase in sliding mode control gains, and the recovery time under the disturbance turns shorter obviously with the increase in sliding mode gains. The results also prove that the robustness is improved along with the increase in sliding mode gains, but the fluctuation in steady state will increase. Thus, considering the dynamic and the steady-state performance, \({k_0} = {k_1} = 5000\) is selected in the following experiment.

Then the proposed method is compared with cascade PI controller, the speed response waveforms of two methods are shown in Fig. 8. The dq-axes current, electromagnetic torque and dq-axes voltage waveforms of the proposed method are shown in Fig. 9. The overshoot of speed is 48 r and 9 r, respectively, and the settling time to the reference speed is 0.6 s and 0.2 s, respectively. The proposed ITSMC has the faster starting performance. When the load disturbance is added or removed, the speed dynamic waveforms are shown in Fig. 10, and the corresponding dq-axes current, electromagnetic torque and dq-axes voltage waveforms are shown in Fig. 11. From Fig. 10, we can see that the two methods (PI and ITSMC) have the fluctuation about 74 r, 66 r, respectively, and the motor speed can recover to the reference value under the disturbance about 0.25 s and 0.35 s, respectively. The results prove that the proposed method has the better transient performance. When the load disturbance is added, the PI control has the faster recover time, but it has the bigger fluctuation.

To further verify the control performance of the proposed method, the reference speed is given as 1000 r/min and 200 r/min, respectively. The speed response waveforms based on PI control and ITSMC are shown in Figs. 12a and 13a. When the load disturbance is added or removed, the speed comparison waveforms are shown in Figs. 12b and 13b. From the figures, we can see that the overshoots under 1000 r/min are 28 r and 84 r, respectively, and the settling time of ITSMC is shorter than PI controller. When the disturbance is added on the motor, the fluctuations of ITSMC and PI are 65 r and 75 r, respectively. The more comparisons are shown in Tab. 2. The results above also prove that the proposed SMC method has the faster response performance. When the load torque is changed, the PI control has the slightly faster recover time and the larger fluctuation.

Next, the experiments are developed to verify the feasibility of the proposed integral-type terminal sliding mode control with disturbance observer, and it is compared with both ITSMC without observer and the traditional terminal sliding mode control (TSMC) with DOB. The magnitude of the observer gains determines the speed of convergence, which means the convergence speed increases with the gains. But too large gains will cause the overshoot in the starting process. Thus, the parameters in the observer gain matrix are chosen by using a trial and error method. The observer gains of the proposed method are set as \({l_1} = {l_2} = 0.8\). In the traditional terminal sliding mode control, the sliding mode surface is designed as \(s = \dot{e} + \beta {e^{p/q}}\), \(\beta > 0\), \(1< p/q < 2\), the approach rate is \(\dot{s} = - {m_1}s - {m_2}\hbox {sign}(s)\), where \(\beta = 1\mathrm{{35}}\), \(q/p = 1.4\), \({m_1} = 1000\), \({m_2} = 10\).

Similarly, to test the dynamic performance of ITSMC+DOB, the reference speed of the motor is given as 600 r/min, 1000 r/min and 200 r/min, respectively. Compared with ITSMC and TSMC+DOB, the speed response waveforms are shown in Fig. 14. The dq-axes current, electromagnetic torque and dq-axes voltage waveforms under 600 r/min are shown in Fig. 15. From the figures under three methods (ITSMC, TSMC+DOB, ITSMC+DOB), we can see that the overshoots with 600 r/min are 9 r, 43 r, 17 r, and the settling time is about 0.2 s, 0.45 s, 0.2 s, respectively. The overshoots with 1000 r/min are 28 r, 76 r, 32 r, and the settling time is about 0.2 s, 0.5 s, 0.2 s, respectively. The overshoots with 200 r/min are 10 r, 23 r, 12 r, and the settling time is about 0.1 s, 0.3 s, 0.1 s, respectively. Through the comparison, the ITSMC has the best starting performance. The proposed composite controller has slightly larger overshoot than ITSMC, and the TSMC+DOB method has the larger overshoot and the slower response speed.

To test the anti-disturbance performance, at \(t=5\) s, the load disturbance 3.5 N m is added on the motor and it is removed at \(t=10\) s, the compared speed waveforms are shown in Fig. 16, and the dq-axes current, electromagnetic torque and dq-axes voltage waveforms under 600 r/min are shown in Fig. 17. As seen in the figures under three methods (ITSMC, TSMC+DOB, ITSMC+DOB), when the reference speed is 600 r/min, the speed drop with load disturbance is 66 r, 62 r, 60 r, respectively. The recover time to the reference speed is 0.35 s, 0.25 s and 0.25 s, respectively. Compared with ITSMC, the proposed composite controller has the faster recover time and the smaller drop with the load disturbance, and it has the stronger robustness for the disturbance. From the figures, although the TSMC+DOB has the faster recover speed, it has the similar time to the reference value with the proposed ITSMC+DOB. The detailed performance comparison of the controllers under different reference speed is shown in Tab. 2.

Table 2 The detailed performance comparison of four kinds of controllers under different reference speed
Full size table

6 Conclusion

A new speed control method is proposed for PMSM in this paper. At first, a continuous integral-type terminal sliding mode control is proposed. Different from the conventional cascade control with the inner current loop and the outer speed loop. The proposed controller adopts the non-cascade structure, and it has the better transient performance. To further improve the robustness of the system, through introducing a nonlinear disturbance observer to the designed sliding mode controller, a composite speed controller is constructed, and the observer is used for the feed-forward compensation. The recovery time for the disturbance is effectively improved. The experimental results prove the effectiveness of the proposed method. At present, the current constraint problem for the designed non-cascade controller has not been solved, and it will be the focus of future research. In addition, the control problem with the proposed method in field-weakening region will be considered in future work.