Adaptive sliding mode control based on a combined state/disturbance observer for the disturbance rejection control of PMSM

Abstract

An improved adaptive sliding mode controller (ASMC) based on a combined state/disturbance observer (CSO) is proposed for the high-performance control of permanent magnet synchronous motor (PMSM). In order to estimate the unknown state and the disturbance including the parameter uncertainty and the external disturbance, the CSO is proposed. Different from the extended state observer (ESO) or generalized ESO (GESO), the CSO uses the linear combination of the extended high-order states to construct the new estimation. The CSO resolves the contradiction between the estimation accuracy and the noise insensitivity, so it is more applicable to time-varying disturbances. Then, the CSO and the ASMC are integrated in the PMSM speed controller by the feed-forward compensation to enhance the system robustness. A simple nonlinear adaptive law is presented to solve the unknown upper bound of the estimation error and minimize the chattering. The theoretical analysis shows that the global stability of the closed-loop system is strictly guaranteed. The simulation and experimental results are presented to demonstrate the effectiveness of the proposed control method.

1 Introduction

Permanent magnet synchronous motor (PMSM) has been widely used in high-performance motion control due to the advantages, such as high power density, high efficiency, and low inertia [1,2,3]. PMSM is one of the systems with strong nonlinearity, uncertain parameters and disturbances. The classical linear control methods, for example, PI scheme, cannot quickly and effectively reject the uncertain and time-varying disturbances, which will degrade the control performance. In order to meet the requirements of high-performance control for PMSM, many nonlinear control methods, such as adaptive control [4,5,6], sliding mode control (SMC) [7], observer-based control [8], and intelligent control [9, 10], have been studied in recent years.

Because of the insensitivity to the uncertainties and the implementation simplicity [11,12,13,14,15,16,17], SMC is regarded as an efficient control method for PMSM speed servo system. In spite of the good robustness, the main drawback of SMC is the well-known chattering which is originated by the switching control. The high-order SMC can effectively reduce the chattering [18,19,20]. But the upper bound of sliding function derivative is required in parameter design, which brings difficulties in implementation.

A feasible solution is introducing a disturbance feed-forward compensation into controller [3, 14, 21]. In this way, it is not necessary to select too large switching gain for guaranteeing the stability, and thus the chattering can be fundamentally reduced with good disturbance rejection. In real applications, it is impossible to directly measure the disturbance, so the observer-based SMC could be a desirable scheme. The extended state observer (ESO) [22] [or its generalization (GESO)] and the disturbance observer (DOB), as the proven disturbance estimation techniques, have been successfully applied in industrial control systems [14, 21, 23,24,25,26]. Since in the actual PMSM system, the measurement noise of the speed sensor is inevitable, the effect of disturbance compensation, to some extent, depends on the estimation accuracy and the noise insensitivity of the observer. For the existing ESO (or GESO) and DOB, it is difficult to simultaneously improve the estimation accuracy and the noise insensitivity [27, 28]. The estimation accuracy and the noise insensitivity have to compromise in the observer design. Especially when the disturbance is time-varying, this contradiction will be more serious, which limits the application of the observer-based schemes. Therefore, to enhance the control performance of PMSM, it is of significance to develop a new disturbance estimation technique which can simultaneously achieve the satisfactory estimation accuracy and the noise insensitivity.

On the other hand, it is difficult to determine an appropriate switching gain of SMC since the upper bound of the disturbance or the disturbance estimation error is unknown. To reduce blindness of selecting switching gain, some adaptive sliding mode control (ASMC) methods are developed to adjust the switching gain real timely [29,30,31,32]. Plestan and Shtessel propose a linear adaptive law which can ensure the switching gain against over-estimated [33]. But, the adaptive law in [33] may lead to an excessively large transient value of the switching gain when the states are far from the sliding surface, and lead to a very slow convergence rate when the states are close to the sliding surface.

Motivated by the above discussion, the main contributions of this work are described here: Based on the analysis of GESO, a combined state/disturbance observer (CSO) is proposed to estimate the lumped disturbance of PMSM and the speed derivative. In the CSO, the linear combination of the extended high-order states is used to construct the new estimation. Compared with the GESO (or other disturbance observer, e.g., linear disturbance observer used in [26]), the CSO resolves the contradiction between the estimation accuracy in low frequency and the noise insensitivity in high frequency. Based on the CSO, a sliding mode controller for PMSM speed control is designed. And a simple nonlinear adaptive law is proposed to eliminate the limitation that the upper bound of the estimation error must be known in advance. The adaptive law avoids the aforementioned problems in [33] and minimizes the chattering. The effectiveness of the proposed method is verified by the simulations and experiments.

The rest of this paper is organized as follows. The mathematical model of PMSM is presented in Sect. 2. The CSO is proposed and analyzed in detail in Sect. 3. In Sect. 4, the adaptive sliding mode controller for PMSM speed control is designed. Then, the simulations and experiments are carried out and the results are given in Sect. 5. Finally, some conclusions are given in Sect. 6.

2 Problem formulation and model dynamics

The model of surface-mounted PMSM in the d–q-axis can be expressed as

$$ \left( \begin{aligned} \dot{i}_{d} \hfill \\ \dot{i}_{q} \hfill \\ {\dot{\omega }} \hfill \\ \end{aligned} \right) = \left( {\begin{array}{*{20}l} {- \frac{{R_{\text{s}} }}{{L_{\text{s}} }}} \hfill & {n_{\text{p}} \omega } \hfill & 0 \hfill \\ { - n_{\text{p}} \omega } \hfill & { - \frac{{R_{\text{s}} }}{{L{}_{\text{s}}}}} \hfill & { - \frac{{n_{\text{p}} \psi_{\text{f}} }}{{L_{\text{s}} }}} \hfill \\ 0 \hfill & {\frac{{1.5n_{\text{p}} \psi_{\text{f}} }}{J}} \hfill & { - \frac{B}{J}} \hfill \\ \end{array} } \right)\left( \begin{aligned} i_{d} \hfill \\ i_{q} \hfill \\ \omega \hfill \\ \end{aligned} \right) + \left( {\begin{array}{*{20}l} {\frac{{u_{d} }}{{L_{\text{s}} }}} \hfill \\ {\frac{{u_{q} }}{{L_{\text{s}} }}} \hfill \\ { - \frac{{T_{\text{L}} + d_{\text{e}} }}{J}} \hfill \\ \end{array} } \right) $$

(1)

where u_d, u_q, i_d, i_q and ω are, respectively, the d–q axes stator voltages, the d–q-axis stator currents and the rotor speed; L_s, R_s and ψ_f are the stator inductance, stator resistance and rotor flux linkage; T_L, n_p, J, B and d_e are the unknown load torque, the number of pole pairs, the moment of inertia, the friction coefficient and the external disturbance.

Figure 1 shows the structure of field-oriented vector control of PMSM. Here, we focus our attention on the speed controller. The motion equation of PMSM is given as

$$ \dot{\omega } = gi_{q} + d(t) $$

(2)

where $g = {{1.5n_{\text{p}} \psi_{\text{f}} } \mathord{\left/ {\vphantom {{1.5n_{\text{p}} \psi_{\text{f}} } J}} \right. \kern-0pt} J}$, and $d(t) = - ({B \mathord{\left/ {\vphantom {B J}} \right. \kern-0pt} J})\omega - {{(T_{\text{L}} + d_{\text{e}} )} \mathord{\left/ {\vphantom {{(T_{\text{L}} + d_{\text{e}} )} J}} \right. \kern-0pt} J}$. In the general PMSM speed controller design, the motion Eq. (2) is replaced by $\dot{\omega } = gi_{q}^{*} + d(t)$ where $i_{q}^{*}$ is the q-axis reference current. Owing to neglecting the current error, the speed control performance will be degraded. So in this paper, a more precise second-order model is adopted, which directly describes the relation between $i_{q}^{*}$ and ω according to [21]. From the PI controller of the q-axis current loop, one has

$$ u_{q} = k_{\text{p}} (i_{q}^{*} - i_{q} ) + k_{\text{i}} \int_{0}^{t} {(i_{q}^{*} - i_{q} ){\text{d}}t} $$

(3)

where k_p and k_i are the proportional and the integral coefficients. From (3), $i_{q} = i_{q}^{*} - {{(u_{q} - k_{\text{i}} \int_{0}^{t} {(i_{q}^{*} - i_{q} ){\text{d}}t} )} \mathord{\left/ {\vphantom {{(u_{q} - k_{\text{i}} \int_{0}^{t} {(i_{q}^{*} - i_{q} ){\text{d}}t} )} {k_{\text{p}} }}} \right. \kern-0pt} {k_{\text{p}} }}$ can be obtained, and substituting it into (2), it yields

$$ \dot{\omega } = g(i_{q}^{*} - {{(u_{q} - k_{\text{i}} \int_{0}^{t} {(i_{q}^{*} - i_{q} ){\text{d}}t} )} \mathord{\left/ {\vphantom {{(u_{q} - k_{\text{i}} \int_{0}^{t} {(i_{q}^{*} - i_{q} ){\text{d}}t} )} {k_{\text{p}} }}} \right. \kern-0pt} {k_{\text{p}} }}) + {\text{d}}(t) $$

(4)

Taking the derivative of (4), we have

$$ \ddot{\omega } = g\dot{i}_{q}^{*} + g\frac{{k_{\text{i}} }}{{k_{\text{p}} }}i_{q}^{*} - g\frac{{k_{\text{i}} }}{{k_{\text{p}} }}i_{q} - \frac{g}{{k_{\text{p}} }}\dot{u}_{q} + \dot{d}(t) $$

(5)

From (2), we get $i_{q} = {{[\dot{\omega } - d(t)]} \mathord{\left/ {\vphantom {{[\dot{\omega } - d(t)]} g}} \right. \kern-0pt} g}$. Then substituting it into (5), it yields

$$ \ddot{\omega } = - \frac{{k_{\text{i}} }}{{k_{\text{p}} }}\dot{\omega } + u + D(t) $$

(6)

where $u = g\dot{i}_{q}^{*} + g({{k_{\text{i}} } \mathord{\left/ {\vphantom {{k_{\text{i}} } {k_{\text{p}} }}} \right. \kern-0pt} {k_{\text{p}} }})i_{q}^{*}$ and $D(t) = - ({g \mathord{\left/ {\vphantom {g {k_{\text{p}} }}} \right. \kern-0pt} {k_{\text{p}} }})\dot{u}_{q} + \dot{d}(t) + ({{k_{\text{i}} } \mathord{\left/ {\vphantom {{k_{\text{i}} } {k_{\text{p}} }}} \right. \kern-0pt} {k_{\text{p}} }})d(t)$. Equation (6) is the second-order motion model. D(t) is considered as the lumped disturbance including the parametric uncertainties, the unmodeled dynamics and the load disturbances.

Fig. 1

Block diagram of PMSM control system

Assumption 1

D(t) is bounded, i.e.,$\left| {D(t)} \right| \le M_{1}$, and there exists a t_F, when t > t_F, the n-order derivative of D(t) exists and is bounded, i.e., $\left| {{{d^{n} D(t)} \mathord{\left/ {\vphantom {{d^{n} D(t)} {dt^{n} }}} \right. \kern-0pt} {dt^{n} }}} \right| \le M_{2}$, n ≥ 1.

3 The CSO and its performance analysis

To estimate the speed derivative and the lumped disturbance D(t), the CSO is proposed in this section. It is well-known that in an actual PMSM system, the high-frequency measurement noise which comes from the sensor is inevitable [34, 35]. If the noise restraining ability of the observer is poor, the measurement noise will be amplified through the observer and influence the stator currents, thus the control performance will be severely degraded. So, the estimation accuracy and the noise insensitivity are two important indexes of the observer.

3.1 Brief analysis of GESO

Since the CSO in this paper is developed on the basis of GESO, first, a brief analysis of GESO is given (it should be noted that the performance of DOB is similar to conventional ESO, and conventional ESO can be regarded as a special case of GESO). If Assumption 1 holds, defining $x_{1} = \omega$, $x_{2} = \dot{\omega } + ({{k_{\text{i}} } \mathord{\left/ {\vphantom {{k_{\text{i}} } {k_{\text{p}} }}} \right. \kern-0pt} {k_{\text{p}} }})\omega$, and $x_{3} = D(t)$, Eq. (6) can be extended as

$$ \left\{ {\begin{array}{*{20}l} {\dot{x}_{1} = x_{2} - ({{k_{\text{i}} } \mathord{\left/ {\vphantom {{k_{\text{i}} } {k_{\text{p}} }}} \right. \kern-0pt} {k_{\text{p}} }})x_{1} } \hfill \\ {\dot{x}_{2} = u + x_{3} } \hfill \\ {\dot{x}_{3} = \dot{D}(t)} \hfill \\ \vdots \hfill \\ {\dot{x}_{n + 2} = D^{(n)} (t)} \hfill \\ \end{array} } \right. $$

(7)

where n is the extended order. Then, design the following system as

$$ \left\{ {\begin{array}{*{20}l} {\dot{z}_{1} = z_{2} - ({{k_{\text{i}} } \mathord{\left/ {\vphantom {{k_{\text{i}} } {k_{\text{p}} }}} \right. \kern-0pt} {k_{\text{p}} }})x_{1} - l_{1} e_{1} } \hfill \\ {\dot{z}_{2} = u + z_{3} - l_{2} e_{1} } \hfill \\ {\dot{z}_{3} = z_{4} - l_{3} e_{1} } \hfill \\ \vdots \hfill \\ {\dot{z}_{n + 1} = z_{n + 2} - l_{n + 1} e_{1} } \hfill \\ {\dot{z}_{n + 2} = - l_{n + 2} e_{1} } \hfill \\ \end{array} } \right. $$

(8)

where $e_{1} = z_{1} - x_{1}$, $l_{i} = k_{\text{i}} \omega_{0}^{i} > 0$ (i = 1, 2, …, n + 2) in which $k_{\text{i}} = (n + 2)!/[i! \times (n + 2 - i)!]$ and $- \omega_{0}$ is the desired pole. In GESO, z_i (i = 1, 2, …, n + 2) is regarded as the estimation of x_i. Then, we can analyze the performance of GESO through the transfer function between z₃(s) and D(s) which is given as

$$ z_{3} (s) = \frac{{l_{3} s^{n - 1} + l_{4} s^{n - 2} + \cdots + l_{n + 2} }}{{s^{n + 2} + l_{1} s^{n + 1} + \cdots + l_{n + 2} }}D(s) $$

(9)

and the estimation error $\tilde{z}_{3} (s) = z_{3} (s) - D(s)$ is given as

$$ \tilde{z}_{3} (s) = \frac{{s^{n + 2} + l_{1} s^{n + 1} + l_{2} s^{n} }}{{s^{n + 2} + l_{1} s^{n + 1} + \cdots + l_{n + 2} }}D(s) $$

(10)

Figure 2 shows the frequency characteristics of the GESO using (9) and (10) with different values of extended order n, here ω₀ is chosen as 100. Figure 2a shows that by increasing 1 of n, the slope of $\tilde{z}_{3} (s)/D(s)$ in low frequency increases 20 dB/dec. Thus, the estimation error decreases with n increasing. On the other hand, from Fig. 2b, as n increases, the frequency magnitude of $z_{3} (s)/D(s)$ shifts to the right, and the slope of $z_{3} (s)/D(s)$ in high frequency remains constant (− 60 dB/dec). Thus, the sensitivity of the observer to the high-frequency noise increases with n increasing. Therefore, the extended order n is limited by this fact, and the estimation accuracy and the noise insensitivity have to be compromised. Especially when the disturbance is time-varying, the higher extended order is required for enough accuracy [28], so the contradiction between accuracy and noise insensitivity becomes more acute, which limits the application of observer-based control methods.

Fig. 2

Frequency characteristics of the GESO with different values of n. a $\tilde{z}_{3} (s)/D(s)$, b $z_{3} (s)/D(s)$

3.2 The CSO

From (9), it can be known that the reason of above contradiction is that in transfer function of GESO, the degrees of the denominator and the numerator cannot be separately designed. If we change the value of n, the degrees of both the denominator and the numerator will be synchronously changed. So it is difficult to attain a trade-off between estimation accuracy in low frequency and noise insensitivity in high frequency.

Therefore, in order to simultaneously improve the estimation accuracy and the noise insensitivity, we need to add a degree of freedom to separately design the denominator and the numerator of transfer function. Note that in GESO, only the state z₃ is employed to estimate D(t), and the other states ($z_{4} ,z_{5} , \ldots ,z_{n + 2}$) are not fully used. Based on this idea, the following CSO is proposed.

By subtracting (7) from (8), the error dynamics can be expressed as

$$ \left\{ {\begin{array}{*{20}l} {\dot{e}_{1} = e_{2} - l_{1} e_{1} } \hfill \\ {\dot{e}_{2} = e_{3} - l_{2} e_{1} } \hfill \\ \vdots \hfill \\ {\dot{e}_{n + 2} = - l_{n + 2} e_{1} - D^{(n)} } \hfill \\ \end{array} } \right. $$

(11)

where $e_{i} = z_{i} - x_{i}$. Via Laplace transform of (11), we have

$$ e_{1} (s) = - \frac{{s^{n} D(s)}}{{s^{n + 2} + l_{1} s^{n + 1} + l_{2} s^{n} + \cdots + l_{n + 2} }} $$

(12)

Substituting $e_{1} (s)$ into the Laplace transform of (8), it yields

$$ \left\{ {\begin{array}{*{20}l} {z_{n + 2} (s) = \frac{{l_{n + 2} s^{n - 1} }}{{s^{n + 2} + l_{1} s^{n + 1} + l_{2} s^{n} + l_{3} s^{n - 1} \cdots + l_{n + 2} }}D(s)} \hfill \\ {z_{n + 1} (s) = \frac{{l_{n + 1} s^{n - 1} + l_{n + 2} s^{n - 2} }}{{s^{n + 2} + l_{1} s^{n + 1} + l_{2} s^{n} + l_{3} s^{n - 1} \cdots + l_{n + 2} }}D(s)} \hfill \\ {z_{n} (s) = \frac{{l_{n} s^{n - 1} + l_{n + 1} s^{n - 2} + l_{n + 2} s^{n - 3} }}{{s^{n + 2} + l_{1} s^{n + 1} + l_{2} s^{n} + l_{3} s^{n - 1} \cdots + l_{n + 2} }}D(s)} \hfill \\ \vdots \hfill \\ {z_{3} (s) = \frac{{l_{3} s^{n - 1} + l_{4} s^{n - 2} \cdots + l_{n + 2} }}{{s^{n + 2} + l_{1} s^{n + 1} + l_{2} s^{n} + l_{3} s^{n - 1} \cdots + l_{n + 2} }}D(s)} \hfill \\ \end{array} } \right. $$

(13)

Then, we will show that by using the linear combination of z_i (i = 3, 4, …, n + 2), the better transfer function between $\hat{x}_{2} (s)$ and x₂(s), $\hat{D}(s)$ and D(s) can be constructed. For convenience, the more compact form of (13) is given.

$$ Z(s) = L_{1} F(s) $$

(14)

where Z(s) = (z_n+2(s), z_n+1(s), …, z₃(s))^T, $F(s) = \left( {\frac{{s^{n - 1} D(s)}}{{s^{n + 2} + \cdots + l_{n + 2} }} ,\frac{{s^{n - 2} D(s)}}{{s^{n + 2} + \cdots + l_{n + 2} }} ,\cdots ,\frac{D(s)}{{s^{n + 2} + \cdots + l_{n + 2} }}} \right)^{\text{T}}$, and $L_{1} = \left( {\begin{array}{*{20}l} {l_{n + 2} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill & \ldots \hfill & 0 \hfill \\ {l_{n + 1} } \hfill & {l_{n + 2} } \hfill & 0 \hfill & 0 \hfill & \ldots \hfill & 0 \hfill \\ {l_{n} } \hfill & {l_{n + 1} } \hfill & {l_{n + 2} } \hfill & 0 \hfill & \ldots \hfill & 0 \hfill \\ {} \hfill & {} \hfill & \vdots \hfill & {} \hfill & {} \hfill & {} \hfill \\ {l_{3} } \hfill & {l_{4} } \hfill & {l_{5} } \hfill & \cdots \hfill & {l_{n + 1} } \hfill & {l_{n + 2} } \hfill \\ \end{array} } \right)$. Note that L₁ is invertible, F(s) can be calculated by F(s) = L⁻¹₁ Z(s), so F(t) = L⁻¹₁ Z(t). With F(t), and define $L_{2} = (l_{2} ,l_{3} , \ldots ,l_{{r_{1} + 1}} ,0, \ldots ,0)$ and $L_{3} = (l_{3} ,l_{4} , \ldots ,l_{{r_{2} + 2}} ,0, \ldots ,0)$ where r₁ and r₂ are integers and 0 ≤ r₁ < n+1, 0 ≤ r₂ < n, the new $\hat{x}_{2} (t)$ and $\hat{D}(t)$ are given as

$$ \hat{x}_{2} (t) = z_{2} (t) - L_{2} F(t) = z_{2} (t) - L_{2} L_{1}^{ - 1} Z(t) $$

(15)

and

$$ \hat{D}(t) = z_{3} (t) - L_{3} F(t) = z_{3} (t) - L_{3} L_{1}^{ - 1} Z(t) $$

(16)

where $Z(t) = (z_{n + 2} (t),z_{n + 1} (t), \ldots ,z_{3} (t))^{\text{T}}$. The proposed CSO consists of Eqs. (8), (15) and (16). It can be noted that when ω₀ is fixed, L₂ and L₃ are only determined by r₁ and r₂. And the GESO can be regarded as a special case of CSO when r₁ = r₂ = 0. The next section will show the performance improvement behind this difference.

3.3 Performance analysis of the CSO

To analyze the performance of CSO, the transfer functions between $\hat{x}_{2} (s)$ and x₂(s), $\hat{D}(s)$ and D(s) are given by

$$ \begin{aligned} \hat{x}_{2} (s) & = \frac{{l_{{r_{1} + 2}} s^{{n - r_{1} }} + l_{{r_{1} + 3}} s^{{n - r_{1} - 1}} + \cdots + l_{n + 2} }}{{s^{n + 2} + l_{1} s^{n + 1} + l_{2} s^{n} + \cdots + l_{n + 1} s + l_{n + 2} }}x_{2} (s) \\ & \quad + \frac{{s^{n + 1} + l_{1} s^{n} + \cdots + l_{{r_{1} + 1}} s^{{n - r_{1} }} }}{{s^{n + 2} + l_{1} s^{n + 1} + l_{2} s^{n} + \cdots + l_{n + 1} s + l_{n + 2} }}u(s) \\ \end{aligned} $$

(17)

and

$$ \hat{D}(s) = \frac{{l_{{r_{2} + 3}} s^{{n - r_{2} - 1}} + l_{{r_{2} + 4}} s^{{n - r_{2} - 2}} + \cdots + l_{n + 2} }}{{s^{n + 2} + l_{1} s^{n + 1} + \cdots + l_{n + 2} }}D(s) $$

(18)

respectively. And the estimation errors are given as

$$ \begin{aligned} \tilde{x}_{2} (s) & = \hat{x}_{2} (s) - x_{2} (s) \\ & = - \frac{{s^{n + 2} + l_{1} s^{n + 1} + \cdots + l_{{r_{1} + 1}} s^{{n - r_{1} + 1}} }}{{s^{n + 2} + l_{1} s^{n + 1} + \cdots + l_{n + 1} s + l_{n + 2} }}x_{2} (s) \\ & \quad + \frac{{s^{n + 1} + l_{1} s^{n} + \cdots + l_{{r_{1} + 1}} s^{{n - r_{1} }} }}{{s^{n + 2} + l_{1} s^{n + 1} + \cdots + l_{n + 1} s + l_{n + 2} }}u(s) \\ \end{aligned} $$

(19)

and

$$ \begin{aligned}\tilde{D}(s) &= \hat{D}(s) - D(s)\\ &= - \frac{{s^{n + 2} + l_{1} s^{n + 1} + \cdots + l_{{r_{2} + 2}} s^{{n - r_{2} }} }}{{s^{n + 2} + l_{1} s^{n + 1} + \cdots + l_{n + 2} }}D(s)\end{aligned} $$

(20)

where $\tilde{x}_{2} (s)$ and $\tilde{D}(s)$ denote the estimation errors. From (17) (or (18)), we can see the degree of denominator is n + 2, and the degree of numerator is $n - r_{1}$ (or $n - r_{2} - 1$). Therefore, by adjusting n and r_1,2, we can separately design the degree of denominator and numerator of transfer function. Using (17)–(20), the frequency characteristics of CSO with different values of n and r_1,2, where ω₀ is chosen as 100, is presented. From Fig. 3, it can be observed that if r_1,2 is fixed (see Fig. 3a), with the increase in n, the estimation error decreases in low frequency, thus the estimation accuracy is improved. And if n is fixed (see Fig. 3b), with the increase in r_1,2, the high-frequency attenuation of $\hat{D}(s)/D(s)$ increases, thus the insensitivity to high frequency noise is improved.

Fig. 3

Frequency characteristics of GESO and CSO with different values of n and r_1,2. a $\tilde{D}(s)/D(s)$, b $\hat{D}(s)/D(s)$

Further, from Fig. 4, where the proportion relation between r_1,2 and n is fixed (i.e., r_1,2 = 2, n = 4, r_1,2 = 3, n = 6, and r_1,2 = 4, n = 8), it can be seen if r_1,2 = 0.5n, every increase 2 of n (and meanwhile, increase 1 of r_1,2), the slope of $\tilde{D}(s)/D(s)$ increases 20 dB/dec in low frequency; and meanwhile, the slope of $\hat{D}(s)/D(s)$ increases − 20 dB/dec in high frequency. Therefore, by tuning the value of n and r_1,2, both the estimation accuracy and the noise restraining effect can be simultaneously improved.

Fig. 4

Frequency characteristics of the CSO where r_1,2 = 0.5n. a $\tilde{D}(s)/D(s)$, b $\hat{D}(s)/D(s)$

From above discussion, we can see a striking advantage of CSO is that the degree of denominator and numerator of the transfer function are decoupled and can be separately designed. So the estimate ability of the observer is greatly enhanced. Furthermore, the proposed CSO can be easily realized by (8), (15) and (16), which does not greatly increase the computation complexity compared with GESO.

3.4 Stability analysis of the CSO

Theorem 1

For the given system (6), a CSO is constructed by (8), (15) and (16), if Assumption 1 holds, the estimation error will be bounded uniformly and ultimately, there are $\lim_{t \to \infty } \left| {\hat{x}_{2} - x_{2} } \right| \le O(\varepsilon^{{n + 1 - r_{1} }} )$and $\lim_{t \to \infty } \left| {\hat{D} - D} \right| \le O(\varepsilon^{{n - r_{2} }} )$where 0 ≤ r₁ < n + 1, 0 ≤ r₂ < n, and ε = 1/ω₀.

The proof of Theorem 1 is presented in Appendix A.

4 Adaptive sliding mode controller

Based on the CSO, an adaptive sliding mode controller is designed for PMSM in this section.

4.1 Controller design

The objective of the speed controller is to force the PMSM rotor speed to track the reference. To do this, the sliding manifold is defined first

$$ \sigma (t) = \hat{\dot{e}}(t) + c \cdot e(t) $$

(21)

where e(t) = ω_r(t) − ω(t), ω_r(t) represents the speed reference, c is a positive constant, and $\hat{\dot{e}}(t) = \dot{\omega }_{r} (t) - \hat{\dot{\omega }}(t)$ in which $\hat{\dot{\omega }}(t)$ is obtained by CSO ($\hat{\dot{\omega }} = \hat{x}_{2} - ({{k_{\text{i}} } \mathord{\left/ {\vphantom {{k_{\text{i}} } {k_{\text{p}} }}} \right. \kern-0pt} {k_{\text{p}} }})\omega$). The sliding manifold (21) can ensure the speed error e(t) converges to zero as long as $\sigma (t) = 0$. In order to make $\sigma (t)$ converge to zero, the control law is designed as

$$ u = \ddot{\omega }_{\text{r}} + ({{k_{\text{i}} } \mathord{\left/ {\vphantom {{k_{\text{i}} } {k_{\text{p}} }}} \right. \kern-0pt} {k_{\text{p}} }})\hat{\dot{\omega }} + c\hat{\dot{e}} + k\text{sgn} (\sigma ) + k_{\text{s}} \sigma - \hat{D}(t) $$

(22)

where k > 0, k_s> 0, $\hat{\dot{\omega }}$ and $\hat{D}(t)$ are provided by CSO. According to the analysis in Sect. 3, the accurate and smooth $\hat{\dot{\omega }}$ and $\hat{D}(t)$ can be obtained. The derivative of σ with respect to time is deduced as

$$ \dot{\sigma } = \ddot{e} + c\dot{e} - \dot{\tilde{x}}_{2} = \ddot{\omega }_{\text{r}} + ({{k_{\text{i}} } \mathord{\left/ {\vphantom {{k_{\text{i}} } {k_{\text{p}} }}} \right. \kern-0pt} {k_{\text{p}} }})\dot{\omega } - D(t) - u + c\dot{e} - \dot{\tilde{x}}_{2} $$

(23)

Substituting the control law (22) into (23), it yields

$$ \dot{\sigma } = - k_{\text{s}} \sigma - k\text{sgn} (\sigma ) + \varGamma (t) $$

(24)

where $\varGamma (t) = \tilde{D}(t) + \left( {c - \frac{{k_{\text{i}} }}{{k_{\text{p}} }}} \right)\tilde{x}_{2} - \dot{\tilde{x}}_{2}$. It can be noted that if $k \ge \varGamma (t)$ is satisfied, there is $\sigma \dot{\sigma } \le 0$, so σ(t) will converge to zero. However, the upper bound of $\varGamma (t)$ is hard to obtain, which brings difficulties for implementation of the control law. To overcome this problem, a simple nonlinear adaptive law is proposed as follows:

$$ \dot{k} = \left\{ {\begin{array}{*{20}l} {k_{m} \left| \sigma \right|^{p} \text{sgn} (\left| \sigma \right| - \varepsilon_{1} )} \hfill & {k > \mu } \hfill \\ \mu \hfill & {k \le \mu } \hfill \\ \end{array} } \right. $$

(25)

where μ and ε₁ are nonzero positive constants, k_m> 0 and 0 < p<1. The parameter μ is used to ensure k > 0. Thereinafter, Theorem 2 indicates that the control law (22) with the adaptive law (25) can ensure that the PMSM speed tracks its reference, and k is not overestimated. Since the chattering of SMC is originated by the switching term ksgn(σ), the avoidance of over-estimation of k minimizes the chattering.

From (25), when the system is in transient state (e.g., starting phase), $\left| \sigma \right|$ is larger, but $\left| {\dot{k}} \right|$ will not be too large because 0 < p < 1, thus avoiding the excessively large value of k in transient process. And when the system states are close to the sliding manifold, the convergence of k will be fast owing to 0 < p < 1. So the steady and fast convergence of the switching gain is achieved.

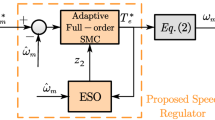
The suggested control scheme (ASMC + CSO) is shown in Fig. 5. The CSO is used to estimate the speed derivative and the lumped uncertain disturbance. The estimated result is compensated to the control law which is given by (22). And the switching gain k is adjusted by the adaptive law (25). The actual output of the speed loop $i_{q}^{*}$ (q-axis reference current) is calculated by $g\left( {\dot{i}_{q}^{*} + \frac{{k_{\text{i}} }}{{k_{\text{p}} }}i_{q}^{*} } \right) = u$, where u is provided by control law (22). $i_{d}^{*}$ and $i_{q}^{*}$ are inputted to the currents control loop to provide u_d and u_q. After coordinate transformation, u_α and u_β are used in SVPWM to generate the on and off signals for the three-phase voltage inverter.

Fig. 5

Block diagram of the designed PMSM speed controller

In practice, $\ddot{\omega }_{\text{r}}$ in (22) can be set as zero when the speed reference is step value. And this will not influence the system stability.

4.2 Stability analysis of closed-loop system

Lemma 1

For the nonlinear function f(x) = −k_sx² − (k − k_d)x + $\frac{1}{\lambda }$(k − k_d)k_mx^p, where k_s> 0, k ≤ k_d, k_m> 0 and 0 < p < 1, there exists a positive real number λ such that f(x) ≤ 0 for all x ≥ 0.

The proof of Lemma 1 is presented in Appendix B.

Theorem 2

If Assumption 1holds for the PMSM system (1), and the control law (22) and the adaptive law (25) are applied, it is guaranteed that the speed tracking error converges to a small neighborhood of zero in a finite time.

Proof

Rewriting (24) as

$$ \dot{\sigma } = - k_{s} \sigma - k\text{sgn} (\sigma ) + \varGamma (t) $$

(26)

According to [33], it can be easy known that the switching gain k has an upper bound that $k_{d} > \sup \left| {\varGamma (t)} \right|$, i.e., k(t) ≤ k_d, $\forall t > 0$. Assuming $\tilde{k} = k - k_{d}$, consider the following positive definite Lyapunov function

$$ V = {{\sigma^{2} } \mathord{\left/ {\vphantom {{\sigma^{2} } 2}} \right. \kern-0pt} 2} + {{\tilde{k}^{2} } \mathord{\left/ {\vphantom {{\tilde{k}^{2} } {2\lambda }}} \right. \kern-0pt} {2\lambda }} $$

(27)

where λ > 0, and k ≤ k_d. The derivative of V is

$$ \dot{V} = \sigma \dot{\sigma } + \frac{1}{\lambda }\tilde{k}\dot{\tilde{k}} = - k_{s} \sigma^{2} - k\left| \sigma \right| - \sigma \varGamma (t) + \frac{1}{\lambda }\tilde{k}\dot{k} $$

(28)

When $\left| \sigma \right| > \varepsilon_{1}$, there is $\dot{k} = k_{m} \left| \sigma \right|^{p} > 0$ according to (25), then $\dot{V}$ can be deduced as

$$ \begin{aligned} \dot{V} & = - k_{s} \left| \sigma \right|^{2} - k\left| \sigma \right| + k_{d} \left| \sigma \right| - k_{d} \left| \sigma \right| - \sigma \varGamma (t) + \frac{1}{\lambda }(k - k_{d} )k_{m} \left| \sigma \right|^{p} \\ & \le ( - k_{s} \left| \sigma \right|^{2} - (k - k_{d} )\left| \sigma \right| + \frac{1}{\lambda }(k - k_{d} )k_{m} \left| \sigma \right|^{p} ) - \left| \sigma \right|(k_{d} - \varGamma (t)) \\ \end{aligned} $$

(29)

Using Lemma 1, there exists a positive real number λ such that $- k_{s} \left| \sigma \right|^{2} - (k - k_{d} )\left| \sigma \right| + \frac{1}{\lambda }(k - k_{d} )k_{m} \left| \sigma \right|^{p} \le 0$, so we have

$$ \dot{V} \le - \left| \sigma \right|(k_{d} - \varGamma (t)) $$

(30)

considering $k_{d} > \sup \left| {\varGamma (t)} \right|$, there is $\dot{V} \le - \left| \sigma \right|(k_{d} - \varGamma (t)) < 0$ when $\left| \sigma \right| > \varepsilon_{1}$. It is guaranteed that σ converges to a domain of $\left| \sigma \right| \le \varepsilon_{1}$ in a finite time from any initial condition $\left| {\sigma \left( 0 \right)} \right| > \varepsilon_{1}$.

When $\left| \sigma \right| < \varepsilon_{1}$, $\dot{k} = - k_{m} \left| \sigma \right|^{p} < 0$, $\dot{V}$ is sign indefinite and $\left| \sigma \right|$ may increase. As soon as $\left| \sigma \right| \ge \varepsilon_{1}$, there is $\dot{V} < 0$, and thus $\left| \sigma \right|$ has a stable finite reaching time dynamics. Therefore, $\left| \sigma \right|$ will converge to $\left| \sigma \right| \le \varepsilon_{1}$ and stay in a bounded domain thereafter, and thus the speed tracking error e will converge to a small neighborhood of zero along the sliding manifold. Thus, Theorem 2 is proved.

It should be noted that the current PI controller has already been considered in second-order model (6), so the Theorem 2 can ensure the stability of the whole system.

Remark 1

From above proof, it can be known that the control accuracy depends on the parameter ε₁. If ε₁ is selected too large, the control accuracy decreases according to Theorem 2. But conversely, if ε₁ is too small, the self-sustained oscillation may be induced due to the finite sampling period in implementation. Considering the discrete-time form of (26), one has

$$ \sigma (t + T) = \sigma (t) - T(k_{s} \sigma (t) + k\text{sgn} (\sigma (t)) + \varGamma (t)) $$

(31)

where T is the sampling period. Given that $\left| {\sigma (t)} \right| \le \varepsilon_{1}$ and $k \ge \sup \left| {\varGamma (t)} \right|$, if ε₁ is too small, $\left| {\sigma (t + T)} \right|$ could be greater than ε₁, thus leading to the self-sustained oscillation. To avoid this problem, $\left| {\sigma (t + T)} \right| \le \varepsilon_{1}$ is required when $\left| {\sigma (t)} \right| \le \varepsilon_{1}$ and $k \ge \sup \left| {\varGamma (t)} \right|$. From (31), considering σ(t) and $T(k_{s} \sigma (t) + k\text{sgn} (\sigma (t)) + \varGamma (t))$ have the same sign when $k \ge \left| {\varGamma (t)} \right|$, so if the following in equation

$$ T\left| {(k_{s} \sigma (t) + k\text{sgn} (\sigma (t)) + \varGamma (t))} \right| \le \varepsilon_{1} $$

(32)

is satisfied,$\left| {\sigma (t + T)} \right| \le \varepsilon_{1}$ can be guaranteed. Considering $\left| {\sigma (t)} \right| \le \varepsilon_{1}$, it yields

$$ \begin{aligned} & T\left| {(k_{s} \sigma (t) + k\text{sgn} (\sigma (t)) + \varGamma (t))} \right| \\ & \quad \le Tk_{s} \varepsilon_{1} + T\left| {k\text{sgn} (\sigma (t))} \right| + T\left| {\varGamma (t)} \right| \le Tk_{s} \varepsilon_{1} + 2Tk \\ \end{aligned} $$

(33)

To ensure (32), it is necessary to make $Tk_{s} \varepsilon_{1} + 2Tk \le \varepsilon_{1}$. Supposing $1 - Tk_{s} > 0$, thus $\varepsilon_{1}$ should be chosen as the following function

$$ \varepsilon_{1} (t) \ge {{2Tk(t)} \mathord{\left/ {\vphantom {{2Tk(t)} {(1 - Tk_{s} }}} \right. \kern-0pt} {(1 - Tk_{s} }}) $$

(34)

5 Simulations and experiments

To test the effectiveness of the proposed method, the simulations and experiments are carried out. The following three control methods are compared.

• 1. The conventional SMC without disturbance compensation and adaptive parameter adjusting.

• 2. The SMC + GESO without adaptive parameter adjusting.

• 3. The proposed method (ASMC + CSO).

The parameters of PMSM are given in Table 1. To evaluate the disturbance rejection performance, the step disturbance, the time-varying disturbance and the parameter uncertainty are, respectively, considered. For a fair comparison, the parameters of the speed controller and the currents controller are well-tuned and same in three methods.

Table 1 Parameters of PMSM

5.1 Simulation results

The saturation limit of q-axis current is ± 10 A. The PI parameters of the currents loop, which are designed according to the stator resistance and stator inductance, are k_p= 48 and k_i= 5000. The parameters of the speed controller and the adaptive law are selected as c = 40, k_s= 20 (satisfies $1 - Tk_{s} > 0$), k_m= 10, μ = 0.5, p = 0.25, $\varepsilon_{1} (t) = {{3Tk(t)} \mathord{\left/ {\vphantom {{3Tk(t)} {(1 - Tk_{s} )}}} \right. \kern-0pt} {(1 - Tk_{s} )}}$ and T = 0.5 × 10⁻⁴ s. The parameters of the CSO are chosen as n = 4, r₁ = r₂ = 2, ω₀ = 120. And the pole location of the GESO in method 2 are also chosen as ω₀ = 120.

• (1) Case 1

The speed reference is 1000 rpm, and a step load disturbance T_L= 1.5 N m is added at 6 s. Figure 6 shows the disturbance estimations by the CSO and the GESO. Comparing Fig. 6a, b, it is obvious that the CSO has better estimation accuracy and noise insensitivity than the GESO. As shown in Fig. 7, a very large switching gain (k = 2×10⁴) is required for the conventional SMC to reject the disturbance, so that the chattering of the control input is very severe (see Fig. 7b). And the speed drop with the conventional SMC is about 50 rpm when the disturbance occurs. From Figs. 8 and 9, both the SMC + GESO (k = 400) and the ASMC + CSO can reject the disturbance due to the disturbance compensation. But when the disturbance occurs, the speed drop is about 27.6 rpm, and the recovery time is about 0.63 s using the SMC + GESO; comparatively, the speed drop and the recovery time are, respectively, about 16.9 rpm and 0.18 s using the ASMC + CSO. Besides, since the estimation accuracy of CSO is higher, the switching gain k converges to 0.5 under the adaptive law (see Fig. 9d), which is much smaller than method 1 and 2. So the chattering of control input is greatly reduced. Detailed comparisons of the control effect are given in Table 2.

Fig. 6

Lumped disturbance estimation (simulation). a CSO. b GESO

Fig. 7

Control effects under the step disturbance with the SMC (simulation). a Speed, b control input, c q-axis current

Fig. 8

Control effects under the step disturbance with the SMC + GESO (simulation). a Speed, b control input, c q-axis current

Fig. 9

Control effects under the step disturbance with the proposed method (simulation). a Speed, b control input, c q-axis current, d switching gain k

Table 2 Control effect under the step disturbance (simulation)

• (2) Case 2

In this case, a time-varying disturbance d_e= (0.3sin(15t) +1.5) N m is added at 1.4 s, and the designed controller is verified at different speeds of 500 rpm, 1200 rpm and 800 rpm. Figure 10 shows that the CSO has smaller estimation error for the time-varying disturbance and more effective restraining action to high-frequency noise than the GESO. As shown in Fig. 11, since the conventional SMC (k = 2×10⁴) cannot completely reject the disturbance, the speed fluctuation exists in steady state and its amplitude is about 8.1 rpm (the speed fluctuation is calculated by ω_max − ω_min). And the chattering of control input is severe as shown in Fig. 11b. From Fig. 12, the disturbance rejection is improved by the SMC + GESO (k = 400). But, owing to larger estimation error of GESO, the speed fluctuation in steady state still exists and its amplitude is about 5.2 rpm. And the control input contains larger noise. Comparatively, in the case of the proposed method, the disturbance influence is greatly suppressed because of the high estimation accuracy of the CSO, and the speed fluctuation in steady state is reduced to 1.3 rpm as shown in Fig. 13a. And the switching gain k converges fast and steadily to a smaller value (k = 7.3) under the adaptive law, which significantly reduces the chattering (see Fig. 13b). And the influence of the measurement noise is effectively attenuated by the CSO. The detailed comparison is given in Table 3.

Fig. 10

Lumped disturbance estimation (simulation). a CSO, b GESO

Fig. 11

Control effects under the time-varying disturbance with SMC (simulation). a Speed, b control input, c q-axis current

Fig. 12

Control effects under the time-varying disturbance with the SMC + GESO (simulation). a Speed, b control input, c q-axis current

Fig. 13

Control effects under the time-varying disturbance with the proposed control method (simulation). a Speed, b control input, c q-axis current, d switching gain k

Table 3 Control effect under the time-varying disturbance (simulation)

• (3) Case 3

In order to validate the operation at low speed, the speed reference is set to 100 rpm at 0 s and zero at 6 s. And to validate the robustness to parameter uncertainty, the nominal value of J is set to 2 J^*, the nominal value of $L_{s}$ is set to 1.3 $L_{s}^{*}$, and the stator resistance of PMSM is changed to R = 3R^* at 3 s, where the superscript “ ^* ” represents the measured value of parameters given in Table 1. And the added load torque is 2 N m. From Fig. 14, it can be observed that the CSO possesses higher disturbance estimation accuracy and better noise insensitivity than the GESO. Comparing Figs. 15, 16 and 17, it can be seen that with the proposed method, the speed drop when resistance is changed, is 20 rpm, which is smaller than the results with SMC and SMC + GESO. And since the switching gain k converges to 0.5 under the adaptive law, the chattering of control input is greatly reduced. The detailed comparison is given in Table 4.

Fig. 14

Lumped disturbance estimation (simulation). a CSO, b GESO

Fig. 15

Control effects under the parameter variation with SMC (simulation). a Speed, b control input, c q-axis current

Fig. 16

Control effects under the parameter variation with the SMC + GESO (simulation). a Speed, b control input, c q-axis current

Fig. 17

Control effects under the parameter variation with the proposed control method (simulation). a Speed, b control input, c q-axis current, d switching gain k

Table 4 Control effect under the parameter uncertainty (simulation)

5.2 Experiment results

The experimental platform is shown in Fig. 18. A switching power is used to provide DC power for PMSM control system. The control algorithm is implemented by the program of TMS320F28069 with a clock frequency of 90 MHz. The PMSM is driven by a three phase voltage source inverter using MOSFET with a switching frequency of 30 kHz. The sampling frequency of the current loop and the speed loop is 15 kHz and 1 kHz. The Hall effect device is used to measure the currents, an incremental encoder of 2500 lines is used to measure the rotor speed, and a torque sensor is adopted to measure the electromagnetic torque. A magnetic remanence brake whose maximum output torque is 3 N m with an adjustable current source is used to provide the load. The parameters of the controller and the adaptive law are the same as the simulation. The experimental data are downloaded from DSP after execution.

Fig. 18

Experimental platform

It should be noted that the torque sensor is used here to ensure that the magnetic remanence brake outputs the required load torque and its value will not exceed the rated torque of PMSM.

• (1) Case 1

The speed reference is 1000 rpm, and a step load disturbance T_L= 1.5 N m is added at 6 s. The control effects with the three methods are shown in Figs. 19, 20 and 21, respectively. It can be seen that when the step disturbance occurs, since there is no disturbance compensation, both the speed drop and the recovery time with the conventional SMC, which, respectively, are 51.4 rpm and 1.2 s (see Fig. 19a), are large. Comparing Figs. 20 and 21, since CSO possesses the better estimation performance for the lumped disturbance, the ASMC + CSO significantly reduces the speed drop and the recovery time. And the switching gain k converges to 0.66 under the adaptive law (see Fig. 21c), which is much smaller than method 1 and 2, thus the chattering is reduced. Besides, owing to the preferable noise-restrain effect of CSO, the influence of the encoder measurement noise is attenuated. The detailed comparisons of the control effect are given in Table 5.

Fig. 19

Control effects under the step disturbance with SMC (experiment). a Speed, b q-axis current

Fig. 20

Control effects under the step disturbance with the SMC + GESO (experiment). a Speed, b q-axis current

Fig. 21

Control effects under the step disturbance with the proposed method (experiment). a Speed, b q-axis current, c switching gain k

Table 5 Control effect under the step disturbance (experiment)

• (2) Case 2

The controller is verified at different speeds of 500 rpm, 1200 rpm and 800 rpm, and a time-varying disturbance d_e= (0.3sin(15t) + 1.5) N m is added at 1.4 s. Figures 22, 23 and 24 show the control effect using the three methods. It can be observed that owing to the accurate disturbance estimation by the CSO, the speed fluctuation in steady state is about 4.8 rpm with the proposed method, which is obviously smaller than the conventional SMC (14.5 rpm) and SMC + GESO (9.4 rpm). Furthermore, the switching gain k converges to 13.8 of a smaller value under the adaptive law. The detailed comparisons are given in Table 6.

Fig. 22

Control effects under the time-varying disturbance with SMC (experiment). a Speed, b q-axis current

Fig. 23

Control effects under the time-varying disturbance with the SMC + GESO (experiment). a Speed, b q-axis current

Fig. 24

Control effects under the time-varying disturbance with the proposed method (experiment). a Speed, b q-axis current, c switching gain k

Table 6 Control effect under the time-varying disturbance (experiment)

• (3) Case 3

In order to validate the operation at low speed, the speed reference is set to 100 rpm at 0 s and zero at 6 s. And to validate the robustness to parameter uncertainty, the nominal value of J is set to 2 J^*, the nominal value of $L_{s}$ is set to 1.3 $L_{s}^{*}$, and the stator resistance of PMSM is changed to R = 3R^* at 3 s. The added load torque is 2 N m. Comparing Figs. 25, 26 and 27, it can be seen that when stator resistance is changed, the speed drop is about 76 rpm with conventional SMC, 56 rpm with SMC + GESO, and 35 rpm with proposed method. And, the switching gain converges to about 0.7 in steady state under the adaptive law, which is much smaller than the one in SMC and SMC + GESO, so the chattering is greatly reduced. Besides, at low speed, the influence of the speed measurement noise is also attenuated by the CSO. The detailed comparison is given in Table 7.

Fig. 25

Control effects under the parameter uncertainty with SMC. a Speed, b q-axis current

Fig. 26

Control effects under the parameter uncertainty with the SMC + GESO (experiment). a Speed, b q-axis current

Fig. 27

Control effects under the parameter uncertainty with proposed method (experiment). a Speed, b q-axis current, c switching gain k

Table 7 Control effect under the parameter uncertainty (simulation)

6 Conclusions

This paper proposes a new disturbance estimation technique called combined state/disturbance observer (CSO), and designs an adaptive sliding mode control (ASMC) based on CSO for PMSM speed control. The CSO is developed to estimate the speed derivative and the lumped disturbance of PMSM including the parameter perturbations and the external disturbances. The theoretical analysis shows that both the estimation accuracy and the noise-restrain ability can be simultaneously improved, which is the main advantage of CSO compared with the generalized extended state observer (GESO). Then, a sliding mode controller for PMSM, in which a disturbance feed-forward compensation is introduced, is designed. Furthermore, a simple nonlinear adaptive law is presented to solve the unknown upper bound of the disturbance estimation error and minimize the chattering. The global stability of the closed-loop system with the proposed method is guaranteed.

In the simulations and the experiments, three control methods are compared under the step disturbance, the time-varying disturbance and the parameter uncertainty, respectively. The results show that the CSO possesses preferable estimation accuracy and noise insensitivity. And the ASMC + CSO has the better speed tracking performance and the smaller chattering in the presence of different disturbances and parameter uncertainty.

Appendices

Appendix A

Proof

Define the following state variables: $x_{0} = \int_{0}^{t} {x_{1} (t)} {\text{d}}t$, $x_{ - 1} = \int_{0}^{t} {x_{0} (t){\text{d}}t}$, …, and $x_{{1 - r_{1} }} = \int_{0}^{t} {x_{{1 - (r_{1} - 1)}} (t){\text{d}}t}$, the system (6) can be rewritten as

$$ \left\{ {\begin{array}{*{20}l} {\dot{x}_{{1 - r_{1} }} = x_{{1 - (r_{1} - 1)}} } \hfill \\ \vdots \hfill \\ {\dot{x}_{1} = x_{2} } \hfill \\ {\dot{x}_{2} = u + x_{3} } \hfill \\ {\dot{x}_{3} = \dot{D}} \hfill \\ \vdots \hfill \\ {\dot{x}_{{n + 2 - r_{1} }} = D^{{(n - r_{1} )}} } \hfill \\ \end{array} } \right. $$

(A1)

For system (A1), a GESO is designed as

$$ \left\{ {\begin{array}{*{20}l} {\dot{\eta }_{{1 - r_{1} }} = \eta_{{1 - (r_{1} - 1)}} - \omega_{0} k_{1} \xi_{1} } \hfill \\ \vdots \hfill \\ {\dot{\eta }_{1} = \eta_{2} - \omega_{0}^{{r_{1} + 1}} k_{{r_{1} + 1}} \xi_{1} } \hfill \\ {\dot{\eta }_{2} = u + \eta_{3} - \omega_{0}^{{r_{1} + 2}} k_{{r_{1} + 2}} \xi_{1} } \hfill \\ {\dot{\eta }_{3} = \eta_{4} - \omega_{0}^{{r_{1} + 3}} k_{{r_{1} + 3}} \xi_{1} } \hfill \\ \vdots \hfill \\ {\dot{\eta }_{{n + 2 - r_{1} }} = - \omega_{0}^{n + 2} k_{n + 2} \xi_{1} } \hfill \\ \end{array} } \right. $$

(A2)

where $\xi_{1} = \eta_{{1 - r_{1} }} - x_{{1 - r_{1} }}$, $k_{i} = \left( {n + 2} \right)!/i! \times (n + 2 - i)!$, and $- \omega_{0}$ is the desired pole. Supposing $\xi = [\xi_{1} , \ldots ,\xi_{n + 2} ] = [\eta_{{1 - r_{1} }} - x_{{1 - r_{1} }} ,\eta_{{1 - (r_{1} - 1)}} - x_{{1 - (r_{1} - 1)}} , \ldots ,\eta_{{n + 2 - r_{1} }} - x_{{n + 2 - r_{1} }} ]$, and subtracting (A1) from (A2) we have

$$ \left\{ {\begin{array}{*{20}l} {\dot{\xi }_{1} = \xi_{2} - \omega_{0} k_{1} \xi_{1} } \hfill \\ {\dot{\xi }_{2} = \xi_{3} - \omega_{0}^{2} k_{2} \xi_{1} } \hfill \\ \vdots \hfill \\ {\dot{\xi }_{n + 2} = - \omega_{0}^{n + 2} k_{n + 2} \xi_{1} - D^{{(n - r_{1} )}} } \hfill \\ \end{array} } \right. $$

(A3)

By using Laplace transform of (A2) and (A3), the following equation can be obtained

$$ \begin{aligned} \eta_{2} (s) & = \frac{{l_{{r_{1} + 2}} s^{{n - r_{1} }} + l_{{r_{1} + 3}} s^{{n - r_{1} - 1}} + \cdots + l_{n + 2} }}{{s^{n + 2} + l_{1} s^{n + 1} + l_{2} s^{n} + \cdots + l_{n + 2} }}x_{2} (s) \\ & \quad + \frac{{s^{n + 1} + l_{1} s^{n} + \cdots + l_{{r_{1} + 1}} s^{{n - r_{1} }} }}{{s^{n + 2} + l_{1} s^{n + 1} + l_{2} s^{n} + \cdots + l_{n + 2} }}u(s) \\ \end{aligned} $$

(A4)

Comparing (A4) with (17), it can be seen that $\hat{x}_{2} (s) = \eta_{2} (s)$, so $\hat{x}_{2} (t) = \eta_{2} (t)$. Then using the theorem in [27], for GESO (A2), there is $\lim_{t \to \infty } \left| {\eta_{2} - x_{2} } \right| \le O(\varepsilon^{{n + 1 - r_{1} }} )$, where ε = 1/ω₀. Thus $\lim_{t \to \infty } \left| {\hat{x}_{2} - x_{2} } \right| \le O(\varepsilon^{{n + 1 - r_{1} }} )$ is satisfied. Similarly, $\lim_{t \to \infty } \left| {\hat{D} - D} \right| \le O(\varepsilon^{{n - r_{2} }} )$ can be proved. Thus, Theorem 1 is proved.

Here, the existing results of GESO are used in the proof of Theorem 1. And it can be seen that the GESO (A2) achieves the same estimation as the CSO. However, (A2) cannot be implemented because the “integral saturation” problem will appear when calculating x₀, $x_{ - 1}$, …, $x_{{1 - r_{1} }}$. The CSO uses the linear combination of the extended high-order states to generate the unknown state and disturbance estimations, so this problem is eliminated.

Appendix B

Proof

When x = 0, it can be easy known f(0) = 0. When x > 0, if k < k_d, defining $g(x) = f^{'} (x) = - 2k_{s} x - (k - k_{d} ) + \frac{1}{\lambda }(k - k_{d} )k_{m} px^{p - 1}$, then $g^{'} (x) = - 2k_{s} + \frac{1}{\lambda }(k - k_{d} )k_{m} p(p - 1)x^{p - 2}$ can be obtained. Supposing $g^{'} (x_{0} ) = 0$, we have

$$ x_{0} = \left(\frac{{2k_{s} \lambda }}{{(k - k_{d} )k_{m} p(p - 1)}}\right)^{{\frac{1}{p - 2}}} $$

(B1)

It can be known that x₀ > 0. Noting $g^{''} (x_{0} ) = (k - k_{d} )k_{m} {{p(p - 1)(p - 2)x_{0}^{p - 3} } \mathord{\left/ {\vphantom {{p(p - 1)(p - 2)x_{0}^{p - 3} } \lambda }} \right. \kern-0pt} \lambda }$, and considering k < k_d, 0 < p < 1 and x₀ > 0, there is $g^{''} (x_{0} ) < 0$. Thus the maximum value of g(x) is g(x₀), i.e., g(x) ≤ g(x₀). Selecting $\lambda = {{(k - k_{d} )k_{m} p(p - 1)} \mathord{\left/ {\vphantom {{(k - k_{d} )k_{m} p(p - 1)} {2k_{s} }}} \right. \kern-0pt} {2k_{s} }} \cdot \left[ { - \frac{1}{{2k_{s} }}(k - k_{d} )} \right]^{p - 2} > 0$, and substituting it into (B1), we have $x_{0} = - \frac{1}{{2k_{s} }}(k - k_{d} )$. Substituting x₀ into g(x), it yields

$$ g(x_{0} ) = {{(k - k_{d} )k_{m} px_{0}^{p - 1} } \mathord{\left/ {\vphantom {{(k - k_{d} )k_{m} px_{0}^{p - 1} } \lambda }} \right. \kern-0pt} \lambda } $$

(B2)

Because x₀ > 0, there is g(x₀) < 0, and thus $f^{'} (x) = g(x) \le g(x_{0} ) < 0$ for all x > 0.

If k = k_d, there is $f(x) = - k_{s} x^{2}$, it is obvious that $f^{'} (x) = - 2k_{s} x < 0$ for all $x > 0$. Therefore, there exists a positive real number λ such that $f^{'} (x) < 0$ for all x > 0. And noting that f(0) = 0 and f(x) is continuous, it can be known that $f(x) \le 0$ for all $x \ge 0$. Lemma 2 is proved.