On suppression of chaotic motion of a nonlinear MEMS oscillator

Abstract

This work investigates the behavior of the linear and nonlinear stiffness terms and damping coefficient related to the dynamics of a microelectromechanical resonator. The system is controlled by forcing it into an orbit obtained from the analytical solution of the harmonic balance method. The control techniques considered are the polynomial expansion of Chebyshev, the Picard interactive method, Lyapunov–Floquet, OLFC control, and SDRE controls. Additionally, in order to study the thermal effects, the effect of damping with fractional-order was implemented. To analyze the behavior of the system in fractional-order, the wavelet-based scale index test was carried out. In addition, the control robustness is investigated analyzing the parametric errors, and the sensitivity of the fractional derivative variation.

1 Introduction

The interest for smaller devices which are capable of measuring minimal electric or mechanical signs has grown in several technological areas. A prominent device is the microelectromechanical system (MEMS), which is of reduced mass, large-scale production, and high sensitivity. Consequently, this technology became popular among manufacturers and attracted many researchers due to their nonlinear behavior, ability to convert mechanical energy into electrical energy and reduced number of variables. MEMS have been used in different applications, such as sensing, and actuation, being considered for spring and damped systems [1], nonlinear RCL circuits [2], nonlinear fluids and surfaces [3].

Microresonators present nonlinear behavior and are mathematically modeled as in [4, 5]. In addition, they have high amplitude and frequency, which makes the initial parameters of the project deviate from the fabrication. As a result, many control strategies are implemented in MEMS.

Firstly, Younis and Nayfeh [3] implemented a high-frequency voltage that suppresses instabilities in electronic MEMS. A similar study with parametric error and applying an optimal linear feedback control was used with fractional-order in Tusset et al. [6, 7]. Further, a time delay feedback controller applied in a microresonator subjected to AC and DC voltages was shown in Shao et al. [8]. A third situation was demonstrated in Rhoads et al. [9], in which the chaotic behavior of a microcantilever beam was studied for a set of parameters. Other studies analyzed the dynamics of these systems through bifurcation diagrams considering limited power and their operating temperature [10].

The presence of damping in MEMS is a challenge due to the high constraint of the dynamics of the system. Squeeze-film damping is the most common damping source of MEMS, which is of great interest in the field. On the other hand, other damping source which is recurrently under interest is the thermoelastic damping, which is caused from the irreversible heat flow generated by the compression and decompression of the oscillation of the resonator [3]. Hence, the thermoelastic effect in the behavior of a MEMS resonator is investigated. The model of the micro resonator is considered with the thermal effect of the damping with fractional-order (FODE system) [11, 12]. In addition, the influence of the damping coefficients neglecting the fractional-order, linear and nonlinear stiffness on the dynamics of the system (ODE system) is studied. The MEMS system is subjected to electrostatic DC and AC voltages excitations such that it can exhibit negative linear stiffness coefficient which modulates the geometric stiffness to the point that it can overcome the positive stiffness coefficient [13,14,15,16].

To confirm whether the behavior is chaotic or periodic, the use of phase diagrams, time histories, bifurcation diagrams and Lyapunov exponents for the ODE system is considered. For the case of the system in fractional-order, the wavelet-based index scale test is carried out [17].

In order to suppress the chaotic behavior, three control techniques are considered and implemented. The control proposals consider feedforward and feedback, the Optimum Linear Feedback (OLFC) control project, and the state-dependent Riccati equation (SDRE) that will drive chaotic behavior to a desired periodic orbit found as a solution of the Harmonic Balance Method [18,19,20,21]. The first applied control technique is obtained by using the polynomial expansion of Chebyshev and the interaction of the Piccard and Lyapunov–Floquet (LF) transformation [22,23,24,25,26]. The second technique, OLFC, is proposed by Rafikov and Balthazar [27]. The theorem formulated by Rafikov and Balthazar [27] provides sufficient conditions that allow the use of a linear feedback control for nonlinear systems. The SDRE technique was proposed by Pearson [28] and then expanded by Wernli and Cook [29]. Subsequently, this technique was studied by Mracek and Cloutier [30] and alluded by Friedland [31]. It is one of the most popular techniques among researchers in the control field. The SDRE method is a nonlinear control technique which produces a feedback control law that is a function of the states. The method linearizes the system by about one point, allowing the use of LQR (Linear Quadratic Regulator).

In this way, the present paper is organized in the following structure: Sect. 2 characterizes the mathematical modeling and dynamic analysis. In Sect. 3, the proposed control by Interaction Piccard Method and Transformation Lyapunov–Floquet, OLFC, and SDRE are implemented and analyzed. Section 4 details the parametric errors and control robustness. In Sect. 5, the chaos is analyzed and the control for MEMS system with a fractional-order is implemented. And finally, the conclusions are given.

2 Microelectromechanical system (MEMS)

Figure 1 shows a schematic of a MEMS which consists of two fixed plates and a movable plate between them, at which is applied a voltage V(t) composed of a polarization voltage (DC) ${V}_{p}$, an alternating voltage (AC) ${V}_{i}$sin(wt), d (distance between the plates), x (horizontal movement) and m (front panel mass).

Fig. 1

Microelectromechanical resonator (MEMS)

Considering as in [32,33,34,35,36], the mathematical model for the MEMS, represented by Fig. 1, can be written as follows:

$$\begin{aligned}&m\ddot{x}+k_1 x+k_3 x^{3}+c\dot{x}\nonumber \\&\quad =\frac{1}{2}\frac{C_0 }{\left( {d-x} \right) ^{2}}\left( {V_p +V_i \sin (wt)} \right) \nonumber \\&\quad -\frac{1}{2}\frac{C_0 }{\left( {d+x} \right) ^{2}}V_p^2 \end{aligned}$$

(1)

where ${C}_{0}$ represents the capacitance of the parallel-plate actuator, $k_{1}$ is the linear stiffness, $k_{3}$ is the nonlinear stiffness and c is the damping coefficient. Equation 1 represents a lumped-parameters model of a MEMS device, which can also be considered for a nonlinear dynamic analysis [5,6,7,8, 12, 13, 25, 26, 32,33,34,35,36].

The nonlinear electrostatic terms of Eq. (1) can be expanded up to the third order based on the Taylor series expansion method, which is represented by the following equation [32,33,34,35,36]:

$$\begin{aligned} \ddot{x}= & {} -\mu {\dot{x}}-k_l x-k_{nl} x^{3}\nonumber \\&\quad +\,\alpha \left( {1+2x+3x^{2}+4x^{3}} \right) \sin (wt) \end{aligned}$$

(2)

where $\mu =\frac{c}{m},k_l =\frac{k_1 }{m} , k_{nl} =\frac{k_3 }{m}, \gamma =\frac{C_{\mathrm{0}} {V}_{p}^{\mathrm{2}} }{2md^{2}}$ and $\alpha =\frac{2\gamma V_i }{V_p }$.

2.1 Dynamical analysis

Consider Eq. (2) in the state-space notation:

$$\begin{aligned} {\dot{x}}_1= & {} x_2 \nonumber \\ {\dot{x}}_2= & {} -\mu x_2 -k_l x_1 -k_{nl} x_1^3 \nonumber \\&+\,\alpha \left( {1+2x_1 +3x_1^2 +4x_1^3 } \right) \sin (wt) \end{aligned}$$

(3)

Figure 2 depicts bifurcation diagrams that show the dynamic behavior of Eq. (3) considering the following initial conditions and parameters: $x_1 (0)=0.0001, x_2 (0)=0.0006, \alpha =0.64, \mu =[0{:}0.8], k_l =[-\,10{:}5], k_{nl} =[4{:}20]$ and $w=1$.

Fig. 2

Bifurcation diagram. a$k_l =[-\,10{:}5], \mu =0.03$ and $k_{nl} =9.296$. b$k_{nl} =[4{:}20], \mu =0.03$ and $k_l =-\,0.352$. c$\mu =[0{:}0.8], k_l =-\,0.352$ and $k_{nl} =9.296$

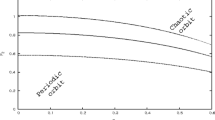
For certain variations of the parameters ($\mu , k_l$, and $k_{nl} )$, the system shows an evidence of chaotic and periodic behaviors. Figure 3 shows the variation of the highest Lyapunov exponent for the same variations of the parameters ($\mu =[0{:}0.8], k_l=[-\,10{:}5]$, and $k_{nl} =[4{:}20])$.

Fig. 3

Highest Lyapunov exponent, a$k_l =[-\,10{:}5]$, b$k_{nl} =[4{:}20]$, c$\mu =[0{:}0.8]$

It is observed that for individual variations of the parameters ($\mu$, $k_l$, and $k_{nl} )$, Eq. (3) presents chaotic behavior. In Fig. 4, it is possible to observe the dynamic behavior of Eq. (3) through the Lyapunov maps varying both three parameters in three different combinations.

Fig. 4

Highest Lyapunov exponent. a$k_{nl} =[4{:}20]$ versus $k_l =[-\,10{:}5]$. b$\mu =[0{:}0.8]$ versus $k_{nl} =[4{:}20]$. c$k_l =[-\,10{:}5]$ versus $k_{nl} =[4{:}20]$

As shown in Fig. 4a, when the linear stiffness coefficient ($k_l )$ is negative, the system obtains the highest value for the Lyapunov exponent. However, the main obstacle that needs to be overcome in the design process is to create a negative linear stiffness ($k_l <0)$. According to the authors in [13], to overcome this seemingly unphysical condition, the movable plate can be chosen so that, under a certain reasonable $V_{p}$, the stiffness ($k_l )$ is negative.

Considering the parameters: $\alpha =0.64$, $\mu =0.03$, $k_l =-\,0.352$, $k_{nl} =9.296$ and $w=1$, Fig. 5 shows the dynamic behavior of the system for these parameters by means of Poincare map, phase plane, time history of displacement, Lyapunov exponent, and FFT. These results show the chaotic behavior of the system, which is even proved by the positive Lyapunov exponent $\uplambda _{1}$ = 0.093 in Fig. 5d.

Fig. 5

Dynamics of the microelectromechanical oscillator (MEMS), a displacement in time, b phase plane, c poincare map, d Lyapunov exponent, e FFT

To find a periodic orbit which is desired for the controls, the harmonic balance method (HBM) is applied and shown in the next section.

2.2 Perturbation technique solution by HBM

The harmonic balance method consists of the application of a harmonic solution to calculate the steady-state response of a nonlinear differential equation. Consider the equation of motion of the system:

$$\begin{aligned}&\ddot{x}+\mu {\dot{x}}+k_l x+k_{nl} x^{3}\nonumber \\&\quad -\,\alpha \left( {1+2x+3x^{2}+4x^{3}} \right) \sin (wt)=0 \end{aligned}$$

(4)

The solution to be considered to solve the system is a linear and a nonlinear part of a harmonic solution, depending on the order of the system. The generalized solution for the HBM is considered as [18,19,20,21]:

$$\begin{aligned} x\left( t \right)= & {} a\sin \left( {\omega t} \right) +b\sin \left( {2\omega t} \right) \nonumber \\&+\,c\cos \left( {2\omega t} \right) +d\sin \left( {3\omega t} \right) +e\cos \left( {3\omega t} \right) \nonumber \\ \end{aligned}$$

(5)

Considering the response of the system of the third order (n = 3), Eq. (5) and their respective derivatives are introduced into Eq. (4), and in addition, manipulating trigonometric terms to reduce their order and selecting each of the respective terms of the given solution, a system of five equations and five variables a, b, c, d,  and e is obtained, which are Eqs. (A.1)–(A.5) in “Appendix A.”

Solving the system of Eqs. (A.1)–(A.5) in “Appendix A,” the values of the constants solved in Real space, that is an approximation of the numerical integration, are $a=0.34309, b=-\,0.00615, c=-\,0.80198, d=0.03027$ and $e=0.02952$.

Then, such response is shown in the phase portrait of the chaotic numerical solution and perturbation technique solution by Eq. (4), which is:

In Fig. 6, it is possible to observe the periodic behavior of Eq. (4) with the solution of the HBM of the third order. The method allowed to study a lot of orbits, stable or not, which are related to the equations of motion. However, most of them are either nonphysical or they are trajectories far from the trajectory drawn by the numerical integration of the equations (the chaotic trajectory of the phase plane). For this reason, this trajectory is the one which fits on the chaotic trajectory, which means that is one predicted from the infinite possible trajectories due to chaos.

With that, the next section will treat about the control of the system by considering this trajectory as the aimed one to lead the chaos to.

3 Control using the optimal control

Chaotic behavior in the system can be avoided with the performance of a control strategy which, in this work, uses an optimal linear feedback control. In this way, there is the objective of finding the optimal control such that the response of the controlled system of Eq. (4) results in a periodic orbit ${\tilde{x}}$ stable asymptotically. Considering the introduction of the control signal U in Eq. (3), it has:

$$\begin{aligned} {\dot{x}}_1= & {} x_2 \nonumber \\ {\dot{x}}_2= & {} -\,\mu x_2 -k_l x_1 -k_{nl} x_1^3 \nonumber \\&+\,\alpha \left( {1+2x_1 +3x_1^2 +4x_1^3 } \right) \sin (wt)+U \end{aligned}$$

(6)

where $x_1 =x, x_2 ={\dot{x}}$ and $U=u+{\tilde{u}}, u$ is the state feedback control and ${\tilde{u}}$ is the feedforward control.

3.1 Control I: control using Picard interaction and Lyapunov–Floquet transformation

Considering that $U=U_1$, where $U_1 =u{ }_1+{\tilde{u}}_1 , u_1$ is the state feedback control, and ${\tilde{u}}_1$ is the feedforward control, the control that maintains the system in the desired trajectory. The feedforward control (${\tilde{u}}_1 )$ is given by Sinha et al. [37]:

$$\begin{aligned} {\tilde{u}}_1= & {} \ddot{{\tilde{x}}}+\mu \dot{\tilde{x}}+k_l {\tilde{x}}+k_{nl} {\tilde{x}}^{3}\nonumber \\&-\,\alpha \left( {1+2\tilde{x}+3{\tilde{x}}^{2}+4{\tilde{x}}^{3}} \right) \sin (wt) \end{aligned}$$

(7)

where ${\tilde{x}}$ is desired periodic orbit Eq. (5).

Substituting Eq. (7) into Eq. (6) and defining the desired trajectory errors as:

$$\begin{aligned} \left[ {{\begin{array}{l} {e_1 } \\ {e_2 } \\ \end{array} }} \right] =\left[ {{\begin{array}{l} {x_1 -{\tilde{x}}_1 } \\ {x_2 -{\tilde{x}}_2 } \\ \end{array} }} \right] \end{aligned}$$

(8)

and substituting $u_1$ in the controlled Eq. (6), it has:

$$\begin{aligned} {\dot{e}}_1= & {} e_2 \nonumber \\ {\dot{e}}_2= & {} -\mu e_2 -k_l e_1 -k_{nl} \left( {e_1 +{\tilde{x}}_1 } \right) ^{3}\nonumber \\&+\,2\alpha \left( {e_1 +{\tilde{x}}_1 } \right) ^{3}\sin (wt)\nonumber \\&+\,3\alpha \left( {e_1 +{\tilde{x}}_1 } \right) ^{2}\sin (wt) \nonumber \\&+\,4\alpha \left( {e_1 +{\tilde{x}}_1 } \right) ^{3}\sin (wt)+u_1 \end{aligned}$$

(9)

Equation (9), whose main period is $T=\pi$, can be rewritten in a normalized space-state form, whose period is one (1), as:

$$\begin{aligned} {{\dot{\mathbf{e}}}{} \mathbf{(t)}}=\mathbf{A(t)e(t)}+\mathbf{B(t)u}_1 \end{aligned}$$

(10)

where

$$\begin{aligned} \mathbf{A(t)}= & {} \mathbf{A}_\mathbf{0} +\mathbf{A}_\mathbf{1} \cos (t)+\mathbf{A}_\mathbf{2} \sin ( t)\nonumber \\&+\,\mathbf{A}_\mathbf{3} \cos (2 t) +\mathbf{A}_\mathbf{4} \sin (2 t) \nonumber \\&+\,\mathbf{A}_\mathbf{5} \cos (3 t) +\mathbf{A}_\mathbf{6} \sin (3t)\nonumber \\&+\,\mathbf{A}_\mathbf{7} \cos (4 t)+\mathbf{A}_\mathbf{8} \sin (4t)+\mathbf{A}_\mathbf{9} \cos (5 t) \nonumber \\&+\,\mathbf{A}_{\mathbf{10}} \sin (5 t)+\mathbf{A}_{\mathbf{11}} \cos (6 t) +\mathbf{A}_{\mathbf{12}} \sin (6 t)\nonumber \\ \end{aligned}$$

(11)

with $\mathbf{A}_\mathbf{0} =\left[ {{\begin{array}{cc} 0&{} 1 \\ {-\,9.3237}&{}\quad {-\,0.03} \\ \end{array} }} \right] ; \mathbf{A}_\mathbf{1} =\left[ {{\begin{array}{cc} 0&{}\quad 0 \\ {0.6849}&{}\quad 0 \\ \end{array} }} \right] ; \mathbf{A}_\mathbf{2} =\left[ {{\begin{array}{cc} 0&{}\quad 0 \\ {-\,3.227}&{}\quad 0 \\ \end{array} }} \right] ; \mathbf{A}_\mathbf{3} =\left[ {{\begin{array}{cc} 0&{}\quad 0 \\ {-\,2.209}&{}\quad 0 \\ \end{array} }} \right] ; \mathbf{A}_\mathbf{4} =\left[ {{\begin{array}{cc} 0&{}\quad 0 \\ {0.1613}&{}\quad 0 \\ \end{array} }} \right] ; \mathbf{A}_\mathbf{5} =\left[ {{\begin{array}{cc} 0&{}\quad 0 \\ {0.0948}&{}\quad 0 \\ \end{array} }} \right] ;\mathbf{A}_\mathbf{6} =\left[ {{\begin{array}{cc} 0&{}\quad 0 \\ {6.35}&{}\quad 0 \\ \end{array} }} \right] ; {} \mathbf{A}_\mathbf{7} =\left[ {{\begin{array}{cc} 0&{}\quad 0 \\ {-\,7.7157}&{}\quad 0 \\ \end{array} }} \right]$; $\mathbf{A}_\mathbf{8} =\left[ {{\begin{array}{cc} 0&{}\quad 0 \\ {-\,0.3213}&{}\quad 0 \\ \end{array} }} \right] ; \mathbf{A}_\mathbf{9} =\left[ {{\begin{array}{cc} 0&{}\quad 0 \\ {0.5989}&{}\quad 0 \\ \end{array} }} \right] ; \mathbf{A}_{\mathbf{10}} =\left[ {{\begin{array}{cc} 0&{}\quad 0 \\ {1.8771}&{}\quad 0 \\ \end{array} }} \right] ; A_{11} =\left[ {{\begin{array}{cc} 0&{}\quad 0 \\ {0.0948}&{}\quad 0 \\ \end{array} }} \right] ; \mathbf{A}_{\mathbf{12}} =\left[ {{\begin{array}{cc} 0&{}\quad 0 \\ {-\,0.0498}&{}\quad 0 \\ \end{array} }} \right]$ and $\mathbf{B(t)}=\left[ {{\begin{array}{cc} 0 \\ 1 \\ \end{array} }} \right]$.

Factoring the monodromy matrix of Eq. (15) as ${\varvec{{\varphi }}}(T)=\mathbf{Q}(t)e^{Rt}$, where $R=\frac{\phi ^{2}(T)}{2T}$ is a real constant matrix, $\mathbf{Q}(t)={\varvec{{\phi }}}(T)e^{-Rt}$ being the Lyapunov–Floquet transformation matrix [33], and applying the Lyapunov–Floquet transformation $z(t)=\mathbf{Q}(t)\mathbf{q}(t)$, original Eq. (10) reduces to a dynamically equivalent time-invariant system [21], which is depicted as:

$$\begin{aligned} {{\dot{\mathbf{q}}}}(t)=\mathbf{Rq}(t)+\mathbf{Q}^{-1}(t)\mathbf{B}(t)\mathbf{u}_1 \end{aligned}$$

(12)

where $\mathbf{R}=\left[ {{\begin{array}{cc} {-\,0.06406215}&{}\quad {-\,0.00345748} \\ {-\,0.35130756}&{}\quad {0.03410286} \\ \end{array} }} \right]$ and $\mathbf{Q}^{-1}(t)$ is the inverse of the Lyapunov–Floquet transformation matrix Q(t). The eigenvalues of Eq. (12) are − 0.07517710 and 0.04521781, indicating the instability of the normalized system. Using the procedures of [21, 37], the state feedback controller $u_1$ is designed to place the unstable poles of system at − 1; − 10, as:

$$\begin{aligned} \mathbf{u}_1 =\mathbf{F}(t)\mathbf{z}(t) \end{aligned}$$

(13)

The term F(t) is the time-varying state feedback matrix defined by:

$$\begin{aligned} \mathbf{F}(t)=\mathbf{BQ}(t){\bar{\mathbf{k}}\mathbf Q}^{-1}(t) \end{aligned}$$

(14)

where $\mathbf{B}^{*}=\left[ {0 \quad 1} \right]$ is a generalized inverse matrix $\mathbf{B}$, and ${\bar{\mathbf{k}}}=\left[ {{\begin{array}{cc} {-\,0.935937}&{}\quad {0.003457} \\ {0.351307}&{}\quad {-\,10.034102} \\ \end{array} }} \right]$ is the matrix of gains that is chosen when applying the pole placement technique.

Figure 7a, b shows the time histories for the controlled systems of Eq. (11). Figure 7c shows the phase portrait of the desired and controlled orbits. Figure 7d shows the desired trajectory errors, and Fig. 7e shows the signal of the control $U_1$. These results show that the proposed control $U_1 =u_1 +{\tilde{u}}_1$ is efficient and could lead the system (Eq. (6)) from the initial state $x_{1_0 }$ and $x_{2_0 }$ to the desired state ${\tilde{x}}_{1_0 }$ and ${\tilde{x}}_{2_0 }$.

Fig. 6

Perturbation technique solution by HBM of third order

3.2 Control II: control using the optimal linear feedback control

Considering now $U=U_2$ where $U_2 =u_2+{\tilde{u}}_2 , u_2$ is the state feedback control, ${\tilde{u}}_2$ is the feedforward control. The feedforward control, which maintains the system in the desired trajectory, is given by:

$$\begin{aligned} {\tilde{u}}_2= & {} \ddot{{\tilde{x}}}+\mu \dot{\tilde{x}}+k_l {\tilde{x}}+k_{nl} {\tilde{x}}^{3}\nonumber \\&-\,\alpha \left( {1+2\tilde{x}+3{\tilde{x}}^{2}+4{\tilde{x}}^{3}} \right) \sin (wt) \end{aligned}$$

(15)

Substituting Eq. (15) into Eq. (6), taking the desired trajectory errors of Eq. (8), and also substituting $u_2$ into Eq. (6), it has:

$$\begin{aligned} {\dot{e}}_1= & {} e_2 \nonumber \\ {\dot{e}}_2= & {} -\,\mu e_2 -k_l e_1 -k_{nl} \left( {e_1 +{\tilde{x}}_1 } \right) ^{3}\nonumber \\&+\,2\alpha \left( {e_1 +{\tilde{x}}_1 } \right) ^{3}\sin (wt)+3\alpha \left( {e_1 +{\tilde{x}}_1 } \right) ^{2}\sin (wt) \nonumber \\&+\,4\alpha \left( {e_1 +{\tilde{x}}_1 } \right) ^{3}\sin (wt)+u_2 \end{aligned}$$

(16)

Equation (16) can be represented in deviation as:

$$\begin{aligned} {{\dot{\mathbf{e}}}}=\mathbf{Ae}+\mathbf{G}(e,{\tilde{x}})+\mathbf{Bu}_2 \end{aligned}$$

(17)

Fig. 7

Time histories: a displacement in time. b Velocity in time. c Phase plane. d Desired trajectory errors. e Signal of the control

According to Tusset et al. [6], if there exist matrices $\mathbf{Q}$ and $\mathbf{R}$with positive definite symmetric matrix such that the matrix:

$$\begin{aligned} { {\tilde{\mathbf{Q}}}}=\mathbf{Q}-\mathbf{G}^{\mathbf{T}}(e,\tilde{x})\mathbf{P}-\mathbf{PG}(e,{\tilde{x}}) \end{aligned}$$

(18)

is positive definite for the limited matrix $\mathbf{G}(e,{\tilde{x}})$, then the control $u_2$ is optimal and transfers Eq. (16) from any initial state to final state $\mathbf{e}(\infty )=0$.

Minimizing the functional:

$$\begin{aligned} J=\mathop {\int }\limits _0^\infty ( \mathbf{e}^{\mathbf{T}}{{\tilde{\mathbf{Q}}}} \mathbf{e}+\mathbf{u}_\mathbf{2}^\mathbf{T} \mathbf{R} \mathbf{u}_\mathbf{2} )\mathrm{d}t \end{aligned}$$

(19)

the control $u_{2}$ can be found by solving:

$$\begin{aligned} \mathbf{u}_\mathbf{2} =-\mathbf{R}^{-\mathbf{1}}{} \mathbf{B}^{\mathbf{T}}{} \mathbf{Pe} \end{aligned}$$

(20)

The symmetric matrix $\mathbf{P}$ can be found from the algebraic Riccati equation:

$$\begin{aligned} \mathbf{PA}+\mathbf{A}^{\mathbf{T}}{} \mathbf{P}-\mathbf{PBR}^{-\mathbf{1}}{} \mathbf{B}^{\mathbf{T}}{} \mathbf{P}+\mathbf{Q}=\mathbf{0} \end{aligned}$$

(21)

According to Rafikov and Balthazar [27], to analyze cases in which the matrix ${ {\tilde{\mathbf{Q}}}}$ is analytically difficult, it is possible to analyze numerically considering the function:

$$\begin{aligned} \mathbf{L}\left( t \right) =\mathbf{e}^{\mathbf{T}}{\tilde{\mathbf{Q}}} \mathbf{e} \end{aligned}$$

(22)

calculated on the optimal debt trajectory, where $\mathbf{L}(t)$ is positive definite for any time interval so that the matrix ${ {\tilde{\mathbf{Q}}}}$ is positive defined.

3.2.1 Application of the optimal linear feedback control

Let the matrices $\mathbf{A}$ and $\mathbf{B}$ of Eq. (16) be represented by:

$$\begin{aligned} \mathbf{A}=\left[ {{\begin{array}{cc} 0&{}\quad 1 \\ {-\,k_l }&{}\quad {-\,\mu } \\ \end{array} }} \right] , ~\hbox {and }~\mathbf{B}=\left[ {{\begin{array}{cc} 0 \\ 1 \\ \end{array} }} \right] \end{aligned}$$

(23)

and defined as:

$$\begin{aligned} \mathbf{Q}=\left[ {{\begin{array}{cc} {100}&{}\quad 0 \\ 0&{}\quad {100} \\ \end{array} }} \right] ,~ \hbox {and}~ \mathbf{R}=\left[ 1 \right] \end{aligned}$$

(24)

Equation (21) is then solved, obtaining:

$$\begin{aligned} \mathbf{P}=\left[ {{\begin{array}{cc} {\hbox {109.95002}}&{}\quad {\hbox {10.3582}} \\ {\hbox {10.3582}}&{}\quad {\hbox {10.95714}} \\ \end{array} }} \right] \end{aligned}$$

(25)

The eigenvalues for the system with control are − 1 and − 10. The control signal is obtained as:

$$\begin{aligned} u_2= & {} - 1 0.3582e_1 - 1 0.9571e_2 \nonumber \\= & {} - 1 0.3582(x_1 -{\tilde{x}}_1 )- 1 0.9571(x_2 -\tilde{x}_2 ) \end{aligned}$$

(26)

Figure 8 shows the analyses of the controlled system comparing to the desired orbit. The times histories of displacement, velocity, and phase portrait, shown in Figs. 8a–c, respectively, show that the control $U_{2}$ led the system to the desired orbit (denoted by Eq. 5) with a very small error (see Fig. 8d). In addition, Figure 8e, f shows the signal of the control and L(t) calculated numerically, respectively. It is observed that L(t) remains positive, demonstrating that control Eq. (26) is optimal and that the matrix ${ {\tilde{\mathbf{Q}}}}$ is positive definite.

Fig. 8

Time histories of a displacement and b velocity, c phase portrait, d desired trajectory error, e signal of the control, fL(t) calculated numerically

3.3 Control III: SDRE control design

The proposed SDRE control uses both feedforward and feedback control [6, 7, 35, 38, 39]. The control input is given as $U=U_3$, where $U_3 =u{ }_3+{\tilde{u}}_3 , u_3$ is the state feedback control, and ${\tilde{u}}_3$ is feedforward control.

Substituting the desired trajectory errors from Eq. (8) into the controlled Eq. (6), it has:

$$\begin{aligned} {\dot{e}}_1= & {} e_2 \nonumber \\ {\dot{e}}_2= & {} -\mu e_2 -k_l e_1 -k_{nl} e_1^3 -k_{nl} 3e_1^2 {\tilde{x}}_1 -k_{nl} 3e_1 {\tilde{x}}_1^2 \nonumber \\&+\,\alpha \left( 2e_1 +3e_1^2 +6e_1 {\tilde{x}}_1 +4e_1^3 +12e_1^2 {\tilde{x}}_1 +12e_1 {\tilde{x}}_1^2 \right) \sin (wt) \nonumber \\&+\,\alpha \left( {1+2{\tilde{x}}_1 +3{\tilde{x}}_1^2 +4{\tilde{x}}_1^3 } \right) \sin (wt)\nonumber \\&-\,\dot{{\tilde{x}}}_2 -\mu {\tilde{x}}_2 -k_l {\tilde{x}}-k_{nl} {\tilde{x}}_1^3 +U_3 \end{aligned}$$

(27)

The feedforward control is given by:

$$\begin{aligned} {\tilde{u}}_3= & {} -\alpha \left( {1+2{\tilde{x}}_1 +3\tilde{x}_1^2 +4{\tilde{x}}_1^3 } \right) \sin (wt)+\dot{{\tilde{x}}}_2 \nonumber \\&+\, \mu {\tilde{x}}_2 +k_l {\tilde{x}}_{1}+k_{nl} {\tilde{x}}_1^3 \end{aligned}$$

(28)

Replacing Eq. (28) into Eq. (27), the system of Eq. (27) can be represented in the following form:

$$\begin{aligned} {\dot{\mathbf{e}}}=\mathbf{A}(e_1 ,e_2)\mathbf{e}+\mathbf{Bu}_3 \end{aligned}$$

(29)

where

$$\begin{aligned} \mathbf{A(}e_1 ,e_2 \mathbf{)}=\left[ {{\begin{array}{cc} 0&{}\quad 1 \\ {\begin{array}{cc} -k_l -k_{nl} e_1^2 -3k_{nl} e_1 {\tilde{x}}-3k_{nl} {\tilde{x}}_1^2 + \\ \alpha \left( {2+3e_1 +6{\tilde{x}}_1 +4e_1^2 +12e_1 {\tilde{x}}_1 +12{\tilde{x}}_1^2 } \right) \sin (wt) \\ \end{array}}&{}\quad {-\mu } \\ \end{array} }} \right] , \quad \mathbf{e}=\left[ {{\begin{array}{cc} {x_1 -{\tilde{x}}_1 } \\ {x_2 -{\tilde{x}}_2 } \\ \end{array} }} \right] \hbox {and }{} \mathbf{B}=\left[ {{\begin{array}{cc} 0 \\ 1 \\ \end{array} }} \right] \end{aligned}$$

The quadratic performance measured for the feedback control problem is given by:

$$\begin{aligned} J=\frac{1}{2}\mathop {\int }\limits _{t_0}^{\infty } \left[ \mathbf{e}^{T}{} \mathbf{Q}\left( \mathbf{e} \right) \mathbf{e}+\mathbf{u}_f^T \mathbf{R}\left( \mathbf{x} \right) \mathbf{u}_f \right] \mathrm{d}t \end{aligned}$$

(30)

where $\mathbf{Q}\left( e \right)$ and $\mathbf{R}\left( e \right)$ are positive definite matrices. Assuming full state feedback, the control law is given by:

$$\begin{aligned} \mathbf{u}_3 =-\mathbf{R}^{-\mathbf{1}}(\mathbf{e})\mathbf{B}^{\mathbf{T}}(\mathbf{e})\mathbf{P}(\mathbf{e})\mathbf{e} \end{aligned}$$

(31)

$\mathbf{P}(\mathbf{e})$ is obtained from the state-dependent Riccati equation, which is given from:

$$\begin{aligned} \mathbf{P}(\mathbf{e})\mathbf{A}(\mathbf{e})+ & {} \mathbf{A}^{\mathbf{T}}(\mathbf{e})\mathbf{P}(\mathbf{e})-\mathbf{P}(\mathbf{e})\mathbf{B}(\mathbf{e})\mathbf{R}^{-\mathbf{1}}(\mathbf{e})\mathbf{B}^{\mathbf{T}}(\mathbf{e})\mathbf{P}(\mathbf{e})\nonumber \\+ & {} \mathbf{Q}(\mathbf{e})=\mathbf{0} \end{aligned}$$

(32)

The $\mathbf{u}_3$ is obtained for each iteration by solving Riccati equation Eq. (32). Another important factor to consider is that the matrix $\mathbf{A}(\mathbf{e})$ cannot violate the controllability of the system. Then, Eq. (29) is controllable if the rank of the matrix $\mathbf{M}$ is 2:

$$\begin{aligned} \mathbf{M}=\left[ {{\begin{array}{cc} \mathbf{B}&{} {\mathbf{A}(\mathbf{e})\mathbf{B}} \\ \end{array} }} \right] \end{aligned}$$

(33)

To obtain a suboptimal solution for the dynamic control problem, the SDRE control technique has the following procedure [37]:

• 1. Define the state-space model with the state-dependent coefficient as in Eq. (27);

• 2. Define $\mathbf{x}(0)=\mathbf{x}_0$, so that the rank of $\mathbf{M}$ is n and choose the coefficients of weight matrices $\mathbf{Q}\left( \mathbf{x} \right)$ and$\mathbf{R}\left( \mathbf{x} \right)$;

• 3. Solve Riccati Eq. (32) for the state $\mathbf{e}(t)$;

• 4. Calculate the input signal from Eq. (31);

• 5. Integrate Eq. (6) and update the state of the system $\mathbf{x}(t)$ with this result;

• 6. Calculate the rank of Eq. (33), if $\hbox {rank}=2$ go to step 3. However, if rank$<2$, the matrix $\mathbf{A}(\mathbf{e})$ is not controllable, therefore, should use the last matrix controllable $\mathbf{A}(\mathbf{e})$ that has been obtained, and thus go to step 3.

Using the matrices:

$$\begin{aligned} \mathbf{Q}=\left[ {{\begin{array}{cc} {100}&{}\quad 0 \\ 0&{}\quad {100} \\ \end{array} }} \right] , ~\hbox {and}~ \mathbf{R}=\left[ 1 \right] \end{aligned}$$

(34)

the feedback control signal $\mathbf{u}_3$ is obtained from Eq. (31).

Figure 9a, b shows the time histories of displacement and velocity, respectively. The phase portrait shown in Fig. 9c, d shows the desired trajectory errors, considering the application of the control $U_3$ in Eq. (12). The proposed control $U_{3}$ is efficient and led Eq. (6) from the initial state $x_{1_0 }$ and $x_{2_0 }$ to the desired state ${\tilde{x}}_{1_0 }$ and ${\tilde{x}}_{2_0 }$. In addition, Fig. 9e shows the signal of the control, which is possible to observe the variation of the proposed control $U_3 =u_3+{\tilde{u}}_3$ gains.

Fig. 9

Time histories: of a displacement and b velocity, c phase portrait, d desired trajectory errors, e signal of the control

4 Analysis of the performance of the proposed controller

Control techniques can, most of time, reach their purpose. However, they are not always feasible due to the minimum time required for the system achieves the desired orbit. Therefore, the analysis of the performance for the minimum time required for the controlled system to achieve a lower system error of 2% is considered. Similar strategy was used in [26, 40].

In Fig. 10, the variation of the control signal and the settling time of the error is observed considering a maximum of 2% of error for the steady state.

Fig. 10

Time histories of displacement of a desired trajectory errors $e_1 =x_1 -{\tilde{x}}_1$, b desired trajectory errors $e_2 =x_2 -{\tilde{x}}_2$, c signal of the control

The three analyzed control techniques were able to keep the controlled system below 2% of steady-state error. In Fig. 10a, it is observed that the control by Picard interaction and Lyapunov–Floquet transformation took approximately 1.8 (t) to stabilize the system below 2% error. The Optimal Linear Feedback control took approximately 1.9 (t) to stabilize the system below 2% error. However, the state-dependent Riccati equation control took approximately 3.7 (t) to stabilize the system below 2% error.

It can be seen in Fig. 10c that the proposed controls used approximately the same control signal, Control I (maximum absolute amplitude: $U_1 =4.746)$, Control II (maximum absolute amplitude: $U_2 =2.16)$, Control III (maximum absolute amplitude: $U_{3}=6.135$).

4.1 Effect of parameter uncertainties

According to Peruzzi et al., Schueller, and Triguero et al. [26, 41, 42], the parametric uncertainties are associated with differences between real values and the parameters of the mathematical model.

To consider the effects of parameter uncertainties on the performance of the controller, the parameters used in the control are taken to have a random error of $\pm \, 20\%$ [7, 26, 42,43,44], as given by: $\bar{{\mu }}=\mu \left( {0.8+0.4r(t)} \right) , \quad \bar{{k}}_l =k_l \left( {0.8+0.4r(t)} \right) , \quad \bar{{k}}_{nl} =k_{nl} \left( {0.8+0.4r(t)} \right)$ and $\bar{{\alpha }}=\alpha \left( {0.8+0.4r(t)} \right)$ where r(t) are distributed random functions.

Figure 11 shows the robustness of the control using Picard interaction and Lyapunov–Floquet transformation when the parameters of the system have random uncertainties. The uncertainties in the parameters increase the error because the control with parametric uncertainties has higher error variations than the control without uncertainties.

Fig. 11

Time histories of displacements of a desired trajectory errors $e_1 =x_1 -{\tilde{x}}_1$, b desired trajectory errors $e_2 =x_2 -{\tilde{x}}_2$

Figure 12 shows the robustness of the control using Optimal Linear Feedback control when the parameters of the system have random uncertainties. The uncertainties in the parameters increase the error of the control because the control with parametric uncertainties has higher variations of error than the control without uncertainties. It can also be observed that the Optimal Linear Feedback control is less sensitive than using Picard interaction and Lyapunov–Floquet transformation.

Fig. 12

Time histories of displacement of a desired trajectory errors $e_1 =x_1 -{\tilde{x}}_1$, b desired trajectory errors $e_2 =x_2 -{\tilde{x}}_2$

Figure 13 shows the robustness of the control using the state-dependent Riccati equation control when the parameters of the system have random uncertainties. The state-dependent Riccati equation control is more robust to parametric variations than the other two controls, as there was no increase in error.

Fig. 13

Time histories of displacement of a desired trajectory errors $e_1 =x_1 -{\tilde{x}}_1$, b desired trajectory errors $e_2 =x_2 -{\tilde{x}}_2$

In Fig. 14, a comparison of the robustness among the three control techniques when the systems parameters have random uncertainties is presented. The three controls were able to keep the error below 2%, demonstrating that they are efficient in carrying and maintaining the system in the desired orbit, even in the case of parametric uncertainties. Analyzing Fig. 14a, b, the control effort using Picard interaction and Lyapunov–Floquet transformation to reduce the error of $e_{1}$ influenced its performance in reducing $e_{2},$ obtaining maximum uncertainty and error magnitude. In addition, comparing the results of Figs. 10b and 14b, it is seen that the parametric uncertainties influenced the control performance using Picard interaction and Lyapunov–Floquet.

Fig. 14

Time histories of displacement of a desired trajectory errors $e_1 =x_1 -{\tilde{x}}_1$, b desired trajectory errors $e_2 =x_2 -{\tilde{x}}_2$

5 Chaos analysis and control for system with a fractional-order

The thermal effect due to the thermoelastic damping on MEMS plays an important role because it makes a high constraint on the motion of the MEMS resonator [3, 31, 44,45,46,47]. The behavior of heat conduction, dielectric polarization, electrode-electrolyte polarization, electromagnetic waves can be properly described by using the fractional-order system theory [48,49,50,51,52]. For the thermal effect, the damping of the microelectromechanical system is modeled in fractional-order, which is the main contribution of this work. To confirm whether the behavior is chaotic or periodic, the wavelet-based scale index test is carried out.

Due to differences between the ODE and the FODE systems, the ODE one cannot be directly extended to the case of the FODE one [11, 50, 51]. FODE may involve Riemann–Liouville Fractional differential operators with $q > 0$, described as [52]:

$$\begin{aligned} D^{q}x(\tau )=\frac{1}{\Gamma \left( {\eta -q} \right) }\mathop {\int }\limits _{\tau _0 }^\tau {\frac{x^{(\eta )}(u)}{\left( {\tau -u} \right) ^{q-\eta +1}}} \mathrm{d}u \end{aligned}$$

(35)

where $\eta$ is the first integer not less than q. It is easily proved that the definition is the usual derivatives when $q=1$, with constraint for the choice of memory length L [52], given by:

$$\begin{aligned} L\ge \frac{1}{\delta _0^2 \Gamma \left( q \right) ^{2}} \end{aligned}$$

(36)

where $\Gamma \left( q \right)$ is the gamma function, and $\delta _0$ is the maximum admissible normalized error. For simplicity and without loss of generality, in the following, it is assumed that: $\tau _0 =0$, $0<q<1$ [52, 53]. Thus, the discretization of the fractional derivative operator into Eq. (35) is carried out, as described in [53].

5.1 The wavelet-based scale index

Wavelet techniques have been used to describe the pattern of motion to verify the presence of chaos in dynamic systems. The scale parameter is analogous to the concept of scales used in maps, thus in small scales, it has more compressed wavelets with rapidly variable details. On large scales, however, there are more enlarged wavelets, more visible features and slowly changing. In other words, small scales provide good resolution in the time domain, while large scales provide good resolution of the frequency domain.

Fig. 15

a Time history of the displacement, b time history of the velocity, c phase portrait

It is possible to find the Continuous Wavelet Transform (CWT) of signal f at time u and scale s. Suppose $f\in L^{2}(\mathbb {R})$, then the CWT is defined as

$$\begin{aligned} Wf\left( {u,s} \right) :=\left\langle {f,\psi _{u,s}^*} \right\rangle =\mathop \int \limits _{-\infty }^{+\infty } {f\left( t \right) \psi _{u,s}^*\left( t \right) \mathrm{d}t} \end{aligned}$$

(37)

where

$$\begin{aligned} \psi _u,s^{*}:= \frac{1}{\sqrt{s}} \psi \left( \frac{t-u}{s}\right) , \quad u \in {\mathbb {R}},\,s>0 \end{aligned}$$

(38)

The frequency component of the signal f as regards to the wavelet $\psi _{u,s}$ at time u and scale s is given by $Wf\left( {u,s} \right)$ [17]. The scalogram of f, denoted by $\wp$, is defined as [17]:

$$\begin{aligned} \wp (s):=\left\| {Wf\left( {u,s} \right) } \right\| =\left( {\mathop \int \limits _{-\infty }^{+\infty } {\left| {Wf\left( {u,s} \right) } \right| ^{2}\mathrm{d}u} } \right) ^{1/2}\nonumber \\ \end{aligned}$$

(39)

Knowing this relationship, it is possible to interpret $\wp (s)$ as the energy of the CWT of f at scale s. The scalogram can be used to detect which is the most representative scale (or frequency) of the signal f [17]. The term inner scalogram of f at scale s was defined in Benítez et al. [17], and can be defined as:

$$\begin{aligned} \wp ^{\mathrm{inner}}(s):= & {} \left\| {Wf\left( {u,s} \right) } \right\| _{J\left( s \right) } \nonumber \\= & {} \left( {\mathop \int \limits _{c\left( s \right) }^{d\left( s \right) } {\left| {Wf\left( {u,s} \right) } \right| ^{2}\mathrm{d}u} } \right) ^{1/2} \end{aligned}$$

(40)

where $J\left( s \right) =\left[ {c\left( s \right) ,d\left( s \right) } \right] \subseteq I$ is the maximal subinterval in I for which the support of $\psi _{u,s}$ is included in I for all $u\in J\left( s \right)$. Therefore, in Benítez et al. [17] it is suggested that the normalization of the inner scalogram be as follows:

$$\begin{aligned} \bar{{\wp }}^{\mathrm{inner}}(s)=\frac{\wp ^{\mathrm{inner}}(s)}{\left( {d\left( s \right) -c\left( s \right) } \right) ^{1/2}} \end{aligned}$$

(41)

Besides, the authors of Benítez et al. [17] introduced the Scale index in the scale interval $\left[ {s_0 ,s_1 } \right]$ defined by relation:

$$\begin{aligned} i_{\mathrm{scale}} :=\frac{\wp (s_{\min } )}{\wp (s_{\max } )} \end{aligned}$$

(42)

where $s_{\max }$ and $s_{\min }$ are the smallest scales such that $\wp (s_{\min } )\le \wp (s)\le \wp (s_{\max } )$ for all $s\in \left[ {s_0 ,s_1 } \right]$. In this way, using the definition of the Scale index $i_{\mathrm{scale}}$, values between 0 and 1 ($0\le i_{\mathrm{scale}} \le 1)$ were taken into account. Therefore, this measure ($i_{\mathrm{scale}} )$ can be used to explore the degree of non-periodicity of the signal, namely if the Scale index is close or equal to zero the signal is periodic, otherwise, the signal is non-periodic [17].

Table 1 Error in RMS (root mean square), and wavelet-based scale index test

Fig. 16

Error the time history of the displacement $y_1=x_{1_{\,(q_3 =1)}}^u -x_{1_{\,(q_3 \ne 1)}}^u$, a control using Picard interaction and Lyapunov–Floquet transformation ($y_{\mathrm{rms(lft})} )$, b optimal linear feedback control ($y_{\mathrm{rms(olfc})} )$, c state-dependent Riccati equation control ($y_{\mathrm{rms(sdre})} )$

5.2 Analysis and control of the fractional-order system

According to Tusset et al. [11], some techniques of fractional calculus can be used to analyze the behavior of Eq. (3) with the fractional-order damping, which is given as:

$$\begin{aligned} \frac{\mathrm{d}^{q_1 }x_1 }{\mathrm{d}\tau ^{q_1 }}= & {} x_2 \nonumber \\ \frac{\mathrm{d}^{q_2 }x_2 }{\mathrm{d}\tau ^{q_2 }}= & {} -\mu \frac{\mathrm{d}^{q_3 }x_3 }{\mathrm{d}\tau ^{q_3 }}-k_l x_1 -k_{nl} x_1^3 \nonumber \\&+\,\alpha \left( {1+2x_1 +3x_1^2 +4x_1^3 } \right) \sin (wt) \nonumber \\ \frac{\mathrm{d}^{q_3 }x_3 }{\mathrm{d}\tau ^{q_3 }}= & {} x_2 \end{aligned}$$

(43)

where $0<q_1 ,q_2 ,q_3 \le 1$. Its order is denoted by $q=\left( {q_1 ,q_2 ,q_3 } \right)$.

Table 2 Error in RMS (root mean square) for $y_1 =x_{1_{\,(q_3 =1)}}^u -x_{1_{\,(q_3 \ne 1)}}^u$

The displacement, velocity and phase portrait for ($q_1 =q_2 =1$ and $q_3 =0.6)$ case are shown in Fig. 15. The displacement of the beam has no defined period demonstrating that the behavior is chaotic. This means that the inclusion of the fractional-order changes the displacement of the beam, whose variation of the chaotic behavior is shown in Table 1, where $i_{\mathrm{scale}}$ is the wavelet-based scale index test, and $e_{\mathrm{rms}}$ is the error variation in RMS.

With the application of the wavelet-based scale index test ($i_{\mathrm{scale}} )$, it is possible to state that the system maintained the chaotic behavior. However, considering the error $e_{\mathrm{rms}}$, the variation of $q_3$ influences the beam movements, generating movements different from those observed for $q_3 =1$.

The MEMS system with control signal U (Eq. 6), in fractional-order, is expressed in the following way:

$$\begin{aligned} \frac{\mathrm{d}^{q_1 }x_1 }{\mathrm{d}\tau ^{q_1 }}= & {} x_2 \nonumber \\ \frac{\mathrm{d}^{q_2 }x_2 }{\mathrm{d}\tau ^{q_2 }}= & {} -\mu \frac{\mathrm{d}^{q_3 }x_3 }{\mathrm{d}\tau ^{q_3 }}-k_l x_1 -k_{nl} x_1^3 \nonumber \\&+\,\alpha \left( {1+2x_1 +3x_1^2 +4x_1^3 } \right) \sin (wt)+\hbox {U }\nonumber \\ \frac{\mathrm{d}^{q_3 }x_3 }{\mathrm{d}\tau ^{q_3 }}= & {} x_2 \end{aligned}$$

(44)

Figure 16 shows the robustness of the control in keeping the system on the same orbit obtained with the control with $q_3 =1$. It is considered that $y_1 =x_{{1}_{\,(q_3 =1)}}^{u}-x_{{1}_{\,(q_3 \ne 1)}}^u$ and $x_{1_{\,(q_3 =1)}}^u$ are the states ($x_1 )$ obtained with the control with $q_3 =1$, and $x_{1 _{\,(q_3 \ne 1)} }^u$ is the state ($x_1 )$ obtained with the control with $q_3 \ne 1$. The three analyzed controls are sensitive to the variation of derivative order $q_3$, demonstrating the importance of a control design that also considers the variation in fractional derivatives.

Table 2 shows the variation of the error in RMS for each of the controls with the variation of $q_3$. The more $q_3$ moves away from $q_3 =1$, the greater the control error is. In addition, the OLFC control is the most robust one for these variations, while the SDRE is the most sensitive one.

6 Conclusions

In this paper, the dynamics of a mathematical model of a MEMS resonator was analyzed. The dynamic system showed to be chaotic and was controlled to a desired periodic orbit through a state feedback control technique based on the Lyapunov–Floquet transformation, Optimum Linear Feedback Control and through the SDRE Control. The desired orbit was obtained by the Harmonic Balance method.

The dynamic analysis of the linear and nonlinear parameters of the stiffness coefficient and the damping coefficient showed that the system has a chaotic behavior for a set of parameters. It was also observed that the nonlinear stiffness has a strong influence on the dynamics of the system. The results demonstrated that the control proposed in [23] and the Optimum Linear Feedback control proposed in [27] are a good choice for the cases in which it is wished to minimize the transitory time of the system to a predetermined orbit. In cases where the control parameters are subject to parametric errors, the results show that the SDRE control is more robust in relation to the other two proposed controls. On the other hand, for the damping with fractional-order, the OLFC control has shown to be robust for variations of the derivative order $q_{3}$.

The main contribution of this work is the results obtained throughout the sensitivity of the controls for parametric errors and fractional derivative variation. There are some results that were not observed in previous works, then demonstrating the importance of the controller design taking into account the parametric errors and order of the fractional derivative, which is related to the effects of memory of the material, such as the behavior observed with thermal phenomenon or with similar behavior. In addition, the error increases as the derivative ($q_3 )$ moves away from the derivative ($q_3 =1)$, which is the value of the derivative normally used in the control design, and that the fractional thermoelastic damping coefficient in the fractional-order plays an important role, since the dynamics of the MEMS can be brought to different responses (see Fig. 15), showing the influence of the order of the derivative on the displacement of the movable plate.

With those results, it is intended for a future work to verify the possibility of improving the robustness of the controls with the application of additional controls as adaptive ones.

Appendix

Variables a, b, c, d,  and e for Eq. (5).

$$\begin{aligned}&-\,4a\omega ^{2}-4\alpha -9a^{2}\alpha -6b^{2}\alpha +\,4c\alpha +24a^{2}c\alpha +6b^{2}c\alpha -6c^{2}\alpha +6c^{3}\alpha +6ad\alpha \nonumber \\&\quad -\,36acd\alpha -6d^{2}\alpha +12cd^{2}\alpha +36abe\alpha -\,6e^{2}\alpha +12ce^{2}\alpha +4ak_l \nonumber \\&\quad +\,3\left( a^{3}-a^{2}d+b^{2}d-c^{2}d+2bce +\,2a\left( {b^{2}+c^{2}+d^{2}+e^{2}} \right) \right) k_{nl} =0 \end{aligned}$$

(A.1)

$$\begin{aligned}&\frac{1}{2}\left( \begin{array}{l} -8b\omega ^{2}-3b\left( {-2a\left( {-1+c} \right) +d+2cd} \right) \alpha +9b^{2}e\alpha \\ +\,\left( {2+9a^{2}-3c+3c^{2}+3d^{2}} \right) e\alpha +3e^{3}\alpha -4c\omega \mu \\ \end{array} \right) \nonumber \\&\quad +\,bk_l +\frac{3}{4}\left( 2a^{2}b+2a\left( {bd+ce} \right) +\,b\left( {b^{2}+c^{2}+2\left( {d^{2}+e^{2}} \right) } \right) \right) k_{nl} =0 \end{aligned}$$

(A.2)

$$\begin{aligned}&\begin{array}{l} \dfrac{1}{2}\left( {\begin{array}{l} -8c\omega ^{2}+4a^{3}\alpha +9c^{2}\left( {a-d} \right) \alpha -2d\alpha -9a^{2}d\alpha -3b^{2}d\alpha -3d^{3}\alpha -3be\alpha \\ -3de^{2}\alpha +3c\left( {-2a+d+2be} \right) \alpha +a\left( {2+3b^{2}+6d^{2}+6e^{2}} \right) \alpha +4b\omega \mu \\ \end{array}} \right) \\ \quad +\,ck_l +\frac{3}{4}\left( 2a^{2}c+a\left( {-2cd+2be} \right) +\,c\left( {b^{2}+c^{2}+2d^{2}+2e^{2}} \right) \right) k_{nl} =0 \\ \end{array} \end{aligned}$$

(A.3)

$$\begin{aligned}&\begin{array}{l} -\,36d\omega ^{2}+3a^{2}\alpha -3b^{2}\alpha -4c\alpha -18a^{2}c\alpha -\,6b^{2}c\alpha +3c^{2}\alpha -6c^{3}\alpha \\ \quad -\,12ad\alpha +24acd\alpha -18cd^{2}\alpha +\,12bde\alpha -6ce^{2}\alpha -12e\omega \mu +4dk_l \\ \quad +\,\left( -a^{3}+3a\left( {b^{2}-c^{2}} \right) +\,6a^{2}d+3d\left( {2b^{2}+2c^{2}+d^{2}+e^{2}} \right) \right) k_{nl} =0 \\ \end{array} \end{aligned}$$

(A.4)

$$\begin{aligned}&\begin{array}{l} \dfrac{1}{2}\left( {\begin{array}{l} 3b^{3}\alpha +b\left( {2+9a^{2}-3c+3c^{2}+3d^{2}} \right) \alpha +9be^{2}\alpha \\ -6e\left( {3\omega ^{2}+\left( {a-2ac+cd} \right) \alpha } \right) +6d\omega \mu \\ \end{array}} \right) +ek_l \\ \quad +\frac{3}{4}\left( {2abc+2a^{2}e+e\left( {2b^{2}+2c^{2}+d^{2}+e^{2}} \right) } \right) k_{nl} =0 \\ \end{array} \end{aligned}$$

(A.5)