Detecting network backbones against time variations in node properties

Abstract

Many real systems can be described through time-varying networks of interactions that encapsulate information sharing between individual units over time. These interactions can be classified as being either reducible or irreducible: reducible interactions pertain to node-specific properties, while irreducible interactions reflect dyadic relationships between nodes that form the network backbone. The process of filtering reducible links to detect the backbone network could allow for identifying family members and friends in social networks or social structures from contact patterns of individuals. A pervasive hypothesis in existing methods of backbone discovery is that the specific properties of the nodes are constant in time, such that reducible links have the same statistical features at any time during the observation. In this work, we release this assumption toward a new methodology for detecting network backbones against time variations in node properties. Through analytical insight and numerical evidence on synthetic and real datasets, we demonstrate the viability of the proposed approach to aid in the discovery of network backbones from time series. By critically comparing our approach with existing methods in the technical literature, we show that neglecting time variations in node-specific properties may beget false positives in the inference of the network backbone.

1 Introduction

Dealing with real, temporal datasets brings forward several challenges. One of the most ambitious goals is to elucidate the role of temporal interactions in complex systems [1,2,3,4,5]. The presence of temporal interactions questions the very basis of a network approach to complex systems. As articulated in [6], temporal links could be related to intrinsic node properties that do not require the truly dyadic nature of a network. Such temporal links are called reducible, whereby they are fully explained by node-specific features. Devising robust methodologies to filter out these reducible links for the inference of the irreducible backbone of temporal interactions is an open research topic.

Fig. 1

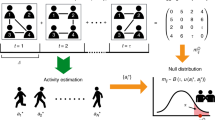
Top: time evolution of a complex system, showing node-specific, reducible interactions (solid red links), and the irreducible backbone (dashed blue links). Bottom: empirical observations of temporal interactions between any node pair are used by a filtering algorithm to reconstruct the backbone. The resulting backbone network is composed of a set of aggregated, static links. Retaining a link in the backbone is informed by a statistical comparison that tests the hypothesis of the link being explained by the null model

A fruitful approach entails the formulation of null models to explain the reducible part of the temporal interactions and guide the process of filtering, as illustrated in Fig. 1. Filtering is carried out within a statistically principled approach, where one seeks to detect links that are incompatible with the null hypothesis of links being produced by the null model [7,8,9,10,11,12,13,14]. More concretely, the approach assigns a “strength” to link candidates and filters out weak links, which are statistically unlikely to pertain to the backbone network.

Despite significant progress, most research studies assume that nodes have time-invariant properties, such that the empirical time series are realizations of stationary stochastic processes. However, time-varying connections might be affected by several factors, such as individual propensity to generate links over time and physical constraints on the network evolution. In addition, connections may vary non-uniformly in time, exhibiting highly dynamic patterns that could challenge the possibility of network reconstruction. The chief objective of our work is to explore the feasibility of inferring the backbone network in the presence of richer time-varying connections.

1.1 Background and related studies

A key step toward the inference of the backbone network is the formulation of reliable and comprehensive null models. A promising modeling paradigm is offered by activity-driven networks (ADNs) [15]. Within the ADN paradigm, individual propensity of generating links over time is encapsulated by a single, heterogeneously distributed parameter, called activity. In its original formulation, the activities of all the nodes are assumed to be constant in time and the process of network assembly is carried out in a discrete-time setting. A similar approach can be undertaken in continuous time [16].

Because of its analytical tractability, activity-driven models have been extended to comprehend features of real networks, such as memory effects in the link wiring [17], self-exciting mechanisms in individual activities [18], presence of communities [19], and spreading over multiple layers [20, 21]. For example, recent studies have examined adaption of individual activities based on the node’s health status [22, 23]. Building on this promising line of research, a predictive model of the 2014 Ebola spreading in Liberia has been established [24]. Finally, circadian and weekly patterns have been included in the ADN paradigm in [25].

Upon formulating a valid null model, the next step to backbone inference entails a statistical test to identify irreducible links. The simplest approach is to set a threshold that filters out links with lower strength [26]. However, such an approach could fail to capture the inherent heterogeneity of many complex systems where the formation of reducible links drastically varies in time and throughout the network. The disparity filter [9], which has been recently extended to consider self-exciting mechanisms [14], could address inference of heterogeneous networks. A more established approach is the statistically validated network (SVN) [10], first introduced to study bipartite networks, and then applied to temporal networks [11, 27,28,29].

The SVN approach works on an aggregated version of the temporal network, that is, a static weighted network formed by retaining all the links occurring at any time instant. Each link has a weight equal to the total number of temporal connections formed over time between two nodes. The SVN approach has helped to elucidate many aspects of real systems, such as connections between the backbone network and the network’s community structure [30], the influence of time correlations [28, 29], and the time evolution of the backbone network [27].

A further improvement on the SVN approach is constituted by the temporal fitness model (TFM) [7]. The TFM utilizes an ADN as a null model, in which individual activities are considered to be constant in time. Their values are identified through maximum likelihood estimation. The approach can be extended to study daily patterns and circadian rhythms, within the so-called $\hbox {TFM}_{\mathrm{rhythm}}$ [7], which utilizes a common function to modulate the overall network evolution. The SVN, TFM, and $\hbox {TFM}_{\mathrm{rhythm}}$ are summarized in “Appendix”.

Overall, these approaches assume that individual properties of the nodes are constant in time. As a result, they cannot be utilized to infer backbone networks in the presence of changes in individual behavior.

1.2 Our contribution

Here, we seek to propose a new methodology to improve the detection of a backbone network in the presence of complex temporal variations of activity patterns. To this end, we introduce an extended version of ADNs, where individual activities are piece-wise constant in time and heterogeneously distributed throughout the network. The null model assumes that all connections are formed uniformly at random, that is, the probability of creating a link at a specific time instant between two nodes is the product of the individual activities of the nodes at that time. In this vein, a very active node is more likely to form connections with another high active node than with a low active one.

Accounting for time-varying activities in the null model calls for two main steps to find irreducible links. First, it is necessary to estimate activity values as piece-wise constant functions of time. Then, links are included in the backbone network if their overall weight is significantly higher than what would be expected from the null model.

While the latter step can be tackled through a statistical test similar to [7, 10], dealing with estimation of activity values requires a novel scheme. Specifically, we divide the total observation window of network evolution in independent intervals, containing a uniform total number of connections. Activities are then estimated according to the weighted configuration model [31, 32], which has been shown to offer reliable estimates for large networks.

Partitioning the observation window into independent intervals is a crucial step that can be carried out in three ways, depending on the available information of the network evolution. If these intervals are known a priori, they can be used as inputs for the estimation of activity values. If only the number of these intervals is known, then a supervised method is necessary, which takes the number of intervals as an input and returns an interval partition. Finally, if no information is available, an unsupervised method is necessary to identify the interval partition from the available time series.

The simplest supervised method entails choosing the length of the intervals at random, such that their sum equals the length of the total observation window. This naïve approach should set a lower bound for the performance of our approach to the backbone inference. Other effective supervised methods include the parsimonious temporal aggregation [33], piece-wise constant approximation [34], and V-optimal histograms [35]. A freeware software that implements these methods is available in [36].

A convenient unsupervised method is the Bayesian blocks (BB) representation [37]. The BB method employs maximum likelihood and marginal posterior functions to separate statistically significant features from random observational errors. In this way, it relaxes common assumptions regarding the smoothness or shape of the overall temporal evolution, without constraining the process of partitioning the observation window. We refer to our methodology toward backbone inference as evolving activity-driven model (EADM), encompassing the null model formulation, the identification of the time-varying activities, and the statistical test.

We acknowledge that partition into intervals is not always necessary. For instance, if a system is stationary, then the number of connections generated at each time step is constant. In this case, the total observation window is contained in only one interval. To investigate such a scenario, we examine a simplified version of the EADM, where only one interval is present so that the EADM reduces to a classical ADN (referred to as $\hbox {EADM}_{I=1}$).

Beyond comparing our approach with its simplest incarnation that utilizes a single time interval, we further consider three different methods, sharing similarities with the EADM: SVN, TFM, and $\hbox {TFM}_{\mathrm{rhythm}}$. We consider both an artificial, synthetic network (benchmark) and seven real-world networks (datasets). For each network (artificial or real), we set the maximum computational time of 24 h, thereby dismissing longer processes.

The synthetic network is useful for validating our model in a controlled setting. In fact, it considers activity values as piece-wise constant functions in time with a ground truth on the backbone network. We consider three different scenarios. First, we assume knowledge about the interval partition, thereby fully exploiting the capabilities of our method. Then, we consider the case in which limited information is available about the interval partition. When only the number of intervals is available, we use the naïve supervised method and estimate the length of the intervals at random. When no information about the interval partition is accessible, we utilize the unsupervised BB method. Afterward, when tackling backbone detection of real systems, we focus on the BB method, as we have no prior knowledge about the interval partition.

1.3 Main results

A critical result of our study is the analytical characterization of the conditions in which one must account for time-varying individual properties to accurately infer backbone networks. Our analysis suggests that considering time-varying properties is necessary when the system is not stationary or when the activation pattern of a node is correlated with the activation pattern of another node.

Further, from the analysis of synthetic networks, we conclude that our methodology outperforms the SVN, TFM, and $\hbox {TFM}_{\mathrm{rhythm}}$, whereby it leads to a more reliable inference of backbone networks in synthetic data, where a ground-truth backbone is known. Interestingly, in both synthetic and real networks, we find that our approach reconstructs a backbone with a subset of links found by other methods, thereby diminishing the number of false positive links (links wrongly identified as part of the backbone network). Overall, the three methods available in the literature result in equivalent inferences, similar to the special case of $\hbox {EADM}_{I=1}$, in which we execute our approach without partitioning the observation window.

Thus, we propose that assuming individual activities to be constant in time could lead to incorrect classification of irreducible links and parts of the backbone network. Considering individual activities as piece-wise constant functions of time offers improved estimates and more reliable results.

1.4 Paper organization

The rest of the paper is organized as follows: In Sect. 2, we introduce the null model and articulate our procedure to detect significant interactions in time-varying networks. In Sect. 3, we describe our main findings by comparing the performance of our approach with other methods on synthetic networks, in which the backbone network is known, and on real datasets where different claims can be formulated depending on the method that is pursued. Finally, in Sect. 4, we draw our main conclusions and outline potential directions for further inquiry.

2 Significant links

In this section, we articulate the EADM, our approach to the detection of the irreducible backbone from the time series of each individual link. First, we present the null model, which defines the process of generating temporal interactions from node-specific and piece-wise constant properties. Then, we elucidate the inference procedure of the nodes’ activities within the null model from available time series, assuming to be able to access the switching events. Further, we present the statistical test from which we filter reducible links and retain irreducible ones, thus finding the backbone network. Finally, we discuss the computational complexity of our methodology.

2.1 Null model

We consider a time-varying network of N nodes evolving in a observation window of $T \gg 1$ time steps, labeled by the discrete time index $t=1,\ldots ,T$, with a unitary resolution. The same modeling framework is valid for a continuous time evolution.

At each time step t, nodes are connected through a binary, possibly disconnected, undirected network whose adjacency matrix, A(t), stochastically varies in time. Each temporal connection is the realization of a Bernoulli variable, whereby the probability that two distinct nodes i and j are connected at time t is equal to

$$\begin{aligned} p_{ij}(t)=a_i(t)a_j(t), \end{aligned}$$

(1)

where $a_i(t)$ and $a_j(t)$ are the so-called activities of nodes i and j at time t, respectively.

Activities vary according to a switching rule, whereby they are kept constant over I disjoint time intervals indexed by $\varDelta = 1, \ldots , I$. The generic $\varDelta$th time interval starts at time $t_{\mathrm {in}}(\varDelta )$ and has a duration $\tau (\varDelta )$, such that $\sum _{\varDelta =1}^{I} \tau (\varDelta ) =T$. The interval partition might be a priori known or it should be determined from the time series as explained below.

When only the number of intervals I is known, a supervised method should be used to determine the interval partition. A crude possibility is to assume a random partition in I intervals, which strains the use of the null model and sets a lower bound for the EADM performance. On the contrary, if I is unknown, then an unsupervised method should be used. Specifically, we use the BB representation [37]. In this case, we analyze the total number of temporal links created at time t

$$\begin{aligned} \varOmega (t) = \sum _{i, j = 1; i < j}^{N} A_{ij}(t), \end{aligned}$$

(2)

where $A_{ij}(t)$ is the ijth entry of the network adjacency matrix at time t. The BB method returns a set of independent intervals containing a uniform total number of connections.

To characterize the network evolution at the intermediate time scale of the switching rule, that is, over successive intervals, we define a weight matrix for each interval, summing the number of occurrences of links between any two nodes. Specifically, in the $\varDelta$th interval we define the random variable

$$\begin{aligned} w_{ij}(\varDelta ) = \sum _{t = t_{\text {in}}(\varDelta )}^{t_{\text {in}}(\varDelta )+\tau (\varDelta )-1} A_{ij}(t). \end{aligned}$$

(3)

To count the overall number of temporal connections between nodes i and j forming a link ij along the observation window, it is sufficient to sum the corresponding weights, resulting in the following aggregated random variable:

$$\begin{aligned} {\overline{w}}_{ij} =\sum _{\varDelta = 1}^{I} w_{ij}(\varDelta ) = \sum _{t=1}^{T} A_{ij}(t). \end{aligned}$$

(4)

By construction, the weight $w_{ij}(\varDelta )$ is a binomial variable and ${\overline{w}}_{ij}$ the sum of non-identical binomial random variables, described through a Poisson binomial distribution. Since no closed-form expression is available for the Poisson binomial distribution, this is usually approximated by the Poisson distribution [38,39,40], with expected value

$$\begin{aligned} \text {E}\left[ {\overline{w}}_{ij} \right] = \sum _{t = 1}^{T} p_{ij}(t). \end{aligned}$$

(5)

From the weight matrix, we define the strength of the ith node in the $\varDelta$th interval as

$$\begin{aligned} s_{i} \left( \varDelta \right) = \sum _{j = 1}^{N} w_{ij}(\varDelta ). \end{aligned}$$

(6)

This quantity encapsulates the total number of temporal links generated by the ith node within an interval. The total number of temporal links generated in the whole network in the $\varDelta$th interval is therefore

$$\begin{aligned} W(\varDelta )=\frac{1}{2} \sum _{i = 1}^{N} s_{i}(\varDelta ). \end{aligned}$$

(7)

Both $s_{i} \left( \varDelta \right)$ and $W(\varDelta )$ can be approximated by Poisson random variables, being linear combinations of independent non-identical binomial random variables.

2.2 Estimation of the activities from time series

In order to compute the probability that two distinct nodes i and j are connected at time t, as given in Eq. (1), we must estimate the time-varying activities $a_i(t)$ and $a_j(t)$, assumed to be piece-wise constant over known successive intervals. A possible line of approach entails the use of the weighted configuration model [31, 32], which implies that the activity of node i in the $\varDelta$th time interval $t_{\text {in}}(\varDelta ), \ldots , t_{\text {in}}(\varDelta )+\tau (\varDelta )-1$ can be estimated from the time series of the temporal connections $A^{\mathrm {ts}}_{ij}(t)$, where we utilize a superscript “$\mathrm {ts}$” to identify that the realizations from the corresponding random variables are experimental or numerical time series.

Hence, we obtain

$$\begin{aligned} \begin{aligned} a_i \left( t \right)&= \frac{s_{i}^{\mathrm {ts}} \left( \varDelta \right) /\tau (\varDelta )}{\sqrt{\left( 2 W^{\mathrm {ts}}(\varDelta )-1\right) /\tau (\varDelta )}} \\&= \frac{s_{i}^{\mathrm {ts}} \left( \varDelta \right) }{\sqrt{\left( 2 W^{\mathrm {ts}}(\varDelta )- 1\right) \tau (\varDelta )}}, \end{aligned} \end{aligned}$$

(8)

where $s_{i}^{\mathrm {ts}} \left( \varDelta \right)$ and $W^{\mathrm {ts}}(\varDelta )$ are estimated from the time series and $\tau (\varDelta )$ is derived from the interval partition. In Eq. (8), the activity $a_i(t)$ in the $\varDelta$th interval is estimated as the ratio between the average number of temporal links created per time step by node i, $s_{i}^{\mathrm {ts}} \left( \varDelta \right) /\tau (\varDelta )$, over a measure of the same quantity for the entire network, $\sqrt{\left( 2 W^{\mathrm {ts}}(\varDelta )-1\right) /\tau (\varDelta )}$. We note that the use of a square root in the denominator is for consistency with the weighted configuration model [31]. Further, when only one link is created in the $\varDelta$th interval, $W^{\mathrm {ts}}(\varDelta ) = 1$, such that, the factor $2 W^{\mathrm {ts}}(\varDelta )-1 = 1$, in agreement with the static configuration model [32]. The accuracy of the estimate relies on the assumption that $W^{\mathrm {ts}}(\varDelta )\gg 1$ and the network is large, that is, a large number of events is occurring in each interval and a large number of nodes is participating in the system’s evolution. In “Appendix”, we examine the accuracy of Eq. (8) as a function of the network size.

By replacing Eq. (8) in Eq. (1), we obtain the probability¹ of observing a link ij in the $\varDelta$th time interval $t_{\text {in}}(\varDelta ), \ldots , t_{\text {in}}(\varDelta )+\tau (\varDelta )-1$ as

$$\begin{aligned} p_{ij} (t) = \frac{s^{\mathrm {ts}}_{i} \left( \varDelta \right) s^{\mathrm {ts}}_{j} \left( \varDelta \right) }{\left( 2 W^{\mathrm {ts}}(\varDelta ) - 1\right) \tau (\varDelta )}. \end{aligned}$$

(9)

2.3 Statistical analysis

To determine whether a link is a node-specific temporal connection or part of the irreducible backbone, we compute a p-value $\alpha _{ij}$ for each link observed at least once in the evolving network and compare it with a proper significance threshold. If the p-value is below the significance threshold, then the corresponding link appears more often than what the null model would predict and should therefore be associated with the backbone.

Thus, we examine the probability distribution of the generic weight of the ijth link over the entire observation window. As previously stated, the distribution is conveniently described by a Poisson distribution as

$$\begin{aligned} \begin{aligned} P \left( x; \text {E}\left[ {\overline{w}}_{ij} \right] \right) = \frac{1}{x!} \text {E}\left[ {\overline{w}}_{ij} \right] ^{x} e^{- \text {E}\left[ {\overline{w}}_{ij} \right] }, \end{aligned} \end{aligned}$$

(10)

where x is the realization of the random variable. The distribution in Eq. (10) can be explicitly computed from empirical data, using Eq. (5) and the estimation of $p_{ij}(t)$ in Eq. (9), as

$$\begin{aligned} P \left( x; \text {E}\left[ {\overline{w}}_{ij} \right] \right)= & {} \frac{1}{x!} \left[ \sum _{\varDelta = 1}^{I} \frac{s_{i}^{\mathrm {ts}} \left( \varDelta \right) s_{j}^{\mathrm {ts}} \left( \varDelta \right) }{2 W^{\mathrm {ts}} (\varDelta ) - 1}\right] ^{x}\times \nonumber \\&\exp \left[ - \sum _{\varDelta =1}^{I} \frac{s_{i}^{\mathrm {ts}} \left( \varDelta \right) s_{j}^{\mathrm {ts}} \left( \varDelta \right) }{2 W^{\mathrm {ts}} (\varDelta ) - 1}\right] . \end{aligned}$$

(11)

The p-value $\alpha _{ij}$ of the link ij in the overall network evolution is then computed according to the cumulative function of the Poisson distribution

$$\begin{aligned} \begin{aligned} \alpha _{ij}&\equiv 1 - \sum _{x = 0}^{{\overline{w}}_{i j}^{\mathrm {ts}}-1} P \left( x; \text {E}\left[ {\overline{w}}_{ij} \right] \right) . \end{aligned} \end{aligned}$$

(12)

Upon computing a p-value for every pair of nodes in the network, one should perform a statistical test on all the links observed at least once in the evolving network. Given that multiple hypotheses are tested, a multiple hypothesis test correction is required [41]. We use the Bonferroni correction which modifies the significance threshold to $\beta ^{*} = \beta /N_\mathrm{E} = 0.01/N_\mathrm{E}$, where $N_\mathrm{E}$ is the number of links observed at least once in the evolving network [42]. This correction ensures that no false positives will be included with probability $1-\beta$. A possible, less restrictive alternative may be a procedure that controls the false discovery rate [43]. Specifically, such a procedure ensures that the fraction of false positive is less than $\beta$.

2.4 Computational complexity

Here, we examine in detail the computational complexity of our method to detect significant links. For clarity, we discuss separately the three required steps: (i) finding the interval partition; (ii) estimating the individual activities $a_i$ and probability $p_{ij}$ in Eqs. (8) and (9); and (iii) computing the p-values $\alpha _{ij}$ in Eq. (12).

To find the interval partition, we use the BB representation [37]. Given a time series composed of T successive time steps, the total number of links $\varOmega (t)$ is computed according to Eq. (2) and used as an input for the BB representation. This method determines whether $\varOmega (t) \ne \varOmega (t+1)$, $\forall t = 1, 2, \ldots , T-1$, to identify the number of change points $T_{\text {cp}}$ (when the time series changes value). From the knowledge of $T_{\text {cp}}$, the maximum number of possible intervals is computed as $I_{\text {max}}= T_{\text {cp}}+1$. The interval partition is calculated with a computational time that scales as ${\mathcal {O}}(I_{\text {max}}^2)$, which is affordable even for $I_{\text {max}} \sim 10^6$ [37].

The next step is to estimate individual activities $a_i$ and probabilities $p_{ij}$ in Eqs. (8) and (9). These empirical estimations depend on the number of intervals I and the amount of temporal links in each interval. The latter might substantially affect the algorithm’s complexity, which ranges from ${\mathcal {O}}(N I)$ for sparse networks, to ${\mathcal {O}}(N^2 I)$ for dense ones.

Finally, the p-values are computed according to Eq. (12), which has a computational complexity of ${\mathcal {O}}(N_\mathrm{E})$, where $N_\mathrm{E}$ is the number of links observed at least once in the evolving network. For sparse networks, this reduces to ${\mathcal {O}}(N)$.

The above three steps are independent, and their computational costs add up, such that for sparse networks, the bottleneck of our approach is either the detection of the interval partition or the computation of the p-values. If the time series is larger than the number of links observed at least once in the evolving network, then the complexity is ${\mathcal {O}}(I_{\text {max}}^2)$. In the opposite scenario, our approach has a computational cost of ${\mathcal {O}}(N)$.

3 Results

In this section, we assess the performance of the EADM in detecting the backbone of temporal networks and we compare such a performance with four models that assume time-invariant activities. We specify our study to the SVN, TFM, $\hbox {TFM}_{\mathrm{rhythm}}$, and $\hbox {EADM}_{I=1}$ (a simplified version of our model that uses time-invariant activities). We limit the computational time for each method to 24 h, on an Intel(R) Xeon(R) CPU E5-2697 v3 @ 2.60 GHz, which we consider a reasonable computational burden for the backbone inference.

First, we analytically determine conditions for which the EADM yields equivalent results to the $\hbox {EADM}_{I=1}$, which allows for speculating when time-varying activities could play a salient role in the backbone detection. This corresponds to cases where the system is not stationary or the activation patterns of the nodes are correlated.

Then, we numerically assess the performance of the EADM, $\hbox {EADM}_{I=1}$, TFM, and SVN in detecting the backbone of temporal networks generated via an artificial network. Given that the $\hbox {TFM}_{\mathrm{rhythm}}$ requires the solution of $N+T-1$ equations, its implementation on synthetic data exceeds the computational time limit of 24 h per simulation. Therefore, its performance is not assessed on synthetic datasets. The key findings of our comparisons are: (i) the EADM offers improved performance with respect to the other methods, thereby reducing the number of false positives in the backbone network; (ii) the $\hbox {EADM}_{I=1}$, TFM, and SVN have comparable performance for all situations under scrutiny; and (iii) the EADM performs better when using the BB method for time interval partitioning, rather than a naïve interval partition.

Finally, we compare the irreducible backbone extracted from all models under study on several real datasets: Primary school, High school, and Museum contact patterns are from the SocioPatterns project [44]; Message, Email, and Stack overflow datasets are from the SNAP database [45]; and Enron email dataset [46]. For the Primary school, High school, and Museum datasets, we remove the time intervals when no links are recorded. Some simulations of the TFM (which solves N equations) and $\hbox {TFM}_{\mathrm{rhythm}}$ exceed our computational time limit. In all the seven datasets, the EADM finds less links than other methods, which perform very similar to each other. This observation is in agreement with numerical computations on the synthetic networks, suggesting that assuming individual activities as constant in time leads to an overestimation in the number of links of the backbone network.

3.1 Analytical derivation

We start by estimating the probability of having the occurrence of link ij in the $\text {EADM}_{I=1}$, that is, when individual activities are constant in time. In this case, Eq. (9) reads as

$$\begin{aligned} p_{ij} = \frac{{\overline{s}}_i^{\mathrm {ts}} {\overline{s}}_j^{\mathrm {ts}}}{\left( 2 {\overline{W}}^{\mathrm {ts}}-1\right) T}, \end{aligned}$$

(13)

where we define the total strength in the overall observation window ${\overline{s}}_{i}^{\mathrm {ts}} = \sum _{\varDelta = 1}^{I} s_{i}^{\mathrm {ts}} \left( \varDelta \right)$, and the total number of temporal links in the overall observation window ${\overline{W}}^{\mathrm {ts}} = \sum _{\varDelta =1}^{I} W^{\mathrm {ts}} (\varDelta )$. Thus, the expected number of links in the $\hbox {EADM}_{I=1}$ is

$$\begin{aligned} \text {E}_{I = 1}\left[ {\overline{w}}_{ij} \right] = T p_{ij} = \frac{{\overline{s}}_{i}^{\mathrm {ts}} {\overline{s}}_{j}^{\mathrm {ts}} }{2 {\overline{W}}^{\mathrm {ts}} - 1}, \end{aligned}$$

(14)

which is equivalent to predictions of the weighted configuration model [31].

In general, $\text {E}_{I=1}\left[ {\overline{w}}_{ij} \right]$ in Eq. (14) is different from $\text {E} \left[ {\overline{w}}_{ij} \right]$ in Eq. (5), thereby begetting different statistical inferences of the backbone. Under the following conditions, we show that the two inferences are similar:

• (i) if the system is stationary, $W^{\mathrm {ts}}(\varDelta ) \approx {\overline{W}}^{\mathrm {ts}}/T$, and

• (ii) if, for any link ij, the activation pattern of node i is independent of the one of node j.

To prove this claim, we compute $\text {E}\left[ {\overline{w}}_{ij} \right]$ and demonstrate that it converges to $\text {E}_{I=1}\left[ {\overline{w}}_{ij} \right]$ for ${\overline{W}}^{\mathrm {ts}} > W^{\mathrm {ts}}(\varDelta ) \gg 1$ and large networks. By replacing Eq. (9) into Eq. (5) for ${\overline{W}}^{\mathrm {ts}} > W^{\mathrm {ts}}(\varDelta ) \gg 1$, we obtain

$$\begin{aligned} \begin{aligned} \text {E}\left[ {\overline{w}}_{ij} \right]&\simeq \sum _{\varDelta = 1}^{I} \frac{s_{i}^{\mathrm {ts}} \left( \varDelta \right) s_{j}^{\mathrm {ts}} \left( \varDelta \right) }{2 W^{\mathrm {ts}} (\varDelta )}. \end{aligned} \end{aligned}$$

(15)

First, we assume the system as stationary, as in condition (i), so that

$$\begin{aligned} \begin{aligned} \text {E}\left[ {\overline{w}}_{ij} \right]&\simeq \frac{T^2}{2 {\overline{W}}^{\mathrm {ts}}} \frac{1}{T} \sum _{\varDelta = 1}^{I} s_{i}^{\mathrm {ts}} \left( \varDelta \right) s_{j}^{\mathrm {ts}} \left( \varDelta \right) . \end{aligned} \end{aligned}$$

(16)

Then, we apply condition (ii), which for large networks supports the mean-field approximation $\langle s_i^{\text {ts}}\left( \varDelta \right) \rangle \langle s_j^{\text {ts}}\left( \varDelta \right) \rangle \simeq \langle s_i^{\text {ts}}\left( \varDelta \right) s_j^{\text {ts}}\left( \varDelta \right) \rangle$, leading to

$$\begin{aligned} \begin{aligned} \text {E}\left[ {\overline{w}}_{ij} \right]&\simeq \frac{T^2}{2 {\overline{W}}^{\mathrm {ts}}} \left[ \frac{1}{T} \sum _{\varDelta =1}^{I} s_{i}^{\mathrm {ts}} \left( \varDelta \right) \right] \\&\quad \times \left[ \frac{1}{T} \sum _{\varDelta ^{\prime }=1}^{I} s_{j}^{\mathrm {ts}} \left( \varDelta ^{\prime } \right) \right] , \end{aligned} \end{aligned}$$

(17)

and, from the time series of ${\overline{s}}_i^{\mathrm {ts}}$ and ${\overline{s}}_j^{\mathrm {ts}}$ in Eqs. (6), we establish

$$\begin{aligned} \begin{aligned} \text {E}\left[ {\overline{w}}_{ij} \right]&\simeq \frac{{\overline{s}}_i^{\mathrm {ts}} {\overline{s}}_j^{\mathrm {ts}}}{2 {\overline{W}}^{\mathrm {ts}}}. \end{aligned} \end{aligned}$$

(18)

Finally, we observe that Eq. (18) corresponds to $\text {E}_{\text {I}=1} \left[ {\overline{w}}_{ij} \right]$ in Eq. (14) under the assumption that ${\overline{W}}^{\mathrm {ts}} \gg 1$, which concludes our proof.

If the system is not stationary or the activation patterns of nodes are correlated, one might expect that the EADM will yield different predictions than the $\hbox {EADM}_{I=1}$, supporting the need for properly partitioning the observation window toward the successful detection of the backbone network.

3.2 Performance comparison on synthetic data

The considered synthetic data begets a temporal network where reducible links, generated by the EADM, coexist with the irreducible backbone. Reducible links evolve over an observation window T, partitioned into I successive intervals. Nodes have interval-dependent (piece-wise constant) activities a(t) drawn from a power law distribution $F(a) \sim a^{-2.1}$, with $a \in [a_{{\min }} , 1]$. The value $a_{{\min }}$ represents the minimum possible value for the individual activity in the system, and it is chosen to be greater than zero to avoid divergence in the distribution [15, 24, 47].

Between two consecutive intervals, $t_{1}\in [t_{\text {in}}(\varDelta -1), t_{\text {in}}(\varDelta -1)+\tau (\varDelta -1)-1]$ and $t_{2} \in [t_{\text {in}}(\varDelta ), t_{\text {in}}(\varDelta )+\tau (\varDelta )-1]$, the activity values vary according to

$$\begin{aligned} a_i (t_2) = a_i (t_1) p + y(1-p), \end{aligned}$$

(19)

where p is an autocorrelation parameter and y a random number extracted from F(a). For $p=1$, individual activities are time-invariant, while for $p<1$, they exhibit temporal correlations.

A small fraction $\delta$ of all the links observed at least once in the network is arbitrarily assigned to the backbone network. An additional parameter $\lambda$ is used to measure the preponderance of the backbone during the observation window, such that if $\lambda =1$, these links are always present, and if $\lambda <1$, they could not be present at all times. Details about the algorithm to construct synthetic data are presented in “Appendix”.

We numerically assess the improvement provided by the EADM in the backbone detection with respect to the TFM, SVN, and $\hbox {EADM}_{I=1}$. Performing our numerical experiments using the $\hbox {TFM}_{\mathrm{rhythm}}$ exceeds our allotted computational time of 24 h, such that its performance could not be tested against this artificial network. Performance is otherwise scored using two well-known metrics, precision and recall [48]. The former is computed as the ratio between the number of links detected, which belong to the irreducible backbone (true positives), divided by the total number of detected links (sum of true and false positives). The latter metric is the ratio between the true positives divided by the total number of links in the irreducible backbone (sum of true positives and false negatives).

First, we assume that the partition into intervals is known and we estimate the activity values according to Eq. (8), thereby applying the EADM. Then, we release this assumption toward choosing the length of the intervals at random or we employ the unsupervised BB method to estimate such a partition.

3.2.1 The EADM improves backbone detection

In our comparison, we assess the role of two important parameters: (i) the autocorrelation parameter p, which regulates the variation of individual activities over time, from $p=0$ (completely uncorrelated individual activities) to $p=1$ (time-invariant activities), and (ii) the ratio between the average interval length and the total length of the observation window $\langle \tau (\varDelta ) \rangle /T$, which quantifies the fraction of switches in activity patterns. For $\langle \tau (\varDelta ) \rangle /T = 1$, individual activities are constant in time, while as $\langle \tau (\varDelta ) \rangle /T$ approaches zero, individual activities rapidly change over time. We select two values of $\lambda$, which lead to different scenarios: a larger value of $\lambda$ that begets an easily detectable backbone where all irreducible links can be discovered, examined in Fig. 2, and a smaller value of $\lambda$ that results in a partially hidden backbone where some irreducible links cannot be discovered, considered in Fig. 3.

Fig. 2

Performance comparison against the synthetic network, assuming a priori knowledge of the interval partition for the EADM implementation. We assess precision and recall as a function of the autocorrelation parameter p and ratio between the average interval length and the total observation window $\langle \tau (\varDelta ) \rangle /T$. The horizontal axis in (b) and (d) is obtained by fixing $T = 5000$ and varying I to span different values of $\langle \tau (\varDelta ) \rangle = T/I$. In a, c we hold $\langle \tau (\varDelta ) \rangle$ and I, fixed to 500 and 10, while in (b) and (d) we set $p=0.4$. Other parameter values are: $N=100$, $\delta = 0.01$, $\lambda = 0.025$, and $a_{{\min }} = [\sqrt{\langle \tau (\varDelta ) \rangle }]^{-1}$. Markers indicate the average of $10^2$ independent simulations; 95% confidence interval is displayed in gray

Fig. 3

Performance comparison against the synthetic network, assuming a priori knowledge of the interval partition for the EADM implementation. We assess precision and recall as a function of the autocorrelation parameter p and ratio between the average interval length and the total observation window $\langle \tau (\varDelta ) \rangle /T$. The horizontal axis in (b) and (d) is obtained by fixing $T = 5000$ and varying I to span different values of $\langle \tau (\varDelta ) \rangle = T/I$. In a, c we hold $\langle \tau (\varDelta ) \rangle$ and I, fixed to 500 and 10, while in (b) and (d) we set $p=0.4$. Other parameter values are: $N=100$, $\delta = 0.01$, $\lambda = 0.010$, and $a_{{\min }} = [\sqrt{\langle \tau (\varDelta ) \rangle }]^{-1}$. Markers indicate the average of $10^2$ independent simulations; 95% confidence interval is displayed in gray

Figure 2a, c supports the claim that the EADM is a valuable approach to infer the backbone networks for any choice of the autocorrelation parameter, since precision and recall are always close to one. Figure 3a, c confirms that no false positive is detected by the EADM even if the backbone is not preponderant; however, some irreducible links cannot be discovered and the recall is lower than one. On the contrary, the TFM, SVN, and $\hbox {EADM}_{I=1}$ are successful only when the value of the autocorrelation parameter approaches 1, such that individual activities are practically time-invariant. In this case, we register values of the precision close to 1.

Figures 2b, d and 3b, d suggest that the EADM outperforms the other methods for intermediate values of the number of switching intervals in terms of precision. Performance is, on the other hand, comparable for the extreme cases of $\langle \tau (\varDelta )/T \rangle$ approaching one or zero. While the comparable predictions that we register for the former case $\langle \tau (\varDelta )/T \rangle \simeq 1$ can be anticipated due to the limited variability of the activity patterns, the similar performance registered for the latter case $\langle \tau (\varDelta )/T \rangle \simeq 0$ deserves some comments. Under fast switching conditions, none of the algorithms leads to large values of the recall, such that only a small fraction of the backbone can be reconstructed, although with high accuracy. In fact, under fast switching conditions, the SVN, TFM, and $\hbox {EADM}_{I=1}$ would practically capture an annealed version of the network that is not representative of the backbone. On the other hand, an algorithm like ours that tracks time variations requires a large number of realizations for performing the statistical test, which become unfeasible for time series of limited length with several switches. The similar performance registered for the TFM, SVN, and $\hbox {EADM}_{I=1}$ is discussed in “Appendix”.

Taken together, the higher precision of the EADM and its comparable recall to other methods suggest that the EADM is successful in reducing the number of false positives. These advantages will be explored and further detailed when we examine real networks.

Table 1 Performance comparison in the synthetic network, assuming limited information of the interval partition for the EADM implementation

3.2.2 The backbone inference does not require knowledge about activity patterns

Thus far, we have assumed complete knowledge about the interval partition, which is used as an input parameter in the EADM. However, this situation is rarely met in reality, where only limited information about the interval partition may be available. To improve the degree of realism of the analysis, we consider two different scenarios. In the first one, we assume knowledge about the number of intervals and choose their length at random. This naïve approach sets a lower bound for the EADM performance. We identify this setting as EADM+R, where “R” stands for random. In the second scenario, we assume no a priori knowledge about the interval partition, and we resort to the unsupervised BB method. We identify this situation as EADM $+$ BB.

In Table 1, we study precision and recall of the five methods for two choices of the parameter values, considered in Figs. 2 and 3 . The two cases pertain to two different choices of $\lambda$, where we were fully successful in reconstructing the backbone or registered a recall less than one with full knowledge about the interval partitions.

Results in Table 1 indicate that all the five methods lead to a comparable recall, which is equivalent to results in Figs. 2 and 3. However, we document a remarkable improvement in precision for the EADM+R and EADM $+$ BB, when compared to the other three methods that do not account for time variations of activity patterns. Given that the EADM $+$ BB does not require any knowledge about the intervals, it should be the approach of choice in backbone inference. In “Appendix”, we report further insight on the comparison between the EADM+R and EADM $+$ BB, which indicate that the EADM+R might lead to inadequate inferences if the number of intervals is not exactly known. This is the case of real networks, which motivates the systematic use of the EADM $+$ BB in the discovery process.

3.3 Application to real networks

Based on our previous assessment on synthetic data, we turn to real networks, where we compare predictions of the EADM $+$ BB with other existing methods.

The comparison is carried out using three different metrics: (i) the number of significant links; (ii) the Jaccard index [49]; and (iii) the overlap coefficient [50]. We denote the set of irreducible links detected by our method as $L_{\text {EADM+BB}}$, and the others as $L_{x}$, where $x =$$\hbox {EADM}_{I=1}$, TFM, $\hbox {TFM}_{\mathrm{rhythm}}$, or SVN. The Jaccard coefficient is defined as

$$\begin{aligned} J(L_{\text {EADM+BB}}, L_{x}) = \frac{| L_{\text {EADM+BB}} \cap L_{x}|}{|L_{\text {EADM+BB}} \cup L_{x}|}, \end{aligned}$$

(20)

where $| \cdot |$ indicates the set cardinality. The overlap coefficient is defined as

$$\begin{aligned} O(L_{\text {EADM+BB}}, L_{x}) = \frac{|L_{\text {EADM+BB}}\cup L_{x}|}{\min \left( |L_{\text {EADM+BB}}|, |L_{x}|\right) }. \end{aligned}$$

(21)

The Jaccard coefficient yields the fraction of common links between the EADM+BB and each of the other methods, while the overlap coefficient quantifies the extent of the overlap between the two detected backbones.

Table 2 Data summary of the seven real datasets under consideration

Each real dataset is examined at four different time resolutions obtained by counting, without repetitions, all the links that occur at the nominal frequency of acquisition of the experimental observation. Table 2 summarizes the seven datasets considered in this work. For ease of illustration, in this main document, we focus on the Primary school and the Museum datasets; “Appendix” contains the analysis of all datasets. Similar to the study of synthetic data, simulations are terminated after 24 h of computational time.

In Fig. 4, we summarize our comparison. In panels (a) and (d), we show a sample of the time series of the total number of temporal links, $\varOmega ^{\text {ts}} (t)$, and the interval partition identified by the BB method. For both datasets, $\varOmega ^{\text {ts}} (t)$ is not stationary, reflecting the complexity of the time evolution where each student or teacher in the Primary school dataset or museum visitor in the Museum dataset will come irregularly into contact with others. In panels (b) and (e), we compare the number of significant links detected by the five methods considered in this work. In agreement with evidence from Figs. 2 and 3 and Table 1 on synthetic data, the EADM+BB identifies a smaller number of links than other methods, whose predictions are equivalent.

We also observe that improving on the resolution of the data, by lowering the time step, increases the number of significant links detected by all the methods. This is related to the decrease in the number of temporal links ${\overline{W}}^{\text {ts}}$ due to the deletion of repeated temporal links. (No multiedges are allowed in a single time step.) Such a deletion affects mostly the nodes with highest activity, which generate many links over time. In this way, the heterogeneity of the system is reduced, reflecting in a lower number of detected significant links. Although all the methods are affected by the time resolution of the dataset, the EADM+BB is the one that shows the strongest tendency, as it requires the identification of switches in the activity patterns, which could be masked by node-specific links in poorly resolved datasets.

In Fig. 5, we compare the detected backbone networks using the Jaccard index and the overlap coefficient. The Jaccard index suggests a strong similarity in the case of the Primary school dataset and a weak similarity in the case of the Museum dataset. On the other hand, the overlap coefficient suggests that in both cases our method identifies a subset of links within those detected by other methods.

Individual activities have different temporal features in the two datasets. In the Primary school dataset, most students and teachers are recorded for the entire observation window and can recurrently interact with each other. As a result, the impact of explicitly considering time-varying activities is limited, and a time-averaged representation of the phenomenon constitutes an acceptable approximation. On the other hand, in the Museum dataset, visitors spend only a few hours in the museum, which comprises a small fraction of the observation window of 81 days. In this case, approximating individual activities with constant quantities along the whole observation window is an oversimplification of the problem that could lead to several false positives in the backbone detection.

Fig. 4

Influence of temporal patterns on backbone detection. In a, d we show the total number of temporal links created over time, $\varOmega ^{\text {ts}} (t)$, for one chosen resolution (indicated in square brackets) of the Primary school and Museum datasets, respectively. For visualization purposes, we select the first 60 time steps. Partition into intervals is performed by applying the Bayesian blocks (BB) method to the time series. Horizontal red segments represent the average number of temporal links in a specific interval. In b, e we compare the number of significant links found by the methods under scrutiny for the same two datasets. Inferences not reported correspond to simulations that exceed our time limit of 24 h. In c, f we display the number of temporal links, ${\overline{W}}^{\text {ts}}$, as a function of the resolution for the same two datasets. The exact values of the resolution are found in Table 2

Fig. 5

Differences and similarities in the backbone networks detected by the EADM+BB and the other methods (indicated in the legends). In a, c we show the Jaccard index for the Primary school and Museum datasets, respectively. In b, d we display the overlap coefficient for the same two datasets. Inferences not reported correspond to simulations that exceed our time limit of 24 h

In Fig. 6, we assess the accuracy of the methods in estimating the overall network connectivity, measured in terms of the total number of links in the observation window. We compare the expected number of temporal links, E$\left[ {\overline{W}} \right]$, with observations in the time series, ${\overline{W}}^{\mathrm {ts}}$. We specifically compute the relative error, $|\text {E}\left[ {\overline{W}} \right] - {\overline{W}}^{\mathrm {ts}}|/{\overline{W}}^{\mathrm {ts}}$, where we use E$\left[ {\overline{W}} \right] = \sum _{i,j=1;i<j}^{N}\sum _{t=1}^{T} p_{ij}(t)$ for the EADM+BB; $\hbox {E}_{I=1}\left[ {\overline{W}} \right] = \sum _{i,j=1;i<j}^{N} T p_{ij}$ for the $\hbox {EADM}_{I=1}$; Eq. (25) in Appendix for the TFM; and Eq. (29) in Appendix for the $\hbox {TFM}_{\mathrm{rhythm}}$. The SVN is excluded from this analysis as it takes ${\overline{W}}^{\text {ts}}$ as an input parameter. For all the considered datasets and all backbone detection methods, relative error is at most 5%, thereby indicating that all the methods are accurate in capturing the evolution of the network connectivity. In agreement with our expectation, the relative error for the TFM and the $\hbox {TFM}_{\mathrm{rhythm}}$ (when available) is lower than that for the $\hbox {EADM}_{I=1}$ and the EADM+BB. In fact, as previously discussed, the TFM and $\hbox {TFM}_{\mathrm{rhythm}}$ refine the estimation of individual activities through a maximum likelihood approach.

While all the methods work with approximately the same number of links throughout the temporal evolution, as shown in Fig. 6, they yield different predictions for the underlying backbone network as shown in Figs. 4 and 5. The most remarkable difference depends on whether one is accounting or not for time-varying activities.

Based on the study of the synthetic datasets in Figs. 2 and 3, we propose that the discovery process of the backbone network should be formulated by assuming, in general, that activity patterns are time-varying.

Fig. 6

Relative error between the total number of temporal links found in the time series, ${\overline{W}}^{\text {ts}}$, and the number of total temporal links estimated from the backbone detection algorithms under consideration. The SVN is discarded from this analysis since it uses ${\overline{W}}^{\text {ts}}$ as an input for filtering reducible links. Inferences not reported correspond to simulations that exceed our time limit of 24 h

4 Discussion

In this paper, we have introduced the evolving activity-driven model, a novel approach to detect the backbone network against time variations of node-specific properties, encapsulated by the activity. The activity of a node represents its propensity to generate links over time, which, in real systems, is seldom constant [51]. Should one look at temporal networks formed by humans, the individual activity might be low during sleeping hours and breaks, while it should be high during working hours. Whether differences in individual behavior modify the backbone network is the topic of our study.

To this end, we analytically identify conditions in which temporal patterns of the activity will have a secondary role on the detection of the backbone. These conditions correspond to the system being stationary and the activation patterns of the nodes not correlated. Based on these claims, we speculate that straining either of these conditions will lead to a salient role of temporal variations of the activity patterns on the backbone detection. Afterward, we compare the backbone networks detected by our methodology with inferences supported by four other approaches, all of which assume that individual activities are constant in time. Specifically, we focus on a modification of the evolving activity-driven model with constant activities, the statistically validated network [10], and two versions of the temporal fitness model [7]. In the first version of the temporal fitness model, activities are kept constant in time and their estimates are refined through a maximum likelihood approach, while in the second one, a time-varying parameter is utilized to encapsulate circadian and weekly patterns.

For both synthetic and real datasets, our approach identifies a subset of the links determined by the other methods. By utilizing a ground-truth backbone network from the synthetic data, we conclude that our methodology reduces the number of links that are incorrectly classified as part of the backbone network (false positives) and improves the precision of the detection process. These results suggest that accounting for temporal variations in the activity plays an important role in backbone detection, potentially leading to the discovery of a different backbone network. The most remarkable differences are noted when nodes display activity patterns that intensively vary in time, without a recurrent behavior. For instance, in the Museum dataset, visitors spend only a few hours in the museum, which is a small fraction of the total observation window of 81 days. In contrast with other methods that all yield equivalent predictions, our approach discovers a smaller backbone network, representative of people visiting museums in small groups. We expect a similar behavior when analyzing airports, restaurants, hotels, websites, and chat rooms, where people access alone or in small groups and only for a limited time.

The size of the backbone network discovered by our approach is influenced by the time resolution of the dataset. Working with poorly resolved data will challenge the feasibility of network inference, which is evident when dealing with visitors in a museum, and calls for the careful selection of a time resolution, which could be a confounding factor in detecting the backbone network of a system. This claim is in line with [52], which focuses on random walks over temporal networks.

The main advantages of the proposed evolving activity-driven methodology are three: (i) its limited computational time, whereby it allows for fast network discovery even when dealing with long time series and large networks (simulations presented in this paper are only a few minutes long); (ii) its ability to cogently model temporal activity patterns, which cannot be addressed by the current state-of-the-art approaches; and (iii) its consistency with the literature, whereby it yields equivalent predictions to existing methods when dealing with time-invariant activity patterns.

Our approach can find applications across several domains of science and engineering, beyond the exemplary social networks examined herein. For example, it could be implemented in the study of functional networks in the brain, which primarily relies on simple thresholding [26], or in the analysis of the World Wide Web, power grids, chemical reaction networks, where topology identification methods [53,54,55] can benefit from a statistically principled approach to discard reducible links.

However, our approach is not free of limitations. We detect switches in the individual activities over successive disjoint intervals by considering the overall system evolution, rather than the individual time series. In principle, we cannot exclude the possibility that individual activities could vary in time in such a way that the overall system evolution remains stationary. In this case, our approach would not be able to detect time variations in individual activities. In principle, we could attempt at working with individual time series, but this would challenge the use of the Bayesian block representation [37] that relies on nodes to activate multiple times—a condition that is not satisfied by the sparse datasets considered in our study. In addition, the overall computational cost would depend also on the size of the system, thereby hindering implementation for large networks. At the same time, we acknowledge that our methodology is not applicable to small networks, composed of only a few tens of nodes, as we conduct the estimates of the individual activities using a weighted configuration model that requires large networks [31].

Future research will involve the formulation of algorithms for the optimal selection of the temporal resolution, which are needed for enhancing the performance of our methodology and the one proposed in [7]. The evolving activity-driven model might be further extended through the detection of individual interval partitions, one for each node in the network, overcoming the assumptions that the interval partition is unique and that all of the activities switch synchronously. More long-term, fruitful lines of research should aim at unraveling the intricate interplay between individual features and the formation of temporal interaction patterns.

4.1 Code availability

Python 2.7 codes are freely available here [56].

Appendix

1.1 Backbone detection methods

Here, we succinctly summarize the temporal fitness model (TFM) [7], the temporal fitness model with rhythm ($\hbox {TFM}_{\mathrm{rhythm}}$) [7], and the statistically validated network (SVN) [10].

1.1.1 Temporal fitness model

The TFM considers a temporal network formed by N nodes evolving over T discrete time steps. All multiple links occurring within the same time step are removed, so that the total number of temporal links between node i and j is bounded by T. First, individual activities are computed according to

$$\begin{aligned} a_i = \frac{{\overline{s}}^{\text {ts}}_i}{\sqrt{2 {\overline{W}}^{ts} T}}. \end{aligned}$$

(22)

Then, their values are refined through a maximum likelihood approach, which requires the solution of N equations

$$\begin{aligned} \sum _{j = 1; j\ne i}^{N} \frac{{\overline{w}}_{ij}^{\text {ts}} - T a_i^*a_j^*}{1 - a_i^*a_j^*} = 0, i = 1, \ldots , N, \end{aligned}$$

(23)

where $\varvec{a^*} = \left( a_1^*, \ldots , a_N^* \right)$ contains the optimal values for the individual activities. Finally, the p-value $\alpha _{i j}$ for the link generated between node i and j is computed from the cumulative function of the Binomial distribution as

$$\begin{aligned} \alpha _{i j} \equiv 1 - \sum _{ x = 0}^{{\overline{w}}^{\text {ts}}_{i j}-1} B \left( x; T, a_i^*a_j^* \right) . \end{aligned}$$

(24)

All p-values, one for each link in the network, are compared with a threshold value $\beta$, properly corrected by using a multiple hypotheses correction [42, 43], and any value lower than $\beta$ adds a link to the backbone network.

For our purposes, we also compute the expected total number of temporal links in the overall temporal evolution

$$\begin{aligned} \text {E} \left[ {\overline{W}} \right] = T \sum _{i,j=1;i<j}^{N} a_i^*a_j^*. \end{aligned}$$

(25)

1.1.2 Temporal fitness model with rhythm

The $\hbox {TFM}_{\mathrm{rhythm}}$ adds to the TFM T time-varying coefficients, one for each time step, $\varvec{\xi } = \left( \xi (1), \ldots , \xi (T) \right)$. First, every element in the time-varying vector is manually set to 0.999, with the exception of $\xi (1)$ that is set equal to one. Individual activities are estimated according to Eq. (22). To determine the optimal values $(\varvec{a^*}, \varvec{\xi }^{*})$ in the maximum likelihood sense, we solve the system of $N+T-1$ equations

$$\begin{aligned} \begin{aligned}&\sum _{t=1}^{T} \sum _{j = 1; j\ne i}^{N} \frac{A_{ij}^{\text {ts}}(t) - a_i^*a_j^*\xi ^*(t)}{1 - a_i^*a_j^*\xi ^*(t)} = 0,&i = 1, \ldots , N,\\&\sum _{i,j = 1; j\ne i}^{N} \frac{A_{ij}^{\text {ts}}(t) - a_i^*a_j^*\xi ^*(t)}{1 - a_i^*a_j^*\xi ^*(t)} = 0,&t = 2, \ldots , T, \end{aligned} \end{aligned}$$

(26)

where $A_{ij}^{\text {ts}}(t)$ is the adjacency matrix at time t estimated from the time series. The expected number of links is computed as

$$\begin{aligned} \text {E} \left[ {\overline{w}}_{ij} \right] = \sum _{t = 1}^{T} a_i^*a_j^*\xi ^*(t). \end{aligned}$$

(27)

Finally, the p-value $\alpha _{i j}$ for the link generated between node i and j is computed from the cumulative function of the Poisson distribution as

$$\begin{aligned} \alpha _{i j} \equiv 1 - \sum _{ x = 0}^{{\overline{w}}^{\text {ts}}_{i j}-1} P \left( x; \text {E}\left[ {\overline{w}}_{ij} \right] \right) . \end{aligned}$$

(28)

All the p-values, one for each link in the network, are compared to a threshold value $\beta$, properly corrected by using a multiple hypotheses correction [42, 43]. Any value lower than $\beta$ leads to a link in the backbone network.

For our purposes, we also compute the expected total number of temporal links in the overall temporal evolution

$$\begin{aligned} \text {E} \left[ {\overline{W}} \right] = \sum _{i,j=1;i<j}^{N} \sum _{t = 1}^{T} a_i^*a_j^*\xi ^*(t). \end{aligned}$$

(29)

1.1.3 Statistically validated network

The SVN considers a temporal network of N nodes evolving over an observation time window that can be either discrete or continuous in time. Temporal links are aggregated to form a weighted static network. The p-value $\alpha _{i j}$ for the link generated between node i and j is computed from the cumulative function of the hypergeometric distribution as

$$\begin{aligned} \begin{aligned} \alpha _{i j}&\equiv 1 - \sum _{ x = 0}^{{\overline{w}}^{\mathrm {ts}}_{i j}-1} H \left( {\overline{w}}_{i j} \bigg |2 {\overline{W}}^{\mathrm {ts}}, {\overline{s}}_{i}^{\mathrm {ts}}, {\overline{s}}_{j}^{\mathrm {ts}} \right) . \end{aligned} \end{aligned}$$

(30)

The p-values are compared with a threshold value $\beta$, properly corrected by using a multiple hypotheses correction [42, 43], and a link is added to the backbone network of the p-value which is less than $\beta$.

1.2 On the similarity among the $\hbox {EADM}_{I=1}$, SVN, and TFM

Here, we discuss why these three methods yield similar results for both synthetic and real datasets. First, we show that the $\hbox {EADM}_{I=1}$ is a valid approximation of the TFM for large networks (hundreds of nodes or more). Then, we analytically examine the convergence of the SVN to the $\hbox {EADM}_{I=1}$.

1.2.1 On the similarity between the TFM and $\hbox {EADM}_{I=1}$

We consider a long observation window T, for which the Binomial distribution in Eq. (24) converges to a Poisson distribution used in our method in Eq. (12). While in the $\hbox {EADM}_{I=1}$ activities are estimated from the dataset using Eq. (8), in the TFM they are identified in a maximum likelihood sense [7]

Fig. 7

Accuracy of the $\hbox {EADM}_{I=1}$ and the TFM in estimating the total number of temporal links in the overall time series. A perfect identification should yield a ratio between E$\left[ {\overline{W}}\right]$ and ${\overline{W}}^{\text {ts}}$ of one (black solid line). In these simulations, we use our artificial network where no backbone is present ($\delta = \lambda = 0$) and activities are constant in time ($T = 5000$, $I=1$, $\langle \tau (\varDelta ) \rangle = T/I = 5000$, $a_{{\min }} = [\sqrt{\langle \tau (\varDelta ) \rangle }]^{-1}$, and $p=0$). Markers indicate the average of $10^2$ independent simulations; 95% confidence interval is displayed in gray

Fig. 8

Sensitivity analysis of the EADM+R to the number of estimated intervals, $I_e$, from $I_e=1$ to $I_e = T-1$. In a, c, we set $a_{{\min }} = [\sqrt{\langle \tau (\varDelta ) \rangle }]^{-1}$ and $\lambda = 0.025$, to attain a dense ADNs and an easy-to-discover backbone. On the contrary, in b, d, we set $a_{{\min }} = [\langle \tau (\varDelta ) \rangle ]^{-1}$ and $\lambda = 0.002$, to attain sparse ADNs and a partially hidden backbone. Other parameter values are: $N=100$, $T = 5000$, $I=20$, $\langle \tau (\varDelta ) \rangle = T/I = 250$, $\delta = 0.01$, and $p=0.4$. Markers indicate the average of $10^2$ independent simulations; 95% confidence interval is displayed in gray

Fig. 9

Number of significant links as a function of the resolution for all real datasets under consideration. Inferences not reported correspond to simulations that exceed our time limit of 24 h

Fig. 10

Jaccard index between EADM+BB and all the other methods as a function of the resolution for all datasets under consideration. Inferences not reported correspond to simulations that exceed our time limit of 24 h

Fig. 11

Overlap coefficient between EADM $+$ BB and all the other models as a function of the resolution for all datasets under consideration. Inferences not reported correspond to simulations that exceed our time limit of 24 h

In Fig. 7, we assess the ability of the $\hbox {EADM}_{I=1}$ and the TFM to estimate the total number of temporal links. We compute the expected values of the number of links for the $\hbox {EADM}_{I=1}$ as $\text {E}\left[ {\overline{W}} \right] = \sum _{i,j=1;i<j}^{N} T p_{ij}$, while we use Eq. (25) for the TFM. These values are compared with the total number of temporal links observed in the time series ${\overline{W}}^{\text {ts}}$. As expected, the TFM works well for any network size, due to the use of the maximum likelihood. Nevertheless, the maximum likelihood approach becomes computational demanding for networks of around 1,000 nodes and beyond, thereby becoming useless for very large networks. On the other hand, the $\hbox {EADM}_{I=1}$ shows poor performance for small networks, while reaching the TFM for networks of 100 nodes. This improvement in performance of the $\hbox {EADM}_{I=1}$ is explained in [31], where it is shown that Eq. (14) is in excellent agreement with numerical simulations for large networks.

1.2.2 On the similarity between the SVN and $\hbox {EADM}_{I=1}$

When ${\overline{W}}^{\mathrm {ts}} \gg 1$, the hypergeometric distribution in Eq. (30) converges to a Poisson distribution and its p-value becomes equivalent to the p-value for the $\hbox {EADM}_{I=1}$

$$\begin{aligned} \begin{aligned} \alpha _{ij} = 1 - \sum _{x = 0}^{{\overline{w}}_{i j}^{\mathrm {ts}}-1} P \left( x; \frac{{\overline{s}}_{i}^{\mathrm {ts}} {\overline{s}}_{j}^{\mathrm {ts}}}{2 {\overline{W}}^{\mathrm {ts}}} \right) . \end{aligned} \end{aligned}$$

(31)

In all the synthetic and real data studied herein ${\overline{W}}^{\mathrm {ts}}$ is very large, so that Eq. (30) converges to Eq. (31).

1.3 Generation of synthetic temporal networks

To examine the precision and recall of irreducible links, we generate synthetic networks. The procedure of network generation is given as follows:

• 1. We consider a temporal network evolving in an observation window of length T, divided into I different intervals. We randomly select without replacement $I-1$ time steps in $\{1,\ldots ,T\}$, which we sort as $t_{\mathrm {in}}(2) \ldots t_{\mathrm {in}}(I)$, and we set $t_{\mathrm {in}}(1)=1$. Each interval $\varDelta$ has different length $\tau (\varDelta )$, so that, in general, the average length of the interval is $\langle \tau (\varDelta ) \rangle = T/I$.

• 2. The N nodes in the network have a time-varying, piece-wise constant, individual activity. We extract activity values from a power law distribution, $F(a) \sim a^{-2.1}$, with $a \in [a_{{\min }}, 1]$. The time-varying activity $a_i (t)$ is selected according to the following procedure:

  • When $\varDelta =1$, N activity values, one for each node in the network, are randomly extracted from F(a), and held constant within $[t_{\text {in}}(1), t_{\text {in}}(1)+\tau (1)-1]$.

  • When $2 \le \varDelta \le I$, activities might be correlated between two successive intervals, $t_{1}\in [t_{\text {in}}(\varDelta -1), t_{\text {in}}(\varDelta -1)+\tau (\varDelta -1)-1]$ and $t_{2} \in [t_{\text {in}}(\varDelta ), t_{\text {in}}(\varDelta )+\tau (\varDelta )-1]$ according to Eq. (19) in the main text.

• 3. We generate a temporal network in the observation window [1, T]. Each pair of nodes ij within an interval $\varDelta$ is connected with probability $a_i(\varDelta ) a_j(\varDelta )$. As a result, we obtain a sequence of T undirected and unweighted networks, with adjacency matrices ${\hat{A}}(1)$, $\ldots$, ${\hat{A}}(T)$. These networks are generated only as a function of the individual activities.

• 4. Based on the node pairs that are connected at least once over T time steps of the observation window, we define the synthetic backbone. Specifically, we randomly assign a fraction $\delta$ of these node pairs to the backbone.

• 5. We construct T new networks A(1), A(2), $\ldots$, A(T) from ${\hat{A}}(1)$, ${\hat{A}}(2)$, $\ldots$, ${\hat{A}}(T)$ by accounting for the synthetic backbone above. First, we set $A_{ij}(t) = {\hat{A}}_{ij}(t)$ for $t = 1, \ldots T$ for all the pairs that do not belong to the backbone. Then, for the generic link ij in the backbone, we initialize $A_{i j}(1) = {\hat{A}}_{ij}(1)$ and we iterate the following steps for $t = 2, \ldots , T$:

  • if ${\hat{A}}_{ij}(t) = 1$, we maintain $A_{ij}(t) = 1$;

  • if ${\hat{A}}_{ij}(t) = 0$, we set $A_{ij}(t) = 1$ with probability $\lambda$ and $A_{ij}(t) = 0$ with probability $1-\lambda$.

  The parameter $\lambda$ measures the preponderance of links associated with the backbone during the observation window.

1.4 Insights on the interval estimation

The EADM+R requires that the number of intervals is known a priori. Nevertheless, when dealing with real networks, our knowledge, $I_e$, might differ from the true value, I. This mismatch might diminish the accuracy of the backbone inference, as examined below for synthetic data. We focus on two sets of parameters, which represent two possible scenarios. In the first case, $a_{{\min }} = [\sqrt{\langle \tau (\varDelta ) \rangle }]^{-1}$ and $\lambda = 0.025$, which correspond to a “dense” ADNs with an easily detectable backbone. In the second case, $a_{{\min }} = [\langle \tau (\varDelta ) \rangle ]^{-1}$ and $\lambda = 0.002$, which represent a “sparse” ADNs with a partially hidden backbone.

In Fig. 8a, c, we show that if the number of estimated intervals, $I_e$, is greater or equal to the true value, I, precision and recall are close to one. On the contrary, in Fig. 8b, d, we observe a more dramatic scenario, in which increasing $I_e$ hinders the performance of the method, leading to filtering out most of the links that belong to the backbone network.

Fig. 12

Total number of temporal links estimated in the time series $W^{\text {ts}}$ as a function of the resolution for all datasets under consideration

Fig. 13

Relative error between the total number of temporal links, ${\overline{W}}^{\mathrm {ts}}$, and the number of total temporal links estimated from the backbone detection algorithms under consideration. The SVN is discarded from this analysis because it uses ${\overline{W}}^{\mathrm {ts}}$ as an input. Inferences not reported correspond to simulations that exceed our time limit of 24 h

1.5 Analysis of all available real datasets

1.5.1 Significant links

We compare the backbone networks from seven real-world datasets inferred by the five methods under consideration in terms of the number of significant links. The EADM+BB always finds less links than any other methods (Fig. 9).

1.5.2 Jaccard index

In Fig. 10, we assess differences in the backbone networks detected by the EADM+BB and four methods on seven real-world datasets, in terms of the Jaccard index. We observe that the EADM+BB finds backbones different from the $\hbox {EADM}_{I=1}$, SVN, TFM, and $\hbox {TFM}_{\mathrm{rhythm}}$, which are equivalent.

1.5.3 Overlap coefficient

Similar to Fig. 10, we examine the overlap coefficient of backbone networks determined by our method and the other four in Fig. 4, confirming that the EADM+BB tends to detect a subset of the links predicted by other methods—which are thus prone to false positives (Fig. 11).

1.5.4 Temporal links

In Fig. 12, we display the total number of temporal links estimated in the time series, ${\overline{W}}^{\mathrm{ts}}$, for all the considered methods on all the seven real-world datasets. We confirm that the number of links decreases as we increase the time resolution of the dataset.

1.5.5 Relative error

We analyze the accuracy of the methods in describing the overall system evolution. We compare the expected number of the total temporal links generated in, E$\left[ {\overline{W}} \right]$, with ${\overline{W}}^{\mathrm {ts}}$. All methods are accurate for the datasets studied herein, with a relative error up to 5% (Fig. 13).