Nonlinear magnetic force and dynamic characteristics of a tri-stable piezoelectric energy harvester

Abstract

In piezoelectric energy harvesters (PEHs) with external magnetic coupling, one main challenge is to obtain a precise magnetic force model to calculate the impacts of the external magnetic force on the vibrational response and energy harvesting performance. A tri-stable piezoelectric energy harvester (TPEH) with two external magnets was considered in this paper. An improved magnetic force model based on the magnetic dipoles theory was originally derived to investigate the formation mechanisms for bi- or tri-stability states at first, and then, a distributed-parameter mathematical model based on the energy method was established by considering the derived nonlinear magnetic force, and was used to investigate the nonlinear dynamic behaviors and power generation performance. Bifurcation analyses were also performed for the equilibrium solution of the derived system model. Experiments were subsequently conducted to validate the theoretical analysis. Simulation and experimental results indicate that the improved model for magnetic force is more applicable compared with the magnetic dipoles model used before. Results also show that the TPEH can significantly enhance the energy harvesting performance compared with the conventional bi-stable piezoelectric energy harvester in a wide frequency range.

1 Introduction

Harvesting energy from ambient vibrations via piezoelectric transducers has inspired extensive attentions over the past decades for the reason that it provides an exciting solution to resolve the costly and tedious replacement issue for some small electronic devices powered by batteries [1,2,3,4,5,6,7,8]. Most of the incipient piezoelectric energy harvesters, which were composed of a piezoelectric cantilever beam with a tip mass, were designed based on linear resonance mechanism. Such linear energy harvesters only perform well when they are excited at their resonance frequencies, which should be synchronized with the excitation frequency [9, 10]. Unfortunately, it is considerately suboptimal for the excitation frequency synchronized with the resonance frequency due to the frequency-varying and wideband characteristics, leading to a significant reduction of the energy harvesting efficiency in the off-resonant frequency region [11]. To overcome this issue, lots of efforts have been made to improve the energy harvesting performance via active and adaptive frequency-tuning methods, multimodal energy harvesting, and nonlinearity techniques [11,12,13]. Particularly, introducing nonlinear phenomenon generated by the magnetic coupling effect into the linear harvesters can achieve a significant enhancement for broadband performance and energy harvesting efficiency [14]. As a result, an extensive investigation of nonlinear piezoelectric energy harvester with external magnetic coupling effect has been carried out to improve the output performances over a wide range of operating frequencies, such as mono-stable, bi-stable, and multi-stable energy harvesters [15,16,17]. Mono-stable piezoelectric energy harvester (MPEH) is the simplest form of a nonlinear energy harvester that has one stable equilibrium state and one oscillating mass [18]. It can result in large oscillations over a wider range of frequencies excited at high external amplitudes, but it exhibits poor performance when the excitations are band-limited [19] and random excitations [20].

To overcome the limitations of MPEHs, bi-stable piezoelectric energy harvesters (BPEH) have been proposed [21,22,23]. A typical bi-stable piezoelectric energy harvester can be realized by using a piezoelectric cantilever beam with tip and external magnets [24, 25]. Such a bi-stable piezoelectric energy harvester has two potential wells separated by a barrier, with the two wells corresponding to two stable equilibrium positions. The BPEH has a unique double-well restoring force potential characteristics which provide three distinct dynamic operating regions (e.g., intrawell vibrations, aperiodic or chaotic interwell vibrations, and large-amplitude interwell vibrations). When the excitation amplitude is sufficiently large, the BPEH can oscillate between the two stable equilibrium positions, leading to large-amplitude interwell vibrations and high output performance. Despite the potential benefits, there exist several limitations to BPEH. The main challenge is that the energy harvesting ability of the BPEH seriously depends on the excitation intensity. Additionally, the BPEH has been recently proved to show inefficient in real-world applications where excitations are random and non-stationary [26].

Recently, multi-stable piezoelectric energy harvesters, such as tri- or quad-stable PEHs, have attracted the researcher’s interests due to their shallower potential wells compared with BPEH [17, 27, 28]. The shallower wells of multi-stable piezoelectric energy harvesters result in higher energy output and greater harvesting efficiency at lower frequencies and weaker excitation intensity [17]. Zhou et al. [27] used a genetic algorithm to identify key parameters and testified that the tri-stable energy harvester can easily achieve interwell motions. They also theoretically and experimentally proved the broadband response characteristics of a tri-stable piezoelectric energy harvester with two rotatable external magnets [28]. Cao et al. [29] numerically and experimentally investigated the influence of potential well depth on tri-stable energy harvesting performance. Kim et al. [30] presented a tri-stable oscillator constructed around a cantilever-based magnetically coupled system and numerically demonstrated the advantages of tri-stable energy harvesters. However, experimental verification would like to be conducted. Zhou et al. [31] studied a method to improve the efficiency of harvesting random energy by snap-through in a quad-stable harvester. Nevertheless, there are several issues regarding the effect of parameter variations, especially the magnetic force, on the dynamic responses of the tri-stable energy harvesters. A comprehensive insight into these effects will help to optimize tri-stable energy harvesters in various applications and further improve the output performance.

Fig. 1

Schematic of the tri-stable energy harvester

In the above-mentioned studies of nonlinear piezoelectric energy harvesters with external magnetic coupling, the magnetic force exerted on the cantilever beam tip is frequently adopted to alter the stiffness of the energy harvester to enhance the conversion abilities. And the tip magnet can also be used to tune the resonant frequency of the energy harvester to match with the excitation frequency, which is ideally suited to efficiently harvest the energy from ambient vibration with slowly varying frequencies. However, it is very difficult to derive a precise model to calculate the magnetic force for the reason that the magnetic force is usually a complicated nonlinear function of the cantilever deflection and the magnets’ interval. Thus, the impact of the nonlinear magnetic force on vibration response and energy harvesting efficiency has become challenging. Zhou et al. [31] and Aboulfotoh et al. [32] measured the magnetic force by experiments and summarized an empirical expression to characterize magnetic force. This method can accurately calculate the magnetic force of that harvester. However, it will lead to a failure in another system once any parameter changes, thus it is difficult to be widely used. Leng et al. [33] studied a method based on equivalent magnetizing current theory to calculate the magnetic force and the potential function with triple wells, while the energy harvester was equivalent as a mass-spring-damper model based on the lumped system analysis method. Stanton et al. [34] and Zhu et al. [35] modeled all the magnets of the energy harvester as magnetic dipoles to obtain the magnetic force calculation expression. In their model, the magnets were modeled as point dipoles only when the magnet’s dimensions are much less than the magnet interval. However, it is very difficult to achieve large power output and energy conversion ratio with small magnets in practice. In fact, large dimension magnets are usually adopted to achieve a good output performance. In this case, the accuracy of this model will be greatly reduced. Further, the magnetic force produced by the magnetic coupling depends on the energy harvester’s structural parameters such as the size of the magnets, the cantilever, and the magnets interval, as well as the magnet state changing with the tip magnet movement. Therefore, the magnetic force has become the key factor that affects the energy harvesting performance, and it is very necessary to build a precise theoretical model to calculate the magnetic force, and this will be helpful to understand the formation mechanism of multi-stability states, nonlinear dynamic behaviors and power generation performance.

Fig. 2

The conventional magnetic force method

In this study, the mathematical modeling, numerical simulation, and experimental validation are performed to further investigate the dynamic responses and energy output of a tri-stable piezoelectric energy harvester. An improved model for calculating magnetic force based on the magnetic dipoles theory is originally built. The simulation and experimental results indicate that the improved model for magnetic force is more applicable for different magnetic intervals compared with the magnetic dipoles model used before. The results also show that the TPEH can enhance the energy harvesting performance significantly compared with the conventional bi-stable piezoelectric energy harvester (BPEH) in a wide frequency range. This paper is organized as follows. The next section provides the illustration and modeling of the TPEH, and an improved model for calculating magnetic force based on the magnetic dipoles theory is originally built and verified by experiment. Also, a distributed-parameter electromechanical model of the TPEH including the derived magnetic force model is established. In Sect. 3, a series of bifurcation analyses, potential wells, and numerical simulation are performed based on the derived model to investigate the dynamic response and energy harvesting performance. The performance comparison between the TPEH and the conventional BPEH are also carried out. In Sect. 4, experiments are conducted to verify the theoretical results of the TPEH. At last, key findings and conclusions are presented and summarized.

2 Magnetic force and dynamic model of TPEH

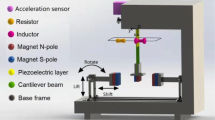
Figure 1 shows the schematic diagram of the TPEH with magnetic coupling considered in this paper [17, 27,28,29,30, 32,33,34,35]. This harvester is mainly composed of a piezoelectric cantilever beam with a tip magnet (A), two external magnets (B and C), and a base that is excited by ambient vibrations. The piezoelectric cantilever beam is fixed at the left wall of the base. Two identical piezoelectric layers (PZTs) are fully bonded on the top and bottom surfaces of the cantilever beam substrate. These two PZTs, poled oppositely in the thickness direction, are covered by conductive electrodes and connected in series to an equivalent load resistance (R) represented a small electronic device. As shown in Fig. 1, magnet A is attached to the tip of the cantilever beam and oriented with opposite polarity to the field of magnets B and C. There is a separation distance (d) measured in the x direction between the tip magnet and the two external magnets. The two external magnets are fixed at the right wall of the base and located parallel to each other in the x direction, and they are separated from each other by a gap distance ($d_{\mathrm{g}}$) measured in the z direction. For this configuration shown in Fig. 1, the TPEH has three equilibrium positions in the static state, i.e., stable 1, stable 2, and stable 3.

As to the TPEH, one challenge is how to precisely calculate the magnetic force exerted on the tip magnet. Therefore, an appropriate method of calculating magnetic force should be solved.

2.1 Conventional magnetic force model of the TPEH

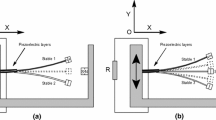
For two mutually exclusively and horizon-alignment magnets B and C in Fig. 1, the magnetic force exerted on magnet A can be calculated by using magnetic dipoles method in the previous works [27,28,29,30, 32,33,34,35]. The configuration of the conventional magnetic force model based on magnetic dipoles method is shown in Fig. 2.

In Fig. 2, all the magnets are modeled as a point dipole when their dimensions are much less than the separation distance d. $Q_{\mathrm{A}}$, $Q_{\mathrm{B}}$ and $Q_{\mathrm{C}}$ are the equivalent point dipoles of magnet A, B and C, respectively. So the magnetic field generated by magnet i ($i =\hbox { B or C}$) upon magnet A can be given by

$$\begin{aligned} \mathbf{B}_{i\mathrm{A}} =-\frac{\mu _0 }{4\pi }\nabla \frac{{\varvec{m}}_i \cdot {{\varvec{r}}}_{i\mathrm{A}} }{\left\| {{\varvec{r}}_{i{\mathrm{A}}} } \right\| _2^3 } \end{aligned}$$

(1)

where $\mu _0$ is the magnetic permeability constant, ${{\varvec{m}}}_i$ represents the magnetic moment vector of $i\hbox {th}$ magnet. ${{\varvec{r}}}_{i\mathrm{A}}$ is the vector direction from the magnet i to magnet A, respectively. $\left\| \cdot \right\| _2$ and $\nabla$ denote Euclidean norm and vector gradient operator, respectively. So the potential energy created by magnet i upon magnet A can be written as

$$\begin{aligned} U_{mi\mathrm{A}} =-{{\varvec{B}}}_{i\mathrm{A}} \cdot {{\varvec{m}}}_{\mathrm{A}} \end{aligned}$$

(2)

where ${{\varvec{m}}}_{\mathrm{A}}$ represents the magnetic moment vector of magnet A. So the potential energy of magnetic field generated by the two external magnets B and C upon magnet A can be obtained.

$$\begin{aligned} U_\mathrm{m} =U_{m\mathrm{BA}} +U_{m\mathrm{CA}} =-{{\varvec{B}}}_{\mathrm{BA}} \cdot {{\varvec{m}}}_{\mathrm{A}} -{{\varvec{B}}}_{\mathrm{CA}} \cdot {{\varvec{m}}}_{\mathrm{A}} \end{aligned}$$

(3)

And then the nonlinear magnetic force can be given by

$$\begin{aligned} F_z ={\partial U_\mathrm{m} }/{\partial w(L,t)} \end{aligned}$$

(4)

where w(L, t) is the tip displacement of the piezoelectric cantilever beam, as shown in Fig. 2.

Fig. 3

Comparison between experimental data and calculated magnetic force of the conventional magnetic dipoles method

Figure 3 shows the magnetic force comparison between experimental result and calculated result using Eq. (4) derived from conventional magnetic dipoles method. It can be seen that there are some distinct differences between the experimental data and calculated magnetic force. The error increases with a decrease in the separation distance d. This is mainly caused by the assumptions that all the magnet’s dimensions are much smaller than the magnet interval. It seems unreasonable because large dimension magnets are usually adopted to achieve a good output performance and energy conversion ratio in practical applications. Therefore, the conventional magnetic dipole method is less suitable to calculate the magnetic force, especially when the separation distance d is small.

Fig. 4

The improved magnetic force calculating method

2.2 Improved magnetic force model of the TPEH

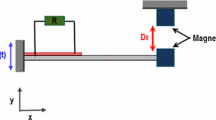
In this subsection, an improved magnetic force model based on the point dipole theory is presented to calculate the magnetic force. As the magnet is magnetized in a magnetic field, there are internal magnetizing current inside it and surface magnetizing current on the surface of the magnet, respectively. For the permanent magnets, the magnetization of the magnet is usually assumed to be constant, that is to say the internal magnetizing current density of the magnets is zero, and only the surface magnetizing currents of the magnets are considered [36]. Therefore, the left and the right polarized surfaces of the magnet A, B, and C are modeled as point dipoles of $Q_1$, $Q_2$, ${Q}'_1$, ${Q}'_2$, ${Q}'_3$ and ${Q}'_4$, respectively, as shown in Fig. 4. In this model,${{\varvec{r}}}_{ij} (i=1,2,3,4,j=1,2)$ is the vector direction from the magnet dipole ${Q}'_i$ to $Q_j ;{{\varvec{M}}}_{\mathrm{A}}$,${{\varvec{M}}}_{\mathrm{B}}$ and ${{\varvec{M}}}_{\mathrm{C}}$ are the magnetization vector of magnet A, B, and C, respectively. w(L, t) is the tip displacement of the cantilever beam, a is the half-length of the three magnets, and $\theta$ is the rotation angle of the tip magnet A.

Assuming that the two external magnets are identical in all aspects and that their magnetizations are uniform throughout the associated surfaces, the magnetic current density can be calculated using the Biot-Savart law once the surface current densities are given. The magnetic current density generated by ${Q}'_i (i = 1, 2, 3, 4)$ at a point $\hbox {P}_{0}$, whose position vector can be denoted by ${{\varvec{X}}}$, can then be given by the following vector form.

$$\begin{aligned} {{\varvec{B}}}_i ({{\varvec{X}}},{{{\varvec{X}}}'})= & {} \frac{\mu _0 }{4\pi }\sum _{i=1}^4 {{Q}'_i } \frac{{{\varvec{X}}}-{{{\varvec{X}}}'}_i }{\left| {{{\varvec{X}}}-{{{\varvec{X}}}'}_i } \right| ^{3}}=\frac{\mu _0 }{4\pi }\sum _{i=1}^4 {{Q}'_i } \frac{{{\varvec{r}}}_i }{\left| {{{\varvec{r}}}_i } \right| ^{3}}\nonumber \\ \end{aligned}$$

(5)

with

$$\begin{aligned} {Q}'_i= & {} -M_{\mathrm{B}} S_{\mathrm{B}} ,M_{\mathrm{B}} S_{\mathrm{B}} ,-M_{\mathrm{C}} S_\mathrm{C} ,M_{\mathrm{C}} S_{\mathrm{C}} ,\nonumber \\&\quad \hbox { for }i=1,2,3,4 \end{aligned}$$

(6)

where ${{{\varvec{X}}}'}_i$ and ${Q}'_i$ are the position vector and the total surface charge for the $i\hbox {th}$ equivalent point charge of the external magnets, respectively. ${{\varvec{r}}}_i$is the vector direction from the $i\hbox {th}$ equivalent point charge ${Q}'_i$ to the point $\hbox {P}_{0}$, and $S_{\mathrm{A}}$, $S_{\mathrm{B}}$ and $S_\mathrm{C}$ are the surface area of the magnets A, B and C, respectively.

Similarly, assuming that the magnetization of the tip magnet is uniform throughout the associated surfaces, using the external magnetic current density given in Eq.(5), the magnetic force exerted on the point dipole $Q_1$ and $Q_2$ can be, respectively, achieved as follows:

$$\begin{aligned} F_1= & {} Q_1 {\varvec{B}}_i ({\varvec{X}}_1 ,{{\varvec{X}}'})=\frac{\mu _0 }{4\pi }\sum _{i=1}^4 {Q_1 {Q}'_i } \frac{{\varvec{X}}_1 -{{\varvec{X}}'}_i }{\left| {{\varvec{X}}_1 -{{\varvec{X}}'}_i } \right| ^{3}}\nonumber \\= & {} \frac{\mu _0 }{4\pi }\sum _{i=1}^4 {Q_1 {Q}'_i } \frac{{\varvec{r}}_{i1} }{\left| {{\varvec{r}}_{i1} } \right| ^{3}} \end{aligned}$$

(7)

$$\begin{aligned} F_2= & {} Q_2 {\varvec{B}}_i ({\varvec{X}}_2 ,{{\varvec{X}}'})=\frac{\mu _0 }{4\pi }\sum _{i=1}^4 {Q_2 {Q}'_i } \frac{{\varvec{X}}_2 -{{\varvec{X}}'}_i }{\left| {{\varvec{X}}_2 -{{\varvec{X}}'}_i } \right| ^{3}}\nonumber \\= & {} \frac{\mu _0 }{4\pi }\sum _{i=1}^4 {Q_2 {Q}'_i } \frac{{\varvec{r}}_{i2} }{\left| {{\varvec{r}}_{i2} } \right| ^{3}} \end{aligned}$$

(8)

where $Q_j =M_{\mathrm{A}} S_{\mathrm{A}} ,-M_{\mathrm{A}} S_{\mathrm{A}}$, for $j=1,2$. And ${{\varvec{X}}}_j (j=1,2)$ is the position vector for the $j\hbox {th}$ equivalent point charge of the tip magnet. Therefore, the total magnetic force of the tip magnet generated by the two external magnets then can be obtained as

$$\begin{aligned} F= & {} F_1 +F_2 =\frac{\mu _0 }{4\pi }\sum _{j=1}^2 {\sum _{i=1}^4 {Q_j {Q}'_i } } \frac{{\varvec{X}}_j -{{\varvec{X}}'}_i }{\left| {{\varvec{X}}_j -{{\varvec{X}}'}_i } \right| ^{3}}\nonumber \\= & {} \frac{\mu _0 }{4\pi }\sum _{j=1}^2 {\sum _{i=1}^4 {Q_j {Q}'_i } } \frac{{\varvec{r}}_{ij} }{\left| {{\varvec{r}}_{ij} } \right| ^{3}} \end{aligned}$$

(9)

From the magnetic configuration shown in Fig. 4, the position vectors ${\varvec{X}}_j$ and ${{\varvec{X}}'}_i$ can be calculated as

$$\begin{aligned} {{\varvec{X}}'}_1= & {} (L+2a+d){\varvec{i}}+0.5d_{\mathrm{g}} {\varvec{k}}\hbox { for }{Q}'_1 \end{aligned}$$

(10a)

$$\begin{aligned} {{\varvec{X}}'}_2= & {} (L+4a+d){\varvec{i}}+0.5{\mathrm{g}} {\varvec{k}}\hbox { for }{Q}'_2 \end{aligned}$$

(10b)

$$\begin{aligned} {{\varvec{X}}'}_3= & {} (L+2a+d){\varvec{i}}-0.5{\mathrm{g}} {\varvec{k}}\hbox { for }{Q}'_3 \end{aligned}$$

(10c)

$$\begin{aligned} {{\varvec{X}}'}_4= & {} (L+4a+d){\varvec{i}}-0.5{\mathrm{g}} {\varvec{k}}\hbox { for }{Q}'_4 \end{aligned}$$

(10d)

$$\begin{aligned} {\varvec{X}}_1= & {} L{\varvec{i}}+w(L,t){\varvec{k}}\hbox { for }Q_1 \end{aligned}$$

(10e)

$$\begin{aligned} {\varvec{X}}_2= & {} (L+2a){\varvec{i}}+[2a\theta +w(L,t)]{\varvec{k}}\hbox { for }Q_2 \end{aligned}$$

(10f)

where $\theta [\theta ={\partial w(L,t)}/{\partial x}]$ is the rotation angle of the tip magnet, and L is the length of the cantilever beam. Here, we assume that the rotation angle is much small with respect to the length of the cantilever beam.${\varvec{i}}$ and ${\varvec{k}}$ represent the unit vector in the x-direction and the z-direction, respectively. Then, the direction vector ${\varvec{r}}_{ij}$ can be obtained as follows:

$$\begin{aligned} {\varvec{r}}_{11}= & {} -(2a+d){\varvec{i}}+[w(L,t)-0.5d_\mathrm{g} ]{\varvec{k}}, \nonumber \\ {\varvec{r}}_{21}= & {} -(4a+d){\varvec{i}}+[w(L,t)-0.5d_\mathrm{g} ]{\varvec{k}}, \nonumber \\ {\varvec{r}}_{31}= & {} -(2a+d){\varvec{i}}+[w(L,t)+0.5d_\mathrm{g} ]{\varvec{k}}, \nonumber \\ {\varvec{r}}_{41}= & {} -(4a+d){\varvec{i}}+[w(L,t)+0.5d_\mathrm{g} ]{\varvec{k}}, \nonumber \\ {\varvec{r}}_{12}= & {} -d{\varvec{i}}+[w(L,t)+2a\theta -0.5d_\mathrm{g} ]{\varvec{k}}, \nonumber \\ {\varvec{r}}_{22}= & {} -(2a+d){\varvec{i}}+[w(L,t)+2a\theta -0.5d_\mathrm{g} ]{\varvec{k}}, \nonumber \\ {\varvec{r}}_{32}= & {} -d{\varvec{i}}+[w(L,t)+2a\theta +0.5d_\mathrm{g} ]{\varvec{k}}, \nonumber \\ {\varvec{r}}_{42}= & {} -(2a+d){\varvec{i}}+[w(L,t)+2a\theta +0.5d_\mathrm{g} ]{\varvec{k}}. \end{aligned}$$

(11)

Substituting Eq. (11) into Eq. (9), the total magnetic force can be rewritten as following expression.

$$\begin{aligned} F=F_x {\varvec{i}}+F_z {\varvec{k}} \end{aligned}$$

(12)

where $F_x$ and $F_z$ are force components exerted on the tip magnet in the x-direction and the z-direction, respectively. Details on the mathematical expressions for $F_x$ and $F_z$ are given in the following forms.

$$\begin{aligned}&F_x = \frac{\mu _0 }{4\pi }\left\{ {\begin{array}{l} \left[ {\frac{M_{\mathrm{A}} S_{\mathrm{A}} M_{\mathrm{B}} S_{\mathrm{B}} (2a+d)}{\left[ {(2a+d)^{2}+(w(L,t)-0.5d_\mathrm{g} )^{2}} \right] ^{3/2}}-\frac{M_{\mathrm{A}} S_{\mathrm{A}} M_{\mathrm{B}} S_{\mathrm{B}} (4a+d)}{\left[ {(4a_\mathrm{t} +d)^{2}+(w(L,t)-0.5d_\mathrm{g} )^{2}} \right] ^{3/2}}} \right] \\ +\left[ {\frac{M_{\mathrm{A}} S_{\mathrm{A}} M_{\mathrm{C}} S_{\mathrm{C}} (2a+d)}{\left[ {(2a+d)^{2}+(w(L,t)+0.5d_\mathrm{g} )^{2}} \right] ^{3/2}}-\frac{M_{\mathrm{A}} S_{\mathrm{A}} M_{\mathrm{C}} S_{\mathrm{C}} (4a+d)}{\left[ {(4a+d)^{2}+(w(L,t)+0.5d_\mathrm{g} )^{2}} \right] ^{3/2}}} \right] \\ -\left[ {\frac{M_{\mathrm{A}} S_{\mathrm{A}} M_{\mathrm{B}} S_{\mathrm{B}} d}{\left[ {d^{2}+(w(L,t)+2a\theta -0.5d_\mathrm{g} )^{2}} \right] ^{3/2}}-\frac{M_\mathrm{A} S_{\mathrm{A}} M_{\mathrm{B}} S_{\mathrm{B}} (2a+d)}{\left[ {(2a+d)^{2}+(w(L,t)+2a\theta -0.5d_\mathrm{g} )^{2}} \right] ^{3/2}}} \right] \\ -\left[ {-\frac{M_{\mathrm{A}} S_{\mathrm{A}} M_{\mathrm{C}} S_{\mathrm{C}} d}{\left[ {d^{2}+(w(L,t)+2a\theta +0.5d_\mathrm{g} )^{2}} \right] ^{3/2}}-\frac{M_\mathrm{A} S_{\mathrm{A}} M_{\mathrm{C}} S_{\mathrm{C}} (2a+d)}{\left[ {(2a+d)^{2}+(w(L,t)+2a\theta +0.5d_\mathrm{g} )^{2}} \right] ^{3/2}}} \right] \\ \end{array}} \right\} \end{aligned}$$

(13a)

$$\begin{aligned}&F_z = \frac{\mu _0 }{4\pi }\left\{ {\begin{array}{l} -\left[ {\frac{M_{\mathrm{A}} S_{\mathrm{A}} M_{\mathrm{B}} S_{\mathrm{B}} (w(L,t)-0.5d_\mathrm{g} )}{\left[ {(2a+d)^{2}+(w(L,t)-0.5d_\mathrm{g} )^{2}} \right] ^{3/2}}-\frac{M_{\mathrm{A}} S_{\mathrm{A}} M_{\mathrm{B}} S_{\mathrm{B}} (w(L,t)-0.5d_\mathrm{g} )}{\left[ {(4a+d)^{2}+(w(L,t)-0.5d_\mathrm{g} )^{2}} \right] ^{3/2}}} \right] \\ -\left[ {\frac{M_{\mathrm{A}} S_{\mathrm{A}} M_{\mathrm{C}} S_{\mathrm{C}} (w(L,t)+0.5d_\mathrm{g} )}{\left[ {(2a+d)^{2}+(w(L,t)+0.5d_\mathrm{g} )^{2}} \right] ^{3/2}}-\frac{M_{\mathrm{A}} S_{\mathrm{A}} M_{\mathrm{C}} S_{\mathrm{C}} (w(L,t)+0.5d_\mathrm{g} )}{\left[ {(4a+d)^{2}+(w(L,t)+0.5d_\mathrm{g} )^{2}} \right] ^{3/2}}} \right] \\ +\left[ {\frac{M_{\mathrm{A}} S_{\mathrm{A}} M_{\mathrm{B}} S_{\mathrm{B}} (w(L,t)+2a\theta -0.5d_\mathrm{g} )}{\left[ {d^{2}+(w(L,t)+2a\theta -0.5d_\mathrm{g} )^{2}} \right] ^{3/2}}-\frac{M_{\mathrm{A}} S_{\mathrm{A}} M_{\mathrm{B}} S_{\mathrm{B}} (w(L,t)+2a\theta -0.5d_\mathrm{g} )}{\left[ {(2a+d)^{2}+(w(L,t)+2a\theta -0.5d_\mathrm{g} )^{2}} \right] ^{3/2}}} \right] \\ +\left[ {\frac{M_{\mathrm{A}} S_{\mathrm{A}} M_{\mathrm{C}} S_{\mathrm{C}} (w(L,t)+2a\theta +0.5d_\mathrm{g} )}{\left[ {d^{2}+(w(L,t)+2a\theta +0.5d_\mathrm{g} )^{2}} \right] ^{3/2}}-\frac{M_{\mathrm{A}} S_{\mathrm{A}} M_{\mathrm{C}} S_{\mathrm{C}} (w(L,t)+2a\theta +0.5d_\mathrm{g} )}{\left[ {(2a+d)^{2}+(w(L,t)+2a\theta +0.5d_\mathrm{g} )^{2}} \right] ^{3/2}}} \right] \\ \end{array}} \right\} \end{aligned}$$

(13b)

Fig. 5

Comparison between experimental data and calculated magnetic force of improved magnetic dipoles method

Here, the force component of $F_z$ in the z direction is preferred to be considered in the following sections as it plays a major role in the dynamic characteristics of the TPEH.

Figure 5 shows the magnetic force comparison between experimental result and calculated result using Eq. (13b). It can be seen that the theoretical results obtained via the improved magnetic dipole method are acceptable in agreement with the experimental data for every separation distance d from 13 mm to 19 mm. Comparison with the results shown in Fig. 3, the improved magnetic dipole method has a significant improvement of the calculating precision for the magnetic force; therefore, it is more applicable to calculate the magnetic force for different magnetic separation distances. More experimental validations of this method are performed in the following sections.

2.3 Dynamic model of the TPEH considering the improved magnetic dipole result

For the TPEH shown in Fig. 1, the vibration displacement w(x, t) of the piezoelectric cantilever beam can be generally approximated by the linear combination of modes based on the Galerkin’s concept.

$$\begin{aligned} w(x,t)=\sum _{i=1}^n {\phi _i } (x)q_i (t) \end{aligned}$$

(14)

with

$$\begin{aligned} \phi _i (x)= & {} \left\{ {\begin{array}{l} \phi _{i1} (x){\begin{array}{ll} ,&{} {0\le x<L_\mathrm{p} } \\ \end{array} } \\ \phi _{i2} (x){\begin{array}{ll} ,&{} {L_\mathrm{p} \le x\le L} \\ \end{array} } \\ \end{array}} \right. \end{aligned}$$

(15)

$$\begin{aligned} \phi _{i1} (x)= & {} C_1 \cos (\beta _{i1} x)+C_2 \cosh (\beta _{i1} x)\nonumber \\&+\,C_3 \sin (\beta _{i1} x)+C_4 \sinh (\beta _{i1} x) \end{aligned}$$

(16)

$$\begin{aligned} \phi _{i2} (x)= & {} D_1 \cos (\beta _{i2} x)+D_2 \cosh (\beta _{i2} x)\nonumber \\&+\,D_3 \sin (\beta _{i2} x)+D_4 \sinh (\beta _{i2} x) \end{aligned}$$

(17)

where $\phi _{i1} (x)$ and $\phi _{i2} (x)$ represent the linear mode shapes of the beams with and without the piezoelectric layers, respectively. $C_k$ and $D_k (k=1,2,3,4)$ are the constant coefficients which can be determined from the boundary conditions, ${q_{i}}(t)$ are the modal coordinates, $\beta _{i1}$ and $\beta _{i2}$ are the eigenvalues of the characteristic equation, and L and $L_\mathrm{p}$ are the lengths of the substrate and the piezoelectric layers, respectively.

Because low-frequency excitations are used in this study, we consider only the first-order bending vibration mode of the cantilever beam based on the Galerkin approach. Thus, the vibration displacement of the cantilever beam of the TPEH can be rewritten as

$$\begin{aligned} w(x,t)=\phi _1 (x)q_1 (t) \end{aligned}$$

(18)

For this paper, we assume that the large-amplitude oscillations in the tri-stable or bi-stable potentials are small enough to maintain the validity of Euler–Bernoulli theory, and the geometric nonlinearity and the axial strain of the cantilever beam of the TPEH are ignored as they play a minor role in the dynamic characteristics of the TPEH. Based on these important assumptions, the dynamic equations of the TPEH can be derived by Euler–Bernoulli beam theory and Lagrange function. The general form of Lagrange function for this system can be given by

$$\begin{aligned} L_a (x,t)=T_\mathrm{s} +T_\mathrm{p} +T_\mathrm{M} +W_\mathrm{p} -U_\mathrm{s} -U_\mathrm{p} -U_\mathrm{m}\nonumber \\ \end{aligned}$$

(19)

where $T_\mathrm{s}$, $T_\mathrm{p}$, and $T_\mathrm{M}$ are the kinetic energy of the substrate, piezoelectric layers, and the tip magnet, respectively; $U_\mathrm{s}$ and $U_\mathrm{p}$ are the elastic potential energy of the substrate and the piezoelectric layers, respectively; $W_\mathrm{p}$ is the electric potential energy of the piezoelectric layers, and $U_\mathrm{m}$ is the nonlinear potential energy produced by the repulsive force between the external magnets and the tip magnet.

The kinetic energy of the substrate and the piezoelectric layers can be obtained by following expressions

$$\begin{aligned} T_\mathrm{s}= & {} \frac{1}{2}\rho _\mathrm{s} A_\mathrm{s} \int _0^{L_\mathrm{p} } {\left( {\phi _{11} (x){\dot{q}}_1 (t)+{\dot{z}}_0 (t)} \right) } ^{2}\hbox {d}x\nonumber \\&+\frac{1}{2}\rho _\mathrm{s} A_\mathrm{s} \int _{L_\mathrm{p} }^L \left( \phi _{12} (x){\dot{q}}_1 (t)\right. \nonumber \\&\left. +{\dot{z}}_0 (t) \right) ^{2}\hbox {d}x \end{aligned}$$

(20)

$$\begin{aligned} T_\mathrm{p}= & {} \rho _\mathrm{p} A_\mathrm{p} \int _0^{L_\mathrm{p} } {\left( {\phi _{11} (x){\dot{q}}_1 (t)+{\dot{z}}_0 (t)} \right) } ^{2}\hbox {d}x \end{aligned}$$

(21)

where $\rho _\mathrm{s}$ and $\rho _\mathrm{p}$ are the densities of the substrate material and piezoelectric layers, respectively; $A_\mathrm{s}$ and $A_\mathrm{p}$ are the section areas of the substrate and piezoelectric layers, respectively, and $z_0 (t)$ is the vibration displacement of the base.

The kinetic energy of the tip magnet is given by

$$\begin{aligned} T_\mathrm{M}= & {} \frac{1}{2}M_\mathrm{t} \left( {\phi _{12} (x)\left| {_{x=L} } \right. {\dot{q}}_1 (t)+{\dot{z}}_0 (t)} \right) ^{2}\nonumber \\&+\frac{1}{2}I_\mathrm{t} \left( {\frac{\partial \phi _{12} (x)}{\partial x}\left| {_{x=L} } \right. {\dot{q}}_1 (t)} \right) ^{2} \end{aligned}$$

(22)

where $M_\mathrm{t}$ is the mass of the tip magnet A; $I_\mathrm{t}$ is the rotational inertia of the tip magnet A.

The elastic potential energy of the substrate can be achieved by

$$\begin{aligned} U_\mathrm{s}= & {} \frac{1}{2}E_\mathrm{s} I_\mathrm{s} \int _0^{L_\mathrm{p} } {\left( {\frac{\partial ^{2}\phi _{11} (x)}{\partial ^{2}x}} \right) ^{2}q_1^2 (t)} \hbox {d}x\nonumber \\&+\frac{1}{2}E_\mathrm{s} I_\mathrm{s} \int _{L_\mathrm{p} }^L {\left( {\frac{\partial ^{2}\phi _{12} (x)}{\partial ^{2}x}} \right) ^{2}q_1^2 (t)} \hbox {d}x \end{aligned}$$

(23)

where $E_\mathrm{s} I_\mathrm{s}$ is the moment of the inertia of the substrate.

The elastic potential energy and the electric potential energy of the piezoelectric layers can be derived by the piezoelectric constitutive equation, respectively.

$$\begin{aligned} U_\mathrm{p}= & {} E_\mathrm{p} I_\mathrm{p} \int _0^{L_\mathrm{p} } {\left( {\frac{\partial ^{2}\phi _{11} (x)}{\partial ^{2}x}} \right) ^{2}q_1^2 (t)\hbox {d}x}\nonumber \\&-\frac{1}{4}e_{31} b_\mathrm{p} (h_\mathrm{s} +h_\mathrm{p} )\frac{\partial \phi _{11} (x)}{\partial x}\left| {_{x=L_\mathrm{p} } } \right. q_1 (t)V(t) \end{aligned}$$

(24)

$$\begin{aligned} W_\mathrm{p}= & {} \frac{1}{4}e_{31} (h_\mathrm{s} +h_\mathrm{p} )b_\mathrm{p} \frac{\partial \phi _{11} (x)}{\partial x}\left| {_{x=L_\mathrm{p} } } \right. q_1 (t)V(t)\nonumber \\&+\frac{1}{4}C_\mathrm{p} V^{2}(t) \end{aligned}$$

(25)

where $E_\mathrm{p} I_\mathrm{p}$ is the moment of the inertia of the substrate and the piezoelectric layers; V(t) is the voltage across the electrodes; $e_{31}$ is the piezoelectric constant, $b_\mathrm{s}$ and $h_\mathrm{s}$ are the width and height of the substrate, $b_\mathrm{p}$ and $h_\mathrm{p}$ are the width and the height of the piezoelectric layers; $C_\mathrm{p} ={\varepsilon _{33}^S b_\mathrm{p} L_\mathrm{p} }/{h_\mathrm{p} }$ is the capacitance through the piezoelectric layers.

Using Eq. (13b), the nonlinear potential energy $U_\mathrm{m}$ generated by the nonlinear magnetic force $F_z$ can be calculated as

$$\begin{aligned} U_\mathrm{m}= & {} \int {F_z } \hbox {d}w(L,t)\nonumber \\= & {} \int {F_z } \frac{\partial \phi _{12} (x)}{\partial x}\left| {_{x=L} } \right. q_1 (t)\hbox {d}x \end{aligned}$$

(26)

Substituting Eqs. (20–26) into Eq. (19) and applying the orthogonal conditions of the Eigen functions, the Lagrange function of the system can be obtained

$$\begin{aligned} L_a (x,t)= & {} \frac{1}{2}{\dot{q}}_1^2 (t)+\chi {\dot{q}}_1 (t){\dot{z}}_0 (t)-\frac{1}{2}\omega _1^2 q_1^2 (t)\nonumber \\&+\vartheta q_1 (t)V(t)\nonumber \\&+\frac{1}{2}M{\dot{z}}_0^2 (t)+\frac{1}{4}C_\mathrm{p} V^{2}(t)-U_\mathrm{m} \end{aligned}$$

(27)

where $\omega _1$ is the first-order bending modal frequency, and

$$\begin{aligned} \chi= & {} M_\mathrm{t} \phi _{12} (L)+(2\rho _\mathrm{p} A_\mathrm{p} +\rho _\mathrm{s} A_\mathrm{s} )\int _0^{L_\mathrm{p} } {\phi _{11} } (x)\hbox {d}x\nonumber \\&+\rho _\mathrm{s} A_\mathrm{s} \int _{L_\mathrm{p} }^L {\phi _{12} } (x)\hbox {d}x \end{aligned}$$

(28)

$$\begin{aligned} M= & {} \rho _\mathrm{s} A_\mathrm{s} L+2\rho _\mathrm{p} A_\mathrm{p} L_\mathrm{p} +M_\mathrm{t} \end{aligned}$$

(29)

$$\begin{aligned} \vartheta= & {} \frac{1}{2}e_{31} b_\mathrm{p} (h_\mathrm{s} +h_\mathrm{p} )\frac{\partial \phi _{11} (x)}{\partial x}\left| {_{x=L_\mathrm{p} } } \right. \end{aligned}$$

(30)

The generalized dissipative force and the generalized current of the system can be expressed as

$$\begin{aligned} F(t)= & {} -2\xi \omega _1 {\dot{q}}_1 (t) \end{aligned}$$

(31)

$$\begin{aligned} {\dot{Q}}(t)= & {} -{V(t)}/R \end{aligned}$$

(32)

where $\xi$ is the corresponding modal damping ratio.

The dynamic equations of the TPEH system then can be derived by

$$\begin{aligned}&\frac{\hbox {d}}{\hbox {d}t}\left( \frac{\partial L_a }{\partial {\dot{q}}_1 (t)}\right) -\left( \frac{\partial L_a }{\partial q_1 (t)}\right) =F(t) \end{aligned}$$

(33)

$$\begin{aligned}&\frac{\hbox {d}}{\hbox {d}t}\left( \frac{\partial L_a }{\partial {\dot{V}}(t)}\right) -\left( \frac{\partial L_a }{\partial V(t)}\right) =Q(t) \end{aligned}$$

(34)

As a consequence, we have

$$\begin{aligned}&\ddot{q}_1 (t)+2\xi \omega _1 {\dot{q}}_1 (t)+\omega _1^2 q_1 (t)-\vartheta V(t)+F_z \nonumber \\&\quad =-\chi \ddot{z}_0 (t) \end{aligned}$$

(35)

$$\begin{aligned}&\vartheta {\dot{q}}_1 (t)+\frac{1}{2}C_\mathrm{p} \dot{V}(t)+{V(t)}/R=0 \end{aligned}$$

(36)

where

$$\begin{aligned}&\alpha _1 =\phi _{12} (L)q_1 (t)-0.5d_\mathrm{g}, \alpha _2 =\phi _{12} (L)q_1 (t)+0.5d_\mathrm{g} \\&\alpha _3 =\phi _{12} (L)q_1 (t)+2a{\phi }'_{12} (L)q_1 (t)-0.5d_\mathrm{g}, \alpha _4 \\&~\quad =\phi _{12} (L)q_1 (t)+2a{\phi }'_{12} (L)q_1 (t)+0.5d_\mathrm{g} \\&K_{BA} =\frac{\mu _0 M_A S_A M_B S_B }{4\pi }, \quad K_{CA} =\frac{\mu _0 M_A S_A M_C S_C }{4\pi } \\&\begin{array}{l} F_z =-\left( {\frac{K_{BA} \alpha _1 }{\left( {(2a+d)^{2}+\alpha _1^2 } \right) ^{3/2}}-\frac{K_{BA} \alpha _1 }{\left( {(4a+d)^{2}+\alpha _1^2 } \right) ^{3/2}}} \right) \\ ~~~~~~~~~-\left( {\frac{K_{CA} \alpha _2 }{\left( {(2a+d)^{2}+\alpha _1^2 } \right) ^{3/2}}-\frac{K_{CA} \alpha _2 }{\left( {(4a+d)^{2}+\alpha _1^2 } \right) ^{3/2}}} \right) \\ ~~~~~~~~~+\left( {\frac{K_{BA} \alpha _3 }{\left( {d^{2}+\alpha _3^2 } \right) ^{3/2}}-\frac{K_{BA} \alpha _3 }{\left( {(2a+d)^{2}+\alpha _3^2 } \right) ^{3/2}}} \right) \\ ~~~~~~~~~+\left( {\frac{K_{CA} \alpha _4 }{\left( {d^{2}+\alpha _3^2 } \right) ^{3/2}}-\frac{K_{CA} \alpha _4 }{\left( {(2a+d)^{2}+\alpha _3^2 } \right) ^{3/2}}} \right) \\ \end{array} \end{aligned}$$

By introducing the state variables $x_1 =q_1 (t)$,$x_2 ={\dot{q}}_1 (t)$, and $x_3 =V(t)$, the dynamic equations given in Eq. (35) and Eq. (36) can be rewritten as the state-space form.

$$\begin{aligned}&\left[ {{\begin{array}{l} {{\dot{x}}_1 } \\ {{\dot{x}}_2 } \\ {{\dot{x}}_3 } \\ \end{array} }} \right] =\left[ {{\begin{array}{c} {x_2 } \\ {-\omega _1^2 x_1 -2\xi \omega _1 x_2 +\vartheta x_3 -F_z -\chi \ddot{z}_0 } \\ {-\frac{2\vartheta }{C_\mathrm{p} }x_2 -\frac{2}{RC_\mathrm{p} }x_3 } \\ \end{array} }} \right] \nonumber \\ \end{aligned}$$

(37)

3 Simulation and analysis

In this section, numerical methods are employed to solve the dynamical equations and simulation is performed to reveal the characteristics of the TPEH under harmonic base excitation. The system’s geometric, material, electromechanical, and magnetic parameters used in simulations are listed in Table 1.

Table 1 Model parameters used for simulation

3.1 Bifurcation analysis for the system’s equilibrium state

Nowadays, many studies have discussed the bifurcation phenomena of the system’s equilibrium solutions of the BPEH [17,18,19,20,21,22,23,24,25], but few have concerned that of the TPEH [17]. Since the equilibrium bifurcation behaviors of the TPEH are more complicated than those of the BPEH, and they are helpful to deeply understand the transition mechanism from the mono-stable state to tri-stable state. Therefore, further investigation of the equilibrium bifurcation behavior of the TPEH is warranted and presented here.

The equilibrium solutions can be achieved from the homogeneous version of Eq. (35) incorporated with steady-state conditions.

$$\begin{aligned} \omega _1^2 q_1 +F_z =0 \end{aligned}$$

(38)

Fig. 6

Bifurcation of the TPEH system

From Eq. (38), we can calculate the bifurcation behaviors of the equilibrium solutions of the TPEH in (d, $d_{\mathrm{g}}$, w) space, as shown in Fig. 6. It can be seen that the bifurcation behaviors of the equilibrium solutions of the TPEH are very complex and closely depend on the geometric parameters (e.g., d and $d_{\mathrm{g}})$ associated with the three magnets. To reveal the transition from mono-stable state to bi-stable or tri-stable state, the bifurcation diagrams, depicted in (d, w) space, for the equilibrium solution of the TPEH with a series of gap distance $d_{\mathrm{g}} (d_{\mathrm{g}}= 0\hbox { mm}$, 5 mm, 5.5 mm, 5.8 mm, 5.97 mm, and 10 mm) are shown in Fig. 7. When the gap distance $d_{\mathrm{g}}=0\hbox { mm}$, the TPEH degenerates into a BPEH. Only one pitchfork bifurcation of the equilibrium solution at point $\hbox {BP}_{1}$ was observed, as shown in Fig. 7a. Such a bifurcation behavior is very similar to that of the BPEH with one external magnet [17,18,19,20,21,22,23,24,25]. However, there are obvious differences between the two PEHs as the gap distance $d_{\mathrm{g}}$ increases. When the gap distance $d_{\mathrm{g}}$ increases to 5 mm, another pitchfork bifurcation is appeared at the point $\hbox {BP}_{2}$ as shown in Fig. 7b. From the point $\hbox {BP}_{1}$, the stable trivial solution starts to bifurcate into one unstable trivial solution and two stable non-trivial braches. In contrast, From the point $\hbox {BP}_{2}$, the unstable trivial solution starts to bifurcate into one stable trivial solution and two unstable non-trivial braches. Due to the two bifurcation points $\hbox {BP}_{1}$ and $\hbox {BP}_{2}$, the given parameter domain of the separation distance d was divided into three regions. In the region of $d <d_{\mathrm{BP2}}$, there are one stable trivial solution, two unstable non-trivial solutions and two stable non-trivial solutions, which makes the TPEH become a tri-stable system due to the magnetic repulsion effect generated by the external magnets B and C. In the region of $d_{\mathrm{BP2}}<d <d_{\mathrm{BP1}}$, the TPEH becomes a bi-stable system with one unstable solution and two stable non-trivial solutions. While in the region of $d >d_{\mathrm{BP1}}$, the TPEH becomes a mono-stable system with one trivial solution. Further increasing the gap distance $d_{\mathrm{g}}$ to 5.5 mm, the pitchfork bifurcation at point $\hbox {BP}_{1}$ degenerates to a codimension-two bifurcation (as shown Fig. 7c) at the point BD, from which a two saddle-node bifurcation is appeared at the points SN in Fig. 7d with the gap distance $d_{\mathrm{g}}$ increases to 5.8 mm. As shown in Fig. 7d, the TPEH gradually exhibits a mono-stable system in the region of $d_{\mathrm{SN}}<d$, bi-stable system in the region of $d_{\mathrm{BP2}}< d < d_{\mathrm{BP1}}$, and tri-stable system in the regions of $d_{\mathrm{BP1}}< d < d_{\mathrm{SN}}$ and $d < d_{\mathrm{BP2}}$ with the decreases of the separation distance d. Additionally, As the gap distance $d_{\mathrm{g}}$ increases, point $\hbox {BP}_{1 }$ moves left and point $\hbox {BP}_{2}$ moves right, leading to the decrease of the region of $d_{\mathrm{BP2}}< d < d_{\mathrm{BP1}}$. When the gap distance $d_{\mathrm{g}}$ increases to 5.97 mm, the two points $\hbox {BP}_{1 }$ and $\hbox {BP}_{2 }$ coincide with each other at the cusp point $\hbox {BP}_{D}$, and the region of $d_{\mathrm{BP2}}< d <d_{\mathrm{BP1}}$ decreases to zero, leading to the bi-stable region completely disappear, as shown in Fig. 7e. Therefore, the TPEH becomes a tri-stable system in the region of $d < d_{\mathrm{SN}}$ and a mono-stable system in the region of $d < d_{\mathrm{SN}}$, respectively. When the gap distance $d_{\mathrm{g}} =10\hbox { mm}$, as shown in Fig. 7f. The two unstable non-trivial solution branches start to separate from the cusp point $\hbox {BP}_{\mathrm{D}}$ and then gradually moves away. Consequently, the TPEH becomes a tri-stable system in the region of $d < d_{\mathrm{SN}}$ and a mono-stable system in the region of $d > d_{\mathrm{SN}}$, respectively.

Fig. 7

Bifurcation diagrams of the equilibrium solutions when $d_{\mathrm{g}}=$a 0, b 5, c 5.5, d 5.8, e 5.97, and f 10 mm; thin solid lines and the dashed lines denote the stable and unstable equilibria, respectively

From above bifurcation analysis, we can find that there are four transitions of the TPEH from the mono-stable state to bi- or tri-stable state in the given parameter domain. The first transition starts directly from the mono-stable state to the bi-stable state, as shown in Fig. 7a, the second transition starts from the mono-stable state, passing through the bi-stable state, then to the tri-stable state, as shown in Fig. 7b and Fig. 7c. The third transition starts from the mono-stable state, successively passing through the tri- and bi-stable states, and finally to the tri-stable state, as shown in Fig. 7d. The fourth transition starts directly from the mono-stable state to the tri-stable state, as shown in Fig. 7e, f.

Fig. 8

Bifurcation diagrams of the equilibrium solutions when $d =$a 6, b 8, and c 10 mm; thin solid lines and the dashed lines denote the stable and unstable equilibria, respectively

Fig. 9

Nonlinear magnetic force and potential wells for $d_{\mathrm{g}}=$a 10 mm, b 17.22 mm, and c 25mm

The bifurcation diagrams, depicted in ($d_{\mathrm{g}}$, w) space, for the equilibrium solution of the TPEH with a series of separation distance $d (d = 6\hbox { mm}$, 8 mm, and 10 mm) are also investigated, as shown in Fig. 8. When the separation distance d is relative small ($d = 6\hbox { mm}$; Fig. 8a), there are one pitchfork bifurcation at the point $\hbox {BP}_{1}$ and two saddle-node bifurcation at the point SN. In the region of $d_{\mathrm{gBP1}}< d_{\mathrm{g}}<d_{\mathrm{gSN}}$, the TPEH exhibits a tri-stable state with one stable trivial solution, two unstable non-trivial and two stable non-trivial solutions. In the region of $d_{\mathrm{g}}<d_{\mathrm{gBP1}}$ and $d_{\mathrm{g}}>d_{\mathrm{gSN}}$, the TPEH exhibits a bi-stable state and a mono-stable state, respectively. As the separation distance d increases, the saddle-node bifurcation point SN moves left and toward to the stable trivial solution, leading to the distance between the point $\hbox {BP}_{1}$ and SN gradually decreases, the region of the TPEH exhibiting a tri-stable state decreases, as shown in Fig. 8b. Further increasing the separation distance $d (d =10\hbox { mm}$; Fig. 8c), the saddle-node bifurcation point SN disappeared; the TPEH only has a pitchfork bifurcation at point $\hbox {BP}_{1}$, which exhibits a bi-stable state in the region of $d_{\mathrm{g}}<d_{\mathrm{gBP1}}$ and a mono-stable state in the region of $d_{\mathrm{g}}> d_{\mathrm{gBP1}}$.

3.2 Nonlinear magnetic force and potential energy wells analysis for the TPEH

We have studied the formation of bi- or tri-stability characteristics of the TPEH in the above subsection via the bifurcation analysis with respect to the equilibrium solutions. In this subsection, the nonlinear magnetic force and the potential well of the TPEH are further investigated to reveal the transition from the mono-stable state to the bi- or tri-stable state. Figure 9 shows the nonlinear magnetic forces (left column) and the potential wells (right column) for three different gap distances, i.e., $d_{\mathrm{g}}=10\hbox { mm}$ (Fig. 9a), 17.2 mm (Fig. 9b), and 25 mm (Fig. 9c). In each of these sub-figures, the nonlinear magnetic force and the potential well for the mono-stable state at the separation distance $d = 60\hbox { mm}$ (plotted by the black and diamond solid line) are presented for the purpose of comparison.

It can be seen from Fig. 9 that the nonlinear magnetic force and the depth of the potential well increase with the decrease of the separation distance d. For the case of $d_{\mathrm{g}}=10\hbox { mm}$ (Fig. 9a), it is easy to find that each nonlinear magnetic force curve has three zero points, i.e., $\hbox {P}_{0}$, $\hbox {P}_{1}$, and $\hbox {P}_{2}$, and $\hbox {P}_{0}$ (0, 0) is the unstable trivial equilibrium solution and the other two are the stable non-trivial equilibrium solutions. In the potential energy diagrams, we can find that each potential energy curve has two symmetric potential wells excepting for the case of $d=60\hbox { mm}$, which is caused by the trivial center bifurcating into one hilltop saddle ($\hbox {P}_{0})$ and two symmetric centers ($\hbox {P}_{1}$, and $\hbox {P}_{2})$ through the pitchfork bifurcation (corresponding to the point $\hbox {BP}_{1}$ shown in Fig. 7a). With the separation distance d decreases, the transition of the TPEH starts from a mono-stable state to a bi-stable state, the corresponding bifurcation characteristic is shown in Fig. 7a.

Fig. 10

Phase portraits (left column) and harvested voltage (right column) for three different systems when the exciting amplitude is $10\,\hbox {m/s}^{2}$ and frequency 5 Hz

Fig. 11

Phase portraits for another three cases when exciting amplitude is $10\hbox { m/s}^{2}$ and frequency 10 Hz. a tri-stable system when $d =12\hbox { mm}$, $d_{\mathrm{g}}=17\hbox { mm}$; b bi-stable system when $d =13\hbox { mm}$, $d_{\mathrm{g}}=10\hbox { mm}$; c mono-stable system when $d =15\hbox { mm}$, $d_{\mathrm{g}}=17\hbox { mm}$

When the gap distance $d_{\mathrm{g}}$ increases to 17.2 mm, as shown in Fig. 9b. The TPEH transits from the mono-stable state, passing through the bi-stable state and then to the tri-stable state with the separation distance d decreasing from 60 mm to 15 mm (the corresponding bifurcation characteristics are shown in Fig. 7b, c). For the tri-stable state, each of the nonlinear magnetic force curves has five zero points, i.e., $\hbox {P}_{0}$, $\hbox {P}_{1}$, $\hbox {P}_{2}$, $\hbox {P}_{3}$, and $\hbox {P}_{4}$, corresponding to the five equilibrium solutions. Among these five equilibrium solutions, $\hbox {P}_{0}$ (0, 0) is the stable trivial equilibrium, $\hbox {P}_{1}$ and $\hbox {P}_{3}$ are the unstable equilibrium solutions, and $\hbox {P}_{2}$ and $\hbox {P}_{4}$ are the stable non-trivial equilibrium solutions. Each of the potential energy curves has three wells, among which the outer two wells are deeper, while the inner one is shallower. The inner potential well is generated by the bifurcation of the hilltop saddle point in the bi-stable state; the hilltop saddle point starts to bifurcate into a trivial center (i.e., $\hbox {P}_{0})$ and two non-trivial saddle points (i.e., $\hbox {P}_{1}$ and $\hbox {P}_{3})$ through the subcritical pitchfork bifurcation (corresponding to the point $\hbox {BP}_{2}$ shown in Fig. 7b, c), leading to the formation of an additional potential energy well at the center of the diagrams.

When the gap distance $d_{\mathrm{g}}$ still increases to 25 mm, the TPEH directly transits from the mono-stable state to the tri-stable state with the separation distance d decreases from 60 mm to 20 mm, as shown in Fig. 9c. For the tri-stable state of this case, there also have five zero points (i.e., $\hbox {P}_{0}$, $\hbox {P}_{1}$, $\hbox {P}_{2}$, $\hbox {P}_{3}$, and $\hbox {P}_{4}$,) in each magnetic force curve and three wells in each potential energy curve. Unlike in Fig. 9b, two non-trivial saddle points (i.e., $\hbox {P}_{1}$, and $\hbox {P}_{3})$ and two non-trivial center points (i.e., $\hbox {P}_{2}$, and $\hbox {P}_{4})$ are newly generated through the saddle-node bifurcations (corresponding to the point SN shown in Fig. 7e, f), leading to the formation of two symmetric outer wells.

From the analysis results of Fig. 9, we can also find that the potential energy functions of the TPEH have different shapes with different d and $d_{\mathrm{g}}$. When $d = 20\hbox { mm}$ and $d_{\mathrm{g}}=25\hbox { mm}$, the inner well depth is larger than that of the two outer wells. In this case, the TPEH can easily pass through the two outer wells, but cannot easily go over the inner well and move to the outer wells. When $d = 22\hbox { mm}$ and $d_{\mathrm{g}}=25\hbox { mm}$, the three wells have a similar depth. The TPEH can easily oscillate in the three wells and generate high energy harvesting output. However, when $d = 25\hbox { mm}$ and $d_{\mathrm{g}}=25\hbox { mm}$, the inner well depth is lower than that of the two outer wells. In this case, the potential energy barrier is large between the inner well and the two outer wells, which requires a relatively large excitation force to overcome the barrier to oscillate between the two outer wells. As mentioned in the previous study [17], the remarkable advantage of the TPEH is that the wider and shallower potential energy wells than those of the BPEH, which can significantly improve the output performance of the TPEH. Therefore, it is important to optimizing design the TPEH structure to obtain wider and shallower potential energy wells, which can be achieved by adjusting the two key parameters of the gap distance $d_{\mathrm{g}}$ and the separation distance d.

3.3 Dynamic characteristics analysis for the TPEH

The dynamic responses of the TPEH are performed with a series of simulations using Eq. (37) in this subsection. Figure 10 shows the phase portraits depicted in (w, $\hbox {d}w/\hbox {d}t$) space (left column) and the harvested output voltage (right column) for three different cases, i.e., tri-stable case with $d =13\hbox { mm}$ and $d_{\mathrm{g}}=17\hbox { mm}$, bi-stable case with $d =13\hbox { mm}$ and $d_{\mathrm{g}}=12\hbox { mm}$, and mono-stable case with $d =13\hbox { mm}$ and $d_{\mathrm{g}}=25\hbox { mm}$. A harmonic excitation force with amplitude $10\hbox { m/s}^{2}$ and frequency 5 Hz is exerted on the base of the TPEH; the load resistance R is $\hbox {1 M}\Omega$. It can be seen that the tri- and bi-stable cases exhibit interwell motion with large output amplitude, while the mono-stable case exhibits one-period intrawell motion with small output amplitude. Compared to the bi- and mono-stable cases, the tri-stable case possesses relatively larger vibration amplitude and output voltage.

Fig. 12

Output performance when $F_{0} = 8\hbox { m/s}^{2}$ and frequency $f = 9\hbox { Hz}$ for both tri-stable system (with $d =13\hbox { mm}$ and $d_{\mathrm{g}}=17\hbox { mm}$) and bi-stable system (with $d=13\hbox { mm}$ and $d_{\mathrm{g}}= 0\hbox { mm}$). a Phase portraits, b output voltage, c output displacement, and d output velocity

Figure 11 shows the phase portraits depicted in (w, $\hbox {d}w/\hbox {d}t$) space for another three cases by adjusting the parameters of d and $d_{\mathrm{g}}$, e.g., (i) $d=12\hbox { mm}$ and $d_{\mathrm{g}}=17\hbox { mm}$ for tri-stable case, (ii) $d=13\hbox { mm}$ and $d_{\mathrm{g}}=10\hbox { mm}$ for bi-stable case, and (iii) $d=15\hbox { mm}$ and $d_{\mathrm{g}}=17\hbox { mm}$ for mono-stable case. A harmonic excitation force with amplitude $10\hbox { m/s}^{2}$ and frequency 10 Hz is applied to excite the base of the TPEH; the load resistance R is $\hbox {1 M}\Omega$. Unlike the one-period interwell motions shown in Fig. 10, the tri- and bi-stable cases exhibit very complicated responses with a chaotic superposition of the intrawell and interwell motions. The mono-stable system still oscillates in a one-period intrawell motion; however, its displacement and velocity amplitudes are greatly improved compared to the mono-stable case of $d =13\hbox { mm}$ and $d_{\mathrm{g}}=25\hbox { mm}$ as shown in Fig. 10. It also can be seen from Fig. 11 that the distance of the potential wells in tri-stable case is the largest among these three cases; this also proves that the tri-stable case has an advantage in dynamic responses and energy harvesting ability.

Fig. 13

Output performance when $F_{0} =10\hbox { m/s}^{2}$ and frequency $f=9\hbox { Hz}$ for both tri-stable system (with $d=13\hbox { mm}$ and $d_{\mathrm{g}}=17\hbox {mm}$) and bi-stable system (with $d=13\hbox { mm}$ and $d_{\mathrm{g}}=\hbox {0mm}$). a Phase portraits, b output voltage, c output displacement, and d output velocity

Fig. 14

Output performance when $F_{0} =10\hbox { m/s}^{2}$ and frequency $f=5\hbox { Hz}$ for both tri-stable system (with $d=13\hbox { mm}$ and $d_{\mathrm{g}}=17\hbox { mm}$) and bi-stable system (with $d=13\hbox { mm}$ and $d_{\mathrm{g}}=0\hbox { mm}$). a Phase portraits, b output voltage, c output displacement, and d output velocity

Fig. 15

(First row) Tip displacement responses, (second row) output voltage and (third row) the associated electric power obtained for TPEH (left column) and BPEH (right column) under swept sine excitation. a$F_{0} = 5\hbox { m/s}^{2}$, b$F_{0} = 10\hbox { m/s}^{2}$, and c$F_{0} = 15\hbox { m/s}^{2}$

Fig. 16

View of the experimental setup. a Prototype of TPEH, b overall view of the experimental devices

As mentioned before, the disadvantage of the conventional BPEH is that it is difficult to achieve the interwell motion when the excitation intensity is not large enough to overcome the potential barrier. This leads to a low output power as is shown in Fig. 12. When the exciting intensity $F_{0}$ is relatively low, for example, $F_{0} =8\hbox { m/s}^{2}$, it is difficult to obtain the interwell motion for the BPEH. In contrast, the TPEH can easily oscillate in interwell motions, leading to a large output performance under the given excitation level. When the excitation intensity $F_{0}$ increases to $10\hbox { m/s}^{2}$, the output performance of the two PEHs is shown in Fig. 13. Although these two PEHs both have enough energy to generate interwell motions, the TPEH has a larger output displacement and output voltage when the load resistance R is $\hbox {1 M}\Omega$. The similar phenomena can also be observed for both the TPEH and the BPEH when the exciting frequency is 5 Hz and the exciting intensity $F_{0}=10\hbox { m/s}^{2}$ as shown in Fig. 14. Figures 13 and 14 indicate that for the same base excitation intensity, the TPEH has a wider frequency band than the BPEH to exhibit larger output displacement and output voltage.

From the above analysis results of the time domain responses (TMR), we can find that the TPEH has better performance at lower excitation intensity, and the TPEH is superior to the BPEH in enhancing output voltage and broadening the bandwidth. This can be further investigated from the frequency domain responses (FDR) of the BPEH and the TPEH. Linearly increasing frequency (forward-sweep) excitation simulations are performed slowly over the frequency range of 0–15 Hz when the load resistance R is $\hbox {1 M}\Omega$. The displacement responses, voltage responses, and the generated powers of the TPEH (left column) and the BPEH (right column) are calculated under three different levels of base acceleration, namely $5\hbox { m/s}^{2}$, $10\hbox { m/s}^{2}$, and $15\hbox { m/s}^{2}$, for each of the sub-figures on the first to the third row of Fig. 15. When the excitation strength is relatively small, e.g., $F_{0} =5\hbox { m/s}^{2}$ (Fig. 15a), the tip magnet oscillates within one of the three potential wells for the TPEH and one of the two potential wells for the BPEH, within most of the interest frequency domain. Only within a very narrow frequency band, both the TPEH and the BPEH oscillate in interwell motions. When the excitation strength increases to $F_{0} =10\hbox { m/s}^{2 }$ (Fig. 15b), a one-period interwell motion generates for the TPEH that is accompanied by a much larger amplitude over a broad frequency band, leading to a much larger voltage and associated electric power. For example, the interwell motion occurs for the TPEH within the range of 3.2–4.8 Hz. On the other hand, the BPEH exhibits a chaotic interwell motion with a smaller voltage and electric power in a narrower frequency range 4.83–6.15 Hz. When the excitation intensity further increases to $15\hbox { m/s}^{2}$ (Fig. 15c), it is observed that the TPEH oscillates in an interwell motion with much larger amplitude within a broader frequency range than that of the BPEH. For example, the TPEH oscillates in an interwell state within the range of 0.3–5.5 Hz; the generated electric power reaches 5 mW. While for the BPEH, such an interwell motion occurs within the range of 4.3–6.6 Hz, the generated electric power is 0.25 mW. The results shown in Fig. 15 obviously indicate that the TPEH is superior to enhance energy harvesting performance in lower excitation levels and broader frequency band than the BPEH.

4 Experimental verification

4.1 TPEH device and the experimental setup

In order to validate the presented magnetic force model and the simulated results, a TPEH device using parameters in Table 1 is manufactured. As shown in Fig. 16a, the cantilever beam is a stainless steel plate; two identical PZT layers (PZT-5A) are bonded on its top and bottom surfaces root, respectively. At the tip of the cantilever beam, a permanent magnet (N35) is attached. Two external magnets with identical size and type are fixed on the right wall of the base, and their polarization directions are opposite to that of the tip magnet. Corresponding experimental setup for the TPEH is shown in Fig. 16b. The TPEH is mounted on a vibrator (JZK-5). A harmonic signal used to simulate the ambient vibration is generated by a signal generator (AFG3102C, Tektronix) and amplified by a power amplifier (YE5871A). The amplified signal is then inputted into the vibrator to excite the TPEH. An accelerometer is attached on the top of the vibrator to measure the acceleration. The tip displacement of the TPEH is measured by a displacement sensor (LK-G3000, KEYENCE), and the tip velocity is acquired by a laser vibrometer (PolyTec OFV303 sensor head with OFV3001 controller). Also, the output voltage is collected with an oscilloscope. All the signals, including the base acceleration, the tip displacement, tip velocity, and harvested output voltage of the TPEH, are collected in acquisition equipment (DH5922) and then recorded in a computer for analysis.

Fig. 17

Experimental setup for magnetic force measuring

Fig. 18

Comparison between experimental data and calculated magnetic force of improved magnetic dipoles method when $d_{\mathrm{g}}=25\hbox { mm}$

4.2 Validation of the magnetic force model

To verify the magnetic force model presented above, an experimental system for measuring the magnetic force is set up as shown in Fig. 17. It is mainly composed of a TPEH, a dynamometer (HF-10), a laser displacement sensor (LK-G3000, KEYENCE), and other auxiliary equipment. The TPEH with magnet A is fixed at the base. Magnet B and C are attached to the micro-dynamometer which can measure the magnetic force acting on the magnet A. The laser displacement sensor is used to measure the tip displacement of the TPEH. The experimental magnetic force and the calculated results are shown in Fig. 5 for the gap distance $d_{\mathrm{g}}$ equaling 17 mm, which demonstrates that the presented magnetic force model has a significant improvement precision for calculating the magnetic force compared to the point dipole model used before. Here, the experiment at the gap distance $d_{\mathrm{g}}$ of 25 mm is also performed, as shown in Fig. 18. It can be seen that the calculated results are reasonable in agreement with the experimental data for every separation distances; both the amplitude and the position of the force peaks for theoretical and experimental curves are almost identical. The experimental and calculated potential energy function with $d=17\hbox { mm}$ and $d_{\mathrm{g}} =25\hbox { mm}$ are also presented as shown in Fig. 19a. We can find that the experimental potential energy function is acceptable in agreement with the calculated results. The potential energy function has three potential wells with three stable equilibrium positions (e.g., stable 1, stable 2, and stable 3), as illustrated in Fig. 19b–d, respectively.

Fig. 19

a Experimental and calculating potential energy when $d =17\hbox { mm}$ and $d_{g }=25\hbox { mm}$, and three stable equilibrium positions, b stable 1, c stable 2, and d stable 3

4.3 Experiments for the dynamic characteristics of the TPEH

In order to validate the numerical analysis, the theoretical and experimental displacement responses of the TPEH without the external magnets are firstly conducted, as shown in Fig. 20. The values of the vertical axis are the output displacements under unit acceleration amplitude with respect to the exciting frequency. It demonstrates the theoretical displacement response is in good agreement with the experimental result. The resonant frequency of the TPEH obtained by experiment is 6.93 Hz, while the theoretical result is 7 Hz. This verifies the presented dynamic model is correct.

Fig. 20

Displacement response of the TPEH without external magnets

When the separation distance d is 12 mm and the gap distance $d_{\mathrm{g}}$ is 13 mm, and the TPEH is excited at 5 Hz with an acceleration of $10\hbox { m/s}^{2}$. The experimental and numerical phase portraits and harvested voltage of the TPEH are shown in Fig. 21. It can be seen that the experimental results are in agreeable with the numerical results both in the phase portrait and the harvested voltage. With the given parameters, the TPEH exhibits a bi-stable behavior and oscillates across the potential well with a large-amplitude output. The displacement and velocity of the tip magnet achieve the maximum values of 20 mm and 600 mm/s, respectively, and the harvested voltage reaches the maximum value of 4.9 V.

When the separation distance d and the gap distance $d_{\mathrm{g}}$ are, respectively, adjusted to 12 mm and 17 mm, the excitation amplitude and frequency are set to be $10\hbox { m/s}^{2}$ and 9 Hz. The experimental and numerical phase portraits and harvested voltage of the TPEH are shown in Fig. 22. It shows that the calculated phase portrait and the harvested voltage are in agreement with that obtained from experiments, which further verifies that the presented dynamic model of the TPEH is correct. With the given parameters and excitation, the TPEH exhibits a tri-stable behavior and experiences a very complicated response with a chaotic superposition of the intrawell and interwell motions. From the obtained results shown in Fig. 22, the maximum values of the tip displacement and velocity of the TPEH achieve 24 mm and 800 mm/s, respectively, and the harvested voltage reaches the maximum value of 8 V. Compared to the results shown in Figs. 21 and 22, we can find that the output performances of the TPEH oscillating in a tri-stable state has obvious enhancement when compared with the condition that TPEH oscillates in a bi-stable motion.

Fig. 21

Dynamic characteristics of the experimental and calculating results for the TPEH when $d =13\hbox { mm}$ and $d_{g }=12\hbox { mm}$. a Phase portrait, b harvested voltage

Fig. 22

Dynamic characteristics of the experimental and calculating results for the TPEH when $d =12\hbox { mm}$ and $d_{g }=17\hbox { mm}$. a phase portrait, b calculating result of harvested voltage, c experimental result of harvested voltage

Fig. 23

Experimental swept voltages (first row) and powers (second row) of the TPEH and BPEH under constant frequency. a Swept forward, b swept backward

As there are not abundant swept-frequency harmonic excitations in real environments. Most of the vibration sources operate at the vicinity of a constant frequency. Therefore, investigating the response of the TPEH under fixed frequency excitation is necessary. Fig. 23 shows the root-mean-square (RMS) value of the experimental output voltage and output power under different excitation frequency for the TPEH and the conventional BPEH with two different separation distances of 23 and 25 mm for both forward (Fig. 23a) and backward sweep (Fig. 23b) at a base acceleration of $20\hbox { m/s}^{2}$ and a load resistance of $7\hbox { M}\Omega$ (which is the optimum resistance). The experimental results indicate that the TPEH has larger voltage and power, as well as wider frequency bandwidth than the conventional BPEH both in forward and backward sweeps. This implies that the TPEH has promise for application in the real environment energy harvesting due to the lower energy required to drive the TPEH response to a high output performance.

At last, we experimentally investigated the influence of load resistance on the output voltage and power for the TPEH and the conventional BPEH under different separation distances, i.e., $d =$ 21, 23, 25, 33 mm, respectively. In this experiment, the excitation amplitude is $15\hbox { m/s}^{2}$ and the frequency is 5 Hz. The load resistance R is increasing by $0.1\hbox { M}\Omega$ every circulation for zero initial conditions. As shown in Fig. 24, both the harvested voltage and power increase with the decrease of the separation distance d; this may be the contribution of the increase of the magnetic force exerted on the tip beam when the separation distance d decreases, leading to a large strain in the cantilever beam. In addition, the harvested voltage also increases with the increase of the load resistance. However, power outputs indicate an optimum value within a certain range of load resistance. For example, both the TPEH and BPEH have an optimum value of $7\hbox { M}\Omega$ at the case of $d=21\hbox { mm}$. The power of the TPEH and BPEH sharply increases before the load resistance reaches the optimum value and then gradually decreases. As to the optimum value, the power of the TPEH and BPEH reach a peaks of $0.62\,\upmu \hbox {W}$ and 0.49 $\upmu \hbox {W}$, respectively. In addition, it is also found that the TPEH has larger voltage and power than the conventional BPEH within the whole range of the resistance at every separation distance, which further shows the advantage of the TPEH for highly efficient energy harvesting.

Fig. 24

Experimental results of the relationship between voltage and resistance (left column), power between resistance (right column) under different separated distance d when the excitation amplitude is $15\,\hbox {m/s}^{2}$ and frequency is 5 Hz. a TPEH, b conventional BPEH

We have noticed from above experimental results that the generated voltages of the TPEH and BPEH are very small. This is due to the low piezoelectric constant and electromechanical coupling factor of the PZT material used in the TPEH and BPEH, resulting in a small energy harvesting and converting ability. In addition, the large height and small surface area of the PZT material with respect to the substrate decrease the strain induced by the vibration, which also decreases the harvesting voltages of the TPEH and BPEH. Therefore, the application of new piezoelectric ceramic materials with high piezoelectric constant and electromechanical coupling factor, as well as large surface area and small height will increase the energy harvesting voltage.

Finally, it should be noted that the piezoelectric beam has very large deformation in the presented TPEH configuration when it oscillates in bi- or tri-stable motions. Therefore, considering the geometric nonlinearity and axial strain of the piezoelectric beam for building the exact dynamic model and analyzing the effects of geometric nonlinearity on the dynamic characteristics of the TPEH could be of great interest for further investigation.

5 Conclusions

Focusing on a tri-stable piezoelectric energy harvester with magnetic coupling for low-frequency excitations, this paper presented an improved magnetic force model to precisely calculate the magnetic force exerted on the cantilever beam based on the magnet point dipole theory. With the derived magnetic force model, the formation mechanism of the bi or tri-stable states was analyzed using the bifurcation and potential well diagrams. The nonlinear dynamic characteristics and broadband energy harvesting of such a tri-stable energy harvester were investigated through a series of numerical simulations and experimental validations. The main findings of the present study are summarized are follows:

• 1. An improved magnetic force model is presented based on the magnetic point dipole theory. Theoretical simulations and experimental validations have shown that the improved magnetic force model has a significant improvement of the calculating precision, and it is more applicable to calculate the magnetic force for different magnetic intervals compared with the conventional magnetic dipoles model.

• 2. With the improved magnetic force model, various bifurcation and potential energy functions of the TPEH were investigated to reveal the formation mechanism of bi- or tri-stable states. Increasing the gap distance between the two external magnets can lead to (i) the generation of a new pitchfork bifurcation of the trivial solution and (ii) the degeneration of the pitchfork bifurcation of the non-hyperbolic trivial solution accompanying with the saddle-node bifurcation of the non-trivial solution.

• 3. From the potential energy diagrams, the TPEH has four transitions with the decrease of the separation distance d, i.e., (i) transition starts from mono-stable state to bi-stable state, (ii) transition starts from mono-stable state, passing through bi-stable state and then to tri-stable state, (iii) transition starts from mono-stable state, directly to tri-stable state, (iv) transition starts from mono-stable state, successively passing through tri-stable state and bi-stable state, and then to tri-stable state.

• 4. The theoretical analysis and experimental validations indicated that the TPEH possesses lower and wider potential energy well, leading to a significant enhancement of the energy harvesting ability in lower excitation and broader frequency bandwidth. This verifies that the TPEH has promise for application in the real environment energy harvesting.

• 5. The TPEH can generate higher output voltage and power at lower frequency excitation under different load resistance. The TPEH has an optimum value of 7 M$\Omega$ at the separation distance d=21 mm. As to the optimum value, the power of the TPEH and BPEH reach 0.62 and 0.49 $\upmu$W, respectively.