1 Introduction

Energy harvesting technologies aim to convert unused ambient energy into electrical energy. Particularly, vibrational energy harvesting from mechanical vibrations [1], structural oscillations [2] or biological contractions [3] provides alternative power for structural health monitoring, wildlife tracking and or pacemakers among different applications. The direct piezoelectric effect is usually exploited in vibrational energy harvesting due to strong electromechanical coupling, large energy density and high-voltage output [4]. Early designs of the piezoelectric energy harvesters are based on linear theory. The most significant shortcoming of operating in the linear regime is the limitation of energy harvesting over a narrow bandwidth. In contrast to harvesters based on the linear performance, harvesters capable of exploiting nonlinear aspects increase the mutual coupling between the structure and the vibration source, which can potentially lead to broadened bandwidth and improved performance of piezoelectric energy harvesters [5,6,7].

One common approach of introducing the nonlinearity is to utilize magnetic interactions. Stanton et al. [8] designed a nonlinear energy harvester with both hardening and softening responses through tuning the position of the stationary magnets with respect to the tip magnet of the cantilever beam. Erturk et al. [9] proposed a similar piezomagnetoelastic device with two fixed magnets interacting with a tip magnet. Tang et al. [10] designed a nonlinear piezoelectric energy harvester with a magnetic oscillator interacting with the tip magnet of the cantilever beam. Zhou et al. [11] designed a piezomagnetoelastic energy harvester with rotatable external magnets. Fan et al. [12] presented a bidirectional nonlinear piezoelectric energy harvester composed of two magnetically coupled cantilever beams that deflect in orthogonal directions. Su et al. [13] designed a tridirectional piezomagnetoelastic energy harvester for expanded broadband performance in three orthogonal directions. Kim et al. [14] investigated the nonlinear dynamics of an energy harvester composed of a bimorph cantilever beam with three permanent magnets using the methods of multiple scales and harmonic balance. A multi-mode piezoelectric energy harvester with nonlinear magnetic force and geometric nonlinearity was presented [15]. High-voltage output with broad band performance was obtained. A piezoelectric energy harvesting array was proposed with magnetically coupled effect [16]. It was demonstrated to satisfy the power requirement of the wireless sensor node. Chen et al. [17] proposed an L-shaped piezoelectric energy harvester with magnetic interaction. Compared to its counterpart without internal resonance, the L-shaped 1:2 internally resonant vibration energy harvester greatly broadened the bandwidth. Harmonic balance method was used to analyze the nonlinear response of the magnetoelectric energy harvester [18]. A semi-analytical approach based on harmonic balance method was later proposed [19]. Energy harvesting studies on L-shaped structures [20, 21], autoparametric vibration absorber with internal resonance [22] and cantilever-beam structure with liquid filled container as the proof mass [23] were also performed for expanding the bandwidth of the energy harvesting frequency range.

In the recent decade, the nonlinear bistable characteristic has been utilized to broaden the energy harvesting bandwidth. A rotational bistable energy harvester with frequency up-conversion capability was proposed. Kinetic energy with low frequency was reported to be effectively harvested [24]. To improve the wave energy conversion result, a bistable performance realized by magnetic interactions was introduced [25]. The capture ratio of the bistable wave energy harvester was about twice its linear counterpart. For large-amplitude impulsive vibration energy scavenge, a bistable energy harvester with plucking effect was presented [26]. Compared to the conventional bistable harvesters, a new bistable energy harvester with the elastic magnifier was observed to exhibit higher broadband electric outputs [27]. Moreover, a lever-based bistable energy harvester was proposed [28]. The nonlinear characterizations showed that the lever-based bistable energy harvester was superior than the bistable energy harvester without the lever effect.

From the electric aspect, bandwidth improvement was also achieved by using the inductive–resistive circuit. Such approach was called as the shunted piezoelectric damping method in vibration control [29] and then used for broadband piezoelectric energy harvesting. The effects of the inductance on the band width and power output were investigated [30]. Inductive–resistive impedance matching was proposed with the equivalent circuit method [31]. The optimal performance was realized by adjusting the inductance and resistance depending on the external frequency. Similar broadband piezoelectric energy harvesters were designed based on gradient optimization method [32]. An electromechanical coupled distributed parameter model was proposed for the piezoelectric energy harvester with the inductive–resistive circuit [33]. Double resonance zones were found for broad band energy harvesting.

Nonlinear dynamic studies are crucial for broadband ambient energy harvesting [34]. Successful applications include powering pacemakers from heartbeat [35], powering wearable devices from human motion [36] and powering wireless sensor nodes from ship and bridge vibration [37]. To the authors’ knowledge, the combined effects of the mechanical and electrical nonlinearities with the magnetic interaction and inductive–resistive circuit have not been investigated for broadband bistable energy harvesting. The complex electromechanical coupled nonlinear phenomena of such a system have not been revealed. To cover this gap, an electromechanical coupled distributed parameter model of a piezoelectric energy harvester with a nonlinear magnetic force and a series-connected inductive–resistive circuit is proposed. The nonlinear boundaries for multiple solutions are then determined based on the discriminant of the cubic function. The Jacobi matrix of the modulation equations is then proposed to determine the stability of the multiple solutions. The upward and downward sweep experiments are performed. Effects of the inductance and cubic magnetic coefficients on the performance of the bistable energy harvester are discussed.

2 Mathematical modeling

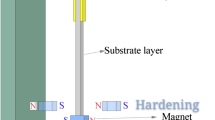
As shown in Fig. 1, the proposed piezoelectric energy harvester consists of a partially covered piezoelectric cantilever beam that is fixed to a base structure undergoing the harmonic excitation in the y direction. The tip mass of the cantilever beam is a magnet that interacts repulsively with two other magnets of the system. The relative positions of the three magnets can be adjusted by the rotation, lifting and shifting of the two magnets. The piezoelectric sheet bonded on the surface of the beam substrate layer is connected to a resistor and an inductor. To establish the electromechanical coupled distributed parameter model for the proposed energy harvester, the extended Hamilton principle [38] is employed which yields

$$\begin{aligned} \begin{array}{l} \displaystyle \int _{{t_{_1}}}^{{t_2}} {[\delta (T - V+ W_\mathrm{nc}}) ]\hbox {d}t = 0 \end{array} \end{aligned}$$
(1)

where T, V and \(W_\mathrm{nc}\) are, respectively, the kinetic energy, potential energy and virtual work due to the nonconservative forces. The kinetic energy T and potential energy V are expressed as

$$\begin{aligned}&{{T}} = \frac{1}{2}{\int _0^l {m(x)\left( {\frac{{\partial {u_\mathrm{rel}}(x,t)}}{{\partial t}} + \frac{{\hbox {d}{u_b}(t)}}{{\hbox {d}t}}} \right) } ^2}\hbox {d}x \nonumber \\&\qquad + \frac{1}{2}{M_t}\left( \frac{{\partial {u_\mathrm{rel}}(l,t)}}{{\partial t}} + {l_c}\frac{{{\partial ^2}{u_\mathrm{rel}}(l,t)}}{{\partial x\partial t}} \right. \nonumber \\&\qquad \left. + \frac{{\hbox {d}{u_b}(t)}}{{\hbox {d}t}} \right) ^2 + \frac{1}{2}{I_c}{\left( {\frac{{{\partial ^2}{u_\mathrm{rel}}(l,t)}}{{\partial x\partial t}}} \right) ^2}\end{aligned}$$
(2)
$$\begin{aligned}&V = \frac{1}{2}{\int _0^l {EI(x)\left( {\frac{{{\partial ^2}{u_\mathrm{rel}}(x,t)}}{{\partial {x^2}}}} \right) } ^2}\hbox {d}x \end{aligned}$$
(3)

where m(x) is the mass of the beam per unit length and expressed as \(m(x) = b{\rho _\mathrm{s}}{h_\mathrm{s}} + 2b{\rho _\mathrm{p}}{h_\mathrm{p}}(H(x) - H(x - {l_\mathrm{p}}))\), b is the width of the substrate and piezoelectric layers, \({\rho _\mathrm{s}}\) and \({\rho _\mathrm{p}}\) are, respectively, the density of the substrate material and piezoelectric sheet, \({h_\mathrm{s}}\) and \({h_\mathrm{p}}\) are, respectively, the thicknesses of the substrate layer and piezoelectric layer, \(l_\mathrm{p}\) is the length of the piezoelectric layer, H(x) is the Heaviside step function, \({u_\mathrm{rel}}(x, t)\) represents the displacement of the piezoelectric cantilever beam in the y direction and is a function of the coordinate x and time t, \({u_b}(t)\) denotes the displacement of the base frame in the y direction, \(M_t\) is the mass of the tip magnet, l is the total length of the beam structure, \(l_c\) denotes the half length of the tip magnet, \(I_c\) represents the rotational inertia of the tip magnet relative to the center of the tip magnet, EI(x) is the stiffness relative to the center of the cross section of the beam and given by EI(x)= \(\frac{1}{12}{b}{E_\mathrm{s}}{h_\mathrm{s}}^3 + \frac{2}{3}{b}{E_\mathrm{p}}[{{({h_\mathrm{p}} + \frac{{{h_\mathrm{s}}}}{2})}^3} - \frac{{{h_\mathrm{s}}^3}}{8}](H(x) - H(x - {l_\mathrm{p}}))\), where \({E_\mathrm{s}}\) and \({E_\mathrm{p}}\) are the Young’s Modulus of the substrate and piezoelectric layers, respectively.

Fig. 1
figure 1

Schematic of the broadband piezoelectric energy harvester

Full size image

The virtual work due to the nonconservative forces is given by

$$\begin{aligned} {W_\mathrm{nc}} = {W_\mathrm{ele}} + {W_\mathrm{damp}} + {W_\mathrm{mag}} \end{aligned}$$
(4)

where \({W_\mathrm{ele}}\), \({W_\mathrm{damp}}\) and \({W_\mathrm{mag}}\) are the virtual works due to the electric, damping and magnetic forces, respectively. The virtual work due to the electric force \({W_\mathrm{ele}}\) is expressed as

$$\begin{aligned} {W_\mathrm{ele}}{\mathrm{= - }}{\int _0^l {{{{M}}_\mathrm{ele}}\left( {\frac{{{\partial ^2}{u_\mathrm{rel}}(x,t)}}{{\partial {x^2}}}} \right) } ^2}\hbox {d}x \end{aligned}$$
(5)

where \({M_\mathrm{ele}}\) is the moment due to the electric effect. For parallelly connecting the upper and lower piezoelectric layers, its expression is calculated as

$$\begin{aligned} {M_\mathrm{ele}}= & {} {b_2}\left( \int _{ - {h_\mathrm{s}}/2 - {h_\mathrm{p}}}^{ - {h_\mathrm{s}}/2} {e_{31}}\frac{{{\mathrm{V(t)}}}}{{{h_\mathrm{p}}}}y\hbox {d}y\right. \nonumber \\&\left. + \int _{{h_\mathrm{s}}/2}^{{h_\mathrm{p}} + {h_\mathrm{s}}/2} { - {e_{31}}\frac{{{\mathrm{V(t)}}}}{{{h_\mathrm{p}}}}y\hbox {d}y} \right) \ \nonumber \\&\qquad \left( {H(x) - H(x - {l_\mathrm{p}})} \right) \end{aligned}$$
(6)

where V(t) is the voltage of the piezoelectric layer, \(e_{31}=E_\mathrm{p} d_{31}\) is the piezoelectric stress coefficient where \(d_{31}\) is piezoelectric strain coefficient. The virtual work due to the damping force \({W_\mathrm{damp}}\) is presented as

$$\begin{aligned} \delta {W_\mathrm{damp}} = \int _0^l {{F_\mathrm{d}}(x,t)\delta {u_\mathrm{rel}}(x,t)\hbox {d}x} \end{aligned}$$
(7)

where \({F_\mathrm{d}}(x,t)\) is the damping force of the cantilever beam and expressed as \({F_\mathrm{d}}(x,t) = - {c_\mathrm{a}}\frac{{\partial {u_\mathrm{rel}}(x,t)}}{{\partial t}} - {c_\mathrm{s}}I\frac{{{\partial ^5}{u_\mathrm{rel}}(x,t)}}{{\partial {x^4}\partial t}}\). In this expression, \(c_\mathrm{s}\) and \(c_\mathrm{a}\) are, respectively, the viscous strain and air damping coefficients of the cantilever beam. The virtual work due to the magnetic force \({W_\mathrm{mag}}\) is given by

$$\begin{aligned} \delta {W_\mathrm{mag}} = {F_\mathrm{mag}}\delta {u_\mathrm{rel}}(l,t) \end{aligned}$$
(8)

where \({F_\mathrm{m}}\) is the magnetic force and modeled as \(F_\mathrm{m}=\mu v_\mathrm{rel}(l,t)+\lambda v_\mathrm{rel}(l,t)^3\), where \(\mu \) and \(\lambda \) are, respectively, the linear and cubic magnetic empirical coefficients [11].

Substituting Eq. (2–4) into the extended Hamilton equation (1) and collecting all terms with the virtual displacement \(\delta {u_\mathrm{rel}}(x,t)\), the electromechanical coupled distributed parameter model for such an energy harvester is then derived as:

$$\begin{aligned}&EI(x)\frac{{{\partial ^4}{u_\mathrm{rel}}(x,t)}}{{\partial {x^4}}} + {c_\mathrm{s}}I(x)\frac{{{\partial ^5}{u_\mathrm{rel}}(x,t)}}{{\partial {x^4}\partial t}} \nonumber \\&\qquad + {c_\mathrm{a}}\frac{{\partial {u_\mathrm{rel}}(x,t)}}{{\partial t}} \nonumber \\&\qquad + m(x)\frac{{{\partial ^2}{u_\mathrm{rel}}(x,t)}}{{\partial {t^2}}}\nonumber \\&\qquad + \left( \frac{{\hbox {d}\delta (x)}}{{\hbox {d}x}} - \frac{{\hbox {d}\delta (x - l_\mathrm{p})}}{{\hbox {d}x}}){\vartheta _\mathrm{p}}(L{\dot{I}}(t)+RI(t)\right) \nonumber \\&\quad = [\mu u_\mathrm{rel}(l,t)+\lambda u_\mathrm{rel}(l,t)^3]\delta (x-l) + [m(x)\nonumber \\&\qquad +{M_t}\delta (x - l)]a_b\cos ({\omega _b}t) \end{aligned}$$
(9)

The first term on the left hand side of Eq. (9) represents the resistance to the bending stiffness of the beam. The second term is due to strain rate damping with \(c_\mathrm{s}\) denoting the viscous strain damping effect of the cantilever beam. The third term is due to the air damping effect around the beam structure. The fourth term is the inertia term of the cantilever beam. The last term on the left of the Eq. (9) is the electromechanical coupled term of the resistive–inductive interface circuit, where \(\delta (x)\) is the Dirac delta function and \(\vartheta _\mathrm{p}\) is the piezoelectric coupling term given by \({\vartheta _\mathrm{p}} =- {e_{31}{b}} (h_\mathrm{p}+h_\mathrm{s})\) where \(e_{31}=E_\mathrm{p} d_{31}\) is the piezoelectric stress coefficient, \(d_{31}\) is piezoelectric strain coefficient, R is the load resistance, L is the inductance and I(t) is the generated current through the interface circuit. The first term on the right hand side of Eq. (9) is the magnetic force. The second term is the excitation force, where \(a_b\) is the base acceleration amplitude, \(\omega _b\) is the base excitation frequency. Besides, four boundary conditions are obtained from the terms of the solved extended Hamilton equation at \(x=0\) and \(x=l\) as

$$\begin{aligned} \begin{array}{*{20}{l}} {\begin{array}{*{20}{l}} {{u_\mathrm{rel}}({x^ + },t) = 0,}&{\frac{{\partial {u_\mathrm{rel}}({x^ + },t)}}{{\partial x}} = 0;} \end{array}}&\quad {\begin{array}{*{20}{l}} \mathrm{for}&{}{x = 0} \end{array}}\\ {{\mathrm{EI}}({x^ - })\frac{{{\partial ^2}{u_\mathrm{rel}}({x^ - },t)}}{{\partial {x^2}}} + ({M_t}{l_c}\frac{{{\partial ^2}{u_\mathrm{rel}}({x^ - },t)}}{{\partial {t^2}}} + {I_t}\frac{{{\partial ^3}{u_\mathrm{rel}}({x^ - },t)}}{{\partial x\partial {t^2}}}) = 0,}\\ {\frac{\partial }{{\partial x}}\left( {{\mathrm{EI}}({x^ - })\frac{{{\partial ^2}{u_\mathrm{rel}}({x^ - },t)}}{{\partial {x^2}}}} \right) - {M_t}(\frac{{{\partial ^2}{u_\mathrm{rel}}({x^ - },t)}}{{\partial {t^2}}} + {l_c}\frac{{{\partial ^3}{u_\mathrm{rel}}({x^ - },t)}}{{\partial x\partial {t^2}}}) = 0.} &{}\quad {\begin{array}{*{20}{l}} \mathrm{for}&{}{x = l} \end{array}} \end{array} \end{aligned}$$
(10)

where the superscripts − and \(+\) denote, respectively, the left and right parts close to the separation points, \(I_t\) represents the rotational inertia of the tip magnet relative to the end of the beam structure. Inspecting the above equation, the inertia of the tip mass has been considered in the boundary condition at \(x = l\).

Since the two pieces of piezoelectric sheets are parallelly connected, Gauss law [39] is introduced to relate the electrical variables with the mechanical deformation as following:

$$\begin{aligned} \frac{\hbox {d}}{{\hbox {d}t}}\int _A { \mathbf {D} \cdot \mathbf {n} \; \hbox {d}A} =\frac{\hbox {d}}{{\hbox {d}t}}\int _A { D_3\; \hbox {d}A }=\frac{I(t)}{2} \end{aligned}$$
(11)

where \(\mathbf {D}\) is the electric displacement vector and \(\mathbf {n}\) is the normal vector to the plane of the beam. The electric displacement component \(D_3\) is given by

$$\begin{aligned} {D_3}(x,t) = e_{31} \varepsilon _{11}(x,t) + \epsilon _{33}^s{E_3} \end{aligned}$$
(12)

where \(\varepsilon _{11}(x,t)=-\frac{1}{h_\mathrm{p}}\int _{h_\mathrm{s}/2}^{h_\mathrm{s}/2+h_\mathrm{p}}\frac{\partial ^2 u_\mathrm{rel}(x,t)}{\partial x^2}y\hbox {d}y=-\frac{h_\mathrm{s}+h_\mathrm{p}}{2}\frac{\partial ^2 u_\mathrm{rel}(x,t)}{\partial x^2}\) is the average strain component in the piezoelectric layers, \(\epsilon ^{s}_{33}\) is the permittivity component at constant strain and \(E_3\) is the electric field which is expressed as \(E_3=-V(t)/h_\mathrm{p}\). Substituting Eq. (12) into Eq. (11), the coupling electrical equation is calculated as

$$\begin{aligned}&- e_{31}(h_\mathrm{p}+h_\mathrm{s}){b} \int _{{0}}^{{l_\mathrm{p}}} \frac{{{\partial ^3}u_\mathrm{rel}(x,t)}}{{\partial t\partial {x^2}}}\mathrm{d}x \nonumber \\&\quad - \frac{{2\epsilon _{33}^s{b}l_\mathrm{p}}}{{{h_\mathrm{p}}}}\frac{{\mathrm{d}(L{\dot{I}}(t)+RI(t))}}{{\mathrm{d}t}} = I(t). \end{aligned}$$
(13)

The first term on the left hand side of Eq. (13) is the electromechanical coupling term. The second term is the current flow through the capacitor of the piezoelectric material.

The Galerkin procedure is then employed to discretize the distributed parameter models [33]. The displacement of the beam, \(u_\mathrm{rel}(x,t)\), is then written as

$$\begin{aligned} u_\mathrm{rel}(s,t) = \sum _{i=1}^N{{\phi _i }} (s){q_i}(t) \end{aligned}$$
(14)

where \({q_i}(t)\) and \( {{\phi _i}} (s)\) are the \(i_\mathrm{th}\) modal coordinate and shape of the cantilever beam, respectively. The exact mode shape of the beam is written as

$$\begin{aligned} \phi _{ij} (x)= & {} A_{ij}\sin \beta _{ij} x + B_{ij}\cos \beta _{ij} x\nonumber \\&+ C_{ij}\sinh \beta _{ij} x + D_{ij}\cosh \beta _{ij} x,\quad j=1,\;2 \end{aligned}$$
(15)

where i represents the \(i_{\mathrm{th}}\) mode, \(j=1\) is for \(0 <x \le l_\mathrm{p}\), \(j=2\) is for \(l_\mathrm{p} <x \le l\), the coefficients of \(\beta _{i1}\) and \(\beta _{i2}\) are related by \(\beta _{i1}=\root 4 \of {EI(l) m(0)/(EI(0) m(l))}\beta _{i2}\), the coefficients \(A_{ij}\), \(B_{ij}\), \(C_{ij}\), \(D_{ij}\) are determined from the boundary equations (10) and the equal displacement, rotational angle, bending moment and shear force between two sides at \(x=l_\mathrm{p}\). After considering Eq. (14), these conditions are simplified as below

$$\begin{aligned} \begin{array}{l} \begin{array}{*{20}{c}} {\phi _{i1} (0) = 0,}&{}{\phi _{i1} '(0) = 0,} {}&{}{\phi _{i1} (l_\mathrm{p}) = \phi _{i2} (l_\mathrm{p}),} \end{array}\\ \phi _{i1}' (l_\mathrm{p}) = \phi _{i2}' (l_\mathrm{p}), \\ EI({l_\mathrm{p}}^ - ){\phi _{i1}}^{\prime \prime }({l_\mathrm{p}}) = E{I}({l_\mathrm{p}}^ + ){\phi _{i2}}^{\prime \prime }({l_\mathrm{p}}),\\ EI({l_\mathrm{p}}^ - )\phi _{i1}^{\prime \prime \prime } (l_\mathrm{p}) =EI({l_\mathrm{p}}^ + ) \phi _{i2}^{\prime \prime \prime } (l_\mathrm{p}),\\ EI(l)\phi _{i2} ^{\prime \prime }(l) - {\omega _i ^2}M_t l_c \phi _{i2} (l) - {\omega _i ^2}I_t\phi _{i2} '(l) = 0,\\ EI(l)\phi _{i2} ^{\prime \prime \prime }(l) + {\omega _i ^2}M_t l_c \phi _{i2} '(l) +{\omega _i ^2}M_t\phi _{i2} (l) = 0. \end{array} \end{aligned}$$
(16)

where the prime indicates the derivative with respect to x, \(\omega _i\) denotes the \(i_\mathrm{th}\) natural frequency of the cantilever beam. To make the equivalent total mass of the governing equation to be equal to 1, the following normalized orthogonality conditions are chosen as

$$\begin{aligned} \begin{array}{l} \displaystyle \int _0^{l_\mathrm{p}} {m(x) {\phi _{q1}}(x){\phi _{r1}}(x)\hbox {d}x} \\ \quad +\int _{l_\mathrm{p}}^l {m(x) {\phi _{q2}}(x){\phi _{r2}}(x)\hbox {d}x} + I_t{\phi _{q2}}^{\prime }(l){\phi _{r2}}^{\prime }(l)\\ \quad +M_t{\phi _{q2}}(l){\phi _{r2}}(l)+ M_t{\phi _{q2}}^{\prime }(l)l_c{\phi _{r2}}(l) \\ \quad + M_t{\phi _{q2}}(l)l_c{\phi _{r2}}^{\prime }(l) = {\delta _{qr}}\\ \displaystyle \int _0^{l_\mathrm{p}} {EI(x){\phi _{q1}}^{\prime \prime }(x){\phi _{r1}}^{\prime \prime }(x)\hbox {d}x}\\ \quad +\int _{l_\mathrm{p}}^l {EI(x){\phi _{q2}}^{\prime \prime }(x){\phi _{r2}}^{\prime \prime }(x)\hbox {d}x} = {\delta _{qr}}\omega _r^2 \end{array} \end{aligned}$$
(17)

where q and r represent the modes, and \(\delta _{qr}\) is the Kronecker delta, which is defined as unity when q is equal to r and zero otherwise. With the experimental work shown in Sect. 4, the first three natural frequencies are determined as 16.35 rad/s, 271.14 rad/s and 583.57 rad/s. Therefore, the second or third natural frequency is much larger than the first one. In the current research work, the effects of the magnetic force and inductance on the nonlinear properties of the system are focused to be analyzed. These nonlinear performances mainly appear near the natural frequency of the energy harvester. To simplify the nonlinear simulation, only the first natural frequency is considered in the following analysis. Substituting Eq. (14) into Eqs. (9) and (13) and using Eqs. (15–17), the distributed parameter models of the first mode shape are reduced as

$$\begin{aligned}&\ddot{q}(t)+2\xi \omega \dot{q}(t)+\omega ^2q(t)-\theta _{p}(L\dot{I}(t)+RI(t))\nonumber \\&\quad =\bar{M} a_{b}\cos \omega _{b}t+\alpha q(t)+\beta q^3(t) \end{aligned}$$
(18)
$$\begin{aligned}&C_\mathrm{p}(L\ddot{I}(t)+R\dot{I}(t))+I(t)+\theta _\mathrm{p}\dot{q}(t)=0 \end{aligned}$$
(19)

where q(t) is the first modal coordinate, \(\xi \) is the structural damping ratio, \(\omega \) is the first natural frequency of the cantilever beam, \(\theta _\mathrm{p}=\phi ^{\prime }(l_\mathrm{p})b_\mathrm{p}E_\mathrm{p}d_{31}(h_\mathrm{p}+h_\mathrm{s})\) is the electromechanical coupling factor, \(\bar{M}=\int ^{l}_{0}m(x)\phi (x)\hbox {d}x+M_t\phi (l)\) is the equivalent mass of the cantilever beam, \(\phi (x)\) is the first mode shape of the cantilever beam, \(\alpha =\mu \phi (l)^2\) is the equivalent linear magnetic coefficient, \(\beta =\lambda \phi (l)^4\) is the equivalent cubic magnetic coefficient, and \(C_\mathrm{p}=\frac{2\epsilon ^s_{33}b_\mathrm{p}l_\mathrm{p}}{h_\mathrm{p}}\) is the capacitance of the piezoelectric sheets. For Eq. (18), it is obtained through integrating Eq. (9) times \(\phi (x)\) along the beam length from \(x=0\) to \(x=l\). Based on the normalized orthogonality conditions shown in Eq. (17), the coefficients of mass and stiffness are, respectively, equal to 1 and \(\omega ^2\). In other words, this distributed parameter model has been normalized through the mode shape \(\phi (x)\) and thus every term of Eq. (18) seems to be divided by the equivalent total mass of the system.

Based on the electromechanical decoupled method [40], the relationships between the mode coordinate q(t) and the electric current I(t) can be determined by the linear electrical equation (19). After that, the electric coupled term \(-\theta _{p}(L\dot{I}_{{\hat{s}}}(t)+RI_{{\hat{s}}}(t))\) in the mechanical domain is treated as additional damping and elastic forces. The equivalent structure representation for the piezoelectric energy harvester with the R–L circuit is then written as

$$\begin{aligned}&\ddot{q}(t)+(2\xi \omega +c_e)\dot{q}(t)+\Omega ^2q(t)-\beta q(t)^3\nonumber \\&\quad =\bar{M}a_b \cos \omega _{b}t \end{aligned}$$
(20)

where the modified frequency \(\Omega \) and electrical damping \(c_e\) due to the electromechanical coupling are obtained as

$$\begin{aligned} \Omega= & {} \sqrt{\omega ^2+\frac{C_\mathrm{p} \omega ^2_b L^2-L+C_\mathrm{p} R^2}{(C_\mathrm{p}\omega _b R)^2+(C_\mathrm{p} \omega ^2_b L-1)^2}\theta ^2_\mathrm{p} \omega ^2_b-\alpha },\end{aligned}$$
(21)
$$\begin{aligned} c_e= & {} \frac{R\theta _\mathrm{p}^2}{(C_\mathrm{p} \omega _b R)^2+(C_\mathrm{p} \omega ^2_b L-1)^2}. \end{aligned}$$
(22)

It is noted from Eq. (20) that the resonance happens when \(\Omega \approx {\omega _b}\). Inspecting Eq. (21), the modified frequency \(\Omega \) is dependent on the external frequency \(\omega _b\) unless \(L=0\). For the case of \(L \ne 0\), there may exist multiple solutions of \(\omega _b\) after substituting \(\Omega = {\omega _b}\) into Eq. (21). In other words, multiple resonant peaks will appear in the energy harvesting system since the inductance L is introduced to the electrical circuit. After solving q(t) from Eq. (20), the tip displacement and harvested power are obtained by the following relationships.

$$\begin{aligned} A_\mathrm{tip}=\phi (l) q_0,\quad P=c_e(\omega _b q_0)^2 \end{aligned}$$
(23)

where \(q_0\) is the amplitudes of q(t).

3 Nonlinear analysis

The method of harmonic balance is implemented to analytically determine the nonlinear response of the energy harvester and their effects on the broadening of the harvester’s response. Inspecting Eq. (20), the solution of q(t) is assumed as \(q(t) = {q_0}\cos ({\omega _b}t + \varphi )\) where \({q_0}\) and \(\varphi \) are the respective amplitude and phase angle of q(t). Substituting the above expression into Eq. (20), the implicit functions for \(q_0\) and \(\varphi \) are obtained as

$$\begin{aligned} \begin{array}{l} ({\Omega ^2} - \omega _b^2){q_0} - \frac{{3\beta }}{4}q_0^3 = {\bar{M}}{a_b}\cos \varphi \\ \quad - (2\xi \omega + {c_e}){\omega _b}{q_0} = {\bar{M}}{a_b}\sin \varphi . \end{array} \end{aligned}$$
(24)

Using x to replace \(q_{0}^{2}\) and eliminating the variable \(\varphi \), Eq. (24) is rewritten as a cubic function.

$$\begin{aligned}&\frac{{9{\beta ^2}}}{{16}}{x^3} - \frac{{3\beta }}{2}\left( {{\Omega ^2} - \omega _b^2} \right) {x^2}\nonumber \\&\quad + \left[ {{{\left( {{\Omega ^2} - \omega _b^2} \right) }^2} + {{\left( {2\xi \omega + c_e} \right) }^2}\omega _b^2} \right] x - {\left( {{\bar{M}}{a_b}} \right) ^2} = 0. \end{aligned}$$
(25)

When \(\beta \) is zero, the coefficients of the cubic and quadratic terms are zero. The solution of the above equation becomes unique. That is because the system turns out to be linear as shown in Eq. (18). In the practical cases, the cubic magnetic coefficient \(\lambda \) is usually not equal to zero. As such, only the case of \(\beta \ne {\mathrm{0}}\) will be discussed in the following work. The discriminant for the number and type of the real roots is expressed as \({\Delta _\mathrm{cubic}} = 18abcd - 4{b^3}d + {b^2}{c^2} - 4a{c^3} - 27{a^2}{d^2}\), where a, b, c and d are the coefficients of the cubic, quadratic, linear and constant terms, respectively. There are three distinct real roots of x when \({\Delta _\mathrm{cubic}}>0\). If \({\Delta _\mathrm{cubic}}=0\), Eq. (25) has a real double root and a real simple root. At this situation, the corresponding external frequency is denoted as \(\omega _b^0\). When \({\Delta _\mathrm{cubic}}<0\), only one real root exists. From the above discussion, it is noted that the number of real solutions will change at \({\Delta _\mathrm{cubic}}=0\). In other word, bifurcation occurs at the point of \({\Delta _\mathrm{cubic}}=0\). As such, only the case of \({\Delta _\mathrm{cubic}}=0\) is focused for the nonlinear theoretical analysis in this section. \({\Delta _\mathrm{cubic}}\) is dependent on six parameters: two electrical variables (R, L), two magnetic coefficients (\(\alpha \), \(\beta \)) and two excitation parameters (\(\omega _b\) and \(a_b\)). In this work, the cubic magnetic coefficient \(\beta \) and the electric inductance L are chosen to analyze the nonlinear responses of the system at specific load resistances and excitations.

3.1 Effect of cubic magnetic coefficient

It is noted from the distributed parameter model of the system (Eqs. 18–19), the coefficient of the only nonlinear term is \(\beta \). As such, \(\beta \) has the most important effect on the nonlinear properties of the system and is analyzed first in this subsection. The discriminant for the real-root number and type is calculated as a quartic polynomial of \(\beta \) as

$$\begin{aligned} {\Delta _\mathrm{cubic}}= & {} - \frac{{2187}}{{256}}{\chi ^4}{\beta ^4} + \frac{1}{{16}}\left( {27{\vartheta ^2} + 243{\kappa ^2}} \right) \vartheta {\chi ^2}{\beta ^3}\nonumber \\&- \frac{9}{4}{\kappa ^2}{\left( {{\vartheta ^2} + {\kappa ^2}} \right) ^2}{\beta ^2} \end{aligned}$$
(26)

where \( \vartheta ={\Omega ^2} - \omega _b^2\), \(\kappa ={\omega _b}\left( {c_e + 2 \xi \omega } \right) \) and \(\chi ={\bar{M}}{a_b}\).

For x or \(q_0^2\) having multiple solutions of a single root and a double root, \(\Delta _\mathrm{cubic}\) is required to be zero, which yields the following quadratic polynomial equation of \(\beta \).

$$\begin{aligned} \eta _1\beta ^2+\eta _2 \beta +\eta _3=0 \end{aligned}$$
(27)

where the coefficients of \(\eta _1\), \(\eta _2\) and \(\eta _3\) are given by \({\eta _1} = - \frac{{2187}}{{256}}{\chi ^4}\), \({\eta _2} = \frac{1}{{16}}{\chi ^2}\vartheta \left( {27{\vartheta ^2} + 243{\kappa ^2}} \right) \) and \({\eta _3} = - \frac{9}{4}{\kappa ^2}{\left( {{\vartheta ^2} + {\kappa ^2}} \right) ^2}\). \(\beta \) is then solved from Eq. (27) as

$$\begin{aligned} \beta _{1,2} = \frac{{ - {\eta _2} \pm \sqrt{\Delta _\beta } }}{{2{\eta _1}}}. \end{aligned}$$
(28)

The corresponding nonlinear magnetic empirical coefficient \(\lambda \) is obtained as

$$\begin{aligned} \lambda _{1,2} = \frac{{ - {\eta _2} \pm \sqrt{\Delta _\beta } }}{{2{\eta _1}\phi {{\left( l \right) }^4}}} \end{aligned}$$
(29)

where \({\Delta _\beta } = \frac{{729}}{{256}}{\chi ^4}{( {\vartheta + \sqrt{3} \kappa })^3}{( {\vartheta - \sqrt{3} \kappa })^3}\). Since \(\Delta _\mathrm{cubic}\) becomes zero as long as Eq. (28) or Eq. (29) is satisfied, Eq. (28) or Eq. (29) is the sufficient and necessary condition for the cyclic-fold bifurcations of the energy harvester. For the existence of \(\beta \) to satisfy \(\Delta _\mathrm{cubic}=0\), \({\Delta _\beta }\) must be greater than or equal to zero, which renders

$$\begin{aligned} \begin{array}{l} \vartheta \ge \sqrt{3}\varphi \quad \text {or}\quad \vartheta \le -\sqrt{3}\varphi . \end{array} \end{aligned}$$
(30)

3.2 Effect of inductance on \(\Delta _\beta \)

In this work, the inductance L is designed in the electrical circuit to broadband the range of the high-efficient energy harvesting with the magnetic force. In this subsection, the effect of L will be analyzed on the nonlinear properties of the system through the parameter \(\beta \). It is noted form Eq. (28) that \(\Delta _\beta =0\) is the critical point to determine the numbers of \(\beta \) for \(\Delta _\mathrm{cubic}=0\). The unique \(\beta \) for \(\Delta _\mathrm{cubic}=0\) (\(\Delta _\beta =0\)) yields the roots of the inductance L representing the softening behavior

$$\begin{aligned} L_{{s1}_{(+, -)}} = \frac{{ - {a_{s2}} \pm \sqrt{{\Delta _{sL1}}} }}{{2{a_{s1}}}} \end{aligned}$$
(31)

with

$$\begin{aligned} \begin{aligned} {a_{s1}}&= {C_\mathrm{p}}\omega _b^4\left[ - \alpha {C_\mathrm{p}} + \theta _\mathrm{p}^2 \right. \\&\quad \left. + {C_\mathrm{p}}\left( {{\omega ^2} - \omega _b^2 - 2\sqrt{3} \xi \omega \omega _b} \right) \right] \\ {a_{s2}}&= \omega _b^2\left[ 2\alpha {C_\mathrm{p}} - \theta _\mathrm{p}^2 \right. \\&\quad \left. + 2{C_\mathrm{p}}\left( { - {\omega ^2} + \omega _b^2 + 2\sqrt{3} \xi \omega \omega _b } \right) \right] \\ {a_{ s3}}&= \left( {1 + C_\mathrm{p}^2{R^2}\omega _b^2} \right) \left( { - \alpha + {\omega ^2} - 2\sqrt{3} \xi \omega {\omega _b}} \right) \\&\quad - \omega _b^2 - {C_\mathrm{p}}{R^2}\omega _b^2\left( { - \theta _\mathrm{p}^2 + {C_\mathrm{p}}\omega _b^2} \right) - \sqrt{3} R\theta _\mathrm{p}^2{\omega _b} \\ \Delta _{sL1}&=a_{s2}^2-4a_{s1}a_{s3} \end{aligned} \end{aligned}$$
(32)

and for the hardening behavior

$$\begin{aligned} L_{{s2}_{(+, -)}} = \frac{{ - {b_{s2}} \pm \sqrt{{\Delta _{sL2}}} }}{{2{b_{s1}}}} \end{aligned}$$
(33)

with

$$\begin{aligned} \begin{aligned} {b_{s1}}&= {C_\mathrm{p}}\omega _b^4\left[ - \alpha {C_\mathrm{p}} + \theta _\mathrm{p}^2\right. \\&\quad \left. + {C_\mathrm{p}}\left( {{\omega ^2} - \omega _b^2 + 2\sqrt{3} \xi \omega \omega _b} \right) \right] \\ {b_{s2}}&= \omega _b^2\left[ 2\alpha {C_\mathrm{p}} - \theta _\mathrm{p}^2 \right. \\&\quad \left. + 2{C_\mathrm{p}}\left( -{{\omega ^2}+ \omega _b^2 - 2\sqrt{3} \xi \omega \omega _b} \right) \right] \\ {b_{s3}}&= \left( {1 + C_\mathrm{p}^2{R^2}\omega _b^2} \right) \left( { - \alpha + {\omega ^2} + 2\sqrt{3} \xi \omega {\omega _b}} \right) \\&\quad - \omega _b^2 + {C_\mathrm{p}}{R^2}\omega _b^2\left( {\theta _\mathrm{p}^2 - {C_\mathrm{p}}\omega _b^2} \right) + \sqrt{3} R\theta _\mathrm{p}^2{\omega _b}\\ \Delta _{sL2}&=b_{s2}^2-4b_{s1}b_{s3}. \end{aligned} \end{aligned}$$
(34)

Inspecting Eqs. (31–34), the critical values of \(L_\mathrm{s}\) are independent of the amplitude of the external base acceleration \(a_b\). In fact, \(\Delta _\beta =0\) becomes zero as long as Eq. (31) or Eq. (33) is satisfied. Therefore, Eqs. (31) and (33) are the sufficient and necessary conditions with which the equality of Eq. (30) holds. These two equations determine the number of real values of \(\beta \) or \(\lambda \) as shown in Eqs. (28) or (29). However, they are not the sufficient conditions for the cyclic-fold bifurcations of the energy harvester.

3.3 Stability

To determine the stability of the equilibrium solutions of \(q_0\) and \(\varphi \) from Eq. (24), it is assumed that \(\gamma = {\omega _b}t + \varphi \). The expression of q(t) is rewritten as \(q(t)=q_0 \cos \gamma \). The time derivative of q(t) is given by

$$\begin{aligned} \dot{q}=-q_0\omega _b \sin \gamma . \end{aligned}$$
(35)

Away from the equilibrium points, \(q_0\) and \(\psi \) become time-varying. At this situation, the time derivative of q(t) is given by

$$\begin{aligned} \dot{q}=\dot{q}_0\cos \gamma -q_0 \omega _b \sin \gamma -q_0 {\dot{\psi }}\sin \gamma . \end{aligned}$$
(36)

Subtracting Eq. (35) from Eq. (36), one obtains one relation between \(\dot{q}_0\) and \({\dot{\psi }}\)

$$\begin{aligned} \dot{q}_0\cos \gamma -q_0{\dot{\psi }}\sin \gamma =0. \end{aligned}$$
(37)

Taking the time derivative of Eq. (35), the acceleration of q(t) near equilibrium points is calculated as

$$\begin{aligned} \ddot{q}=-\dot{q}_0\omega _b\sin \gamma -q_0\dot{\psi }\omega _b\cos \gamma -q_0\omega _b^2\cos \gamma . \end{aligned}$$
(38)

Substituting Eqs. (35) and (38) into Eq. (20), one obtains a second relation between \(\dot{q}_0\) and \(\dot{\psi }\)

$$\begin{aligned} -\dot{q}_0\sin \gamma -q_0\dot{\psi } \cos \gamma =\frac{f+F}{\omega _b} \end{aligned}$$
(39)

where \(f=(2\xi \omega +c_e)\omega _b q_0 \sin \gamma +(\omega _b^2-\Omega ^2)q_0\cos \gamma +\beta q_0^3 \cos ^3\gamma \) and \(F=\bar{M}a_b\cos (\omega _b t)\). Based on Eqs. (37) and (39), the time variation of the amplitude and phase angle of q(t) near equilibrium points are calculated as

$$\begin{aligned} \begin{array}{l} {{\dot{q}}_0} = - \frac{{f + F}}{{{\omega _b}}}\sin \gamma \\ {\dot{\psi }} = - \frac{{f + F}}{{{\omega _b}{q_0}}}\cos \gamma . \end{array} \end{aligned}$$
(40)

Near the equilibrium points, \(q_0\) and \(\psi \) are almost constant with a period \(\gamma =\omega _b t+\psi \). As such, the modulation equations of \(q_0\) and \(\psi \) are obtained as

$$\begin{aligned} \begin{array}{l} \dot{q}_0=-\frac{Q(q_0,\psi )}{2\omega _b}\\ \dot{\psi }=-\frac{P(q_0,\psi )}{2\omega _b q_0} \end{array} \end{aligned}$$
(41)

where \(Q(q_0,\psi )\) and \(P(q_0,\psi )\) are modulation coefficients for a period of \(\gamma \) and expressed as \(Q(q_0,\psi )=\frac{1}{\pi }\int _0^{2\pi } {(f + F)} \sin \gamma \mathrm{d}\gamma =(2\xi \omega +c_e)\omega _b q_0+\bar{M}a_b \sin \psi \) and \(P(q_0,\psi )=\frac{1}{\pi }\int _0^{2\pi } {(f + F)} \cos \gamma \mathrm{d}\gamma =(\omega _b^2-\Omega ^2)q_0+\frac{3}{4}\beta q_0^3+\bar{M}a_b \cos \psi \), respectively. The stability of fixed point \(q_0\) can be analyzed by the Jacobi matrix of modulation equation (41) as following

$$\begin{aligned} -\frac{1}{2\omega _b} \begin{bmatrix} (2\xi \omega +c_e)\omega _b &{} \bar{M}a_b\cos \psi \\ \frac{3}{2}\beta q_0-\bar{M}a_b q_0^{-2}\cos \psi &{} -\bar{M}a_b q_{0}^{-1}\sin \psi \end{bmatrix}\nonumber \\ \end{aligned}$$
(42)

If the two eigenvalues \({\lambda _i}\) have negative real parts, then the fixed point is a sink (stable). Otherwise, the equilibrium point will form a saddle or a source (unstable).

4 Experimental setup

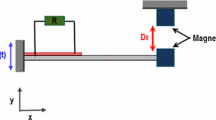
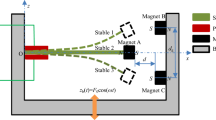
The experimental setup is consisted of a vertical cantilever beam that is partially covered with a piezoelectric sheet and forced at its base in the horizontal direction with a shaker (JZK-100). The tip mass of the cantilever beam is a magnet that repulsively interacts with two other magnets. As shown in Fig. 2, the shaker was excited with sinusoidal signal generated using a digital function generator (YE1311) and amplified using a power amplifier (YE5878). The amplified signal finally determined the motion of the shaker. The piezoelectric energy harvester was connected to the shaker through the base frame. An acceleration sensor (1A314E) was placed on the base frame near the fixed end of the cantilever beam to measure the acceleration of the base excitation. A NdFeB permanent magnet was attached to the free end of the cantilever beam. Two other NdFeB permanent magnets were placed on the left and right of the magnet of the beam with the same poles facing each other. The relative positions between the magnets could be adjusted via the slide slots on the base frames. The positive and negative electrodes of the piezoelectric material bonded on the cantilever beam were connected to the load resistance box and the inductance box. The response of the cantilever beam was determined by the simultaneous actions of the base excitation, nonlinear magnetic forces and electromechanical coupling with the inductance. The vibration displacement of the cantilever beam was measured using a laser displacement sensor (IL-300). The acceleration of the base excitation, output voltage of the energy harvester and vibration displacement of the cantilever beam were collected by a data acquisition system (DH8303). In the upward sweep and downward sweep tests, the amplitude of the acceleration was kept constant at \(2.5\,\hbox {m/s}^2\). Based on extensive testing for different values, the load resistance R and inductance L were chosen as \(10^3\) ohm and 10 H.

Fig. 2
figure 2

The experimental setup of the broadband piezoelectric energy harvester

Full size image

5 Results

5.1 Model validation

To validate the analytical model, the predicted amplitudes of the tip displacement and harvested power during upward and downward sweeps of external frequency are compared with experimentally measured values and plotted in Fig. 3. The analytical solutions are determined from the frequency-response equations (25) and (23). The stability of the solutions is determined by the matrix in Eq. (42). The solid lines represent the stable solutions while the dashed lines indicate the unstable ones. The hardening nonlinearity due to the inductance and magnetic force bends the frequency-response curve to the right. The plots show two stable and one unstable solutions. To validate the predicted jumps, experimental upward and downward sweeps performed. During the upward sweep, the response amplitudes of the tip displacement and harvested voltage increase along the curve ABC until C is reached. After that, a slight increase in the value of the external frequency leads to the observed jump from C to D. Further increase in the excitation frequency results in the decrease in the response amplitude along the curve DE. During downward sweep, the excitation frequency is reduced while maintaining the amplitude of the acceleration constant. As the frequency is decreased from values larger than the natural frequency, \(\Omega \), the amplitudes of the tip displacement and harvested voltage increase slightly along the curve EDF. An abrupt upward jump is noted at near frequency denoted by F. As the frequency is decreased further, the amplitude of the response is decreased along the curve BA. Both analytical and experimental results show the hysteresis in the region between BC and FD. The dashed indicates an unstable saddle point that underlines the dependence of the response on initial conditions. These detailed nonlinear properties will be analyzed in Sect. 5.3. The difference in the power spectra of the harvested power and phase portraits of the tip displacement and tip velocity obtained from the measurements during the upward and downward sweeps, as shown in Fig. 4, denotes the variation in the frequency of the response, which is always equal to the excitation frequency in addition to the variations in the amplitude of the response.

Fig. 3
figure 3

Variations of a the tip displacement amplitude and b harvested voltage amplitude with the excitation frequency (\(a_b=0.25g\), \(L=10\) H and \(R=10^3\) ohm). ‘Upward sweep’ or ‘Downward sweep’ indicates that the excitation frequency, respectively, increases or decreases monotonically when the amplitude of the base acceleration is kept constant

Full size image
Fig. 4
figure 4

Variations of a, b power spectra of the harvested voltage and c, d phase portraits of the tip displacement and tip velocity with the excitation frequency (\(a_b=0.25g\)). ‘Upward sweep’ or ‘Downward sweep’ indicates the excitation frequency, respectively, increases or decreases monotonically when the amplitude of the base acceleration is kept constant

Full size image

5.2 Multi-hardening and multi-softening characterization

To enhance the performance of the harvester, the effects of the inductance L and cubic magnetic coefficient \(\lambda \) are analyzed next. The excitation frequency boundaries where multiple solutions are observed are set by letting \(\Delta _\mathrm{cubic}=0\). The variations in the excitation frequency with the inductance L when \({\Delta _\beta } = 0\) for a load resistance R of \(10^3\) ohm and linear magnetic coefficient \(\mu \) of 0.2 N/mm are presented in Fig. 5. This relationship is determined through using Eqs. (31) and (33). Six curves of \(\omega _b^o-L\) are noted and marked as two \(L_{s1-}\), one \(L_{s1+}\), two \(L_{s2-}\) and one \(L_{ s2+}\) with different colors. The ‘\(+\)’ and ‘−’ subscripts, respectively, represent the plus and minus determined from Eqs. (31) and (33). In fact, \(L_{ s1}\) denotes the softening behavior, while \(L_{s2}\) denotes the hardening behavior. The intersection of \(L_{ s1+}\) and \(L_{ s1-}\) occurs at \(\Delta _{sL1}=0\), and the intersection of \(L_{ s2+}\) and \(L_{ s2-}\) takes place at \(\Delta _{sL2}=0\). As the inductance L is increased from 0 to 300 H, the number of the solutions of \(\omega _b^o\) is successively 2, 3, 4, 5, 6, 5, 4.

Fig. 5
figure 5

Variation in the excitation frequency for \(\Delta _\mathrm{cubic}=0\), \(\omega _b^o\), with the inductance L for \({\Delta _\beta } = 0\) when \(a_b=1g\), \(R=1000\) ohm and \(\mu =0.2\) N/mm

Full size image

Regions of hardening and softening responses as a function of the nonlinear magnetic coefficients for different values of the inductance \(L=10, \,21.48, \,50, 100,\, 200\) H are shown in Fig. 6a–e and discussed in below. At \(L=10\) H, the change in \(\omega _b^o\) with the cubic magnetic coefficient, \(\lambda \), is shown in Fig. 6a.Two solutions of \(\omega _b^o\) at \({\Delta _\beta } = 0\) represented by the yellow circle (on \(L_{ s2-}\)) and orange circle (on \(L_{ s1-}\)) are noted in Fig. 5. They, respectively, correspond to one hardening and one softening. These two points are the boundary for nonlinear hardening and softening. There is no \(\omega _b^o\) appearing the range between these two points, in which the system exhibits only linear phenomenon for all nonlinear magnetic cubic coefficient. The nonlinear hardening occurs at \(\lambda <0\). With the same \(\lambda \), \(\omega _b^o\) of the red line is higher than \(\omega _b^o\) of the blue line for the hardening case. In contrast, the nonlinear softening appears at \(\lambda >0\) with \(\omega _b^o\) of the blue line higher than \(\omega _b^o\) of the red line or zero for the same \(\lambda \). The intersection of the blue and red curves is marked as the yellow and orange circles in Fig. 6a, which corresponds to the same symbol in Fig. 5. The line of \(\omega _b^o=\Omega _\mathrm{s}\) shown in cerulean separates the hardening and softening regions. \(\Omega _\mathrm{s}\) is the special modified frequency which satisfies both Eq. (21) and \(\Omega =\omega _b\). The hardening occurs at \(\omega _b^o>\Omega _\mathrm{s}\), while the softening appears at \(\omega _b^o<\Omega _\mathrm{s}\). A plot for positive \(\lambda \) values is also shown in Fig. 6a. The plot reveals a region of \(\lambda \) with three solutions of \(\omega _b^o\) (one in blue and two in red). In this region, a special nonlinear softening between zero and the lower \(\omega _b^o\) shown in red appears with the typical nonlinear softening between the higher \(\omega _b^o\) in red and \(\omega _b^o\) in blue.

At \(L=21.48\) H, one more solution represented by the black circle is observed at \(\Delta _{sL2}=0\) in addition to the two solutions marked by the yellow and orange circles in Fig. 5. Unlike the yellow and orange circles, the black circle appears at relatively large negative values of \(\lambda \), which is not shown in Fig. 6a. Typical nonlinear hardening and typical nonlinear softening responses are observed with a special nonlinear hardening between the two higher \(\omega _b^o\) in red. The zoomed plot in Fig. 6b reveals that nonlinear softening between zero and the lower \(\omega _b^o\) also exists at \(L=21.48\) H. Similar as the case of \(L=10\) H, the system exhibits as linear one between the hardening and softening points. These points represent softening and hardening boundaries.

At \(L=50\) H, four solutions for \(\omega _b^o\) at \({\Delta _\beta } = 0\) represented by the pink, green, yellow and orange circles are illustrated in Fig. 5. The pink, green and yellow circles (on \(L_{{{\hat{s}}}2}\)) correspond to nonlinear hardening, while the orange circle (\(L_{{{\hat{s}}}1-}\)) corresponds to nonlinear softening. Figure 6c shows the variations of \(\omega _b^o\) of this case with the cubic magnetic coefficient \(\lambda \). The intersections of the red and blue lines are represented by the circles with the same colors as shown in Fig. 5 except the green circle, which appears at very large negative \(\lambda \) values. When the value of \(\lambda \) is changed from negative to positive, the response successively exhibits double hardening, single hardening, single softening, double softening and single softening for \(L=50\) H. Three lines of \(\omega _b^o=\Omega _\mathrm{s}\) are shown in cerulean and purple. The purple line separates the two typical nonlinear hardening regions with a cerulean line. The rest cerulean line separates the typical nonlinear hardening and softening regions.

When L is increased to 100 H, there are six solutions of \(\omega _b^o\) at \({\Delta _\beta } = 0\) shown as the circles in Figs. 5 and 6d. The three circles on \(L_{{{\hat{s}}}2}\) indicate double hardening and the other three circles on \(L_{ s1}\) imply double softening. As L is increased to 200 H, the single hardening (one circle on \(L_{s2}\)) appears with the double softening (three circles on \(L_{ s1}\)) in Fig. 6e. The cerulean circles that appear at relatively large \(\lambda \) are not shown in Fig. 6d, e. When \(\lambda \) is changed from negative to positive, the response successively exhibits single hardening, double hardening, single hardening, single softening, double softening, single softening, double softening and single softening for \(L=100\,\hbox {H}\). At \(L=200\,\hbox {H}\), the response successively exhibits single hardening, single softening, double softening, triple softening, double softening and single softening. The purple line separates the two typical nonlinear hardening regions and two typical nonlinear softening regions in Fig. 6d, while it only separates the two typical nonlinear softening regions in Fig. 6e.

Fig. 6
figure 6

Regions of hardening and softening responses as a function of the nonlinear magnetic coefficients \(\lambda \) for a–e different values of the inductances L at \(a_b=1g\), \(R=10^3\) ohm and \(\mu =0.2\) N/mm

Full size image
Fig. 7
figure 7

Variations of the amplitudes of a the tip displacement and b harvested power with the excitation frequency at \(a_b=1g\), \(R=1000\,\hbox {ohm}\) and \(\mu =0.2\,\hbox {N/mm}\). In the legend, ‘AM’ and ‘NM’ indicate the analytical and numerical approaches, respectively

Full size image
Fig. 8
figure 8

The phase space determined from the modulation equation (41) for different external excitation frequencies: a\(\frac{{{\omega _b}}}{{2\pi }}=49\,\hbox {Hz}\), b\(\frac{{{\omega _b}}}{{2\pi }}=55\,\hbox {Hz}\) and c\(\frac{{{\omega _b}}}{{2\pi }}=78\,\hbox {Hz}\) when \(a_b=1g\), \(R=1000\,\hbox {ohm}\), \(\mu =0.2\,\hbox {N/mm}\), \(L=50\,\hbox {H}\) and \(\lambda =-2.5\,\hbox {N/mm}^3\)

Full size image

5.3 Bistable analysis

Two approaches are taken to determine the responses of the energy harvesting system. In the first approach, we solve Eqs. (18) and (19) simultaneously using the Runge–Kutta method, which is referred to the numerical approach. In the second approach, we solve the modal coordinate \(q_0\) from Eq. (24) and obtain the responses with their relations expressed by Eq. (23), which is called as the analytical approach. The variations of the tip displacement and harvested power with the excitation frequency using both approaches are presented in Fig. 7 for the double hardening case. The frequency band over which energy is harvested is observed to be significantly extended by the multiple nonlinear behavior. The excitation frequencies obtained from \(\Delta _{cubic}=0\) (Eq. 26), \(\omega _b^o\), and represented by the red and blue vertical lines in Fig. 7. The red lines denote the intersection of the unstable solution and the stable solution corresponding to a large initial condition, while the blue line stands for the intersection of the unstable solution and the stable solution corresponding to the small initial condition. Between the blue (lower bound) and red (higher bound) vertical lines, multiple solutions of the responses exist. Since bistable solutions are obtained, we use the pink diamonds to represent numerical solutions obtained with the large initial conditions and the green circles to denote solutions obtained using the small initial conditions. Overlaid with the symbols, the solid lines are stable analytical solutions determined by the stability analysis in Sect. 3.3. The dash lines between the stable solutions are determined as the unstable solutions. Inspecting Fig. 7, the numerical solutions confirm the analytical stable solutions. As discussed in Sect. 2, the frequency \(\Omega \) of the equivalent mechanical system (Eq. 20) varies with the external frequency \(\omega _b\) when the inductance is introduced in the electrical circuit. As such, \(L=50\) H leads to the double hardening phenomenon in the current case.

To characterize the bistable–monostable–bistable dynamic change through increasing the excitation frequency, the phase space as obtained from the modulation equation (41) for three representative external excitation frequencies is presented in Fig. 8. The slope field of \(\psi \) and \(q_0\) is plotted with gray dashed lines. The blue trajectories and arrows present how the responses with different initial conditions move toward the steady-state solutions as time increases. When the external excitation frequency is set as \(\frac{{{\omega _b}}}{{2\pi }}\)=49 Hz, there exist three steady-state solutions as shown in Fig. 8a. Two sinks and a saddle are observed corresponding to the bistable solutions and one unstable solution in Fig. 7, respectively. Except two special red trajectories that approach the saddle point, all other manifold move to one of the two sinks. These two special red trajectories form a separatrix (basin boundary), which separates two domains of attraction for the two sinks. The basin boundary passes the saddle point. Besides, the slope fields change their directions to different sink points near the basin boundary. For the yellow domain of the large \(q_0\), the initial condition is usually large and thus only large initial conditions can excite it as shown in Fig. 7. To better present the difference of different initial conditions, the time history, phase portrait and power spectra of reduced governing equations (18) and (19) are plotted in Fig. 9. The larger initial condition leads to a larger stable amplitude of the cantilever beam than the smaller one. However, the same frequency is observed for both large and small initial conditions. As shown in the range of BC or FD in Fig. 3, there are two stable solutions: the sink corresponding to the smaller amplitude on curve FD and the sink of the larger amplitude on segment BC. For the case of upward sweep, the initial condition will be near the sink of the larger amplitude, and thus, it moves along the curve BC. Similarly, the initial condition is closer to the sink of the smaller amplitude and responses will remain on the segment DF for the case of downward sweep. This can be explained for the interval between BC and FD through upward and downward sweep experimental results. At the excitation frequency \(\frac{{{\omega _b}}}{{2\pi }}\)=55 Hz, only one sink is observed as shown in Fig. 8b. This sink corresponds to the monostable solution in Fig. 7. As expected, one stable dynamic motion with different initial conditions is obtained from the numerical method as shown in Fig. 9. As the excitation frequency \(\frac{{{\omega _b}}}{{2\pi }}\) is increased to 78 Hz (Fig. 8c), two sinks and a saddle are observed corresponding to the bistable solutions and one unstable solution as observed in Fig. 7. There exist two different types of stable motions with different initial conditions using the numerical method in figure  9. The smaller domain of attraction for the sink corresponding to the large amplitude is noted in Fig. 8c than that in Fig. 8a, suggesting more difficulty to excite the large stable response.

As the magnetic cubic coefficient \(\lambda \) becomes positive, the impact of the double softening phenomenon on the variations in the tip displacement and harvested power with the external excitation frequency can be deduced from plots presented in Fig. 10. Specifically, the frequency bandwidth over which energy can be harvested is greatly enhanced. In contrast with the response observed in the double hardening phenomenon, the double softening starts from the zero excitation frequency which is very beneficial for energy harvesting from low-frequency excitations, which are abundant in industrial and natural environment. The numerical results with large and small initial conditions agree well with the analytical solutions. The phase space calculated from the modulation equation (41) for the different excitation frequencies of \(\frac{{{\omega _b}}}{{2\pi }}=10\,\hbox {Hz}\), \(\frac{{{\omega _b}}}{{2\pi }}=28\,\hbox {Hz}\) and \(\frac{{{\omega _b}}}{{2\pi }}=32\,\hbox {Hz}\) are plotted in Fig. 11. Compared with the double hardening cases in Fig. 8, the manifolds of the double softening spiral more circles until they reach the sinks. The time history, phase portrait and power spectra of the numerical simulations prove that different initial conditions lead to the different stable dynamic motions as shown in Fig. 12. As in the case of double hardening, the frequency of the motion for double softening is the same for both sinks.

Fig. 9
figure 9

The a, d, g time history, b, e, h phase portrait and c, f, i power spectra of reduced governing equations (18) and (19) with different external excitation frequencies: a, b, c\(\frac{{{\omega _b}}}{{2\pi }}=49\,\hbox {Hz}\), d, e, f\(\frac{{{\omega _b}}}{{2\pi }}=55\,\hbox {Hz}\) and g, h, i\(\frac{{{\omega _b}}}{{2\pi }}=78\,\hbox {Hz}\) when \(a_b=1g\), \(R=1000\,\hbox {ohm}\), \(\mu =0.2\,\hbox {N/mm}\), \(L=50\,\hbox {H}\) and \(\lambda =-2.5\,\hbox {N/mm}^3\)

Full size image
Fig. 10
figure 10

Variations of the amplitudes of a the tip displacement and b harvested power with the excitation frequency at \(a_b=1g\), \(R=1000\,\hbox {ohm}\) and \(\mu =0.2\,\hbox {N/mm}\). In the legend, ‘AM’ and ‘NM’ indicate the analytical and numerical approaches, respectively

Full size image
Fig. 11
figure 11

The phase space determined from the modulation equation (41) for different external excitation frequencies: a\(\frac{{{\omega _b}}}{{2\pi }}=10\,\hbox {Hz}\), b\(\frac{{{\omega _b}}}{{2\pi }}=28\,\hbox {Hz}\) and c\(\frac{{{\omega _b}}}{{2\pi }}=32\,\hbox {Hz}\) when \(a_b=1g\), \(R=1000\,\hbox {ohm}\), \(\mu =0.2\,\hbox {N/mm}\), \(L=200\,\hbox {H}\) and \(\lambda =1\,\hbox {N/mm}^3\)

Full size image
Fig. 12
figure 12

The a, d, g time history, b, e, h phase portrait and c, f, i power spectra of reduced governing equations (18) and (19) with different external excitation frequencies: a, b, c\(\frac{{{\omega _b}}}{{2\pi }}=10\,\hbox {Hz}\), d, e, f\(\frac{{{\omega _b}}}{{2\pi }}=28\,\hbox {Hz}\) and g, h, i\(\frac{{{\omega _b}}}{{2\pi }}=32\,\hbox {Hz}\) when \(a_b=1g\), \(R=1000\) ohm, \(\mu =0.2\,\hbox {N/mm}\), \(L=200\,\hbox {H}\) and \(\lambda =1\,\hbox {N/mm}^3\)

Full size image
Fig. 13
figure 13

Variations of the a tip displacement and b harvested power with the excitation frequency for double hardening cases at \(a_b=1g\), \(R=1000\) ohm and \(\mu =0.2\,\hbox {N/mm}\)

Full size image
Fig. 14
figure 14

Variations of the a tip displacement and b harvested power with the excitation frequency for double softening cases at \(a_b=1g\), \(R=1000\,\hbox {ohm}\) and \(\mu =0.2\,\hbox {N/mm}\)

Full size image

5.4 Ultra-broadband by multi-hardening and multi-softening

The effects of the inductance and cubic magnetic coefficients on broadband performance via the multi-hardening and multi-softening are, respectively, presented in Figs. 13 and 14. At \(L=10\,\hbox {H}\) and \(\lambda =-2\,\hbox {N/mm}^3\), a single hardening behavior is noted in Fig. 13. The nonlinear range for energy harvesting extends from 52.61 to 73.95 Hz with harvested power levels between 1.852 and 15.88 mW. At \(L=21.48\,\hbox {H}\) and \(\lambda =-15\,\hbox {N/mm}^3\), double nonlinear hardening is realized. The nonlinear range extends from 60.25 to 75.24 Hz with harvested power levels between 1.758 and 22.70 mW and from 96.48 to 125.5 Hz with harvested power levels between 25.63 and 6.196 mW. Under linear resonance, the peak harvested power is 1.906 mW at 85.95 Hz. For \(L=50\,\hbox {H}\) and \(\lambda =-2.5\,\hbox {N/mm}3\), the double-hardening phenomenon is observed. The nonlinear range in the lower frequency is from 47.39 to 49.45 Hz with harvested power levels between 11.02 and 21.49 mW. The higher frequency is between 62.41 and 84.80 Hz with harvested power levels between 17.24 and 5.067 mW. The decrease in the harvested power with the excitation frequency in the nonlinear region with the higher frequency is caused mainly by the precipitous decline of the electric damping with the excitation frequency. At \(L=100\,\hbox {H}\) and \(\lambda =-4\,\hbox {N/mm}^3\), two nonlinear hardening regions are found in addition to the linear resonance. The linear resonance results in a power peak of 13.17 mW at 36.55 Hz, which is near the frequency of the displacement peak (purple line). The nonlinear region in the low frequency is close to the linear resonance and very narrow. The nonlinear range in the higher frequency is between 59.42 and 95.3 Hz with harvested power levels between 0.6004 and 0.4188 mW.

At \(L=10\) H and \(\lambda =2\,\hbox {N/mm}^3\), a single softening phenomenon is observed between zero and \(\frac{\omega _b^o}{2\pi }=24.94\,\hbox {Hz}\) with harvested power levels between 0 and 0.311 mW as shown in Fig. 14. The two power peaks of 0.427 mW and 0.315 mW are not in the nonlinear response region and take place at the excitation frequencies of 36.1 Hz and 123.8 Hz. At \(L=21.48\,\hbox {H}\) and \(\lambda =0.01\,\hbox {N/mm}^3\), a different type of softening between 0 Hz and \(\frac{\omega _b^o}{2\pi }=9.018\,\hbox {Hz}\) with harvested power levels between 0 and 8.646 mW is noted. Outside the nonlinear region, there are two peaks with values of 12.42 mW and 1.87 mW at 39.85 Hz and 85.95 Hz, respectively. At \(L=50\) H and \(\lambda =0.0584\,\hbox {N/mm}^3\), a double-softening phenomenon and a linear resonance are noted. The nonlinear energy harvesting over the low-frequency band is extended further to values between 0 Hz and \(\frac{\omega _b^o}{2\pi }=28.58\) Hz as denoted by the left red line with the harvested power of \(0-13.45\,\hbox {mW}\). The second nonlinear range is \(29.69-35.46\,\hbox {Hz}\) with harvested power levels between 14.01 and 14.16 mW. At the relatively high frequency of 59.3 Hz, the linear resonance occurs yielding a harvested power level of 15.51 mW. Except for a small region, all of the low frequency band between 10 and 62 Hz can almost be exploited for energy harvesting. At \(L=100\,\hbox {H}\) and \(\lambda =1.25\,\hbox {N/mm}^3\), a different double-softening phenomenon is noted. The first nonlinear range is between 0 and 25.09 Hz with harvested power levels between 0 and 1.131 mW. The second nonlinear range between 43.16 and 44.09 Hz yield harvested power levels between 22.43 and 14.76 mW. The power peak between the two nonlinear regions occurs at 34.55 Hz with a harvested power level of 3.69 mW. In comparison with the previous case, only the medium frequency region between 25 and 50 Hz can be exploited for energy harvesting.

6 Conclusion

Nonlinear magnetic interaction and inductive–resistive interface circuit are exploited and integrated for the purpose of expanding the range of broadband piezoelectric energy harvesting. Toward that objective, we presented an electromechanical coupled distributed parameter model for the broadband energy harvester. The implicit analytical solution of the responses for such a system was determined based on the equivalent mechanical representation and the method of harmonic balance. The analytical expression of the modified natural frequency indicates that multiple resonances caused by the inductance may occur. The cubic-function discriminant of the implicit analytical expression was introduced to determine the nonlinear boundaries for multiple solutions. These nonlinear boundaries determine the bandwidth of the energy harvester for effective energy harvesting. The Jacobi matrix of the modulation equation was derived to determine the stability of the multiple solutions. Upward and downward sweep experiments were performed to validate the jump phenomenon due to the effect of the inductance and magnetic force. The analytical solutions were found to be in agreement with the experimental results. To better analyze the bistable phenomenon, plots of the phase space as determined from the modulation equation were employed to determine the basin boundary of the stable solutions (sinks). Over the nonlinear region, the initial condition showed a great impact on the dynamic motion of the system and lead to the jump phenomenon for both upward and downward sweep experiments. The impacts of the cubic magnetic coefficient and electric inductance were then analytically analyzed over the range of the broadband energy harvesting. Plots for the analytical expression of \({\Delta _\beta } = 0\) varied by the electric inductance are very effective to determine the types of the nonlinear phenomena. Based on this expression, single, double and triple nonlinear hardening and softening phenomena were observed. Different nonlinear types were found, including typical nonlinear hardening and softening with two stable and one unstable solutions, special nonlinear hardening and softening with one stable and one unstable solutions. Overall, the results show that the cubic magnetic coefficient and inductance are crucial parameters to design effective energy harvester with a great potential to cover up to 40 Hz in the low-frequency range when using the right parameters.